Optimal selection of number and location of rain gauge stations for areal estimation of annual rainfall using a procedure based on inverse distance weighting estimator

Abstract

One basic demand toward advancement of economic growth is the need for reliable data on quantity and quality of water. Optimum design of rain gauge network in space leads to reliable data on water input. A conventional paradigm in rain gauge network design is to cast the optimization problem in a stochastic framework using geostatistical tools, which calls for an extensive matrix inversion to compute measure of accuracy. Deterministic schemes rely solely on network topology for interpolation and do not require matrix inversion and they are quite easy to use and understand. This feature might be a good reason to invest on network design based on deterministic methods. Changing the support size and assigning a measure of accuracy to the block-wise estimate are two basic challenges associated with working on a deterministic scheme. A new areal variance-based estimator using stochastic inverse distance weighting (Stc-IDW) is developed to design a rain gauge network. A new criterion is defined to move from point to block and cast the measure of accuracy for the entire study area. To evaluate the effectiveness of the proposed methodology, the coupled algorithm is applied to a case study with 25,000 km² and 34 rain gauge stations in Iran. Development of measure of accuracy versus number of stations is achieved via both Stc-IDW and block kriging estimators, and the results are compared and contrasted to one another. Surprisingly, the optimum network configuration for various combinations of rain gauges shares almost identical goodness of fit criteria. Based on the results, the minimum of eleven stations are found to reach the maximum accuracy for both methods.

Introduction

In many hydrological analysis and watershed management problems such as water budget studies, flood frequency analysis and sewer drainage design, availability of accurate rainfall data with an appropriate coverage in both time and space is considered a classic issue in surface water hydrology. Rainfall data can be obtained from both ground-based (rain gauge stations) and air-based (radar or satellite) instruments. Even if one uses an air-based measurement, discrete ground-based data are still required for validation and calibration purposes.

For the last one hundred years or so, optimum delineation of rain gauges in both time and space was considered as a classic problem in operational hydrology. Network density will affect the accuracy of long-term average rainfall value over the study area. While the flat region of central part of Iran calls for low network density due to less variability in rainfall, the mountainous region of west calls for denser network due to high variability of rainfall in those regions. As a result, intelligent delineation of rain gauge network in various parts of the country is considered necessary.

Numerous factors affect a representative rain gauge network design. These factors include but not limited to overall objective of designing a network (e.g., water balance studies, reservoir operation, flood forecasting), the process considered (e.g., evaporation, rainfall), the attribute of the process under consideration (e.g., rainfall depth, rainfall duration), the temporal scale (e.g., hourly, daily, monthly, annual rainfall data), the spatial scale (e.g., catchment, regional, countrywide), the topographic setting (flat, rolling, mountainous, etc.), the types of precipitation (e.g., orographic, convective, cyclonic) and the type of objective functions (e.g., variance-based, entropy-based, fractal-based and distance-based techniques). Some factors are selected based on the characteristics of the study area (i.e., spatial scale, topographic setting and the types of precipitation), while the objective behind the operation of rain gauge network might dictate the time scale required. It should be noted that there is a close interaction between the process time scale and the type of objective function used. In particular, entropy-based approaches are more customized to short time scale suitable for flood forecasting, while long time scale is more suitable for refining component of water budget studies very consistent with variance-based approaches. In our case, as we specified the study area (i.e., southwest of Iran) and the objective of the whole network design (i.e., long-term water balance studies), a few factors including, process (i.e., precipitation), attribute (i.e., rainfall depth), time scale (i.e., annual), the extend of the study area are fixed, and we have to specify the objective function consistent with the overall aim behind network design. In this study, a deterministic interpolant so-called IDW scheme is defined in a stochastic framework (i.e., Stc-IDW) and coupled with variance-based method to delineate the optimum number and spatial location of rain gauges over the study area. It is expected that selection of such a deterministic-based estimator might make the whole process more efficient and robust as it does not require any matrix inversion.

Objective functions typically used for network design problems based on ground-based point measurement, include methods such as variance-based techniques (Rodriguez-Iturbe and Mejia 1974; Bras and Rodriguez-Iturbe 1976; Bastin et al. 1984; Bogardi and Bardossy 1985; Rouhani 1985; Kassim and Kottegoda 1991; Cheng et al. 2008; Shafiei et al. 2014; Adhikary et al. 2015), distance-based methods (Van Groenigen et al. 2000; Barca et al. 2008), entropy-based techniques (Krstanovic and Singh 1992; Al-Zahrani and Husain 1998; Yoo et al. 2008; Chen et al. 2008), fractal-based approaches (Korvin et al. 1990; Mazzarella and Tranfaglia 2000) and also some multi-objective models (Werstuck and Coulibaly 2016). Depending on the nature of the network under consideration (e.g., data gathering vs. service network), one will decide on the objective function to be used. Distance-based objective function is more often used in service network. One of the most frequently used techniques considered for rain gauge network design is variance-based method, which will be used in this study.

In variance-based methods, the goodness of fit criterion for network evaluation is some measure of accuracy such as variance of residuals. The objective (measure of accuracy) in such methods is to minimize point and/or areal variance of residuals. In rain gauge network design, minimization of variance of residuals corresponds to maximization of network information content. In turn, enhancement of information content could be interpreted as collection of data with higher accuracy and precision. It is hoped that this higher accuracy would eventually lead to lower construction cost with more useful information. Among a variety of variance-based techniques, geostatistical interpolation methods such as various flavors of kriging have often been extensively implemented to design a representative rain gauge network. Due to numerous back and forth interaction between the optimizer and the objective function, one basic shortcoming of kriging for rain gauge network design is that it takes a considerable time to find the numerical value of the objective function due to numerous matrix inversions during the design process. Such inappropriate feature of kriging gives rise to numerous simplifications in rain gauge network design (Bastin et al. 1984; Kassim and Kottegoda 1991; Nour et al. 2006). Could it be possible to delineate an estimator, which does not require matrix inversion? In this paper, a deterministic-based method so-called inverse distance weighting (IDW) approach is proposed to go for rain gauge network design.

To the best of authors’ knowledge, this is the first time that a process based on IDW is used for rain gauge network design. At this stage, it might help to justify its lack of usage in network design and try to address and resolve the issues involved. Due to its very deterministic nature, estimation at an un-sampled point is not equipped with measure of accuracy. As a result, the very first task is to cast a stochastic framework for IDW (i.e., Stc-IDW). In addition, as the results have to be compared with a conventional paradigm in network design (e.g., BK) for independent verification, one has to propose a mechanism to convert point estimation of IDW-based procedure to block-wise estimation, to make the objective function unique and comparable to block kriging (BK). Cheng et al. (2008) considered point ordinary kriging to design a rain gauge network in northern Taiwan. As their goodness of fit criterion was not unique and would change from one point to another, they developed the concept of “area with acceptable accuracy” to move from point-wise to block-wise goodness of fit. Shafiei et al. (2014) extended a methodology to evaluate and augment the rain gauge network using the same concept as Cheng et al. (2008), based on a tool in ArcGIS software applied to the network in Northern Iran. However, their proposal lacks independent verification, which is required due to numerous ad hoc assumptions considered in Cheng et al. (2008). These challenges along with independent verification of Cheng et al. (2008) study are to be addressed in some detail in subsequent paragraphs and sections.

This paper is organized as follows; the next section is devoted to an in-depth theoretical background on concepts used in this study touching on geostatistical framework (especially BK) and IDW estimator (especially Stc-IDW and the proposed methodology). Then, the following section describes materials and methods summarizing the description of the study area, materials and step-by-step procedure of variance-based estimation accuracy using BK and Stc-IDW estimators. In “Results and discussion” section, the results of conventional variance-based criterion in the network design are compared and contrasted to the proposed scheme. The last section includes the conclusions, which can be drawn from this study.

Theoretical background

To design a rain gauge network, it is assumed that annual rainfall depth P(s_i) observed at rain gauges in spatial locations s_i, i = 1, …, N are regionalized variables and can be considered as a single partial realization of a random function:

$$P = \left[ {P\left( {\varvec{s}_{1} } \right),P\left( {\varvec{s}_{2} } \right), \ldots ,P\left( {\varvec{s}_{N} } \right)} \right]^{\text{T}} .$$

(1)

It should be noted that P at every spatial location consists of large-scale variation invariably called mean function or the trend function, m(s), and a small-scale variation, W(s). The mean function is modeled deterministically, while W(s) is modeled stochastically with zero expectation. The associated parent random function is given by:

$$P\left( \varvec{s} \right) = m\left( \varvec{s} \right) + W\left( \varvec{s} \right).$$

(2)

At every point in space, one has to differentiate between three types of random variables. These three types of random variables can be stated as:

• P_o(s₀): The observed value of P at spatial location s₀,

• P(s₀): The true value of P at spatial location s₀ which is not accessible,

• $\hat{P}\left( {\varvec{s}_{0} } \right)$: The estimated value of P at spatial location s₀.

All interpolation methods (either deterministic or stochastic) share the following equation in estimating the attribute under consideration at a point which is not sampled. The difference among methods (e.g., IDW and BK estimators) is somehow related to computation of weighting coefficients.

$$\hat{P}\left( {\varvec{s}_{0} } \right) = \mathop \sum \limits_{i = 1}^{N} \lambda_{i} \left( {\varvec{s}_{0} } \right)P_{\text{o}} \left( {\varvec{s}_{i} } \right),$$

(3)

where N is the total number of rain gauge stations, s₀ is the estimation location and s_i is the sample location. $\hat{P}\left( {\varvec{s}_{0} } \right)$ is the estimated precipitation at location s₀, and λ_i(s₀) is the weighting coefficient associated with the observed rainfall depth at s_i, i.e., P_o(s_i). For the sake of paper integrity and completeness, a brief overview on two interpolation methods, BK and IDW, will be provided in subsequent subsections.

An overview on block ordinary kriging

Keeping in mind $P = \left[ {P\left( {\varvec{s}_{1} } \right), P\left( {\varvec{s}_{2} } \right), \ldots ,P\left( {\varvec{s}_{N} } \right)} \right]^{\text{T}}$ as a realization of a random function, the mean areal precipitation over block V centered at s₀, i.e., $\hat{P}_{\text{V}}^{\text{BK}} \left( {\varvec{s}_{0} } \right)$ can be obtained through the following relationship:

$$\hat{P}_{\text{V}}^{\text{BK}} \left( {\varvec{s}_{0} } \right) = \mathop \sum \limits_{i = 1}^{N} \lambda_{i}^{\text{BK}} \left( {\varvec{s}_{0} } \right)P_{\text{o}} \left( {\varvec{s}_{i} } \right),$$

(4)

$\lambda_{i}^{\text{BK}}$’s are weighting coefficients associated with observed precipitation data.

Computation of weighting coefficients requires imposing further assumptions on the parent random function. One such limitation concerns with stationarity of the parent RF. According to the theory of regionalized variable, a random function is said to be first-order stationary if the covariance function is a function of separation vector throughout the entire domain and the variance at any location is independent of spatial location (Deutsch 2002). Therefore, it can be written as:

$$\begin{aligned} & E\left[ {P\left( {\varvec{s}_{i} } \right)} \right] = m, \\ & {\text{COV}}\left[ {P\left( {\varvec{s}_{i} } \right),P\left( {\varvec{s}_{j} } \right)} \right] = C\left( {\varvec{s}_{i} - \varvec{s}_{j} } \right) = C\left( \varvec{h} \right). \\ \end{aligned}$$

(5)

Two conditions have to be imposed on residuals [$R_{\text{V}} \left( {\varvec{s}_{0} } \right) = \hat{P}_{\text{V}} \left( {\varvec{s}_{0} } \right) - P_{\text{V}} \left( {\varvec{s}_{0} } \right)$] to cast the kriging system either in terms of covariance or variogram functions. After imposing the minimum variance of residuals condition and implementing the unbiasedness condition, one can cast the BK system as:

$$\begin{aligned} & \mathop \sum \limits_{j = 1}^{N} \lambda_{j}^{\text{BK}} \left( {\varvec{s}_{0} } \right)\gamma \left( {\varvec{s}_{i} ,\varvec{s}_{j} } \right) - \mu \left( {\varvec{s}_{0} } \right) \\ & \quad = \frac{1}{M}\mathop \sum \limits_{k = 1}^{M} \gamma \left( {\varvec{s}_{i} ,\varvec{s}_{k}^{'} } \right),\quad \forall i = 1,2, \ldots ,N \\ & \mathop \sum \limits_{i = 1}^{N} \lambda^{\text{BK}}_{i} \left( {s_{0} } \right) = 1, \\ \end{aligned}$$

(6)

where “′” referred to the discretized points inside a typical block. M is the number of grid points inside a discretized block, µ is the Lagrange multiplier and $\left( {\varvec{s}_{i} ,\varvec{s}_{k}^{'} } \right)$ are spatial location corresponding to observed point i and mesh grid point k (k = 1, …, M), respectively. By substituting $\lambda_{i}^{\text{BK}} \left( {\varvec{s}_{0} } \right)$ calculated from Eq. (6) into Eq. (4), mean areal precipitation can be calculated. Subsequently, the variance of residuals over block V centered at s₀ as a measure of accuracy is given by:

$$\begin{aligned} {\text{VAR}}\left[ {R_{\text{V}}^{\text{BK}} \left( {\varvec{s}_{0} } \right)} \right] & = - \mu \left( {\varvec{s}_{0} } \right) + \frac{1}{M}\mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{k = 1}^{M} \lambda^{\text{BK}}_{i} \left( {\varvec{s}_{0} } \right)\gamma \left( {\varvec{s}_{i} ,\varvec{s}_{k}^{'} } \right) \\ & \quad - \frac{1}{{M^{2} }}\mathop \sum \limits_{k = 1}^{M} \mathop \sum \limits_{j = 1}^{M} \gamma \left( {\varvec{s}_{j}^{'} ,\varvec{s}_{k}^{'} } \right) \\ & = \sigma_{{R_{\text{V}} }}^{{2{\text{BK}}}} \left( {\varvec{s}_{0} } \right), \\ \end{aligned}$$

(7)

where $R_{\text{V}}^{\text{BK}} \left( {\varvec{s}_{0} } \right)$ is the residual over block V. As one can get from Eq. (7), block variance of the residuals [i.e., $\sigma_{{R_{\text{V}} }}^{{2{\text{BK}}}} \left( {\varvec{s}_{0} } \right)$] depends only on the number and spatial location of rain gauge stations in place.

An overview on inverse distance weighting interpolation (IDW)

Keeping in mind $P = \left[ {P\left( {\varvec{s}_{1} } \right), P\left( {\varvec{s}_{2} } \right), \ldots ,P\left( {\varvec{s}_{N} } \right)} \right]^{\text{T}}$ as a realization of a random function, estimation of mean areal precipitation using IDW interpolation method is:

$$\hat{P}^{\text{IDW}} \left( {\varvec{s}_{0} } \right) = \mathop \sum \limits_{i = 1}^{N} \lambda_{i}^{\text{IDW}} \left( {\varvec{s}_{0} } \right)P_{\text{o}} \left( {\varvec{s}_{i} } \right),$$

(8)

where $\hat{P}^{\text{IDW}} \left( {\varvec{s}_{0} } \right)$ is the estimated value of precipitation at spatial location s₀ and $\lambda_{i}^{\text{IDW}}$ is the weighting coefficient associated with sample point s_i. The weights are determined via:

$$\begin{aligned} & \lambda_{i}^{\text{IDW}} \left( {\varvec{s}_{0} } \right) = \frac{{\left( {\frac{1}{{d^{\beta } \left( {\varvec{s}_{i} ,\varvec{s}_{0} } \right)}}} \right)}}{{\mathop \sum \nolimits_{i = 1}^{N} \left( {\frac{1}{{d^{\beta } \left( {\varvec{s}_{i} ,\varvec{s}_{0} } \right)}}} \right)}}\quad {\text{and}} \\ & \mathop \sum \limits_{i = 1}^{N} \lambda_{i}^{\text{IDW}} \left( {\varvec{s}_{0} } \right) = 1 ,\quad i = 1, \ldots ,N, \\ \end{aligned}$$

(9)

where d(s_i, s₀) is the Euclidian distance between estimation location s₀ and sample point s_i, β is the distance decay parameter (i.e., power) which controls the degree of smoothness of the approximation function $\hat{P}^{\text{IDW}} \left( {\varvec{s}_{0} } \right)$. The approximation function would be sharp in the case of $0 \le \beta \le 1$, and it will be smooth in the case of $\beta \ge 1$. It is common to choose β = 2, but any other value for power can be chosen. As power decreases to zero, IDW collapses to arithmetic mean method, and as the power increases to infinity, the interpolated value gives a unit weight to the most nearest station and zero to others, invariably called Thiessen polygons method. After discretizing the study area into a mesh and finding the amount of precipitation at every grid point inside the region, areal estimation of precipitation can be found as:

$$\begin{aligned} \hat{P}_{\text{V}}^{\text{IDW}} \left( {{\mathbf{s}}_{0} } \right) & = \frac{1}{M}\mathop \sum \limits_{j = 1}^{M} \hat{P}^{\text{IDW}} \left( {{\mathbf{s}}_{j} } \right) \\ & = \frac{1}{M}\mathop \sum \limits_{j = 1}^{M} \mathop \sum \limits_{i = 1}^{N} \lambda_{i}^{\text{IDW}} \left( {{\mathbf{s}}_{j} } \right)P_{\text{o}} \left( {{\mathbf{s}}_{i} } \right), \\ \end{aligned}$$

(10)

where $\hat{P}_{\text{V}}^{\text{IDW}} \left( {{\mathbf{s}}_{0} } \right)$ is the areal estimation of precipitation over block V centered at a generic point s₀ inside the block as large as the study area. To find a measure of accuracy for the rain gauge network using IDW estimator, either a measure of similarity or variability should be assigned to the parent random function. Babak and Deutsch (2009) used such measures to select optimal support domain size (i.e., number of neighbor stations) and power in IDW estimator. Their approach was based on the assumption of stationarity and the known variogram model of the parent random function. To reach our goal, the stochastic framework for IDW scheme is used in this study which we named “Stc-IDW.”

Development of stochastic framework for IDW scheme (Stc-IDW)

As mentioned earlier, one has to assign a measure of goodness to the block-wise average using IDW approach. In this section, a stochastic framework is developed to define such measure, named Stc-IDW. This stochastic framework could help to design a typical rain gauge network effectively utilizing the lack of need for matrix inversion in IDW scheme. Such need for development of a stochastic framework would arise as we have only access to a single partial realization of the random function. In light of this, one has to impose stationarity on data to be able to assign a measure of goodness to each estimated value. Fortunately, IDW scheme is equipped with such interesting features whereby those characteristics can help to honor stationary in IDW. As an example, the sum of weighting coefficients in IDW is one. This feature can easily help to show that the expected values of both the sampled as well as the un-sampled points are independent of spatial location (Babak and Deutsch 2009). Furthermore, in reference to stationary assumption, the variance of the estimated value can be represented by covariance to be a function of at most separation vector. This variance can be used to compute variance of residuals at all un-sampled points using Stc-IDW as follows:

$$\begin{aligned} {\text{VAR}}\left[ {R\left( {\varvec{s}_{0} } \right)} \right] & = {\text{VAR}}\left[ {\hat{P}\left( {\varvec{s}_{0} } \right) - P\left( {\varvec{s}_{0} } \right)} \right] \\ & = \sigma^{2} - 2\mathop \sum \limits_{i = 1}^{N} \lambda_{i}^{\text{IDW}} \left( {\varvec{s}_{0} } \right){\text{COV}}\left( {\varvec{s}_{i} ,\varvec{s}_{0} } \right) \\ & \quad + \mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{j = 1}^{N} \lambda_{i}^{\text{IDW}} (\varvec{s}_{0} )\lambda_{j}^{\text{IDW}} \left( {\varvec{s}_{0} } \right){\text{COV}}\left( {\varvec{s}_{i} ,\varvec{s}_{j} } \right), \\ \end{aligned}$$

(11)

where σ² is the global variance. At this stage, the variance of residuals is expressed in terms of covariance function. As variogram function is more conventional in stochastic framework, one can also represent the variance of residuals in terms of variogram function [${\text{COV}}\left( {\mathbf{h}} \right) = \sigma^{2} - \gamma \left( \varvec{h} \right)$]. The resulting equation in terms of variogram function can be written as follows:

$$\begin{aligned} {\text{VAR}}\left[ {R\left( {\varvec{s}_{0} } \right)} \right] & = 2\mathop \sum \limits_{i = 1}^{N} \lambda_{i}^{\text{IDW}} \left( {\varvec{s}_{0} } \right)\gamma \left( {\varvec{s}_{i} ,\varvec{s}_{0} } \right) \\ & \quad - \mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{j = 1}^{N} \lambda_{i}^{\text{IDW}} \left( {\varvec{s}_{0} } \right)\lambda_{j}^{\text{IDW}} \left( {\varvec{s}_{0} } \right)\gamma \left( {\varvec{s}_{i} ,\varvec{s}_{j} } \right) \\ & = \sigma_{R}^{{2{\text{IDW}}}} \left( {\varvec{s}_{0} } \right), \\ \end{aligned}$$

(12)

where $\sigma_{R}^{{2{\text{IDW}}}} \left( {\varvec{s}_{0} } \right)$ is the point-wise variance of residuals at an un-sampled point s₀ inside the region. $\lambda_{i}^{\text{IDW}} \left( {\varvec{s}_{0} } \right)$ is the weighing coefficient of Stc-IDW estimator at sampled point s_i. It should be noted that the support size for variance of residuals is still of point-wise and we have to devise a procedure to convert it to block as large as the study area. This block-wise measure will be addressed below.

Proposed methodology using Stc-IDW approach

As mentioned before, in deterministic-based estimation (i.e., IDW), the support size for estimation is the same as the support size for observation. This characteristic still remains for Stc-IDW. In such an approach, one cannot easily move from point-wise to block-wise, making the subsequent objective function unique. In light of this, one should devise an innovative approach to move from point-wise to block-wise estimation and subsequent goodness of fitness criterion. This is the subject which had not been addressed in previous studies. To achieve this goal, the definition of acceptable accuracy in the study area should be represented. Cheng et al. (2008) applied this procedure using “ordinary kriging” for rain gauge network evaluation and augmentation based on the percentage of the total area with acceptable accuracy. Acceptable accuracy method is presented in the following subsection. In the current study, Stc-IDW is used in place of point ordinary kriging for point estimation, and the cited measure is used to move from point to block to design the rain gauge network.

Mathematical description of the acceptable accuracy

Estimation of precipitation at an un-gauged point s₀, $[\hat{P}(\varvec{s}_{0} )]$ can be calculated using annual rainfall measurements P(s_i) using IDW interpolation method [i.e., Eq. (8)]. On the other hand, estimation is considered to be acceptable, only if it falls within a given range of the true value:

$$\left| {R\left( {\varvec{s}_{0} } \right)} \right| = \left| {\hat{P}\left( {\varvec{s}_{0} } \right) - P\left( {\varvec{s}_{0} } \right)} \right| < r,$$

(13)

where r > 0 and R(s₀) refers to estimation error (residual). Standard deviation can be used to express the acceptable range for the estimation error which means:

$${\text{Prob}}\left[ {\left| {\hat{P}\left( {\varvec{s}_{0} } \right) - P\left( {\varvec{s}_{0} } \right)} \right| < k\sigma } \right] \ge \alpha ,$$

(14)

where “Prob” means the probability and α is a threshold for acceptable probability level. It means that the probability of the estimated value to be “falling in the range $\left[ {P\left( {\varvec{s}_{0} } \right) - k\sigma ,P\left( {\varvec{s}_{0} } \right) + k\sigma } \right]$” should be more than α percent. Parameters k and α are chosen based on available budget for rain gauge installation or maintenance. The coefficient k dictates the area under the probability density function where the random variable might belong to the corresponding interval. In a sense, assuming k = 1 implies that the probability of X being in interval (− σ, σ) is 0.64. After some trial and error, an appropriate value of α was found to be 0.8 for this study. The rationale behind such a selection will be explained later.

Moreover, residual or estimation error [R(s₀)] has normal distribution with zero mean {i.e., $E\left[ {\hat{P}\left( {\varvec{s}_{0} } \right) - P\left( {\varvec{s}_{0} } \right)} \right] = E\left[ {\hat{P}\left( {\varvec{s}_{0} } \right)} \right] - E\left[ {P\left( {\varvec{s}_{0} } \right)} \right] = 0$} and variance equal to $\sigma_{R}^{2} \left( {\varvec{s}_{0} } \right)$ {i.e., $R\left( {\varvec{s}_{0} } \right) = N\left[ {0,\sigma_{R}^{2} \left( {\varvec{s}_{0} } \right)} \right]$}. Therefore, the probability of estimation error can be calculated to fall within the desired range (− σ, σ) using cumulative probability of standard normal distribution. By dividing [R(s₀)] to residual’s standard deviation at point s₀ [i.e., $\sigma_{R} \left( {\varvec{s}_{0} } \right)$], standardized estimation error can be found as:

$$\begin{aligned} {\text{Prob}}\left[ {\left| {R\left( {\varvec{s}_{0} } \right)} \right| < \sigma } \right] & = {\text{Prob}}\left[ {\frac{{\left| {R\left( {\varvec{s}_{0} } \right)} \right|}}{{\sigma_{R} \left( {\varvec{s}_{0} } \right)}} < \frac{\sigma }{{\sigma_{R} \left( {\varvec{s}_{0} } \right)}}} \right] \\ & = {\text{Prob}}\left[ {\left| {R^{*} \left( {\varvec{s}_{0} } \right)} \right| < \frac{\sigma }{{\sigma_{R} \left( {\varvec{s}_{0} } \right)}}} \right] \\ & = A_{\text{point}} \left( {\varvec{s}_{0} } \right), \\ \end{aligned}$$

(15)

where $R^{*} \left( {\varvec{s}_{0} } \right)$ is the standardized estimation error and has standard normal distribution [i.e., N(0, 1)]. A_point(s₀) is the “acceptable probability” at an un-sampled point s₀. In other words, A_point(s₀) is the probability of the estimation error at point s₀ to be less than σ. According to Eq. (14), accuracy of estimation at an un-gauged location s₀ can be considered to be acceptable only if the associated “acceptable probability” is not less than α [$A_{\text{point}} \left( {\varvec{s}_{0} } \right) > \alpha$]. As a result, one can argue that the estimation at the point under consideration has the acceptable accuracy in light of honoring the aforementioned inequality. In order to better understand the process, the estimation error with different variances is compared and contrasted in Fig. 1. $\sigma_{{\varvec{s}1}}^{ 2} , \sigma_{{\varvec{s}2}}^{2}$ are point variances of two generic points within the study area. It is assumed that $\sigma_{{\varvec{s}1}}^{ 2} < \sigma_{{\varvec{s}2}}^{2}$. Point s₂ with higher variance has less area inside the acceptable range and therefore has lower acceptable probability. This elaboration could ensure that high variance points have lower A_point(s₀). On the other hand, points associated with higher acceptable probability (compared to the threshold α) are more accurate.

Fig. 1

Probability distribution of the estimation error considering different IDW variances

A_point(s₀) is a point-wise measure of accuracy. To find a block-wise criterion, a new parameter called “Percentage of area with acceptable accuracy” (hereafter denoted by A_Areal) is introduced. It is the percentage of area that their acceptance probability [i.e., A_point(s₀)] is greater than α. In other words, A_Areal is the percentage of area within which the probability of the error variance at s₀ falling within the range (− σ, σ) is more than α percent. In order to effectively utilize Stc-IDW for rain gauge network design using this procedure, $\sigma_{R} \left( {\varvec{s}_{0} } \right)$ in Eq. (15) will be replaced by $\sigma_{R}^{\text{IDW}} \left( {\varvec{s}_{0} } \right)$ computed via Eq. (12). For this purpose, the study area will be discretized into a mesh and A_point(s₀) will be calculated for each grid point. In this study, after testing a few grid spacing, we use the optimum grid spacing, which has minimal effect on subsequent results.

Materials and methods

Numerous studies focus on kriging and IDW methods as appropriate kernels to evaluate the performance of a representative rain gauge network design. These estimators can be effectively utilized to estimate precipitation at a point which is not sampled. A majority of studies try to compare and contrast these estimators and argue that a particular estimator has a better performance compared to another. When it comes to goodness of fit criteria, error measures associated with IDW are quite arbitrary due to the deterministic nature of this method and cannot be easily compared to other estimators. In this section, an appropriate measure will be developed to evaluate the performance of a method based on IDW estimator and then compare the results with those of kriging. In addition, the study area, parameter estimation of Stc-IDW and also variogram modeling will be presented. Subsequently, a methodology for measuring the areal accuracy of Stc-IDW and BK estimators will also be provided.

Description of the study area

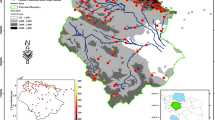
A plain region of Kohkiloyeh-Bouyerahmad and Khouzestan provinces in southwest of Iran is selected as the study area. The total area of this region is about 25,000 km², as illustrated in Fig. 2. It is located between longitude 49°17′ and 51°22′ east, and between latitude 30°2′ and 31°56′ north. The physiography within the study area is the near-horizontal depositional surfaces of the Gachsaran and Dehdasht regions.

Fig. 2

Location and rain gauge stations in the study area

The overall rainfall pattern in the region is affected by Mediterranean low-pressure systems which enter from the west throughout the year. The precipitation of this region occurs mostly in the form of rain, which usually results from frontal storm systems traveling eastward. However, summer precipitation results from localized convective-type storms, which usually has no major contribution to the total annual precipitation.

A total number of 34 non-recording rain gauge stations with annual precipitation, for at least a 10-year period, is used for this study. The spatial distribution of rain gauges is illustrated in Fig. 2. The UTM coordinates, elevation and average annual rainfall depth (mm) of each rain gauge station are summarized in Table 1. The mean annual rainfall ranges from 249.9 to 901.4 mm. This difference in rainfall numerical values shows a great spatial variability over the study area.

Table 1 Precipitation data used for characterizing rainfall spatial variability

Variogram modeling

Within a stochastic framework, every estimator requires model of spatial similarity or variability. In spatial data analysis, variogram is considered to be an appropriate model of spatial variability. Within the last 3–4 decades, its modeling was the focus of extensive research because of its generality compared to measure of similarity. At early stage of variogram modeling, one has to identify the experimental omnidirectional variogram and then try to delineate an appropriate theoretical variogram which will best represent the experimental variogram. Generally speaking, variogram, i.e., $\gamma \left( {\varvec{s}_{i} , \varvec{s}_{j} } \right)$ is defined as half of the variance of the first increment in attribute values. When it comes to computation of experimental variogram, the variance can be replaced by a summation in light of intrinsic hypothesis.

$$\hat{\gamma }\left( {\varvec{s}_{i} , \varvec{s}_{j} } \right) = \frac{1}{2 }\sum \left[ {P\left( {\varvec{s}_{i} } \right) - P\left( {\varvec{s}_{j} } \right)} \right]^{2} ,$$

(16)

where N(h_ij) is the number of data pairs whose separation distance belongs to $\varvec{h}_{ij} = \varvec{s}_{i} - \varvec{s}_{j}$. There are various functions cited in the literature to represent theoretical variogram (i.e., exponential, power, Gaussian). Selection of theoretical variogram is considered to be a simple exercise in nonlinear curve fitting. In the current study, exponential structure is found to represent the experimental variogram in an efficient way. The exponential variogram can be stated as:

$$\gamma \left( {\varvec{h}_{ij} } \right) = \sigma^{2} \left[ {1 - \exp \left( { - \frac{{\varvec{h}_{ij} }}{a}} \right)} \right],$$

(17)

where σ² is the sill value and “a” is the range which is defined as the distance whereby the correlation value tend to a small ignorable value. For an anisotropic phenomenon, the semi-variance will be a function of separation vector. However, for isotropic process, the model of spatial variability will solely be a function of separation distance. In this study, the process under consideration is considered to be isotropic. After conducting a nonlinear curve fitting on omnidirectional experimental variogram, the parameters of exponential variogram are found to be σ² = 37511 mm² and a = 68,997 m. Figure 3 demonstrates the result of variogram modeling related to the data used in this study.

Fig. 3

Experimental variogram along with the best fit to theoretical exponential model

Calibration of Stc-IDW’s parameters

To use Stc-IDW estimator for network design, it is an inevitable task to find its optimal parameters such as “power” and number of neighbor stations surrounding the point under consideration invariably called “support domain size.” Optimal parameters can be found by cross-validation procedure whereby one is obliged to leave one data out and then use the kernel to estimate the attribute at the point pretended not to be sampled. Toward the end of this exercise, at each station, we have two numbers, i.e., the observed and the simulated one for each pair of power and support domain size. Optimum values of power and support domain size correspond to minimum root mean square error. Figure 4a, b demonstrates variation of RMSE as a function of power and support domain size in 2D dimensions, respectively. According to this figure, optimal value of power is found to be 3 and support domain size is 10. Needless to say, in rain gauge network design, scenarios with number of gauges less than 10 would not be affected by limitation imposed by support domain size.

Fig. 4

RMSE of IDW, changing the number of data (a) and distance decay parameter (b)

Implementation of the estimators

It is quite important to obtain the exponentially decaying measure of network accuracy versus the number of stations for both BK and Stc-IDW. In relevant literature, there are numerous approaches conducted to go for rain gauge network design. Two of the most widespread usage of these methods are those of Bastin et al. (1984) and Kassim and Kottegoda (1991). In subsequent paragraphs, Bastin’s approach is considered to design the rain gauge network using both Stc-IDW-based and BK-based estimations using the proposed methodology.

Procedure to implement Stc-IDW approach

To implement the proposed methodology using Stc-IDW in this research, a few key parameters are defined for our study area. In our study, σ [used in Eq. (15)] is the sill value of the theoretical variogram. It is also vital to obtain an appropriate value for α. Based on our findings in Fig. 5, at α = 0.8, about 98% of the total area has acceptable accuracy (i.e., A_Areal = 98%). On the other hand, A_Areal is about 60% at α = 0.9 which is very low. Moreover, α = 0.7, leads to A_Areal = 90% and α = 0.6 do not cover the acceptable accuracy range at all (i.e., it covers 60–100% which is not logical). As a result, α = 0.8 is selected as the best amount of α for the current study area. Similar result for α has also been used by Cheng et al. 2008. The size of the grid nodes for discretization has to be also obtained. Among different grids pacing (13, 10, 8, 7, 6, 5 km), the results of the proposed approach remain invariant at grid spacing with 7 km or less. Therefore, the grid spacing of 7 km * 7 km is adopted in this study.

Fig. 5

Comparison between different amounts of α

The step-by-step procedure to delineate optimal combination for a particular set of rain gauges out of the total number of rain gauges using Stc-IDW is documented as follows:

• Step 1 Identify the theoretical variogram function for the attribute under consideration.

• Step 2 Find appropriate values of Stc-IDW parameters using cross-validation statistics.

• Step 3 Discretize the whole study area into a set of grid nodes with 7-km grid spacing.

• Step 4 Develop the MATLAB code for Stc-IDW estimator to generate n-rain gauge station(s) scenario considering that n − 1 stations have already been selected at previous steps. In other words, one rain gauge scenario consists of finding the best station that maximize A_Areal over the entire study area. It means that one has to first compute the variance of residuals at each grid node using Eq. (12) and then compute A_point(s₀) for each grid point and subsequently calculate A_Areal for the scenario under consideration and repeat this procedure N times out of which the scenario corresponding to maximum A_Areal will be chosen. When it comes to two rain gauge scenario, it is assumed that one of them has already been selected at previous step and then the second one will be chosen out of N − 1 possibilities using the same procedure. This procedure will be repeated for other combinations up to the end.

Procedure to implement BK approach

In block kriging, the support size for observation is point-wise while that of estimation is block-wise. Indeed, the variance of residuals over the entire study area can be considered as an objective function to be minimized for an optimum configuration and spatial distribution of rain gauges over the region [i.e., Eq. (7)]. As BK approach is not sensitive to the grid spacing, the same grid spacing as Stc-IDW (7 km * 7 km) is adopted for BK in this study. Step-by-step procedure to delineate optimal combination for a particular set of rain gauges out of the total number of rain gauges is documented as follows:

• Step 1 Identify the theoretical variogram function for the attribute under consideration.

• Step 2 Discretize the whole study area into a set of grid nodes with 7-km grid spacing.

• Step 3 Develop the MATLAB code for BK estimator to generate n-rain gauge station(s) scenario considering that n − 1 stations have already been selected at previous steps. In other words, one rain gauge scenario consists of finding the best station that minimize variance of residuals over the entire study area. For this purpose, the variance of residuals will be computed N times out of which the scenario corresponding to minimum variance will be chosen. Needless to say, computation of kriging coefficients (i.e., $\lambda_{i}^{\text{BK}}$ in Eq. 4) will be considered as a prerequisite for minimum variance computation. When it comes to two rain gauge scenario, it is assumed that one of them has already been selected at previous step and then the second one will be chosen out of N − 1 possibilities using the same procedure. This procedure will be repeated for other combinations up to the end.

Results and discussion

As mentioned earlier, in a given rain gauge network design, the sole independent decision variables are considered to be the number and spatial location of rain gauges. Minimization of residuals and/or maximization of information content (i.e., network accuracy) is more frequently used objective functions for such problems. According to information theory, as the number of rain gauges increases, the information content and/or measure of accuracy becomes independent of the number of rain gauges and approaches an asymptote, hence, a truly optimization problem in its own right.

The main objective of rain gauge network design in this study is to present a new accuracy criterion based on one of the popular deterministic-based interpolation methods (i.e., IDW with some changes) which is based on the number and location of stations and evaluate the quality of the network performance through comparing and contrasting the end results with those of stochastic-based methods (i.e., BK). Indeed, to the best of authors’ knowledge, such comparison is missing from the existing literature on rain gauge network design. In subsequent subsections, the results along with its critical discussion will be provided for both approaches.

Result of Stc-IDW approach

Figure 6 illustrates the result of prioritization of the rain gauge network in the southwest of Iran using the new proposed criterion and Stc-IDW estimator. Percentage of area with acceptable accuracy varies from 8%, when selecting 1 station, to 100% when selecting more than 11 stations. In reference to the content of Fig. 6, for a single rain gauge scenario, the first most accurate station that represents the areal annual precipitation in the region is station #13. For a two rain gauge scenario, the tradition is to assume every scenario has station #13 in common trying to find the second best station which will best represent the measure of accuracy. In our case, station #18 is found to be the most accurate location to represent the two rain gauge scenario. In other words, accurate set of “two-station scenario” using IDW estimator is stations “13, 18.” Similarly, stations “13, 18, 30” have achieved the maximum accuracy among other possibilities (e.g., three-rain gauge scenario). As the number of selected stations increases, the accuracy criterion approaches to its plateau and becomes independent of additional stations. In particular, after selecting 11 stations, no further improvement can be traced in measure of accuracy.

Fig. 6

Optimum delineation of various rain gauge combinations using IDW method

Result of BK approach

In order to evaluate the network performance cited above under similar condition (i.e., different estimators), the result of network design using BK approach is represented in Fig. 7. As shown in Fig. 7, the variance of residuals over the entire study area reaches a plateau value after choosing 11 stations. When selecting BK as the estimator, the one-station scenario is station #7. Other accurate optimum combinations can be seen in Fig. 7.

Fig. 7

Optimum delineation of various rain gauge combinations using BK method

Comparison of the implemented schemes

At this stage, it might be useful to compare and contrast the two approaches to better rationalize the results. BK and Stc-IDW approaches presented in this paper both provide areal accuracy criterion belonging to the block as large as the study area. Moreover, both methods need to break down the study area into grid nodes to compute the measure of accuracy. In addition, BK and Stc-IDW can both require some sort of system identification. More specifically, system identification in BK corresponds to variogram modeling, while in Stc-IDW approach, before estimation, one needs some sort of parameter calibration. On the other hand, there are some differences between the two approaches. In BK approach, weighting coefficients are based on network topology as well as process attribute value in an implicit way, while in Stc-IDW approach, the network topology will be the sole factor in computation of weighting coefficients. Furthermore, BK and Stc-IDW approaches are different because computation of weighting coefficients in BK requires matrix inversion. These similarities and differences would pave the road to better rationalize the results emerging from the two approaches.

A procedure is presented in this section to compare the results and measure the efficiency of the new proposed accuracy estimation criterion. It should be mentioned that all parameters of the two estimators including the study area, size and the number of grid nodes and variogram models are the same. The only source of variability can be attributed to the estimator (i.e., interpolant) and associated accuracy criterion. Efficiency of network design using the proposed criterion can be traced by converting one of the method’s prioritization stations into the other method’s accuracy estimation. In other words, we kept the exponentially decaying function of BK’s quite intact and tried to convert results of Stc-IDW to the former one for comparison purposes. In this way, both methods use the same measure of accuracy, and the performance of the proposed criterion can be examined as done in Fig. 8. As noted in Fig. 8, beside each station, one can notice two station numbers. The first number is associated with BK approach while that of Stc-IDW procedure is associated with the second number. Interestingly enough, the results of the two approaches are almost identical in terms of variance of residuals for various combinations as shown in Fig. 8.

Fig. 8

Comparison of error variance of BK and IDW interpolation methods

The task of prioritizing the rain gauge stations in BK and Stc-IDW methods tend to decrease in a rapid rate at early stage of rain gauge addition and then changes more slowly as the number of stations saturated toward a lower asymptote. Even though, one can notice a minor change in delineating station number between the two approaches, as soon as the measure of accuracy reaches the constant value, around 55% of the total number of stations selected is exactly the same (i.e., #13, 17, 21, 24, 30, 31 are selected for both procedures as part of 11-stations scenario) in both approaches and the difference between variance of residuals among the two approaches is quite marginal.

As shown in Fig. 8, one can notice that the first holding station for both methods may not be the same. When it comes to two rain gauge scenario, BK and IDW resulted in stations “7, 25” and “13, 18” which both methods selected one station at the center of the study area and one station at one corner of the study area. For three-rain gauge scenario, stations “7, 25, 13” and “13, 18, 30” are singled out by the two methods. Looking at network configuration as depicted in Fig. 1, three selected stations in both methods cover the study area. Upon further elaboration on delineating the best scenarios for various combinations, Fig. 8 clearly shows that the number of stations selected for eleven-rain gauge scenario (i.e., the turning point of exponentially decaying curve) is “7, 25, 13, 19, 21, 24, 15, 11, 17, 31, 30” for BK method and “13, 18, 30, 29, 21, 31, 20, 33, 32, 24, 17” for Stc-IDW method which contains 6 identical stations and 5 stations near each other. This has a major implication for rain gauge network design when it comes to resorting to deterministic-based approaches.

It is worth noting that even though the Stc-IDW approach is based on totally different scientific backgrounds, it provided exponentially decaying function very similar to that of BK approach. In other words, the proposed areal accuracy estimation criterion of Stc-IDW interpolant is in good agreement with conventional, routinely implemented variance-based BK approach. One could easily rationalize the similar results emerging from the two approaches by noting that in Stc-IDW, areas with less “percentage of area with acceptable accuracy” correspond to high variance of residuals, hence, demanding for higher number of stations.

Conclusions

The accuracy of precipitation estimation over a given study area in a rain gauge network design is directly related to the number and spatial location of stations. Existing literature on rain gauge network design calls for development of a systematic procedure to define and implement an accuracy criterion based on one of the deterministic-based methods over the entire study area. The relevant literature is quite silent on how to move from point-wise estimation to block-wise average in deterministic-based methods. Perhaps the need for such transformation emerges from the fact that in deterministic-based approaches, the kernel does not require any matrix inversion. The current study intended to effectively benefit from this lack of need for matrix inversion in Stc-IDW scheme, critical assessment of results emerging from such approach, and also propose a mechanism for independent verification of rain gauge network design elaborated by Cheng et al. (2008).

To fulfill this gap, a new criterion is presented to move from point-wise estimation to block-wise average, and its independent verification is achieved via comparing and contrasting the results with that of BK. According to the proposed criterion, for the first time, a probability-based measure is coupled with IDW interpolation method (i.e., Stc-IDW) to design a rain gauge network in southwest of Iran. After implementing the proposed methodology on an existing rain gauge network to prioritize the gauges, the result is compared with a variance-based interpolation method (i.e., BK). Good agreement is observed between the new proposed scheme and BK results.

An interesting exercise would be to use a time-consuming approach or a random search procedure such as genetic algorithm to find the best set of stations among all potential candidates using the proposed criterion and better acknowledge the efficiency and robustness of Stc-IDW as a typical deterministic-based method for rain gauge network design, which does not require matrix inversion. Moreover, other IDW/Stc-IDW parameters such as anisotropy ratio and anisotropy angle may also be used to better interpolate the attribute under consideration over the entire study area.