1 Introduction

The dynamic behaviours of circular plates have been a subject of great research interest for the past few decades. In such research, it has been shown that thin circular plates may exhibit a flexural vibration, having the same order as the thickness of the plate. In that case, linear model is not sufficient enough to predict the dynamic behaviour of the circular plates because physical scenario such as resonance, jump phenomenon and hysteresis are often encountered (Nayfeh and Mook 1979). In order to describe the vibration of the structure under such condition, Von Kármán equation is used to include the geometric nonlinearities in the vibration governing equation, taking cognisance of the stretching of the midplane. One of such studies was presented by Dumir (1986) where the dynamic behaviour of circular plates resting on elastic foundation was analysed using a semi-analytical method. The author made consideration to plates with edges restrained against rotation and in-plane displacement using Von Kármán principle. Touzé et al. (2002) studied asymmetric nonlinear vibrations of free-edge circular plates using multiple scales method with introduction of slight imperfections into the plate. The authors focused on the scenario where one configuration that is not directly excited by the load obtains energy via nonlinear coupling with other configurations. Von Kármán equations are considered in the modelling of the governing equation. Subsequently, Dai et al. (2011) investigated nonlinear plates vibration based on Von Kármán principle using Galerkin method resulting in tangential stiffness matrix. In another study, Xie and Xu (2013) determined general solution for nonlinear oscillations based on Von Kármán’s theory along with quasi-steady aerodynamic theory in establishing the governing equation. In a later work, Dai et al. (2014) re-examined deflection of Von Kármán plate with imperfect initial deflection using semi-analytical method.

Foundations are important parts of systems owing to the preponderant application in engineering. The role of foundation in protecting structural system under vibration from failure cannot be underestimated. Part of the aims of the authors is to investigate the dynamic behaviour of viscoelastic nonlinear foundation on a thin vibrating isotropic circular plate. Zhu et al. (2015) examined the nonlinear viscoelastic foundation model as a three-parameter model, meaning the layers are indicated by linear elastic springs, cubic nonlinearity elastic springs and shear deformation. The investigation of dynamic response of beam resting on elastic foundation was performed by Yankelevsky et al. (1989), based on the findings nonlinear model is more practical and more realistic than linear model. In another study, Wu and Thompson (2004) conducted a research on the effect of linearity and nonlinearity on the wheel–rail impact. It was concluded that the linear model is not suitable for wheel–rail impact problem. In a similar work, Senalp et al. (2010) investigated the effects of speed and damping of load on nonlinear dynamic response of beams resting on nonlinear foundation. Also, Civalek (2013) based on his study stated that the influence of nonlinear and shear parameters on the amplitude of oscillations is vastly significant compared to the linear model. In a further study, Kanani et al. (2014) examined the influence of nonlinear foundation on large amplitude of a beam. The foundation was modelled to include shear layer of Pasternak and nonlinear Winkler foundations. The authors realized that increasing the nonlinear parameter of the foundation can augment the system nonlinearity. Meanwhile, shear and linear parameters can weaken the nonlinearity. Since the nonlinearity of the system is affected by the above-mentioned parameters, the system nonlinearity can be controlled by linear and shear. Younesian et al. (2019) reviewed elastic and viscoelastic foundations on linear and nonlinear model. Based on the authors’ finding, there are limitations in the use of elastic foundation compared to adoption of viscoelastic element. Other studies on related field are reported by Haciyev et al. (2019), Sofiyev et al. (2017), Lin and Dangal (2017), Lin et al. (2018) and Linlin and Xing (2019).

Various analytical studies in the previous work have shown that analysis of nonlinear models is very difficult to handle using exact method, and recourse is made to semi-analytical and numerical method. In an attempt to obtain numerical solution for structure on nonlinear foundation, Allahverdizadeh et al. (2008) employed Kantorovich averaging method to analyse nonlinear free and forced vibration of functionally graded plates. However, for semi-analytical solutions, El Kaak et al. (2016) studied geometrical nonlinearity of free axisymmetric vibrations of functionally graded circular plate using iterative and explicit semi-analytical solution. In another work, Yazdi (2016) assessed the use of homotopy perturbation method on forced vibration of orthotropic circular plate on elastic nonlinear foundation. The effect of elastic foundation parameter was considered. According to the findings, the influence of Winkler and Pasternak foundation on the frequency ratio is much significant. Also, Togun and Bagdatl (2016) examined the free and forced vibration of nanobeam resting on Winkler and Pasternak foundation using Perturbation series. In a further work, Sobamowo (2017) used differential transformation method (DTM) to analysis carbon nanotube resting on Pasternak foundation. DTM is adopted as the method of solution for this study based on the fact that the method is a closed form series solution with fast convergence coupled with being easier to use and reduction of computational cost compared to other methods of solutions like numerical method with huge volume of calculation and convergence study limitation. More so, for perturbation method, the need for small parameter is also a limitation. Likewise, the restriction of HPM to weakly nonlinear and lack of proper guideline on choice of initial approximation in iterative method are some of the difficulties DTM overcome.

Various studies are presented in the literature including axisymmetric vibration of circular plate resting on elastic foundation, meanwhile investigation on the symmetric vibration on viscoelastic three-parameter medium is still limited. Therefore, this study examines forced vibration of symmetric and axisymmetric circular plate resting on viscoelastic three foundation parameters. Most of the above works are mainly related with the amplitude–frequency response of the circular plates. However, damping and forcing effect included studies on the nonlinear vibration properties of plate systems are also rather limited. The damping effects are considered, and nonlinear vibration behaviours of the circular plates are illustrated. Practical application of problem includes liquid storage tanks, pipelines and slab track for floating railway track to mention a few.

2 Problem Formulation and Mathematical Analysis

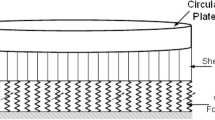
Considering a circular plate as shown in Fig. 1, the plate is considered resting on Pasternak and Winkler foundations under simply supported and clamped edge conditions. Von Kármán’s deflection theory by Touzé et al. (2002) is considered in the modelling of the governing equation based on the following assumptions:

  1. (1)

    Thin plate is assumed.

  2. (2)

    Kirchhoff–Love hypotheses are assumed to be satisfied.

  3. (3)

    Only the nonlinear terms of lowest order are kept in the expression of the strains as functions of the displacement.

  4. (4)

    The in-plane and rotatory inertia terms are neglected.

Fig. 1
figure 1

Showing uniform thickness circular plate resting on four-parameter foundations

Full size image

The governing differential equations as reported by Kerr (1964), Dumir (1986) and Yamaki (1961) are

$$\begin{aligned} & D\nabla^{4} w^{*} (r,\theta ,t) + \overline{k}_{{\text{w}}} w^{*} (r,\theta ,t) - \overline{k}_{{\text{s}}} \nabla^{2} w^{*} (r,\theta ,t) - \overline{k}_{{\text{p}}} w^{3*} (r,\theta ,t) \\ & \quad + c\frac{{\partial w^{*} (r,\theta ,t)}}{\partial t} + \rho h\frac{{\partial^{2} w^{*} (r,\theta ,t)}}{{\partial t^{2} }} - \frac{h}{r}\frac{\partial }{\partial r}\left( {\frac{\partial F}{{\partial r}}\frac{{\partial w^{*} }}{\partial r}} \right) = q\cos (\omega t), \\ \end{aligned}$$
(1)
$$\nabla^{4} F = - \left( \frac{E}{r} \right)\frac{{\partial w^{*} }}{\partial r}\frac{{\partial^{2} w^{*} }}{{\partial r^{2} }},$$
(2)

where \(t\) is the time, \(r\) is the radial coordinate, \(w^{*}\) is the transverse deflection, \(E\) is the Young’s modulus of the plate. The foundation of the circular plate is visco-Pasternak medium, \(k_{{\text{w}}}\) is the Winkler foundation, \(k_{{\text{s}}}\) is the Pasternak foundation, \(k_{{\text{p}}}\) is the nonlinear Winkler, \(q\) is the uniformly distributed transverse load, \(\omega\) is the excitation frequency, c is the damper modulus parameters, while \(\rho\) is the material density, \(h\) is the thickness of the plate, flexural rigidity \(D = Eh^{3} /12(1 - \nu^{2} )\), \(F\) is the Airy stress function, \(\nabla\) is the Laplacian and Poisson’s ratio is \(\nu\).

The transverse deflection of the plate is assumed to be

$$w\left( {R,\theta ,t} \right) = \sum\limits_{m = 0}^{\infty } {w^{*} } \left( {R,t} \right)\cos \left( {m\theta } \right),$$

\(w^{*}\) is the vertical displacement at a given point of coordinates with respect to spatial coordinate and time of the middle surface of the plate.

Using dimensionless parameters

$$w = \frac{{w^{*} }}{h},\quad F = \frac{{F^{*} }}{{Eh^{2} }},\quad R = \frac{r}{a},\quad D = \frac{{Eh^{3} }}{{12(1 - \nu^{2} )}},$$

we arrived at the following equations

$$\begin{aligned} & \frac{1}{{12(1 - \nu^{2} )}}\left( {\frac{{\partial^{4} w}}{{\partial R^{4} }} + \frac{2}{R}{\mkern 1mu} \frac{{\partial^{3} w}}{{\partial R^{3} }} - \left( {\frac{{2m^{2} + 1}}{{R^{2} }}} \right)\frac{{\partial^{2} w}}{{\partial R^{2} }} + \left( {\frac{{2{\mkern 1mu} m^{2} + 1}}{{R^{3} }}} \right)\frac{\partial w}{{\partial R}} - \left( {\frac{{4{\mkern 1mu} m^{2} - m^{4} }}{{R^{4} }}} \right)w} \right) - \frac{1}{R}\frac{\partial }{\partial R}\left( {\frac{\partial F}{{\partial R}}\frac{\partial w}{{\partial R}}} \right) \\ & \quad = Q_{0} \cos \left( {\omega {\mkern 1mu} \tau } \right) - \frac{1}{{12(1 - \nu^{2} )}}\frac{{\partial^{2} w}}{{\partial \tau^{2} }} - k_{{\text{s}}} \frac{{\partial^{2} w}}{{\partial R^{2} }} + \frac{{k_{{\text{s}}} }}{R}\frac{\partial w}{{\partial R}} - k_{{\text{w}}} w + \frac{3}{4}{\mkern 1mu} {\mkern 1mu} k_{{\text{p}}} w^{3} - \frac{C}{{12(1 - \nu^{2} )}}\frac{\partial w}{{\partial \tau }}, \\ \end{aligned}$$
(3)
$$\frac{{\partial^{2} F}}{{\partial R^{2} }} + \frac{1}{R}\frac{\partial F}{{\partial R}} - \frac{1}{{R^{2} }}F = - \left( \frac{1}{R} \right)\frac{\partial w}{{\partial R}}\frac{{\partial^{2} w}}{{\partial R^{2} }},$$
(4)

where

$$\tau = \left[ {\sqrt {\frac{D}{{\gamma^{*} ha^{4} }}} } \right]t,\,\,\,k_{{\text{w}}} = \frac{{\overline{k}_{{\text{w}}} a^{4} }}{{Eh^{3} }},\,\,k_{{\text{p}}} = \frac{{\overline{k}_{{\text{p}}} a^{4} }}{Eh},\,\,k_{{\text{s}}} = \frac{{\overline{k}_{{\text{s}}} a^{2} }}{{Eh^{3} }},\,\,\,Q_{0} = \frac{{qa^{4} }}{{Eh^{4} ,}}\,\,\,\,C = \frac{{ca^{4} }}{{Eh^{3} }}$$
(5)

2.1 Boundary Condition

The following boundary conditions are used (Figs. 2, 3):

  • Clamped edge condition

    $$\begin{aligned} & \left. W \right|_{R = 1} = 0,\left. {\frac{\partial W}{{\partial R}}} \right|_{R = 1} = 0, \\ & \left. W \right|_{R = 0} = 0,\left. {\frac{\partial W}{{\partial R}}} \right|_{R = 0} = 0, \\ \end{aligned}$$
    (6)

  • Simply Supported edge condition

    $$\begin{aligned} & \left. W \right|_{R = 1} = 0,\left. {\left( {\frac{{\partial^{2} W}}{{\partial R^{2} }} + \frac{\nu }{R}\frac{\partial W}{{\partial R}}} \right)} \right|_{R = 1} = 0, \\ & \left. W \right|_{R = 0} = 0,\left. {\left( {\frac{{\partial^{2} W}}{{\partial R^{2} }} + \frac{\nu }{R}\frac{\partial W}{{\partial R}}} \right)} \right|_{R = 0} = 0, \\ \end{aligned}$$
    (7)

  • The initial conditions:

    $$\left. W \right|_{\tau = 0} = T_{o} ;\quad \left. {\frac{\partial W}{{\partial \tau }}} \right|_{\tau = 0} = 0,$$
    (8)
Fig. 2
figure 2

Schematic of a clamped–clamped supported condition

Full size image
Fig. 3
figure 3

Schematic of a simply supported conditions at both edges of the rectangular plate

Full size image

For the Airy stress functions, free edge and constrained immovable edge are considered. The boundary conditions in dimensionless form are

$$R = 1:\quad \frac{\partial F}{{\partial R}} = 0,\quad \frac{{\partial^{2} F}}{{\partial R^{2} }} - \frac{\nu }{R}\frac{\partial F}{{\partial R}} = 0.$$
(9)

3 Method of Solution: Differential Transformation Method

3.1 Principle of Differential Transformation Method

Differential transformation method (DTM) proposed by Zhao (1986) is a closed form series approximate solution, very powerful, reliable and easy to comprehend semi-analytical method for solving linear, nonlinear, partial and ordinary differential equations. DTM involves transformation techniques which are applied to the governing equation along with the governing boundary conditions to form algebraic equations. The resulting solution of the algebraic equations form the solution of the system in series form. The accuracy of the results compared to numerical method and experimental is very high. The basic definitions and operational properties are as follows:

Considering a function \(\varphi (t)\) that is analytic in the domain \(t\), the function \(\varphi (t)\) will be differentiated continuously with rest to space \(t\)

$$\frac{{{\text{d}}^{k} \varphi (t)}}{{\partial t^{k} }} = \phi \left( {t,k} \right),\quad {\text{for}}\,{\text{all}}\;\; t\, \in \tau$$
(10)

For \(t = t_{i}\), then \(\phi \left( {t,k} \right) = \phi \left( {t_{i} ,k} \right)\), where \(k\) belongs to the set of nonnegative integers, denoted as the \(k{\text{-domain}}\). Therefore, Eq. (10) is written as

$$\vartheta (k) = \phi \left( {t_{i} ,k} \right) = \left[ {\frac{{{\text{d}}^{k} \varphi (t)}}{{\partial t^{k} }}} \right]_{{t = t_{i} }} ,$$
(11)

where \(\vartheta_{k}\) is the spectrum of \(\varphi \left( t \right)\) at \(t = t_{i}\).

\(\varphi \left( t \right)\) is expressed in Taylor’s series, then \(\varphi \left( t \right)\) is presented as

$$\varphi \left( t \right) = \sum\limits_{k}^{\infty } {\left[ {\frac{{\left( {t - t_{i} } \right)^{k} }}{k!}} \right]\varphi \left( k \right).}$$
(12)

Equation (12) is the inverse of \(\vartheta (k)\) transverse deflection using the symbol “\(D\)” representing the differential transform process, and combining Eqs. (11) and (12), we have (Table 1)

$$\varphi \left( t \right) = \sum\limits_{k}^{\infty } {\left[ {\frac{{\left( {t - t_{i} } \right)^{k} }}{k!}} \right]\vartheta (k) = D^{ - 1} \vartheta (k).}$$
(13)
Table 1 Operational properties of differential transformation method
Full size table

3.2 Transformation of the Governing Equation to Ordinary Differential Equation

An approximate solution is obtained by assuming the nonlinear free vibrations to have the same spatial shape, i.e.

$$w(r,\tau ) = \left( {c_{4} {\mkern 1mu} r^{4} + c_{2} {\mkern 1mu} r^{2} + 1} \right)\varphi \left( t \right).$$
(14)

Substituting Eqs. (14) into (4) and solving the ordinary differential equation (ODE) provides

$$F(r,t) = \frac{{c_{1} }}{r} - c_{3} r + \frac{{(\varphi (t))^{2} r^{3} \left( {2{\mkern 1mu} c_{4}^{2} r^{4} + 4{\mkern 1mu} c_{2} {\mkern 1mu} c_{4} {\mkern 1mu} r^{2} + 3{\mkern 1mu} c_{2}^{2} } \right)}}{6}.$$
(15)

The value of \(F\) is accordingly found to be finite at the origin \(c_{1} = 0\). Additionally, \(c_{3}\) is the constant of integration to be determined from in-plane boundary conditions.

The substitution of the expressions for \(w\) and \(F\) given by Eqs. (14) and (15), respectively, into Eq. (3), also with application of the Galerkin procedure in the nonlinear time differential equation obtained in the form

$$\int\limits_{0}^{1} {L^{\prime}} (w,F)w\,\,r\,\,{\text{d}}r = 0.$$
(16)

We reached

$$M\ddot{\varphi }_{{\text{s}}} (t) + G\dot{\varphi }_{{\text{s}}} (t) + K\varphi_{{\text{s}}} (t) - V\varphi_{{\text{s}}}^{3} (t) = Q_{o} \cos \omega t,$$
(17)

where

$$M = \frac{{25{\mkern 1mu} c_{4}^{2} }}{3822} + \frac{{\left( {10 + \frac{{25{\mkern 1mu} c_{2} }}{3}} \right)c_{4} }}{546} + \frac{{25{\mkern 1mu} c_{2} }}{1092} + \frac{{5{\mkern 1mu} c_{2}^{2} }}{546} + \frac{25}{{1638}},$$
(18)
$$\begin{aligned} K &= \frac{{5{\mkern 1mu} c_{4}^{2} }}{546}\left( {\frac{{39{\mkern 1mu} k_{{\text{w}}} }}{5} - \frac{{728{\mkern 1mu} c_{3} }}{5} - \frac{{728{\mkern 1mu} k_{{\text{s}}} }}{5} + 64} \right) + \frac{{5{\mkern 1mu} c_{4} }}{546}\left( \begin{gathered} \left( {80 + \frac{{91{\mkern 1mu} k_{{\text{w}}} }}{5} - \frac{{1092{\mkern 1mu} c_{3} }}{5} - \frac{{1092{\mkern 1mu} k_{{\text{s}}} }}{5}} \right)c_{2} + \frac{{546{\mkern 1mu} k_{{\text{w}}} }}{25} - \hfill \\ \frac{{1092{\mkern 1mu} c_{3} }}{5} - \frac{{1092{\mkern 1mu} k_{{\text{s}}} }}{5} + \frac{320}{3} \hfill \\ \end{gathered} \right) \\ & \quad + \frac{{5{\mkern 1mu} c_{2}^{2} }}{546}\left( { - \frac{{273{\mkern 1mu} k_{{\text{s}}} }}{5} + \frac{{273{\mkern 1mu} k_{{\text{w}}} }}{25} - \frac{{273{\mkern 1mu} c_{3} }}{5}} \right) + \frac{{5{\mkern 1mu} c_{2} }}{546}\left( {\frac{{273{\mkern 1mu} k_{{\text{w}}} }}{10} - \frac{{364{\mkern 1mu} c_{3} }}{5} - \frac{{364{\mkern 1mu} k_{{\text{s}}} }}{5}} \right) + \frac{{k_{{\text{w}}} }}{6}, \\ \end{aligned}$$
(19)
$$\begin{aligned} V &= \frac{{5{\mkern 1mu} c_{4}^{4} }}{546}\left( { - \frac{{819{\mkern 1mu} k_{{\text{p}}} }}{220} + \frac{728}{9}} \right) + \frac{{5{\mkern 1mu} c_{4}^{3} }}{546}\left( {\left( {273 - \frac{{819{\mkern 1mu} k_{{\text{p}}} }}{50}} \right)c_{2} - \frac{{91{\mkern 1mu} k_{{\text{p}}} }}{5} + 104} \right) \\ &\quad + \frac{{5{\mkern 1mu} c_{4}^{2} }}{546}\left( {\left( {364 - \frac{{273{\mkern 1mu} k_{{\text{p}}} }}{10}} \right)c_{2}^{2} + \left( {\frac{728}{3} - \frac{{2457{\mkern 1mu} k_{{\text{p}}} }}{40}} \right)c_{2} - \frac{{351{\mkern 1mu} k_{{\text{p}}} }}{10}} \right) \\ &\quad + \frac{{5{\mkern 1mu} c_{4} }}{546}\left( {\left( {\frac{1092}{5} - \frac{{819{\mkern 1mu} k_{{\text{p}}} }}{40}} \right)c_{2}^{3} + \left( {\frac{1092}{5} - \frac{{351{\mkern 1mu} k_{{\text{p}}} }}{5}} \right)c_{2}^{2} - \frac{{819{\mkern 1mu} c_{2} {\mkern 1mu} k_{{\text{p}}} }}{10} - \frac{{819{\mkern 1mu} k_{{\text{p}}} }}{25}} \right) \\ &\quad + \frac{{5{\mkern 1mu} c_{2}^{4} }}{546}\left( { - \frac{{117{\mkern 1mu} k_{{\text{p}}} }}{20} + \frac{1092}{{25}}} \right) + \frac{{5{\mkern 1mu} c_{2}^{3} }}{546}\left( { - \frac{{273{\mkern 1mu} k_{{\text{p}}} }}{10} + \frac{273}{5}} \right) - \frac{{9{\mkern 1mu} c_{2}^{2} k_{p} }}{20} - \frac{3}{8}c_{2} {\mkern 1mu} k_{{\text{p}}} - \frac{{k_{{\text{p}}} }}{8}, \\ \end{aligned}$$
(20)
$$G = \frac{{25{\mkern 1mu} Cc_{4}^{2} }}{3822} + \frac{{\left( {10{\mkern 1mu} C + \frac{{25{\mkern 1mu} Cc_{2} }}{3}} \right)c_{4} }}{546} + \frac{{25{\mkern 1mu} Cc_{2} }}{1092} + \frac{{5{\mkern 1mu} Cc_{2}^{2} }}{546} + \frac{{25{\mkern 1mu} C}}{1638}.$$
(21)

The initial and boundary conditions are

$$\varphi (0,r) = a,\,\,\dot{\varphi }(0,r) = 0.$$
(22)

For a plate with an elastically restrained outer edge, with rotational and in-plane stiffnesses \(k_{{\text{b}}}^{*}\) and \(k_{{\text{i}}}^{*}\), subjected to an applied in-plane radial force resultant \(N^{*}\) at the outer edge, the boundary conditions are

$$r = a:\quad M_{r} = k_{{\text{b}}}^{*} \frac{{\partial w^{*} }}{\partial r},\quad N_{r} = N^{*} - k_{{\text{i}}}^{*} u^{*} ,$$
(23)

where \(u^{*}\) is the radial displacement at midplane. Introduce dimensionless parameters \(k_{b} ,k_{i}\) and \(N\)

$$k_{{\text{b}}} = \frac{{12k_{{\text{b}}}^{*} a}}{{Eh^{3} }},\quad N = \left( {\frac{{N^{*} }}{Eh}} \right)\left( \frac{a}{h} \right)^{2} ,\quad k_{{\text{i}}} = \frac{{k_{{\text{i}}}^{*} a}}{Eh}.$$
(24)

The dimensionless boundary conditions are

$$R = 1:\quad W = 0,$$
(25)
$$\,\left[ {(1 - \nu^{2} )k_{{\text{b}}} + \nu } \right]\frac{\partial W}{{\partial R}} + \frac{{\partial^{2} W}}{{\partial R^{2} }} = 0,$$
(26)
$$\,k_{{\text{i}}} \left( {\frac{{\partial^{2} F}}{{\partial R^{2} }} - \nu \frac{\partial F}{{\partial R}}} \right) + \frac{\partial F}{{\partial R}} = N.$$
(27)

Equations (25) and (26) are used to find the constants \(c_{2}\) and \(c_{4}\) while the constant of integration \(c_{3}\) is obtained using Eq. (27). The constants values under simply supported conditions are

$$c_{2} = - \frac{{2{\mkern 1mu} (k_{{\text{b}}} {\mkern 1mu} \nu^{2} - k_{{\text{b}}} - \nu - 3)}}{{k_{{\text{b}}} {\mkern 1mu} \nu^{2} - k_{{\text{b}}} - \nu - 5}},\quad c_{4} = \frac{{k_{{\text{b}}} {\mkern 1mu} \nu^{2} - k_{{\text{b}}} - \nu - 1}}{{k_{{\text{b}}} {\mkern 1mu} \nu^{2} - k_{{\text{b}}} - \nu - 5}},$$
(28)
$$c_{3} = - \frac{{\left( \begin{gathered} 3{\mkern 1mu} Nk_{{\text{b}}}^{2} \nu^{4} - 5{\mkern 1mu} k_{{\text{b}}}^{2} \nu^{5} + 10{\mkern 1mu} k_{{\text{b}}}^{2} \nu^{4} - 6{\mkern 1mu} Nk_{{\text{b}}}^{2} \nu^{2} - 6{\mkern 1mu} Nk_{{\text{b}}} {\mkern 1mu} \nu^{3} + 10{\mkern 1mu} k_{{\text{b}}}^{2} \nu^{3} + 10{\mkern 1mu} k_{{\text{b}}} {\mkern 1mu} \nu^{4} - 30{\mkern 1mu} Nk_{{\text{b}}} {\mkern 1mu} \nu^{2} - 20{\mkern 1mu} k_{{\text{b}}}^{2} \nu^{2} \hfill \\ + 22{\mkern 1mu} k_{{\text{b}}} {\mkern 1mu} \nu^{3} + 3{\mkern 1mu} Nk_{{\text{b}}}^{2} + 6{\mkern 1mu} Nk_{{\text{b}}} {\mkern 1mu} \nu + 3{\mkern 1mu} N\nu^{2} - 5{\mkern 1mu} k_{{\text{b}}}^{2} \nu - 94{\mkern 1mu} k_{{\text{b}}} {\mkern 1mu} \nu^{2} - 5{\mkern 1mu} \nu^{3} + 30{\mkern 1mu} Nk_{{\text{b}}} + 30{\mkern 1mu} N\nu + 10{\mkern 1mu} k_{{\text{b}}}^{2} - 22{\mkern 1mu} k_{{\text{b}}} {\mkern 1mu} \nu \hfill \\ - 32{\mkern 1mu} \nu^{2} + 75{\mkern 1mu} N + 84{\mkern 1mu} k_{{\text{b}}} - 25{\mkern 1mu} \nu + 218 \hfill \\ \end{gathered} \right)}}{{3{\mkern 1mu} \left( {k_{{\text{b}}} {\mkern 1mu} \nu^{2} - k_{{\text{b}}} - \nu - 5} \right)^{2} \left( { - 2 + \nu } \right)}},$$
(29)

while for Clamped edge condition they are

$$c_{2} = - 2,\,\,\,\,c_{4} = 1,\,\,c_{3} = - \frac{{3{\mkern 1mu} N + 10 - 5{\mkern 1mu} \nu }}{{ - 6 + 3{\mkern 1mu} \nu }}.$$
(30)

3.3 Determination of Nonlinear Natural Frequency Ratio

The dynamic response of the structural analysis is carried out under the transformation

$$\tau = e^{iwt} ,$$
(31)

Applying Eqs. (31) on (17), we have

$$M\ddot{\varphi }_{s} (t) + G\dot{\varphi }_{s} (t) + K\varphi_{s} (t) - V\varphi_{s}^{3} (t) = Q\cos \omega t,$$
(32)

\(G = 0\) for undamped condition

$$M\ddot{\varphi }_{s} (t) + K\dot{\varphi }_{s} (t) - V\varphi_{s}^{3} (t) = Q_{o} \cos \omega t.$$
(33)

In order to find the periodic solution of Eq. (33), assume an initial approximation for zero-order deformation as

$$\varphi_{0} (\tau ) = A\cos \tau .$$
(34)

Substituting Eqs. (34) into (33) gives

$$- M\omega_{0}^{2} A\cos \tau + KA\cos \tau - VA^{3} \cos^{3} \tau = Q_{o} \cos \omega t,$$
(35)

which gives

$$- M\omega_{0}^{2} A\cos \tau + KA\cos \tau - VA^{3} \left( {\frac{3\cos \tau + \cos 3\tau }{4}} \right) = Q_{o} \cos \omega t,$$
(36)

collect like term

$$\left( {KA - M\omega_{0}^{2} A - \frac{{3VA^{3} }}{4}} \right)\cos \tau - \frac{1}{4}VA^{3} \cos 3\tau = Q_{o} \cos \omega t;$$
(37)

eliminating the secular term, one arrives at

$$\left( {KA - M\omega_{0}^{2} A - \frac{{3VA^{3} }}{4}} \right) = Q.$$
(38)

Thus, zero-order nonlinear natural frequency becomes

$$\omega_{0} \approx \sqrt {\frac{K}{M} + \frac{{3VA^{2} }}{4M} - \frac{Q}{MA}} .$$
(39)

Therefore, ratio of zero-order nonlinear natural frequency\(\omega_{0}\) to the linear frequency \(\omega_{b}\)

$$\frac{{\omega_{0} }}{{\omega_{b} }} = \sqrt {1 + \frac{{3VA^{2} }}{4K} - \frac{Q}{AK}.}$$
(40)

Following the same procedural approach, the first-order nonlinear natural frequency is

$$\omega_{1} \approx \sqrt {\frac{1}{2}\left\{ {\left[ {\left( \frac{K}{M} \right) - \left( {\frac{{3VA^{2} }}{4M}} \right)} \right] + \sqrt {\left[ {\left( \frac{K}{M} \right) - \left( {\frac{{3VA^{2} }}{4M}} \right)} \right]^{2} - \left( {\frac{{3V^{2} A^{4} }}{{32M^{2} }}} \right)} } \right\} - \frac{Q}{AK}} .$$
(41)

The ratio of the first-order nonlinear frequency\(\omega_{1}\) to the linear frequency \(\omega_{b}\) gives,

$$\frac{{\omega_{1} }}{{\omega_{b} }} \approx \sqrt {\frac{1}{2}\left\{ {\left[ {1 - \left( {\frac{{3VA^{2} }}{4K}} \right)} \right] + \sqrt {\left[ {1 - \left( {\frac{{3VA^{2} }}{4K}} \right)} \right]^{2} - \left( {\frac{{3V^{2} A^{4} }}{32K}} \right)} } \right\} - \frac{Q}{AK}} .$$
(42)

Primary resonance of damped Duffing system is given as

$$\left[ {1 - \left( {\frac{\Omega }{{\omega_{0} }}} \right)^{2} + \frac{3}{4}\frac{{\varepsilon kA^{2} }}{{\omega_{0}^{2} }}} \right]^{2} + \left( {2\varsigma \frac{\Omega }{{\omega_{0} }}} \right)^{2} = \left( {\frac{Q}{{A\omega_{0}^{2} }}} \right)^{2} ,$$
(43)

where the frequency ratio is represented by \(\frac{\Omega }{{\omega_{0} }}\), where \(\varsigma\) is the damping coefficient, \(\Omega\) is excited frequency \(k\), \(\varepsilon\) and \(Q\) are constants, \(A\) is the amplitude of vibration, and \(\omega_{0}\) is the natural frequency of the underlying linear system.

3.4 Modified Differential Transform Method Procedure

The small domain limitation of semi-analytical method has been overcome by the introduction of after treatment method in power series method. Laplace–Padè approximant has proven to be very reliable approach that also increases the convergence rate of the iteration. The Padè is a form of converting the analytical solution obtained through DTM method to polynomial rational form. The basic procedure are as follows:

  1. 1.
    $${\text{Apply}}\;{\text{Laplace}}\;{\text{transform}}\;{\text{to}}\;{\text{the}}\;{\text{series}}\;{\text{solution}}\;{\text{and}}\;{\text{setting}}\;s = \frac{1}{t}.$$
    (44)
  2. 2.

    Apply Padè approximation to the solution from previous step to obtain the following approximation in the following rational form:

    $$\left[ \frac{L}{M} \right] = \frac{{P_{0} + P_{1} t + P_{2} t^{2} + \cdots P_{L} t^{L} }}{{q_{0} + q_{1} t + q_{2} t^{2} + \cdots q_{M} t^{M} }}\quad {\text{and}}\,{\text{setting}}\,t = \frac{1}{s}.$$
    (45)
  3. 3.
    $${\text{Apply}}\;{\text{inverse}}\;{\text{Laplace}}\;{\text{transform}}\;{\text{on}}\;\left[ \frac{L}{M} \right]\;{\text{approximant}}{.}$$
    (46)

3.5 Application of Differential Transformation Method to the Duffing Equation

Applying DTM to the Duffing oscillation Eq. (17), along with the initial condition Eq. (8), we get

$$\varphi \left[ {k + 2} \right] = \frac{{\left\{ { - K\varphi \left[ k \right] - V\sum\nolimits_{l = 0}^{k} {\sum\nolimits_{p = 0}^{l} {\varphi \left[ {l - p} \right]\varphi \left[ p \right]\varphi \left[ {k - l} \right] + G(k + 1)\varphi \left[ {k + 1} \right] + Q\frac{{\omega^{k} }}{k!}\sin \left( {\frac{\pi k}{2}} \right)} } } \right\}}}{M(k + 1)(k + 2)}.$$
(47)

Initial condition are

$$\varphi \left[ 0 \right] = A:\,\,\,\,\,\,\,\,\varphi \left[ 1 \right] = 0,$$
(48)

3.5.1 The Solution Procedure

For \(k\) from 0, 1, 2, 3, 4, 5, 6, 7, we have the following:

$$\varphi \left[ 2 \right] = \frac{1}{2}\left( {\frac{{ - VA^{3} - KA + Q\omega }}{M}} \right),{\mkern 1mu}$$
(49)
$$\varphi \left[ 3 \right] = - \frac{{G\left( { - VA^{3} - KA + Q\omega } \right)}}{{6M^{2} }},$$
(50)
$$\varphi \left[ 4 \right] = \frac{1}{12}{\mkern 1mu} \frac{1}{M}\left( \begin{gathered} - \frac{1}{2}{\mkern 1mu} \frac{{K\left( { - VA^{3} - KA + Q\omega } \right)}}{M} - \frac{{3{\mkern 1mu} }}{2}\frac{{VA^{2} \left( { - VA^{3} - KA + Q\omega } \right)}}{M} \hfill \\ + \frac{1}{2}\frac{{G^{2} \left( { - VA^{3} - KA + Q\omega } \right)}}{{M^{2} }} - \frac{1}{2}Q\omega \hfill \\ \end{gathered} \right),$$
(51)
$$\varphi \left[ 5 \right] = \frac{1}{20}{\mkern 1mu} \frac{1}{M}\left( \begin{gathered} - \frac{{KG\left( { - VA^{3} - KA + Q\omega } \right)}}{{6M^{2} }} - \frac{1}{2}{\mkern 1mu} \frac{{VA^{2} G\left( { - VA^{3} - KA + Q\omega } \right)}}{{M^{2} }} - \hfill \\ \frac{1}{3}\frac{G}{M}\left( \begin{gathered} \frac{1}{2}\frac{{K\left( { - VA^{3} - KA + Q\omega } \right)}}{M} - \frac{3}{2}\frac{{VA^{2} \left( { - VA^{3} - KA + Q\omega } \right)}}{M} \hfill \\ + \frac{1}{2}\frac{{G^{2} \left( { - VA^{3} - KA + Q\omega } \right)}}{{M^{2} }} - \frac{1}{2}Q\omega \hfill \\ \end{gathered} \right){\mkern 1mu} \hfill \\ \end{gathered} \right).$$
(52)

Using the definition of DTM, solution of Eq. (18) is given as

$$\vartheta (t) = \sum\limits_{j = 0}^{n} {\varphi (j)t^{j} } ,$$
(53)

Substituting the values obtained for \(K,M,V\) from Eqs. (18)–(20) into Eq. (53), we have

$$\begin{aligned} \varphi (t) & = \frac{1}{10} + \frac{{94277{\mkern 1mu} t^{2} }}{47251} - \frac{{59081{\mkern 1mu} t^{3} }}{29611} - \frac{{840837{\mkern 1mu} t^{4} }}{3959} + \frac{{335612{\mkern 1mu} t^{5} }}{1329} + \frac{{4365731{\mkern 1mu} t^{6} }}{499} - \frac{{1613849{\mkern 1mu} t^{7} }}{143} - \frac{{6125021{\mkern 1mu} t^{8} }}{32} \\ & \quad + \frac{{10655874{\mkern 1mu} t^{9} }}{41} + \frac{{28318184{\mkern 1mu} t^{10} }}{11} - \frac{{40017257{\mkern 1mu} t^{11} }}{11} - \frac{{138629879{\mkern 1mu} t^{12} }}{6}. \\ \end{aligned}$$
(54)

The accuracy of the DTM is improved using the principle of Modified differential transform method (MDTM). Apply Laplace transform to the series solution Eq. (54) as

$$\begin{aligned} L\left[ {w(t)} \right] & = \frac{1}{10s} + \frac{188554}{{47251{\mkern 1mu} s^{3} }} - \frac{352810}{{29471{\mkern 1mu} s^{4} }} - \frac{871633}{{171{\mkern 1mu} s^{5} }} + \frac{6151624}{{203{\mkern 1mu} s^{6} }} + \frac{44094758}{{7{\mkern 1mu} s^{7} }} - \frac{56879713}{{s^{8} }} \\ & \quad - \frac{{7.71 \times 10^{7} {\mkern 1mu} }}{{s^{9} }} + \frac{{9.43 \times 10^{8} }}{{s^{10} }}{\mkern 1mu} + \frac{{9.34 \times 10^{10} }}{{s^{11} }} - \frac{{1.45 \times 10^{12} }}{{s^{12} }} - \frac{{1.10 \times 10^{14} }}{{s^{13} }}. \\ \end{aligned}$$
(55)

Also, replacing \(s = \frac{1}{t}\) and calculating Padè approximant of \(\left[ \frac{5}{6} \right]\) and letting \(t = \frac{1}{s}\) gives the following,

$$\left[ \frac{5}{6} \right]\, = \frac{{\frac{s}{10} + \frac{5935}{{6624{\mkern 1mu} s^{2} }} + \frac{698288}{{1179{\mkern 1mu} s^{3} }} + \frac{1423780}{{661{\mkern 1mu} s^{4} }} + \frac{17909531}{{30{\mkern 1mu} s^{5} }}}}{{1 + \frac{29675}{{3312{\mkern 1mu} s}} + \frac{2253116}{{383{\mkern 1mu} s^{2} }} + \frac{4494714}{{211{\mkern 1mu} s^{3} }} + \frac{40509958}{{7{\mkern 1mu} s^{4} }} + \frac{2560431}{{325{\mkern 1mu} s^{5} }} + \frac{34624657}{{6{\mkern 1mu} s^{6} }}}}.$$
(56)

Applying the inverse Laplace transform to the Padè approximant of Eq. (56), the MDTM solution is

$$\begin{aligned} \varphi (t) & = \left( {\frac{4}{219654619} + \frac{i}{355614789}} \right){\text{e}}^{{\left( { - \frac{61199}{{20529}} - \frac{{525887{\kern 1pt} i}}{7753}} \right)t}} + \left( {\frac{4}{219654619} - \frac{i}{355614789}} \right){\text{e}}^{{\left( { - \frac{61199}{{20529}} + \frac{{525887{\kern 1pt} i}}{7753}} \right)t}} \\ & \quad - \left( {\frac{1063}{{651429}} + \frac{{389{\mkern 1mu} i}}{5352618}} \right){\text{e}}^{{\left( { - \frac{36757}{{24505}} - \frac{{215193{\kern 1pt} i}}{6082}} \right)t}} - \left( {\frac{1063}{{651429}} - \frac{{389{\mkern 1mu} i}}{5352618}} \right){\text{e}}^{{\left( { - \frac{36757}{{24505}} + \frac{{215193{\kern 1pt} i}}{6082}} \right)t}} \\ & \quad + \left( {\frac{8559}{{165770}} + \frac{{183{\mkern 1mu} i}}{2866424}} \right){\text{e}}^{{\left( {\frac{3433}{{2964589}} - \frac{{44888{\kern 1pt} i}}{44929}} \right)t}} + \left( {\frac{8559}{{165770}} - \frac{{183{\mkern 1mu} i}}{2866424}} \right){\text{e}}^{{\left( {\frac{3433}{{2964589}} + \frac{{44888{\kern 1pt} i}}{44929}} \right)t}} . \\ \end{aligned}$$
(57)

4 Results and Discussion

The problem titled forced vibration analysis of isotropic circular plate resting on viscoelastic foundation is analysed and presented here. The accuracy and reliability of the presented analytical solution are established and validated with results presented in the cited literature Haterbouch and Benamar (2003). The validations are displayed in Table 3 and confirmed in good harmony with maximum 5% difference. Two cases were considered, when the number of nodal diameter \(m = 0\) (symmetric case, even number) and while \(m = 1\) (axisymmetric case, odd numbers). The physical properties of the material used for the analysis are as follows:

Young's modulus = 210.0 GPa, Poisson's ratio = 0.3, and mass density = 7850 kg/m3 and plate thickness of 3 mm. The amplitude of vibration considered is \(Q_{o} = 0.1\).

4.1 Convergence Criteria

The convergence criteria are illustrated along with the computational time in Table 2. It is shown that the iteration converges at n = 4; therefore, extending the iterations beyond n = 4 only further increases the computational time without substantial difference in the solution (Table 3).

Table 2 Convergence criteria based on the number of iteration (n) in the solutions of circular plate deflection
Full size table
Table 3 Frequency ratio for an isotropic circular plate for different values of non-dimensional vibration amplitudes
Full size table

4.2 Effect of Foundation Parameters

The variation of the amplitude with nonlinear frequency ratio is shown in Figs. 4, 5, 6 and 7. The frequencies are obtained taking into consideration the physical geometry properties of the plate and also taking into consideration non-dimensional analysis. Invariably, the results are effective for any thickness-to-radius ratios. It is shown in Fig. 4 that increase in the value of the nonlinear Winkler foundation parameter results in a reduction in the frequency ratio. This is a case of softening nonlinearity properties.

Fig. 4
figure 4

Influence of nonlinear foundation stiffness variation on amplitude of vibration for symmetric case

Full size image
Fig. 5
figure 5

Influence of Pasternak foundation variation on amplitude of vibration for symmetric case

Full size image
Fig. 6
figure 6

Influence of Winkler foundation parameter variation on amplitude of vibration for symmetric case

Full size image
Fig. 7
figure 7

Influence of combine foundation stiffness variation on amplitude of vibration for symmetric case

Full size image

In Figs. 5, 6 and 7, the nonlinear frequency against the amplitude curve of the isotropic circular plate is shown for linear foundation parameter variation. From the results, it is observed that nonlinear frequency of the circular plate increases with the increase in elastic linear foundation parameters. The Pasternak parameter has a pronounced effect on the nonlinear frequency amplitude curve of the circular plate. The values of nonlinear frequency has a direct relationship with the Winkler and Pasternak values. The parameters can be used to control the nonlinearity of structures. Same scenario is observed for symmetric and axisymmetric cases likewise under the two boundary conditions considered.

4.3 Effect of Radial Force

Figures 8 and 9 show the influence of outer edge radial force consequent on nonlinear frequency ratio. Figure 8 illustrates the results obtained for tensile force, while Fig 9 depicts that of compressive force. It is observed clearly from the figures that nonlinear frequency ratio increases for tensile force with an increase in the value of N, while the contrary is observed for compressive force. The effect of a compressive force is more pronounced than that of a tensile force. This is attributed to the fact that variation of radial force N may affect the stiffness of the isotropic circular plate.

Fig. 8
figure 8

Influence of tensile force variation on amplitude of vibration for symmetric case

Full size image
Fig. 9
figure 9

Influence of compressive force variation on amplitude of vibration for symmetric case

Full size image

4.4 Effect of Viscoelastic Foundation

The influence of the viscoelastic foundation is presented in Figs. 10 and 11. As the viscoelastic parameter increases, the deflection on the plate decreases. The excitation of the vibration decays with time due to the presence of damper. Attenuation of the deflection of the circular plate is observed meaning that damages in the system can be reduced with the presence of viscoelastic foundation.

Fig. 10
figure 10

Influence of viscoelastic foundation on vibration of the circular plate for symmetric case

Full size image
Fig. 11
figure 11

Influence of viscoelastic foundation on vibration of the circular plate for axisymmetric case

Full size image

Figure 12 shows the comparison of linear with nonlinear vibration of the isotropic circular plate, and it is observed that the difference is more significant with an increase in value of maximum vibration of the structure, while Fig. 13 shows the relationship between results obtained with DTM and MDTM. The advantage of MDTM is illustrated by extending the domain of the results.

Fig. 12
figure 12

Comparison of midpoint deflection time history for the linear and nonlinear analysis

Full size image
Fig. 13
figure 13

Midpoint deflection time history for the nonlinear analysis of isotropic circular plate

Full size image

4.5 Effect of Symmetric and Antisymmetric Cases

To illustrate the study of symmetric and axisymmetric case considered. Results obtained from the analysis are shown graphically in Fig. 14. From the result, axisymmetric case is shown to possess better results than the symmetric case. The frequency ratio is lower for axisymmetric case compared to symmetric case due to higher stiffness possessed by axisymmetric case. This shows that spatial property of the circular plate has an impact on vibration of the circular plate.

Fig. 14
figure 14

Influence of asymmetric and symmetric parameter m on the nonlinear amplitude–frequency response curves of the isotropic circular plate

Full size image

4.6 Primary Resonance Response

Figure 15 shows the primary resonance response of the isotropic circular plate. From the results, it is observed that vibration amplitude is lower than the thickness of the plate meaning that the result is reliable. It is also inferred from the figure that the nonlinear frequency is a function of amplitude. Increasing the forcing term increases function amplitude of vibration.

Fig. 15
figure 15

Influence of varying vibration amplitude on the nonlinear amplitude–frequency response curves of the isotropic circular plate

Full size image

4.7 Effect of Boundary Condition

Figures 16 and 17 depict the effect of boundary conditions on the nonlinear amplitude frequency response curve of the isotropic circular plate. From the results, case of softening nonlinearity is observed.

Fig. 16
figure 16

Influence of simply supported boundary conditions on the nonlinear amplitude–frequency response curves of the isotropic circular plate

Full size image
Fig. 17
figure 17

Influence of clamped edge boundary conditions on the nonlinear amplitude–frequency response curves of the isotropic circular plate

Full size image

5 Conclusions

In this study, the forced vibration analysis of isotropic circular plate resting on nonlinear viscoelastic foundation is investigated. The governing coupled partial differential equation is transformed into nonlinear ordinary differential equation using Galerkin decomposition method. The ODE is solved analytically using DTM with Padè Laplace approximant technique. Symmetric and axisymmetric cases are considered. The results obtained are verified with results published in the cited literature, and good harmony is observed. The developed analytical solutions are used to investigate the effect of elastic foundations, radial force, damper and varying amplitude on the dynamic behaviour of the isotropic circular plate. Based on the parametric studies, the following were observed.

  1. 1.

    Nonlinear Winkler foundation parameter results in reduction in the frequency ratio, while nonlinear frequency ratio increases with increase linear elastic foundation. Pasternak parameter has a pronounced effect on the nonlinear frequency

  2. 2.

    Nonlinear frequency ratio increases for tensile force, whereas contrariwise is observed for compressive force. The effect of compressive force is more pronounced than that of tensile force.

  3. 3.

    The deflection of the circular plate decreases as the viscoelastic foundation parameters increases.

  4. 4.

    For primary resonance obtained, vibration amplitude is lower than the thickness of the plate and maximum amplitude occurs at \(Q = 0\).

  5. 5.

    Axisymmetric case of vibration gives lower frequency ratio compared to symmetric case.

  6. 6.

    Same softening nonlinearity is observed for both simply supported and clamped edge condition.

The present study reveals major elements controlling the nonlinearity of vibrating thin circular plate under external force. Also, the versality of DTM with Padè-approximant technique has been demonstrated. It is hoped that the present study will improve understanding in theory of vibration of circular plate.