1 Introduction

Plate is an important part of structural system in civil, mechanical, naval, marine and aeronautic engineering. However, with wide application of plate in engineering, investigating the dynamic behavior of plate is very important. Many engineering problems like railway, structural foundations and storage tank foundation require information on dynamic behavior of plate embedded on foundation before proceeding on the design. The easiest form of modelling mechanical behavior of soil foundation interaction is by Winkler foundation. Winkler foundation suffers the setback of non-interaction between the lateral spring thereby resulting into unreliable results. Two-parameter elastic foundations are developed to account for this interaction. Adoption of two-parameter elastic foundations provides a true account of soil foundation interaction. Incorporating two-parameter foundations results in circular plates exhibiting huge flexural vibrations of the ‘same order with the plate thickness’ [1]. Thereby, resulting into a wrong prediction of dynamic behaviour of plate by the linear model. To mitigate this, recourse is hereby made to the von Kármán equations which comprise of geometrical non-linearities in the local vibration equations also, taking into consideration the stretching of the plate mid-plane. In the study of vibration of plate resting on elastic foundations, Dumir [2] obtained an analytical solution for the large deflection responses of isotropic thin circular plates place on nonlinear Winkler foundations. Based on the findings of the study, buckling with the linear natural frequency increased with the foundation parameters and the edge support rotational stiffness. Also, Wang [3] in an effort to obtain the exact axisymmetric post-buckling equilibrium, adopted the power series method in analysing the nonlinear differential equations of thin circular plates. Eihab et al. [4] incorporated the von Kármán thin plate theory to justify for large static deformations of axisymmetric annular plates. The natural frequencies and mode shapes were obtained numerically considering series of uniform loads. In another work, Civalek and Ersoy [5] investigated large deflection of circular plate on elastic foundation using numerical method. In another study, Gupta et al. [6] analysed the vibration and buckling of circular plate embedded on Winkler foundation. On application of semi-analytical method, Ghannadi et al. [7] used indirect Trefftz method to analyze free vibration of circular plate.

Earlier studies show that, inherent singularity issue and non-trivial solution of circular plate are not easy to handle. Numerical method is a reliable method of solution for handling governing equation of related challenges but, the convergence studies, volume of iterations and stability studies associated with numerical increase the computation time and cost. Meanwhile, exact method of solution suffers from setback of handling nonlinear problem coupled with sound knowledge of mathematics that is required. Therefore, in an attempt to obtain symbolic solution for dynamic behavior of circular plate resting on Winkler and Pasternak foundations, Yasser et al. [8] investigated the deflection of circular plate under load using Homotopy perturbation method (HPM). In a later study, Yin-shan et al. [9] also, used HPM to analyze the deflection of large circular plate. In a related study, Yalcin et al. [10] adopted differential transform method (DTM) for free vibration of circular plate. Also, Zur and Jankowski [11] investigated free vibration of porous functional graded material using exact method. DTM is equally a very versatile method, good in handling singularity and non-trivial differential system of equation but, requires the need to manipulate the governing equation before the singularity problem is resolved and subsequently, involve transforming the governing equation to algebraic form. The volumes of iterations in DTM are very cumbersome compared to Galerkin of weighted residual. Meanwhile, HPM also suffers the setback of finding the embedded parameter and initial approximation of the governing equation that satisfies the given conditions. Nonetheless, several research on free vibration of circular plate using different methods have been presented in literature [12,13,14,15]. Moreover, the reliability and flexibility of Galerkin weighted residual [16,17,18,19] has made it more effective than any other semi-numerical methods. The method is much simpler than any other approximating method of solutions. Galerkin of weighted residual handles circular plate vibration problem without any manipulation of governing equation with very precise results compared to experimental with few iterations. Other recent publications reported on vibration are [20,21,22,23,24,25].

Previous studies show that, dynamic analysis of circular plate on Winkler and Pasternak foundation has not been investigated using Galerkin of weighted residual. Therefore, the present study focuses on application of Galerkin of weighted residual for dynamic analysis of circular plate resting on Winkler and Pasternak foundations. Part of the novelties of the present study also include, resolving the singularities problem associated with circular plate without modifying the governing equation. The analytical solutions obtained are used for the parametric study.

2 Problem formulation and mathematical analysis

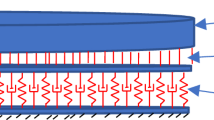
Circular plate of uniform thickness and homogenous material resting on Winkler and Pasternak foundation in Fig. 1 is considered under various boundary conditions simply supported, free and clamped edge conditions. The following assumptions are considered in the model of governing equation based on von Kármán’s deflection theory [1, 26].

  1. 1.

    Normal to the middle plane before bending remain straight and normal to the middle plane after bending.

  2. 2.

    Slopes produced by flexure are moderately large, but small in comparison with unity.

  3. 3.

    Normal stresses are small compared with other stress components and may be neglected in the stress–strain relations.

  4. 4.

    Loads and deflections of the plates are symmetrical with respect to the z-axis.

  5. 5.

    Assuming there is Perfect bonding between the foundation and the plate.

Fig. 1
figure 1

Circular plate resting on two-parameter foundations

Full size image

The von Kármán model for geometrically nonlinear vibrations of thin plates for analysing the solutions for the transverse displacement \(w(r,t)\) and the Airy stress function \(F(r,t)\) [1, 27].

$$\nabla^{4} F = - \frac{E}{r}\frac{\partial w}{\partial r}\frac{{\partial^{2} w}}{{\partial r^{2} }},$$
(1)
$$L^{\prime } (w,F) = D\nabla^{4} w + \rho h\frac{{\partial^{2} w}}{{\partial t^{2} }} - \frac{h}{r}\frac{\partial }{\partial r}\left( {\frac{\partial F}{\partial r}\frac{\partial w}{\partial r}} \right) + k_{w} w - k_{p} w^{3} - g_{s} \nabla^{2} w = 0,$$
(2)

For the linear analysis, the differential governing equation of circular plate as shown in Fig. 1 may be written as [28, 29]

$$D\nabla^{4} w(r,\theta ,t) + \rho h\frac{{\partial^{2} w(r,\theta ,t)}}{{\partial t^{2} }} + k_{w} w(r,\theta ,t) - g_{s} \nabla^{2} w(r,\theta ,t) = 0$$
(3)

For free vibration equation, the solution be presented in this form based on Kantorovich-type approximation

$$w(r,\theta ,t) = \tilde{w}(r,\theta )e^{i\omega t}$$
(4)

Assumed deflection of the plate:

$$w = f(r)\cos (m\theta )$$
(5)

Presenting the solution in a more general form, the following dimensionless parameters are used \(r = \frac{{\bar{r}}}{b},\quad f = \frac{{\bar{f}}}{h},\quad \varOmega^{2} = \frac{{\rho hb^{4} }}{D}\omega^{2} ,\quad k_{w} = \frac{{\bar{k}_{w} b^{4} }}{D},\quad g_{s} = \frac{{\bar{g}_{s} b^{2} }}{D}\),

Applying Eqs. (4) and (5) on Eq. (3), we have

$$\frac{{d^{4} f}}{{dr^{4} }} + \frac{2}{r}\frac{{d^{3} f}}{{dr^{3} }} - \frac{B}{{r^{2} }}\frac{{d^{2} f}}{{dr^{2} }} + \frac{B}{{r^{3} }}\frac{df}{dr} + \frac{A}{{r^{4} }}f + k_{w} f - g_{s} \left( {\frac{{d^{2} f}}{{dr^{2} }} - \frac{1}{r}\frac{df}{dr}} \right) = \varOmega^{2} f,$$
(6)

where, \(f\) is the deflection,\(r\) is the radius, \(k_{w}\) is the Winkler parameter, \(g_{s}\) is the Pasternak parameters, \(k_{p}\) is the nonlinear Winkler parameter, \(\varOmega^{2}\) is natural frequency \(A = m^{4} - 4m^{2}\) and \(B = 2m^{2} + 1\) respectively.

2.1 Boundary conditions

The boundary conditions considered as earlier stated are simply support, clamped and free edge conditions. The dimensionless form of the boundary conditions may be presented in terms of the deflection \(f(r)\) as follows [10]

  • Clamped

    $$\left. {f\left( r \right)} \right|_{r = 1} = 0,\quad \left. {\frac{df}{dr}} \right|_{r = 1} { = 0,}$$
    (7)

  • Simply supported

    $$\left. {f\left( r \right)} \right|_{r = 1} = 0,\quad \left. {M_{r} } \right|_{r = 1} = - \,D\left[ {\frac{{d^{2} f}}{{dr^{2} }} + \nu \left( {\frac{1}{r}\frac{df}{dr} + \frac{{m^{2} }}{{r^{2} }}f} \right)} \right] = 0,$$
    (8)

  • Free edge

    $$\left. {M_{r} } \right|_{{_{r = 1} }} = - \,D\left[ {\frac{{d^{2} f}}{{dr^{2} }} + \nu \left( {\frac{1}{r}\frac{df}{dr} + \frac{{m^{2} }}{{r^{2} }}f} \right)} \right] = 0,\quad \left. {V_{r} } \right|_{r = 1} = \left[ {\frac{{d^{3} f}}{{dr^{3} }} + \frac{1}{r}\frac{{d^{2} f}}{{dr^{2} }} + \left( {\frac{{m^{2} \nu - 2m^{2} - 1}}{{r^{2} }}} \right)\frac{df}{dr} + \left( {\frac{{3m^{2} - m^{2} \nu }}{{r^{3} }}} \right)f} \right] = 0,$$
    (9)

Bending moment is represented as \(M_{r}\) the radial shear force per unit length is represented as \(V_{r}\) while \(m\) is an integer. As generally accepted, a nth-order differential equation requires n-number of boundary condition. Since the dimensionless Eq. (6) is a fourth-order governing equation then, four boundary conditions are expected for resolving the equation. Two of the conditions may be obtained from the external condition of the plate while the rest two are obtained from the condition at the center of the plate. The regularity conditions at the center are given as,

2.1.1 Symmetric case

$$\left. {\frac{df}{dr}} \right|_{r = 0} { = 0, }\quad \left. {{\text{V}}_{r} } \right|_{r = 0} = \frac{{d^{3} f}}{{dr^{3} }}{ = 0,}\quad for\left( {m = 0,2,4, \ldots } \right),$$
(10)

2.1.2 Axisymmetric case

$$\left. {f\left( r \right)} \right|_{r = 0} = 0,\quad \left. {M_{r} } \right|_{r = 0} = \left. {\frac{{d^{2} f}}{{dr^{2} }}} \right|_{r = 0} = 0\quad for\;\left( {m = 1,3,5, \ldots } \right).$$
(11)

3 Linear analysis: principle of Galerkin weighted residual

Galerkin method was first proposed by Walther Ritz but was credited to Soviet Engineer called Boris Galerkin [16]. The method is used for handling differential equations. The approximate solutions of the differential equations are presumed to be thoroughly approximated by a finite sum of test functions. However, the chosen method of weighted residual is used to obtain the coefficients value of each resulting test function \(\varphi_{i}\). The corresponding coefficients are made to reduce the error between the linear combination of test functions, and actual solution, in a chosen standard. The technique is a reliable estimated solution capable of solving series of problems that eliminate the search for vibrational formulation. Assuming the governing equation to be

$$L\left( T \right) = 0\;in\;\varOmega ,$$
(12)
$$T \approx \bar{T} \approx \sum\limits_{i = 1}^{n} {a_{i} N_{i} \left( r \right)} ,$$
(13)

Putting Eqs. (12) into (13) gives

$$L\left( {\bar{T}} \right) \ne 0 = R\;\left( {Residual} \right),$$
(14)

The concept requires the determination of \(a_{1} ,a_{2} , \ldots ,a_{n}\) that satisfy,

$$\int\limits_{\varOmega } {w_{i} \left( r \right)} Rdr = 0\quad where\;i = 1,2, \ldots ,n$$
(15)

where the function \(w_{i} \left( r \right)\;and\;n\) are arbitrary weighting function which are found through either, Galerkin of weighted residual, collocation, sub-domain, or least square method. For the purpose of this study Galerkin approach is adopted.where \(w_{i} \left( r \right) = N_{i} \left( r \right)\), meaning it is the same trial function as used in \(T\left( r \right)\)

$$\int\limits_{\varOmega } {N_{i} \left( r \right)} Rdr = 0\quad where\;i = 1,2, \ldots ,n,$$
(16)

The weight or shape function is \(N_{i} \left( r \right)\), \(R\) is the residual and \(i\) represent the node in the domain.

3.1 Application of Galerkin of weighted residual to the governing equation

For the sake of brevity, symmetric case regularity condition and simply supported edge condition is presented here while the same approach is used to determine the other conditions treated in this study. The choice of the polynomial solution is based on the highest order of the derivative of the governing equation. This is a fourth-order derivative equation so; the chosen polynomial is of the order five.

Assume a polynomial solution for order four differential equation

$$F\left( r \right) = a + br + \frac{{cr^{2} }}{2!}{\mkern 1mu} + \frac{{dr^{3} }}{3!} + \frac{{{\mkern 1mu} er^{4} }}{4!} + \frac{{gr^{5} }}{5!},$$
(17)

Applying the boundary conditions at \(r = 0\), symmetric case in Eq. (17)

  • Simply Supported edge

    $$f^{\prime } \left( 0 \right) = b = 0,$$
    (18)
    $$f^{\prime \prime \prime } \left( 0 \right) = d = 0,$$
    (19)
    $$f\left( 1 \right) = a + \frac{c}{2} + \frac{e}{24} + \frac{f}{120} = 0,$$
    (20)
    $$- \,D\left[ {f^{\prime \prime } \left( 1 \right) + \nu \left( {\frac{1}{r}f^{\prime } \left( 1 \right) + \frac{{m^{2} }}{{r^{2} }}f\left( 1 \right)} \right)} \right] \Rightarrow - \,\frac{{221793{\mkern 1mu} c}}{1000} - \frac{{187671{\mkern 1mu} e}}{2000} - \frac{{244541{\mkern 1mu} f}}{8000} = 0,$$
    (21)

where values of flexural rigidity \(D\) and Poisson’s \(\nu\) ratio given in Table 1. Symmetric case \(m = 0\). Solving the simultaneous equation [Eqs. (20) and (21)] to find the unknowns and substitute back to Eq. (17).

$$F \Rightarrow R\left( r \right) = a + \frac{1}{2}{\mkern 1mu} cr^{2} + \frac{1}{24}{\mkern 1mu} \left( { - \frac{{5160{\mkern 1mu} a}}{83} - \frac{{2268{\mkern 1mu} c}}{83}} \right)r^{4} + \left( {\frac{{6360{\mkern 1mu} c}}{83} + \frac{{15840{\mkern 1mu} a}}{83}} \right)\frac{{r^{5} }}{120},$$
(22)

Chain function \(N_{i} \left( r \right)\) in Eq. (22) are \(a\) and \(c\), As reported in Eqs. (7–9) the boundary condition range is \(0 \Rightarrow 1\),invariably the integral limit for this Galerkin method is 0–1.

$$Galerkin\;equation\;\int\limits_{0}^{1} {N_{i} \left( r \right)} \times R\left( r \right)dr = 0,$$
(23)
Table 1 Validation of fundamental natural frequency for symmetric condition
Full size table

  • Chain function

    $$N_{1} = \frac{dR\left( r \right)}{da} \Rightarrow 1 - \frac{{215{\mkern 1mu} r^{4} }}{83} + \frac{{132{\mkern 1mu} r^{5} }}{83},$$
    (24)
    $$N_{2} = \frac{dR\left( r \right)}{dc} \Rightarrow \frac{1}{2}r^{2} - \frac{{189{\mkern 1mu} r^{4} }}{166} + \frac{{53{\mkern 1mu} r^{5} }}{83},$$
    (25)

Applying Eq. (20) and obtain simultaneous equation based on the chain function;

$$\int\limits_{0}^{1} {\left( {1 - \frac{{215{\mkern 1mu} r^{4} }}{83} + \frac{{132{\mkern 1mu} r^{5} }}{83}} \right)} \left( \begin{aligned} \frac{{d^{4} R(r)}}{{dr^{4} }} + \frac{2}{r}\frac{{d^{3} R(r)}}{{dr^{3} }} - \frac{B}{{r^{2} }}\frac{{d^{2} R(r)}}{{dr^{2} }} + \frac{B}{{r^{3} }}\frac{dR(r)}{dr} + \frac{A}{{r^{4} }}dR(r) + k_{w} R\left( r \right) - g_{s} \left( {\frac{{d^{2} R(r)}}{{dr^{2} }} - \frac{1}{r}\frac{dR(r)}{dr}} \right) - \varOmega^{2} R\left( r \right) \end{aligned} \right)dr = 0,$$
(26)
$$\int\limits_{0}^{1} {\left( {\frac{1}{2}r^{2} - \frac{{189{\mkern 1mu} r^{4} }}{166} + \frac{{53{\mkern 1mu} r^{5} }}{83}} \right)} \left( \begin{aligned} \frac{{d^{4} R(r)}}{{dr^{4} }} + \frac{2}{r}\frac{{d^{3} R(r)}}{{dr^{3} }} - \frac{B}{{r^{2} }}\frac{{d^{2} R(r)}}{{dr^{2} }} + \frac{B}{{r^{3} }}\frac{dR(r)}{dr} + \frac{A}{{r^{4} }}dR(r)+ k_{w} R\left( r \right) - g_{s} \left( {\frac{{d^{2} R(r)}}{{dr^{2} }} - \frac{1}{r}\frac{dR(r)}{dr}} \right) - \varOmega^{2} R\left( r \right) \end{aligned} \right)dr = 0,$$
(27)

Validating the analytical solutions require setting the controlling parameters as zero. The resulting simultaneous equation obtained may be written in this form

$$\begin{aligned} \psi_{11}^{\left( n \right)} \left( \varOmega \right)f_{0} + \psi_{12}^{\left( n \right)} \left( \varOmega \right)f_{2} = 0 \hfill \\ \psi_{21}^{\left( n \right)} \left( \varOmega \right)f_{0} + \psi_{22}^{\left( n \right)} \left( \varOmega \right)f_{2} = 0 \hfill \\ \end{aligned}$$
(28)

The polynomials \(\psi_{11} ,\psi_{12} ,\psi_{21} \;and\;\psi_{22}\) are represented in terms of the natural frequency \(\varOmega\). Meanwhile \(\psi_{11} ,\psi_{12} ,\psi_{21} \;and\;\psi_{22}\) are representing a series expression obtained after resolving Eqs. (26) and (27). Therefore, Eq. (28) may be written in matrix form as

$$\left[ {\begin{array}{*{20}c} {\psi_{11}^{\left( n \right)} \left( \varOmega \right)} & {\psi_{12}^{\left( n \right)} \left( \varOmega \right)} \\ {\psi_{21}^{\left( n \right)} \left( \varOmega \right)} & {\psi_{22}^{\left( n \right)} \left( \varOmega \right)} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {f_{0} } \\ {f_{2} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \right\},$$
(29)

The following Characteristic determinant is obtained applying the non-trivial condition

$$\left[ {\begin{array}{*{20}c} {\psi_{11}^{\left( n \right)} \left( \varOmega \right)} & {\psi_{12}^{\left( n \right)} \left( \varOmega \right)} \\ {\psi_{21}^{\left( n \right)} \left( \varOmega \right)} & {\psi_{22}^{\left( n \right)} \left( \varOmega \right)} \\ \end{array} } \right] = 0,$$
(30)

Solving Eq. (30), one gets the Eigen value

$$- \frac{{14923{\mkern 1mu} \varOmega^{2} }}{46030} - \frac{28704}{3259} + \frac{{\sqrt {\left( {4.17 \times 10^{19} {\mkern 1mu} \varOmega^{4} + 2.52 \times 10^{21} {\mkern 1mu} \varOmega^{2} + 2.52 \times 10^{22} } \right)} }}{{2.00 \times 10^{8} }},$$
(31)

Solving the quadratic Eq. (31) gives the natural frequency;

$$\varOmega = 4. 9 5 7 1 7 5 8 5 4 , { - }\, 4. 9 5 7 1 7 5 8 5 4 ,$$
(32)

Substitute the positive root obtained in Eq. (32) into Eq. (29) gives,

$$\left[ {\begin{array}{*{20}c} { - \frac{137865}{4058}} & { - \frac{111560}{8717}} \\ {\frac{35062}{31091}} & {\frac{22757}{53569}} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} a \\ c \\ \end{array} } \right\}_{(1)} = \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \right\},$$
(33)

Putting \(c = 1\) in Eq. (33), then \(a\) is calculated as,

$$\left\{ {\begin{array}{*{20}c} a \\ c \\ \end{array} } \right\}_{(1)} = \left\{ {\begin{array}{*{20}c} { - \,2.654608759} \\ 1 \\ \end{array} } \right\},$$
(34)

Same procedure from (33) is repeated for second mode. Therefore, the deflection solution of the governing Eq. (6) gives

$$f\left( r \right) = 1 - \frac{{25785{\mkern 1mu} r^{2} }}{20356} + \frac{{32609{\mkern 1mu} r^{4} }}{93147} - \frac{{9721{\mkern 1mu} r^{5} }}{116589}.$$
(35)

3.2 Nonlinear analysis: von Kármán model for thin plates

The classical Kirchhoff theory for linear plate bending is accurate only for small deflection problems \((w \le 0.2h)\) ignoring the middle surface strains and the corresponding in-plane stresses. As the external force increases, the lateral deflection may be relatively large \((w \ge 0.3h)\).

Dimensionless form of Eqs. (1) and (2) according to [1, 17] are

$$k_{p} = \frac{{\bar{k}_{p} a^{4} }}{D},\quad w = \frac{{\bar{w}}}{h},\quad F = \frac{{\bar{F}}}{{Eh^{2} }},\quad r = \frac{{\bar{r}}}{b},$$
(36)
$$\frac{1}{{12(1 - \nu^{2} )}}\left( {\frac{{\partial^{2} w}}{{\partial t^{2} }} + \nabla^{4} w} \right) + k_{w} w - k_{p} w^{3} - g_{s} \nabla^{2} w - \frac{1}{r}\frac{\partial }{\partial r}\left( {\frac{\partial F}{\partial r}\frac{\partial w}{\partial r}} \right) = 0,$$
(37)
$$\nabla^{4} F = \frac{1}{r}\frac{\partial w}{\partial r}\frac{{\partial^{2} w}}{{\partial r^{2} }}.$$
(38)

3.2.1 Boundary condition

Simply supported and Clamped case are considered for the isotropic circular plate.

  • Simply supported

    $$w = \frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{\nu }{r}\frac{\partial w}{\partial r} = 0,$$
    (39)

  • Clamped edge support

    $$w = \frac{\partial w}{\partial r} = 0$$
    (40)

For the Airy stress conditions, stress free edge and constrained immovable conditions are considered.

$$Eu_{r} = r(\sigma_{\theta } - \nu \sigma_{r} )$$
(41)

The following are considered at \(r = R\):

$$\frac{\partial F}{\partial r} = 0,$$
(42)
$$\frac{{\partial^{2} F}}{{\partial r^{2} }} - \frac{\nu }{r}\frac{\partial F}{\partial r} = 0,$$
(43)

Approximate solution of the plate deflection \(w(r,t)\) is expressed as

$$w(r,t) = \psi (t)\left( {1 + c_{1} r^{2} + c_{2} r^{4} } \right),$$
(44)

where \(\psi (t)\) represents the maximum deflection at the center of the circular plate, a function of time \(t\) alone, while \(c_{1} {\text{ and }}c_{2}\) in each case are defined by the boundary conditions Eqs. (42) and (43) and given as:

  • Edges are free from stresses

    $$c_{1} = - \frac{6 + 2\nu }{5 + \nu },\,\,\,c_{2} = \frac{1 + \nu }{5 + \nu },$$
    (45)

  • Constrained immovable

    $$c_{1} = - 2,\,\,\,\,c_{2} = 1,$$
    (46)

Assuming, \(F = f \times \psi^{2} (t)\), then substitute Eq. (44) into Airy stress function Eq. (38), integrating the resulting equation making use of the boundary condition Eqs. (42) and (43), we have

$$F = - \varphi^{2} (t)\left[ {c_{3} r^{2} + \frac{1}{16}c_{1}^{2} r^{4} + \frac{1}{18}c_{1} c_{2} r^{6} + \frac{1}{48}c_{2}^{2} r^{8} } \right],$$
(47)

where \(c_{3}\) is a constant obtained by substituting Eq. (47) into Eqs. (42) and (43). One obtains

  1. 1.
    $$c_{3} = -\, \frac{1}{24}\left( {3c_{1}^{2} + 4c_{1} c_{2} + 2c_{2}^{2} } \right),$$
    (48)
  2. 2.
    $$c_{3} = -\, \frac{1}{24(1 - \nu )}\left[ {3(3 - \nu )c_{1}^{2} + 4(5 - \nu )c_{1} c_{2} + 2(7 - \nu )c_{2}^{2} } \right],$$
    (49)
    $$\int\limits_{0}^{R} {L^{\prime}} (w,F)w\,\,r\,\,dr = 0$$
    (50)

The Substitution of the expressions for \(w\) and \(F\) given by Eqs. (44) and (47) respectively into Eq. (37) and the application of the Galerkin procedure Eq. (50) in the nonlinear time differential equation obtained in the form.

We have

$$M\ddot{u}_{s} (t) + Ku_{s} (t) - Vu_{s}^{3} (t) = 0,$$
(51)

where

$$M = \frac{737}{625571},$$
(52)
$$K = \frac{{800{\mkern 1mu} g_{s} }}{8427} + \frac{{5137{\mkern 1mu} k_{w} }}{399297} + \frac{9449}{80711},$$
(53)
$$V = -\, \frac{{1151{\mkern 1mu} k_{p} }}{351586} - \frac{1683}{179389}.$$
(54)

3.3 Determination of non-natural frequencies

To determine the nonlinear natural frequency of the circular plate, the dynamic response is analysis is carried out following the assumption that [30]

$$\tau = e^{iwt} ,$$
(55)

Applying Eq. (55) on Eq. (51), we have

$$M\omega^{2} \ddot{u}(\tau ) + Ku(t) - Vu_{s}^{3} (t) = 0,$$
(56)

In order to find the periodic solution of Eq. (56), assume an initial approximation for zero-order deformation as

$$u_{0} (\tau ) = A\cos \tau ,$$
(57)

Substitute Eq. (57) into Eq. (56), we have;

$$- \,M\omega_{0}^{2} A\cos \tau + KA\cos \tau - VA^{3} \cos^{3} \tau = 0,$$
(58)

Which gives

$$-\, M\omega_{0}^{2} A\cos \tau + KA\cos \tau - VA^{3} \left( {\frac{3\cos \tau + \cos 3\tau }{4}} \right) = 0,$$
(59)

Collect like term

$$\left( {KA - M\omega_{0}^{2} A - \frac{{3VA^{3} }}{4}} \right)\cos \tau - \frac{1}{4}VA^{3} \cos 3\tau = 0,$$
(60)

Eliminate secular term, we have

$$\left( {KA - M\omega_{0}^{2} A - \frac{{3VA^{3} }}{4}} \right) = 0,$$
(61)

Thus, zero-order nonlinear natural frequency becomes

$$\omega_{0} \approx \sqrt {\frac{K}{M} - \frac{{3VA^{2} }}{4M}} ,$$
(62)

Therefore, ratio of zero-order nonlinear natural frequency, \(\omega_{0}\) to the linear frequency \(\omega_{b}\)

$$\frac{{\omega_{0} }}{{\omega_{b} }} = \sqrt {1 - \frac{{3VA^{2} }}{4K},}$$
(63)

Following the same procedural approach, the first-order nonlinear natural frequency is

$$\omega_{1} \approx \sqrt {\frac{1}{2}\left\{ {\left[ {\left( {\frac{K}{M}} \right) - \left( {\frac{{3VA^{2} }}{4M}} \right)} \right] + \sqrt {\left[ {\left( {\frac{K}{M}} \right) - \left( {\frac{{3VA^{2} }}{4M}} \right)} \right]^{2} - \left( {\frac{{3V^{2} A^{4} }}{{32M^{2} }}} \right)} } \right\}} ,$$
(64)

The ratio of the first-order nonlinear frequency,\(\omega_{1}\) to the linear frequency \(\omega_{b}\) gives,

$$\frac{{\omega_{1} }}{{\omega_{b} }} \approx \sqrt {\frac{1}{2}\left\{ {\left[ {1 - \left( {\frac{{3VA^{2} }}{4K}} \right)} \right] + \sqrt {\left[ {1 - \left( {\frac{{3VA^{2} }}{4K}} \right)} \right]^{2} - \left( {\frac{{3V^{2} A^{4} }}{32K}} \right)} } \right\}} .$$
(65)

4 Results and discussion

The analytical solution of governing equation of motion of the circular plate under various boundary conditions with Galerkin method of weighted residual is hereby presented. The material properties for the thin uniform thickness, homogenous circular plate used are \(E = 207\,{\text{GPa}}\) material density \(\rho = 7850\,{\text{kg/m}}^{3}\) thickness of the plate \(h = 0.03\,{\text{m}}\) and Poisson’s ratio \(\nu = 0.3\) respectively.

To validate the analytical solution of free vibration of circular plate resting on Winkler and Pasternak foundations using Galerkin method of weighted residual, application is made to the numeric data stated above given by [31]. Galerkin method of weighted residual determined the natural frequency in dimensionless form. However, the accuracy of the analytical solutions obtained are compared with results as reported in literature [28] and confirm in good agreement along the entire values under different boundary conditions and presented in Tables 1 and 2. Since dimensionless value of the natural frequency \(\varOmega\) is obtained in the analysis, the results are valid for all thickness to radius ratio. Also the parametric studies of the controlling factors are presented in both tabular and graphical form.

Table 2 Validation of fundamental natural frequency for axisymmetric condition
Full size table

The iteration of the Galerkin method of weighted residual is a determinant of order of the assumed polynomial chosen. In this study, fifth order polynomial is chosen for fourth order governing differential equation. The analytical solutions obtained though are limited to first two natural frequencies but, its good enough to predict the behaviour of the plate and the results are observed similar to results reported in literature [28]. Moreso, when the same analytical solutions are compared to results reported in literature [10] which are obtained using another semi-analytical method DTM, for the fundamental natural frequency DTM requires ten iterations while for fifth order assumed polynomial chosen here, first two natural frequencies already obtained and converged. It is also observed that, to obtain higher node of natural frequencies there is need to increase the order of the assumed polynomial choosen at the beginning of the analysis. Results shown in Tables 1 and 2 illustrate the fundamental natural frequencies obtained which give a reasonable prediction of the circular plate behaviour with minimal iterations.

Tables 1 and 2 also show comparison of results for symmetric and axisymmetric case of the present study with reported work in literature review. There is good agreement between the present study and the results reported [28], Hence, it can be concluded that the present procedure is very effective. Maximum Percentage variation of 0.4%.

4.1 Effect of foundation parameter on natural frequency

To further investigate the effect of elastic foundation on free vibration of circular plate, the natural frequencies \(\varOmega\) of the solutions obtained are plotted against the foundation parameters variation. The results are obtained by setting m = 1 and m = 0 respectively as shown in Figs. 2, 3 and 4. Tables 3, 4 and 5 present the dimensionless symmetric natural frequency \(\varOmega = \omega a^{2} \sqrt {\rho h/D}\) for different values of the elastic foundation parameters. The numeric value of natural frequencies obtained are given as \(\varOmega_{1}\) and \(\varOmega_{2}\) in the tables. In this study, Consideration is given to

  • Elastic Winkler type foundation (\(g_{s} = 0,\;k_{w} = 0,30,120,200\))

  • Shear elastic Pasternak type foundation (\(k_{w} = 0,\;g_{s} = 10,50,100\))

Fig. 2
figure 2

Influence of Winkler foundation variations on simply supported edge condition symmetric case

Full size image
Fig. 3
figure 3

Influence of Pasternak foundation variation on clamped edge condition symmetric case

Full size image
Fig. 4
figure 4

Influence of Winkler and Pasternak foundation variation on free edge condition symmetric case

Full size image
Table 3 Variation of elastic foundation on natural frequency symmetric case m = 0
Full size table
Table 4 Shear Pasternak variation effect on natural frequency
Full size table
Table 5 Winkler and Pasternak variation effect on natural frequency symmetric case
Full size table

Figures 2, 3 and 4 show that as the elastic foundation parameter (shear stiffness) of the elastic medium increase, the natural frequency of vibration of the uniform thickness, homogenous circular plate increase. As a result of increased value of the elastic medium stiffness, the shear stiffness make the uniform circular plate stronger/stiffer and vibrate at higher natural frequency. Although, it a known character of plate to be affected by characteristic of elastic foundation, Moreover, it is also observed that, effect of the difference in natural frequencies are more significant for higher mode of the circular plate. By comparing the results in Tables 3 and 4 with Tables 1 and 2, one observed that, analytical solutions obtained with Galerkin method of weighted residual increase with increasing the elastic foundation parameters. Furthermore, the effect of foundation is lesser in lower modes. Same effect are observed under Pasternak foundation and when the plate is resting on combined Winkler and Pasternak foundations.

4.2 Mode shapes

The mode shape for the dimensionless natural frequencies are shown in Figs. 5, 6, 7, 8, 9 and 10 respectively. It is important to note that, the mode shape obey the classical theory of vibration.

Fig. 5
figure 5

Mode shape for simply supported edge condition symmetric case

Full size image
Fig. 6
figure 6

Mode shape for simply supported edge condition asymmetric case

Full size image
Fig. 7
figure 7

Mode shape for clamped edge condition symmetric case

Full size image
Fig. 8
figure 8

Mode shape for clamped edge condition asymmetric case

Full size image
Fig. 9
figure 9

Mode shape for free edge condition symmetric case

Full size image
Fig. 10
figure 10

Mode shape for free edge condition asymmetric case

Full size image

4.3 Nonlinear natural frequency

To further investigate the influence of nonlinear foundation. The model is converted into Duffing equation using Galerkin method. The ratio of linear to nonlinear natural frequency on the amplitude is obtained. The frequency ratio is obtained taking into consideration the constant parameter of linear Winkler and shear Pasternak foundation while the nonlinear foundation stiffness is varied from (\(k_{p} = 2,10,20\)). However, the effect of nonlinear foundation is studied. Figures 11, 12 and 13 illustrate the relationship between ratio of natural frequency to the amplitude. It is observed that, nonlinear frequency is a function of amplitude. The more the amplitude the more the significance in variation between the nonlinear to linear natural frequency.

Fig. 11
figure 11

Influence of nonlinear Winkler foundation on nonlinear natural frequency

Full size image
Fig. 12
figure 12

Influence of shear Pasternak foundation on nonlinear natural frequency

Full size image
Fig. 13
figure 13

Influence of shear Pasternak and nonlinear Winkler foundation on nonlinear natural frequency

Full size image

Figure 11 shows the influence of nonlinear foundation on the nonlinear frequency ratio-amplitude response curves of circular plate. It is observed that, as the nonlinear foundation increases, the nonlinear vibration frequency ratio decreases. This is a case of softening nonlinearity. Figure 12 illustrates the influence of shear Pasternak foundation on nonlinear amplitude-frequency response curve. It is observed that, as shear Pasternak foundation increases, the nonlinear vibration foundation ratio increases. This is a case of softening nonlinearity. Figure 13 reveals that Winkler and Pasternak foundations have significant effect on nonlinearity of the circular plates therefore, the paramount is important in controlling the nonlinearity of circular plates. The increase of nonlinear Winkler foundation only attenuates the amplitude of vibration while increase elastic linear foundations increases the amplitude of vibration (Table 6).

Table 6 Results of different deflection values
Full size table

5 Conclusion

In this study, free vibration of circular plate resting on Winkler and Pasternak foundations using Galerkin of weighted residual method is investigated. From the parametric studies, it was established that

  1. 1.

    The natural frequency of circular plate increases with increase in elastic Winkler foundation Parameter.

  2. 2.

    The natural frequency of circular plate increases with increase in elastic Pasternak foundation Parameter.

  3. 3.

    As the nonlinear foundation increases, the nonlinear vibration frequency ratio decreases.

The present study emphasis the effect of elastic foundation and fluid on dynamic behaviour of thin circular plate. Also, singularities issue of circular plate is handle with ease using Galerkin of weighted residual. It is expected that the present study will contribute to the understanding of the study of dynamic behaviour of circular plate under various parameters.