Extremal Trees with Respect to Bi-Wiener Index

Abstract

In this paper we introduce and study a new graph-theoretic invariant called the bi-Wiener index. The bi-Wiener index $W_b(G)$ of a bipartite graph G is defined as the sum of all (shortest-path) distances between two vertices from different parts of the bipartition of the vertex set of G. We start with providing a motivation connected with the potential uses of the new invariant in the QSAR/QSPR studies. Then we study its behavior for trees. We prove that, among all trees of order $n\ge 4$, the minimum value of $W_b$ is attained for the star $S_n$, and the maximum $W_b$ is attained at path $P_n$ for even n, or at path $P_n$ and $B_n(2)$ for odd n where $B_n(2)$ is a broom with maximum degree 3. We also determine the extremal values of the ratio $W_b(T_n)/W(T_n)$ over all trees of order n. At the end, we indicate some open problems and discuss some possible directions of further research.

1 Introduction

All graphs considered in this paper are finite, undirected, simple and connected. If $G=(V(G), E(G))$ is a graph, we will use $n(G) = |V(G)|$ for its order and $m(G) = |E(G)|$ for its size. The degree $d_G(v)$ of $v\in V(G)$ is the number of vertices in G adjacent to v. We denote by $N_{G}(v)$ the open neighborhood of vertex v in G. For two vertices $u,v\in V(G)$, we use $d_G(u,v)$ to denote the (shortest-path) distance between u and v in G. If the graph G is clear from the context, $d_G(v)$ and $d_G(u,v)$ will be simplified into d(v) and d(u, v), respectively. The eccentricity $\varepsilon _G(v)$ of a vertex $v\in V(G)$ is the maximum distance from v to any other vertex of G. The complement of G is denoted with $G^c$. A vertex $v\in V(G)$ with maximum eccentricity is a diametral vertex in G. Moreover, the vertex with the second maximum eccentricity is a semi-diametral vertex. For a connected graph G, its distance matrix D(G) is a square matrix whose rows and columns are indexed by the vertices of G and whose entry (i, j) is equal to the shortest-path distance between the vertices i and j. Clearly, the distance matrix of an undirected simple graph is symmetric and has zeros on its main diagonal. Once computed, the distance matrix encodes all information about distances, eccentricities, and all other distance-related concepts such as the diameter, the radius, the center, the periphery, etc. We refer the readers to [4] and also to [9] for more on distances in graphs.

We denote by $S_{n}$ and $P_n$ the star and the path on n vertices, respectively. Other undefined notations and terminologies on graph theory can be found in [3].

A graphical invariant is a function from the set of graphs to the reals which is invariant under graph isomorphisms. In the chemical literature, graphical invariants are also known as topological indices and as molecular descriptors. The oldest topological index in chemical graph theory is the Wiener index [16]. Despite being introduced in 1947 and studied ever since, it still generates a lot of interest [5,6,7, 10, 11, 13, 15, 17,18,19]. For a connected graph G, its Wiener index is defined as $W(G)=\sum \nolimits _{\{u,v\}\subseteq V(G)}d_G(u,v)$. It is the sum of all entries in the upper (or in the lower) triangle of D(G).

Let G be a bipartite graph with the bipartition $V(G) = A\cup B$. By considering only the distances between the vertices belonging to different classes of bipartition, one arrives at the following modification of the Wiener index:

$$\begin{aligned} W_b(G)=\sum \limits _{(u,v)\in A\times B}d_G(u,v). \end{aligned}$$

We call the new invariant the bi-Wiener index of G and denote it by $W_b(G)$. Clearly, the bi-Wiener index of a bipartite graph G cannot exceed its full Wiener index, an observation which we will formalize shortly.

Before presenting in more detail the properties of the new invariant, we make a short digression to provide some motivation. It is reasonable to expect that the bi-Wiener index, like the full Wiener index, but often easier to calculate, correlates well with various properties of molecules, including "boiling point, molar volume, refractive index, heat of isomerization, heat of vaporization, density, critical pressure, surface tension, viscosity, chromatographic retention time and sound velocity, $\cdots \cdots$" [12].

Although the Wiener index is closely correlated with the boiling points of linear and branched hydrocarbons, it does not work well for some cyclic molecules and their corresponding isomers. In Table 1 below, we compare the Wiener and the bi-Wiener indices for cyclohexane and methylcyclohexane with some of their corresponding substituted cyclobutyl counterparts. The Wiener index of cyclohexane is 27 and its bi-Wiener index is 15. Compared to the Wiener index of cyclohexane, only the isomeric 1,1-dimethylcyclobutane has a smaller Wiener index, while for 1,3-dimethylcyclobutane is larger. On the other hand, the bi-Wiener indices for both isomers (the 1,3-dimethylcyclobutane and 1,1-dimethylcyclobutane) are smaller than the bi-Wiener of cyclohexane. Thus bi-Wiener index appears to be a better indicator to predict the physical properties of the isomers, consistent with the lower boiling points and densities of the cyclobutyl isomers compared to that of cyclohexane.

Another example involves comparison of the Wiener and bi-Wiener indices of methylcyclohexane and its corresponding trisubstituted cyclobutyl counterparts. The Wiener index of methylcyclohexane is 42, while its bi-Wiener index is 22. Of all the three possible isomeric trisubstituted cyclobutyl counterparts, namely 1,1,2-trimethylcyclobutane, 1,2,3-trimethylcyclobutane, and the 1,1,3-trimethylcyclobutane, only the latter has been successfully synthesized (Table 1). While the Wiener index for this isomer is the same as that of methylcyclohexane, its bi-Wiener index is much smaller than that of methylcyclohexane. The smaller bi-Wiener index for 1,1,3-trimethylcyclobutane is consistent with its lower boiling point compared to that of methylcyclohexane. Moreover, the values of the densities also fall in the expected range as predicted by the lower bi-Wiener indices (Table 1).

The two examples illustrated in this article, namely the cyclohexane and methylcyclohexane and their corresponding cyclobutyl isomeric counterparts, show that the bi-Wiener index is a better predictor for physical properties compared to that of the Wiener index. To test the generality of our approach, we will investigate the di-and trisubstituted cyclohexanes in order to compare their Wiener and bi-Wiener indices with their isomeric substituted cylobutyl counterparts.

In general, for many of the cyclic molecules that are bipartite, the value of the bi-Wiener index conforms with the Wiener index in predicting the physical properties of the various isomers as noted above.

Table 1 Comparison of the Wiener and the bi-Wiener indices of Cyclohexane, Methylcyclohexane and some of their corresponding substituted cyclobutyl counterparts

In chemical graph theory, trees are frequently used as models for studying chemical and physical properties of acyclic molecules, in particular the alkanes [16]. A vertex of degree at least 3 is a branching vertex in a tree. A vertex adjacent to a leaf of a tree is a support vertex. Clearly, any diametral vertex in a tree T must be a leaf, and any semi-diametral vertex must be a support vertex to a diametral leaf. A tree T of order n with a unique branching vertex v with $T-v=P_{n_1}\cup P_{n_2}\cup \ldots \cup P_{n_k}$, with $n_1\le n_2\le \cdots \le n_k$ satisfying $\sum \nolimits _{i=1}^kn_i=n-1$, will be denoted by $T=T_n(n_1,n_2,\ldots ,n_k)$. (Such trees are known as starlike trees and also as spiders; see [1] for some recent applications in chemical context.) If $n_j$ appears $\ell _j\ge 2$ times in $T_n(n_1,n_2,\ldots ,n_k)$, then we write $n_j^{\ell _j}$ in it. For example, $T_{11}(1,2,2,2,3)$ will be denoted with $T_{11}(1,2^3,3)$. In particular, $T_n(1^k, n-k-1)$ with $k\ge 2$ is a broom and denoted by $B_n(k)$ in the following. Denote by $H(n-a-b,a,b)$ the bi-broom obtained by attaching a and b pendant vertices, respectively, to the two leaves of a path $P_{n-a-b}$, where $a\ge b\ge 2$. Moreover, for convenience, $P_n$ can be viewed as the special case of $B_n(k)$ with $k=1$ and $B_n(a)$ is the special case of $H(n-a-b,a,b)$ with $b\in \{0,1\}$. Throughout this paper, we use the notation $[k]=\{1,2,\ldots ,k\}$ for any positive integer k.

For any positive integer $n\le 3$, there is a unique tree of order n. Therefore, in what follows, we only consider the trees of order $n\ge 4$.

2 Preliminary Results

In this section, we prove some preliminary results. Most of them are concerned with trees, but we start with some valid for all bipartite graphs. The following results are direct consequences of the definition of bipartite graphs and hold at a glance.

Proposition 2.1

If G is a bipartite graph with a vertex bipartition $A\cup B$, then $d_G(u,v)$ is odd for any vertex $u\in A$ and any vertex $v\in B$.

Corollary 2.2

The bi-Wiener index of a graph G is the sum of all odd entries in the upper triangle of the distance matrix D(G) of G.

Corollary 2.3

For a bipartite graph G, $W_b(G) \le W(G)$ with equality if and only if $G \cong K_2$.

Proof

If a bipartite graph G has at least 3 vertices, then its diameter is at least 2, and there is at least a pair of vertices at distance 2 in G. Hence, at least one element of D(G) is even, and the difference $W(G) - W_b(G)$ is positive. $\square$

Corollary 2.4

Let G be a bipartite graph with the bipartition $V(G) = A\cup B$. Then $W_b(G)$ is odd if and only if both |A| and |B| are odd.

Proof

It has been known for a long time [2] that the Wiener index of a bipartite graph G is odd if and only if both classes of the bipartition of V(G) have odd cardinalities. The claim now follows from the fact that the difference $W(G) - W_b(G)$ is always an even number, being the sum of even entries in the upper triangle of D(G). $\square$

Corollary 2.5

Let G be a bipartite graph of odd order. Then $W_b(G)$ is even.

Since trees are bipartite, all of the above results are valid for trees. In the rest of this section, we restrict our attention to trees and study a number of transformations which affect their bi-Wiener numbers.

Denote by $\gamma (G,k)$ the number of vertex pairs with distance k in a graph G. For a bipartite graph G with vertex bipartition $A\cup B$ with $|A|=p\ge q=|B|$, we say that $A\cup B$ is a (p, q)-bipartition of G. Below we provide a new formula for computing the value of $W_b$.

Proposition 2.6

For a bipartite graph G with a vertex bipartition $A\cup B$ and $V_0\subseteq V(G)$, $V_1=V(G)\setminus V_0$, $W_{b_1}(G)=\sum \limits _{\begin{array}{c} u\in A\cap V_0 \\ v\in B\cap V_0 \end{array}}d_G(u,v)$, $W_{b_2}(G)=\sum \limits _{\begin{array}{c} u\in A\cap V_1\\ v\in B\cap V_1 \end{array}}d_G(u,v)$, $W_{b_3}(G)=\sum \limits _{\begin{array}{c} u\in A\cap V_0\\ v\in B\cap V_1 \end{array}}d_G(u,v)+\sum \limits _{\begin{array}{c} u\in B \cap V_0\\ v\in A\cap V_1 \end{array}}d_G(u,v)$. Then

$$\begin{aligned} W_b(G)=W_{b_1}(G)+W_{b_2}(G)+W_{b_3}(G). \end{aligned}$$

Let T be a tree of order n with a (p, q)-bipartition $A\cup B$. Let $P=u_1u_2\dots u_{t-1}u_t~(t\ge 4)$ be a diametral path of T. Let $u_i$ ($3\le i\le t-1$) be a branching vertex with $d_T(u_2,u_i)$ as small as possible. Let $D_1$ be the component of $T-\{u_{i-1}u_i,u_iu_{i+1}\}$ containing $u_i$, $v_m$ be a leaf of $D_1$ with a path $P'=u_i(=v_0)v_1\dots v_hv_{h+1}\dots v_m$ $(0\le h<m,m+1\le i)$ where $v_h$ is the closest branching vertex to $v_m$ in $D_1$. Let $D_2$ be the component of $T-\{u_{i-1}u_i\}$ containing $u_i$ and $W_1=D_2\setminus P'$. Without loss of generality, we assume that $u_1\in A$. Next we introduce five transformations.

Fig. 1

Graphs T and $T^{\prime }$ associated with Transformation I

Transformation I Let T be the aforementioned tree with a (p, q)-bipartition with $d(u_2)=2$, $d(u_2,u_i)$ and $d(u_i,v_m)$ having the same parity. Clearly, $d(u_i,v_m)+1\le d(u_1,u_i)$. We construct a new tree $T'=T-\{v_hv_{h+1}\}+\{v_mu_1\}$ and say that $T'$ is obtained from T by running Transformation I for path $P''=v_hv_{h+1}\dots v_m$. Since $u_1\in A$, we have $v_m\in B$ and $T'$ is also a tree with a (p, q)-bipartition (Fig. 1).

Lemma 2.7

Let $T,T'$ be trees in Transformation I. Then $W_b(T')> W_b(T)$.

Proof

Let $T,T'$ be trees in Transformation I and $V_0=\{v_{h+1},v_{h+2},\dots ,v_m\}$ with $W_2=V(T)-V_0-W_1$. Then $V_1=W_1\cup W_2$. Based on the structures of $T,T'$ and Proposition 2.6, it suffices to prove $W_{b_3}(T')> W_{b_3}(T)$.

For every $u\in V_0\cap A, v\in W_1\cap B$ (or $u\in V_0\cap B, v\in W_1\cap A$), we have $d_{T}(u,v)=d_{T}(u,v_j)+d_{T}(v_j,v)$, $d_{T'}(u,v)=d_{T'}(u,v_j)+d_{T'}(v_j,v)$, where $v_j\in V(P')$ ($0\le j\le h$) is the closest vertex from v to $P'$. Note that $d_{T}(u,v_j)<d_{T'}(u,v_j)$, $d_{T}(v_j,v)=d_{T'}(v_j,v)$. Then $d_{T'}(u,v)>d_{T}(u,v)$. It follows that

$$\begin{aligned}&\sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in W_1\cap B \end{array}}d_{T'}(u,v)+\sum \limits _{\begin{array}{c} u\in V_0\cap B\\ v\in W_1\cap A \end{array}}d_{T'}(u,v)>\sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in W_1\cap B \end{array}}d_{T}(u,v)+\sum \limits _{\begin{array}{c} u\in V_0\cap B\\ v\in W_1\cap A \end{array}}d_{T}(u,v), \\&\sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in W_2\cap B \end{array}}d_{T'}(u,v)+\sum \limits _{\begin{array}{c} u\in V_0\cap B\\ v\in W_2\cap A \end{array}}d_{T'}(u,v)=\sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in W_2\cap B \end{array}}d_{T}(u,v)+\sum \limits _{\begin{array}{c} u\in V_0\cap B\\ v\in W_2\cap A \end{array}}d_{T}(u,v). \end{aligned}$$

Therefore

$$\begin{aligned} W_{b_3}(T')&=\sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in W_1\cap B \end{array}}d_{T'}(u,v)+\sum \limits _{\begin{array}{c} u\in V_0\cap B\\ v\in W_1\cap A \end{array}}d_{T'}(u,v)+\sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in W_2\cap B \end{array}}d_{T'}(u,v)\\&\quad +\sum \limits _{\begin{array}{c} u\in V_0\cap B\\ v\in W_2\cap A \end{array}}d_{T'}(u,v)\\&>W_{b_3}(T). \end{aligned}$$

That is, we have $W_b(T')>W_b(T)$, finishing the proof. $\square$

Fig. 2

Graphs T and $T^{\prime }$ associated with Transformation II

Transformation II Let T be the aforementioned tree with a (p, q)-bipartition with $d(u_2)\ge 3$ such that $d(u_2,u_i)$ and $d(u_i,v_m)$ have the same parity, $d(v_m,v_h)$ is even. Clearly, $d(u_i,v_m)+1\le d(u_1,u_i)$. We construct a new tree $T'=T-\{v_hv_{h+1},u_2u_3\}+\{u_3v_m,u_2v_{h+1}\}$ and say that $T'$ is obtained from T by running Transformation II for path $P''=v_hv_{h+1}\dots v_m$. For $u_1\in A$, we have $v_m,v_h\in B$. Thus $T'$ is also a tree with a (p, q)-bipartition.

Lemma 2.8

Let $T,T'$ be trees in Transformation II. Then $W_b(T')> W_b(T)$.

Proof

Let $T,T'$ be trees in Transformation II with $d(u_2)=x+1$ where $x\ge 2$ and $N_T(u_2)\setminus \{u_3\}=\{u_1,z_1,\dots ,z_{x-1}\}$. Let $V_0=\{u_1,u_2,z_1,\dots ,z_{x-1},v_{h+1},\dots ,v_m\}$, $W_2=V(T)-V_0-W_1$. Then $V_1=W_1\cup W_2$. By the structures of $T,T'$ and Proposition 2.6, we have

$$\begin{aligned} W_{b_1}(T)&=\sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in V_0\cap B \end{array}}d_{T}(u,v)\\&=\sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in V_0\cap B \end{array}}d_{T'}(u,v)+\frac{d_{T}(v_m,v_h)}{2}d_{T}(u_2,v_h)+\frac{d_{T}(v_m,v_h)}{2}d_{T}(u_2,v_h)x\\&=W_{b_1}(T')+(x+1)d_{T}(u_2,v_h)\frac{d_{T}(v_m,v_h)}{2},\\ W_{b_2}(T)&=\sum \limits _{\begin{array}{c} u\in V_1\cap A\\ v\in V_1\cap B \end{array}}d_{T}(u,v)=W_{b_2}(T'). \end{aligned}$$

Similarly as the proof in Lemma 2.7, we have

$$\begin{aligned}&\sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in W_1\cap B \end{array}}d_{T'}(u,v)+\sum \limits _{\begin{array}{c} u\in V_0\cap B\\ v\in W_1\cap A \end{array}}d_{T'}(u,v)>\sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in W_1\cap B \end{array}}d_{T}(u,v)+\sum \limits _{\begin{array}{c} u\in V_0\cap B\\ v\in W_1\cap A \end{array}}d_{T}(u,v), \\&\sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in W_2\cap B \end{array}}d_{T'}(u,v)=\sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in W_2\cap B \end{array}}d_{T}(u,v)+2\frac{d_{T}(v_m,v_h)}{2}|W_2\cap B|+xd_{T}(v_m,v_h)|W_2\cap B|\\&\!\!\qquad \qquad \qquad \qquad \quad =\sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in W_2\cap B \end{array}}d_{T}(u,v)+(x+1)d_{T}(v_m,v_h)|W_2\cap B|,\\&\sum \limits _{\begin{array}{c} u\in V_0\cap B\\ v\in W_2\cap A \end{array}}d_{T'}(u,v)=\sum \limits _{\begin{array}{c} u\in V_0\cap B\\ v\in W_2\cap A \end{array}}d_{T}(u,v)-2\frac{d_{T}(v_m,v_h)}{2}|W_2\cap A|+d_{T}(v_m,v_h)|W_2\cap A|\\&\qquad \qquad \qquad \qquad \quad =\sum \limits _{\begin{array}{c} u\in V_0\cap B\\ v\in W_2\cap A \end{array}}d_{T}(u,v). \end{aligned}$$

Therefore, we have

$$\begin{aligned} W_{b_3}(T')>W_{b_3}(T)+(x+1)d_{T}(v_m,v_h)|W_2\cap B|. \end{aligned}$$

Since $|W_2\cap B|=\frac{d_{T}(u_2,v_h)}{2}$, we have

$$\begin{aligned} W_b(T')&>W_{b_1}(T)-(x+1)d_{T}(v_m,v_h)|W_2\cap B|+W_{b_2}(T)+W_{b_3}(T)\\&\quad +(x+1)d_{T}(v_m,v_h)|W_2\cap B|\\&=W_b(T). \end{aligned}$$

This completes the proof. $\square$

Fig. 3

Graphs T and $T^{\prime }$ associated with Transformation III

Transformation III Let T be the aforementioned tree with a (p, q)-bipartition and $d(u_2)\ge 3$ such that $d(u_2,u_i)$ and $d(u_i,v_m)$ have a same parity, $d(v_m,v_h)$ is odd. Clearly, $d(u_i,v_m)+1\le d(u_1,u_i)$. We construct a new tree $T'=T-\{v_hv_{h+1},u_2u_3\}+\{u_3v_m,u_1v_{h+1}\}$ and say that $T'$ is obtained from T by running Transformation III for path $P''=v_hv_{h+1}\dots v_m$. For $u_1\in A$, we have $v_m\in B$, $v_h\in A$. Thus $T'$ is also a tree with a (p, q)-bipartition (Fig. 3).

Lemma 2.9

Let $T,T'$ be trees in Transformation III. Then $W_b(T')> W_b(T)$.

Proof

Let $T,T'$ be trees in Transformation III with $d(u_2)=x+1$ where $x\ge 2$ and $N_T(u_2)\setminus \{u_3\}=\{u_1,z_1,\dots ,z_{x-1}\}$. Let $V_0=\{u_1,u_2,z_1,\dots ,z_{x-1},v_{h+1},\dots ,v_m\}$, $W_2=V(T)-V_0-W_1$. Then $V_1=W_1\cup W_2$. By the structures of $T, T'$ and Proposition 2.6, we have

$$\begin{aligned} W_{b_1}(T)&=\sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in V_0\cap B \end{array}}d_{T}(u,v)\\&=\sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in V_0\cap B \end{array}}d_{T'}(u,v)+\frac{d_{T}(v_m,v_h)-1}{2}d_{T}(u_3,v_{h})\\&\quad +\frac{d_{T}(v_m,v_h)+1}{2}d_{T}(u_3,v_{h})(x-1)+\frac{d_{T}(v_m,v_h)+1}{2}d_{T}(u_1,v_{h}),\\ W_{b_2}(T)&=\sum \limits _{\begin{array}{c} u\in V_1\cap A\\ v\in V_1\cap B \end{array}}d_{T}(u,v)=W_{b_2}(T'). \end{aligned}$$

Similarly as the proof in Lemma 2.7, we have

$$\begin{aligned} \sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in W_1\cap B \end{array}}d_{T'}(u,v)+\sum \limits _{\begin{array}{c} u\in V_0\cap B\\ v\in W_1\cap A \end{array}}d_{T'}(u,v)&>\sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in W_1\cap B \end{array}}d_{T}(u,v)+\sum \limits _{\begin{array}{c} u\in V_0\cap B\\ v\in W_1\cap A \end{array}}d_{T}(u,v), \\ \sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in W_2\cap B \end{array}}d_{T'}(u,v)&=\sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in W_2\cap B \end{array}}d_{T}(u,v)+(d_{T}(v_m,v_h)-1)|W_2\cap B|\\&+(x-1)(d_{T}(v_m,v_h)+1)|W_2\cap B|, \\ \sum \limits _{\begin{array}{c} u\in V_0\cap B\\ v\in W_2\cap A \end{array}}d_{T'}(u,v)&=\sum \limits _{\begin{array}{c} u\in V_0\cap B\\ v\in W_2\cap A \end{array}}d_{T}(u,v)+(d_{T}(v_m,v_h)+1)|W_2\cap A|,\\ |W_2\cap A|&=|W_2\cap B|+1. \end{aligned}$$

Then it follows that

$$\begin{aligned} W_{b_3}(T')&>W_{b_3}(T)+(d_{T}(v_m,v_h)-1)|W_2\cap B|+x(d_{T}(v_m,v_h)+1)|W_2\cap B|\\&\quad +d_{T}(v_m,v_h)+1. \end{aligned}$$

Since $|W_2\cap B|=\frac{d_{T}(u_3,v_{h})}{2}$, we have

$$\begin{aligned} W_b(T')&>W_{b_1}(T)-(d_{T}(v_m,v_h)-1)|W_2\cap B|-\Big [d_{T}(v_m,v_h)+1\Big ]\\&\quad -\Big [d_{T}(v_m,v_h)+1\Big ]|W_2\cap B|-(x-1)\Big [d_{T}(v_m,v_h)+1\Big ]|W_2\cap B|\\&\quad +W_{b_2}(T)+W_{b_3}(T)+(d_{T}(v_m,v_h)-1)|W_2\cap B|\\&\quad +x\Big [d_{T}(v_m,v_h)+1\Big ]|W_2\cap B|+d_{T}(v_m,v_h)+1\\&=W_b(T). \end{aligned}$$

This completes the proof. $\square$

Fig. 4

Graphs T and $T^{\prime }$ associated with Transformation IV

Transformation IV Let T be the tree defined above with a (p, q)-bipartition with $d(u_2)\ge 2$ such that $d(u_2,u_i)$ and $d(u_i,v_m)$ have different parity, $d(v_m,v_h)$ is even. Clearly, $d(u_i,v_m)\le d(u_1,u_i)$. We construct a new tree $T'=T-\{u_2u_3,v_hv_{h+1}\}+\{u_2v_m,v_{h+1}u_3\}$ and say that $T'$ is obtained from T by running Transformation IV for path $P''=v_hv_{h+1}\dots v_m$. Since $u_1\in A$, we have $v_m,v_h\in A$. Then $T'$ is also a tree with a (p, q)-bipartition (Fig. 4).

Lemma 2.10

Let $T,T'$ be trees in Transformation IV. Then $W_b(T')>W_b(T)$.

Proof

Let $T,T'$ be trees in Transformation IV with $d(u_2)=x+1$ where $x\ge 1$. If $x=1$, we have $N_T(u_2)\setminus \{u_3\}=\{u_1\}$ and assume that $V_0=\{u_1,u_2,v_{h+1},\dots ,v_m\}$. For $x\ge 2$, we have $N_T(u_2)\setminus \{u_3\}=\{u_1,z_1,\dots ,z_{x-1}\}$ and assume that $V_0=\{u_1,u_2,z_1,\dots ,z_{x-1},v_{h+1},\dots ,v_m\}$. Let $W_2=V(T)-V_0-W_1$. Then $V_1=W_1\cup W_2$. By the structures of $T,T'$ and Proposition 2.6, we have

$$\begin{aligned} W_{b_1}(T)&=\sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in V_0\cap B \end{array}}d_{T}(u,v)\\&=\sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in V_0\cap B \end{array}}d_{T'}(u,v)+\frac{d_{T}(v_m,v_h)}{2}\Big [d_{T}(u_2,v_{h+1})+d_{T}(u_3,v_{h})x\Big ],\\ W_{b_2}(T)&=\sum \limits _{\begin{array}{c} u\in V_1\cap A\\ v\in V_1\cap B \end{array}}d_{T}(u,v)=W_{b_2}(T'). \end{aligned}$$

Similarly as the proof in Lemma 2.7, we have

$$\begin{aligned} \sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in W_1\cap B \end{array}}d_{T'}(u,v)+\sum \limits _{\begin{array}{c} u\in V_0\cap B\\ v\in W_1\cap A \end{array}}d_{T'}(u,v)&>\sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in W_1\cap B \end{array}}d_{T}(u,v)+\sum \limits _{\begin{array}{c} u\in V_0\cap B\\ v\in W_1\cap A \end{array}}d_{T}(u,v), \\ \sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in W_2\cap B \end{array}}d_{T'}(u,v)&=\sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in W_2\cap B \end{array}}d_{T}(u,v)+xd_{T}(v_m,v_h)|W_2\cap B|,\\ \sum \limits _{\begin{array}{c} u\in V_0\cap B\\ v\in W_2\cap A \end{array}}d_{T'}(u,v)&=\sum \limits _{\begin{array}{c} u\in V_0\cap B\\ v\in W_2\cap A \end{array}}d_{T}(u,v)+d_{T}(v_m,v_h)|W_2\cap A|. \end{aligned}$$

Therefore

$$\begin{aligned} W_{b_3}(T')>W_{b_3}(T)+xd_{T}(v_m,v_h)|W_2\cap B|+d_{T}(v_m,v_h)|W_2\cap A|.\\ \end{aligned}$$

Note that $|W_2\cap A|=\frac{d_{T}(u_2,v_{h+1})}{2}$, $|W_2\cap B|=\frac{d_{T}(u_3,v_{h})}{2}$. We have

$$\begin{aligned} W_b(T')&>W_{b_1}(T)-d_{T}(v_m,v_h)|W_2\cap A|-xd_{T}(v_m,v_h)|W_2\cap B|+W_{b_2}(T)\\&\quad +W_{b_3}(T)+xd_{T}(v_m,v_h)|W_2\cap B|+d_{T}(v_m,v_h)|W_2\cap A|=W_b(T). \end{aligned}$$

This finishes the proof. $\square$

Fig. 5

Graphs T and $T^{\prime }$ associated with Transformation V

Transformation V Let T be the tree defined above with a (p, q)-bipartition with $d(u_2)\ge 2$ such that $d(u_2,u_i)$ and $d(u_i,v_m)$ have different parity, $d(v_m,v_h)$ is odd. Clearly, $d(u_i,v_m)\le d(u_1,u_i)$. We construct a new tree $T'=T-\{u_2u_3,v_hv_{h+1},v_mv_{m-1}\}+\{u_2v_m,v_{h+1}u_2,v_{m-1}u_3\}$ for $m>h+1$ and $T'=T-\{v_hv_{h+1}\}+\{v_{h+1}u_{2}\}$ for $m=h+1$ and say that $T'$ is obtained from T by running Transformation V for path $P''=v_hv_{h+1}\dots v_m$. Since $u_1\in A$, we have $v_m\in A$, $v_h\in B$. Then $T'$ is also a tree with a (p, q)-bipartition (Fig. 5).

Lemma 2.11

Let $T,T'$ be the trees in Transformation V. Then $W_b(T')\ge W_b(T)$ with equality if and only if T is a bi-broom with even diameter.

Proof

Let $T,T'$ be trees in Transformation V with $d(u_2)=x+1$ where $x\ge 1$. If $x=1$, we have $N_T(u_2)\setminus \{u_3\}=\{u_1\}$ and assume that $V_0=\{u_1,u_2,v_{h+1},\dots ,v_m\}$. For $x\ge 2$, we have $N_T(u_2)\setminus \{u_3\}=\{u_1,z_1,\dots ,z_{x-1}\}$ and assume that $V_0=\{u_1,u_2,z_1,\dots ,z_{x-1},v_{h+1},\dots ,v_m\}$. Let $W_2=V(T)-V_0-W_1$. Thus $V_1=W_1\cup W_2$. By the structures of $T,T'$ and Proposition 2.6, we have

$$\begin{aligned} W_{b_1}(T)&=\sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in V_0\cap B \end{array}}d_{T}(u,v)\\&=\sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in V_0\cap B \end{array}}d_{T'}(u,v)+\frac{d_{T}(v_m,v_h)+1}{2}d_{T}(u_2,v_{h})\\&\quad +\frac{d_{T}(v_m,v_h)-1}{2}d_{T}(u_2,v_{h+2})x-x(d_{T}(v_m,v_h)-1)\\&=\sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in V_0\cap B \end{array}}d_{T'}(u,v)+\frac{d_{T}(v_m,v_h)+1}{2}d_{T}(u_2,v_{h})\\&\quad +\frac{d_{T}(v_m,v_h)-1}{2}d_{T}(u_2,v_{h})x,\\ W_{b_2}(T)&=\sum \limits _{\begin{array}{c} u\in V_1\cap A\\ v\in V_1\cap B \end{array}}d_{T}(u,v)=W_{b_2}(T'). \end{aligned}$$

Similarly as the proof in Lemma 2.7, we have

$$\begin{aligned}&\sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in W_1\cap B \end{array}}d_{T'}(u,v)+\sum \limits _{\begin{array}{c} u\in V_0\cap B\\ v\in W_1\cap A \end{array}}d_{T'}(u,v)\ge \sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in W_1\cap B \end{array}}d_{T}(u,v)+\sum \limits _{\begin{array}{c} u\in V_0\cap B\\ v\in W_1\cap A \end{array}}d_{T}(u,v), \\&\sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in W_2\cap B \end{array}}d_{T'}(u,v)=\sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in W_2\cap B \end{array}}d_{T}(u,v)+2\frac{d_{T}(v_m,v_h)+1}{2}|W_2\cap B|\\&\qquad \qquad \qquad \qquad \quad +x(d_{T}(v_m,v_h)-1)|W_2\cap B|,\\&\sum \limits _{\begin{array}{c} u\in V_0\cap B\\ v\in W_2\cap A \end{array}}d_{T'}(u,v)=\sum \limits _{\begin{array}{c} u\in V_0\cap B\\ v\in W_2\cap A \end{array}}d_{T}(u,v). \end{aligned}$$

Therefore

$$\begin{aligned} W_{b_3}(T')\ge W_{b_3}(T)+(d_{T}(v_m,v_h)+1)|W_2\cap B|+x(d_{T}(v_m,v_h)-1)|W_2\cap B|. \end{aligned}$$

Since $|W_2\cap B|=\frac{d_{T}(u_2,v_{h})}{2}$, we have

$$\begin{aligned} W_b(T')&\ge W_{b_1}(T)-(d_{T}(v_m,v_h)+1)|W_2\cap B|-x(d_{T}(v_m,v_h)-1)|W_2\cap B|\\&\quad +W_{b_2}(T)+W_{b_3}(T)+(d_{T}(v_m,v_h)+1)|W_2\cap B|\\&\quad +x(d_{T}(v_m,v_h)-1)|W_2\cap B|\\&=W_b(T) \end{aligned}$$

with equality holding if and only if $d(u_2,u_i)$ is even and $d(u_i,v_m)=1$, $i=t-1$, that is, T is a bi-broom of order n with a (p, q)-bipartition with even diameter, completing the proof. $\square$

3 Main Result

In this section we focus on the determination of extremal trees with respect to bi-Wiener index among all trees of order $n\ge 4$. Let $\mathcal {T}_n$ be the set of all trees of order $n=p+q\ge 4$ with a (p, q)-bipartition with $d(u_2)=2$ where $P=u_1u_2\dots u_t$ is a diametral path. We first give a characterization of minimum trees with respect to $W_b$.

Theorem 3.1

Let T be a tree of order $n\ge 4$. Then $W_b(T)\ge n-1$ with equality if and only if $T\cong S_n$.

Proof

Assume that $A\cup B$ is an (a, b)-bipartition of T with $|A|=a\le b=n-a=|B|$. By Proposition 2.1, we have $\gamma (T,1)+\gamma (T,3)+\ldots +\gamma (T,k)=a(n-a)$ where k is the maximum odd distance between two vertices from A and B, respectively. Note that $\gamma (T,1)=n-1$. From the definition of bi-Wiener index, we have

$$\begin{aligned} W_b(T)= & {} \gamma (T,1)+3\gamma (T,3)+\ldots +k\gamma (T,k)\\\ge & {} n-1+3[a(n-a)-(n-1)]\\\ge & {} n-1. \end{aligned}$$

The above equalities holds simultaneously if and only if $a=1$, that is, $T\cong S_n$. This completes the proof. $\square$

Next we turn to determine the maximum trees with respect to $W_b$.

Lemma 3.2

Let $G\in \mathcal {T}_n$ with maximum bi-Wiener index. Then G must be a broom.

Proof

Let $G\in \mathcal {T}_n$ with a (p, q)-bipartition and maximum bi-Wiener index. If $q=1$, then $G\cong S_n$. Therefore, suppose in the following that $p\ge q\ge 2$. Let $P=u_1u_2\dots u_{t-1}u_t$ be a diametral path of G, clearly $t\ge 4$. Using $d(u_2)=2$, to prove that G is a broom, it suffices to show $d(u_i)=2$ $(3\le i\le t-2)$. Assuming that there exists $d(u_j)\ge 3$ where $3\le j\le t-2$, let $u_i$ ($3\le i\le t-2$) be such a vertex such that $d(u_2,u_i)$ is as small as possible and $D_1$ be the component of $G-\{u_{i-1}u_i, u_iu_{i+1}\}$ containing $u_i$. Then, let m be a leaf in $D_1$ with $h\in V(D_1)$ being a closest branching vertex to it.

Suppose that $d(u_2,u_i)$ and $d(u_i,m)$ are all even (or odd), then $G_1$ can be obtained from G by running Transformation I. By Lemma 2.7, we have $W_b(G_1)>W_b(G)$, a contradiction.

Suppose that $d(u_2,u_i)$ is odd (even) and $d(u_i,m)$ is even (odd), d(m, h) is even. Then by running Transformation IV for G, we can obtain $G_2$, and by Lemma 2.10, we have $W_b(G_2)>W_b(G)$, a contradiction.

Suppose that $d(u_2,u_i)$ is odd (even) and $d(u_i,m)$ is even (odd), d(m, h) is odd, then $G_3$ can be obtained from G by running Transformation V. By Lemma 2.11, we have $W_b(G_3)>W_b(G)$, a contradiction.

This completes the proof of the lemma. $\square$

Lemma 3.3

Let $T^*$ be a tree of order $n\ge 4$ with maximum bi-Wiener index. Then $T^*$ must be a bi-broom with even diameter or a broom.

Proof

Let T be a tree of order n with a (p, q)-bipartition $A\cup B$. If $q=1$, then $T\cong S_n$. Therefore suppose in the following that $p\ge q\ge 2$ and k is the number of branching vertices in T. Now we prove the result by induction on k.

For $k=0$, the result holds trivially since $T\cong P_n$ with $P_n=B_n(1)$ from the assumption.

If $k=1$, then T is a starlike tree. Let u be the branching vertex of T with $\{u\}=\bigcap \limits _{i=1}^{\ell }P_{n_i}$ where $2\le n_1\le n_2\le \dots \le n_\ell$ and there exist x odd paths and $\ell -x$ even paths. If $n_{\ell -1}=2$, then T is a broom and there is nothing to prove. So we assume that $n_{\ell -1}>2$ in the following. Then $P_{n_\ell }\cup P_{n_{\ell -1}}$ is a diametral path of T. Next we will run transformations for paths other than $P_{n_\ell }$ and $P_{n_{\ell -1}}$.

Assume that $P_{n_\ell },P_{n_{\ell -1}}$ are both even paths. When $x=0$, there exist $\ell$ even paths, and we can obtain $P_n$ by repeating Transformation IV on $\ell -2$ even paths. By Lemma 2.10, we have $W_b(T)<W_b(P_n)$. If $x\ge 1$, we can obtain $G_1$ by running Transformation IV on $\ell -2-x$ even paths with $W_b(G_1)>W_b(T)$ by Lemma 2.10; and then by running Transformation I on an odd path of $G_1$, we get $G_2$ with $W_b(G_2)>W_b(G_1)$ by Lemma 2.7. At last we get $B_n(x)$ by repeating Transformation V on $x-1$ odd paths of $G_2$. Moreover, we have $W_b(B_n(x))>W_b(G_2)$ by Lemma 2.11.

Assume that $P_{n_\ell },P_{n_{\ell -1}}$ are both odd paths. We can firstly obtain $G_3$ by running successively Transformation I on $\ell -x$ even paths with $W_b(G_3)>W_b(T)$ from Lemma 2.7. Next by repeating Transformation V on $x-2$ odd paths of $G_3$, in view of Lemma 2.11, we get $B_n(x-1)$ with $W_b(B_n(x-1))>W_b(G_3)$.

Assume that $P_{n_\ell }$ is an odd (or even) path and $P_{n_{\ell -1}}$ is an even (or odd) path. Firstly, we can obtain $G_4$ by repeating Transformation I on $\ell -x-1$ even paths with $W_b(T)<W_b(G_4)$ by Lemma 2.7. Then we can obtain $B_n(x)$ by running Transformation V on $x-1$ odd paths in $G_4$ with $W_b(B_n(x))>W_b(G_4)$ by Lemma 2.11.

Therefore, for $k=1$, the broom maximizes the bi-Wiener index among all trees with a (p, q)-bipartition where $p+q=n$.

For $k=2$, we assume that $P=u_1u_2\dots u_{t-1}u_t$ is a diametral path of T. If $d(u_2)=2$, we have proven the desired result in Lemma 3.2. Thus it suffices to deal with the case when $d(u_2)\ge 3$. Let $u_2$ be a branching vertex with $d(u_2)=r+1$ and $u_i$ ($3\le i\le t-1$) be another branching vertex at which s pendant paths, that are x odd paths and $s-x$ even paths, are attached except $P'=u_i\dots u_t$. Then we will run transformations for the above s paths.

Assume that $d(u_2,u_i)$ is even. We can obtain $B_n(r+x)$ by performing Transformation II on $s-x$ even paths and Transformation V on x odd paths in sequence. By Lemmas 2.8 and 2.11, we have $W_b(B_n(r+x))\ge W_b(T)$. The equation holds if T is a bi-broom with even diameter.

Assume that $d(u_2,u_i)$ is odd. By running Transformation IV on $s-x$ even paths and Transformation III on x odd paths successively, we can get $G_5$ satisfying $d_{G_5}(u_i)=2$ or $d_{G_5}(v_2)=2$ where $v_2$ is a semi-diametral vertex of $G_5$. By Lemmas 2.10 and 2.9, we have $W_b(G_5)>W_b(T)$. If $d_{G_5}(u_i)=2$, then $G_5$ is a broom; if $d_{G_5}(v_2)=2$, by Lemma 3.2, the result follows. Thus the result holds for $k=2$.

We assume henceforth that $k\ge 3$. Let T be a (p, q)-bipartition tree with k branching vertices and a diametral path $P=u_1u_2\dots u_{t-1}u_t$ in it. By Lemma 3.2, it suffices to show the case of $d(u_{t-1})\ge d(u_2)\ge 3$. Let $u_i$ ($3\le i\le t-1$) be a vertex of degree at least 3 with $d_T(u_2,u_i)$ as small as possible and $D_1$ be the component of $T-\{u_{i-1}u_i, u_iu_{i+1}\}$ containing $u_i$. Let $d_T(u_i)=r+2$. Next we divide into the following two cases based on the existence of branching vertices in $D_1-u_i$.

Case 1. There is no branching vertex in $D_1-u_i$.

In this case there are r pendant paths attaching to $u_i$ including x odd paths, $r-x$ even paths. Assume that $d(u_2,u_i)$ is even. We can obtain $T_1$ with $d_{T_1}(u_i)=2$ by performing Transformation II on $r-x$ even paths and Transformation V on x odd paths in sequence. Thus there are $k-1$ branching vertices in $T_1$. And, by Lemmas 2.8 and 2.11, we have $W_b(T_1)\ge W_b(T)$. The equation holds if and only if T is a bi-broom with even diameter. Then from the induction hypothesis, the result holds for $k\ge 3$.

Assume that $d(u_2,u_i)$ is odd. By running Transformation IV on $r-x$ even paths and Transformation III on x odd paths successively until we get $T_2$ with $d_{T_2}(u_i)=2$ or $d_{T_2}(v_2')=2$ where $v_2'$ is a semi-diametral vertex of $T_2$. Then there are at most $k-1$ branching vertices in $T_2$. By Lemmas 2.10 and 2.9, we have $W_b(T_2)>W_b(T)$. Then our result for $k\ge 3$ follows from the induction hypothesis.

Case 2. There is at least one branching vertex in $D_1-u_i$.

Let h be the farthest branching vertex from $u_i$ with $d_T(h)=s+1$. Then there exist s pendant paths attaching to h including y odd paths, $s-y$ even paths.

Assume that $d(u_2,u_i)$ and $d(u_i,h)$ are all even (or odd). We can obtain $T_3$ with $d_{T_3}(u_i)=1$ by performing Transformation II on $s-y$ even paths and Transformation V on y odd paths in sequence. Thus there exist $k-1$ branching vertices in $T_3$. And by Lemmas 2.8 and 2.11, we have $W_b(T_3)>W_b(T)$. Then by the induction hypothesis, our result holds for $k\ge 3$.

Assume that $d(u_2,u_i)$ is odd (or even) and $d(u_i,h)$ is even (or odd). By running Transformation IV on $s-y$ even paths and Transformation III on y odd paths successively, we can get $T_4$ with $d_{T_4}(u_i)=2$ or $d_{T_4}(c_2)=2$ where $c_2$ is a semi-diametral vertex of $T_4$. Then there are at most $k-1$ branching vertices in $T_4$. By Lemmas 2.10 and 2.9, we have $W_b(T_4)>W_b(T)$. Then by the induction hypothesis, our result holds for $k\ge 3$.

Combining the above arguments, we complete the proof of the result. $\square$

Lemma 3.4

Let $k\ge 3$, $n\ge 5$ be two integers. Then $W_b(B_n(k-2))> W_b(B_n(k))$.

Proof

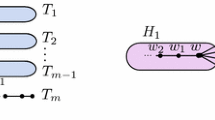
Let $H_1=B_n(k)$ with $k\ge 3$ be a broom of order n with a (p, q)-bipartition $A\cup B$ and a branching vertex $u_1$ with $p+q=n$, $p>q$. We have $p=\frac{n+k-1}{2}$, $q=\frac{n-k+1}{2}$ if $n-k$ is odd or $p=\frac{n+k}{2}$, $q=\frac{n-k}{2}$ if $n-k$ is even. Let $N_{H_1}(u_1)=\{w_1,\dots ,w_k,u_2\}$ with $d_{H_1}(w_i)=1$ for $i\in [k]$, $P=w_1u_1\dots u_{n-k}$ be a diametral path of $H_1$. Next we set $H_2=H_1-\{u_1w_1, u_1w_2\}+\{u_{n-k}w_1,w_1w_2\}$. Clearly, $H_2=B_n(k-2)$ is a broom with $(p-1,q+1)$-bipartition. Setting $V_0=\{w_1,w_2\}$, by the structures of $H_1,H_2$ and Proposition 2.6, we have

$$\begin{aligned} W_b(H_1)&=0+W_{b_2}(H_1)+W_{b_3}(H_1)=W_{b_2}(H_1)+2\sum \limits _{i=1}^q(2i-1),\\ W_b(H_2)&=1+W_{b_2}(H_2)+W_{b_3}(H_2)\\&=W_{b_2}(H_2)+1+\sum \limits _{i=1}^q(2i-1)+\sum \limits _{i=2}^q(2i-1)+(p-q-1)(2q+1)\\&=W_{b_2}(H_1)+2\sum \limits _{i=1}^q(2i-1)+(p-q-1)(2q+1)~if~n-k~ is~ odd,\\ W_b(H_2)&=1+W_{b_2}(H_2)+W_{b_3}(H_2)\\&=W_{b_2}(H_2)+1+\sum \limits _{i=1}^q(2i+1)+\sum \limits _{i=1}^q(2i-1)+(p-q-2)(2q+1)\\&=W_{b_2}(H_1)+2\sum \limits _{i=1}^q(2i-1)+(p-q-1)(2q+1)~ if~ n-k~ is~ even. \end{aligned}$$

Since $k\ge 3$, we have $p-q-1>0$. Therefore, regardless of the parity of $n-k$, we still have $W_b(H_2)-W_b(H_1)=(p-q-1)(2q+1)>0$, completing the proof. $\square$

Lemma 3.5

Let $a\ge b\ge 2$, $n\ge 6$ be three integers. If $n-a-b+2$ is odd, then we have $W_b(H(n-a-b+2,a,b-2))> W_b(H(n-a-b,a,b))$.

Proof

Let $H_1=H(n-a-b,a,b)$ be a bi-broom of order n obtained by attaching a (b, respectively) pendant vertices to the end vertex $w_{n-a-b}$ ($w_1$, respectively) of path $P_{n-a-b}=w_1w_2\dots w_{n-a-b}$ with a (p, q)-bipartition $A\cup B$. Let $N(w_1)\setminus \{w_2\}=\{z_1,z_2\dots ,z_b\}$. Recall that $|A|=p\ge q=|B|$. Thus $w_1\in B$, $z_1,z_2\in A$. Let $H_2=H_1-\{w_1w_2,z_1w_1\}+\{z_1z_2+z_1w_2\}$. Now we have $z_1\in B$ in $H_2$. Therefore $H_2=H(n-a-b+2,a,b-2)$ is a bi-broom with $(p-1,q+1)$-bipartition. Setting $V_0=\{w_1,z_1\dots ,z_b\}$, $V_1=V(H_1)\setminus V_0$ and $k=\frac{p-a-b-1}{2}$, by the structures of $H_1,H_2$ and Proposition 2.6, we have

$$\begin{aligned} W_{b_1}(H_2)&=b-1+1+3(b-2)=4b-6>b=W_{b_1}(H_1),~~~~\\ W_{b_2}(H_2)&=W_{b_2}(H_1),\\ W_{b_3}(H_1)&=\sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in V_1\cap B \end{array}}d_{H_1}(u,v)+\sum \limits _{\begin{array}{c} u\in V_0\cap B\\ v\in V_1\cap A \end{array}}d_{H_1}(u,v)\\&=\sum \limits _{v\in V_1\cap A}d_{H_1}(w_1,v)+b\sum \limits _{i=1}^{k}(2i+1),\\ W_{b_3}(H_2)&=\sum \limits _{\begin{array}{c} u\in V_0\cap A\\ v\in V_1\cap B \end{array}}d_{H_2}(u,v)+\sum \limits _{\begin{array}{c} u\in V_0\cap B\\ v\in V_1\cap A \end{array}}d_{H_2}(u,v)\\&=\sum \limits _{v\in V_1\cap A}d_{H_2}(z_1,v)+\sum \limits _{v\in V_1\cap A}d_{H_2}(w_1,v)\\&\quad +\sum \limits _{i=1}^{k}(2i+1)+(b-2)\sum \limits _{i=1}^{k}(2i+3);\\ \sum \limits _{v\in V_1\cap A}d_{H_1}(w_1,v)&=\sum \limits _{v\in V_1\cap A}d_{H_2}(z_1,v),\quad \sum \limits _{v\in V_1\cap A}d_{H_2}(w_1,v)>\sum \limits _{i=1}^{k}(2i+1). \end{aligned}$$

Therefore we have

$$\begin{aligned} W_b(H_2)=W_{b_1}(H_2)+W_{b_2}(H_2)+W_{b_3}(H_2)>W_{b}(H_1), \end{aligned}$$

completing the proof. $\square$

Corollary 3.6

Let $a\ge b\ge 2$, $n\ge 6$ be three integers. If $n-a-b+2$ is odd, then $W_b(B_n(a))> W_b(H(n-a-b,a,b))$.

Theorem 3.7

Let T be a tree of order $n\ge 4$. Then

$$\begin{aligned} W_b(T)\le f(n)={\left\{ \begin{array}{ll}\frac{n(n^2-1)}{12},~n~is~odd \\ \frac{n(n^2+2)}{12},~n~is~even\end{array}\right. } \end{aligned}$$

with equality holding if and only if $T\cong P_n$ for even n or $T\in \{P_n, B_n(2)\}$ for odd n.

Proof

Let $T^*$ be the tree of order $n\ge 4$ with maximum $W_b$. By Lemma 3.3, $T^*$ must be a bi-broom with even diameter or a broom. By Corollary 3.6, $T^*$ cannot a bi-broom with even diameter. If $T^*$ is a broom, by Lemma 3.4, we find that $P_n$ is the broom with maximum bi-Wiener index with $W_b(B_n(2))=W_b(P_n)$ if n is odd. So $T^*\cong P_n$ for even n or $T^*\in \{P_n, B_n(2)\}$ for odd n. Moreover, we have $W_b(P_n)=W_b(B_n(2))=\frac{k(k+1)(2k+1)}{3}$ for $n=2k+1$, or $W_b(P_n)=\frac{k(2k^2+1)}{3}$ for $n=2k$. Thus $W_b(T)\le f(n)$ with $f(n)={\left\{ \begin{array}{ll}\frac{n(n^2-1)}{12},~n~is~odd \\ \frac{n(n^2+2)}{12},~n~is~even\end{array}\right. }$ with equality holding if and only if $T\cong P_n$ for even n or $T\in \{P_n, B_n(2)\}$ for odd n. $\square$

Combining Theorems 3.1 and 3.7, we arrive at the main result as follows.

Theorem 3.8

Let T be a tree of order $n\ge 4$. Then

$$\begin{aligned} n-1\le W_b(T)\le {\left\{ \begin{array}{ll}\frac{n(n^2-1)}{12},~n~is~odd \\ \frac{n(n^2+2)}{12},~n~is~even\end{array}\right. } \end{aligned}$$

with left equality holding if and only if $T\cong S_n$ and right equality holding if and only if $T\cong P_n$ for even n or $T\in \{P_n, B_n(2)\}$ for odd n.

4 Concluding Remarks

In this paper we have introduced and studied a new topological index, called the bi-Wiener index. We have established some of its basic properties and determined its extremal values over all trees on a given number of vertices. However, many other interesting problems remain unresolved even for trees. We address here maybe the most natural one, namely the one about the largest value of the ratio $W_b(T_n)/W(T_n)$ over all trees of order n. We have shown that $\lim \limits _{n\rightarrow \infty }\frac{W_b(S_n)}{W(S_n)}=0$ and that $\lim \limits _{n\rightarrow \infty }\frac{W_b(P_{2n+1})}{W(P_{2n+1})}=\frac{1}{2}$, but what can happen for general trees? It turns out, somewhat unexpectedly, that this cannot be bounded away from one when n tends to infinity.

Theorem 4.1

Let $\mathcal {T}$ denote the set of all trees on $n \ge 4$ vertices. Then

$$\begin{aligned} \sup \limits _{T \in \mathcal {T}} \frac{W_b(T)}{W(T)}=1. \end{aligned}$$

Proof

Assume that $T_n^*=H(k+1, (n-k-1)/2, (n-k-1)/2)$ with k being odd. Let us denote $m = (n-k-1)/2$ and consider trees $H(k+1,m,m)$. It follows by a straightforward computation that their bi-Wiener and ordinary Wiener indices are given by

$$\begin{aligned} W_b((H(k+1,m,m)) = (k+2)\,m^2 + \frac{(k+1)^2}{2}\,m + \frac{1}{12} (k^3 + 3k^2 + 5k + 3) \end{aligned}$$

and

$$\begin{aligned} W(H(k+1,m,m)) = (k+4)\,m^2 + k(k+3)\,m + \frac{1}{6}k(k+1)(k+2), \end{aligned}$$

respectively. Now, their ratio is given by

$$\begin{aligned} \frac{W_b(H(k+1,m,m))}{W(H(k+1,m,m))} = \frac{(k+2)\,m^2 + \frac{(k+1)^2}{2}\,m + \frac{1}{12} (k^3 + 3k^2 + 5k + 3)}{(k+4)\,m^2 + k(k+3)\,m + \frac{1}{6}k(k+1)(k+2)}. \end{aligned}$$

For large enough m (and hence large enough n), this will behave as the ratio of leading terms, $\frac{k+2}{k+4}$, and this, in turn, can be made arbitrarily close to 1 by choosing large enough k.

The supremum value of 1 is never achieved, since, by Corollary 2.3, the ratio remains strictly below one for the number of vertices greater than two. It is reached for $P_2$, though, if we consider all trees.

The above proof works for even n. It would require only a minor modification to work also for n odd, but the conclusion would remain the same, settling the case for all trees.$\square$

The problem still remains, though, if we consider all trees on a given number of vertices. Since those are finite sets, there we can ask about the maximum value of the ratio.

Problem 4.2

What is the maximum value of the ratio $\frac{W_b(T_n)}{W(T_n)}$ among all trees $T_n$ of a given order $n\ge 4$?

The results of Theorem 4.1 could be refined in several ways. For example, it would be interesting to investigate for which rational numbers p/q between 0 and 1 one could construct a sequence of trees so that the considered ratio tends to p/q. Also, one could ask are the stars the only trees with the ratio tending to zero.

It is natural to ask what happens for bipartite graph which are not trees, i.e., which contain cycles.

Problem 4.3

What is the supremum of the ratio $\frac{W_b(G)}{W(G)}$ over all bipartite graphs which contain a cycle? What is the maximum value of the ratio $\frac{W_b(G_n)}{W(G_n)}$ among all bipartite graphs $G_n$ of a fixed order $n\ge 4$ containing at least one cycle?

In particular, what can be said about bipartite graphs with low cyclomatic numbers?

The bi-Wiener index could (and maybe should) be generalized in many (if not all) of the ways the original index was generalized. For example, one could consider its additively and multiplicatively weighted variants [14], then the terminal variant, the polarity variant, etc. It might be also interesting to investigate the corresponding polynomials [8]. Some work on those topics is under way and we hope to be able to report on it soon.

More generally, it may be interesting to extend the definition of the bi-Wiener index of a bipartite graph to the k-Wiener index for k-partite graphs with integer $k\ge 3$.