General Degree-Eccentricity Index of Trees

Abstract

For a connected graph G and $a,b \in \mathbb {R}$, the general degree-eccentricity index is defined as $\mathrm{DEI}_{a,b}(G) = \sum _{v \in V(G)} d_{G}^{a}(v) \mathrm{ecc}_{G}^{b}(v)$, where V(G) is the vertex set of G, $d_{G} (v)$ is the degree of a vertex v and $\mathrm{ecc}_{G}(v)$ is the eccentricity of v in G. We obtain sharp upper and lower bounds on the general degree-eccentricity index for trees of given order in combination with given matching number, independence number, domination number or bipartition. The bounds hold for $0< a < 1$ and $b > 0$, or for $a > 1$ and $b < 0$. Many bounds hold also for $a = 1$. All the extremal graphs are presented.

1 Introduction

Topological indices are invariants which play an important role in chemistry, pharmaceutical sciences, materials science and engineering, because they can be correlated with many properties of molecules. Eccentricity-based indices have shown very good correlations with respect to both physical and biological properties of chemical substances; see [12]. They provide an excellent predictive power for pharmaceutical properties, for example, for predicting anti-HIV activity of chemical substances; see [5].

Let G be a simple connected graph with vertex set V(G) and edge set E(G). The number of vertices of G is called the order. The number of edges incident to a vertex $v \in V(G)$ is the degree of v, denoted by $d_G (v)$. A vertex of degree one is a pendant vertex. For $u , v \in V(G)$, the number of edges in a shortest path between u and v is the distance $d_G (u,v)$ between u and v. The distance between v and any vertex furthest from v in G is the eccentricity $\mathrm{ecc}_{G}(v)$ of v. The distance between any two furthest vertices in G is the diameter of G. A shortest path between any two furthest vertices is a diametral path in G. A tree is a connected graph without cycles. The path and star of order n are denoted by $P_n$ and $S_n$, respectively. Let $P_k = v_1 v_2 \dots v_k$ be a path with $V(P_k) = \{ v_1, v_2, \dots , v_k \}$ and $E(P_k) = \{ v_1v_2, v_2v_3, \dots , v_{k-1}v_k \}$.

For $a,b \in \mathbb {R}$, we propose the concept of the general degree-eccentricity index, which is defined for a connected graph G as

$$\begin{aligned} \mathrm{DEI}_{a,b}(G) = \sum _{v \in V(G)} d_{G}^{a}(v) \mathrm{ecc}_{G}^{b}(v). \end{aligned}$$

Several important eccentricity-based indices are special cases of this general index. Note that $\mathrm{DEI}_{a,1}(G)$ is the general eccentric connectivity index, $\mathrm{DEI}_{1,1}(G)$ is the classical eccentric connectivity index, $\mathrm{DEI}_{1,-1}(G)$ is the connective eccentricity index, $\mathrm{DEI}_{0,1}(G)$ is the total eccentricity index, and $\mathrm{DEI}_{0,2}(G)$ is the first Zagreb eccentricity index of G.

The eccentric connectivity index has been extensively studied. Sharp upper and lower bounds on the eccentric connectivity index for trees with prescribed order were obtained in [24], tight upper and lower bounds for trees in terms of order and diameter were given in [16] and [24], sharp bounds for trees with given maximum degree were obtained in [10], and the tight lower bound and upper bound for trees of prescribed order and number of pendant vertices were presented in [9] and [24], respectively. Trees with respect to degree sequence were studied in [22], upper bounds for graphs with prescribed order and vertex connectivity/edge connectivity were given in [17], the eccentric connectivity index for generalized thorn graphs was given in [20], values of this index for polyacenic nanotubes were presented in [13], values for 3-fence graphs and their line graphs were given in [14], and composite graphs were considered in [4].

Zagreb eccentricity indices have been investigated a lot as well. For example, upper and lower bounds on those indices for trees and general graphs were given in [2] and [23], and bounds for trees of given domination number or bipartition were determined in [19].

Sharp upper and lower bounds on the general eccentric connectivity index of trees with prescribed order and diameter/number of pendant vertices were given in [21], exact values on the connective eccentricity index for several classes of path-thorn graphs were obtained in [11], and the total eccentricity index was studied in [3].

Several other indices which contain the eccentricity have been studied. For example, the eccentric distance sum of trees was investigated in [6] and [15], the eccentric connectivity coindex was studied in [8], and the eccentric adjacency index was investigated in [1].

We obtain upper and lower bounds on the general degree-eccentricity index for trees of given order and matching number, independence number, domination number or bipartition. The bounds hold for $0< a < 1$ and $b > 0$, or for $a > 1$ and $b < 0$. Many bounds hold also for $a = 1$. We show that all our bounds are best possible by presenting the extremal graphs.

2 Preliminary Results

The following lemma was presented in [21]. This lemma is used in the proofs of several theorems and lemmas.

Lemma 1

Let $x, y, c, a \in \mathbb {R}$, where $1 \le x < y$ and $c > 0$. For $0< a < 1$, we have

$$\begin{aligned} (x+c)^a - x^a > (y+c)^a - y^a. \end{aligned}$$

For $a > 1$ and $a < 0$, we have

$$\begin{aligned} (x+c)^a - x^a < (y+c)^a - y^a. \end{aligned}$$

For integers $l \ge 2$ and $r \ge t \ge 1$, let $P_l (r, t)$ be the tree of order n obtained from the path $P_l = v_1v_2 \dots v_l$ by joining $v_1$ to r pendant vertices and $v_l$ to t pendant vertices; see Fig. 1. Clearly, $r + t = n - l$.

Fig. 1

Tree $P_l (r,t)$

We study the general degree-eccentricity index of the trees $P_l (r, t)$.

Lemma 2

Let $l \ge 2$ and $r \ge t \ge 2$. Then, for any $b \in \mathbb {R}$, we have

• (i) $\mathrm{DEI}_{a,b}(P_l (r, t)) > \mathrm{DEI}_{a,b}(P_l (r+1, t-1))$ if $0< a < 1$,

• (ii) $\mathrm{DEI}_{a,b}(P_l (r, t)) < \mathrm{DEI}_{a,b}(P_l (r+1, t-1))$ if $a > 1$,

• (iii) $\mathrm{DEI}_{a,b}(P_l (r, t)) = \mathrm{DEI}_{a,b}(P_l (r+1, t-1))$ if $a = 1$.

Proof

Let $T' \cong P_l (r, t)$, where $P_l = v_1v_2 \dots v_l$, and let u be any pendant vertex adjacent to $v_l$ in $T'$. Let $T''$ be the tree with $V(T'') = V(T')$ and $E(T'') = \{ uv_1 \} \cup E(T') {\setminus } \{ uv_l \}$. So, $T'' \cong P_l (r+1, t-1)$. Then $d_{T'} (v_1) = r+1$, $d_{T''} (v_1)=r+2$, $d_{T'} (v_l)=t+1$, $d_{T''} (v_l)=t$ and $d_{T'} (x)=d_{T''} (x)$ for each $x\in V(T') {\setminus } \{v_1, v_l \}$. It is clear that $\mathrm{ecc}_{T'} (z) = \mathrm{ecc}_{T''} (z)$ for all $z \in V(T')$ and $\mathrm{ecc}_{T'} (v_1) = \mathrm{ecc}_{T''} (v_l) = l$. We obtain

$$\begin{aligned} \mathrm{DEI}_{a,b}(T') - \mathrm{DEI}_{a,b} (T'')= & {} d_{T'}^{a}(v_1)\mathrm{ecc}_{T'}^{b}(v_1)- d_{T''}^{a}(v_1)\mathrm{ecc}_{T''}^{b}(v_1)\\&+ d_{T'}^{a}(v_l)\mathrm{ecc}_{T'}^{b}(v_l)- d_{T''}^{a}(v_l)\mathrm{ecc}_{T''}^{b}(v_l)\\= & {} [(r+1)^{a} - (r+2)^{a}+ (t+1)^{a} - t^{a}] l^{b}. \end{aligned}$$

For $0< a < 1$, by Lemma 1, we have $(t+1)^{a} - t^{a} > (r+2)^{a} - (r+1)^{a}$, so $(r+1)^{a} - (r+2)^{a}+ (t+1)^{a} - t^{a} > 0$ and $\mathrm{DEI}_{a,b}(T') > \mathrm{DEI}_{a,b} (T'')$.

For $a > 1$, we get $(t+1)^{a} - t^{a} < (r+2)^{a} - (r+1)^{a}$, so $(r+1)^{a} - (r+2)^{a}+ (t+1)^{a} - t^{a} < 0$ and $\mathrm{DEI}_{a,b}(T') < \mathrm{DEI}_{a,b} (T'')$.

For $a = 1$, we obtain $(r+1)^{a} - (r+2)^{a}+ (t+1)^{a} - t^{a} = 0$ and $\mathrm{DEI}_{a,b}(T') = \mathrm{DEI}_{a,b} (T'')$. $\square$

From Lemma 2, we obtain sharp lower and upper bounds on the general degree-eccentricity index of the trees $P_l (r, t)$.

Corollary 1

Let T be any tree of order $n = l + r + t$ having the form $P_l (r, t)$, where $l \ge 2$ is fixed and $r \ge t \ge 1$.

If $0< a < 1$, then

$$\begin{aligned} \mathrm{DEI}_{a,b}(P_l (n-l-1, 1)) \le \mathrm{DEI}_{a,b}(T) \le \mathrm{DEI}_{a,b}\left( P_l \left( \left\lceil \frac{n-l}{2}\right\rceil , \left\lfloor \frac{n-l}{2}\right\rfloor \right) \right) \end{aligned}$$

with equalities if and only if T is $P_l (n-l-1, 1)$ and $P_l(\lceil \frac{n-l}{2}\rceil , \lfloor \frac{n-l}{2}\rfloor )$, respectively.

If $a > 1$, then

$$\begin{aligned} \mathrm{DEI}_{a,b}\left( P_l \left( \left\lceil \frac{n-l}{2}\right\rceil , \left\lfloor \frac{n-l}{2}\right\rfloor \right) \right) \le \mathrm{DEI}_{a,b}(T) \le \mathrm{DEI}_{a,b}(P_l (n-l-1, 1)) \end{aligned}$$

with equalities if and only if T is $P_l(\lceil \frac{n-l}{2}\rceil , \lfloor \frac{n-l}{2}\rfloor )$ and $P_l (n-l-1, 1)$, respectively.

In Lemmas 3 and 4 we compare the general degree-eccentricity indices of trees having the same order, but different diameters.

Lemma 3

Let $l \ge 2$, $r \ge 2$ and $t \ge 1$. Let $T \cong P_{l+1} (r-1, t)$ if $r > t$ and $T \cong P_{l+1} (t, r-1)$ if $r = t$. Then, for $0 < a \le 1$ and $b > 0$, we have

$$\begin{aligned} \mathrm{DEI}_{a,b}(P_l (r, t)) < \mathrm{DEI}_{a,b}(T). \end{aligned}$$

Proof

Let $T' \cong P_l (r, t)$, where $P_l = v_1v_2 \dots v_l$, and let u be any pendant vertex adjacent to $v_1$ in $T'$. Let T be the tree with $V(T) = V(T')$ and $E(T) = \{ uv_2 \} \cup E(T') {\setminus } \{ v_1v_2 \}$. So $T \cong P_{l+1} (r-1, t)$ if $r > t$ and $T \cong P_{l+1} (t, r-1)$ if $r = t$. Then, $d_{T'} (v_1) = r+1$, $d_{T} (v_1) = r$, $d_{T'} (u) = 1$, $d_{T} (u) = 2$ and $d_{T'} (x) = d_{T} (x)$ for all $x\in V(T') {\setminus } \{v_1, u \}$.

For all $z \in V(T') {\setminus } \{ u \}$, we have $\mathrm{ecc}_{T'} (z) \le \mathrm{ecc}_{T} (z)$, which implies that $\mathrm{ecc}^b_{T'} (z) \le \mathrm{ecc}^b_{T} (z)$ for $b > 0$. Note that $\mathrm{ecc}_{T'} (v_1) = l$, $\mathrm{ecc}_{T} (v_1) = l+1$, $\mathrm{ecc}_{T'} (u) = l+1$ and $\mathrm{ecc}_{T} (u) = l$. Thus,

$$\begin{aligned} \mathrm{DEI}_{a,b}(T') - \mathrm{DEI}_{a,b} (T)\le & {} d_{T'}^{a}(v_1)\mathrm{ecc}_{T'}^{b}(v_1)- d_{T}^{a}(v_1)\mathrm{ecc}_{T}^{b}(v_1)\\&+ \ d_{T'}^{a}(u)\mathrm{ecc}_{T'}^{b}(u)- d_{T}^{a}(u)\mathrm{ecc}_{T}^{b}(u)\\= & {} (r+1)^{a} l^b - r^{a} (l+1)^b + 1^{a} (l+1)^b - 2^{a} l^{b}\\= & {} [(r+1)^{a} - 2^{a}] l^b + [1^{a} - r^{a}] (l+1)^{b}\\< & {} [(r+1)^{a} - 2^{a} + 1^{a} - r^{a}] (l+1)^{b}. \end{aligned}$$

For $0< a < 1$, by Lemma 1, we have $(r+1)^{a} - 2^{a} < r^{a} - 1^{a}$, so $(r+1)^{a} - 2^{a} + 1^{a} - r^{a} < 0$. If $a = 1$, then $(r+1)^{a} - 2^{a} + 1^{a} - r^{a} = 0$. Then, $\mathrm{DEI}_{a,b}(T') < \mathrm{DEI}_{a,b} (T)$. $\square$

Lemma 4

Let $l \ge 2$, $r \ge 2$ and $t \ge 1$. Let $T \cong P_{l+1} (r-1, t)$ if $r > t$ and $T \cong P_{l+1} (t, r-1)$ if $r = t$. Then, for $a \ge 1$ and $b < 0$, we have

$$\begin{aligned} \mathrm{DEI}_{a,b}(P_l (r, t)) > \mathrm{DEI}_{a,b}(T). \end{aligned}$$

Proof

Let us present those parts of the proof of Lemma 4 which are different from the proof of Lemma 3.

For all $z \in V(T') {\setminus } \{ u \}$, we have $\mathrm{ecc}_{T'} (z) \le \mathrm{ecc}_{T} (z)$, which implies that $\mathrm{ecc}^b_{T'} (z) \ge \mathrm{ecc}^b_{T} (z)$ for $b < 0$. Thus

$$\begin{aligned} \mathrm{DEI}_{a,b}(T') - \mathrm{DEI}_{a,b} (T)\ge & {} d_{T'}^{a}(v_1)\mathrm{ecc}_{T'}^{b}(v_1)- d_{T}^{a}(v_1)\mathrm{ecc}_{T}^{b}(v_1)\\&+ \ d_{T'}^{a}(u)\mathrm{ecc}_{T'}^{b}(u)- d_{T}^{a}(u)\mathrm{ecc}_{T}^{b}(u)\\= & {} [(r+1)^{a} - 2^{a}] l^b + [1^{a} - r^{a}] (l+1)^{b}\\> & {} [(r+1)^{a} - 2^{a} + 1^{a} - r^{a}] (l+1)^{b}. \end{aligned}$$

For $a > 1$, by Lemma 1, we have $(r+1)^{a} - 2^{a} > r^{a} - 1^{a}$. If $a = 1$, then $(r+1)^{a} - 2^{a} + 1^{a} - r^{a} = 0$. It follows that $\mathrm{DEI}_{a,b}(T') > \mathrm{DEI}_{a,b} (T)$. $\square$

3 Trees of Given Order

In this section, we generalize results on the general eccentric connectivity index for trees of given order which were presented in [21]. We include results on the general degree-eccentricity index for trees with given order also because Theorems 1 and 2 are used in the proofs of bounds for trees with domination number $\lceil \frac{n}{3} \rceil$.

The only tree with two vertices is $P_2$ and the unique tree with three vertices is $P_3$; thus, we prove the bounds given in this section for $n \ge 4$.

Theorem 1

Let T be any tree with n vertices, where $n \ge 4$. For $0 < a \le 1$ and $b > 0$,

$$\begin{aligned} \mathrm{DEI}_{a,b} (T) \le \mathrm{DEI}_{a,b} (P_n) \end{aligned}$$

with equality if and only if T is $P_n$.

Proof

Let $T'$ be any tree with the maximum $\mathrm{DEI}_{a,b}$ index among trees of order n. We show that $T'$ is $P_n$.

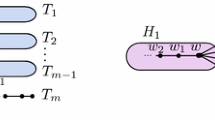
Suppose to the contrary that $T'$ is not $P_n$. Let $u_0 u_1 u_2 \dots u_d$ be a diametral path in $T'$. Then, $T'$ has a pendant vertex $w_1$ other than $u_0$ and $u_d$. Let us denote the vertex joined to $w_1$ in $T'$ by w. For any vertex z in $T'$, we get $\mathrm{ecc}_{T'} (z) = d_{T'} (z, u_0)$ or $\mathrm{ecc}_{T'} (z) = d_{T'} (z, u_d)$. Thus, we can assume that $\mathrm{ecc}_{T'} (w) = d_{T'} (w, u_0)$.

Let $T''$ be the tree with $V(T'') = V(T')$ and $E(T'') = \{ u_0 w_1 \} \cup E(T') {\setminus } \{ w w_1 \}$. For all $z \in V(T')$, we get $\mathrm{ecc}_{T''}(z) \ge \mathrm{ecc}_{T'} (z)$; thus, $\mathrm{ecc}^b_{T''}(z) \ge \mathrm{ecc}^b_{T'} (z)$. Note that $\mathrm{ecc}_{T''} (w) = d_{T''} (w, w_1) = \mathrm{ecc}_{T'} (w)+1$ and $\mathrm{ecc}_{T'}(u_0) = \mathrm{ecc}_{T''} (u_0) = d$.

Let $d_{T'} (w)=p \ge 2$. Then $d_{T''}(w) = p-1$, $d_{T'} (u_0) = 1$, $d_{T''}(u_0)= 2$, and $d_{T''}(z)= d_{T'} (z)$ for $z \in V(T') {\setminus } \{ u_0, w \}$. Then,

$$\begin{aligned}&\mathrm{DEI}_{a,b}(T'') - \mathrm{DEI}_{a,b}(T')\\\ge & {} d_{T''}^{a}(w) \mathrm{ecc}^b_{T''} (w) - d_{T'}^{a}(w) \mathrm{ecc}^b_{T'} (w) + d_{T''}^{a}(u_0) \mathrm{ecc}^b_{T''} (u_0) - d_{T'}^{a}(u_0) \mathrm{ecc}^b_{T'} (u_0)\\= & {} (p-1)^{a} [\mathrm{ecc}_{T'}(w)+1]^b -p^{a} \mathrm{ecc}^b_{T'}(w) + 2^{a} d^b - 1^{a} d^b\\> & {} [(p-1)^{a}-p^{a}] \mathrm{ecc}^b_{T'}(w) + (2^{a}-1) d^b\\\ge & {} [(p-1)^{a}-p^{a}]\mathrm{ecc}^b_{T'}(w) + (2^{a}-1) \mathrm{ecc}^b_{T'}(w). \end{aligned}$$

If $a = 1$ or $p = 2$, then $(p-1)^{a}-p^{a} + 2^{a}-1 = 0$. If $0< a < 1$ and $p > 2$, then by Lemma 1, we have $2^{a}-1 > p^{a}-(p-1)^{a}$, so $(p-1)^{a}-p^{a} + 2^{a}-1 > 0$. This implies that $\mathrm{DEI}_{a,b}(T'') - \mathrm{DEI}_{a,b}(T') > 0$ and $\mathrm{DEI}_{a,b}(T'') > \mathrm{DEI}_{a,b}(T')$, a contradiction. Hence, $P_n$ is the tree with the maximum $\mathrm{DEI}_{a,b}$ index. $\square$

Theorem 2

Let T be any tree with n vertices, where $n \ge 4$. For $a \ge 1$ and $b < 0$,

$$\begin{aligned} \mathrm{DEI}_{a,b} (T) \ge \mathrm{DEI}_{a,b} (P_n) \end{aligned}$$

with equality if and only if T is $P_n$.

Proof

We present only those parts of the proof of Theorem 2 which are different from the proof of Theorem 1.

Let $T'$ be any tree with the minimum $\mathrm{DEI}_{a,b}$ index among trees of order n. Let us show by contradiction that $T'$ is $P_n$.

For all $z \in V(T')$, we have $\mathrm{ecc}_{T''}(z) \ge \mathrm{ecc}_{T'} (z)$; thus, $\mathrm{ecc}^b_{T''}(z) \le \mathrm{ecc}^b_{T'} (z)$. Then,

$$\begin{aligned}&\mathrm{DEI}_{a,b}(T'') - \mathrm{DEI}_{a,b}(T')\\&\quad \le d_{T''}^{a}(w) \mathrm{ecc}^b_{T''} (w) - d_{T'}^{a}(w) \mathrm{ecc}^b_{T'} (w) + d_{T''}^{a}(u_0) \mathrm{ecc}^b_{T''} (u_0) - d_{T'}^{a}(u_0) \mathrm{ecc}^b_{T'} (u_0)\\&\quad = (p-1)^{a} [\mathrm{ecc}_{T'}(w)+1]^b -p^{a} \mathrm{ecc}^b_{T'}(w) + 2^{a} d^b - 1^{a} d^b\\&\quad < [(p-1)^{a}-p^{a}] \mathrm{ecc}^b_{T'}(w) + (2^{a}-1) d^b\\&\quad \le [(p-1)^{a}-p^{a}]\mathrm{ecc}^b_{T'}(w) + (2^{a}-1) \mathrm{ecc}^b_{T'}(w). \end{aligned}$$

If $a = 1$ or $p = 2$, then $(p-1)^{a}-p^{a} + 2^{a}-1 = 0$. If $a > 1$ and $p > 2$, then by Lemma 1, we have $2^{a}-1 < p^{a}-(p-1)^{a}$, so $(p-1)^{a}-p^{a} + 2^{a}-1 < 0$. This implies that $\mathrm{DEI}_{a,b}(T'') - \mathrm{DEI}_{a,b}(T') < 0$ and $\mathrm{DEI}_{a,b}(T'') < \mathrm{DEI}_{a,b}(T')$, a contradiction. Hence, $P_n$ is the tree with the minimum $\mathrm{DEI}_{a,b}$ index. $\square$

Theorem 3

Let T be any tree with n vertices, where $n \ge 4$. For $0< a < 1$ and $b > 0$,

$$\begin{aligned} \mathrm{DEI}_{a,b} (T) \ge (n-1)^{a}+ (n-1) 2^b \end{aligned}$$

with equality if and only if T is $S_n$.

Proof

The star $S_n$ has one vertex of degree $n-1$ and eccentricity 1, and $n-1$ vertices of degree 1 and eccentricity 2; therefore, $\mathrm{DEI}_{a,b} (S_n) = (n-1)^{a}+ (n-1) 2^b$.

Let $T'$ be a tree with the minimum $\mathrm{DEI}_{a,b}$ index among trees of order n. We show by contradiction that $T'$ is $S_n$.

Suppose that $T'$ is not $S_n$. Let $u_0 u_1 u_2 \dots u_d$ be a diametral path in $T'$. Then $d \ge 3$. Let $d_{T'} (u_1) = p$ and $d_{T'} (u_{d-1}) = q$. Without loss of generality, $p \ge q$. Let $V(T'') = V(T')$ and $E(T'') = \{ u_1 u_d \} \cup E(T') {\setminus } \{ u_{d-1}u_{d} \}$. We have $d_{T''}(u_1) = p+1$ and $d_{T''}(u_{d-1}) = q-1$. Moreover, $\mathrm{ecc}_{T'} (u_{d-1}) = \mathrm{ecc}_{T''} (u_{d-1}) = \mathrm{ecc}_{T'} (u_1) = d-1$ and $d-2 \le \mathrm{ecc}_{T''}(u_1) \le d-1$. For each $z \in V(T') {\setminus } \{u_1, u_{d-1}\}$, $d_{T'}(z) = d_{T''} (z)$ and $\mathrm{ecc}_{T'}(z) \ge \mathrm{ecc}_{T''} (z)$. Thus, $\mathrm{ecc}^b_{T'}(z) \ge \mathrm{ecc}^b_{T''} (z)$ and

$$\begin{aligned} \mathrm{DEI}_{a,b} (T') - \mathrm{DEI}_{a,b} (T'')\ge & {} d_{T'}^{a}(u_1) \mathrm{ecc}^b_{T'} (u_1) - d_{T''}^{a}(u_1) \mathrm{ecc}^b_{T''}(u_1)\\&+ d_{T'}^{a} (u_{d-1}) \mathrm{ecc}^b_{T'} (u_{d-1}) - d_{T''}^{a}(u_{d-1}) \mathrm{ecc}^b_{T''}(u_{d-1})\\\ge & {} [p^{a}-(p+1)^{a}](d-1)^b + [q^{a}-(q-1)^{a}](d-1)^b. \end{aligned}$$

From Lemma 1, we have $q^{a}-(q-1)^{a} > (p+1)^{a} - p^{a}$, so $p^{a}-(p+1)^{a} + q^{a}-(q-1)^{a} > 0$. Hence, $\mathrm{DEI}_{a,b} (T') > \mathrm{DEI}_{a,b} (T'')$, which is a contradiction. $\square$

Theorem 4

Let T be any tree with n vertices, where $n \ge 4$. For $a > 1$ and $b < 0$,

$$\begin{aligned} \mathrm{DEI}_{a,b} (T) \le (n-1)^{a}+ (n-1) 2^b \end{aligned}$$

with equality if and only if T is $S_n$.

Proof

We present those parts of the proof of Theorem 4 which are different from the proof of Theorem 3.

Let $T'$ be a tree with the maximum $\mathrm{DEI}_{a,b}$ index among trees of order n. Let us show by contradiction that $T'$ is $S_n$.

Since $\mathrm{ecc}_{T''}(u_1) \le d-1$, we obtain $\mathrm{ecc}^b_{T''}(u_1) \ge (d-1)^b$. For each $z \in V(T')$, $\mathrm{ecc}_{T'}(z) \ge \mathrm{ecc}_{T''} (z)$. Thus, $\mathrm{ecc}^b_{T'}(z) \le \mathrm{ecc}^b_{T''} (z)$ and

$$\begin{aligned} \mathrm{DEI}_{a,b} (T') - \mathrm{DEI}_{a,b} (T'')\le & {} d_{T'}^{a}(u_1) \mathrm{ecc}^b_{T'} (u_1) - d_{T''}^{a}(u_1) \mathrm{ecc}^b_{T''}(u_1)\\&+ d_{T'}^{a} (u_{d-1}) \mathrm{ecc}^b_{T'} (u_{d-1}) - d_{T''}^{a}(u_{d-1}) \mathrm{ecc}^b_{T''}(u_{d-1})\\\le & {} [p^{a}-(p+1)^{a}](d-1)^b + [q^{a}-(q-1)^{a}](d-1)^b. \end{aligned}$$

From Lemma 1, for $a > 1$, we have $q^{a}-(q-1)^{a} < (p+1)^{a} - p^{a}$, so $p^{a}-(p+1)^{a} + q^{a}-(q-1)^{a} < 0$, Hence, $\mathrm{DEI}_{a,b} (T') < \mathrm{DEI}_{a,b} (T'')$, which is a contradiction. $\square$

4 Trees of Given Order and Matching Number

In Theorems 5 and 6, we present sharp bounds on the general degree-eccentricity index for trees with perfect matchings. In Theorems 7 and 8, we obtain bounds for trees with matching number $\beta \ge 3$. Bounds for trees with matching number 2 are given in Theorems 9 and 10. Then, in Theorems 11, 12 and 13, we present sharp bounds for trees with given independence number.

A matching is a set of edges of a graph G such that no two edges have a vertex in common. The cardinality of a maximum matching in G is the matching number of G. Obviously, for any tree of order n and matching number $\beta$, we have

$$\begin{aligned} 1 \le \beta \le \frac{n}{2}. \end{aligned}$$

The lower bound is achieved only by stars, and the upper bound is achieved by trees with perfect matchings.

The following lemma about matchings in trees was proved by Hou and Li [7].

Lemma 5

Let T be any tree of order $n \ge 3$ and matching number $\beta$, where $n > 2\beta$. Then, T has a maximum matching M and a pendant vertex v such that M does not match v.

It is easy to bound the maximum degree of a tree with respect to order and matching number.

Lemma 6

Let T be a tree of order n, matching number $\beta$ and maximum degree $\Delta$. Then, $\Delta \le n - \beta$.

Proof

Assume to the contrary that T contains a vertex, say v, of degree at least $n - \beta +1$. Since at most one edge incident to v is in every matching of T, at least $n - \beta$ edges of T are not in the matching, which implies that at most $\beta - 1$ edges of T are in the matching. A contradiction. Hence, every vertex of T is of degree at most $n - \beta$. $\square$

For positive integers n and $\beta$, where $3 \le \beta \le \frac{n}{2}$, let $T_{n,\beta }$ be the tree that contains one vertex v of degree $n - \beta$, where v is adjacent to $n - 2\beta +1$ pendant vertices and $\beta -1$ vertices of degree 2; thus, each vertex of degree 2 is adjacent to one pendant vertex. Then, $T_{n,\beta }$ has order n and matching number $\beta$; see Fig. 2. The tree $T_{n,\beta }$ contains one vertex of degree $n - \beta$ and eccentricity 2, $n - 2\beta +1$ vertices of degree 1 and eccentricity 3, $\beta -1$ vertices of degree 1 and eccentricity 4, and $\beta -1$ vertices of degree 2 and eccentricity 3. Therefore,

$$\begin{aligned} \mathrm{DEI}_{a,b} (T_{n,\beta }) = (n-\beta )^{a} 2^b + (\beta -1)(2^a 3^b + 4^b) + (n-2\beta +1)3^b. \end{aligned}$$

(1)

Fig. 2

Tree $T_{n,\beta }$

A tree with a perfect matching is called a conjugated tree. Obviously, a conjugated tree with the matching number $\beta$ has $2\beta$ vertices. The only conjugated tree with matching number 1 is $P_2$ and the only conjugated tree with matching number 2 is $P_4$, so we present bounds for trees with perfect matchings for $\beta \ge 3$.

Theorem 5

Let T be any tree of order $2\beta$ with matching number $\beta \ge 3$. Then, for $0 < a \le 1$ and $b > 0$, we have

$$\begin{aligned} \mathrm{DEI}_{a,b} (T) \ge \beta ^{a} 2^b + (\beta -1)( 2^a 3^b + 4^b) + 3^b \end{aligned}$$

with equality if and only if T is $T_{2\beta ,\beta }$.

Proof

Let $T'$ be a tree with the minimum $\mathrm{DEI}_{a,b}$ index among trees of order $2\beta$ with matching number $\beta \ge 3$. We prove Theorem 5 by induction on $\beta$. For $\beta = 3$, we have two trees, $P_6$ and $T_{6,3}$. Since $\mathrm{DEI}_{a,b}(P_6) > \mathrm{DEI}_{a,b}(T_{6,3})$, Theorem 5 holds for $\beta = 3$. We assume that Theorem 5 holds for $\beta - 1$ and prove that it holds for $\beta \ge 4$.

The only trees of diameter 2 are stars with $\beta = 1$, and all the trees of diameter 3 (double stars) have matching number 2; therefore, the diameter of $T'$ is $d \ge 4$.

Let $D = v_0 v_1 \dots v_d$ be a diametral path of $T'$. Obviously, $v_0$ is a pendant vertex and the edge $v_0 v_1$ is in a maximum matching. The vertex $v_1$ is not adjacent to any other pendant vertex; otherwise, that vertex is not matched by a maximum matching. The vertex $v_1$ cannot be adjacent to a non-pendant vertex except for $v_2$; otherwise, D is not a diametral path. Thus, $d_{T'} (v_1) = 2$. Let $V(T'') = V(T') {\setminus } \{v_0, v_1\}$ and $E(T'') = E(T') {\setminus } \{v_0v_1, v_1v_2 \}$.

Then $T''$ is a tree of order $2\beta -2$ with matching number $\beta -1$. By the induction hypothesis, we have

$$\begin{aligned} \mathrm{DEI}_{a,b}(T'') \ge \mathrm{DEI}_{a,b}(T_{2\beta -2,\beta -1}) = (\beta -1)^{a} 2^b + (\beta -2)(2^{a} 3^b +4^b) + 3^b. \end{aligned}$$

Let $d_{T'}(v_2) = p$. By Lemma 6, we obtain $p \le \beta$. We have $d_{T''}(v_2) = p-1$ and $d_{T''}(x) = d_{T'}(x)$ for each $x \in V(T'') {\setminus } \{ v_2 \}$. Moreover, $\mathrm{ecc}_{T'}(v_0) = d$, $\mathrm{ecc}_{T'}(v_1) = d-1$, $\mathrm{ecc}_{T'}(v_2) = \mathrm{ecc}_{T''}(v_2) = d-2$ and $\mathrm{ecc}_{T'}(x) \ge \mathrm{ecc}_{T''}(x)$ for all $x \in V(T'') {\setminus } \{ v_2 \}$. Then $\mathrm{ecc}^b_{T'}(x) \ge \mathrm{ecc}^b_{T''}(x)$ and

$$\begin{aligned}&\mathrm{DEI}_{a,b}(T') - \mathrm{DEI}_{a,b}(T'')\\&\quad = \sum _{x\in V(T'') {\setminus } \{ v_2 \} } [ d^{a}_{T'}(x) \mathrm{ecc}^b_{T'}(x) - d^{a}_{T''}(x) \mathrm{ecc}^b_{T''}(x) ]\\&\qquad + \ [ d^{a}_{T'}(v_2) - d^{a}_{T''}(v_2) ] \mathrm{ecc}^b_{T'}(v_2) + d^{a}_{T'}(v_1) \mathrm{ecc}^b_{T'}(v_1) + d^{a}_{T'}(v_0) \mathrm{ecc}^b_{T'}(v_0)\\&\quad \ge [ p^{a} - (p-1)^{a} ] (d-2)^b + 2^a (d-1)^b + d^b. \end{aligned}$$

If $0< a < 1$ and $p < \beta$, then by Lemma 1, we have $p^{a} - (p-1)^{a} > \beta ^{a} - (\beta -1)^{a}$. If $a = 1$ or $p = \beta$, then $p^{a} - (p-1)^{a} = \beta ^{a} - (\beta -1)^{a}$. Thus $p^{a} - (p-1)^{a} \ge \beta ^{a} - (\beta -1)^{a}$ and $\mathrm{DEI}_{a,b}(T')$

$$\begin{aligned}\ge & {} \mathrm{DEI}_{a,b}(T'') + [ p^{a} - (p-1)^{a} ] (d-2)^b + 2^a (d-1)^b + d^b\\\ge & {} (\beta -1)^{a} 2^b + (\beta -2) (2^a 3^b + 4^b) + 3^b + [p^{a} - (p-1)^{a}] 2^b + 2^a 3^b + 4^b\\\ge & {} (\beta -1)^{a} 2^b + (\beta -2) (2^a 3^b + 4^b) + 3^b + [ \beta ^{a} - (\beta -1)^{a} ] 2^b + 2^a 3^b + 4^b\\= & {} \beta ^{a} 2^b + (\beta -1)( 2^a 3^b + 4^b) + 3^b \end{aligned}$$

with the first equality holding if and only if $\mathrm{ecc}_{T'}(x) = \mathrm{ecc}_{T''}(x)$ for all $x \in V(T'') {\setminus } \{ v_2 \}$, the second equality if and only if $T'' \cong T_{2\beta -2, \beta -1}$ and $d =4$, and the third equality if and only if $p = \beta$. So $T'$ is $T_{2\beta , \beta }$. By (1), we have $\mathrm{DEI}_{a,b} (T_{2\beta ,\beta }) = \beta ^{a} 2^b + (\beta -1)( 2^a 3^b + 4^b) + 3^b$; thus, the proof is complete. $\square$

Theorem 6

Let T be a tree of order $2\beta$ with matching number $\beta \ge 3$. Then, for $a \ge 1$ and $b < 0$, we have

$$\begin{aligned} \mathrm{DEI}_{a,b}(T) \le \beta ^{a} 2^b + (\beta -1)( 2^a 3^b + 4^b) + 3^b \end{aligned}$$

with equality if and only if T is $T_{2\beta ,\beta }$.

Proof

The proofs of Theorems 5 and 6 are similar. We present only those parts of the proof of Theorem 6 which are different from the proof of Theorem 5.

We consider a tree $T'$ having the maximum $\mathrm{DEI}_{a,b}$ index among trees of order $2\beta$ with matching number $\beta \ge 3$. We have $\mathrm{DEI}_{a,b}(P_6) < \mathrm{DEI}_{a,b}(T_{6,3})$. By the induction hypothesis,

$$\begin{aligned} \mathrm{DEI}_{a,b}(T'') \le \mathrm{DEI}_{a,b}(T_{2\beta -2,\beta -1}) = (\beta -1)^{a} 2^b + (\beta -2)(2^{a} 3^b +4^b) + 3^b. \end{aligned}$$

Since $\mathrm{ecc}_{T'}(x) \ge \mathrm{ecc}_{T''}(x)$ for all $x \in V(T'') {\setminus } \{ v_2 \}$, we obtain $\mathrm{ecc}^b_{T'}(x) \le \mathrm{ecc}^b_{T''}(x)$. If $a > 1$ and $p < \beta$, then by Lemma 1, we have $p^{a} - (p-1)^{a} < \beta ^{a} - (\beta -1)^{a}$. Hence, $\mathrm{DEI}_{a,b}(T')$

$$\begin{aligned}\le & {} \mathrm{DEI}_{a,b}(T'') + [ p^{a} - (p-1)^{a} ] (d-2)^b + 2^a (d-1)^b + d^b\\\le & {} (\beta -1)^{a} 2^b + (\beta -2) (2^a 3^b + 4^b) + 3^b + [p^{a} - (p-1)^{a}] 2^b + 2^a 3^b + 4^b\\\le & {} (\beta -1)^{a} 2^b + (\beta -2) (2^a 3^b + 4^b) + 3^b + [ \beta ^{a} - (\beta -1)^{a} ] 2^b + 2^a 3^b + 4^b\\= & {} \beta ^{a} 2^b + (\beta -1)( 2^a 3^b + 4^b) + 3^b. \end{aligned}$$

$\square$

In the next two theorems, we obtain the tree having the minimum $\mathrm{DEI}_{a,b}$ index among trees with given order and matching number $\beta \ge 3$.

Theorem 7

Let T be a tree of order n with matching number $\beta$, where $3 \le \beta \le \frac{n}{2}$. Then, for $0 < a \le 1$ and $b > 0$, we have

$$\begin{aligned} \mathrm{DEI}_{a,b}(T) \ge (n-\beta )^{a} 2^b + (\beta -1)(2^a 3^b + 4^b) + (n-2\beta +1)3^b \end{aligned}$$

with equality if and only if T is $T_{n,\beta }$.

Proof

Let $T'$ be a tree of order $n\ge 2\beta$ and matching number $\beta \ge 3$ having the minimum $\mathrm{DEI}_{a,b}$ index. We prove Theorem 7 by induction on n. From Theorem 5 we know that Theorem 7 holds for $n= 2\beta$. We assume that Theorem 7 holds for $n - 1$ and prove that it holds for $n > 2\beta$. Then, by Lemma 5, there is a maximum matching and a pendent vertex v in $T'$ which is not matched by that matching. Let u be the vertex adjacent to v in $T'$. Let $T''$ be the tree with $V(T'') = V(T') {\setminus } \{ v \}$ and $E(T'') = E(T') {\setminus } \{ vu \}$. So $T''$ is a tree having order $n-1$ and matching number $\beta$. By the induction hypothesis, we have

$$\begin{aligned} \mathrm{DEI}_{a}(T'') \ge \mathrm{DEI}_{a} (T_{n-1, \beta }) = (n-\beta -1)^{a} 2^b + (\beta -1)(2^a 3^b + 4^b) + (n-2\beta )3^b. \end{aligned}$$

Since v is a pendant vertex of $T'$ and $T'$ is not a star, we know that $\mathrm{ecc}_{T'} (v) \ge 3$. So $\mathrm{ecc}_{T'} (u) = \mathrm{ecc}_{T''} (u) \ge 2$. Let $d_{T'} (u) = p$. By Lemma 6, we obtain $p\le n-\beta$. Then, $d_{T''} (u) = p-1$. For each $x\in V(T') {\setminus } \{ u \}$, we obtain $d_{T'} (x) = d_{T''}(x)$ and $\mathrm{ecc}_{T'}(x) \ge \mathrm{ecc}_{T''} (x)$. Then, $\mathrm{ecc}^b_{T'}(x) \ge \mathrm{ecc}^b_{T''}(x)$ and

$$\begin{aligned} \mathrm{DEI}_{a,b} (T') - \mathrm{DEI}_{a,b} (T'')= & {} \sum _{x\in V(T'')} [ d^{a}_{T'}(x) \mathrm{ecc}^b_{T'}(x) - d^{a}_{T''}(x) \mathrm{ecc}^b_{T''}(x) ]\\&+ [d^{a}_{T'}(u) - d^{a}_{T''}(u)] \mathrm{ecc}^b_{T'}(u) + d^{a}_{T'} (v) \mathrm{ecc}^b_{T'} (v)\\\ge & {} [p^{a} - (p-1)^{a}] \mathrm{ecc}^b_{T'}(u) + 1^a \mathrm{ecc}^b_{T'} (v). \end{aligned}$$

If $0< a < 1$ and $p < n - \beta$, then by Lemma 1, we have $p^{a} - (p-1)^{a} > (n-\beta )^{a} - (n-\beta -1)^{a}$. If $a = 1$ or $p = n - \beta$, then $p^{a} - (p-1)^{a} = (n-\beta )^{a} - (n-\beta -1)^{a}$. Thus, $p^{a} - (p-1)^{a} \ge (n-\beta )^{a} - (n-\beta -1)^{a}$ and

$$\begin{aligned} \mathrm{DEI}_{a,b} (T')\ge & {} \mathrm{DEI}_{a,b}(T'') + [p^{a} - (p-1)^{a}] \mathrm{ecc}^b_{T'}(u) + \mathrm{ecc}^b_{T'} (v)\\\ge & {} (n-\beta -1)^{a} 2^b + (\beta -1)(2^a 3^b + 4^b) + (n-2\beta )3^b\\&+ \ [(n-\beta )^{a} - (n-\beta -1)^{a}] 2^b + 3^b\\= & {} (n-\beta )^{a} 2^b + (\beta -1)(2^a 3^b + 4^b) + (n-2\beta +1)3^b \end{aligned}$$

with the first equality holding if and only if $\mathrm{ecc}_{T'}(x) = \mathrm{ecc}_{T''}(x)$ for all $x \in V(T'') {\setminus } \{ u \}$ and the second equality if and only if $T'' \cong T_{n-1, \beta }$, $p = n-\beta$ and $\mathrm{ecc}_{T'}(v) = 3$. That is, $T'$ is $T_{n, \beta }$. By (1), we have $\mathrm{DEI}_{a,b} (T_{n,\beta }) = (n-\beta )^{a} 2^b + (\beta -1)(2^a 3^b + 4^b) + (n-2\beta +1)3^b$; thus, the proof is complete. $\square$

Theorem 8

Let T be a tree of order n with matching number $\beta$, where $3 \le \beta \le \frac{n}{2}$. Then, for $a \ge 1$ and $b<0$, we have

$$\begin{aligned} \mathrm{DEI}_{a,b}(T) \le (n-\beta )^{a} 2^b + (\beta -1)(2^a 3^b + 4^b) + (n-2\beta +1)3^b \end{aligned}$$

with equality if and only if T is $T_{n,\beta }$.

Proof

We present only those parts of the proof of Theorem 8 which are different from the proof of Theorem 7.

Let $T'$ be a tree of order $n\ge 2\beta$ with matching number $\beta \ge 3$ having the minimum $\mathrm{DEI}_{a,b}$ index. For $T''$, by the induction hypothesis, we have

$$\begin{aligned} \mathrm{DEI}_{a,b}(T'')\le & {} \mathrm{DEI}_{a,b} (T_{n-1, \beta }) = (n-\beta -1)^{a} 2^b\\&+ (\beta -1)(2^a 3^b + 4^b) + (n-2\beta )3^b. \end{aligned}$$

Since $\mathrm{ecc}_{T'}(x) \ge \mathrm{ecc}_{T''}(x)$ for $x \in V(T'') {\setminus } \{ u \}$, we obtain $\mathrm{ecc}^b_{T'}(x) \le \mathrm{ecc}^b_{T''}(x)$. If $a > 1$ and $p < n - \beta$, then by Lemma 1, we have $p^{a} - (p-1)^{a} < (n-\beta )^{a} - (n-\beta -1)^{a}$. We obtain

$$\begin{aligned} \mathrm{DEI}_{a,b} (T')\le & {} \mathrm{DEI}_{a,b}(T'') + [p^{a} - (p-1)^{a}] \mathrm{ecc}^b_{T'}(u) + \mathrm{ecc}^b_{T'} (v)\\\le & {} (n-\beta -1)^{a} 2^b + (\beta -1)(2^a 3^b + 4^b) + (n-2\beta )3^b\\&+ \ [(n-\beta )^{a} - (n-\beta -1)^{a}] 2^b + 3^b\\= & {} (n-\beta )^{a} 2^b + (\beta -1)(2^a 3^b + 4^b) + (n-2\beta +1)3^b. \end{aligned}$$

$\square$

In Theorems 7 and 8, we presented bounds for matching number $\beta \ge 3$. Since the only trees with matching number 1 are stars, it remains to find bounds for matching number 2.

Theorem 9

Let T be a tree of order $n \ge 4$ with matching number 2. Then for $0< a < 1$ and $b > 0$, we have

$$\begin{aligned} \mathrm{DEI}_{a,b}(T) \ge [(n-2)^a + 2^a] 2^b + (n-2) 3^b \end{aligned}$$

with equality if and only if T is $P_2 (n-3, 1)$.

Proof

The only trees having matching number 2 are $P_2 (r_2 , t_2)$, where $r_2 + t_2 = n-2$, and $P_3 (r_3 , t_3)$, where $r_3 + t_3 = n-3$. From Corollary 1, we know that among trees of the form $P_2 (r_2 , t_2)$, where $r_2 + t_2 = n-2$, the tree $P_2 (n-3, 1)$ has the minimum $\mathrm{DEI}_{a,b}$ index. Similarly, $P_3 (n-4, 1)$ is the tree having the minimum $\mathrm{DEI}_{a,b}$ index among trees of the form $P_3 (r_3 , t_3)$, where $r_3 + t_3 = n-3$. Finally, by Lemma 3, we have $\mathrm{DEI}_{a,b}(P_2 (n-3, 1)) < \mathrm{DEI}_{a,b}(P_3 (n-4, 1))$, which means that $P_2 (n-3, 1)$ is the tree with the minimum $\mathrm{DEI}_{a,b}$ index among trees of order n and matching number 2. We have $\mathrm{DEI}_{a,b}(P_2 (n-3, 1)) = [(n-2)^a + 2^a] 2^b + (n-2) 3^b$. $\square$

Theorem 10

Let T be a tree of order $n \ge 4$ with matching number 2. Then, for $a > 1$ and $b < 0$, we have

$$\begin{aligned} \mathrm{DEI}_{a,b}(T) \le [(n-2)^a + 2^a] 2^b + (n-2) 3^b \end{aligned}$$

with equality if and only if T is $P_2 (n-3, 1)$.

Proof

Let us present only the parts of the proof which are different from the proof of Theorem 9. By Corollary 1, among trees of the form $P_2 (r_2 , t_2)$, where $r_2 + t_2 = n-2$, the tree $P_2 (n-3, 1)$ has the maximum $\mathrm{DEI}_{a,b}$ index. Similarly, among trees of the form $P_3 (r_3 , t_3)$, where $r_3 + t_3 = n-3$, the tree $P_3 (n-4, 1)$ has the maximum $\mathrm{DEI}_{a,b}$ index. By Lemma 4, we have $\mathrm{DEI}_{a,b}(P_2 (n-3, 1)) > \mathrm{DEI}_{a,b}(P_3 (n-4, 1))$, which means that $P_2 (n-3, 1)$ is the tree with the maximum $\mathrm{DEI}_{a,b}$ index among trees of order n and matching number 2. $\square$

A subset S of V(G) is called an independent set of a graph G if no two vertices from S are adjacent in G. The independence number of G is the cardinality of a largest independent set. It is well known that for any tree of order n, independence number $\alpha$ and matching number $\beta$, we have

$$\begin{aligned} \alpha + \beta = n. \end{aligned}$$

Since $1 \le \beta \le \frac{n}{2}$, we obtain the bounds

$$\begin{aligned} \frac{n}{2} \le \alpha \le n-1. \end{aligned}$$

The only trees with independence number $n-1$ are stars. We present Theorems 11 and 12 for $\frac{n}{2} \le \alpha \le n-3$. In Theorem 13, we consider the case $\alpha = n-2$.

Since we have the equality $\alpha + \beta = n$, Theorem 7 says that if T is a tree of order n with matching number $n - \alpha$, where $3 \le n - \alpha \le \frac{n}{2}$, then for $0 < a \le 1$ and $b > 0$, we have

$$\begin{aligned} \mathrm{DEI}_{a,b}(T) \ge \alpha ^{a} 2^b + (n - \alpha -1)(2^a 3^b + 4^b) + (2\alpha {n} +1) 3^b \end{aligned}$$

with equality if and only if T is $T_{n, n-\alpha }$. Thus, from Theorem 7, we easily obtain Theorem 11.

Theorem 11

Let T be a tree of order n with independence number $\alpha$, where $\frac{n}{2} \le \alpha \le n-3$. Then, for $0 < a \le 1$ and $b > 0$, we have

$$\begin{aligned} \mathrm{DEI}_{a,b}(T) \ge \alpha ^{a} 2^b + (n - \alpha -1)(2^a 3^b + 4^b) + (2\alpha {n} +1) 3^b \end{aligned}$$

with equality if and only if T is $T_{n, n-\alpha }$.

Similarly, from Theorem 8 we get Theorem 12. Let us note that the inequality $\frac{n}{2} \le n-3$ implies that $n \ge 6$.

Theorem 12

Let T be a tree of order n with independence number $\alpha$, where $\frac{n}{2} \le \alpha \le n-3$. Then, for $a \ge 1$ and $b < 0$, we have

$$\begin{aligned} \mathrm{DEI}_{a,b}(T) \le \alpha ^{a} 2^b + ( n-\alpha -1)(2^a 3^b + 4^b) + (2\alpha {n} +1)3^b \end{aligned}$$

with equality if and only if T is $T_{n, n-\alpha }$.

Theorems 9 and 10 yield Theorem 13.

Theorem 13

Let T be a tree of order $n \ge 4$ with independence number $n-2$. Then, for $0< a < 1$ and $b > 0$, we have

$$\begin{aligned} \mathrm{DEI}_{a,b}(T) \ge [(n-2)^a + 2^a] 2^b + (n-2) 3^b. \end{aligned}$$

For $a > 1$ and $b < 0$, we have

$$\begin{aligned} \mathrm{DEI}_{a,b}(T) \le [(n-2)^a + 2^a] 2^b + (n-2) 3^b. \end{aligned}$$

The equalities hold if and only if T is $P_2 (n-3, 1)$.

5 Trees of Given Order and Bipartition

A graph G is bipartite if V(G) can be partitioned into the subsets $V_1$ and $V_2$, where every edge joins a vertex in $V_1$ with a vertex in $V_2$. If $V_1$ contains p vertices and $V_2$ contains q vertices, where $p + q = n$, then G has a (p, q)-bipartition. We can suppose that $p \ge q \ge 1$.

We state bounds on the general degree-eccentricity index for trees with a (p, q)-bipartition for $p \ge q \ge 2$, since the only tree with a (p, 1)-bipartition is the star $S_{p+1}$.

Theorem 14

Let T be any tree with n vertices and a (p, q)-bipartition, where $p \ge q \ge 2$. Then, for $0 < a \le 1$ and $b > 0$, we have

$$\begin{aligned} \mathrm{DEI}_{a,b}(T) \ge (p^a+q^a)2^b + (n-2)3^b \end{aligned}$$

with equality if and only if T is $P_2 (p-1, q-1)$.

Proof

Let T be any tree with n vertices and a (p, q)-bipartition having the minimum $\mathrm{DEI}_{a,b}$ index. We show that $T'$ is $P_2(p-1, q-1)$.

Suppose to the contrary that $T'$ is not $P_2(p-1, q-1)$. Let $v_0v_1\dots v_d$ be a diametral path of $T'$. For $p \ge q \ge 2$, there is no tree of diameter $d \le 2$ and the unique tree with diameter 3 is $P_2(p-1, q-1)$; therefore, $d\ge 4$. Without loss of generality, suppose that $v_0$ is in the partite set $V_2$. Then, $v_1\in V_1$ and $v_2 \in V_2$. Let $u_1, u_2 , \dots , u_{r}$ be all the (pendant) vertices adjacent to $v_{d-1}$ in $T'$. Note that $v_d$ is one of them, so $r\ge 1$. We consider three cases.

Case 1: d is odd.

Then, we have $v_{d-1}\in V_2$ and $v_d\in V_1$. Let $V(T'') = V(T')$ and $E(T'') = \{ v_2 u_1$, $v_2 u_2, \dots , v_2 u_r \} \cup E(T') {\setminus } \{ v_{d-1}u_1, v_{d-1}u_2, \dots , v_{d-1}u_r \}$. Then the tree $T''$ has n vertices and a (p, q)-bipartition. Let $d_{T'}(v_2) = t \ge 2$. Then, $d_{T''} (v_2) = t+r$, $d_{T'}(v_{d-1}) = r+1$, $d_{T''}(v_{d-1}) = 1$ and $d_{T'}(x) = d_{T''}(x)$ for $x\in V(T') {\setminus } \{v_2, v_{d-1}\}$. For each $x \in V(T')$, we obtain $\mathrm{ecc}_{T'}(x) \ge \mathrm{ecc}_{T''}(x)$, so $\mathrm{ecc}^b_{T'}(x) \ge \mathrm{ecc}^b_{T''}(x)$. Note that $\mathrm{ecc}_{T'}(v_2) = d-2$, $\mathrm{ecc}_{T''}(v_2) \le d-2$ and $\mathrm{ecc}_{T'}(v_{d-1}) = \mathrm{ecc}_{T''}(v_{d-1}) = d-1$. Thus

$$\begin{aligned} \mathrm{DEI}_{a,b}(T')- \mathrm{DEI}_{a,b}(T'')\ge & {} d^{a}_{T'}(v_2) \mathrm{ecc}^b_{T'}(v_2) - d^{a}_{T''}(v_2) \mathrm{ecc}^b_{T''}(v_2)\\&+ d^{a}_{T'}(v_{d-1}) \mathrm{ecc}^b_{T'}(v_{d-1}) - d^{a}_{T''}(v_{d-1}) \mathrm{ecc}^b_{T''}(v_{d-1})\\\ge & {} [t^a- (t+r)^a] (d-2)^b + [(r+1)^{a} - 1^{a}] (d-1)^b\\> & {} ([t^a - (t+r)^a] + [(r+1)^{a} - 1^{a}]) (d-2)^b\\\ge & {} 0, \end{aligned}$$

since by Lemma 1, we have $(r+1)^{a}- 1^{a} > (t+r)^{a} - t^{a}$ for $0< a <1$ and $[t^a - (t+r)^a] + [(r+1)^{a} - 1^{a}] = 0$ for $a=1$. Hence, $\mathrm{DEI}_{a,b}(T') > \mathrm{DEI}_{a,b}(T'')$.

Case 2: d is even and $0< a < 1$.

Then $v_{d-1}\in V_1$ and $v_d\in V_2$. Let $T''$ be the tree with $V(T'') = V(T')$ and $E(T'') = \{ v_1 u_1, v_1 u_2, \dots , v_1 u_r \} \cup E(T') {\setminus } \{ v_{d-1}u_1, v_{d-1}u_2, \dots , v_{d-1}u_r \}$. Let $d_{T'}(v_1) = t \ge 2$. Then, $d_{T''} (v_1) = t+r$, $d_{T'}(v_{d-1}) = r+1$, $d_{T''}(v_{d-1}) = 1$ and $d_{T'}(x) = d_{T''}(x)$ for all $x\in V(T') {\setminus } \{v_1, v_{d-1}\}$. For each $x \in V(T')$, we obtain $\mathrm{ecc}_{T'}(x) \ge \mathrm{ecc}_{T''}(x)$, so $\mathrm{ecc}^b_{T'}(x) \ge \mathrm{ecc}^b_{T''}(x)$. Note that $\mathrm{ecc}_{T'}(v_1) = d-1$, $\mathrm{ecc}_{T''}(v_1) \le d-1$ and $\mathrm{ecc}_{T'}(v_{d-1}) = \mathrm{ecc}_{T''}(v_{d-1}) = d-1$. Thus,

$$\begin{aligned} \mathrm{DEI}_{a,b}(T')- \mathrm{DEI}_{a,b}(T'')\ge & {} d^{a}_{T'}(v_1) \mathrm{ecc}^b_{T'}(v_1) - d^{a}_{T''}(v_1) \mathrm{ecc}^b_{T''}(v_1)\\&+ d^{a}_{T'}(v_{d-1}) \mathrm{ecc}^b_{T'}(v_{d-1}) - d^{a}_{T''}(v_{d-1}) \mathrm{ecc}^b_{T''}(v_{d-1})\\\ge & {} [t^a- (t+r)^a] (d-1)^b + [(r+1)^{a} - 1^{a}] (d-1)^b\\> & {} 0, \end{aligned}$$

since by Lemma 1, we have $(r+1)^{a}- 1^{a} > (t+r)^{a} - t^{a}$ for $0< a < 1$. Hence, $\mathrm{DEI}_{a,b}(T') > \mathrm{DEI}_{a,b}(T'')$.

Case 3: d is even and $a = 1$.

Let $u_1, u_2, \dots , u_{s}$ be all the (pendant) vertices at distance d from $v_0$ in $T'$. Note that $v_d$ is one of them, so $s\ge 1$. Let $u'_i$ be the neighbor of $u_i$ in $T'$, where $i = 1, 2, \dots , s$. The vertices in the set $U' = \{ u'_1, u'_2, \dots , u'_{s} \}$ are not necessarily different, so we have $|U'| = l$, where $1 \le l \le s$.

For the tree $T''$, let $V(T'') = V(T')$ and $E(T'') = \{ v_1 u_1$, $v_1 u_2, \dots , v_1 u_s \} \cup E(T') {\setminus } \{ u'_1 u_1$, $u'_2 u_2, \dots , u'_s u_s \}$. Then, the tree $T''$ has n vertices and a (p, q)-bipartition. Let $d_{T'}(v_1) = t \ge 2$. Then $d_{T''} (v_1) = t+s$. All the vertices in $U'$ have degree 1 in $T''$; therefore, $\sum _{u' \in U'} d_{T''} (u') = l$. We know that $\sum _{u' \in U'} d_{T'} (u') = l + s$. For $x\in V(T') {\setminus } (U' \cup \{v_1 \} )$, we obtain $d_{T'}(x) = d_{T''}(x)$.

For each $x \in V(T')$, we get $\mathrm{ecc}_{T'}(x) \ge \mathrm{ecc}_{T''}(x)$, so $\mathrm{ecc}^b_{T'}(x) \ge \mathrm{ecc}^b_{T''}(x)$. Note that $\mathrm{ecc}_{T'}(v_1) = d-1$, $\mathrm{ecc}_{T''}(v_1) = d-2$ and $\mathrm{ecc}_{T'}(u') = \mathrm{ecc}_{T''}(u') = d-1$ for every $u' \in U'$. Thus,

$$\begin{aligned} \mathrm{DEI}_{1,b}(T')- \mathrm{DEI}_{1,b}(T'')\ge & {} \sum _{u' \in U'} [ d_{T'} (u') \mathrm{ecc}^b_{T'}(u') - d_{T''} (u') \mathrm{ecc}^b_{T''}(u') ]\\&\ + d_{T'}(v_1) \mathrm{ecc}^b_{T'}(v_1) - d_{T''}(v_1) \mathrm{ecc}^b_{T''}(v_1)\\= & {} [(l+s)- l] (d-1)^b + t (d-1)^b - (t+s) (d-2)^b\\= & {} (t+s) [(d-1)^b - (d-2)^b]\\> & {} 0. \end{aligned}$$

Hence, $\mathrm{DEI}_{1,b}(T') > \mathrm{DEI}_{1,b}(T'')$.

In all 3 cases we showed that $T'$ does not have the minimum $\mathrm{DEI}_{a,b}$ index, which is a contradiction.

Thus, $T'$ is $P_2(p-1, q-1)$. The graph $P_2(p-1, q-1)$ contains $p+q-2 = n-2$ vertices having degree 1 and eccentricity 3, one vertex having degree p and eccentricity 2, and one vertex of degree q and eccentricity 2. Hence,

$$\begin{aligned} \mathrm{DEI}_{a,b}(P_2(p-1, q-1)) = (p^a+q^a)2^b + (n-2)3^b. \end{aligned}$$

$\square$

Theorem 15

Let T be any tree with n vertices and a (p, q)-bipartition, where $p \ge q \ge 2$. Then, for $a \ge 1$ and $b<0$, we have

$$\begin{aligned} \mathrm{DEI}_{a,b}(T) \le (p^a+q^a)2^b + (n-2)3^b \end{aligned}$$

with equality if and only if T is $P_2 (p-1, q-1)$.

Proof

We present the parts of the proof of Theorem 15 which are different from the proof of Theorem 14.

Let T be any tree with n vertices and a (p, q)-bipartition having the maximum $\mathrm{DEI}_{a,b}$ index. Suppose to the contrary that $T'$ is not $P_2(p-1, q-1)$.

In Case 1, where d is odd, for each $x \in V(T')$, we obtain $\mathrm{ecc}_{T'}(x) \ge \mathrm{ecc}_{T''}(x)$, so $\mathrm{ecc}^b_{T'}(x) \le \mathrm{ecc}^b_{T''}(x)$. Since $\mathrm{ecc}_{T''}(v_2) \le d-2$, we get $\mathrm{ecc}^b_{T''}(v_2) \ge (d-2)^b$ and

$$\begin{aligned} \mathrm{DEI}_{a,b}(T')- \mathrm{DEI}_{a,b}(T'')\le & {} d^{a}_{T'}(v_2) \mathrm{ecc}^b_{T'}(v_2) - d^{a}_{T''}(v_2) \mathrm{ecc}^b_{T''}(v_2)\\&+ d^{a}_{T'}(v_{d-1}) \mathrm{ecc}^b_{T'}(v_{d-1}) - d^{a}_{T''}(v_{d-1}) \mathrm{ecc}^b_{T''}(v_{d-1})\\\le & {} [t^a- (t+r)^a] (d-2)^b + [(r+1)^{a} - 1^{a}] (d-1)^b\\< & {} ([t^a - (t+r)^a] + [(r+1)^{a} - 1^{a}]) (d-2)^b\\\le & {} 0, \end{aligned}$$

since by Lemma 1, we have $(r+1)^{a}- 1^{a} < (t+r)^{a} - t^{a}$ for $a > 1$ and $[t^a - (t+r)^a] + [(r+1)^{a} - 1^{a}] = 0$ for $a=1$. Hence, $\mathrm{DEI}_{a,b}(T') < \mathrm{DEI}_{a,b}(T'')$.

Case 2 is for even d and $a > 1$. For each $x \in V(T')$, we get $\mathrm{ecc}_{T'}(x) \ge \mathrm{ecc}_{T''}(x)$, so $\mathrm{ecc}^b_{T'}(x) \le \mathrm{ecc}^b_{T''}(x)$. Note that $\mathrm{ecc}_{T''}(v_1) \le d-1$; therefore, $\mathrm{ecc}^b_{T''}(v_1) \ge (d-1)^b$. We have

$$\begin{aligned} \mathrm{DEI}_{a,b}(T')- \mathrm{DEI}_{a,b}(T'')\le & {} d^{a}_{T'}(v_1) \mathrm{ecc}^b_{T'}(v_1) - d^{a}_{T''}(v_1) \mathrm{ecc}^b_{T''}(v_1)\\&+ d^{a}_{T'}(v_{d-1}) \mathrm{ecc}^b_{T'}(v_{d-1}) - d^{a}_{T''}(v_{d-1}) \mathrm{ecc}^b_{T''}(v_{d-1})\\\le & {} [t^a- (t+r)^a] (d-1)^b + [(r+1)^{a} - 1^{a}] (d-1)^b\\< & {} 0, \end{aligned}$$

since by Lemma 1, we obtain $(r+1)^{a}- 1^{a} < (t+r)^{a} - t^{a}$ for $a > 1$. Hence, $\mathrm{DEI}_{a,b}(T') < \mathrm{DEI}_{a,b}(T'')$.

Case 3 is for even d and $a = 1$. For each $x \in V(T')$, we get $\mathrm{ecc}_{T'}(x) \ge \mathrm{ecc}_{T''}(x)$, so $\mathrm{ecc}^b_{T'}(x) \le \mathrm{ecc}^b_{T''}(x)$. Thus

$$\begin{aligned} \mathrm{DEI}_{1,b}(T')- \mathrm{DEI}_{1,b}(T'')\le & {} \sum _{u' \in U'} [ d_{T'} (u') \mathrm{ecc}^b_{T'}(u') - d_{T''} (u') \mathrm{ecc}^b_{T''}(u') ]\\&+ \ d_{T'}(v_1) \mathrm{ecc}^b_{T'}(v_1) - d_{T''}(v_1) \mathrm{ecc}^b_{T''}(v_1)\\= & {} (t+s) [(d-1)^b - (d-2)^b]\\< & {} 0. \end{aligned}$$

Hence, $\mathrm{DEI}_{1,b}(T') < \mathrm{DEI}_{1,b}(T'')$.

Hence, $T'$ is not a tree having the maximum $\mathrm{DEI}_{a,b}$ index, which is a contradiction. $\square$

6 Trees of Given Order and Domination Number

A dominating set $\Gamma$ in a graph G is a subset of V(G) such that each vertex not in $\Gamma$ is adjacent to a vertex in $\Gamma$. The domination number of G is the cardinality of a smallest dominating set. From the work of Ore [18], we know that for any connected graph with n vertices and domination number $\gamma$, we have

$$\begin{aligned} 1 \le \gamma \le \frac{n}{2}. \end{aligned}$$

Both bounds can be achieved by trees, since stars have domination number 1 and for the trees $T_{2\gamma , \gamma }$ defined in Sect. 4, we have $\gamma = \frac{n}{2}$.

In Theorems 16 and 17, we state sharp bounds for the general degree-eccentricity index of trees having domination number 2. Bounds for trees with domination number $\lceil \frac{n}{3}\rceil$ are given in Theorems 18 and 19.

The only trees of order $n \le 5$ and domination number 2 are $P_4$, $P_5 \cong P_3 (1,1)$ and $P_2 (2,1)$. By Lemma 3, for $0< a < 1$ and $b > 0$, we have $\mathrm{DEI}_{a,b}(P_2 (2,1)) < \mathrm{DEI}_{a,b} (P_3 (1,1))$. By Lemma 4, for $a > 1$ and $b < 0$, we have $\mathrm{DEI}_{a,b}(P_2 (2,1)) > \mathrm{DEI}_{a,b} (P_3 (1,1))$. Thus, in Theorems 16 and 17, we investigate bounds for $n \ge 6$.

Theorem 16

Let T be a tree having order $n \ge 6$ and domination number 2. Then for $0< a < 1$ and $b > 0$,

$$\begin{aligned} \mathrm{DEI}_{a,b}(T) \le \left( \left\lceil \frac{n-2}{2}\right\rceil ^{a}+\left\lfloor \frac{n-2}{2}\right\rfloor ^{a}\right) 4^b + 2^{a+1} 3^b + (n-4) 5^b \end{aligned}$$

with equality if and only if T is $P_4 ( \lceil \frac{n-4}{2}\rceil , \lfloor \frac{n-4}{2}\rfloor )$.

Proof

The only trees with domination number 2 are $P_2 (r_2 , t_2)$, where $r_2 + t_2 = n-2$, $P_3 (r_3 , t_3)$, where $r_3 + t_3 = n-3$ and $P_4 (r_4 , t_4)$, where $r_4 + t_4 = n-4$. From Corollary 1, we know that among trees of the form $P_2 (r_2 , t_2)$, where $r_2 + t_2 = n-2$, the tree $P_2 ( \lceil \frac{n-2}{2}\rceil , \lfloor \frac{n-2}{2}\rfloor )$ has the maximum $\mathrm{DEI}_{a,b}$ index. Among trees of the form $P_3 (r_3 , t_3)$, where $r_3 + t_3 = n-3$, the tree $P_3 ( \lceil \frac{n-3}{2}\rceil , \lfloor \frac{n-3}{2}\rfloor )$ has the maximum $\mathrm{DEI}_{a,b}$ index. Similarly, $P_4 ( \lceil \frac{n-4}{2}\rceil , \lfloor \frac{n-4}{2}\rfloor )$ is the tree having the maximum $\mathrm{DEI}_{a,b}$ index among trees of the form $P_4 (r_4 , t_4)$, where $r_4 + t_4 = n-4$. We need to compare $\mathrm{DEI}_{a,b}(P_2 ( \lceil \frac{n-2}{2}\rceil , \lfloor \frac{n-2}{2}\rfloor ))$, $\mathrm{DEI}_{a,b}(P_3 ( \lceil \frac{n-3}{2}\rceil , \lfloor \frac{n-3}{2}\rfloor ))$ and $\mathrm{DEI}_{a,b}(P_4 ( \lceil \frac{n-4}{2}\rceil , \lfloor \frac{n-4}{2}\rfloor ))$. By Lemma 3, $\mathrm{DEI}_{a,b}(P_2 ( \lceil \frac{n-2}{2}\rceil , \lfloor \frac{n-2}{2}\rfloor ))< \mathrm{DEI}_{a,b}(P_3 ( \lceil \frac{n-3}{2}\rceil , \lfloor \frac{n-3}{2}\rfloor )) < \mathrm{DEI}_{a,b}(P_4 ( \lceil \frac{n-4}{2}\rceil , \lfloor \frac{n-4}{2}\rfloor ))$, which implies that $P_4 ( \lceil \frac{n-4}{2}\rceil , \lfloor \frac{n-4}{2}\rfloor )$ is the tree with the maximum $\mathrm{DEI}_{a,b}$ index among trees of order n and domination number 2. The tree $P_4 ( \lceil \frac{n-4}{2}\rceil , \lfloor \frac{n-4}{2}\rfloor )$ contains $n-4$ vertices of degree 1 and eccentricity 5, two vertices of degree 2 and eccentricity 3, a vertex of degree $\lceil \frac{n-2}{2} \rceil$ and eccentricity 4 and a vertex of degree $\lfloor \frac{n-2}{2} \rfloor$ and eccentricity 4. Therefore,

$$\begin{aligned}&\mathrm{DEI}_{a,b} \left( P_4 \left( \left\lceil \frac{n-4}{2}\right\rceil , \left\lfloor \frac{n-4}{2}\right\rfloor \right) \right) \\&\quad = \left( \left\lceil \frac{n-2}{2}\right\rceil ^{a}+\left\lfloor \frac{n-2}{2}\right\rfloor ^{a}\right) 4^b + 2^{a+1} 3^b + (n-4) 5^b. \end{aligned}$$

$\square$

The proof of Theorem 17 is similar to the proof of Theorem 16.

Theorem 17

Let T be a tree having order $n \ge 6$ and domination number 2. Then, for $a > 1$ and $b < 0$,

$$\begin{aligned} \mathrm{DEI}_{a,b}(T) \ge \left( \left\lceil \frac{n-2}{2}\right\rceil ^{a}+\left\lfloor \frac{n-2}{2}\right\rfloor ^{a}\right) 4^b + 2^{a+1} 3^b + (n-4) 5^b \end{aligned}$$

with equality if and only if T is $P_4 ( \lceil \frac{n-4}{2}\rceil , \lfloor \frac{n-4}{2}\rfloor )$.

Theorem 18

Let T be a tree having order $n \ge 4$ and domination number $\lceil \frac{n}{3}\rceil$. Then, for $0 < a \le 1$ and $b > 0$,

$$\begin{aligned} \mathrm{DEI}_{a,b} (T) \le \mathrm{DEI}_{a,b}(P_n) \end{aligned}$$

with equality if and only if T is $P_n$.

Proof

By Theorem 1, the path $P_n$ is the only tree having the maximum $\mathrm{DEI}_{a,b}$ index among trees of order n. Thus, it suffices to show that $\gamma (P_n) = \lceil \frac{n}{3}\rceil$.

Let $n=3k - \epsilon$, where $k \ge 2$ and $0 \le \epsilon \le 2$ and let $P_{3k - \epsilon } = v_1v_2\dots v_{3k - \epsilon }$. We use the set $S = \{v_2, v_5,\dots , v_{3k-4} \}$ of $k-1$ vertices. If $n=3k-2$, then $S \cup \{v_{3k-2} \}$ is a dominating set of $P_n$. If $n=3k-1$ or $n=3k$, then $S \cup \{v_{3k-1}\}$ is a dominating set of $P_n$. Thus, $\gamma (P_n) \le k = \lceil \frac{n}{3}\rceil$.

The path $P_n$ has at least $3(k-1) + 1$ vertices. If $P_n$ has a dominating set $\Gamma$, where $| \Gamma | \le k-1$, then $P_n$ contains a vertex, say $u \in \Gamma$, which dominates 3 vertices of $P_n$ other than u, which is not possible. Hence, $\gamma (P_n) = k = \lceil \frac{n}{3}\rceil$, which means that $P_n$ is the tree with the maximum $\mathrm{DEI}_{a,b}$ index among trees with n vertices and domination number $\lceil \frac{n}{3}\rceil$. $\square$

By Theorem 2, the path $P_n$ is the only tree having the minimum $\mathrm{DEI}_{a,b}$ index among trees of order n for $a \ge 1$ and $b < 0$. Since the domination number of $P_n$ is $\lceil \frac{n}{3}\rceil$, we obtain the following theorem.

Theorem 19

Let T be a tree having order $n \ge 4$ and domination number $\lceil \frac{n}{3}\rceil$. Then, for $a \ge 1$ and $b < 0$,

$$\begin{aligned} \mathrm{DEI}_{a,b} (T) \ge \mathrm{DEI}_{a,b}(P_n) \end{aligned}$$

with equality if and only if T is $P_n$.

From [18], we know that $1 \le \gamma \le \frac{n}{2}$ for any tree of order n and domination number $\gamma$. The only trees of domination number 1 are stars. We found sharp bounds on the $\mathrm{DEI}_{a,b}$ index only for $\gamma = 2$ and $\gamma = \lceil \frac{n}{3}\rceil$. It would be interesting to know sharp bounds also for $3 \le \gamma \le \frac{n}{2}$, where $\gamma \ne \lceil \frac{n}{3}\rceil$. This remains an open problem.