The Implicit Equation of a Holditch Curve

Abstract

Holditch’s theorem is a classical geometrical result on the areas of a given closed curve and another one, its Holditch curve, which is constructed as the locus of a fixed point dividing a chord of constant length that moves with its endpoints over the given curve and that returns back to its original position after some full revolution. Holditch curves have already been studied from the parametric point of view, although numerical methods and approximations are often necessary for their computation. In this paper, implicit equations of Holditch curves of algebraic curves are studied. The implicit equations can be simply found from the computation of a resultant of two polynomials. With the same techniques, Holditch curves of two initial algebraic curves are also considered. Moreover, the use of implicit equations allows to find new and explicit parameterizations of non-trivial Holditch curves, such as in the case of having an ellipse as an initial curve.

1 Introduction

Given $p\in \left[ 0,1\right]$ and a planar curve $\alpha$, consider that a chord of constant length $\ell >0$ can be positioned with its two endpoints over $\alpha$. A smooth motion of such a chord with its endpoints always lying on $\alpha$ may be allowed while trying to return to its original position after possibly some full revolutions. We say that $H_{p}$ is a p-Holditch curve of $\alpha$ for a chord length $\ell$ if it is the locus of points that split the chord of constant length $\ell$ in a ratio $p:1-p$ for all its possible positions during its smooth motion (see Fig. 1).

Fig. 1

A p-Holditch curve $H_p$ of a convex curve $\alpha$, for $p=\frac{1}{3}$. Holditch’s theorem gives the shaded area between both curves

Holditch’s theorem is a classical geometrical result [1] that states that the difference between the (algebraic) areas of a closed curve $\alpha$ and a p-Holditch curve $H_p$ of $\alpha$ for a chord length $\ell$ is only dependent on $\ell$ and p. More specifically, it holds

$$\begin{aligned} \mathcal {A}(\alpha ) - \mathcal {A}(H_p) = \pi \,p\,(1-p)\,\ell ^2. \end{aligned}$$

There are many works treating Holditch’s theorem and related scenarios, the interested reader can see [2,3,4,5,6,7] and their references therein.

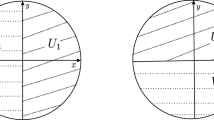
The initial position of the moving chord is decisive, as it could give rise to a different p-Holditch curve (see Fig. 2). In addition, notice that retrograde movements may be necessary in some cases to complete the motion. These happen when an endpoint of the moving chord passes through the same point for different time instants.

Fig. 2

Two $\frac{1}{2}$-Holditch curves of a Cassini oval for the same chord length. The initial position of the chord determines the curve that is found during the motion

The analytical parametric computation of Holditch curves is often difficult and numerical approximations are needed, particularly in the cases where retrograde movements appear. In this paper, we study Holditch curves using implicit equations. We will see that this approach is also useful for finding explicit parameterizations of Holditch curves.

In Sect. 2, given a planar curve $\alpha$ and $p\in \left[ 0,1\right]$, we define the geometric p-Holditch curve of $\alpha$ for a chord length $\ell >0$ as the locus of points that split in a ratio $p:1-p$ any chord of constant length $\ell$ positioned with its endpoints over $\alpha$. We have mentioned that different p-Holditch curves can be obtained depending on the initial position of the moving chord. In essence, the geometric p-Holditch curve is the union (possibly disconnected) of all p-Holditch curves for a chord length $\ell$. This means that in the geometric p-Holditch curve any initial position of the moving chord and any movement is considered. In particular, we show that the geometric p-Holditch curve also includes the set of points given by a $(1-p)$-Holditch curve (Proposition 1).

With the same idea used for the definition of a geometric Holditch curve, one can find simple parameterizations of some Holditch curves by using the implicit equation of the initial curve, even in the case of retrograde movements. We study the case of a parabola in Example 1.

Later, in Sect. 3, we focus on real algebraic curves. We solve an implicitization problem for Holditch curves, in the sense that we find a real algebraic curve that contains the geometric Holditch curve (Theorem 1). The proof is constructive and allows a way to find implicit equations of geometric Holditch curves by computing a resultant of two polynomials. The derived implicit equation will consist of all the possible p-Holditch curves for a chord length $\ell$ that can be considered for such an algebraic curve. That is, it will include all the possible p-Holditch curves that can be found depending on the initial position of the moving chord. We show several examples, including the ellipse and the hyperbola.

The polynomial defined by the resultant could include extraneous factors and undesired points [8], that is, points which do not actually belong to the geometric Holditch curve but that can appear from the implicitization process. In particular we would also like to mention the paper [9] in which the authors study implicit equations for offset curves. In such a paper, the implicit equation gives a double-offset and it is showed that it cannot be factorized into two factors, each of which containing a one-sided offset. In the same way, for our case we observe that in general, for $p\ne \frac{1}{2}$, we cannot split our implicit equation into two factors, one of them containing a p-Holditch curve and the other a $(1-p)$-Holditch curve (Remark 3).

In Sect. 4 we extend the results to the case of having a Holditch curve of two initial curves. In particular, we also have that if the two initial curves are algebraic, then the geometric Holditch curve that we define in this case is included in an algebraic curve (Theorem 2).

Finally, in Sect. 5, we focus on the Holditch curve of an ellipse. Thanks to the implicit equation of its Holditch curve we are able to obtain an explicit parameterization of the endpoints of the moving chord along the ellipse, even in the case of retrograde motion. As a result, we obtain an explicit parameterization of the Holditch curve of an ellipse. Up to our knowledge, this is the first explicit parameterization of the Holditch curve of an ellipse making unnecessary the use of numerical methods.

2 The Geometric Holditch Curve

Let us suppose that a planar curve ${{\mathcal {C}}}$ is defined by an implicit equation

$$\begin{aligned} f(x,y) = 0. \end{aligned}$$

Given $p\in \left[ 0,1\right]$ and $\ell >0$, let us define the geometric p-Holditch curve of $\mathcal {C}$ for a chord length $\ell$, ${{\mathcal {H}}}_p$, as the set of points $(x,y)\in {{\mathbb {R}}}^2$ such that there exists an angle $t\in {{\mathbb {R}}}$ for which

$$\begin{aligned} (x,y)-p\,\ell \,\bigl (\cos t,\,\sin t\bigr )\in {{\mathcal {C}}} \qquad \textrm{and}\qquad (x,y)+(1-p)\,\ell \,\bigl (\cos t,\,\sin t\bigr )\in {{\mathcal {C}}}. \end{aligned}$$

Equivalently, such that

$$\begin{aligned} f(x-p\,\ell \cos t,\,y-p\,\ell \sin t)&= 0,\nonumber \\ f\bigl (x+(1-p)\,\ell \cos t,\,y+(1-p)\,\ell \sin t\bigr )&=0. \end{aligned}$$

(1)

See a geometric p-Holditch curve of an ellipse in Fig. 3.

Fig. 3

Plot of a geometric p-Holditch curve of an ellipse for a chord length $\ell$

As an immediate consequence from the definition, we have the following property, which shows how the geometric p-Holditch curve is composed by both a p-Holditch curve and a $(1-p)$-Holditch curve (see Fig. 4).

Fig. 4

The geometric p-Holditch curve is composed by a p-Holditch curve and a $(1-p)$-Holditch curve for the same chord length

Proposition 1

Let $\mathcal {C}$ be a planar curve defined by an implicit equation $f(x,y)=0$ and let $\mathcal {H}_p$ be its geometric p-Holditch curve for a chord lengh $\ell >0$ and $p\in \left[ 0,1\right]$. If $(x,y)\in {{\mathcal {H}}}_p$, then $(x,y)+(1-2\,p)\,\ell \,(\cos t,\,\sin t)\in {{\mathcal {H}}}_p$.

Proof

The point $(x,y)+(1-2\,p)\,\ell \,(\cos t,\,\sin t)$ belongs to $\mathcal {H}_p$ because by definition we have the angle $t+\pi$ such that

$$\begin{aligned}&(x,y) + (1-2\,p)\,\ell \,(\cos t,\,\sin t)-p\,\ell \,\bigl (\cos (t+\pi ),\,\sin (t+\pi )\bigr )\\&\quad =(x,y) + (1-p)\,\ell \,(\cos t,\,\sin t) \end{aligned}$$

and

$$\begin{aligned}&(x,y) + (1-2\,p)\,\ell \,(\cos t,\,\sin t)+(1-p)\,\ell \,\bigl (\cos (t+\pi ),\,\sin (t+\pi )\bigr )\\&\quad =(x,y) - p\,\ell \,(\cos t,\,\sin t) \end{aligned}$$

are points of $\mathcal {C}$. $\square$

Remark 1

Notice that the points of Proposition 1 are the same if $p=\frac{1}{2}$:

$$\begin{aligned} (x,y) + (1-2\,p)\,\ell \,(\cos t,\,\sin t) = (x,y). \end{aligned}$$

This means that the geometric $\frac{1}{2}$-Holditch curve coincides with the $\frac{1}{2}$-Holditch curve (see an example in Fig. 5).

Fig. 5

Example of a geometric $\frac{1}{2}$-Holditch curve of an ellipse

Example 1

Consider the parabola $\alpha (t) = (t,\,a\,t^2)$, where $a\in {\mathbb {R}}\setminus \{0\}$ and let us try to compute the Holditch curve of $\alpha$ for a chord length $\ell >0$.

If we assume that there is no retrograde motion for the moving chord (i.e., taking a small enough chord length), we can suppose that the first endpoint can be parameterized by $\alpha (t)$, so that the second endpoint must be some $\alpha (s)$ such that

$$\begin{aligned} \bigl \Vert \alpha (t)-\alpha (s)\bigr \Vert ^2=\ell ^2. \end{aligned}$$

Explicitly, this can be written as

$$\begin{aligned} (t-s)^2+a^2\bigl (t^2-s^2\bigr )^2=\ell ^2. \end{aligned}$$

which is an equation of 4th degree in t and s. It is technically possible to find s in terms of t (although the expressions are complicated). However, to get a continuous function $s=f(t)$ different solutions must be considered and the function has to be defined piecewise. After that, the p-Holditch curve can be parameterized by

$$\begin{aligned} H_p(t) = (1-p)\,\alpha (t) + p\,\alpha \bigl (f(t)\bigr ). \end{aligned}$$

We are going to show how the use of the implicit equation $y-a\,x^2=0$ of the parabola can help us to find an easier parameterization of the Holditch curve that will also work in the case of a retrograde motion. Suppose now that if $\alpha (t)$ is the first endpoint of the moving chord, then the second endpoint is $\alpha (t) + \ell \,(\cos u,\,\sin u)$, for some $u\in \left[ 0,2\pi \right]$. Since the second endpoint must lie in the parabola, it must satisfy its implicit equation. This leads to

$$\begin{aligned} 2\,a\cos (u)\,t+a\,\ell \cos ^2(u)-\sin (u)=0. \end{aligned}$$

It is easier if we solve this equation for t instead of solving it for u:

$$\begin{aligned} t=\frac{\sin (u)-a\,\ell \cos ^2(u)}{2\,a\cos (u)}, \end{aligned}$$

where notice that $\cos (u)\ne 0$ because the moving chord is never vertical. This gives a parameterization of the first endpoint as:

$$\begin{aligned} \alpha _1(u)=\Biggl (\frac{\sin (u)-a\,\ell \cos ^2(u)}{2\,a\cos (u)},\,a \left( \frac{\sin (u)-a\,\ell \cos ^2(u)}{2\,a\cos (u)}\right) ^2 \Biggr ). \end{aligned}$$

The second endpoint is

$$\begin{aligned} \alpha _2(u) = \alpha _1(u) + \ell \,(\cos u,\,\sin u). \end{aligned}$$

Thus, given $p\in \left[ 0,1\right]$, the p-Holditch curve can be parameterized by

$$\begin{aligned} H_p(u) = (1-p)\,\alpha _1(u) + p\,\alpha _2(u),\quad u\in \left]-\frac{\pi }{2},\frac{\pi }{2}\right[. \end{aligned}$$

If we consider the domain $u\in \left]-\pi ,-\pi /2\right[ \cup \left]\pi /2,\pi \right[,$ the $(1-p)$-Holditch curve is obtained by the same expression (see Fig. 6).

Fig. 6

On the left, a parabola $\alpha$ and its p-Holditch curve $H_p$, for $a=1$, $\ell =2$ and $p=1/3$, as a parametric curve for $u\in \left]-\pi /2,\pi /2\right[$. On the right, a $(1-p)$-Holditch curve is also obtained for $u\in \left]-\pi ,-\pi /2\right[ \cup \left]\pi /2,\pi \right[$

3 Geometric Holditch Curve of an Algebraic Curve

Given a real algebraic curve $\mathcal {C}$, this is,

$$\begin{aligned} \mathcal {C}=\bigl \{(x,y)\in {\mathbb {R}}^2: f(x,y) = 0\bigr \}, \end{aligned}$$

where $f\in {\mathbb {R}}[x,y]$ is non-zero, we are interested now in their geometric Holditch curves.

Recall that the resultant of two non-zero polynomials over a field F is a polynomial expression of their coefficients that is equal to zero if and only if the polynomials have a common root in some extension of F (see e.g. [10,11,12]). Using the notion of a resultant of two polynomials, we aim to solve an implicitization problem for geometric Holditch curves. For technical issues we will need first the following lemma.

Lemma 1

Let $p,q\in {\mathbb {C}}[u]$ be polynomials of degree m and n, respectively. Consider the polynomials

$$\begin{aligned} {\widehat{p}}(u) \mathrel {\mathop :}=u^m\,p \left( -\frac{1}{u}\right) \quad \text {and}\quad {\widehat{q}}(u)\mathrel {\mathop :}=u^n\,q \left( -\frac{1}{u}\right) . \end{aligned}$$

• 1. If 0 is neither a root of p nor q, then

  $$\begin{aligned} {\text {Res}}_u(p,q)={\text {Res}}_u({\widehat{p}},{\widehat{q}}). \end{aligned}$$

• 2. If 0 is a root of p of multiplicity k, then

  $$\begin{aligned} {\text {Res}}_u(p,q) = \bigl ((-1)^{n}\,q(0)\bigr )^{k}\, {\text {Res}}_u({\widehat{p}},{\widehat{q}}). \end{aligned}$$

Proof

We can write

$$\begin{aligned} p(u)&= a\,(u-u_1)\,(u-u_2)\,\cdots \,(u-u_m),\\ q(u)&= b\,(u-v_1)\,(u-v_2)\,\cdots \,(u-v_n). \end{aligned}$$

Suppose that $u_i\ne 0$ and $v_j\ne 0$ for all i, j. Using the expression of the resultant of two polynomials in terms of their roots, we have

$$\begin{aligned} {\text {Res}}_u(p,q) = a^n\,b^m\,\prod _{i,j}(u_i-v_j). \end{aligned}$$

The polynomials ${\widehat{p}}$ and ${\widehat{q}}$ can be written as

$$\begin{aligned} {\widehat{p}}(u)&= (-1)^m\,a\,(1+u\,u_1)\,(1+u\,u_2)\,\cdots \,(1+u\,u_m),\\ {\widehat{q}}(u)&= (-1)^n\,a\,(1+u\,v_1)\,(1+u\,v_2)\,\cdots \,(1+u\,v_n), \end{aligned}$$

whose leading coefficients are $(-1)^m\,a\,\prod _{i}u_i$ and $(-1)^n\,b\,\prod _jv_j$, respectively, and their roots are $-1/u_i$ and $-1/v_j$. Therefore,

$$\begin{aligned} {\text {Res}}_u({\widehat{p}},{\widehat{q}})&=\biggl ((-1)^m\,a\,\prod _iu_i\biggr )^n\,\biggl ((-1)^n\,b\, \prod _jv_j\biggr )^m\prod _{i,j} \left( -\frac{1}{u_i}+\frac{1}{v_j}\right) \\&=a^nb^m\prod _{i,j}(u_i-v_j) = {\text {Res}}_u(p,q). \end{aligned}$$

Now, suppose that 0 is a root of p of multiplicity $k\ge 1$. If q has also the root 0, then both resultants are zero and the equality of the statement is satisfied. Thus, suppose that all $v_j$ are non-zero. Let I be the set of indices $1\le i\le m$ such that $u_i\ne 0$. Thus,

$$\begin{aligned} p(u)=a\,u^k\,\prod _{i\in I}(u-u_i) \end{aligned}$$

and

$$\begin{aligned} {\text {Res}}_u(p,q)=a^nb^m\biggl (\prod _j( -v_j)\biggr )^k\prod _{i\in I,j}(u_i-v_j). \end{aligned}$$

We have

$$\begin{aligned} {\widehat{p}}(u)&=u^m\,p \left( -\frac{1}{u}\right) =u^m\,a\, \left( -\frac{1}{u}\right) ^k \,\prod _{i\in I} \left( -\frac{1}{u}-u_i\right) \\&=u^{m-k}\,a\,(-1)^k\,(-1)^{m-k}\prod _{i\in I} \left( \frac{1+u\,u_i}{u}\right) = a\,(-1)^m\prod _{i\in I}(1+u\,u_i), \end{aligned}$$

which is a polynomial of degree $m-k$. Its leading coefficient is $a\,(-1)^m\prod _{i\in I}u_i$. Thus,

$$\begin{aligned} {\text {Res}}_u({\widehat{p}},{\widehat{q}})&=\biggl ((-1)^m\,a\,\prod _{i\in I}u_i\biggr )^n\, \biggl ((-1)^n\,b\,\prod _jv_j\biggr )^{m-k}\prod _{i\in I,j} \left( -\frac{1}{u_i}+\frac{1}{v_j}\right) \\&=a^nb^{m-k}\,(-1)^{nk}\prod _{i\in I,j}(u_i-v_j). \end{aligned}$$

Therefore,

$$\begin{aligned} b^k\,\biggl (\prod _jv_j\biggr )^k{\text {Res}}_u ({\widehat{p}},{\widehat{q}}) = {\text {Res}}_u(p,q). \end{aligned}$$

From this, by noticing that

$$\begin{aligned} q(0)= b\,(-1)^n\prod _{j=1}^n v_j, \end{aligned}$$

the expression of the statement is found. $\square$

Theorem 1

If $\mathcal {C}$ is an irreducible real algebraic curve and $\mathcal {H}_p$ is a geometric p-Holditch curve of $\mathcal {C}$, then there exists a real algebraic curve that contains $\mathcal {H}_p$.

Proof

Suppose that $\mathcal {C}$ is described by a non-zero polynomial f(x, y) of degree n.

The geometric p-Holditch curve ${{\mathcal {H}}}_p$ for a chord length $\ell >0$ is the set of points $(x,y)\in {\mathbb {R}}^2$ such that Eqs. (1) are satisfied for some angle $t\in {\mathbb {R}}$. Under the change of variables $t\rightarrow 2\arctan (u)$ we have

$$\begin{aligned} (\cos t,\,\sin t) = \left( \frac{1-u^2}{1+u^2},\,\frac{2\,u}{1+u^2}\right) , \end{aligned}$$

which provides, for $u\in {\mathbb {R}}$, a rational parameterization of ${\mathbb {S}}^1\setminus \{(-1,0)\}$.

Looking at Eqs. (1) with the new variable u, consider the set $\mathcal {H}^{*}_p$ of points $(x,y)\in {\mathbb {R}}^2$ such that there exists $u\in {\mathbb {R}}$ such that

$$\begin{aligned} g_1(x,y,u)&\mathrel {\mathop :}=\bigl (1+u^2\bigr )^k\,f \left( x-p\,\ell \,\frac{1-u^2}{1+u^2},\, y-p\,\ell \,\frac{2\,u}{1+u^2}\right) = 0,\nonumber \\ g_2(x,y,u)&\mathrel {\mathop :}=\bigl (1+u^2\bigr )^k\,f \left( x+(1-p)\,\ell \,\frac{1-u^2}{1+u^2},\,y+(1-p)\,\ell \,\frac{2\,u}{1+u^2}\right) =0, \end{aligned}$$

(2)

where $k\le n$ is the minimum natural number that makes $g_1$ and $g_2$ polynomials in u. Notice that $\mathcal {H}^{*}_p$ is included in $\mathcal {H}_p$.

Suppose that $g_1$ and $g_2$, as polynomials in ${\mathbb {R}}[x,y][u]$, have a common factor. This is, suppose that

$$\begin{aligned} g_1(x,y,u)&=\lambda (x,y,u)\,h_1(x,y,u),\\ g_2(x,y,u)&=\lambda (x,y,u)\,h_2(x,y,u), \end{aligned}$$

where $\gcd _u(h_1,h_2)=1$. The first observation is that $\lambda (x,y,u)$ cannot depend on (x, y). Indeed, given $u_0\in {\mathbb {R}}$, notice that $g_1(x,y,u_0)$ and $g_2(x,y,u_0)$ are translations of f(x, y), in its coordinates, multiplied by a constant factor depending on $u_0$. However, since f(x, y) is irreducible, any translation $f(x+a,y+b)$ must be irreducible as well. Therefore, $\lambda (x,y,u_0)$ cannot depend on (x, y). Thus, we have that

$$\begin{aligned} g_1(x,y,u)&=\lambda (u)\,h_1(x,y,u),\\ g_2(x,y,u)&=\lambda (u)\,h_2(x,y,u), \end{aligned}$$

for all $u\in {\mathbb {R}}$. Now, note that $\lambda (u)$ has no real roots, because otherwise there would exist some $u_0\in {\mathbb {R}}$ such that $g_1(x,y,u_0)=g_2(x,y,u_0)=0$ for all $(x,y)\in {\mathbb {R}}^2$, which implies that the set $\mathcal {H}^{*}_p$ is equal to ${\mathbb {R}}^2$ (and this cannot happen because a geometric p-Holditch curve cannot be ${\mathbb {R}}^2$).

Since $\lambda (u)$ has no real roots, we have

$$\begin{aligned} \mathcal {H}^{*}_p&= \bigl \{(x,y)\in {\mathbb {R}}^2 :\quad \exists u\in {\mathbb {R}}\quad g_1(x,y,u) = g_2(x,y,u) = 0\bigr \}\\&=\bigl \{(x,y)\in {\mathbb {R}}^2 :\quad \exists u\in {\mathbb {R}}\quad h_1(x,y,u) = h_2(x,y,u) = 0\bigr \}. \end{aligned}$$

Consider the resultant of the polynomials $h_1$ and $h_2$ with respect to u:

$$\begin{aligned} h(x,y)\mathrel {\mathop :}={\text {Res}}_u(h_1,h_2)\in {\mathbb {R}}[x,y], \end{aligned}$$

which is a non-zero polynomial because $\gcd _u(h_1,h_2)=1$.

Therefore, we have

$$\begin{aligned} \mathcal {H}^{*}_p\subseteq \bigl \{(x,y) \in {\mathbb {R}}^2: h(x,y) = 0\bigr \}. \end{aligned}$$

Now, it is left to justify that in fact the whole curve $\mathcal {H}_p$ also satisfies this relation (the points corresponding to $u=\infty$ are not included in $\mathcal {H}^{*}_p$).

Suppose that we consider now

$$\begin{aligned} - \left( \frac{1-u^2}{1+u^2},\,\frac{2\,u}{1+u^2}\right) , \end{aligned}$$

which is a rational parameterization of ${\mathbb {S}}^1\setminus \bigl \{(1,0)\bigr \}$ that includes the point $(-1,0)$. This parameterization can also be found by making the variable change $u\mapsto -1/u$ in the rational parameterization we considered above. Thus, define now the set $\widetilde{\mathcal {H}}^{*}_p$ of points $(x,y)\in {\mathbb {R}}^2$ such that there exists $u\in {\mathbb {R}}$ such that

$$\begin{aligned} {\widetilde{g}}_1(x,y,u)&\mathrel {\mathop :}=\bigl (1+u^2\bigr )^k\,f \left( x+p\,\ell \,\frac{1-u^2}{1+u^2},\, y+p\,\ell \,\frac{2\,u}{1+u^2}\right) = 0,\nonumber \\ {\widetilde{g}}_2(x,y,u)&\mathrel {\mathop :}=\bigl (1+u^2\bigr )^k\,f \left( x-(1-p)\,\ell \,\frac{1-u^2}{1+u^2},\,y-(1-p)\,\ell \,\frac{2\,u}{1+u^2}\right) =0. \end{aligned}$$

(3)

Analogously as above, we can write

$$\begin{aligned} {\widetilde{g}}_1(x,y,u)&={\widetilde{\lambda }}(u)\,{\widetilde{h}}_1(x,y,u),\\ {\widetilde{g}}_2(x,y,u)&={\widetilde{\lambda }}(u)\,{\widetilde{h}}_2(x,y,u), \end{aligned}$$

where $\gcd _u({\widetilde{h}}_1,{\widetilde{h}}_2)=1$. Notice that

$$\begin{aligned} u^{2k}\,g_i \left( x,y,-\frac{1}{u}\right) = {\widetilde{g}}_i(x,y,u),\qquad i=1,2. \end{aligned}$$

These are equalities of polynomials in u. With the notation of Lemma 1, we denote by ${\widehat{g}}_i$ the left-hand side polynomials, so that

$$\begin{aligned} {\widehat{g}}_i(x,y,u) = {\widetilde{g}}_i(x,y,u),\qquad i=1,2. \end{aligned}$$

Thus, we have

$$\begin{aligned} {\widetilde{\lambda }}(u)\,{\widetilde{h}}_i(x,y,u) = {\widehat{\lambda }}(u)\,{\widehat{h}}_i(x,y,u),\qquad i=1,2. \end{aligned}$$

We have that $u_0\in {\mathbb {C}}$ is a root of ${\widetilde{g}}_1$ and ${\widetilde{g}}_2$ for all $(x,y)\in {\mathbb {R}}^2$ if and only if it is a root of ${\widehat{g}}_1$ and ${\widehat{g}}_2$ for all $(x,y)\in {\mathbb {R}}^2$. Thus, by definition of $\lambda$ and ${\widetilde{\lambda }}$, we deduce that ${\widetilde{\lambda }}(u) = {\widehat{\lambda }}(u)$, up to a constant factor. Therefore, since $\gcd _u({\widetilde{h}}_1,{\widetilde{h}}_2)=1$, we have

$$\begin{aligned} 0\ne {\text {Res}}_u\Bigl ({\widetilde{h}}_1(x,y,u), \,{\widetilde{h}}_2(x,y,u)\Bigr )={\text {Res}}_u \Bigl ({\widehat{h}}_1(x,y,u),\,{\widehat{h}}_2(x,y,u)\Bigr ), \end{aligned}$$

up to a constant factor. Now, by Lemma 1, the set

$$\begin{aligned} \bigl \{(x,y)\in {\mathbb {R}}^2: {\text {Res}}_u\bigl ({\widetilde{h}}_1 (x,y,u),{\widetilde{h}}_2(x,y,u)\bigr ) = 0\bigr \} \end{aligned}$$

is equal to

$$\begin{aligned} \bigl \{(x,y)\in {\mathbb {R}}^2: h(x,y) = 0\bigr \}. \end{aligned}$$

Therefore,

$$\begin{aligned} \widetilde{\mathcal {H}}^{*}_p\subseteq \bigl \{(x,y)\in {\mathbb {R}}^2: h(x,y) = 0\bigr \}. \end{aligned}$$

Since $\mathcal {H}_p = \mathcal {H}^{*}_p\cup \widetilde{\mathcal {H}}^{*}_p$, we conclude that

$$\begin{aligned} \mathcal {H}_p\subseteq \bigl \{(x,y)\in {\mathbb {R}}^2: h(x,y) = 0\bigr \}, \end{aligned}$$

which is what we wanted to prove. $\square$

Remark 2

Consider the case $p=\frac{1}{2}$. Let $\mathcal {H}$ be the algebraic curve of Theorem 1 that contains the geometric p-Holditch curve $\mathcal {H}_p$ and let $(x,y)\in \mathcal {H}$. If $(x,y)\in \mathcal {H}_p$, then there exists a common root $u\in {\mathbb {R}}$ of $g_1$ and $g_2$ from Eqs. (2). If $u\ne 0$ this happens if and only if $-1/u$ is also a common root of $g_1$ and $g_2$. If $u=0$, then $u=0$ is also a common root of ${\widetilde{g}}_1$ and ${\widetilde{g}}_2$ from Eqs. (3). So, all the points $(x,y)\in \mathcal {H}_p$ are double.

Now, if $(x,y)\in \mathcal {H}\setminus \mathcal {H}_p$, which might happen due to extraneous factors or undesired points, it means that there exists a common root $u\in {\mathbb {C}}\setminus {\mathbb {R}}$ of $g_1$ and $g_2$. In such a case, the conjugated root ${\bar{u}}\in {\mathbb {C}}\setminus {\mathbb {R}}$ is also a common root of $g_1$ and $g_2$. So, these points are also double.

To sum up, if $p=\frac{1}{2}$, all the points of $\mathcal {H}$ are double.

Example 2

(Holditch curve of a circle) Consider a circle of radius r centered at (0, 0):

$$\begin{aligned} f(x,y) = x^2+y^2-r^2. \end{aligned}$$

We have

$$\begin{aligned} g_1(x,y,u)&= \bigl (1+u^2\bigr )\,\bigl (\ell ^2\,p^2-r^2+x^2+y^2\bigr )-2\,p\,\ell \, \bigl ((1-u^2)\,x+2\,u\,y\bigr ),\\ g_2(x,y,u)&= \bigl (1+u^2\bigr )\,\bigl ((1-p)^2\ell ^2-r^2+x^2+y^2 \bigr )\\ {}&\quad +2\,(1-p)\,\ell \,\bigl ((1-u^2)\,x+2\,u\,y\bigr ). \end{aligned}$$

The resultant of $g_1$ and $g_2$ is

$$\begin{aligned} h(x,y) = 16\,\ell ^2\,\bigl (x^2+y^2\bigr )\, \bigl (x^2+y^2+p\,(1-p)\,\ell ^2-r^2\bigr )^2. \end{aligned}$$

Notice that $x^2+y^2$ is an undesired extraneous factor that must be discarded. Therefore, the geometric p-Holditch curve for a chord length $\ell >0$ is given by

$$\begin{aligned} x^2+y^2 = r^2-p\,(1-p)\,\ell ^2, \end{aligned}$$

which is a circle.

Example 3

(Holditch curve of an ellipse) Consider an ellipse with half-axes a and b:

$$\begin{aligned} f(x,y) = \frac{x^2}{a^2}+\frac{y^2}{b^2}-1. \end{aligned}$$

Although that the resultant of $g_1$ and $g_2$ can be computed, it leads to a wide expression. However, it can be greatly simplified if $p=\frac{1}{2}$, which gives

$$\begin{aligned}{} & {} 16\,\ell ^8\,(a-b)^2(a+b)^2\Bigl (4\,a^6y^2\bigl (y^2-b^2\bigr ) +a^4b^2y^2\,\bigl (\ell ^2+4\,x^2\bigr )\\{} & {} \quad +a^2b^4x^2\,\bigl (\ell ^2 -4\,b^2+4\,y^2\bigr )+4\,b^6x^4\Bigr )^2. \end{aligned}$$

Therefore, the geometric $\frac{1}{2}$-Holditch curve for a chord length $\ell >0$ is given by

$$\begin{aligned} 4\,a^6y^2\bigl (y^2-b^2\bigr )+a^4b^2y^2\,\bigl (\ell ^2+4\,x^2 \bigr )+a^2b^4x^2\,\bigl (\ell ^2-4\,b^2+4\,y^2\bigr )+4\,b^6x^4=0.\nonumber \\ \end{aligned}$$

(4)

An example is plotted in Fig. 5.

Notice that the algebraic equation we have found can include undesired points that do not belong to the geometric Holditch curve. For instance, (0, 0) is a point that satisfies (4) for any $a,b,\ell >0$ but that does not belong to the geometric Holditch curve. Other undesired points different from the origin of coordinates can appear, as we will point out later in Remark 3.

Example 4

(Holditch curve of a hyperbola) Consider the hyperbola given by the implicit equation

$$\begin{aligned} f(x,y) = \frac{x^2}{a^2}-\frac{y^2}{b^2}-1=0. \end{aligned}$$

Similarly as with the ellipse, the resultant of $g_1$ and $g_2$ can be computed but it leads to a wide expression except for the case $p=\frac{1}{2}$. In such a case, the resultant of $g_1$ and $g_2$ is reduced to

$$\begin{aligned}{} & {} 16\,\ell ^8\,\bigl (a^2+b^2\bigr )^2\Bigl (-4\,a^6y^2\bigl (b^2 +y^2\bigr )+a^4b^2y^2\bigl (\ell ^2+4\,x^2\bigr )\\{} & {} \quad -a^2b^4x^2\bigl (\ell ^2 +4\,b^2+4y^2\bigr )+4\,b^6x^4\Bigr )^2. \end{aligned}$$

Therefore, the geometric $\frac{1}{2}$-Holditch curve is given by

$$\begin{aligned} -4\,a^6y^2\bigl (b^2+y^2\bigr )+a^4b^2y^2\bigl (\ell ^2+4\,x^2\bigr ) -a^2b^4x^2\bigl (\ell ^2+4\,b^2+4y^2\bigr )+4\,b^6x^4=0. \end{aligned}$$

See some examples in Fig. 7.

Fig. 7

The geometric p-Holditch curve of the hyperbola $f(x,y)=0$, with $a=\frac{1}{4}$ and $b=\frac{1}{3}$, for a chord length $\ell =1$ and $p=\frac{1}{2}$ (left) and $p=\frac{1}{3}$ (right)

Remark 3

In general, if $p\ne \frac{1}{2}$ the implicit equation of a geometric p-Holditch curve cannot be factorized in such a way that a factor provides the implicit equation of a p-Holditch curve and the other factor gives that of a $(1-p)$-Holditch curve.

Consider the ellipse from Example 3. If we take $a=2$, $b=1$ and $p=1/4$, the implicit equation of the geometric p-Holditch curve for a chord length $\ell >0$ can be reduced to

$$\begin{aligned} h(x,y)&=144+54 \left( \ell ^2-32\right) y^2+\frac{9}{16} \left( 9 \left( \ell ^2-64\right) \ell ^2+11776\right) y^4\\ {}&\quad +270 \left( \ell ^2-32\right) y^6\\&\quad +3600\,y^8-\frac{9}{2} \left( 3\,\ell ^2+16\right) x^2 +\frac{9}{32} \left( 9\,\ell ^4-240\,\ell ^2+4864\right) x^2 y^2\\&\quad +27 \left( 5\,\ell ^2-136\right) x^2 y^4+2376\,x^2 y^6 +\frac{9}{256} \left( 3\,\ell ^2+16\right) ^2 x^4\\&\quad +\frac{27}{8} \left( 5\,\ell ^2-112\right) x^4 y^2 +513\,x^4 y^4+36\,x^6 y^2. \end{aligned}$$

Notice that in this case there is no term in $x^8$. Assume that it is possible to split

$$\begin{aligned} h(x,y)=h_1(x,y)\,h_2(x,y), \end{aligned}$$

(5)

with $h_1(x,y)$ and $h_2(x,y)$ being the implicit equations of the p-Holditch curve and the $(1-p)$-Holditch curve, respectively, supposed to be of degree 4. In fact, by symmetry, we have $h_2(x,y) = h_1(x,-y)$ and, explicitly, we can write

$$\begin{aligned} h_1(x,y) = \sum _{i+j\le 4}q_{i,j}\,x^{i}y^{j}. \end{aligned}$$

The coefficient of $x^8$ of $h_1(x,y)\,h_1(x,-y)$ is $q_{4,0}^2$, which by the equality (5) must be equal to zero, i.e. $q_{4,0}=0$. Now, the coefficient of $x^6y^2$ of $h_1(x,y)\,h_1(x,-y)$, which is

$$\begin{aligned} 2\,q_{2,2}\,q_{4,0}-q_{3,1}^2 = -q_{3,1}^2, \end{aligned}$$

must be equal to the coefficient, 36, of $x^6y^2$ of h(x, y), but this is impossible for real coefficients. Therefore, a factorization of this kind is not possible.

Finally, note that

$$\begin{aligned} h(0,y) = \frac{9}{16}\,\Bigl (16+3\,\bigl (\ell ^2-32\bigr ) y^2+80\,y^4\Bigr )^2. \end{aligned}$$

This expression equal to zero has four real solutions

$$\begin{aligned} y=\pm \frac{\sqrt{96-3\,\ell ^2\pm \sqrt{9\,\ell ^4-576\,\ell ^2+4096}}}{4\,\sqrt{10}}, \end{aligned}$$

for any $\ell \in \left[ -2,2\right]$. Two solutions correspond to points belonging to the geometric p-Holditch curve, but the other two are undesired points. For example, if $\ell =\frac{3}{2}$, the points $(0,\,\pm 0.94404)$ belong to the geometric p-Holditch curve. However, $(0,\,\pm 0.473723)$ are points that satisfy the implicit equation $h(x,y)=0$ but that do not belong to the geometric p-Holditch curve.

4 An Extension to Two Initial Curves

It is well-known that Holditch’s theorem can be extended to the case where the endpoints of the moving chord of constant length lie on two different curves. This extension is due to Woolhouse (see page 96 of [13]) and, more recently, this case was also considered by other authors [2, 14]. Let $\alpha$ and $\beta$ be the two initial curves. If $H_p$ is a p-Holditch curve of $\alpha$ and $\beta$ for a chord length $\ell >0$, then their algebraic areas are related through the expression

$$\begin{aligned} \mathcal {A}(H_p) = (1-p)\,\mathcal {A}(\alpha ) + p\,\mathcal {A}(\beta ) - n\,\pi \,p\,(1-p)\,\ell ^2, \end{aligned}$$

where n is the number of chord revolutions (the number of counterclockwise full revolutions minus the number of clockwise full revolutions of the moving chord). An example is shown in Fig. 8.

Fig. 8

Two initial curves $\alpha$ and $\beta$ and a $\frac{1}{3}$-Holditch curve $H_p$ of $\alpha$ and $\beta$ for a chord of constant length that does not make any full revolution during its motion

If the two initial curves $\mathcal {C}_1$ and $\mathcal {C}_2$ are given by implicit equations $f(x,y) = 0$ and $g(x,y) = 0$, respectively, we can define a geometric p-Holditch curve of $\mathcal {C}_1$ and $\mathcal {C}_2$ analogously as we have done in Sect. 2. Given $p\in \left[ 0,1\right]$ and $\ell >0$, the geometric p-Holditch curve of $\mathcal {C}_1$ and $\mathcal {C}_2$ for a chord length $\ell$, $\mathcal {H}_p$, is the set of points $(x,y)\in {\mathbb {R}}^2$ such that there exists an angle $t\in {\mathbb {R}}$ for which

$$\begin{aligned} (x,y)-p\,\ell \,\bigl (\cos t,\,\sin t\bigr )\in \mathcal {C}_1 \qquad \textrm{and}\qquad (x,y)+(1-p)\,\ell \,\bigl (\cos t,\,\sin t\bigr )\in \mathcal {C}_2. \end{aligned}$$

Equivalently, such that

$$\begin{aligned} f(x-p\,\ell \cos t,\,y-p\,\ell \sin t)&= 0,\nonumber \\ g\bigl (x+(1-p)\,\ell \cos t,\,y+(1-p)\,\ell \sin t\bigr )&=0. \end{aligned}$$

(6)

There is an important difference with the case of a single initial curve, which is that an extended version of Proposition 1 is not possible. This means that here we can distinguish with a separate implicit equation geometric p-Holditch curves and geometric $(1-p)$-Holditch curves. This is due to the fact that from the beginning, each endpoint of the constant length chord is associated with one of the two curves and with either p or $1-p$ and so a later interchange is not possible. See an example in Fig. 9.

Fig. 9

A straight line $\alpha$ and a circle $\beta$ as two initial curves, their geometric p-Holditch curve $\mathcal {H}_p$ and their geometric $(1-p)$-Holditch curve $\mathcal {H}_{1-p}$, which are different curves defined by different implicit equations

However, an extended version of Theorem 1 is still possible, which provides a way to construct algebraic equations for geometric Holditch curves of two initial algebraic curves by using a resultant.

Theorem 2

If $\mathcal {C}_1$ and $\mathcal {C}_2$ are irreducible real algebraic curves and $\mathcal {H}_p$ is a geometric p-Holditch curve of $\mathcal {C}_1$ and $\mathcal {C}_2$, then there exists a real algebraic curve that contains $\mathcal {H}_p$.

Proof

The proof is analogous to that of Theorem 1. In this case, if $f(x,y)=0$ and $g(x,y)=0$ are the polynomial equations that describe $\mathcal {C}_1$ and $\mathcal {C}_2$, respectively, we must consider the polynomials

$$\begin{aligned} g_1(x,y,u)&\mathrel {\mathop :}=\bigl (1+u^2\bigr )^{k_1}\,f \left( x-p\,\ell \, \frac{1-u^2}{1+u^2},\, y-p\,\ell \,\frac{2\,u}{1+u^2}\right) = 0,\\ g_2(x,y,u)&\mathrel {\mathop :}=\bigl (1+u^2\bigr )^{k_2}\,g \left( x+(1-p)\,\ell \, \frac{1-u^2}{1+u^2},\,y+(1-p)\,\ell \,\frac{2\,u}{1+u^2}\right) =0, \end{aligned}$$

where $k_1$ and $k_2$ are the minimum integers that make $g_1$ and $g_2$, respectively, polynomials in u. $\square$

Fig. 10

A $\frac{1}{3}$-Holditch curve of two secant lines, which is an ellipse

Example 5

The most famous example of a Holditch curve for two initial curves is that of two line segments orthogonal at their midpoint, which corresponds to the device known as the Trammel of Archimedes [15] used to construct ellipses. A similar construction can also be done for two line segments which make a non-right angle at their midpoint (sometimes also known as Da Vinci’s ellipsograph [16]), see Fig. 10.

By the definition of a geometric p-Holditch curve, it suffices if we consider as initial curves the two straight lines:

$$\begin{aligned} f(x,y) = y,\qquad \text {and}\qquad g(x,y) = m\,x-y, \end{aligned}$$

where $m\in {\mathbb {R}}$. We have

$$\begin{aligned} g_1(x,y,u)&= -2\,\ell \,p\,u+u^2\,y+y,\\ g_2(x,y,u)&= \ell \,(1-p)\,\Bigl (m\,\bigl (1-u^2\bigr ) -2\,u\Bigr )+\bigl (1+u^2\bigr )\,(m\,x-y). \end{aligned}$$

The resultant of $g_1$ and $g_2$ with respect to u is

$$\begin{aligned} 4\,\ell ^2\Bigl (-\ell ^2m^2(1-p)^2p^2+m^2\bigl (p^2x^2 +(1-p)^2y^2\bigr )-2\,m\,p\,x\,y+y^2\Bigr ). \end{aligned}$$

From this we get the implicit equation of the p-Holditch curve for a chord length $\ell$,

$$\begin{aligned} m^2p^2x^2-2\,m\,p\,x\,y+\bigl (1+m^2(1-p)^2\bigr )\,y^2 - \ell ^2m^2(1-p)^2p^2=0, \end{aligned}$$

which represents a conic. The discriminant of the quadratic equation is

$$\begin{aligned} \Delta = -4m^4(1-p)^2p^2 <0, \end{aligned}$$

so that the p-Holditch curve is an ellipse.

5 Explicit Parameterization of the p-Holditch Curve of an Ellipse

In Example 3, we found the implicit equation of the p-Holditch curve of an ellipse

$$\begin{aligned} f(x,y) = \frac{x^2}{a^2}+\frac{y^2}{b^2}-1, \end{aligned}$$

for a chord length $0<\ell \le \max (2a,2b)$ and $p=1/2$. Thanks to this implicit equation, the first observation is that we can easily parameterize the $\frac{1}{2}$-Holditch curve through polar coordinates as

$$\begin{aligned} H(t) = \rho (t)(\cos t,\,\sin t), \end{aligned}$$

(7)

where

$$\begin{aligned} \rho (t) = \frac{a\,b\,\sqrt{a^2\bigl (4\,a^2-\ell ^2\bigr )\sin ^2(t) +b^2\bigl (4\,b^2-\ell ^2\bigr )\cos ^2(t)}}{2\,\sqrt{\bigl (a^2 \sin ^2(t)+b^2\cos ^2(t)\bigr )\,\bigl (a^4\sin ^2(t)+b^4\cos ^2(t)\bigr )}}, \end{aligned}$$

if $\ell$ is less than or equal to the minor axis of the ellipse. This expression is found by simply substituting (7) in the implicit equation and solving it for $\rho (t)$.

Now, we are going to find a parameterization of the p-Holditch curve for any value of $p\in \left[ 0,1\right]$. The implicit equation is quite more difficult in the case $p\ne 1/2$, but we don’t need it. The main remark is that the case $p=1/2$ suffices to know the movement of the chord of constant length and this will allow us to parameterize its endpoints.

Fig. 11

A p-Holditch curve $h_p$ of an ellipse with $a=2$, $b=1$, $\ell =3/2$ and $p=1/3$

To ease a simplification, let $H(t) = \bigl (x(t),y(t)\bigr )$. The endpoints of the moving chord, which can be written as

$$\begin{aligned} \alpha _1(t,u)&= H(t) - \frac{\ell }{2}\,(\cos u,\sin u),\\ \alpha _2(t,u)&= H(t) + \frac{\ell }{2}\,(\cos u,\sin u), \end{aligned}$$

must lie in the ellipse and so must satisfy its implicit equation. Thus, we have two equations

$$\begin{aligned} g_1(t,u)\mathrel {\mathop :}=f\bigl (\alpha _1(t,u)\bigr ) = 0\quad \text {and}\quad g_2(t,u)\mathrel {\mathop :}=f\bigl (\alpha _2(t,u)\bigr ) = 0. \end{aligned}$$

A great simplification can be done if we consider

$$\begin{aligned} \frac{1}{2}\bigl (g_2(t,u)-g_1(t,u)\bigr ) = \frac{\ell \cos (u)\,x(t)}{a^2}+\frac{\ell \sin (u)\,y(t)}{b^2}=0. \end{aligned}$$

Substituting the values of x(t) and y(t), this equation implies that

$$\begin{aligned} a^2 \sin (t) \sin (u)+b^2 \cos (t) \cos (u)=0. \end{aligned}$$

A continuous solution of this equation for u satisfies

$$\begin{aligned} \cos (u)&=-\frac{a^2\sin (t)}{\sqrt{a^4\sin ^2(t)+b^4\cos ^2(t)}},\\ \sin (u)&=\frac{b^2\cos (t)}{\sqrt{a^4\sin ^2(t)+b^4\cos ^2(t)}}. \end{aligned}$$

Therefore, we can directly obtain the parameterization of the p-Holditch curve as follows:

$$\begin{aligned} h_p(t)&= (1-p)\,\alpha _1(t,u)+p\,\alpha _2(t,u)= H(t) +\frac{\ell }{2}\,(2\,p-1)\,\bigl (\cos (u),\sin (u)\bigr )\\&= H(t) \!+\!\frac{\ell }{2}\,(2\,p\!-\!1)\, \left( -\frac{a^2 \sin (t)}{\sqrt{a^4 \sin ^2(t)\!+\!b^4 \cos ^2(t)}},\frac{b^2 \cos (t)}{\sqrt{a^4 \sin ^2(t)\!+\!b^4 \cos ^2(t)}}\right) , \end{aligned}$$

for $t\in \left[ 0,2\pi \right]$. See an example in Fig. 11.