Phase Portraits of a Class of Cubic Systems with an Ellipse and a Straight Line as Invariant Algebraic Curves

Abstract

In this paper we classify the phase portraits in the Poincaré disc of a class of cubic polynomial differential systems having an invariant ellipse and an invariant straight line. We prove that such a class of cubic polynomial differential systems have exactly 43 topologically different phase portraits in the Poincaré disc. Also we obtain that the invariant ellipse in two of these phase portraits is a limit cycle.

Introduction and Statements of the Main Results

The phase portrait of a differential system defined in the plane $\mathbb {R}^2$ consists in describing $\mathbb {R}^2$ as union of all the orbits of the differential system. The phase portrait of a differential system provides the maximal qualitative information about its dynamics. This is the best information which can be given for a differential system whose orbits cannot be given explicitly in function of the time.

A polynomial differential system in the plane $\mathbb {R}^2$ is a differential system of the form

$$\begin{aligned} \frac{dx}{dt}= \dot{x}= P(x,y), \qquad \frac{dy}{dt}= \dot{y}= Q(x,y), \end{aligned}$$

(1)

where P and Q are real polynomials in the variables x and y, and the independent variable t usually is called the time. The maximum degree of the polynomials P and Q is called the degree of the polynomial differential system. The vector field $\mathcal {X}$ associated to system (1) is

$$\begin{aligned} \mathcal {X}=P(x,y)\dfrac{\partial }{\partial x}+Q(x,y)\dfrac{\partial }{\partial y}, \end{aligned}$$

or simply $\mathcal {X}=(P,Q)$.

The phase portrait of a polynomial differential system in the plane usually is presented in the Poincaré disc because then we can control the orbits which go to or come from the infinity. Roughly speaking the Poincaré disc is the closed unit disc centered at the origin of $\mathbb {R}^2$, its interior is identified with $\mathbb {R}^2$, and its boundary the circle $\mathbb {S}^1$ is identified with the infinity of $\mathbb {R}^2$. Note that in the plane $\mathbb {R}^2$ we can go to infinity in as many directions as points in the circle $\mathbb {S}^1$. See subsection 2.2 for more details on the Poincaré compactification and the Poincaré disc.

The polynomial differential systems of degree one are the linear differential systems, and it is well known that these differential systems can be solved explicitly and their phase portraits are known, see for instance Example 1.8 of [10]. So the next polynomial differential systems are the ones of degree two usually called quadratic systems. There are more than one thousand of papers about these systems, see for instance the books of Artés et al. [3], Reyn [24] and Ye Yanquian [28], and the references cited in these books. Many subclasses of quadratic systems have been studied, thus for instance the phase portraits of all quadratic systems having centers (see [4, 6, 13, 14, 25, 26, 29]), or the phase portraits of all quadratic Hamiltonian systems (see [2, 5, 12]), or the phase portraits of all quadratic systems having an invariant ellipse (see [15, 16, 22]), or the phase portraits of all quadratic systems having an invariant ellipse and an invariant straight line (see [17]), or the phase portraits of all quadratic systems with invariant conics (see [20,21,22].

After the quadratic systems come the cubic systems, i.e. the polynomial differential systems of degree three. Very few things are known for the cubic systems with respect the things that we know for the quadratic systems. A nice application of the cubic systems is to the Higgins–Selkov and Selkov systems which allow to study the biological nonlinear glycolytic oscillations, see [4] and the references cited there.

The phase portraits of all cubic systems are unknown, only we know the phase portrais of some subclasses of cubic centers, or the cubic Hamiltonian systems, or of the cubic systems having an ellipse, ... Here we start the classification of the phase portraits of the cubic systems having an invariant ellipse and an invariant straight line.

Let f(x, y) be a real polynomial in the variables x and y. We recall that the algebraic curve $f(x,y)=0$ in $\mathbb {R}^2$ is an invariant algebraic curve of system (1) if

$$\begin{aligned} Pf_x+Qf_y=Kf, \end{aligned}$$

for some polynomial K(x, y), which is called the cofactor of $f(x,y)=0$. As usual we denote by $f_x$ and $f_y$ the partial derivatives of f with respect to x and y, respectively.

In the next result we characterize all the cubic systems having an invariant ellipse and an invariant straight line.

Proposition 1

Every cubic system having an invariant ellipse and an invariant straight line after an affine change of variables can be written into the form:

$$\begin{aligned} \dot{x}=df-(ax+by+c)f_y,\qquad \dot{y}=ef+(ax+by+c)f_x, \end{aligned}$$

(2)

where $f=f(x,y)=(x^2+y^2-1)(x-r)$ with $r\ge 0$.

The cubic system (2) have six parameters a, b, c, d, e, r, too much parameters for doing all their phase portraits. We restrict our study to the subclass of cubic system (2) of the form

$$\begin{aligned} \dot{x}=-(by+c)f_y,\qquad \dot{y}=ef+(by+c)f_x, \end{aligned}$$

(3)

where $f=f(x,y)=(x^2+y^2-1)(x-r)$ with $r\ge 0$. The cubic system (3) have four parameters b, c, e and r.

Doing a rescaling of the time if $e\ne 0$ we can assume that $e=1$. So the objective of this paper is to characterize the phase portraits of the class of cubic system (3) in the Poincaré disc with $e=1$ and with $e=0$. Also we observe that system (3) is invariant by the change $(x,y,t,b,c,r)\rightarrow (x,-y,-t,-b,c,r)$. That is why it is enough to prove the main results only for $b\ge 0$.

Our main results are the following two theorems.

Theorem 2

System (3) with $e=1$ has 32 topologically different phase portraits which are given in Figs. 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26. Also we show that the invariant ellipse in two phase portraits is a limit cycle.

Theorem 3

System (3) with $e=0$ has 11 topologically different phase portraits which are given in Figs. 27, 28, 29, 30, 31.

This paper is organized as follows. In section 2 we introduce the definitions concerning the classification of singularities of planar polynomial vector fields and we describe the Poincaré compactification. Finally, in section 3 we prove Theorems 2 and 3.

Preliminary Results

In this section we summarize some basic results that we shall need for proving our results.

Singular Points

A point $p\in \mathbb {R}^2$ is said to be a singular point of the vector field $\mathcal {X}=(P,Q)$ if $P(p) = Q(p) = 0$. The Jacobian matrix of system (1) at the point p is

$$\begin{aligned} J(p)=\left[ \begin{array}{cc} \dfrac{\partial P}{\partial x}(p)&{}\dfrac{\partial P}{\partial y}(p)\\ \dfrac{\partial Q}{\partial x}(p)&{}\dfrac{\partial Q}{\partial y}(p)\end{array} \right] . \end{aligned}$$

The determinant and the trace of the Jacobian matrix are

$$\begin{aligned} \det (p)=P_{x}(p)Q_y(p)-P_{y}(p)Q_{x}(p),\quad \text {tr}(p)=P_{x}(p)+Q_y(p), \end{aligned}$$

respectively. The singular point p is called hyperbolic if the two eigenvalues of J(p) have real part different from 0. p is a linear center if the eigenvalues of J(p) are purely imaginary without being zero. In this case and if the vector field $\mathcal {X}$ is analytic, p is either a center or a (weak) focus. Moreover p is a saddle if $\det (p)< 0$; a node if $\det (p)>0$ and $\text {tr}(p)^{2} \ge 4\det (p) > 0$, stable if $\text {tr}(p)< 0$, and unstable if $\text {tr}(p)>0$; a focus if $\det (p)>0$ and $4\det (p)>\text {tr}(p)^{2}>0$, stable if $\text {tr}(p)< 0$, and unstable if $\text {tr}(p)> 0$.

If $\det (p)=0$ but $\text {tr}(p) \ne 0$, then the singular point p is semi-hyperbolic. Hyperbolic and semi-hyperbolic singularities are also called elementary.

The singular point p is called nilpotent if both eigenvalues of J(p) are equal to 0 but $J(p)\not \equiv 0$, and the singular point p is called linearly zero if $J(p)\equiv 0$; for more details see [10].

Poincaré Compactification

Due to the fact that system (3) is polynomial we can compactify it in the Poincaré disc $\mathbb D$. This disc is the closed disc of radius one and center at the origin of coordinates of $\mathbb {R}^2$. The plane $\mathbb R^2$ where is defined system (3) is diffeomorphic to the interior of $\mathbb D$, and its boundary $\mathbb S^1$ corresponds to the infinity of $\mathbb R^2$. System (3) can be extended to the closed disc $\mathbb D$ in a unique analytic way in such manner that $\mathbb S^1$, the boundary of $\mathbb D$, is invariant by the extended flow, i.e. if an orbit of the extend flow has a point in $\mathbb S^1$ the whole orbit is contained in $\mathbb S^1$. This extension is called the Poincaré compactification, for more details on this compactification (Figs. 1, 2) see Chapter 5 of [10].

Fig. 1

The local charts $U_i$ and $V_i$, for $i=1,2$ of the Poincaré disc $\mathbb D$

Fig. 2

The coordinates (u, v) in the local charts $U_1$ and $U_2$

In order to work with the Poincaré disc we need four local charts $(U_k,\phi _k)$ and $(V_k,\psi _k)$ for $i=1,2$, where

$$\begin{aligned} \begin{aligned} U_1&=\{ (x,y) \in \mathbb R^2: x>0\},\qquad U_2=\{ (x,y) \in \mathbb R^2: y>0\},\\ V_1&=\{ (x,y) \in \mathbb R^2: x<0\},\qquad V_2=\{ (x,y) \in \mathbb R^2: y<0\}, \end{aligned} \end{aligned}$$

and the diffeomorphisms $\phi _k: U_k \rightarrow \mathbb D$ and $\psi _k:V_k \rightarrow \mathbb D$ for $k=1,2$ are defined as follows

$$\begin{aligned} \phi _1(x,y)=\left( \dfrac{y}{x}, \dfrac{1}{x} \right) =(u,v),\qquad \phi _2(x,y)=\left( \dfrac{1}{y}, \dfrac{x}{y} \right) =(u,v), \end{aligned}$$

and $\psi _k=-\phi _k$ for $k=1,2$.

If $\dot{x}= P(x,y), \,\, \dot{y}=Q(x,y)$ is a polynomial differential system and d is the maximum of the degrees of P and Q, then the expression of the extended flow in the local chart $(U_1, \phi _1)$ is

$$\begin{aligned} \begin{aligned} \dot{u}=&v^d\left[ -u P\left( \dfrac{1}{v}, \dfrac{u}{v} \right) + Q\left( \dfrac{1}{v}, \dfrac{u}{v} \right) \right] , \qquad \dot{v}=&-v^{d+1} P\left( \dfrac{1}{v}, \dfrac{u}{v} \right) . \end{aligned} \end{aligned}$$

The expression in the local chart $(U_2, \phi _2)$ is

$$\begin{aligned} \begin{aligned} \dot{u}=&v^d\left[ P\left( \dfrac{u}{v}, \dfrac{1}{v} \right) - u Q\left( \dfrac{u}{v}, \dfrac{1}{v} \right) \right] , \qquad \dot{v}=&-v^{d+1} Q\left( \dfrac{u}{v}, \dfrac{1}{v} \right) . \end{aligned} \end{aligned}$$

The expressions in the local charts $(V_k, \psi _k)$, for $k=1,2$ are the same than in the chart $(U_k, \phi _k)$ multiplied by $(-1)^{d-1}$. We note that $v=0$ corresponds to the infinity $\mathbb S^1$ in all the local charts. In the Poincaré disc the singular points which are in its interior are called finite singular points, while the singular points which are in its boundary are called infinite singular points.

Note that for studying the infinite singular points it is sufficient to study the infinite singular points which are in the local chart $U_1$, and to see if the origin of the local chart $U_2$ is or not an infinite singular point.

If $\mathcal {X}=(P,Q)$ is the vector field associated to the polynomial differential system (1), then $p(\mathcal {X})$ denotes the vector field associated to the analytic system defined in the Poincaré disc which comes from the extension of the vector field $\mathcal {X}$ to the boundary of the Poincaré disc. Usually we call the vector field $p(\mathcal {X})$ the Poincaré compactification of $\mathcal {X}$.

Phase Portraits in the Poincaré Disc

In this subsection we shall see how to characterize the global phase portraits in the Poincaré disc of the cubic system (3).

A separatrix of $p(\mathcal {X})$ is an orbit which is either a singular point, or a limit cycle, or a trajectory which lies in the boundary of a hyperbolic sector at a finite or infinite singular point. Neumann [19] proved that the set formed by all separatrices of $p(\mathcal {X})$; denoted by $S(p(\mathcal {X}))$ is closed. We denote by S the number of separatrices of the phase portrait of $p(\mathcal {X})$.

The open connected components of $\mathbb {D}\setminus S(p(\mathcal {X}))$ are called canonical regions of $p(\mathcal {X})$. We denote by R the number of canonical regions of the phase portrait of $p(\mathcal {X})$.

We define a separatrix configuration of a polynomial vector field $\mathcal {X}$ as a union of $S(p(\mathcal {X}))$ plus one solution chosen from each canonical region. Two separatrix configurations $S(p(\mathcal {X}))$ and $S(p(\mathcal {Y}))$ are said to be topologically equivalent if there is an orientation preserving or reversing homeomorphism which maps the trajectories of $S(p(\mathcal {X}))$ into the trajectories of $S(p(\mathcal {Y}))$. The following result is due to Markus [18], Neumann [19] and Peixoto [23].

Theorem 4

The phase portraits in the Poincaré disc of the two compactified polynomial differential systems $p(\mathcal {X})$ and $p(\mathcal {Y})$ are topologically equivalent if and only if their separatrix configurations $S(p(\mathcal {X}))$ and $S(p(\mathcal {Y}))$ are topologically equivalent.

To determine the local phase portraits at the singular points of a system, we shall use the following result.

Theorem 5

(Poincaré-Hopf Theorem). For every continuous vector field on the sphere $\mathbb {S}^2$ with a finite number of singular points, the sum of the (topological) indices of their singular points is 2.

The Directional Blow-up Technique

For studying the local phase portraits at the finite and infinite singularities the blow-up technique is necessary, so we present a summary of the directional blow-up technique, for more details see [1].

Consider a real planar polynomial differential system of the form

$$\begin{aligned} \begin{aligned} \dot{x}=&P(x,y)=P_{m}(x,y)+...,\\ \dot{y}=&Q(x,y)=Q_{m}(x,y)+..., \end{aligned} \end{aligned}$$

(4)

where P and Q are coprime polynomials, $P_m$ and $Q_m$ are homogeneous polynomials of degree $m\in \mathbb {N}$. We note that we are assuming that the origin is a singular point, since $m > 0.$

The directional blow-up in the vertical direction (respectively, horizontal) is the mapping $(x, z) \mapsto (x, xz) =(x, y)$ (respectively, $(z, y)\mapsto (yz, y) = (x, y)$), where z is a new variable. This map transforms the origin of (4) into the straight line $y = 0$ (respectively, $x = 0$). The expression of system (4) after a vertical blow-up is

$$\begin{aligned} \dot{x}=P(x,xz),\qquad \dot{y}=\dfrac{Q(x,xz)-zP(x,xz)}{x}, \end{aligned}$$

that is always well-defined since we are assuming that the origin is a singularity. After the blow-up, we cancel an appearing common factor $x^{m-1}$ ($x^{m}$ if $xQ_{m}(x, y) - y P_{m}(x, y)\equiv 0$).

Moreover, the mapping swaps the second and the third quadrants in the vertical blow-up and the third and the fourth quadrants in the horitzontal blow-up, which writes as

$$\begin{aligned} \dot{z}= \dfrac{P(yz,y)-zQ(yz,y)}{y},\qquad \dot{x}= P(yz,y). \end{aligned}$$

The key point is that doing a finite number of blow ups we can determine the local phase portrait of any singular point of an analytic differential system in the plane, see for details [9].

Proof of the Results

We shall start proving Proposition 1 and for this we shall need the following two results, the first is proved in [8], and the second in [11].

Lemma 6

Assume that the polynomial system (1) of degree m has an invariant algebraic curve $f(x,y)=0$, and that there are no points at which $f(x,y)=0$ and their first derivatives are all vanish. If $f_x$ and $f_y$ are coprime, then system (1) has the following normal form

$$\begin{aligned} \dot{x}=Af-Df_y,\qquad \dot{y}=Bf+Df_x, \end{aligned}$$

(5)

where A, B and D are suitable polynomials.

Lemma 7

Suppose that a polynomial system (1) admits q algebraic solutions $f_i=0$ for $i=1,\ldots ,q.$ We denote by $F=\mathop {\prod }\limits _{i=1}^{q}f_i,F_x=\partial F/ \partial x,$ $F_y=\partial F/\partial y, d=\gcd (F_x,F_y),$ $H_1,H_2,H_3,K,P_K,Q_K\in \mathbf{F}[x,y]$ satisfying $F_xP_K+F_yQ_K=KF.$ Then the differential system can be written in the form

$$\begin{aligned} \dot{x}=\frac{1}{H_3}\left( H_1P_K-H_2\frac{F_y}{d}\right) ,\qquad \dot{y}=\frac{1}{H_3}\left( H_1Q_K+H_2\frac{F_x}{d}\right) , \end{aligned}$$

with suitable $H_1,H_2,H_3,K,P_K$ and $Q_K,$ such that $H_1P_K-H_2\frac{F_y}{d}$ and $H_1Q_K+H_2\frac{F_x}{d}$ are polynomials divisible by $H_3$.

Proof of Proposition 1

Assume that we have a cubic system having an invariant ellipse and an invariant straight line. Then doing a convenient affine transformation this ellipse can be written as the circle $x^2+y^2-1=0$. After doing a rotation with respect to the origin of coordinates the invariant straight line can be written as $x-r=0$ with $r\ge 0$. Then we apply Lemma 6 to the polynomial $f(x,y)= (x^2+y^2-1)(x-r)$ when $r> 1$ choosing the polynomials A, B and D in order that the polynomial differential system (5) has degree three, and we obtain the cubic system (2) for $r>1$. Finally using Lemma 7 we again obtain the cubic system (2) for $r\in [0,1]$. $\square$

Infinite Singular Points

We will study of the local phase portraits at the infinite singular points of the local chart $U_1$ and at the origin of $U_2$ of system (3) with $e=1$ and $e=0$.

Infinite Singular Points of System (3) with $e=1$

Let $\mathcal {X}$ be the vector field associated to system (3) with $e=1$. Then the expression for $p(\mathcal {X})$ in the local chart $U_1$ is

$$\begin{aligned} \begin{aligned} \dot{u}=&1+3\,bu+ \left( 3\,c-r \right) v+{u}^{2}-2\,brvu-\left( 2\,cr+1 \right) {v}^{2}+3\,b{u}^{3}+ \left( 3\,c-r \right) v{u}^{2}-b{v}^{2}u\\&+ \left( r-c\right) {v}^{3}-2\,brv{u}^{3}-2\,cr{v}^{2}{u}^{2},\\ \dot{v}=&-2\,v \left( bu+cv \right) u \left( rv-1 \right) . \end{aligned} \end{aligned}$$

Then in order to study the infinite singular points of system (3) with $e=1$ in the local chart $U_1$ we must study the singular points of the form (u, 0). Therefore on $U_1$ there is a unique infinite singular point at $q=\left( -1/(3b), 0\right)$ if $b> 0$, and there is no singular points if $b=0$. The eigenvalues of the Jacobian of the system in the local chart $U_1$ at the point q are $(9\,{b}^{2}+1)/(3b)$ and 2/(9b). Hence the singular point q is an unstable node if $b>0$. Since the degree of $\mathcal {X}$ is odd, the diametrically opposite point p in $V_1$ is also another unstable node.

In the local chart $U_2$ the Poincaré compactification of system (3) is

$$\begin{aligned} \begin{aligned} \dot{u}=&-3\,bu+2\,brv-{u}^{2}+ \left( r -3\,c\right) vu+2\,cr{v}^{2}-3\,b{u}^ {3}+2\,brv{u}^{2}+b{v}^{2}u-{u}^{4}+ \left( r -3\,c\right) v{u}^{3}\\&+ \left( 2\,cr+1 \right) {v}^{2}{u}^{2}+ \left( c-r \right) {v}^{3}u,\\ \dot{v}=&-bv-vu+ ( r-c){v}^{2}-3\,bv{u}^{2}+ 2\,br{v}^{2}u+b{v}^{3 }-v{u}^{3}+ \left( r-3\,c\right) {v}^{2}{u}^{2}+ \left( 2\,cr+1 \right) {v}^{3}u+ \left( c-r \right) {v}^{4}. \end{aligned} \end{aligned}$$

(6)

In order to complete the study of the infinite singular points of system (3) with $e=1$ we only need to study if the origin of local chart $U_2$ is or not a singular point. The eigenvalues of the Jacobian of system (6) at the origin are $-3b$ and $-b$, so the singular point is a stable node if $b>0$. Similarly the diametrically opposite point of $V_2$ is also an unstable node.

If $b=0$, then the origin of $U_2$ is linearly zero. We need to do blow-ups to understand the local behavior at this point. We perform the directional blow-up $(u,v)\mapsto (u,w)$ with $w=v/u$ and we obtain

$$\begin{aligned} \begin{array}{l} \dot{u}={u}^{2} \left( 2\,cr{u}^{2}{w}^{2}+c{u}^{2}{w}^{3}-r{u}^{2}{w}^{3}+2\, cr{w}^{2}-3\,c{u}^{2}w+r{u}^{2}w+{u}^{2}{w}^{2}-3\,cw+rw-{u}^{2}-1 \right) ,\\ \dot{w}=-2\,c{w}^{2}u \left( rw-1 \right) . \end{array} \end{aligned}$$

Using a reparametrization of time we eliminate the common factor u between $\dot{u}$ and $\dot{w}$, and we get

$$\begin{aligned} \begin{array}{l} \dot{u}={u} \left( 2\,cr{u}^{2}{w}^{2}+c{u}^{2}{w}^{3}-r{u}^{2}{w}^{3}+2\, cr{w}^{2}-3\,c{u}^{2}w+r{u}^{2}w+{u}^{2}{w}^{2}-3\,cw+rw-{u}^{2}-1 \right) ,\\ \dot{w}=-2\,c{w}^{2} \left( rw-1 \right) . \end{array} \end{aligned}$$

(7)

For $r>0$ the singular points of system (7) on $u=0$ are (0, 0) and (0, 1/r). The eigenvalues of the linear part of system (7) at the points (0, 0) are $-1$ and 0, and at the point (0, 1/r) are $-c/r$ and $-2c/r$. So the point (0, 0) is a semi-hyperbolic point. Using Theorem 2.19 of [10] it is a saddle-node point. If $c>0$ then the point (0, 1/r) is a stable node and an unstable node if $c<0$. Going back through the blow-ups we obtain the local phase portrait at the origin of $U_2$, it is formed by two elliptic sectors, a repelling parabolic sector, and an attracting parabolic sector as it is shown in Fig. 3.

Fig. 3

The local phase portraits at the origin of $U_2$ when $b=0$ and $r>0$

When $r=0$ system (7) on $u=0$ has the unique singular point (0, 0) and the eigenvalues of the Jacobian matrix at the origin are $-1$ and 0. The origin is a semi-hyperbolic point. Using Theorem 2.19 of [10] it is a saddle-node point. Going back through the change of variables until the coordinates (u, v), the origin of the local chart $U_2$ in the variables (u, v) has the local phase portrait of Fig. 4.

Fig. 4

The local phase portraits at the origin of $U_2$ when $b=0$ and $r=0$

Infinite Singular Points of System (3) with $e=0$

Now suppose that $\mathcal {X}$ is the vector field associated to (3) with $e=0$.

Case (I) If $b> 0$, then the degree of $\mathcal {X}$ is three and the expression for $p(\mathcal {X})$ in the local chart $U_1$ is

$$\begin{aligned} \dot{u}=- \left( bu+cv \right) \left( 2\,r{u}^{2}v+2\,rv-3\,{u}^{2}+{v}^{2}-3 \right) ,\quad \dot{v}=-2\,v \left( bu+cv \right) u \left( rv-1 \right) . \end{aligned}$$

Therefore on $U_1$ there is a unique infinite singular point at the origin. Note that the origin is a non-isolated singular point because the straight line $bu+cv=0$ is filled of singularities.

On the local chart $U_2$ system (3) with $e=0$ becomes

$$\begin{aligned} \dot{u}=\left( cv+b \right) \left( 2\,r{u}^{2}v-3\,{u}^{3}+u{v}^{2}+2\,rv-3\,u \right) ,\quad \dot{v}=v \left( cv+b \right) \left( 2\,ruv-3\,{u}^{2}+{v}^{2}-1 \right) . \end{aligned}$$

The origin of $U_2$ is a singular point, and the eigenvalues of the Jacobian matrix at the origin are $-3b$ and $-b$. So the origin of $U_2$ is a stable node. In this case the degree of $\mathcal {X}$ is odd and the diametrically opposite point of $V_2$ is also a stable node.

Case (II) If $b=0$, then the degree of $\mathcal {X}$ is two and the expression for $p(\mathcal {X})$ in the local chart $U_1$ is

$$\begin{aligned} \dot{u}=-c \left( 2\,r{u}^{2}v+2\,rv-3\,{u}^{2}+{v}^{2}-3 \right) ,\quad \dot{v}=-2\,vcu \left( rv-1 \right) . \end{aligned}$$

Therefore there are no infinite singular point in the local chart $U_1$.

The expression for $p(\mathcal {X})$ in the local chart $U_2$ is

$$\begin{aligned} \dot{u}=c \left( 2\,r{u}^{2}v-3\,{u}^{3}+u{v}^{2}+2\,rv-3\,u \right) ,\quad \dot{v}=vc \left( 2\,ruv-3\,{u}^{2}+{v}^{2}-1 \right) . \end{aligned}$$

So the origin of $U_2$ is an infinite singular point. Since this point has eigenvalues $-c$ and $-3c$, then it is a stable node if $c>0$, and an unstable node if $c<0$. Since the degree of $\mathcal {X}$ is even the diametrically opposite point of $V_2$ is an unstable node and a stable node, respectively.

Finite Singular Points

Here we will study the finite singular points of system (3) with $e=1$, and $e=0$.

Finite Singular Points of System (3) with $e=1$ and $c\ne 0$

In this case the finite singular points are given in Table 1, where $x_{i}^{*}$, $i=1,2,3$ are the three real roots of the equation

$$\begin{aligned} {x}^{3}+ \left( 3\,c-r \right) {x}^{2}- \left( 2\,cr+1 \right) x-c+r=0. \end{aligned}$$

(8)

We claim that Eq. (8) always has three distinct real roots if $c\ne 0$. In fact if we compute its discriminant with respect to x we get

$$\begin{aligned} p(r)=b_0 r^4+b_1 r^3+b_2 r^2+b_3 r+b_4, \end{aligned}$$

where

$$\begin{aligned} b_{0}= 4\,{c}^{2}+4,\quad b_{1}=8\,{c}^{3}, \quad b_{2}= 36\,{c}^{4}+24\,{c}^{2}-8,\quad b_{3}=-72\,{c}^{3},\quad b_{4}=108\,{c}^{4}+36\,{c}^{ 2}+4, \end{aligned}$$

with $b_0\ne 0$, and define

$$\begin{aligned} \begin{array}{rl} D_3=&{} 16 b_0^2 b_2 b_4 - 18 b_0^2 b_3^2 - 4 b_0 b_2^3 + 14 b_0 b_1 b_2 b_3 - 6 b_0 b_1^2 b_4 + b_1^2 b_2^2 - 3 b_1^3 b_3,\\ D_4=&{} 256 b_0^3 b_4^3 - 27 b_0^2 b_3^4 - 192 b_0^2 b_1 b_3 b_4^2 - 27 b_1^4 b_4^2 - 6 b_0 b_1^2 b_3^2 b_4 + b_1^2 b_2^2 b_3^2 - 4 b_0 b_2^3 b_3^2 +\, 18 b_1^3 b_2 b_3 b_4 + 144 b_0 b_1^2 b_2 b_4^2\\ &{} - 80 b_0 b_1 b_2^2 b_3 b_4 + 18 b_0 b_1 b_2 b_3^3 - 4 b_1^2 b_2^3 b_4 - 4 b_1^3 b_3^3 +\, 16 b_0 b_2^4 b_4 - 128 b_0^2 b_2^2 b_4^2 + 144 b_0^2 b_2 b_3^2 b_4. \end{array} \end{aligned}$$

Since $D_4>0$ and $D_3\le 0$ the four roots of the polynomial p(r) are non-real, for more details see [27]. It follows that the discriminant of Eq. (8) is always positive, and consequently Eq. (8) has three distinct real roots.

Table 1 Finite singular points of system (3) with $e=1$ and $c\ne 0$

Now we classify the local phase portrait of the finite singular points according with the twelve cases of Table 1, and after knowing all the local phase portraits at the finite and infinite singular points together with the fact that the circle $x^2+y^2=1$ and the straight line $x=r$ are invariant, we shall determine the phase portraits in the Poincaré disc of these cases.

Case (I) $(\mathbf{I} )$. If $r\in [0,1)$ and $(\mathbf{I1} )$ $r\ne \pm \sqrt{b^{2}-c^{2}}/b$ then system (3) with $e=1$ has eight distinct finite singular points, namely

$$\begin{aligned} p_{1}=\left( r,-\frac{c}{b}\right) , p_{2,3}=\left( r, \pm \sqrt{1-r^{2}}\right) , p_{4,5}=\left( \pm \frac{\sqrt{b^{2}-c^{2}}}{b}, -\frac{c}{b}\right) , p_{i+5}=(x_{i}^{*},0),~~i=1,2,3. \end{aligned}$$

The Jacobian of system (3) is

$$\begin{aligned} J=\left[ \begin{array}{cc} -(by+c)f_{yx}&{}-(b\,f_{y}+(by+c)f_{yy})\\ f_{x}+(by+c)f_{xx}&{}f_{y}+bf_{x}+(by+c)f_{xy} \end{array} \right] . \end{aligned}$$

The eigenvalues of the Jacobian matrix at $p_1$ are 0 and $(\left( {r}^{2}-1 \right) {b}^{2}+{c}^{2})/b$, so it is semi-hyperbolic. Using Theorem 2.19 in [10], it is a saddle-node point. The determinants of the Jacobian matrices at the points $p_2$ and $p_3$ are

$$\begin{aligned} \det J(p_{2})=&4\left( r^{2}-1\right) \left( -{b}^{2}{r}^{2}+2\,bc\sqrt{1-{r}^{2}}+{b}^{2}+{c}^{2}\right) ,\\ \det J(p_{3})=&4\left( r^{2}-1\right) \left( -{b}^{2}{r}^{2}-2\,bc\sqrt{1-{r}^{2}}+{b}^{2}+{c}^{2}\right) . \end{aligned}$$

Since these determinants are negative, these two points are hyperbolic saddles. Computing the determinant and the trace of the Jacobian matrix at the point $p_4$ we have

$$\begin{aligned} \det J(p_{4})=-\dfrac{4cf_{1}(r)}{b^3},\quad \text {tr}J(p_{4})=-\dfrac{2g_{1}(r)}{b^{2}}, \end{aligned}$$

where

$$\begin{aligned} f_{1}(r)=&{b}^{2}\sqrt{b^{2}-c^{2}}{r}^{2}-2b\left( b^{2}-c^{2}\right) r+\sqrt{b^{2}-c^{2}} \left( b^{2}-c^{2}\right) ,\\ g_{1}(r)=&b\left( b \sqrt{b^{2}-c^{2}}-c\right) r-b(b^{2}-c^{2})+c\sqrt{b^{2}-c^{2}}. \end{aligned}$$

The expression $f_{1}(r)$ is positive, therefore the point $p_4$ is a hyperbolic saddle if $c>0$, and a hyperbolic node or focus if $c<0$, because the trace of Jacobian matrix at this point is non-zero. In a similar way we obtain that the point $p_5$ is a hyperbolic saddle if $c<0$, and a hyperbolic node or focus if $c>0$. The determinant and trace of the Jacobian matrix at the point $p_6$ are

$$\begin{aligned} \det J(p_{6})=&-\frac{2}{3}\,{\frac{Kc}{ M^{\frac{2}{3}}}},\quad \text {tr}J(p_{6}) =\frac{1}{3}\,{\frac{bL}{{M}^{\frac{2}{3}}}}, \end{aligned}$$

where

$$\begin{aligned} K=&\left( 27\,{c}^{3}+6\,r{c}^{2}+c{r}^{2}+3\,c+8\,r \right) {M}^{2/3}\\&+\left( -81\,{c}^{4}-18\,{c}^{3}r-12\,{c}^{2}{r}^{2}+c{r}^{3}-36\,{c}^{2}-9\,r + \left( 3\,c+2\,r \right) \sqrt{-T}i\right) M^{1/3}\\ {}&+\left( 9\,{c}^{2}+{r}^{2}+3 \right) \left( 27\,{c}^{3}+6\,r{c}^{2}+c {r}^{2}+3\,c+8\,r \right) -2\, \left( 9\,{c}^{2}+{r}^{2}+3 \right) \sqrt{-T}i,\\ L=&\left( 27\,{c}^{2}+{r}^{2}+3 \right) {M}^{2/3}+ \left( -81\,{c}^{3}-6 \,c{r}^{2}+{r}^{3}-18\,c-9\,r +3\,\sqrt{-T}i\right) M^{1/3}\\&+243\,{c}^{4}+18\,{c}^{2}{r}^{2}-6\,c{r}^{3}+{r}^{4}+54\,{c}^{ 2}+54\,cr+6\,{r}^{2}+9-18\,c\sqrt{-T}i, \\ M=&-27\,{c}^{3}+{r}^{3}-9\,r+3\,\sqrt{-T}i,\\ T=&\left( -3\,{c}^{2}-3 \right) {r}^{4}-6\,{c}^{3}{r}^{3}+ \left( -27\,{ c}^{4}-18\,{c}^{2}+6 \right) {r}^{2}+54\,{c}^{3}r-81\,{c}^{4}-27\,{c}^ {2}-3. \end{aligned}$$

First we show that $T<0$ if $c\ne 0$. Indeed, we consider T as a function of r, then

$$\begin{aligned} \begin{aligned} D_{3}&=-324\,{c}^{2} \left( 648\,{c}^{12}+2295\,{c}^{10}+2592\,{c}^{8}+606\,{ c}^{6}-328\,{c}^{4}+32\,{c}^{2}+128 \right) <0,\\ D_{4}&=11664\,{c}^{4} \left( 54\,{c}^{6}+81\,{c}^{4}+72\,{c}^{2}+16 \right) ^{3}>0. \end{aligned} \end{aligned}$$

Therefore from [27] we get that the four roots of the polynomial T are non-real, and consequently $T<0$. The resultant with respect to c between the polynomials $-27\,{c}^{3}+{r}^{3}-9r$ and $-T$ is

$$\begin{aligned} \begin{aligned} k(r)=&5832\,{r}^{18}-78732\,{r}^{16}+1299078\,{r}^{14}-8798301\,{r}^{12}+ 68024448\,{r}^{10}-199290375\,{r}^{8}+806727438\,{r}^{6}\\&+674398629\,{r }^{4}+172186884\,{r}^{2}+14348907. \end{aligned} \end{aligned}$$

By applying the Sturm’s Theorem we get that $k(r)>0$ for all $r\in [0, \infty )$. Thus $-27\,{c}^{3}+{r}^{3}-9\,r$ and $-T$ have no common roots, and this fact implies that M is different from zero.

Now we will prove that the expressions K and L are non-zero. Taking $M^{1/3}=Y$ the expressions K and L change to the form

$$\begin{aligned} \begin{aligned} K=&\left( 27\,{c}^{3}+6\,r{c}^{2}+c{r}^{2}+3\,c+8\,r \right) Y^{2}\\&+ \left( -81\,{c}^{4}-18\,{c}^{3}r-12\,{c}^{2}{r}^{2}+c{r}^{3}-36\,{c}^{2}-9\,r+ \left( 3\,c+2\,r \right) \sqrt{-T}i\right) Y\\ {}&+\left( 9\,{c}^{2}+{r}^{2}+3 \right) \left( 27\,{c}^{3}+6\,r{c}^{2}+c {r}^{2}+3\,c+8\,r \right) -2\, \left( 9\,{c}^{2}+{r}^{2}+3 \right) \sqrt{-T}i,\\ L=&\left( 27\,{c}^{2}+{r}^{2}+3 \right) Y^{2}+ \left( -81\,{c}^{3}-6 \,c{r}^{2}+{r}^{3}-18\,c-9\,r +3\,\sqrt{-T}i\right) Y\\&+243\,{c}^{4}+18\,{c}^{2}{r}^{2}-6\,c{r}^{3}+{r}^{4}+54\,{c}^{ 2}+54\,cr+6\,{r}^{2}+9-18\,c\sqrt{-T}i. \end{aligned} \end{aligned}$$

After finding the two roots $Y_1$ and $Y_2$ of $K=0$ and the two roots $\bar{Y}_1$ and $\bar{Y}_2$ of $L=0$ we have

$$\begin{aligned} \begin{aligned} M-Y_{j}^{3}&=\pm 216(R(r,c)+iI(r,c)\sqrt{-T})=0,\quad j=1,2,\\ M-\bar{Y}_{j}^{3}&=\pm 72(\bar{R}(r,c)+i\bar{I}(r,c)\sqrt{-T})=0,\quad j=1,2, \end{aligned} \end{aligned}$$

respectively, where

$$\begin{aligned} \begin{aligned} R(r,c)&=c \left( r^{2}-1 \right) W(r) R_{1}(r,c),\qquad I(r,c)=-6\,c \left( r^{2}-1 \right) W(r) I_{1}(r,c),\\ \bar{R}(r,c)&=(r^{2}-1)^{2}R_{1}(r,c),\qquad \bar{I}(r,c)=-6(r^{2}-1)^{2}I_{1}(r,c), \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} W(r)&=\left( {c}^{2}+1 \right) {r}^{4}+2\,{c}^{3}{r}^{3}+ \left( 9\,{c}^{4} +6\,{c}^{2}-2 \right) {r}^{2}-18\,{c}^{3}r+27\,{c}^{4}+9\,{c}^{2}+1,\\ R_{1}(r,c)&=729\,{c}^{6}-243\,{c}^{4}{r}^{2}-108\,{c}^{3}{r}^{3}-27\,{c}^{2}{r}^{4 }+{r}^{6}-729\,{c}^{4}+972\,{c}^{3}r-162\,{c}^{2}{r}^{2}-45\,{r}^{4}- 243\,{c}^{2}\,+135\,{r}^{2}-27,\\ I_{1}(r,c)&=27\,{c}^{3}-{r}^{3}+9\,r. \end{aligned} \end{aligned}$$

The function W(r) is always positive because

$$\begin{aligned} \begin{aligned} D_{3}&=-4\,{c}^{2} \left( 648\,{c}^{12}+2295\,{c}^{10}+2592\,{c}^{8}+606\,{c} ^{6}-328\,{c}^{4}+32\,{c}^{2}+128 \right) <0,\\ D_{4}&=16\,{c}^{4} \left( 54\,{c}^{6}+81\,{c}^{4}+72\,{c}^{2}+16 \right) ^{3}>0. \end{aligned} \end{aligned}$$

On the other hand the resultant between $R_{1}(r,c)$ and $I_{1}(r,c)$ with respect to c is

$$\begin{aligned} l(r)=&-3099363912\,{r}^{18}+41841412812\,{r}^{16}-690383311398\,{r}^{14}+ 4675777881741\,{r}^{12}-36150980669568\,{r}^{10}\\&+105911076180375\,{r}^{8}-428728036378158\,{r}^{6}-358403081794389\, {r}^{4}-91507169819844\, {r}^{2}\\&-7625597484987, \end{aligned}$$

and using the Sturm’s theorem we see that there is no root for all $r\in [0, \infty )$. Thus, $R_{1}(r,c)$ and $I_{1}(r,c)$ have no common roots. These facts imply that K and L are different from zero, therefore the singular point $p_6$ is hyperbolic. Then the determinant and the trace verify

$$\begin{aligned} \begin{aligned}&\det J(p_{6})\vert _{\{r=\frac{1}{2}, c=1\}}=2.310040050- 0.000000003667457936\,i,\\&\det J(p_{6})\vert _{\{r=\frac{1}{2}, c=-1\}}=- 59.94103202- 0.000000005049604033\,i,\\&\text {tr}J(p_{6})\vert _{\{r=\frac{1}{2},c=1\}}=\left( 0.1083508522+ 0.0000000008913180476\,i \right) b, \end{aligned} \end{aligned}$$

and since these functions are continuous it follows that the singular point $p_6$ is a saddle if $c<0$ and an unstable node or focus if $c>0$.

Similarly we can obtain that the singular points $p_{7}$ and $p_8$ are hyperbolic and they are saddles, or nodes or foci.

Using the information about the infinite singular points and the Poincaré-Hopf Theorem we get that the sum of the indices of the singular points at $p_6$, $p_7$ and $p_8$ is one. Therefore two points of these points must be nodes or foci and the other is a saddle. The local phase portraits of the finite singular points are given in Tables 2 and 3.

Now we want to know if the focus or node points, inside the circle $x^{2}+y^{2}-1=0$, are surrounded by limit cycles or not? For this we shall use the Dulac-Bendixson criterion (for a proof see for instance [10]):

Theorem 8

If there exists a $C^1$ function B(x, y) in a simply connected region R such that $\partial (BP)/\partial x+\partial (BP)/\partial y$ has constant sign and is not zero in R, then the $C^1$ differential system

$$\begin{aligned} \dot{x}=P(x,y),\qquad \dot{y}=Q(x,y), \end{aligned}$$

does not have periodic orbits in R.

Fig. 5

Local phase portrait in the Poincaré disc for case (I1) when $b^{2}(r^{2}-1)+c^{2}<0$ and $b,c>0$

Consider the two regions $R_{1}=\lbrace (x,y): x^{2}+y^{2}<1, x-r>0\rbrace$ and $R_{2}=\lbrace (x,y): x^{2}+y^{2}<1, x-r<0\rbrace$, and the Dulac function

$$\begin{aligned} B(x,y)={\frac{1}{ \left( by+c \right) \left( x-r \right) \left( {x}^{2}+{y}^{2}-1 \right) }}. \end{aligned}$$

By applying the Dulac-Bandixson criterion to the differential system (3) with $e=1$ in the regions $R_1$ and $R_2$ with the function B(x, y), we get

$$\begin{aligned} \begin{aligned} \dfrac{\partial (BP)}{\partial x}+\dfrac{\partial (BQ)}{\partial y}=-{\frac{b}{ \left( by+c \right) ^{2}}}. \end{aligned} \end{aligned}$$

Since the straight line $y=-c/b$ is transversal with respect to the flow of the differential system (3) with $e=1$, from Theorem 8 there is no periodic orbits in the regions $R_1$ and $R_2$.

Now we shall describe how we obtain the left phase portrait in the Poincaré disc of Fig. 6, in a similar way are obtained all the other global phase portraits which appear in the paper.

Table 2 The local phase portraits of the finite singular points for case $(\mathbf{I1} )$ when $b^{2}(r^{2}-1)+c^{2}<0$

We consider the local phase portrait corresponding to $c>0$ and $b^{2}(r^{2}-1)+c^{2} <0$. In this case system (3) has eight distinct finite singular points which are described in Table 2. Since $r\in [0,1)$, the invariant straight line $x=r$ intersect the invariant circle $x^{2}+y^{2}=1$ in two points $p_2$ and $p_3$. The point $p_1$ is on the invariant straight line $x=r$ and inside the circle. It is clear that the points $p_4$ and $p_5$ are on the invariant circle and on the line $y=-c/b$. We do not have any explicit solution for the remain points $p_6$, $p_7$ and $p_8$ but we can compute numerically where they are located. Also the local phase portraits at the infinite singular points of the local chart $U_1$ and at the origin of $U_2$ of system (3) are presented in section 3.1 (see Fig. 5).

Now we describe how we find the global phase portrait. We start describing the two global phase portraits coming from the two local phase portraits described in Table 2. Since the infinite singular point p sends orbits to the origins of $U_2$ and $V_2$ one of the stable separatrices of the finite singular point $p_7$ must start at p. The two unstable separatrices of $p_7$ only can go to either to the origin of $U_2$, or to the origin of $V_2$, but both cannot go simultaneously to one of these origins. So one unstable separatrix of $p_7$ goes to the origin of $U_2$ and the other to the origin of $V_2$. Hence the remaining stable separatrix of $p_7$ only can come from the unstable node $p_5$. Clearly the unstable separatrix of $p_1$ must go to the stable singular point $p_8$. On the other hand one of the stable separatrices of $p_4$ must come from the unstable singular point $p_6$, and the other stable only can come from the infinite singular point q. This completes the description of the left global phase portrait of Fig. 6. The right global phase portrait of Fig. 6 can be obtained in the same way. Also we note that every different class of phase portrait is denoted by a different number in the above of the global phase portrait, and we will use the same number for the topologically equivalent classes. Thus in Fig. 6 both phase portraits have the number (1).

Fig. 6

Global phase portraits in the Poincaré disc for case (I1) when $b^{2}(r^{2}-1)+c^{2}<0$

Table 3 The local phase portraits of the finite singular points for case $(\mathbf{I1} )$ when $b^{2}(r^{2}-1)+c^{2}>0$

Fig. 7

Global phase portraits in the Poincaré disc for case (I1) when $b^{2}(r^{2}-1)+c^{2}>0$

$(\mathbf{I2} )$ $r= \sqrt{b^{2}-c^{2}}/b$, then system (3) with $e=1$ has six distinct finite singular points, namely

$$\begin{aligned} p_{1}=\left( \frac{\sqrt{b^{2}-c^{2}}}{b}, \frac{c}{b}\right) , p_{2,3}=\left( \pm \frac{\sqrt{b^{2}-c^{2}}}{b}, -\frac{c}{b}\right) , p_{i+3}=(x_{i}^{*},0),~~i=1,2,3, \end{aligned}$$

where $x_i^*$ are the roots of the cubic polynomial

$$\begin{aligned} x^3+\frac{\left( 3 b c-\sqrt{b^2-c^2}\right) }{b}x^2-\frac{\left( 2 c \sqrt{b^2-c^2}+b\right) }{b}x-\frac{b c-\sqrt{b^2-c^2}}{b}. \end{aligned}$$

The singular points $p_j$ for $j=4,5,6$ only exits when $x_j^*$ is real.

The points $p_i$, $i=1, 3, 4, 5, 6$ are hyperbolic, because the eigenvalues of the Jacobian matrix are real and non-zero. The Jacobian matrix at $p_2$ is linearly zero and then we need blow-ups to understand its local phase portrait.

We move $p_{2}=\left( \sqrt{b^{2}-c^{2}}/b, -c/b\right)$ to the origin, then the differential system becomes

$$\begin{aligned} \begin{array}{l} \dot{x}=-2\,bx{y}^{2}+2\,cxy,\\ \dot{y}=-2\,{\frac{cxy}{b}}+{x}^{3}+4\,\sqrt{{b}^{2}-{c}^{2}}xy+3\,b{x}^{2}y +2\,{\frac{\sqrt{{b}^{2}-{c}^{2}}{x}^{2}}{b}}+x{y}^{2}+b{y}^{3}-2\,c {y}^{2}. \end{array} \end{aligned}$$

(9)

Now we do the blow-up $(x,y)\mapsto (x,w)$ with $w=y/x$ and eliminating the common factor x, we have

$$\begin{aligned} \begin{array}{l} \dot{x}=-2\,wx \left( bwx-c \right) ,\\ \dot{w}=\frac{1}{b}\left( 3\,{b}^{2}{w}^{3}x+3\,{b}^{2}xw+x{w}^{2}b-4\,c{w}^{2}b+4\, \sqrt{{b}^{2}-{c}^{2}}wb+bx-2\,wc+2\,\sqrt{{b}^{2}-{c}^{2}}\right) . \end{array} \end{aligned}$$

(10)

When $x=0$ in system (10), we have that $\dot{w}=0$ if and only if

$$\begin{aligned} w=-\frac{1}{2b},w={\frac{\sqrt{{b}^{2}-{c}^{2}}}{c}}. \end{aligned}$$

So on the w-axis system (10) has two singular points. The eigenvalues of the Jacobian matrix at the point $(0,-1/(2b))$ are $-c/b$ and $(4\,b\sqrt{{b}^{2}-{c}^{2}}+2c)/b$, and at the point $(0,(\sqrt{{b}^{2}-{c}^{2}})/c)$ are $2\,\sqrt{{b}^{2}-{c}^{2}}$ and $-(4\,b\sqrt{{b}^{2}-{c}^{2}}+2c)/b$. Therefore when $c>0$ the points $(0, 1/(-2b))$ and $(0, \sqrt{{b}^{2}-{c}^{2}}/c)$ are saddles. If $c<0$ and $c +2b \sqrt{{b}^{2}-{c}^{2}}>0$, then the point $(0, 1/(-2b))$ is an unstable node and the point $(0, \sqrt{{b}^{2}-{c}^{2}}/c)$ is a saddle. If $c<0$ and $c +2b \sqrt{{b}^{2}-{c}^{2}}<0$, then the point $(0, 1/(-2b))$ is a saddle and the point $(0, \sqrt{{b}^{2}-{c}^{2}}/c)$ is an unstable node (Fig. 7). Going back through the change of variables until the coordinates (x, y), the origin of system (9) in the variables (x, y) has the local phase portraits of Fig. 8. The local phase portraits of the finite singular points are given in Table 4. We classify all the global phase portraits of this case in Fig. 9.

Fig. 8

The local phase portraits at $p_2$ in the case (I2)

Table 4 The local phase portraits of the finite singular points for case (I2)

Fig. 9

Global phase portraits in the Poincaré disc for case (I2)

Case (II). There are six distinct finite singular points, namely

$$\begin{aligned} p_{1}=\left( r,-\frac{c}{b}\right) , p_{2,3}=\left( r, \pm \sqrt{1-r^{2}}\right) , p_{i+3}=(x_{i}^{*},0),~~i=1,2,3. \end{aligned}$$

The points $p_{i}$, $i=2,...,6$ are hyperbolic and $p_{1}$ is a semi-hyperbolic point. Using Theorem 2.19 of [10] we find that $p_1$ is a saddle-node. The local phase portraits of the finite singular points in this case are shown in Table 5. For the global phase portraits of this case see Fig. 10.

Table 5 The local phase portraits of the finite singular points for case (II)

Fig. 10

Global phase portraits in the Poincaré disc for case (II)

Case (III). If $r\in [0,1)$ and

(III1) $r\in (0,1)$ then system (3) with $e=1$ has seven distinct finite singular points, namely

$$\begin{aligned} p_{1}=\left( r,-\frac{c}{b}\right) , p_{2,3}=\left( r, \pm \sqrt{1-r^{2}}\right) , p_{4}=\left( 0, -\frac{c}{b}\right) ,p_{i+4}=(x_{i}^{*},0),~~i=1, 2, 3. \end{aligned}$$

The points $p_{1}$ and $p_4$ are semi-hyperbolic, and using Theorem 2.19 in [10] we obtain that both are saddle-node. The rest of singular points are hyperbolic, see Table 6. The global phase portraits of this case are given in Fig. 11.

Table 6 The local phase portraits of the finite singular points for case (III1)

Fig. 11

Global phase portraits in the Poincaré disc for case (III1)

(III2) $r=0$ then it has five distinct finite singular points, namely

$$\begin{aligned} p_{1}=\left( 0, 1\right) , p_{2}=\left( 0, -1\right) ,p_{i+2}=(x_{i}^{*},0),~~i=1, 2, 3. \end{aligned}$$

The points $p_i$, $i=3, 4,5$ are hyperbolic, the point $p_1$ is hyperbolic if $c>0$, and it is linearly zero if $c<0$, and the point $p_2$ is hyperbolic if $c<0$, and it is a linearly zero if $c>0$. So we need to do the blow-up techniques to study these linearly zero points.

At first we move $p_{1}=(0, 1)$ to the origin and assume that $b=-c$, then we get

$$\begin{aligned} \begin{array}{l} \dot{x}=2\,cxy \left( y+1 \right) ,\\ \dot{y}=-3\,c{x}^{2}y-c{y}^{3}-2\,c{y}^{2}+{x}^{3}+x{y}^{2}+2\,xy. \end{array} \end{aligned}$$

(11)

Doing the blow-up $(x,y)\mapsto (x,w)$ with $w=y/x$ and eliminating the common factor x, we have

$$\begin{aligned} \begin{array}{l} \dot{x}=2\,cxw \left( wx+1 \right) ,\\ \dot{w}=-3\,c{w}^{3}x-4\,c{w}^{2}-3\,cxw+{w}^{2}x+2\,w+x. \end{array} \end{aligned}$$

(12)

When $x=0$, system (12) has the singular points (0, 0) and (0, 1/(2c)). The linear part of system (12) at a point (0, w) is

$$\begin{aligned} \left[ \begin{array}{cc} 2\,cw&{}0\\ -3\,c{w}^{3}-3 \,cw+{w}^{2}+1&{}-8\,cw+2\end{array} \right] . \end{aligned}$$

Therefore the origin of system (12) is a semi-hyperbolic. Using Theorem 2.19 in [10] it is a saddle-node and the point (0, 1/(2c)) is a hyperbolic saddle. Going back through the change of variables until system (11), the local phase portrait at the point $p_1$ is given in Fig. 12.

Fig. 12

The local phase portrait at $p_1$ in the case (III2)

In a similar way we can study the local phase portrait at the point $p_2$, see Fig. 13. The local phase portraits of the finite singular points of this case are shown in Table 7. The global phase portraits of this case are shown in Fig. 14.

Fig. 13

The local phase portrait at $p_2$ in the case (III2)

Table 7 The local phase portraits of the finite singular points for case (III2)

Fig. 14

Global phase portraits in the Poincaré disc for case (III2)

Case (IV). System (3) with $e=1$ and $b=0$ becomes

$$\begin{aligned} \begin{array}{l} \dot{x}=2\,cy \left( -x+r \right) ,\\ \dot{y}=-2\,crx+3\,c{x}^{2}+c{y}^{2}-r{x}^{2}-r{y}^{2}+{x}^{3}+x{y}^{2}-c+r-x. \end{array} \end{aligned}$$

(13)

We know that the cubic system (13) has an invariant ellipse $x^{2}+y^{2}-1=0$ and an invariant straight line $x-r=0$. Using the Darboux theory (see Theorem 8.7 of [10]), it is easy to obtain that

$$\begin{aligned} H(x,y)=e^x (r-x)^c \left( x^2+y^2-1\right) ^c, \end{aligned}$$

is a first integral of system (13) in the open and dense subset of $\mathbb {R}^2$ where it is defined.

System (13) has five distinct finite singular points, namely

$$\begin{aligned} p_{1,2}=\left( r, \pm \sqrt{1-r^{2}}\right) ,p_{i+2}=(x_{i}^{*},0),~~i=1, 2, 3. \end{aligned}$$

The eigenvalues of the Jacobian matrix of system (13) evaluated at $p_i$, $i=1,2$ are equal to $2\,c\sqrt{1-{r}^{2}}$ and $-2\,c\sqrt{1-{r}^{2}}$. Therefore these points are hyperbolic saddles. Since the trace of the Jacobian matrix at the points $p_i$, $i=3,4,5$ is equal to zero and their determinant is non-zero, these points can be either saddle or center or focus. But since the first integral H is not zero on them these points must be a center or a saddle. The local phase portraits of the finite singular points in this case are given in Table 8. The global phase portraits are shown in Fig. 15.

Table 8 The local phase portraits of the finite singular points for case (IV)

Fig. 15

Global phase portraits in the Poincaré disc for case (IV)

Case (V). System (3) with $e=1$ has six distinct finite singular points, namely

$$\begin{aligned} p_{1}=\left( 1,-\frac{c}{b}\right) , p_{2,3}=\left( \pm \frac{\sqrt{b^{2}-c^{2}}}{b}, -\frac{c}{b}\right) , p_{4}=(x_{1}^{*},0)=(1,0),p_{i+3}=(x_{i}^{*},0),~~i=2, 3. \end{aligned}$$

The points $p_{2}$, $p_{3}$ and $p_{6}$ are hyperbolic. The point $p_1$ is semi-hyperbolic and the point $p_4$ is nilpotent, using Theorem 2.19 and Theorem 3.5 in [10], respectively, we know that $p_1$ is a saddle-node and $p_4$ is a saddle. The local phase portrait of the finite singular points in this case are shown in Table 9. We show the global phase portraits in this case in Fig. 16.

Table 9 The local phase portraits of the finite singular points for case (V)

Fig. 16

Global phase portraits in the Poincaré disc for case (V)

Case (VI). System (3) with $e=1$ has four distinct finite singular points, namely

$$\begin{aligned} p_{1}=\left( 1,-\frac{c}{b}\right) , p_{2}=(x_{1}^{*},0)=(1,0),p_{i+1}=(x_{i}^{*},0),~~i=2, 3. \end{aligned}$$

The points $p_{3}$ and $p_{4}$ are hyperbolic. The point $p_1$ is semi-hyperbolic and the point $p_2$ is nilpotent, using Theorem 2.19 and Theorem 3.5 in [10], respectively, we know that $p_1$ is a saddle-node and $p_2$ is a saddle. The local phase portraits of the finite singular points in this case are shown in Table 10. The global phase portraits in this case are classified in Fig. 17.

Table 10 The local phase portraits of the finite singular points for case (VI)

Fig. 17

Global phase portraits in the Poincaré disc for case (VI)

Case (VII). System (3) with $e=1$ has five distinct finite singular points, namely

$$\begin{aligned} p_{1}=\left( 1,-\frac{c}{b}\right) , p_{2}=\left( 0,-\frac{c}{b}\right) , p_{3}=(x_{1}^{*},0)=(1,0),p_{i+2}=(x_{i}^{*},0),~~i=2, 3. \end{aligned}$$

The points $p_{4}$ and $p_{5}$ are hyperbolic. The points $p_1$ and $p_2$ are semi-hyperbolic and the point $p_3$ is nilpotent, using Theorem 2.19 and Theorem 3.5 in [10], respectively, we know that $p_1$ and $p_2$ are saddle-nodes and $p_3$ is a saddle. The local phase portrait of the finite singular points in this case are shown in Table 11. The global phase portraits in this case are classified in Fig. 18.

Table 11 The local phase portraits of the finite singular points for case (VII)

Fig. 18

Global phase portraits in the Poincaré disc for case (VII)

Case (VIII). System (3) with $e=1$ has three distinct finite singular points, namely

$$\begin{aligned} p_{1}=(x_{1}^{*},0)=(1,0),p_{i+1}=(x_{i}^{*},0),~~i=1, 2. \end{aligned}$$

When $c>0$ the point $p_3$ is a hyperbolic saddle and the point $p_2$ is a center or focus, but the first integral in this case is non-zero (see Case (IV)), hence this point is a center. When $c<0$ the point $p_2$ is a hyperbolic saddle and the point $p_3$ is a center for the same reason. The point $p_1$ is nilpotent, again using Theorem 3.5 of [10] it is a saddle. The local phase portraits of the finite singular points in this case are shown in Table 12. The global phase portraits in this case are shown in Fig. 19.

Table 12 The local phase portraits of the finite singular points for case (VIII)

Fig. 19

Global phase portraits in the Poincaré disc for case (VIII)

Case (IX). System (3) with $e=1$ has six distinct finite singular points, namely

$$\begin{aligned} p_{1}=\left( r,-\frac{c}{b}\right) , p_{2,3}=\left( \pm \frac{\sqrt{b^{2}-c^{2}}}{b}, -\frac{c}{b}\right) , p_{i+3}=(x_{i}^{*},0),~~i=1, 2, 3. \end{aligned}$$

The points $p_i$, $i=2,...,6$ are hyperbolic and the point $p_1$ is semi-hyperbolic, using Theorem 2.19 of [10], it is a saddle-node. The local phase portraits of the finite singular points in this case are shown in Table 13. The global phase portraits in this case are given in Fig. 20.

Table 13 The local phase portraits of the finite singular points for case (IX)

Fig. 20

Global phase portraits in the Poincaré disc for case (IX)

Case (X). System (3) with $e=1$ has four distinct finite singular points, namely

$$\begin{aligned} p_{1}=\left( r,-\frac{c}{b}\right) , p_{i}=(x_{i}^{*},0),~~i=2, 3, 4. \end{aligned}$$

The points $p_i$, $i=2, 3, 4$ are hyperbolic and the point $p_1$ is semi-hyperbolic, using Theorem 2.19 in [10], it is a saddle-node.

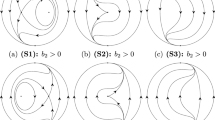
By Theorem 1 of [7] in this case there is only one hyperbolic limit cycle $x^2+y^2=1$. The local phase portrait of the finite singular points in this case are shown in Table 14. The global phase portraits in this case are classified in Fig. 21.

Table 14 The local phase portraits of the finite singular points for case (X)

Fig. 21

Global phase portraits in the Poincaré disc for case (X)

Case (XI). System (3) with $e=1$ has five distinct finite singular points, namely

$$\begin{aligned} p_{1}=\left( r,-\frac{c}{b}\right) ,p_{2}=\left( 0,-\frac{c}{b}\right) , p_{i}=(x_{i}^{*},0),~~i=2, 3, 4. \end{aligned}$$

The points $p_i$, $i=3, 4, 5$ are hyperbolic, and the points $p_1$ and $p_2$ are semi-hyperbolic, using Theorem 2.19 of [10], they are saddle-nodes. The local phase portrait of the finite singular points in this case are shown in Table 15. The global phase portraits in Poincaré disc in this case are given in Fig. 22.

Table 15 The local phase portraits of the finite singular points for case (XI)

Fig. 22

Global phase portraits in the Poincaré disc for case (XI)

Case (XII). System (3) with $e=1$ has three distinct finite singular points, namely

$$\begin{aligned} p_{i}=(x_{i}^{*},0),~~i=1, 2, 3. \end{aligned}$$

The point $p_1$ is a hyperbolic saddle. If $c>0$ the point $p_2$ is a hyperbolic saddle and the point $p_3$ can be either a center or a focus, but the first integral at this point is non-zero (see Case (IV)), hence this point is a center. If $c<0$ the point $p_3$ is a hyperbolic saddle and the point $p_2$ is a center for the same reason. The local phase portraits of the finite singular points in this case are shown in Table 16. These local phase portraits provide three global phase portraits shown in Fig. 23, the first (respectively, the third) phase portrait presented in Fig. 23 is verified by $c=3, r=2$ (respectively, $c=1, r=2$). Therefore by continuity it exists the phase portrait (27) of Fig. 23.

Table 16 The local phase portraits of the finite singular points for case (XII)

Fig. 23

Global phase portraits in the Poincaré disc for case (XII)

In the next sections we shall see that the phase portraits can be obtained directly by the analysis of the corresponding system of polynomial differential equations. So we decided to omit the corresponding tables of description of local phase portraits.

Finite Singular Points of System (3) with $e=1$, $c=0$ and $b> 0$

Under these assumptions system (3) becomes

$$\begin{aligned} \begin{array}{l} \dot{x}=-2\,b{y}^{2} \left( x-r \right) ,\\ \dot{y}=-2\,brxy+3\,b{x}^{2}y+b{y}^{3}-r{x}^{2}-r{y}^{2}+{x}^{3}+x{y}^{2}-by+r-x. \end{array} \end{aligned}$$

(14)

Now we consider three cases as follows:

Case $(\mathbf{i} )$. If $r\in [0,1)$ then system (14) has five distinct finite singular points, namely

$$\begin{aligned} p_{1}=\left( r, 0\right) , p_{2,3}=\left( r, \pm \sqrt{1-r^{2}}\right) , p_{4,5}=\left( \pm 1, 0\right) . \end{aligned}$$

The eigenvalues of the Jacobian matrix at the point $p_1$ are 0 and $b(r^{2}-1)$, therefore it is a semi-hyperbolic point. Using Theorem 2.19 in [10], it is a stable node. The eigenvalues of the Jacobian matrix at the points $p_2$ and $p_3$ are $-2b(r^{2}-1)$ and $2b(r^{2}-1)$, so these points are saddles. The eigenvalues of the Jacobian matrix at the points $p_4$ and $p_5$ are 0, $-2b(r-1)$ and 0, $2b(r+1)$, respectively, therefore these points are semi-hyperbolic, after using Theorem 2.19 of [10] we obtain that these points are saddle-nodes. The global phase portraits in this case are shown in Fig. 24 (i).

Fig. 24

Global phase portraits in the Poincaré disc for case $e=1$, $c=0$

Case $(\mathbf{ii} )$. If $r= 1$ then system (14) has two distinct finite singular points, namely

$$\begin{aligned} p_{1}=\left( 1, 0\right) , p_{2}=\left( -1, 0\right) . \end{aligned}$$

The eigenvalues of the Jacobian matrix at the point $p_2$ are 0 and 4b, therefore it is a semi-hyperbolic point. Using Theorem 2.19 of [10], it is saddle-node. The point $p_1$ is linearly zero, so we need to apply the blow-up technique to determine the local phase portrait at this point. First we move $p_{1}=(0, 1)$ to the origin, then we get

$$\begin{aligned} \begin{array}{l} \dot{x}=-2\,b{y}^{2}x,\\ \dot{y}=3\,b{x}^{2}y+b{y}^{3}+4\,bxy+{x}^{3}+x{y}^{2}+2\,{x}^{2}. \end{array} \end{aligned}$$

(15)

Doing the blow-up $(x,y)\mapsto (x,w)$ with $w=y/x$ and eliminating the common factor x, we have

$$\begin{aligned} \begin{array}{l} \dot{x}=-2\,b{w}^{2}{x}^{2},\\ \dot{w}=3\,b{w}^{3}x+3\,bwx+{w}^{2}x+4\,bw+x+2. \end{array} \end{aligned}$$

(16)

On $x=0$ system (16) has the singular point $(0, -1/(2b))$. The eigenvalues of the Jacobian matrix of system (16) are 0 and 4b. Therefore the singular point $(0, -1/(2b))$ is semi-hyperbolic. Using Theorem 2.19 of [10] it is a saddle-node. Going back through the change of variables until system (15), the local phase portraits of the point $p_1$ are given in Fig. 25.

Fig. 25

The local phase portrait at $p_1$ in the case (ii)

In summary the global phase portraits in this case in Fig. 24 (ii).

Case $(\mathbf{iii} )$. If $r> 1$ then system (14) has three distinct singular points, namely

$$\begin{aligned} p_{1}=\left( r, 0\right) , p_{2,3}=\left( \pm 1, 0\right) . \end{aligned}$$

The points $p_1$, $p_2$ and $p_3$ are semi-hyperbolic, using Theorem 2.19 of [10], these points are a saddle, a saddle-node and a saddle-node, respectively. Then the global phase portraits in the Poincaré disc in this case are given in Fig. 24 (iii).

Finite Singular Points of System (3) with $e=1$, $c=0$ and $b= 0$

Under these assumptions system (3) becomes

$$\begin{aligned} \dot{x}=&0,\\ \dot{y}=&\left( {x}^{2}+{y}^{2}-1 \right) \left( x-r \right) . \end{aligned}$$

We see that the circle ${x}^{2}+{y}^{2}=1$ and the straight line $x=r$ are filled of singular points, and that there are no more singularities. Consequently the global phase portraits in this case are shown in the Fig. 26.

Fig. 26

Global phase portraits in the Poincaré disc for case $e=1$, $c=0$ and $b=0$

Finite Singular Points of System (3) with $e=0$

Here system (3) becomes

$$\begin{aligned} \begin{array}{l} \dot{x}=-2\, \left( by+c \right) y \left( x-r \right) ,\\ \dot{y}=- \left( by+c \right) \left( 2\,xr-3\,{x}^{2}-{y}^{2}+1 \right) . \end{array} \end{aligned}$$

(17)

At first we see that the line $by+c=0$ is filled with singular points. By reparametrization of time we eliminate this common factor, then system (17) changes to the form

$$\begin{aligned} \begin{array}{l} \dot{x}=2\, y \left( x-r \right) ,\\ \dot{y}= 2\,xr-3\,{x}^{2}-{y}^{2}+1. \end{array} \end{aligned}$$

(18)

Note that we cannot consider the case $b=c=0$, otherwise system (17) would become the null system. Using the Darboux theory of integrability (see for instance Chapter 8 of [10]) we obtain that

$$\begin{aligned} H(x,y)=(r-x) \left( x^2+y^2-1\right) , \end{aligned}$$

is a first integral of system (18).

Now we assume $0\le r<1$ then there are four distinct finite singular points of system (17), namely

$$\begin{aligned} p_{1,2}=\left( r, \pm \sqrt{1-r^{2}}\right) , p_{3,4}=\left( \dfrac{r\pm \sqrt{{r}^{2}+3}}{3}, 0\right) . \end{aligned}$$

The Jacobian matrix of system (18) at a generic point $(x^{*},y^{*})$ is given by

$$\begin{aligned} \left[ \begin{array}{cc} -2\,y^{*}&{}-2\,x^{*}+2\,r\\ -2\,r+ 6\,x^{*}&{}2\,y^{*}\end{array} \right] . \end{aligned}$$

The eigenvalues of the Jacobian matrix in $p_1$ and $p_2$ are equal to $2\,\sqrt{-{r}^{2}+1}$ and $-2\,\sqrt{-{r}^{2}+1}$. Consequently, these points are saddles. Computing the determinant and the trace of the Jacobian matrix in the points $p_3$ and $p_4$ we obtain that these points are either a center, or a focus. Since the first integral H is defined on these point they are centers.

Next we assume $r=1$ then there are two distinct finite singular points for system (18), namely

$$\begin{aligned} p_{1}=(1,0),\qquad p_{2}=\left( -\frac{1}{3},0\right) . \end{aligned}$$

Then both eigenvalues of the Jacobian matrix at the point $p_1$ are zero, but $J(p_{1})\not \equiv 0$, so this point is nilpotent. Using Theorem 3.5 in [10], we find that it is a saddle. The determinant of the Jacobian matrix at the point $p_2$ is 32/3 and the trace is equal to zero, therefore it can be either a center or focus. Using the first integral of system (18) we get that this point is a center.

Fig. 27

Global phase portraits in the Poincaré disc for case $e=0$ and $b=0$

Finally we assume $r>1$ then there are two finite distinct singular points for system (18), namely

$$\begin{aligned} p_{1,2}=\left( \dfrac{r\pm \sqrt{{r}^{2}+3}}{3}, 0\right) . \end{aligned}$$

Computing the determinant and the trace of the Jacobian matrix in these points we see that $p_1$ is a hyperbolic saddle and $p_2$ can be either a center, or focus, and for the same reason as in the two previous cases it must be a center.

Using the above information, the global phase portraits of system (17) with $b=0$ are given in Fig. 27 and the global phase portraits of system (17) and the line $by + c = 0$ filled of singular points are shown in Figs. 28, 29, 30, 31.

Fig. 28

Global phase portraits in the Poincaré disc for case $e=0$ and $c=0$

Fig. 29

Global phase portraits in the Poincaré disc for case $e=0$, $|b|>|c|$ and $c>0$

Fig. 30

Global phase portraits in the Poincaré disc for case $e=0$, $b=c>0$

Fig. 31

Global phase portraits in the Poincaré disc for case $e=0$, $|b|<|c|$ and $c>0$

Topological Equivalent Phase Portraits

In Table 17 we summarize the number of canonical regions R and the number of separatrices S of all the phase portraits of system (3) with the parameter $e=1$. Of course the phase portraits which do not share their pair (R, S) with any other phase portraits of the table, clearly are not topological equivalent with any other phase portrait of the table. Now we shall analyze the phase portraits of the table which share their pair (R, S) with some other phase portraits of the table.

Table 17 R and S denotes the number of canonical regions and the number of separatrices of the corresponding phase portraits in the Poincaré disc only of systems (1) with $e=1$

For the systems with $(R,S)=(6,14)$ we analyze all the configurations of separatrices of systems (18) and (26) we see that they are topologically equivalent, so by Theorem 4 these two phase portraits are topologically equivalent. The same occurs with the configurations of separatrices of systems (19) and (28) hence their phase portraits are topologically equivalent. But the configuration of separatrices of (18) and (19) are not topologically equivalent.

Consider the phase portraits (14) and (15) sharing $(R,S)=(7,21)$. They are not topologically equivalent because the phase portrait (14) has a canonical region having in its boundary the invariant circle and a point of the infinity, while the phase portrait (15) has a canonical region having in its boundary the invariant circle and an arc of the infinity.

Now we anayze the systems with $(R,S)=(8,25)$. System (7) has two saddles on the invariant circle which are connected by a separatrix contained in the interior of the unit disc, this does not occur for the systems (16), (17) and (29), so the phase portrait of system (7) is not topologically equivalent to the phase portraits of systems (16), (17) and (29). System (29) has no finite singular points outside the unit disc, since systems (16) and (17) have finite singular points outside the unit disc (recall that the boundary of the unit disc is the invariant circle formed by separatrices), therefore the phase portrait of system (29) is not topologically equivalent to the phase portraits of systems (16) and (17). In the phase portraits of system (17) there is an orbit connecting the saddle and the saddle-node which are outside the unit disc, and this is not the case for the phase portrait of system (17). In summary the phase portraits of systems (7), (16), (17) and (29) are not topologically equivalent.

Consider the systems (4) and (5) having $(R,S)=(8,26)$. The same argument used for proving that the phase portraits (14) and (15) are not topologically equivalent works here.

Again the same argument used for proving that the phase portraits (14) and (15) are not topologically equivalent shows that the phase portraits of the systems (12) and (13), of the systems (8) and (9), of the systems (22) and (23), and of the systems (2) and (3) are not topologically equivalent.

The saddle on the invariant circle of system (21) has a separatrix going to infinity, this is not the case for the saddle of system (20) on the invariant circle. Hence the phase portraits of these two systems are not topologically equivalent.

In summary, from the 31 phase portraits of system (3) with $e=1$ and $b^2+c^2\ne 0$ only 29 are topologically non-equivalent.

Clearly the phase portraits (32), (33) and (34) of system (3) with $e=1$ and $b^2+c^2= 0$ are not topologically equivalent between them, and with all the other phase portraits because are the unique phase portraits having the invariant circle filled up with singular points.

The phase portraits from (35) to (49) are the ones of system (3) with $e=0$. Then using the separatrix configurations and Theorem 4 is easy to verify that the phase portraits of (36) and (37), of (39) and (40), of (42) and (43), and finally of (48) and (49) are topologically equivalent. That is from the 15 phase portraits of system (3) with $e=0$ only 11 are topologically non-equivalent.

Bifurcation Diagrams

Fig. 32

The bifurcation diagrams for the system (3) with $e=1$ and $b^2+c^2\ne 0$. Here $k=c/\sqrt{1-r^2}$. The number x denotes the phase portrait (x) for the values of the parameters b and c in the region or in the straight line where this number appears

Fig. 33

The bifurcation diagrams for the system (3) with $e=0$ and $b^2+c^2\ne 0$. The number x denotes the phase portrait (x) for the values of the parameters b and c in the region or in the straight line where this number appears

In Fig. 32 we provide the bifurcations diagrams of the differential system (3) with $e=1$ and $b^2+c^2\ne 0$ in the half-plane of parameters $\{(c,b): b\ge 0\}$ for the different values of the parameter $r\ge 0$.

While in Fig. 33 we provide the bifurcations diagrams of the differential system (3) with $e=0$ and $b^2+c^2\ne 0$ in the half-plane of parameters $\{(c,b): b\ge 0\}$ for the different values of the parameter $r\ge 0$.

The bifurcation diagram of the differential system (3) with $e=1$ and $b=c=0$ on the half straight line $r\ge 0$ is given by the phase portrait (32) when $0\le r<1$, for the phase portrait (33) when $r=1$, and for the phase portrait (34) if $r>1$.