1 Introduction

Over the past decades, the problem of stability and control for neural networks has attracted much attention due to its both practical and theoretical importance [13, 14, 20,21,22, 31]. However, most of the results have been concerned with the asymptotic stability defined over an infinite-time interval. In many practical applications, the main concern is the behavior of the system over a fixed finite-time interval, for example, large values of the state are not acceptable in the presence of saturations. In this case, the traditional Lyapunov method is not applicable and the finite-time stability method is introduced [1, 5, 29]. Many valuable results on finite-time stability and control of continuous-time and discrete-time neural networks can be found in [2, 16, 23, 30, 32] and in the references therein. It should be noticed that in some systems we must consider their character of dynamic and state at the same time. Up to now, a wide variety of design methods for control of delayed neural networks have been studied mainly including stabilization, adaptive control, fuzzy control. The \(H_{\infty }\) control problem is to design state feedback controllers such that, in addition to the requirement of the robust finite-time stability of the closed-loop system, a specified performance level is also required to be achieved. In the literature, singular systems (also referred to as differential-algebraic equations, implicit systems, descriptor systems or generalized state-space systems) arise in a variety of practical systems such as biological systems, artificial electronic systems, system recognition, target tracking, static image processing and associative memory [4, 9, 29]. Both delay-independent and delay-dependent stability conditions for singular time delay systems have been extensively obtained by using the SVD approach and Lyapunov function method [7, 8, 10, 15, 24,25,26]. Meanwhile, considering the singular neural networks is of great significance [11, 12, 19]. Since the singular neural networks are usually described by nonlinear time delay equations, the results on stability and control of such systems are relative few. The main difficulty in studying singular neural networks is to solve the problem of existence and uniqueness of solutions. Some delay-dependent sufficient conditions for optimizing the size of singular neural networks using SVD approach can be found in [11]. The authors of Kumaresan and Balasubramaniam [12] provided solutions to optimal control for stochastic linear singular systems using neural networks with quadratic performance. More interesting criteria for stochastic stability of discrete-time singular neural networks with Markovian jump and time-varying delays were given in [19]. It is also worth mentioning that the problem of existence of the solution and the time-varying delays are not taken into account in the mentioned papers. For nonlinear discrete-time singular systems, since problems of existence and uniqueness of solutions and finite-time stability, regularity, causality need to be considered simultaneously, the finite-time stability analysis for such systems is more complicated and the methods of analyzing the existence and uniqueness of solution to singular systems in the mentioned papers are difficult to be applied. On the other hand, it should be noticed that almost the existing results for singular nonlinear discrete-time systems were developed in the context of Lyapunov asymptotic stability and control while very little attention has been paid to the finite-time stability and control of such systems. To the best of the our knowledge, the problems of the existence of solutions and the finite-time \(H_{\infty }\) control for singular discrete-time neural networks with delay have not been yet investigated, these problems are important and challenging in both theory and practice.

In this paper, we consider \(H_{\infty }\) finite-time stability and control of nonlinear singular discrete-time delay neurals network-based systems. First, by using the implicit function theorem and singular value decomposition method, LMI sufficient conditions are established which guarantees that the discrete-time singular neural networks are regular, causal and have unique solution in a neighborhood of the origin. Then, based on Lyapunov function method, delay-dependent sufficient conditions for designing state feedback controllers of \(H_{\infty }\) finite-time control are derived in terms of LMIs. The design of such controllers can be carried out in a systematic and computationally efficient manner via the use of LMI-based algorithms [6]. The result of this paper can be considered as a further development of the results obtained in [11, 12, 19]. Last, numerical examples are provided to illustrate the validity and effectiveness of the proposed results.

The structure of the paper is as follows. Section 2 presents problem statement and some technical propositions needed for the proof of the main results. Sufficient conditions for the existence and uniqueness of the solution and for designing state feedback controllers for robust \(H_{\infty }\) control problem are presented in Sect. 3. Numerical examples illustrated that the obtained results are given in Sect. 4.

Notation

\(Z_{+}\) denotes the set of all nonnegative integers; \({R}^{n}\) denotes the n-dimensional space with the scalar product \(x^{\top }y;\,{R}^{n \times r}\) denotes the space of \((n\times r)-\)dimension matrices; \(A^{\top }\) denotes the transpose of matrix A; A is positive definite \((A > 0)\) if \(x^{\top }Ax > 0\) for all \(x \not = 0;\, A > B\) means \(A - B > 0\). The notation diag\(\{\ldots \}\) stands for a block-diagonal matrix. The symmetric term in a matrix is denoted by \(*\).

2 Problem Formulation and Preliminaries

Consider the following discrete-time singular neural networks with time-varying delays and disturbances

$$\begin{aligned} {\left\{ \begin{array}{ll} Ex(k+1) = Ax(k) + Wf(x(k))+W_1g(x(k-h(k))) + Bu(k) + C\omega (k), k\in Z_{+}, \\ z(k) = A_1x(k) + Dx(k-h(k)) + B_1u(k), \\ x(k) = \varphi (k),\ k\in \left\{ -h_2,\ldots ,0\right\} , \end{array}\right. } \end{aligned}$$
(1)

where \(x(k)\in {R}^n\) is the state; \(u(k) \in {R}^m\) is the control input; \(z(k)\in {R}^p\) is the observation output; n is the number of neural; \( f(x(k)) = [f_1(x_1(k)), f_2(x_2(k)), \ldots , f_n(x_n(k))],g(x(k-h(k))) = [g_1(x_1(k-h(k))), g_2(x_2(k-h(k))), \ldots , g_n(x_n(k-h(k)))]\) are activation functions, where \(f_{i}, g_{i}, i=\overline{1,n},\) satisfy the following conditions

$$\begin{aligned} \exists a_i> & {} 0{:}\quad | f_{i}(\xi )| \leqslant a_{i}| \xi |, \quad \forall i=\overline{1,n},\; \forall \xi \in {R},\nonumber \\ \exists b_i> & {} 0{:}\quad | g_{i}(\xi ) | \leqslant b_{i}| \xi |, \quad \forall i=\overline{1,n},\; \forall \xi \in {R}. \end{aligned}$$
(2)

The matrix \(E\in {R}^{n\times n}\) is singular and rank\((E) = r \leqslant n.\) The diagonal matrix \(A=\text{ diag }\{\overline{a}_{1}, \overline{a}_{2},\ldots , \overline{a}_{n}\},|\overline{a}_i| < 1\; \forall i=\overline{1,n}\) represents the self-feedback term; the matrices \(W, W_1\in {R}^{n\times n}\) are the connection weight matrices; \(B\in {R}^{n\times m}, B_1\in {R}^{p\times m}\) are the control matrices; \(C\in {R}^{n\times q}\) is the disturbance matrix; \(A_1, D\in {R}^{p\times n}\) are the observation matrix; the time-varying delay functions h(k) satisfy the condition

$$\begin{aligned} 0 < h_1 \leqslant h(k) \leqslant h_2 \quad \forall k\in {\mathbb {Z}}_{+}, \end{aligned}$$
(3)

where \(h_1, h_2\) are given positive integers; \(\varphi (k)\) is the initial function; the external disturbance \(\omega (k)\in {R}^q\) satisfies the condition

$$\begin{aligned} \sum _{k=0}^N\omega ^{\top }(k)\omega (k) < d, \end{aligned}$$
(4)

where \(d > 0\) is a given number.

Definition 1

[4] The pair (E, A) is said to be regular if characteristic polynomial det\((sE - A)\), where \(s\in {C}\), is not identical zero. The pair (E, A) is said to be causal if \(\text {deg(det}(sE - A)) = \text {rank}(E)\). System (1) with \(u(k) =0\) is said to be regular and causal if the pair (E, A) is regular and causal.

Definition 2

(Robust finite-time stability [5]) Given positive numbers \(N, c_1, c_2, c_1<c_2,\) and a symmetric positive-definite matrix R, unforced system (1) (\(u(k) =0\)) is robustly finite-time stable w.r.t. \((c_1, c_2, R, N)\) if

$$\begin{aligned} \max _{k\in \{-h_2,\ldots ,0\}}\varphi ^{\top }(k)R\varphi (k) \leqslant c_1 \; \Longrightarrow x^{\top }(k)Rx(k) < c_2 \quad \forall k = 1, 2,\ldots , N \end{aligned}$$

for all disturbances \(\omega (k)\) satisfying (4).

Definition 3

(\(H_{\infty }\)finite-time stability [1]) Given positive numbers \(\gamma , N, c_1, c_2, c_1<c_2,\) and a symmetric positive-definite matrix R, unforced system (1) (\(u(k) =0\)) is \(H_{\infty }\) finite-time stable w.r.t. \((c_1, c_2, R, N)\) if the following two conditions hold:

  1. (i)

    System (1) is robustly finite-time stable w.r.t. \((c_1, c_2, R, N)\).

  2. (ii)

    Under the zero initial condition (i.e., \(\varphi (k) = 0 \; \forall k\in \{-h_2, -h_2+1, \ldots , 0\}\)), the output z(k) satisfies

    $$\begin{aligned} \sum _{k=0}^Nz^{\top }(k)z(k) \leqslant \gamma \sum _{k=0}^N\omega ^{\top }(k)\omega (k) \end{aligned}$$
    (5)

    for all disturbances \(\omega (k)\) satisfying (4).

Definition 4

(\(H_{\infty }\)finite-time control) Given positive numbers \(\gamma , N, c_1, c_2, c_1<c_2,\) and a symmetric positive-definite matrix R, the finite-time \(H_{\infty }\) control problem for system (1) has a solution if there exists a state feedback controller \(u(k)=Kx(k)\) such that the resulting closed-loop system is \(H_{\infty }\) finite-time stable w.r.t. \((c_1, c_2, R, N).\)

Proposition 1

(Schur Complement Lemma [3]) Given constant matrices X, Y, Z with appropriate dimensions satisfying \(X=X^{\top }, Y=Y^{\top }>0,\) then

$$\begin{aligned} X+Z^{\top }Y^{-1}Z<0 \quad \Longleftrightarrow \quad \begin{bmatrix} X&\quad Z^{\top }\\ Z&\quad -Y\\ \end{bmatrix} <0. \end{aligned}$$

Proposition 2

(The Implicit Function Theorem [28]) Suppose that V is open in \({R}^{n+p}\), and \(F = (F_1, \ldots , F_n){:}\,V \longrightarrow {R}^{n}\) is \(C^1\) on V. Suppose further that \(F(x_0, t_0) = 0\) for some \((x_0, t_0) \in V\), where \(x_0 \in {R}^{n}\) and \(t_0 \in {R}^{p}\). If Jacobian matrix

$$\begin{aligned} \frac{\partial (F_1, \ldots , F_n)}{\partial (x_1, \ldots , x_n)} (x_0, t_0) \end{aligned}$$

is nonsingular, then there is an open set \(W\subset {R}^{p},\) containing \(t_0\) and a unique continuously differentiable function \(g{:}\,W\longrightarrow {R}^{n}\) such that \(g(t_0) = x_0\), and \(F(g(t), t) = 0\) for all \(t\in W\).

3 Main Results

Consider singular discrete-time neural networks (1). Due to rank\((E) = r \le n,\) there are two nonsingular matrices \(M, G \in {R}^{n\times n}\) such that \(MEG = \begin{bmatrix} I_r&\quad 0\\ 0&\quad 0\\ \end{bmatrix}\). Let us denote

$$\begin{aligned}&M=\begin{bmatrix} M_1\\ M_2\\ \end{bmatrix},\; \bar{M}=\begin{bmatrix} 0&\quad 0\\ 0&\quad I_{n-r}\\ \end{bmatrix}M, \; MAG =\begin{bmatrix} A_{11}&\quad A_{12}\\ A_{21}&\quad A_{22}\end{bmatrix},\; \\&M^{-\top } PM ^{-1}=\begin{bmatrix} P_{11}&\quad P_{12}\\ P_{21}&\quad P_{22} \end{bmatrix},\\&F = \text {diag}\{a_1, \ldots , a_n\},\, H = \text {diag}\{b_1, \ldots , b_n\},\; \varPhi _{12}=\varPhi _{13} = 0,\; \varPhi _{14}= A_1^{\top }D,\\&\varPhi _{11} = - \delta E^{\top } PE + (h_2-h_1+1)Q + S_1 + A_1^{\top }A_1 + F^2 - P\bar{M}A - A\bar{M}^{\top }P, \\&\varPhi _{15} = -P\bar{M} W,\; \varPhi _{16} = - P\bar{M}W_1,\; \varPhi _{17} = - P\bar{M} C,\; \varPhi _{2i} = 0, i=\overline{3,8},\\&\varPhi _{22} = \delta ^{h_1}(-S_1 + S_2), \\&\varPhi _{18} = AP,\; \varPhi _{44} = - \delta ^{h_1}{Q} + D^{\top }D + H^2,\; \varPhi _{3i} = 0, i=\overline{4,8},\; \varPhi _{4i} = 0, i =\overline{5,8},\\&\varPhi _{55}=\varPhi _{66} = -I,\; \varPhi _{33} = -\delta ^{h_2}S_2,\; \varPhi _{56} =\varPhi _{57}=\varPhi _{67} =0,\; \varPhi _{58} = W^{\top }P,\\&\varPhi _{68} = W_1^{\top }P,\,\, \varPhi _{77} = \frac{-\gamma }{\delta ^N} I, \; \varPhi _{78} = C^{\top }P, \; \varPhi _{88} = -P. \end{aligned}$$

We first show the existence and uniqueness of the solution and the regularity and causality of system (1).

Theorem 1

Given positive constants \(\gamma , N, \delta \ge 1\) unforced system (1) \((u(k) =0)\) is regular, causal and has unique solution if there exist symmetric positive-definite matrices \(P, Q, S_1, S_2\) such that the following LMI holds\(\mathrm{:}\)

$$\begin{aligned} \varPhi = \left[ \begin{array}{l} \varPhi _{ij} \\ \end{array}\right] _{8\times 8} < 0. \end{aligned}$$
(6)

Proof

First, we prove that unforced system (1) is regular and causal. From (6), it follows that \(\varPhi _{11} < 0\). Since \(Q> 0, S_1> 0, F > 0\) and G is nonsingular, we have \(G^{\top }(-\delta E^{\top } PE - P\bar{M}A - A\bar{M}^{\top }P)G <0\) and hence

$$\begin{aligned}&-\delta G^{\top }E^{\top }M^{\top }M^{-\top }PM^{-1}MEG - G^{\top }P\bar{M}AG - G^{\top }A\bar{M}^{\top }PG< 0 \\&\Longleftrightarrow -\delta \begin{bmatrix} P_{11}&\quad 0\\ 0&\quad 0 \end{bmatrix} - \begin{bmatrix} (G^{\top }P)_{12}A_{21}&\quad (G^{\top }P)_{12}A_{22}\\ (G^{\top }P)_{22}A_{21}&\quad (G^{\top }P)_{22}A_{22} \end{bmatrix} \\&\qquad -\,\begin{bmatrix} (G^{\top }P)_{12}A_{21}&\quad (G^{\top }P)_{12}A_{22}\\ (G^{\top }P)_{22}A_{21}&\quad (G^{\top }P)_{22}A_{22} \end{bmatrix}^{\top }< 0 \\&\Longleftrightarrow \begin{bmatrix} \star&\quad \star \\ \star&\quad -(G^{\top }P)_{22}A_{22} - A_{22}^{\top }(G^{\top }P)_{22}^{\top }\end{bmatrix} < 0, \end{aligned}$$

where \(\star \) represents matrices that are not relevant in the discussion. The last inequality shows that \((G^{\top }P)_{22}A_{22} + A_{22}^{\top }(G^{\top }P)_{22}^{\top } > 0.\) Assume that \(A_{22}\) is singular, then there exists a vector \(0\ne \eta \in \mathbb {R}^{n-r}\) such that \(A_{22}\eta = 0\). We have

$$\begin{aligned} \eta ^{\top }\left[ (G^{\top }P)_{22}A_{22} + A_{22}^{\top }(G^{\top }P)_{22}^{\top }\right] \eta = \eta ^{\top }(G^{\top }P)_{22}A_{22}\eta \eta ^{\top }A_{22}^{\top }(G^{\top }P)_{22}^{\top }\eta = 0, \end{aligned}$$

i.e., the matrix \((G^{\top }P)_{22}A_{22} + A_{22}^{\top }(G^{\top }P)_{22}^{\top }\) is not positive definite. This contradiction enable us to confirm that \(A_{22}\) is nonsingular matrix. Hence, according to Definition 1 and [4], the system is regular and causal. We now are in position to prove that the system has a unique solution. By setting

$$\begin{aligned} \gamma _i= & {} \frac{\mathrm{d}}{\mathrm{d}(x_i(k))}f_i(x_i(k))\Bigl |_{x_i(k) = 0},\\ \lambda _i= & {} \frac{\mathrm{d}}{\mathrm{d}(x_i(k-h(k)))}g_i(x_i(k-h(k)))\Bigl |_{x_i(k-h(k)) = 0}, \end{aligned}$$

the functions \(f_i(x_i(k))\) and \(g_i(x_i(k-h(k)))\) can be presented in a neighborhood of the origin as

$$\begin{aligned} \begin{aligned}&f_i(x_i(k)) = \gamma _i x_i(k) + \alpha _i (x_i(k)),\\&g_i(x_i(k-h(k))) = \lambda _i x_i(k-h(k)) + \beta _i (x_i(k-h(k))), \end{aligned} \end{aligned}$$

where \(\alpha _i(0) = 0,\; \beta _i(0) = 0\) and

$$\begin{aligned} \begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}(x_i(k))}\alpha _i(x_i(k))\Bigl |_{x_i(k) = 0} = 0, \, \lim _{x_i(k) \rightarrow 0} \frac{\alpha _i(x_i(k))}{x_i(k)}= 0,\\&\frac{\mathrm{d}}{\mathrm{d}(x_i(k-h(k)))}\beta _i (x_i(k-h(k)))\Bigl |_{x_i(k-h(k)) = 0} \\&\quad = 0, \, \lim _{x_i(k-h(k)) \rightarrow 0} \frac{\beta _i(x_i(k-h(k)))}{x_i(k-h(k))}= 0.\\ \end{aligned} \end{aligned}$$

We then have

$$\begin{aligned} \begin{aligned} f(x(k))&= \varGamma x(k) + \alpha (x(k)),\\ g(x(k-h(k)))&= \varLambda x(k-h(k)) + \beta (x(k-h(k))), \end{aligned} \end{aligned}$$
(7)

where \(\varGamma = \text {diag}\{\gamma _1, \ldots , \gamma _n\}, \varLambda = \text {diag}\{\lambda _1, \ldots , \lambda _n\}\) and

$$\begin{aligned} \begin{aligned}&\alpha (x(k)) = \bigl [\alpha _1 (x_1(k)), \ldots , \alpha _n (x_n(k))\bigl ]^{\top },\; \beta (x(\cdot )) = \bigl [\beta _1 (x_1(\cdot )), \ldots , \beta _n (x_n(\cdot ))\bigl ]^{\top },\\&\lim _{x(k) \rightarrow 0} \frac{\alpha (x(k))}{\Vert x(k)\Vert }= 0,\, \lim _{x(k-h(k)) \rightarrow 0}\frac{\beta (x(k-h(k)))}{\Vert x(k-h(k))\Vert }= 0. \end{aligned} \end{aligned}$$

Therefore, unforced system (1) can be represented by

$$\begin{aligned} E x(k+1)= & {} (A + W\varGamma ) x(k) + W_1\varLambda x(k-h(k)) + W\alpha (x(k)) \\&+\,W_1\beta (x(k-h(k))) + C\omega (k). \end{aligned}$$

Combining conditions (2) and (7) gives

$$\begin{aligned}&x^{\top }(k) \varGamma ^2 x(k) + 2x^{\top }(k) \varGamma \alpha (x(k)) + \alpha ^{\top } (x(k))\alpha (x(k))\\&\quad = f^{\top }(x(k))f(x(k)) \le x^{\top }(k) F^2 x(k). \end{aligned}$$

Letting \(\Vert x(k)\Vert \rightarrow 0\), we can see that

$$\begin{aligned} \varGamma ^2 \leqslant F^2. \end{aligned}$$
(8)

Let \( \varUpsilon := \begin{bmatrix} I_{4\times 4}&\quad 0\\ \varGamma _{4,0}&\quad I_{4\times 4} \end{bmatrix},\, \varGamma _{4,0} = \begin{bmatrix}\varGamma&\quad 0&\quad 0&\quad 0\\0&\quad 0&\quad 0&\quad 0\\0&\quad 0&\quad 0&\quad 0\\0&\quad 0&\quad 0&\quad 0\end{bmatrix}, \) then

$$\begin{aligned} \varPhi< 0 \quad \Longleftrightarrow \quad \bar{\varPhi } := \varUpsilon ^{\top }\varPhi \varUpsilon < 0 \end{aligned}$$

where \(\bar{\varPhi } = \begin{bmatrix} \bar{\varPhi } _{ij} \end{bmatrix}_{8\times 8}\) with

$$\begin{aligned} \bar{\varPhi }_{11}= & {} -\delta E^{\top } PE + (h_2 - h_1 +1)Q + S_1 + A_1^{\top }A_1 + F^2 - \varGamma ^2 \\&- P\bar{M}(A+W\varGamma ) - (A+W\varGamma )^{\top }\bar{M}^{\top }P. \end{aligned}$$

From (8) and \(\bar{\varPhi }_{11} < 0\), we get

$$\begin{aligned} -\delta E^{\top } PE - P\bar{M}(A+W\varGamma ) - (A+W\varGamma )^{\top }\bar{M}^{\top }P < 0. \end{aligned}$$

Similar to the proof of (E, A) being regular and causal in the first step, it can be obtained that the pair \((E, A + W\varGamma )\) is regular and causal. That is the approximation system of unforced system (1) in a neighborhood of the origin:

$$\begin{aligned} E x(k+1) = (A + W\varGamma ) x(k) + W_1\varLambda x(k-h(k)) + C\omega (k) \end{aligned}$$
(9)

is regular and causal. Setting

$$\begin{aligned} \begin{aligned}&MW \varGamma G = \begin{bmatrix} \widehat{\varGamma }_{11}&\quad \widehat{\varGamma }_{12}\\ \widehat{\varGamma }_{21}&\quad \widehat{\varGamma }_{22}\\ \end{bmatrix},\quad G^{-1}x(k) = \begin{bmatrix} x^1(k)\\ x^2(k)\\ \end{bmatrix}, \\&\quad G^{-1}x(k-h(k))= \begin{bmatrix} x^1(k-h(k))\\ x^2(k-h(k))\\ \end{bmatrix},\\&\quad G^{-1}\varphi (k) = \begin{bmatrix} \varphi ^1(k)\\ \varphi ^2(k)\\ \end{bmatrix},\quad MW f(x(k))\\&\quad = \begin{bmatrix} f^1\left( x^1(k), x^2(k)\right) \\ f^2(x^1(k), x^2(k))\\ \end{bmatrix},\quad MC\omega (k) = \begin{bmatrix} \omega ^1(k)\\ \omega ^2(k)\\ \end{bmatrix}\\&MW _1g(x(k-h(k))) = \begin{bmatrix} g^1\left( x^1(k-h(k)), x^2(k-h(k))\right) \\ g^2\left( x^1(k-h(k)), x^2(k-h(k))\right) \\ \end{bmatrix}, \end{aligned} \end{aligned}$$

unforced system (1) is restricted system equivalent to the following system

$$\begin{aligned} \begin{aligned} x^1(k+1) =&\ A_{11}x^1(k) + A_{12}x^2(k) + f^1(\cdot ) + g^1(\cdot ) + \omega ^1(k)\\ 0 =&\ A_{21}x^1(k) + A_{22}x^2(k) + f^2(\cdot ) + g^2(\cdot ) + \omega ^2(k), \\ x^1(k) =&\ \varphi ^1(k),\, x^2(k) = \varphi ^2(k),\, k\in \{-h_2,\ldots ,0\}. \end{aligned} \end{aligned}$$
(10)

Since system (9) is regular and causal, the matrix

where \(F(x^1,x^2,f^2,g^2,w^2):= A_{21}x^1(k) + A_{22}x^2(k) + f^2(\cdot ) + g^2(\cdot ) + \omega ^2(k),\) is nonsingular. From Proposition 2, it follows that in a neighborhood of (0, 0, 0, 0, 0),  there exists a unique continuous differentiable function \(\hat{f}^2(x^1(k), x^1(k-h(k)), x^2(k-h(k)), \omega ^2(k))\) on \(x^1(k), x^1(k-h(k)), x^2(k-h(k)), \omega ^2(k)\) such that

$$\begin{aligned} 0 = A_{21}x^1(k) + A_{22}\hat{f}^2(\cdot ) + f^2(\cdot ) + g^2(\cdot ) + \omega ^2(k), \end{aligned}$$

and \(\hat{f}^2(0,0,0,0) = 0.\) That is in a neighborhood of (0, 0, 0, 0, 0), the second equation of (10) has a unique solution:

$$\begin{aligned} x^2(k) = \hat{f}^2(x^1(k), x^1(k-h(k)), x^2(k-h(k)), \omega ^2(k)),\, \hat{f}^2(0,0,0,0) = 0. \end{aligned}$$

Substituting the above solution to the first equation of (10), we obtain

$$\begin{aligned} x^1(k+1) = A_{11}x^1(k) + A_{12}\hat{f}^2(\cdot )+ f^1(\cdot )+ g^1(\cdot ) + \omega ^1(k) \end{aligned}$$

So the system has a unique solution. This completes the proof of the theorem. \(\square \)

Remark 1

It should be mentioned that the existence of a solution is a fundamental issue for nonlinear singular systems. The authors in [18] provided a sufficient condition for the existence and uniqueness of the solution of discrete systems with nonlinear perturbation by using the fixed point principle. In Theorem 1, using the implicit function theorem we propose a sufficient condition for not only the existence and uniqueness of the solution of system (1), but also the regularity and casualty of the system. The condition is given in terms of LMIs, which can be efficiently solved by using LMI control toolbox algorithm [6].

In the sequel, we give the solution to \(H_{\infty }\) finite-time stability of unforced system (1).

Theorem 2

Given positive numbers \(\gamma , N, \delta \ge 1, c_1, c_2\) and a symmetric positive-definite matrix R. Unforced system (1) is \(H_{\infty }\) finite-time stable w.r.t. \((c_1, c_2, R, N)\) if there exist symmetric positive-definite matrices \(P, Q, S_1, S_2\), positive scalars \(\lambda _i, i = \overline{1,5}\) such that the following LMIs hold\(\mathrm{:}\)

$$\begin{aligned}&\varPsi = \begin{bmatrix} \varPsi _{ij} \end{bmatrix}_{11\times 11} < 0, \end{aligned}$$
(11)
$$\begin{aligned}&E^{\top } PE< \lambda _1 R,\; Q< \lambda _2 R, \; \lambda _3 R< S_1< \lambda _4 R,\; S_2 < \lambda _5 R, \end{aligned}$$
(12)
$$\begin{aligned}&\begin{bmatrix} v_{ij} \end{bmatrix}_{5\times 5} < 0, \end{aligned}$$
(13)

where

$$\begin{aligned} \varPsi _{11}&= -\delta E^{\top } PE + (h_2 - h_1 +1)Q + S_1 - P\bar{M}A- A\bar{M}^{\top }P,\; \varPsi _{15} = -P\bar{M}W,\\ \varPsi _{16}&= -P\bar{M}W_1,\; \varPsi _{17} = -P\bar{M}C,\; \varPsi _{19} = A_1^{\top },\; \varPsi _{1,10} = F,\; \varPsi _{22} =\; \varPhi _{22},\\ \varPsi _{33}&= -\delta ^{h_2}S_2,\; \varPsi _{44} = -\delta ^{h_1}Q,\; \varPsi _{49} =D^{\top },\; \varPsi _{4,11} = H, \; \\ \varPsi _{18}&= AP,\; \varPsi _{55} = \varPsi _{66} = \varPsi _{99} = -I,\\ \varPsi _{10,10}&= \varPsi _{11,11} = -I,\; \varPsi _{58} = W^{\top }P,\; \varPsi _{68} = W_1^{\top }P,\; \varPsi _{77} = -\frac{\gamma }{\delta ^N}I,\; \\ \varPsi _{78}&= C^{\top }P,\; \varPsi _{88} = -P,\\ \varPsi _{ij}&= 0 \, \mathrm{for\,any\,other}\,i, j{:}\; j> i,\; \varPsi _{ij} = \;\varPsi _{ji}^{\top }, \, i > j,\; \\ \rho&= c_1\tfrac{h_2(h_2+1) - h_1(h_1-1)}{2}\delta ^{N+h_2},\\ v_{11}&= \gamma d-c_2\lambda _3,\; v_{12} = c_1\delta ^{N+1}\lambda _1,\; v_{13} = \rho \lambda _2,\; v_{33}= -\rho \lambda _2,\; v_{14}\\&= c_1\delta ^{N+h_1}h_1\lambda _4,\\ v_{22}&= -c_1\delta ^{N+1}\lambda _1, \; v_{15}= c_1\delta ^{N+h_2}(h_2 - h_1)\lambda _5,\; v_{23} =v_{24} =v_{25} = v_{34}\\&= v_{35} = v_{45} = 0, v_{44} = -c_1\delta ^{N+h_1}h_1\lambda _4, \; v_{55}= -c_1\delta ^{N+h_2}(h_2 - h_1)\lambda _5. \end{aligned}$$

Proof

Consider the following nonnegative quadratic functions: \( V(k) = \sum _{i=1}^3V_i(k)\) where

$$\begin{aligned} \begin{aligned} V_1(k)&= x^{\top }(k)E^{\top } PE x(k),\\ V_2(k)&= \sum _{s=-h_2+1}^{-h_1+1}\sum _{t=k-1+s}^{k-1}\delta ^{k-1-t}x^{\top }(t)Qx(t),\\ V_3(k)&= \sum _{s=k-h_1}^{k-1}\delta ^{k-1-s}x^{\top }(s)S_1x(s) + \sum _{s=k-h_2}^{k-h_1-1}\delta ^{k-1-s}x^{\top }(s)S_2x(s). \end{aligned} \end{aligned}$$

Denoting \(\eta (k):= [x^{\top }(k), f^{\top }(\cdot ), g^{\top }(\cdot ), \omega ^{\top }(k)]^{\top }, \mathcal {M} := [A, W, W_1, C]\) and taking the difference variation of \(V_{i}(k), i = 1, 2, 3,\) we have

$$\begin{aligned} V_1(k+1) -\delta V_1(k)&= x^{\top }(k+1)E^{\top } PE x(k+1) - \delta x^{\top }(k)E^{\top } PE x(k)\\&=\eta ^T(k)\mathcal {M}^{\top }P\mathcal {M}\eta (k)- \delta x^{\top }(k)E^{\top } PE x(k),\\ V_2(k+1) -\delta V_2(k)&= \sum _{s=-h_2+1}^{-h_1+1}\sum _{t=k+s}^{k}\delta ^{k-t}x^{\top }(t){Q}x(t)\\&\quad -\,\sum _{s=-h_2+1}^{-h_1+1}\sum _{t=k-1+s}^{k-1}\delta ^{k-t}x^{\top }(t){Q}x(t) \\&\leqslant (h_2-h_1+1)x^{\top }(k){Q}x(k) - \delta ^{h_1}x^{\top }(k-h(k)){Q}x(k-h(k))\\ V_3(k+1) -\delta V_3(k)&= \sum _{s=k+1-h_1}^{k}\delta ^{k-s}x^{\top }(s)S_1x(s)- \sum _{s=k-h_1}^{k-1}\delta ^{k-s}x^{\top }(s)S_1x(s)\\&\quad +\,\sum _{s=k+1-h_2}^{k-h_1}\delta ^{k-s}x^{\top }(s)S_2x(s) - \sum _{s=k-h_2}^{k-h_1-1}\delta ^{k-s}x^{\top }(s)S_2x(s)\\&= x^{\top }(k)S_1x(k) + x^{\top }(k-h_1)\left[ \delta ^{h_1}(-S_1 + S_2)\right] x(k-h_1)\\&\quad -\,\delta ^{h_2}x^{\top }(k-h_2)S_2x(k-h_2). \end{aligned}$$

Thus we get

$$\begin{aligned} V(k+1) - \delta V(k)&\le \eta ^{\top }(k)\mathcal {M}^{\top }P\mathcal {M}\eta (k)+ x^{\top }(k)[- \delta E^{\top } PE \nonumber \\&\quad +\,(h_2-h_1+1){Q} + S_1 \nonumber \\&\quad +\,A_1^{\top }A_1]x(k) + 2x^{\top }(k)A_1^{\top }Dx(k-h(k))\nonumber \\&\quad +\,x^{\top }(k-h_1)\left[ \delta ^{h_1}(-S_1 + S_2)\right] x(k-h_1)\nonumber \\&\quad +\,x^{\top }(k-h_2)\left[ -\delta ^{h_2}S_2\right] x(k-h_2)\nonumber \\&\quad +\,x^{\top }(k-h(k))\left[ - \delta ^{h_1}{Q} + D^{\top }D\right] x(k-h(k)) \nonumber \\&\quad +\,\omega ^{\top }(k)\left[ - \frac{\gamma }{\delta ^N}I \right] \omega (k) + \frac{\gamma }{\delta ^N}\omega ^{\top }(k)\omega (k) \nonumber \\&\quad -\,z^{\top }(k)z(k). \end{aligned}$$
(14)

The following estimations hold true by the assumption (2):

$$\begin{aligned} 0\le & {} - f^{\top }(x(k))f(x(k)) + x^{\top }(k)F^2x(k),\nonumber \\ 0\le & {} - g^{\top }(x(k-h(k)))g(x(k-h(k))) + x^{\top }(k-h(k))H^2x(k-h(k)). \end{aligned}$$
(15)

Multiplying by \(-2x^{\top }(k)P\bar{M}\) the both side of Eq. (1) and note that \(\bar{M}E = 0\), we obtain

$$\begin{aligned} 0&= - 2x^{\top }(k)P\bar{M}Ax(k) - 2x^{\top }(k)P\bar{M}Wf(x(k))\nonumber \\&\quad -\,2x^{\top }(k)P\bar{M}W_1g(x(k-h(k)))- 2x^{\top }(k)P\bar{M}C\omega (k). \end{aligned}$$
(16)

By setting

$$\begin{aligned} \xi (k):= & {} \left[ x^{\top }(k), x^{\top }(k - h_1), x^{\top }(k - h_2), x^{\top }(k\right. \\&\left. -\,h(k)), f^{\top }(x(k)), g^{\top }(x(k-h(k))), \omega ^{\top }(k)\right] ^{\top } \end{aligned}$$

we see that

$$\begin{aligned} \eta ^{\top }(k)\mathcal {M}^{\top }P\mathcal {M}\eta (k)=\xi ^{\top }(k)\varUpsilon ^{\top }P^{-1}\varUpsilon \xi (k), \end{aligned}$$

where \(\varUpsilon :=\begin{bmatrix} PA&\quad 0&\quad 0&\quad 0&\quad PW&\quad PW _1&\quad PC \end{bmatrix}.\) Combining (14), (15), (16) gives

$$\begin{aligned} V(k+1) -\delta V(k) \le \xi ^{\top }(k)(\widetilde{\varPhi }+ \varUpsilon ^{\top }P^{-1}\varUpsilon ) \xi (k) + \frac{\gamma }{\delta ^N}\omega ^{\top }(k)\omega (k)- z^{\top }(k)z(k) \end{aligned}$$
(17)

where

$$\begin{aligned} \widetilde{\varPhi } = \begin{bmatrix} \varPhi _{11}&\quad 0&\quad 0&\quad \varPhi _{14}&\quad \varPhi _{15}&\quad \varPhi _{16}&\quad \varPhi _{17}\\ *&\quad \varPhi _{22}&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0\\ *&\quad *&\quad -\delta ^{h_2}S_2&\quad 0&\quad 0&\quad 0&\quad 0\\ *&\quad *&\quad *&\quad \varPhi _{44}&\quad 0&\quad 0&\quad 0\\ *&\quad *&\quad *&\quad *&\quad -I&\quad 0&\quad 0\\ *&\quad *&\quad *&\quad *&\quad *&\quad -I&\quad 0\\ *&\quad *&\quad *&\quad *&\quad *&\quad *&\quad - \frac{\gamma }{\delta ^N}I\\ \end{bmatrix}. \end{aligned}$$

Furthermore, if we set

$$\begin{aligned} {\widehat{\varPhi }}_{11} = -\delta E^{\top } PE + (h_2 - h_1 +1)Q + S_1 + F^2 - P\bar{M}A - A\bar{M}^{\top }P, \end{aligned}$$

then the following relations holds

$$\begin{aligned} \widetilde{\varPhi }+ \varUpsilon ^{\top }P^{-1}\varUpsilon< 0 \Longleftrightarrow \, \varPhi< 0 \Longleftrightarrow \, \varPsi < 0. \end{aligned}$$

As a result, from (11) and (17) it follows that

$$\begin{aligned} V(k+1) \le \delta V(k) + \frac{\gamma }{\delta ^N}\omega ^{\top }(k) \omega (k) \quad \forall k\in \mathbb {Z}_{+}. \end{aligned}$$
(18)

By iteration, and taking assumption (4) into account, the inequality (18) implies

$$\begin{aligned} V(k+1)&\le \delta ^{k+1} V(0) + \frac{\gamma }{\delta ^N}\sum _{s=0}^{k}\delta ^{k-s}\omega ^{\top }(s)\omega (s)\nonumber \\&< \delta ^{N+1} V(0) + \gamma d, \quad \forall k = 0, 1, \ldots , N. \end{aligned}$$
(19)

Using assumption (12) and \(x(k) = \varphi (k), k\in \{-h_2,-h_2+1,\ldots ,0\},\) it is easily seen that

$$\begin{aligned} V(0)&= x^{\top }(0)E^{\top } PE x(0) + \sum _{s=-h_2+1}^{-h_1+1}\sum _{t=-1+s}^{-1}\delta ^{-1-t}x^{\top }(t)Qx(t)\nonumber \\&\quad +\,\sum _{s=-h_1}^{-1}\frac{1}{\delta ^{1+s}}x^{\top }(s)S_1x(s) + \sum _{s=-h_2}^{-h_1-1}\frac{1}{\delta ^{1+s}}x^{\top }(s)S_2x(s)\nonumber \\&\quad <\,\Bigl [\lambda _1 + \lambda _2\displaystyle \frac{h_2(h_2+1)-h_1(h_1-1)}{2}\delta ^{h_2-1} + \lambda _4h_1\delta ^{h_1-1}\nonumber \\&\quad +\,\lambda _5(h_2 - h_1)\delta ^{h_2-1}\Bigl ] c_1. \end{aligned}$$
(20)

Associating (19) with (20), we get

$$\begin{aligned} V(k+1) < \delta ^{N+1} \sigma + \gamma d\quad \forall k = 0, 1, \ldots , N, \end{aligned}$$
(21)

where

$$\begin{aligned} \sigma = \left[ \lambda _1 + \lambda _2\frac{h_2(h_2+1)-h_1(h_1-1)}{2\delta ^{1-h_2}} + \lambda _4h_1\delta ^{h_1-1} + \lambda _5(h_2 - h_1)\delta ^{h_2-1}\right] c_1. \end{aligned}$$

On the other hand, according to (12) again, the following estimation holds

$$\begin{aligned} V(k+1)\ge V_3(k+1)\ge & {} \sum _{s=k+1-h_1}^{k}\delta ^{k-s}x^{\top }(s)S_1x(s)\nonumber \\\ge & {} x^{\top }(k)S_1x(k) > \lambda _3 x^{\top }(k)Rx(k). \end{aligned}$$
(22)

Moreover, by the Schur complement lemma ([3]) condition (13) is equivalent to

$$\begin{aligned}&\gamma d - c_2\lambda _3 + c_1\delta ^{N+1}\lambda _1 + \rho \lambda _2 + c_1\delta ^{N+h_1}h_1\lambda _4 + c_1\delta ^{N+h_2}(h_2 - h_1)\lambda _5< 0\nonumber \\&\quad \Longleftrightarrow \gamma d - c_2\lambda _3 + \delta ^{N+1}\sigma <0. \end{aligned}$$
(23)

Consequently, we get from (21), (22) and (23) that:

$$\begin{aligned} x^{\top }(k)Rx(k)< \frac{1}{\lambda _3}[\delta ^{N+1}\sigma + \gamma d ] < c_2 \; \forall k = 1, 2,\ldots , N, \end{aligned}$$

which implies that the unforced system is robustly finite-time stable w.r.t. \((c_1, c_2, R, N)\). To complete the proof of the theorem, it remains to show the \(\gamma \)-level condition (5). For this, from (17) it follows that

$$\begin{aligned} V(k+1) \leqslant \delta V(k) + \frac{\gamma }{\delta ^N}\omega ^{\top }(k)\omega (k) - z^{\top }(k)z(k), \end{aligned}$$

and hence by iteration it derives that

$$\begin{aligned} V(k) \leqslant \delta ^k V(0) + \sum _{s=0}^{k-1}\frac{1}{\delta ^{1+s-k}} \Big [\frac{\gamma }{\delta ^N}\Vert \omega (s)\Vert ^2- \Vert z(s)\Vert ^2\Big ]. \end{aligned}$$

Since \(V(0) =0,\) the above inequality implies

$$\begin{aligned} \sum _{s=0}^{k-1}\delta ^{k-1-s}z^{\top }(s)z(s)\; \leqslant \; \sum _{s=0}^{k-1}\delta ^{k-1-s} \frac{\gamma }{\delta ^N}\omega ^{\top }(s)\omega (s) \end{aligned}$$

For \(k=N+1,\) we have

$$\begin{aligned} \sum _{s=0}^{N}\delta ^{N-s}z^{\top }(s)z(s)\; \leqslant \; \gamma \sum _{s=0}^{N} \frac{\delta ^{N-s}}{\delta ^N}\omega ^{\top }(s)\omega (s). \end{aligned}$$
(24)

Since \(1\le \delta ^{N-s}\le \delta ^{N}\; \forall s\in \{0, 1, \ldots , N\}\), (24) immediately yields

$$\begin{aligned} \sum _{s=0}^N z^{\top }(s)z(s) \le \gamma \sum _{s=0}^{N}\omega ^{\top }(s)\omega (s), \end{aligned}$$

which implies that condition (5) holds. The proof of the theorem is completed. \(\square \)

We are now in position to solve the problem of finite-time \(H_{\infty }\) control for system (1) by designing a state feedback controller \(u(k)=Kx(k)\) such that the resulting closed-loop system

$$\begin{aligned} Ex(k+1)&= (A + BK)x(k) + Wf(x(k)) +W_1g(x(k-h(k))) + C\omega (k), \, k\in {\mathbb {Z}}_{+},\nonumber \\ z(k)&= (A_1 + B_1K)x(k) + Dx(k-h(k)),\nonumber \\ x(k)&= \varphi (k),\ k\in \{-h_2,-h_2+1,\ldots ,0\}, \end{aligned}$$
(25)

is \(H_{\infty }\) finite-time stable.

Theorem 3

Given positive constants \(\gamma , N, \delta \ge 1, c_1, c_2\) and a symmetric positive-definite matrix R. The finite-time \(H_{\infty }\) control problem of system (1) has a solution if there exist symmetric positive-definite matrices \(U_i, V_j\) with \(i = \overline{1,4}, j = \overline{1,5}, \) a matrix Y such that the following LMIs hold:

$$\begin{aligned}&\; \varOmega = \begin{bmatrix} \varOmega _{ij} \end{bmatrix}_{11\times 11} < 0, \end{aligned}$$
(26)
$$\begin{aligned}&\begin{bmatrix} -V_1&U_1E^{\top }\\ *&-U_1\\ \end{bmatrix} < 0, \end{aligned}$$
(27)
$$\begin{aligned}&\; U_2< V_2, \quad U_3< V_4, \quad U_4 < V_5, \end{aligned}$$
(28)
$$\begin{aligned}&[V_{ij}]_{5\times 5} < 0, \end{aligned}$$
(29)
$$\begin{aligned}&\begin{bmatrix} V_3 - c_2 U_3&\quad \gamma d U_1R \\ *&\quad -\gamma d R \end{bmatrix} < 0. \end{aligned}$$
(30)

Moreover, the state feedback controller is given by

$$\begin{aligned} u(k)=YU_1^{-1}x(k),\quad k\in \mathbb {Z}_{+}, \end{aligned}$$

where \(\rho = c_1\tfrac{h_2(h_2+1)-h_1(h_1-1)}{2}\delta ^{N+h_2}\) and

$$\begin{aligned}&\varOmega _{11} = \delta U_1 + (h_2 - h_1 + 1)U_2 + U_3 + \delta (U_1E^{\top } + EU _1) - \bar{M}(AU_1 + BY)\\&\quad -\,(U_1A + Y^{\top }B^{\top })\bar{M}^{\top },\\&\varOmega _{15} = -\bar{M}W,\; \varOmega _{16} = -\bar{M}W_1,\; \varOmega _{17} = -\bar{M}C, \; \varOmega _{18} = U_1A+Y^{\top }B^{\top },\\&\varOmega _{19} = U_1A_1^{\top }+Y^{\top }B_1^{\top },\; \varOmega _{1,10} = U_1F,\; \varOmega _{22} = \delta ^{h_1}(-U_3 + U_4),\; \varOmega _{33} = -\delta ^{h_2}U_4,\\&\varOmega _{44} = -\delta ^{h_1}U_2, \; \varOmega _{49} = U_1D^{\top },\; \varOmega _{4,11} = U_1H,\; \varOmega _{68} =W_1^{\top },\; \varOmega _{55} = \varOmega _{66} = -I,\\&\varOmega _{99} = \varOmega _{10,10} = \varOmega _{11,11} = -I,\; \varOmega _{77} = -\frac{\gamma }{\delta ^N}I,\; \varOmega _{78} = C^{\top },\; \\&\quad \varOmega _{88}= -U_1,\; \varOmega _{58} = W^{\top },\\&\varOmega _{ij} = 0 \;\;\textit{for any other i, j:}\; j> i,\; \varOmega _{ij} = \varOmega _{ji}^{\top }, \, i > j,\\&V_{11} = -V_3,\; V_{12} = c_1\delta ^{N+1}V_1,\; V_{13} = \rho V_2,\; V_{14} = c_1\delta ^{N+h_1}h_1V_4,\; V_{15}\\&\quad = c_1\delta ^{N+h_2}(h_2 - h_1)V_5,\\&V_{22}= -c_1\delta ^{N+1}V_1,\; V_{23} = V_{24} = V_{25} =0,\; V_{33} = -\rho V_2,\; V_{34} = V_{35} = V_{45}= 0,\\&V_{44} = -c_1\delta ^{N+h_1}h_1V_4,\; V_{55} = -c_1\delta ^{N+h_2}(h_2 - h_1)V_5. \end{aligned}$$

Proof

Using Theorem 2, closed-loop system (25) is \(H_{\infty }\) finite-time stable if there exist symmetric positive-definite matrices \(P, Q, S_1, S_2\), positive scalars \(\lambda _i, i = \overline{1,5},\) such that conditions (11), (12) and (13), where matrices \(A+BK, A_1+B_1K\) will in place of the matrices \(A, A_1,\) hold. In other words, in proportion to (11), we have

$$\begin{aligned} \varTheta = \begin{bmatrix} \varTheta _{ij} \end{bmatrix}_{11\times 11} < 0, \end{aligned}$$
(31)

where

$$\begin{aligned} \varTheta _{11}&= -\delta E^{\top } PE + (h_2 - h_1 +1)Q + S_1 - P\bar{M}(A+BK) - (A+BK)^{\top }\bar{M}^{\top }P,\\ \varTheta _{18}&= (A+BK)^{\top }P,\; \varTheta _{19} = (A_1+B_1K)^{\top },\; \varTheta _{ij} \\&= \varPsi _{ij} \;\; \text {for any other}\; i, j{:}\; j \geqslant i,\; \varTheta _{ij} = \varTheta _{ji}^{\top }, \, i > j. \end{aligned}$$

Pre- and post-multiplying (31) by the matrix:

$$\begin{aligned} \mathrm{diag}\left\{ P^{-1}, P^{-1}, P^{-1}, P^{-1}, I, I, I, P^{-1}, I, I, I\right\} >0 \end{aligned}$$

and then define new matrix variables as follows:

$$\begin{aligned} U_1 = P^{-1}, \quad U_2 = P^{-1}QP^{-1},\quad U_3 = P^{-1}S_1P^{-1},\quad U_4 = P^{-1}S_2P^{-1}, \end{aligned}$$

we easily obtain the following equivalent inequality

$$\begin{aligned} \bar{\varTheta } < 0, \end{aligned}$$
(32)

where \(\bar{\varTheta } = \begin{bmatrix} \bar{\varTheta }_{ij} \end{bmatrix}_{11\times 11}\) with

$$\begin{aligned} \bar{\varTheta }_{11}&= -\delta U_1E^{\top }U_1^{-1} EU _1 + (h_2 - h_1 +1)U_2 + U_3 - \bar{M}(A+BK)U_1 \\&\quad -\,U_1(A+BK)^{\top }\bar{M}^{\top },\\ \bar{\varTheta }_{18}&= U_1(A+BK)^{\top },\; \bar{\varTheta }_{19} = U_1(A_1+B_1K)^{\top },\; \\ \bar{\varTheta }_{ij}&= \varOmega _{ij} \;\; \text {for any other}\; i, j:\; j \geqslant i,\; \bar{\varTheta }_{ij} = \bar{\varTheta }_{ji}^{\top }, \, i > j. \end{aligned}$$

Letting \(Y^{\top } = U_1K^{\top }, K= YU_1^{-1},\) (32) becomes

$$\begin{aligned} \bar{\varOmega } < 0, \end{aligned}$$
(33)

where \(\bar{\varOmega } = \begin{bmatrix} \bar{\varOmega }_{ij} \end{bmatrix}_{11\times 11}\) with

$$\begin{aligned} \bar{\varOmega }_{11}&= -\delta U_1E^{\top }U_1^{-1} EU _1 + (h_2 - h_1 +1)U_2 + U_3 - \bar{M}(AU_1+BY) \\&\quad -\, (U_1A+Y^{\top }B^{\top })\bar{M}^{\top },\\ \bar{\varOmega }_{18}&= U_1A+Y^{\top }B^{\top },\quad \bar{\varOmega }_{19} = U_1A_1^{\top }+Y^{\top }B_1^{\top },\\ \bar{\varOmega }_{ij}&= \varOmega _{ij}, \quad \text {for any other},\quad i, j: j \geqslant i, \, \bar{\varOmega }_{ij} = \bar{\varOmega }_{ji}^{\top },\, \forall i, j:\; i > j. \end{aligned}$$

It is easy to see that

$$\begin{aligned} -\delta U_1E^{\top }U_1^{-1} EU _1 \leqslant \delta (U_1E^{\top } + EU _1 + U_1), \end{aligned}$$

hence condition (33) holds if condition (26) holds. For getting (29), post-multiplying matrix (13): \([v_{ij}I]_{5\times 5}\) by the matrix \(diag \{R, R, R, R, R\}>0\) and then pre- and post-multiplying the derived matrix again by the matrix diag\(\{P^{-1}, P^{-1}, P^{-1}, P^{-1},P^{-1}\}>0,\) and setting new variables

$$\begin{aligned} \begin{aligned} V_1&= P^{-1}(\lambda _1R)P^{-1}, \quad V_2 = P^{-1}(\lambda _2R)P^{-1},\\ V_3&= -\gamma d P^{-1} RP ^{-1} + c_2P^{-1}(\lambda _3R)P^{-1},\\ V_4&= P^{-1}(\lambda _4R)P^{-1}, \quad V_5 = P^{-1}(\lambda _5R)P^{-1}, \end{aligned} \end{aligned}$$

we reach (29) as expected. To obtain the inequalities (27) and (28), we just pre- and post-multiplying (12) by the matrix \(P^{-1}\). Indeed, we prove (27) as illustrator

$$\begin{aligned} \begin{aligned} E^{\top } PE< \lambda _1R&\Longleftrightarrow P^{-1}E^{\top } PEP ^{-1}< P^{-1}(\lambda _1R)P^{-1} \\&\Longleftrightarrow U_1E^{\top }U_1^{-1} EU _1< V_1 \\&\Longleftrightarrow -V_1 + U_1E^{\top }U_1^{-1} EU _1 < 0, \end{aligned} \end{aligned}$$

which is equivalent to (27) by Proposition 1. Finally, note that

$$\begin{aligned} \begin{aligned} V_3&= -\gamma \mathrm{d}P^{-1} RP ^{-1} + c_2P^{-1}(\lambda _3R)P^{-1}< -\gamma \mathrm{d}P^{-1} RP ^{-1} + c_2P^{-1}S_1P^{-1}\\&= -\gamma \mathrm{d}U_1 RU _1 + c_2U_3, \end{aligned} \end{aligned}$$

we get \( V_3 - c_2 U_3 + \gamma \mathrm{d}U_1R[\gamma \mathrm{d}R]^{-1}\gamma \mathrm{d} RU _1 < 0, \) which is evidently equivalent to (30) by Proposition 1. The proof of the theorem is complete. \(\square \)

Remark 2

The results obtained in Theorems 2 and 3 can be regarded as an extension of the results of [11, 12, 19] on \(H_{\infty }\) control for discrete-time neural network (1). To the best of our knowledge, this is the first time that the problem of \(H_{\infty }\) control of nonlinear singular discrete-time neural network systems with time-varying delays and disturbances. Note that Theorems 2 and 3 provide delay-dependent sufficient conditions for the \(H_{\infty }\) finite-time stability and control of the singular neural networks with time-varying delays. The obtained conditions are formulated in terms of LMIs, which can be efficiently solved by using various convex optimization algorithm.

4 Numerical Examples

In this section, we provide some numerical examples. It is worth noting that the finite-time stability and control problem for system (1) is first time studied and solved in our paper and there have not been any similar results obtained for system (1) such that the following examples are given to illustrate the validity and effectiveness of the derived conditions only. In the case, when the discrete-time neural networks (1) reduce to the nonsingular system (\(E= I\)), our result can be viewed as an extension of existing results [13, 19, 22, 27].

Example 1

Consider unforced system (1) (\(u(k) = 0\)), where

$$\begin{aligned} E= & {} \begin{bmatrix} 1&\quad -\,1.1 \\ 1&\quad -\,1.1 \end{bmatrix},\quad A=\begin{bmatrix} 0.95&\quad 0\\ 0&\quad 0.2 \end{bmatrix},\quad W=\begin{bmatrix} -\,0.025&\quad 0.02\\ 0.015&\quad 0.025 \end{bmatrix},\quad \\ W_1= & {} \begin{bmatrix} 0.02&\quad 0.01\\ -\,0.025&\quad 0.02 \end{bmatrix},\\ C= & {} \begin{bmatrix} 0.35 \\ 0.25 \end{bmatrix},\quad F=\begin{bmatrix} 0.25&\quad 0\\ 0&\quad 0.35 \end{bmatrix},\quad H=\begin{bmatrix} 0.2&\quad 0\\ 0&\quad 0.2 \end{bmatrix},\\ A_1= & {} \begin{bmatrix} 0.7&\quad -\,0.3 \end{bmatrix},\quad D=\begin{bmatrix} 0.2&\quad -\,0.1 \end{bmatrix},\quad R = \begin{bmatrix} 1.7&\quad 0\\ 0&1.3 \end{bmatrix},\\ h(k)= & {} 2 + 13\cos ^2\frac{k\pi }{2}, k\in {\mathbb {Z}}_{+}.\ \end{aligned}$$

By simple calculation, we can find

$$\begin{aligned} M=\begin{bmatrix} 1&\quad 0 \\ 1&\quad -1 \end{bmatrix},\quad G=\begin{bmatrix} 1&\quad 1.1 \\ 0&\quad 1 \end{bmatrix},\quad MEG =\begin{bmatrix} 1&\quad 0 \\ 0&\quad 0 \end{bmatrix}, \quad \bar{M}=\begin{bmatrix} 0&\quad 0 \\ 1&\quad -1 \end{bmatrix}. \end{aligned}$$

For given \(h_1=2,\; h_2=15,\; N=60,\; d=1,\; c_1=1,\; c_2=8\) and \(\gamma =1\), the LMIs (11)–(13) are feasible with \(\delta =1.0001\) and

$$\begin{aligned} P= & {} \begin{bmatrix} 0.0078&\quad -\,0.1673\\ -\,0.1673&\quad 12.0088 \end{bmatrix},\quad Q=\begin{bmatrix} 0.0899&\quad -\,0.0249\\ -\,0.0249&\quad 0.0525 \end{bmatrix},\\ S_1= & {} \begin{bmatrix} 7.5618&\quad -\,0.0008\\ -\,0.0008&\quad 5.7823 \end{bmatrix},\quad S_2 =\begin{bmatrix} 0.0017&\quad 0\\ 0&\quad 0.0013 \end{bmatrix},\\ \lambda _1= & {} 17.7476,\quad \lambda _2 = 0.0646,\quad \lambda _3 = 4.4471,\quad \lambda _4 = 4.4506, \quad \lambda _5 = 0.0015. \end{aligned}$$

Since the inequalities (6) and (11) are equivalent, the system is regular, causal, and it has a unique solution and is robustly \(H_{\infty }\) finite-time stable w.r.t. (1, 8, R, 60).

Example 2

Consider singular system (1), where

$$\begin{aligned} E= & {} \begin{bmatrix} 1&\quad -\,1.1 \\ 1&\quad -\,1.1 \end{bmatrix},\quad A=\begin{bmatrix} 0.35&\quad 0 \\ 0&\quad 0.15 \end{bmatrix},\quad W=\begin{bmatrix} -\,0.02&\quad 0.015 \\ 0.01&\quad 0.02 \end{bmatrix}, \quad \\ W_1= & {} \begin{bmatrix} 0.01&\quad 0.015 \\ -\,0.02&\quad 0.025 \end{bmatrix},\\ B= & {} \begin{bmatrix} 0.25 \\ 0.45 \end{bmatrix},\quad C=\begin{bmatrix} 0.15 \\ 0.3 \end{bmatrix},\quad F=\begin{bmatrix} 0.25&\quad 0 \\ 0&\quad 0.15 \end{bmatrix},\quad H=\begin{bmatrix} 0.15&\quad 0 \\ 0&\quad 0.2 \end{bmatrix},\quad \\ A_1= & {} \begin{bmatrix} 0.75&\quad -\,0.15 \end{bmatrix},\\ D= & {} \quad \begin{bmatrix} -\,0.15&\quad 0.1 \end{bmatrix},\quad B_1=0.2,\quad R = \begin{bmatrix} 1.2&\quad 1 \\ 1&\quad 1.4 \end{bmatrix},\quad \\ h(k)= & {} 2 + 12\sin ^2\frac{k\pi }{2}. \end{aligned}$$

We can find that

$$\begin{aligned} M=\begin{bmatrix} 2&\quad 0 \\ 2&\quad -2 \end{bmatrix},\quad G=\begin{bmatrix} 0.5&\quad 0.55 \\ 0&\quad 0.5 \end{bmatrix},\quad MEG=\begin{bmatrix} 1&\quad 0 \\ 0&\quad 0 \end{bmatrix}, \quad \bar{M}=\begin{bmatrix} 0&\quad 0 \\ 2&\quad -2 \end{bmatrix}. \end{aligned}$$

For given \(h_1=2,\; h_2=14,\; N=40,\; d=1,\; c_1=2,c_2 =25\) and \(\gamma =1\), the LMIs (26)–(30) are feasible with \(\delta =1.0001\) and

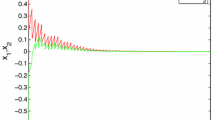
$$\begin{aligned} U_1= & {} \begin{bmatrix} 0.1054&\quad 0.2102\\ 0.2102&\quad 0.4589 \end{bmatrix},\quad U_2=\begin{bmatrix} 0.0022&\quad 0.0048\\ 0.0048&\quad 0.0107 \end{bmatrix},\\ U_3= & {} \begin{bmatrix} 0.0844&\quad 0.1942\\ 0.1942&\quad 0.4585 \end{bmatrix},\quad U_4 =\begin{bmatrix} 0.0012&\quad 0.0032\\ 0.0032&\quad 0.0102 \end{bmatrix},\\ V_1= & {} \begin{bmatrix} 0.5522&\quad 1.2965\\ 1.2965&\quad 3.0661 \end{bmatrix},\quad V_2=\begin{bmatrix} 0.0023&\quad 0.0049\\ 0.0049&\quad 0.0110 \end{bmatrix},\\ V_3= & {} \begin{bmatrix} 1.9826&\quad 4.5768\\ 4.5768&\quad 10.8473 \end{bmatrix},\quad V_4=\begin{bmatrix} 0.0869&\quad 0.2012\\ 0.2012&\quad 0.4841 \end{bmatrix},\\ V_5= & {} \begin{bmatrix} 0.0018&\quad 0.0048\\ 0.0048&\quad 0.0156 \end{bmatrix}, \quad Y=\begin{bmatrix} -\,0.2115&\quad -\,1.0007 \end{bmatrix}. \end{aligned}$$

The \(H_{\infty }\) finite-time control problem of system (1), by Theorem 3, has a solution, and the state feedback controller is given by

$$\begin{aligned} u(k) = \begin{bmatrix} 27.1655&-14.6259 \end{bmatrix} x(k),\quad k\in \mathbb {Z}_{+}. \end{aligned}$$

Figure 1 shows the response solution with the initial condition

$$\begin{aligned} \varphi (k)=\begin{bmatrix} 0.4 \\ 0.8 \end{bmatrix}, \quad k\in \{-14,-13,\ldots ,0\}. \end{aligned}$$
Fig. 1
figure 1

Response solution of the closed-loop system

Full size image

5 Conclusion

The problem of \(H_{\infty }\) finite-time stability and control of nonlinear singular discrete-time neural networks with time-varying delays and disturbances has been studied in this paper. Based on the singular systems theory and Lyapunov functional method, we have provided new delay-dependent sufficient conditions for the existence and uniqueness of solutions and the \(H_{\infty }\) finite-time control for such systems. The conditions for the existence of state feedback controllers are easy to check by using MATLAB LMI control toolbox.