1 Introduction

Over the recent decades there have been extensive studies of neural networks (NNs) including time-varying delays. The existence of time delays may result in instability or oscillation of a neural network system. Therefore, the stability of neural networks with time delay has been attracting the interest of a great number of researchers and has obtained some achievements [1,2,3,4,5,6,7,8,9,10], and the references cited therein. In general, neural networks model is similar to the general dynamical system with time-delay, and the condition of the stability of time-delay neural network can be divided into two parts: delay-independent conditions and delay-dependent conditions [11,12,13]. At present, there are a lot of studies, which focus on the delay-dependent conditions, because the delay-dependent case is less conservative than delay-independent case. Chen [14] obtained the delay-dependent exponential stability for a class of linear neural network condition with the technique of model transformation. A less conservative delay-dependent condition is proposed, through establishing a new Lyapunov-functional and applying S-procedure in [15]. What’s more, in order to reduce the conservatism of the stability criterion, the authors utilized the method of free weighting matrices in [16]. In some of earlier articles, a lot of important parts are ignored, such as the process in the derivative of Lyapunov function and the calculation of the upper limit for the derivative. However, in [17,18,19], the authors considered these items and obtained a less conservative for network systems.

Obviously, the neutral type descriptor system is more general than neutral system and descriptor system. Many practical processes can be modeled as general neutral type descriptor system, such as circuit analysis, computer aided design, real-time simulation of mechanical systems and optimal control [20, 21]. The neutral type descriptor systems contain delays in both its states and the derivatives of states. At the same time, it has the nature of the regular, impulse free, which lead to the search of the neutral-type singular neural network system is more hard to find the criterion of the stability. Recently, the neutral type descriptor system with time-delay has been studied in [22,23,24,25], and some valuable results are obtained. In [23, 24], the authors studied the stability of neutral type descriptor system with mixed delays and multiple time-varying delays, respectively. Han et al. [25] investigated the delay-dependent robust stability for uncertain singular neutral differential system with time-varying and distributed delays. In [26,27,28], Synchronization of singular complex dynamical networks with time-varying delays has been studied. However, the research for exponential stability of neutral type singular networks system is still very rare.

Motivated by the above discussion, in this paper, we consider the problem of the exponential stability of neutral type singular networks system. The main contributions of this paper are summarized as follows: (1) this paper is based on predecessors’ research about the neural network system, a typical network model is considered. (2) A new construction method of Lyapunov functional is adopted. (3) A new stability theorem about singular neutral system is obtained. (4) The simulation results demonstrate the feasibility of the method.

In addition, the liberty of matrix and integral inequality methods are applied, which ensure that the neutral type singular neural network system is globally exponential stability with a unique equilibrium point. These conditions are expressed in terms of linear matrix inequality, which can be solved by using developed techniques in Matlab toolbox. Finally, numerical examples are provided to show the less conservatism and valid of the proposed LMI conditions.

2 System description and assumptions

Consider the neutral type descriptor neural networks with varying delays described by:

$$\left\{ \begin{gathered} E\dot {x}\left( t \right)= - Ax\left( t \right)+B\dot {x}\left( {t - \tau \left( t \right)} \right)+Cf\left( {x\left( t \right)} \right)+Df\left( {x\left( {t - \tau \left( t \right)} \right)} \right)+J, \hfill \\ x(t)=\phi (t),\quad t \in [ - \tau ,0]. \hfill \\ \end{gathered} \right.$$
(1)

where \(x(t)={\left[ {{x_1}(t)\;{x_2}(t) \cdots {x_n}(t)} \right]^T} \in {R^n}\) is the neuron state vector; the integer \(n \geq 2\) denotes the number of units in neural network; \(J={\left[ {{J_1}\;{J_2} \cdot \cdot \cdot {J_n}} \right]^T} \in {R^n}\) is a constant input vector; \(A={\text{diag}}\left\{ {\left. {{a_1},\;{a_2}, \cdots {a_n}} \right\}} \right. \in {R^n}\) denotes the diagonal matrix of passive decay rates, and satisfying \({a_i}>0\) for \(i=1,2, \cdot \cdot \cdot ,n\); \(\dot {x}\left( {t - \tau (t)} \right)={\left[ {{{\dot {x}}_1}(t - \tau (t))\;{{\dot {x}}_2}(t - \tau (t)) \cdots {{\dot {x}}_n}(t - \tau (t))} \right]^T} \in {R^n}\) is the neutral item; \(E\) is a singular matrix and satisfy \(rank(E)=r \leq n\); \(A\), \(B\), \(C\) and \(D \in {R^{n \times n}}\)are the interconnection matrices representing the weight coefficient of the neurons. \(\tau \left( t \right)\) is time-varying continuously function satisfies \(0 \leq \tau \left( t \right) \leq \tau\), \(0<\dot {\tau }\left( t \right) \leq \bar {\tau }\), \(\tau\) and \(\bar {\tau }\)are constants. The initial vector \(\phi \left( \cdot \right)\) is bounded and continuously differential on\(\left[ { - \tau ,0} \right].\)

Now letting \(\tilde {x}={\left[ {{{\tilde {x}}_1}\;{{\tilde {x}}_2} \cdots {{\tilde {x}}_n}} \right]^T} \in {R^n}\) is an equilibrium point of system (1), which is

$${\tilde {x}^ * }\left( t \right) \equiv 0,\;{\tilde {x}^ * }\left( {t - \tau \left( t \right)} \right) \equiv 0.$$

Implying from (1) that

$$0= - A{x^ * }\left( t \right)+Cf\left( {{x^ * }\left( t \right)} \right)+Df\left( {{x^ * }\left( {t - \tau \left( t \right)} \right)} \right)+J.$$

Introducing the state deviation from equilibrium

$$z(t)=x\left( t \right) - \tilde {x}={\left[ {{z_1}\left( t \right)\;{z_2}\left( t \right) \cdots {z_n}\left( t \right)} \right]^T}.$$

So the system (1) is equivalent to the following:

$$\left\{ \begin{gathered} E\dot {z}\left( t \right)= - Az\left( t \right)+B\dot {z}\left( {t - \tau \left( t \right)} \right)+Cg\left( {z\left( t \right)} \right)+Dg\left( {z\left( {t - \tau \left( t \right)} \right)} \right) \hfill \\ z\left( t \right)=\phi \left( t \right) - \tilde {x},t \in \left[ { - \tau ,0} \right], \hfill \\ \end{gathered} \right.$$
(2)

where

$$\begin{gathered} z(t) = [z_{1} (t)\;z_{2} (t) \cdots z_{n} (t)]^{T} , \hfill \\ z(t) = [g_{1} (z_{1} (t))\quad g_{2} (z_{2} (t)) \cdots g_{n} (z_{n} (t))]^{T} , \hfill \\ \dot{z}(t - \tau (t)) = [\dot{z}_{1} (t - \tau (t))\;\dot{z}_{2} (t - \tau (t)) \cdots \dot{z}_{n} (t - \tau (t))]^{T} = \dot{x}(t - \tau (t)) - \tilde{x}, \hfill \\ {\text{g}}(z(t - \tau (t))) = [g_{1} (z_{1} (t - \tau (t))) \cdots g_{n} (z_{n} (t - \tau (t)))]^{T} , \hfill \\ {\text{g}}_{i} (z_{i} (t)) = f_{i} (x_{i} (t)) - f_{i} (\tilde{x}_{i} ) = f_{i} (z_{i} (t) - \tilde{x}_{i} ) - f_{i} (\tilde{x}_{i} ),g_{i} (0) = 0, \hfill \\ g_{i} (z_{i} (t - \tau (t))) = f_{i} (x(t - \tau (t))) - f_{i} (\tilde{x}_{i} ) = f_{i} (z_{i} (t - \tau (t)) - \tilde{x}_{i} ) - f_{i} (\tilde{x}_{i} ). \hfill \\ \end{gathered}$$

Assumption 2.1

The nonlinear function \(~f{\text{ }}:{\text{ }}{R^n} \to {R^n}\) satisfies

$${\left[ {f\left( x \right) - f\left( y \right) - U\left( {x - y} \right)} \right]^T}\left[ {f\left( x \right) - f\left( y \right) - V\left( {x - y} \right)} \right] \leq 0,\forall x,y \in {R^n},$$
(3)

where U and V are constant matrices with appropriate dimensions.

Definition 2.1

Consider the linear system (2), if there exist two scalars \(\varepsilon>0\) and \(\gamma \geq 1\) such that

$$\left\| {z\left( t \right)} \right\| \leq \gamma {e^{ - \varepsilon t}}{\left\| z \right\|_s},\quad t \geq 0,$$

Let \({\left\| z \right\|_s}=\mathop {{\text{sup}}}\limits_{{ - d \leq s \leq 0}} \sqrt {{{\left\| {z\left( s \right)} \right\|}^2}+{{\left\| {\dot {z}\left( s \right)} \right\|}^2}} ,\) then the system (2) is exponentially stable, where \(\varepsilon\) is called the exponential convergence rate, in which \(\left\| \cdot \right\|\) denotes the Euclidean norm.

Definition 2.2 ([29])

The systems (2) is said to be regular and impulse-free, if and only if the pair (E, A) is said to be regular, impulse free.

Before proceeding with the main results, several lemmas are necessary.

Lemma 2.3 ([30])

For any scalars \({\tau _2}>{\tau _1}>0\) and any constant matrix \(Z>0\), if there are a vector function \(\xi \left( t \right):\left[ {{\tau _1},{\tau _2}} \right] \to {R^m}\) such that the integrations in the following are well-defined, then

$$- \int_{{ - {\tau _2}}}^{{ - {\tau _1}}} {\int_{{t+\theta }}^{t} {{\xi ^T}(t)Z\xi (t){\text{d}}s{\text{d}}\theta \leq - \frac{1}{{{\tau _s}}}} } \int_{{ - {\tau _1}}}^{{ - {\tau _2}}} {\int_{{t+\theta }}^{t} {{\xi ^T}(t){\text{d}}s{\text{d}}\theta } } \times Z \times \int_{{ - {\tau _1}}}^{{ - {\tau _2}}} {\int_{{t+\theta }}^{t} {\xi (t){\text{d}}s{\text{d}}\theta } } ,$$

where \({\tau _s}={{\left( {\tau _{2}^{2} - \tau _{1}^{2}} \right)} \mathord{\left/ {\vphantom {{\left( {\tau _{2}^{2} - \tau _{1}^{2}} \right)} 2}} \right. \kern-0pt} 2}\).

Lemma 2.4 ([31])

For a given symmetric positive definite matrix R > 0, any functions any differential signal ω in \(\left[ {a,b} \right] \to {R^n}\) and any twice differential function \(\left[ {a,b} \right] \to {R^n}\), then the following inequality holds:

$$\int_{a}^{b} {\dot {\omega }\left( u \right)R\left( {\dot {\omega }} \right)\left( u \right){\text{d}}u} \geq \frac{{{\mu ^T}\left( {a,b} \right)R\eta \left( {a,b} \right)}}{{b - a}}+\frac{{v_{0}^{T}\left( {a,b} \right)Rv\left( {a,b} \right)}}{{b - a}},$$

where \(\eta \left( {a,b} \right)=\omega \left( b \right) - \omega \left( a \right),{v_0}\left( {a,b} \right)=\frac{{\omega \left( b \right)+\omega \left( a \right)}}{2} - \frac{1}{{b - a}}\int_{a}^{b} {\omega \left( u \right){\text{d}}u} .\)

3 The main results

Theorem 3.1

The neutral type descriptor neural networks system (2) is global exponential stability with convergence rate\(\alpha>0\), if there exist some positive definite matrices\(P\), \({Q_1},{Q_2},{Q_3},{Q_4},R\)and\(H\), a matrix two nonnegative constants\(\mu\)and\(v\), such that the following LMI condition is satisfied:

$${E^T}P={P^T}E \geq 0.$$
(4)
$$\prod {=\left[ {\begin{array}{*{20}{c}} {{\Pi _{11}}}&{{\Pi _{12}}}&{{\Pi _{13}}}&0&{{P^T}B}&{{\Pi _{16}}}&{{P^T}D}&{{\Pi _{18}}} \\ * &{{\Pi _{22}}}&0&0&{{\Pi _{25}}}&{{\Pi _{26}}}&{{E^T}{M^T}D}&0 \\ * & * &{{\Pi _{33}}}&0&0&0&0&{{\Pi _{38}}} \\ * & * & * &{{\Pi _{44}}}&0&0&0&0 \\ * & * & * & * &{{\Pi _{55}}}&0&0&0 \\ * & * & * & * & * &{{\Pi _{66}}}&0&0 \\ * & * & * & * & * & * &{{\Pi _{77}}}&0 \\ * & * & * & * & * & * & * &{{\Pi _{88}}} \end{array}} \right]} \leq 0.$$
(5)

where \({\Pi _{11}}=2\alpha {E^T}P - {P^T}A - {A^T}P+{Q_1}+{Q_2} - {\tau ^2}H - \lambda \frac{{{U^T}V+{V^T}U}}{2} - \frac{5}{4}{e^{ - 2\alpha \tau }}R,\) \({\Pi _{12}}={A^T}ME,\) \({\Pi _{13}}=\frac{5}{4}{e^{ - 2\alpha \tau }}R,\) \({\Pi _{16}}={P^T}C - \lambda \frac{{{U^T}+{V^T}}}{2},\) \({\Pi _{18}}=\tau H+\frac{1}{{2\tau }}{e^{2\alpha \tau }}R,\) \({\Pi _{22}}={Q_3}+{\tau ^2}R - \frac{{{\tau ^4}}}{4}H - {E^T}\left( {{M^T}+M} \right)E,\) \({\Pi _{25}}={E^T}{M^T}B,\) \({\Pi _{26}}={E^T}{M^T}C,\) \({\Pi _{33}}= - {e^{ - 2\alpha \tau }}{Q_2} - \frac{5}{4}{e^{ - 2\alpha \tau }}R,\) \({\Pi _{38}}= - \frac{1}{{2\tau }}{e^{ - 2\alpha \tau }}R,\) \({\Pi _{44}}= - \left( {1 - \bar {\tau }} \right){e^{ - 2\alpha \tau }}{Q_1},\) \({\Pi _{55}}= - \left( {1 - \bar {\tau }} \right){e^{ - 2\alpha \tau }}{Q_3},\) \({\Pi _{66}}={Q_4} - \lambda I,\) \({\Pi _{44}}= - \left( {1 - \bar {\tau }} \right){e^{ - 2\alpha \tau }}{Q_4},\) \({\Pi _{88}}= - H - \frac{4}{{{\tau ^2}}}{e^{ - 2\alpha \tau }}R.\)

Proof

Firstly, we prove the system (2) is regular and impulse free. From Eq. (5), we can obtain the inequality \({\Pi _{11}}<0\), that is to say \(- {P^T}A - {A^T}P<0\). Then, combining with Eq. (4), the pair \(\left( {E,A} \right)\) is regular and impulse free. Thus, the system (2) is regular and impulse free.

Next, we shall show the exponential stability of system (2) is global exponential stability.

For positive definite matrices \(P\), \({Q_1}\), \({Q_2}\), \({Q_3}\), \({Q_4}\), \(R\) and \(H\). Let us consider the Lyapunov functional candidate to be

$$V\left( {{z_t}} \right)={V_1}\left( {{z_t}} \right)+{V_2}\left( {{z_t}} \right)+{V_3}\left( {{z_t}} \right)+{V_4}\left( {{z_t}} \right)+{V_5}\left( {{z_t}} \right)+{V_6}\left( {{z_t}} \right)+{V_7}\left( {{z_t}} \right),$$
(6)

where

$$\begin{gathered} {V_1}\left( {{z_t}} \right)={e^{2\alpha t}}{z^T}\left( t \right){E^T}Pz\left( t \right); \hfill \\ {V_2}\left( {{z_t}} \right)=\int_{{t - \tau \left( t \right)}}^{t} {{e^{2\alpha s}}{z^T}\left( s \right){Q_1}z\left( s \right)} {\text{d}}s; \hfill \\ {V_3}\left( {{z_t}} \right)=\int_{{t - \tau }}^{t} {{e^{2\alpha s}}{z^T}\left( s \right){Q_2}z\left( s \right)} {\text{d}}s; \hfill \\ {V_4}\left( {{z_t}} \right)=\int_{{t - \tau \left( t \right)}}^{t} {{e^{2\alpha s}}{{\dot {z}}^T}\left( s \right){Q_3}\dot {z}\left( s \right)} {\text{d}}s; \hfill \\ {V_5}\left( {{z_t}} \right)=\int_{{t - \tau \left( t \right)}}^{t} {{e^{2\alpha s}}{g^T}\left( s \right){Q_4}g\left( {z\left( s \right)} \right)} {\text{d}}s; \hfill \\ {V_6}\left( {{z_t}} \right)=\tau \int_{{ - \tau }}^{0} {\int_{{t+\beta }}^{t} {{e^{2\alpha s}}{{\dot {z}}^T}\left( s \right)R\dot {z}\left( s \right)} } {\text{d}}s{\text{d}}\beta ; \hfill \\ {V_7}\left( {{z_t}} \right)=\frac{{{\tau ^2}}}{2}\int_{{ - \tau }}^{0} {\int_{\theta }^{0} {\int_{{t+\beta }}^{t} {{e^{2\alpha s}}{{\dot {z}}^T}\left( s \right)H\dot {z}\left( s \right)} {\text{d}}s} } {\text{d}}\beta {\text{d}}\theta . \hfill \\ \end{gathered}$$

Taking the time derivative of \(V\left( t \right)\) along the trajectories of system (2) yields

$$\dot {V}\left( {{z_t}} \right)={\dot {V}_1}\left( {{z_t}} \right)+{\dot {V}_2}\left( {{z_t}} \right)+{\dot {V}_3}\left( {{z_t}} \right)+{\dot {V}_4}\left( {{z_t}} \right)+{\dot {V}_5}\left( {{z_t}} \right)+{\dot {V}_6}\left( {{z_t}} \right)+{\dot {V}_7}\left( {{z_t}} \right),$$
(7)

where

$$\begin{aligned} \dot{V}_{1} (z_{t} ) = & 2\alpha e^{{2\alpha t}} z^{T} (t)E^{T} Pz(t) + 2\alpha e^{{2\alpha t}} z^{T} (t)P^{T} E\dot{z}(t) \\ = & e^{{2\alpha t}} (z^{T} (t)(2\alpha E^{T} P - P^{T} A - A^{T} P)z(t)) + 2z^{T} (t)P^{T} Cg(z(t)) \\ & + 2z^{T} (t)P^{T} B\dot{z}(t - \tau (t)) + 2z^{T} (t)P^{T} Dg(z(t - \tau (t))); \\ \dot{V}_{2} \left( {z_{t} } \right) \le & e^{{2\alpha t}} \left[ {z^{T} \left( t \right)Q_{1} z\left( t \right) - e^{{ - 2\alpha t}} z^{T} \left( {t - \tau \left( t \right)} \right)Q_{1} z\left( {t - \tau \left( t \right)} \right)\left( {1 - \bar{\tau }} \right)} \right]; \\ \dot{V}_{3} \left( {z_{t} } \right) \le & e^{{2\alpha t}} \left[ {z^{T} \left( t \right)Q_{2} z\left( t \right) - e^{{ - 2\alpha t}} z^{T} \left( {t - \tau } \right)Q_{2} z\left( {t - \tau } \right)} \right]; \\ \dot{V}_{4} \left( {z_{t} } \right) \le & e^{{2\alpha t}} \left[ {\dot{z}^{T} \left( t \right)Q_{3} \dot{z}\left( t \right) - e^{{ - 2\alpha t}} \dot{z}^{T} \left( {t - \tau \left( t \right)} \right)Q_{3} \dot{z}\left( {t - \tau \left( t \right)} \right)\left( {1 - \bar{\tau }} \right)} \right]; \\ \dot{V}_{5} (z_{t} ) \le & e^{{2\alpha t}} \left[ {g^{T} (z(t))Q_{4} g(z(t))} \right] - e^{{2\alpha t}} \left[ {e^{{ - 2\alpha \tau }} g^{T} (z(t - \tau (t)))Q_{4} g(z(t - \tau (t)))(1 - \bar{\tau })} \right]; \\ \dot{V}_{6} \left( {z_{t} } \right) \le & e^{{2\alpha t}} \left[ {\tau ^{2} \dot{z}^{T} \left( t \right)R\dot{z}\left( t \right) - e^{{ - 2\alpha t}} \tau \int_{{t - \tau }}^{t} {\dot{z}^{T} \left( s \right)R\dot{z}\left( s \right){\text{d}}s} } \right]; \\ \dot{V}_{7} \left( {z_{t} } \right) \le & e^{{2\alpha t}} \left[ { - \frac{{\tau ^{4} }}{4}\dot{z}^{T} \left( t \right)H\dot{z}\left( t \right) - \frac{{\tau ^{2} }}{2}\int_{{ - \tau }}^{t} {\int_{{t + \theta }}^{t} {\dot{z}^{T} \left( s \right)H\dot{z}\left( s \right){\text{d}}s{\text{d}}\theta } } } \right]. \\ \end{aligned}$$

According to Lemma 2.3, we can obtain

$$\begin{gathered} - \frac{{{\tau ^2}}}{2}\int_{{t+\theta }}^{0} {\int_{{t+\theta }}^{t} {{{\dot {z}}^T}\left( s \right)H\dot {z}\left( s \right)} } {\text{d}}s{\text{d}}\theta \leq - {z^T}\left( t \right){\tau ^2}Hz\left( t \right)+{z^T}\left( t \right)\tau H\int_{{t - \tau }}^{t} {z\left( s \right)} {\text{d}}s \\ +\int_{{t - \tau }}^{t} {{z^T}\left( s \right)} {\text{d}}s\left( {\tau H} \right)z\left( t \right) - \int_{{t - \tau }}^{t} {{z^T}\left( s \right)} {\text{d}}sH\int_{{t - \tau }}^{t} {z\left( s \right){\text{d}}s} . \\ \end{gathered}$$

Then, according to Lemma 2.4, it can get,

$$\begin{aligned} {{\dot {V}}_6}\left( {{z_t}} \right) \leq & \,{e^{ - 2\alpha t}}{\tau ^2}{{\dot {z}}^T}\left( t \right)R\dot {z}\left( t \right) - {e^{2\alpha \left( {t - \tau } \right)}}{\left( {z\left( t \right) - z\left( {t - \tau } \right)} \right)^T}R\left( {z\left( t \right) - z\left( {t - \tau } \right)} \right) \\ & - \frac{1}{4}{e^{2\alpha \left( {t - \tau } \right)}}{\left( {z\left( t \right) - z\left( {t - \tau } \right) - \frac{2}{\tau }\int_{{t - \tau }}^{t} {z\left( s \right){\text{d}}s} } \right)^T}R\left( {z\left( t \right) - z\left( {t - \tau } \right) - \frac{2}{\tau }\int_{{t - \tau }}^{t} {z\left( s \right){\text{d}}s} } \right). \\ \end{aligned}$$

On the other hand, based on Assumption 2.1, we have that any \(\lambda>0\),

$$y\left( t \right)=\lambda {\left[ {\begin{array}{*{20}{c}} {z\left( t \right)} \\ {g\left( {z\left( t \right)} \right)} \end{array}} \right]^T}\left[ {\begin{array}{*{20}{c}} {\bar {U}}&{\bar {V}} \\ * &I \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {z\left( t \right)} \\ {g\left( {z\left( t \right)} \right)} \end{array}} \right] \leq 0,$$
(8)

where \(\bar {U}=\frac{{{U^T}V+{V^T}U}}{2}\), \(\bar {U}=\frac{{{U^T}+{V^T}}}{2}\).

Then, according to the system (2) can get the following equation:

$$\begin{aligned} 0= & {{\dot {z}}^T}(t){E^T}{M^T}( - Az(t)+B\dot {z}(t - \tau (t))+Cg(z(t))+Dg(z(t - \tau (t)))) - Az(t) \\ & +B\dot {z}{(t - \tau (t)+Cg(z(t))+Dg(z(t - \tau (t))))^T}ME\dot {z}(t) - {{\dot {z}}^T}(t){E^T}({M^T}+M)E\dot {z}(t). \\ \end{aligned}$$
(9)

Substituting (8) and (9) into (7) yield that

$$\dot {V}\left( {{z_t}} \right) \leq {e^{2\alpha t}}Z_{1}^{T}\Pi {Z_1}.$$

Define the extended vector

$$\begin{gathered} Z_{1}^{T}=\left[ {{z^T}\left( t \right){{\dot {z}}^T}\left( t \right){z^T}\left( {t - \tau } \right){z^T}\left( {t - \tau \left( t \right)} \right){{\dot {z}}^T}\left( {t - \tau \left( t \right)} \right)} \right. \\ \left. {{g^T}\left( {z\left( t \right)} \right){g^T}\left( {z\left( {t - \tau \left( t \right)} \right)} \right)\int_{{t - \tau }}^{t} {{z^T}\left( s \right){\text{d}}s} } \right], \\ \end{gathered}$$

If \(\Pi <0\), that is to say \(\dot {V}\left( {{z_t}} \right)<0\).

Based on the Lyapunov method, then system (2) is asymptotically stable, that is to say, the system (1) is asymptotically stable.

Furthermore, we prove the exponential stability of the neural networks:

According to \(\dot {V}\left( {{z_t}} \right)<0\), we can get the inequality\(V\left( {{z_t}} \right)<V\left( {{z_0}} \right)\),where

$$\begin{aligned} V({z_0})= & {z^T}(0)Pz(0)+\int_{{t - \tau (0)}}^{0} {{e^{2\alpha s}}{z^T}(s){Q_1}z(s)ds} +\int_{{t - \tau }}^{0} {{e^{2\alpha s}}{z^T}(s){Q_2}z(s)ds} \\ & +\int_{{t - \tau (0)}}^{0} {{e^{2\alpha s}}{{\dot {z}}^T}(s){Q_3}\dot {z}(s)ds} +\int_{{t - \tau (0)}}^{0} {{e^{2\alpha s}}{g^T}({z^T}(s)){Q_4}g(z(s))ds} \\ & +\tau \int_{\beta }^{0} {{e^{2\alpha s}}{{\dot {z}}^T}(s)R\dot {z}(s)dsd\beta } +\frac{{{\tau ^2}}}{2}\int_{{t - \tau }}^{0} {\int_{\beta }^{0} {{e^{2\alpha s}}{{\dot {z}}^T}(s)H\dot {z}(s)dsd\beta d\theta } } \\ \leq & \left( {{\lambda _M}(P)+4\tau {\lambda _M}({Q_i})+{\tau ^3}{\lambda _M}(R)+{\tau ^5}{\lambda _M}(H)} \right) \cdot \left\| z \right\|_{s}^{2}. \\ \end{aligned}$$

Letting \({\delta _0}={\lambda _M}\left( P \right)+\tau {\lambda _M}\left( {{Q_1}} \right)+{\lambda _M}\left( {{Q_2}} \right)+\tau {\lambda _M}\left( {{Q_3}} \right)+{\tau ^3}{\lambda _M}\left( R \right)\), then \({\lambda _M}\left( P \right)\), \({\lambda _M}\left( {{Q_1}} \right)\), \({\lambda _M}\left( {{Q_2}} \right)\), \({\lambda _M}\left( {{Q_3}} \right)\) and \({\lambda _M}(R)\) stand for the largest characteristic value of matrix \(P,{Q_1},{Q_2},{Q_3},{Q_4}\) and \(R\), respectively. For any variable \(t\), form the chosen Lyapunov functional, we can get the following inequality:

$$V\left( {{z_t}} \right) \geq {e^{2\alpha t}}{z^T}\left( t \right)Pz\left( t \right) \geq {\lambda _m}\left( P \right){e^{2\alpha t}}{\left\| {z\left( t \right)} \right\|^2},$$

which leads us to

$$\left\| {z\left( t \right)} \right\| \leq \sqrt {\frac{{{\delta _0}}}{{{\lambda _m}\left( P \right)}}} {\left\| z \right\|_s}{e^{ - \alpha t}},\quad t \geq 0.$$

By Definition 2.1, the system (2) is global exponential stability with a convergence rate \(\alpha\). This implies that the equilibrium point \(\tilde {x}\) of system (2) is globally exponentially stable with convergence rate α. The proof is completed.

Remark 1

When \(E=I\), the system (1) reduces to the traditional neutral type neural networks system:

$$\dot {x}\left( t \right)= - A\left( x \right)+B\dot {x}\left( {t - \tau \left( t \right)} \right)+Cf\left( {x\left( t \right)} \right)+Df\left( {x\left( {t - \tau \left( t \right)} \right)} \right)+J.$$

We can transform the neutral type neural networks system to the system in [28, 29]. However, the system in this paper is more widely used than the traditional neutral type system.

4 Numerical examples

Example 4.1

Considering the system (2):

$$E\dot {z}\left( t \right)= - Az\left( t \right)+B\dot {z}\left( {t - \tau \left( t \right)} \right)+Cg\left( {z\left( t \right)} \right)+Dg\left( {z\left( {t - \tau \left( t \right)} \right)} \right),$$

with the following parameter:

$$\begin{gathered} E=\left[ {\begin{array}{*{20}{c}} 1&0 \\ 0&0 \end{array}} \right],A=\left[ {\begin{array}{*{20}{c}} 1&2 \\ 3&1 \end{array}} \right],B=\left[ {\begin{array}{*{20}{c}} { - 1}&{0.5} \\ {0.5}&{ - 1} \end{array}} \right],C=\left[ {\begin{array}{*{20}{c}} { - 0.5}&{0.5} \\ {0.5}&{0.5} \end{array}} \right], \hfill \\ D=\left[ {\begin{array}{*{20}{c}} { - 2}&{0.1} \\ {0.1}&{ - 0.4} \end{array}} \right],\quad \dot {\tau }\left( t \right)=0.1,\alpha =\mu =v=0.1. \hfill \\ \end{gathered}$$

Using MATLAB LMI Toolbox and Theorem 3.1, we obtain maximum allowable upper bounds \(\tau (t)<4.5\). we choice \(f(z)=\tanh (z)\), by condition (3) in Assumption 2.1, which we can obtain

$$U=\left[ {\begin{array}{*{20}{c}} { - 0.5}&{0.2} \\ 0&{0.95} \end{array}} \right],V=\left[ {\begin{array}{*{20}{c}} { - 0.3}&{0.2} \\ 0&{0.2} \end{array}} \right].$$

and have the following results:

$$\begin{gathered} P=\left[ {\begin{array}{*{20}{c}} {1.498}&{0.4403} \\ {0.4403}&{6.3053} \end{array}} \right],{Q_1}=\left[ {\begin{array}{*{20}{c}} {19.6132}&{ - 0.2745} \\ { - 0.2745}&{23.0388} \end{array}} \right],{Q_2}=\left[ {\begin{array}{*{20}{c}} {12.7215}&{ - 0.1907} \\ { - 0.1907}&{15.8559} \end{array}} \right], \hfill \\ {Q_3}=\left[ {\begin{array}{*{20}{c}} {48.2162}&{ - 1.7476} \\ { - 1.7476}&{49.6480} \end{array}} \right],{Q_4}=\left[ {\begin{array}{*{20}{c}} {3.2815}&{0.0013} \\ {0.0013}&{3.4988} \end{array}} \right],R=\left[ {\begin{array}{*{20}{c}} {40.4538}&{0.4348} \\ {0.4348}&{32.0820} \end{array}} \right], \hfill \\ H=\left[ {\begin{array}{*{20}{c}} {8.8263}&{0.0088} \\ {0.0088}&{7.1792} \end{array}} \right]. \hfill \\ \end{gathered}$$

It is straightforward to check that the conditions in Theorem 3.1 hold. It follows from Theorem 3.1 that system (2) can be exponential stability.

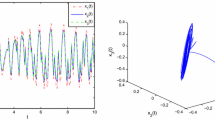
We can simulate the results shown in Fig. 1. The Fig. 1 shows that the singular neutral type neural networks systems are stabilized to zero after a while, and we can say the systems are global exponential stability.

Fig. 1
figure 1

State response of system with vary-time delays

Full size image

Example 4.2

Considering the system (2):

$$E\dot {z}\left( t \right)= - Az\left( t \right)+B\dot {z}\left( {t - \tau \left( t \right)} \right)+Cg\left( {z\left( t \right)} \right)+Dg\left( {z\left( {t - \tau \left( t \right)} \right)} \right),$$

with

$$E=\left[ {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right],A=\left[ {\begin{array}{*{20}{c}} 2&0 \\ 0&{3.5} \end{array}} \right],C=\left[ {\begin{array}{*{20}{c}} { - 1}&{0.5} \\ {0.5}&{ - 1} \end{array}} \right],D=\left[ {\begin{array}{*{20}{c}} { - 0.5}&{0.5} \\ {0.5}&{0.5} \end{array}} \right],\quad B=0,\alpha =0.25.$$
(10)
$$E=\left[ {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right],A=\left[ {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right],C=\left[ {\begin{array}{*{20}{c}} { - 0.1}&{0.1} \\ {0.1}&{ - 0.1} \end{array}} \right],D=\left[ {\begin{array}{*{20}{c}} { - 0.1}&{0.2} \\ {0.2}&{0.1} \end{array}} \right],\quad B=0,\alpha =0.05.$$
(11)

By applying our criteria and using MATLAB LMI toolbox, we have the following comparative result listed in Tables 1 and 2. From Tables 1 and 2, we can see our results are much less conservative than those in [32, 33].

Table 1 Some upper bounds for the time delays of system (2) with (10)
Full size table
Table 2 Some upper bounds for the time delays of system (2) with (11)
Full size table

Remark 2

In this paper, through the comparison with the article [32, 33] in constant and time varying delays, the conclusion was obtained. The conclusion of this paper has better conservation.

Remark 3

A rare integral inequality and model transformation technique make the results have less conservative than some existing literatures.

5 Conclusions

This paper solve the global exponentially stable of neutral type singular networks with time-varying delays. In terms of LMI approach, model transformation technique and a new integral inequality, by using a new Lyapunov–Krasovskii functional, a less conservative criterion of global exponential stability for the networks system is given. The criterion is presented in terms of linear matrix inequalities, which can be easily solved by MATLAB Toolbox. Finally, two examples are presented to illustrate the effectiveness of the method.