1 Introduction

Fractional partial differential equations (FPDEs) have gained more and more attention since many phenomena could be modeled by these equations in science and engineering [20]. Some publications have summarized the historical developments of fractional calculus, such as Oldham and Spanier [16], Miller and Ross [14], and Podlubny [17] and so on. Due to the important applications of FPDEs in engineering and science, some numerical methods including finite difference methods, finite element methods and spectral methods have been developed and analyzed; for details, the readers can refer to [2, 13, 18, 19, 22].

In recent years the study of distributed-order differential equations has attracted much attention of many researchers. The distributed-order partial differential equations could be viewed as a natural generalization of the multi-term fractional differential equation. It has important application in modeling ultraslow diffusion where a plume of particles spreads at a logarithmic rate [10]. Luchko [12] studied the generalized distributed-order time-fractional diffusion equation on bounded domains and proved its uniqueness and continuous dependence on initial conditions. Ford and Morgado [5] studied the existence and uniqueness of solutions of the distributed-order differential equations.

Some scholars have proposed different numerical methods to solve the distributed-order differential equations. B. Jin and his coworkers [8] studied the Galerkin finite element method for the distributed-order time-fractional diffusion and established error estimates optimal with respect to data regularity in \(L^2\) and \(H^1\) norms for both smooth and nonsmooth initial data. Katsikadelis [9] presented an efficient numerical method to solve linear and nonlinear distributed-order differential equations. Diethelm and Ford [4] developed an effective numerical method to solve the distributed-order fractional ordinary differential equations. Morgado and Rebelo [15] proposed and analyzed an implicit scheme for the distributed-order time-fractional reaction–diffusion equation. Ye, Liu and Anh [25] studied a compact finite difference scheme for a distributed-order time-fractional diffusion-wave equation. Li and Wu [11] proposed a numerical method to solve the distributed-order diffusion equations. In [1] Alikhanov presented a finite difference method for the multi-term variable distributed-order diffusion equation. Gao and Sun [6] studied the finite difference methods for the distributed-order differential equations and also proved its stability and convergence. However, up to our knowledge, the study on numerical methods for distributed-order differential equations is just beginning. The development of easy-to-use and higher-order numerical methods for such equations is still an important issue.

Consider the following distributed-order time-fractional reaction–diffusion equation in the Caputo sence

$$\begin{aligned}&\mathcal {D}_t^wu(x,t)=\frac{\partial ^{2}u(x,t)}{\partial x^{2}}-\rho u(x,t)+f(x,t), ~~~~~~x\in (a,b), t\in (0,T],\nonumber \\&u(x,0)=0,~~~~~~x\in [a,b], \end{aligned}$$
(1.1)

\(\rho >0\) is the constant reaction rate, and

$$\begin{aligned}&\mathcal {D}_t^wu(x,t)=\int _0^1w(\alpha )_0^CD_t^{\alpha }u(x,t)d\alpha ,~~~w(\alpha )\ge 0,~~~\int _0^1w(\alpha )d\alpha =c_0>0,\\&_0^CD_t^{\alpha }u(x,t)=\frac{1}{\Gamma (1-\alpha )}\int _0^t\frac{\partial u(x,s)}{\partial s}\frac{ds}{(t-s)^{\alpha }},~t>0,~0<\alpha <1. \end{aligned}$$

Here \(\Gamma (\cdot )\) denotes the Gamma function, and the periodic or compactly supported boundary condition considered in this paper.

The discontinuous Galerkin method, which has many good features of a finite element and a finite volume method, is a very attractive method to solve partial differential equations due to its flexibility in terms of mesh and shape functions and can achieve a high order of convergence. In this paper, we first present a finite difference scheme to approximate the time-fractional derivatives, and then a fully discrete method for the distributed-order time-fractional reaction–diffusion equation in which the spatial direction is approximated by a LDG method is presented and analyzed.

The paper is organized as follows. In Sect. 2 we will introduce some basic notations and theoretic results. Then in Sect. 3 we present our finite difference/local discontinuous Galerkin method for the distributed-order time-fractional reaction–diffusion equation and discuss the stability and give an error estimate in Sect. 4. In Sect. 5, numerical results are also given to illustrate the accuracy of convergence and capability of the method, and the concluding remarks are included in the final section.

2 Notations and Auxiliary Results

Let \(\Omega =\bigcup _jI_j\) be the partition of \(\Omega =[a,b]\), and \(I_{j}=\left[ x_{j-\frac{1}{2}}, x_{j+\frac{1}{2}}\right] ,\) for \(j=1,\ldots N\). The cell lengths \(\Delta x_j=x_{j+\frac{1}{2}}-x_{j-\frac{1}{2}},~1\le j\le N,\) and \(h=\max \limits _{1\le j\le N}\Delta x_j\).

Denote by \(u_{j+\frac{1}{2}}^+\) and \(u_{j+\frac{1}{2}}^-\) the traces from the right cell \(I_{j+1}\) and the left cell \(I_j\), respectively. \(\left[ u_h^n\right] _{j-\frac{1}{2}}\) is used to denote \(\left( u_h^n\right) _{j-\frac{1}{2}}^+-\left( u_h^n\right) _{j-\frac{1}{2}}^-\), i.e., the jump of \(u_h^n\) at each element boundary point, and the jump will be zero for a continuous function.

The associated discontinuous Galerkin element space \(V_h^k\) is defined as the space of piecewise polynomials of the degree up to k,

$$\begin{aligned} V_h^k=\{v:v\in P^k\left( I_j\right) , j=1,2,\ldots N\}. \end{aligned}$$

For error estimates, we will use the projections \(\mathcal {P}\) and \(\mathcal {P}^\pm \) in [a, b], for \(j=1,\ldots N\),

$$\begin{aligned}&\int _{I_j}(\mathcal {P}\mu (x)-\mu (x))\omega (x)=0,~~~~~\forall \omega \in P^k(I_j), \end{aligned}$$
(2.1)
$$\begin{aligned}&\int _{I_j}(\mathcal {P}^+\mu (x)-\mu (x))\omega (x)=0,~~~~~\forall \omega \in P^{k-1}(I_j),\nonumber \\&\mathcal {P}^+\mu \left( x_{j-\frac{1}{2}}^+\right) =\mu \left( x_{j-\frac{1}{2}}\right) , \end{aligned}$$
(2.2)

and

$$\begin{aligned}&\int _{I_j}(\mathcal {P}^-\mu (x)-\mu (x))\omega (x)=0,~~~~~\forall \omega \in P^{k-1}(I_j), \nonumber \\&\mathcal {P}^-\mu \left( x_{j+\frac{1}{2}}^-\right) =\mu \left( x_{j+\frac{1}{2}}\right) . \end{aligned}$$
(2.3)

The above projections \(\mathcal {P}\) and \(\mathcal {P}^\pm \) satisfy the following inequality [23, 24, 26]

$$\begin{aligned} \Vert \mu ^e\Vert +h\Vert \mu ^e\Vert _{\infty }+h^{\frac{1}{2}}\Vert \mu ^e\Vert _{\tau _h}\le Ch^{k+1}, \end{aligned}$$
(2.4)

here \(\mu ^e=\mathcal {P}\mu -\mu \) or \(\mu ^e=\mathcal {P}^\pm \mu -\mu \). The positive constant C is independent of h and solely depends on \(\mu \). \(\tau _h\) denotes the set of boundary points of all elements \(I_j\).

Divide the interval [0, T] uniformly with a time-step size \(\Delta t=\frac{T}{M}\), \(M \in \mathbb {N}\), \(t_{n}=n\Delta t, n=0,1,\ldots ,M\) be the mesh points.

Divide the integral interval [0, 1] into 2L-subintervals with \(\Delta \alpha =\frac{1}{2L}\) and \(\alpha _j=j\Delta \alpha , j=0,1, 2,\ldots , 2L\).

In order to discretize the distributed-order time derivative, we introduce the following composite Simpson formula.

Lemma 2.1

(The composite Simpson formula)

      If \(s(\alpha )\in C^{(4)}[0,1]\), then we have

$$\begin{aligned} \int _0^1 s(\alpha )d\alpha =\Delta \alpha \sum \limits _{j=0}^{2L}d_js(\alpha _j)-\frac{\Delta \alpha ^4}{180}s^{(4)}(\xi ),~~~\xi \in (0,1), \end{aligned}$$

where

$$\begin{aligned} d_j=\left\{ \begin{aligned} \frac{1}{3},&\quad j=0, 2L \\ \frac{2}{3},&\quad j=2,4,\dots , 2L-2 \\ \frac{4}{3},&\quad j=1,3,\dots , 2L-1. \end{aligned} \right. \end{aligned}$$

Next some definitions about fractional calculus will be given. The left-sided Riemann–Liouville fractional derivative is defined as

$$\begin{aligned} _a^{RL}D_t^{\alpha }f(t)=\frac{1}{\Gamma (n-\alpha )} \frac{\mathrm{d}^n}{\mathrm{d}t^n}\int _{a}^t\frac{f(s)}{(t-s)^{\alpha }}\mathrm{d}s, \end{aligned}$$

and the left-sided Caputo fractional derivative

$$\begin{aligned} _0^CD_t^{\alpha }f(t)=\frac{1}{\Gamma (n-\alpha )}\int _0^t \frac{f^{(n)}(s)}{(t-s)^{\alpha }}\mathrm{d}s, \end{aligned}$$

when \(n-1<\alpha <n\).

Lemma 2.2

[17] For \(0<\alpha <1, t>0\), the left-sided Caputo fractional derivative

$$\begin{aligned} _0^CD_t^{\alpha }f(t)=\frac{1}{\Gamma (1-\alpha )}\int _0^t \frac{f'(s)}{(t-s)^{\alpha }}\mathrm{d}s \end{aligned}$$

is equivalent to the Riemann–Liouville fractional derivative

$$\begin{aligned} _0^{RL}D_t^{\alpha }f(t)=\frac{1}{\Gamma (1-\alpha )} \frac{\mathrm{d}}{\mathrm{d}t}\int _{0}^t\frac{f(s)}{(t-s)^{\alpha }}\mathrm{d}s, \end{aligned}$$

when \(f(0)=0\).

Denote

$$\begin{aligned} \mathfrak {I}^{2+\alpha }(R)=\{f|f\in \L ^{1}(R):\int _{-\infty }^{\infty }(1+|\xi |)^{2+\alpha }|\widehat{f}(\xi )|d\xi < \infty \}, \end{aligned}$$

where \(\widehat{f}(\xi )=\int _{-\infty }^{\infty }e^{i\xi t}f(t) \mathrm{d}t\) is the Fourier transformation of f(t).

In order to approximate the Riemann–Liouville fractional derivative, and using the weighted and shifted Grünwald difference operator, we have

Lemma 2.3

[3, 6, 7] Suppose \(f\in \mathfrak {I}^{2+\alpha }(R)\) with \(0\le \alpha \le 1\). We have

$$\begin{aligned} _0^{RL}D_t^{\alpha }u(x,t_{n})=\frac{1}{(\Delta t)^{\alpha }}\sum \limits _{j=0}^{n}\mu _j^\alpha u(x,t_{n-j})+O\left( (\Delta t)^2\right) , \end{aligned}$$

where

$$\begin{aligned} \mu _j =\left\{ \begin{array}{ll} \displaystyle \left( 1+\frac{\alpha }{2}\right) g_0^{\alpha }, &{}\quad j=0 \\ \displaystyle \left( 1+\frac{\alpha }{2}\right) g_j^{\alpha }-\frac{\alpha }{2}g_{j-1}^{\alpha },&{} \mathrm{otherwise}. \end{array} \right. \end{aligned}$$

The coefficients \(g_j^{\alpha }\) satisfy the following properties

$$\begin{aligned} g_0^{\alpha }&=1,~~~g_1^{\alpha }=-\alpha \le 0,\nonumber \\ g_2^{\alpha }&\le g_3^{\alpha }\le g_4^{\alpha }\le \dots 0,\nonumber \\ \sum \limits _{k=0}^{\infty }g_k^{\alpha }&=0,~~~\sum \limits _{k=0}^{n}g_k^{\alpha }\ge 0,~n\ge 1, \end{aligned}$$
(2.5)

and they can be evaluated recursively by

\(g_0^{\alpha }=1, g_k^{\alpha }=\left( 1-\frac{\alpha +1}{k}\right) g_{k-1}^{\alpha },~~~ k\ge 1. \)

For \(0\le \alpha \le 1\), after some manual calculation we know

$$\begin{aligned} \mu _0^\alpha&=1+\frac{\alpha }{2}>0,\nonumber \\ \mu _1^\alpha&=-\frac{1}{2}(\alpha +3)\alpha \le 0,\nonumber \\ \mu _2^\alpha&=\frac{1}{4}(\alpha ^2+3\alpha -2)\alpha ,\nonumber \\ \mu _j^\alpha&\le 0,~~~j\ge 3. \end{aligned}$$
(2.6)

Lemma 2.4

[6, 21] Suppose \((\delta _0,\delta _1,\delta _2,\ldots ,\delta _m)^{T}\in R^{m+1}\) is a real vector, \(m\in N^+\). Then the coefficients \(\{\mu _j^\alpha \}_{j=0}^\infty \) defined in Lemma 2.3 satisfy the following inequality

$$\begin{aligned} \sum \limits _{n=0}^{m}\left( \sum \limits _{j=0}^{n}\mu _j^\alpha \delta _{n-k}\right) \delta _n\ge 0, \end{aligned}$$

In the present paper C will be used as a positive constant which may have a different value in different occurrences. We denote the piecewise derivative of the function w(x) by \(w_x\) and the \(L^2\) norm on D by \(\Vert \cdot \Vert _{D}\), respectively. If \(D=\Omega \), we drop D.

3 The Scheme

In this section, we introduce the numerical scheme for the solution of Eq. (1.1).

In virtue of Lemmas 2.1, 2.2 and 2.3, we have [6]

$$\begin{aligned} \mathcal {D}_t^wu(x,t_n)&=\int _0^1w(\alpha )_0^CD_{t_n}^{\alpha }u(x,t_n)\mathrm{d}\alpha \nonumber \\&=\int _0^1\frac{w(\alpha )}{\Gamma (1-\alpha )}\int _0^{t_n}\frac{\partial u(x,s)}{\partial s}\frac{\mathrm{d}s}{(t_n-s)^{\alpha }}\mathrm{d}\alpha \nonumber \\&=\Delta \alpha \sum \limits _{j=0}^{2L}d_j w(\alpha _j) \frac{1}{(\Delta t)^{\alpha _j}} \sum \limits _{k=0}^{n}\mu _k^{\alpha _j}u(x,t_{n-k})+r^n, \end{aligned}$$
(3.1)

where the truncation error \(|r^n|\le C\left( (\Delta t)^2+\Delta \alpha ^4\right) .\)

For Eq. (1.1) we first consider the equivalent first-order system

$$\begin{aligned}&p=u_x,~~~\mathcal {D}_t^wu(x,t)=p_x-\rho u(x,t) +f(x,t). \end{aligned}$$
(3.2)

Let \(u_h^n, p_h^n\in V_h^k\) be the approximation of \(u(\cdot ,t_n), p(\cdot ,t_n)\), respectively, \(f^n(x)=f(x,t_n)\). We seek the approximation solutions \(u_h^n, p_h^n \in V_h^k,\) such that for test functions \(v, \xi \in V_h^k,\)

$$\begin{aligned}&\left( \rho +\Delta \alpha \sum \limits _{j=0}^{2L}d_j w(\alpha _j) \frac{1}{(\Delta t)^{\alpha _j}} \mu _0^{\alpha _j}\right) \int _{\Omega }u_h^nv\mathrm{d}x+\int _{\Omega }p_h^nv_x\mathrm{d}x\nonumber \\&\qquad -\sum \limits _{j=1}^{N}\left( \left( \widehat{p_h^n}v^-\right) _{j+\frac{1}{2}}-\left( \widehat{p_h^n}v^+\right) _{j-\frac{1}{2}}\right) \nonumber \\&\quad =\Delta \alpha \sum \limits _{j=0}^{2L}d_j w(\alpha _j) \frac{1}{(\Delta t)^{\alpha _j}}\sum \limits _{k=1}^{n}\left( -\mu _k^{\alpha _j}\right) \int _{\Omega }u_h^{n-k}v\mathrm{d}x+\int _{\Omega }f^n v \mathrm{d}x,\nonumber \\&\int _{\Omega }p_h^n\xi \mathrm{d}x+\int _{\Omega }u_h^n\xi _x\mathrm{d}x-\sum \limits _{j=1}^{N}\left( \left( \widehat{u_h^n}\xi ^-\right) _{j+\frac{1}{2}}-\left( \widehat{u_h^n}\xi ^+\right) _{j-\frac{1}{2}}\right) =0. \end{aligned}$$
(3.3)

The initial conditions \(u_h^0\) are taken as the \(L^2\) projections of u(, 0)

$$\begin{aligned} \int _{\Omega }u_h^{0}\phi \mathrm{d}x&=\int _{\Omega }\mathcal {P}u(x,0)\phi \mathrm{d}x=\int _{\Omega }u_0(x)\phi \mathrm{d}x,\\ ~~~\forall v\in V_h^k. \end{aligned}$$

The “hat” terms in (3.3) in the cell boundary terms from integration by parts are the so-called numerical fluxes, which are single-valued functions defined on the edges and should be designed based on different guiding principles for different PDEs to ensure stability. It turns out that we can take the simple choices such that

$$\begin{aligned} \widehat{u_h^n}=\widetilde{u_h^n}+\tau \left[ p_h^n\right] ,\widetilde{u_h^n}=\left( u_h^n\right) ^-,\widehat{p_h^n}=\left( p_h^n\right) ^+, \end{aligned}$$
(3.4)

where \(\tau >0\) is a constant. We remark that the choice for fluxes (3.4) is not unique. In fact the crucial part is taking \(\widetilde{u_h^n}\) and \(\widehat{p_h^n}\) from opposite sides [23, 24, 26].

4 Stability and Convergence

Theorem 4.1

Fully discrete LDG scheme (3.3) is unconditionally stable for any \(\Delta t>0\),

$$\begin{aligned} \frac{\rho \Delta t}{2}\sum \limits _{n=1}^{m}\Vert u_h^n\Vert ^2+\Delta t\sum \limits _{n=1}^{m}\left( \Vert p_h^n\Vert ^2+\tau \sum \limits _{j=1}^{N}[p_h^n]^2_{j-\frac{1}{2}}\right)&\le \chi \Delta t\Vert u_h^0\Vert ^2+\frac{\Delta t}{2\rho }\sum \limits _{n=1}^{m}\Vert f^n\Vert ^2,\\&~~~1\le m\le M, \end{aligned}$$

where \(\chi =\Delta \alpha \sum _{j=0}^{2L}d_j w(\alpha _j) \frac{1}{(\Delta t)^{\alpha _j}}\mu _0^{\alpha _j}.\)

Proof

Scheme (3.3) can be rewritten as

$$\begin{aligned}&\rho \int _{\Omega }u_h^nv\mathrm{d}x+\Delta \alpha \sum \limits _{j=0}^{2L}d_j w(\alpha _j) \frac{1}{(\Delta t)^{\alpha _j}}\sum \limits _{k=0}^{n}\left( \mu _k^{\alpha _j}\right) \int _{\Omega }u_h^{n-k}v\mathrm{d}x\nonumber \\&\quad +\int _{\Omega }p_h^nv_x\mathrm{d}x-\sum \limits _{j=1}^{N}\left( \left( \widehat{p_h^n}v^-\right) _{j+\frac{1}{2}}-\left( \widehat{p_h^n}v^+\right) _{j-\frac{1}{2}}\right) =\int _{\Omega }f^n v \mathrm{d}x,\nonumber \\&\int _{\Omega }p_h^n\xi \mathrm{d}x+\int _{\Omega }u_h^n\xi _x\mathrm{d}x-\sum \limits _{j=1}^{N}\left( \left( \widehat{u_h^n}\xi ^-\right) _{j+\frac{1}{2}}-\left( \widehat{u_h^n}\xi ^+\right) _{j-\frac{1}{2}}\right) =0. \end{aligned}$$
(4.1)

Taking the test functions \(v=u^n_h, \xi =p^n_h\) in (4.1) and with fluxes choice (3.4) we obtain

$$\begin{aligned}&\rho \Vert u_h^n\Vert ^2+\Delta \alpha \sum \limits _{j=0}^{2L}d_j w(\alpha _j) \frac{1}{(\Delta t)^{\alpha _j}}\sum \limits _{k=0}^{n}\left( \mu _k^{\alpha _j}\right) \int _{\Omega }u_h^{n-k}u_h^n\mathrm{d}x+\tau \sum \limits _{j=1}^{N}\left[ p_h^n\right] ^2_{j-\frac{1}{2}}\nonumber \\&\qquad +\Vert p_h^n\Vert ^2+\sum \limits _{j=1}^{N}\left( \Psi \left( u_h^n,p_h^n\right) _{j+\frac{1}{2}} -\Psi \left( u_h^n,p_h^n\right) _{j-\frac{1}{2}}+\Theta \left( u_h^n,p_h^n\right) _{j-\frac{1}{2}}\right) \nonumber \\&\quad =\int _{\Omega }f^nu^n_h\mathrm{d}x\nonumber \\&\quad \le \frac{1}{2\rho }\Vert f^n\Vert ^2+\frac{\rho }{2}\Vert u_h^n\Vert ^2. \end{aligned}$$
(4.2)

here

$$\begin{aligned} \Psi \left( u_h^n,p_h^n\right)&=\left( p_h^n\right) ^-\left( u_h^n\right) ^--\widehat{p_h^n}\left( u_h^n\right) ^--\widehat{u_h^n}\left( p_h^n\right) ^-,\\ \Theta \left( u_h^n,p_h^n\right)&=\left( p_h^n\right) ^-\left( u_h^n\right) ^--\left( p_h^n\right) ^+\left( u_h^n\right) ^+-\widehat{p_h^n}\left( u_h^n\right) ^-+\widehat{p_h^n}\left( u_h^n\right) ^+ -\widehat{u_h^n}\left( p_h^n\right) ^-+\widehat{u_h^n}\left( p_h^n\right) ^+. \end{aligned}$$

After some calculations, we can easily obtain \(\Theta (u_h^n,p_h^n)=0\).

Then we can get

$$\begin{aligned}&\frac{\rho }{2}\Vert u_h^n\Vert ^2+\Delta \alpha \sum \limits _{j=0}^{2L}d_j w(\alpha _j) \frac{1}{(\Delta t)^{\alpha _j}}\sum \limits _{k=0}^{n}\left( \mu _k^{\alpha _j}\right) \int _{\Omega }u_h^{n-k}u_h^n\mathrm{d}x\nonumber \\&\quad \ +\Vert p_h^n\Vert ^2+\tau \sum \limits _{j=1}^{N}\left[ p_h^n\right] ^2_{j-\frac{1}{2}} \le \frac{1}{2\rho }\Vert f^n\Vert ^2. \end{aligned}$$
(4.3)

Denoting \(\chi =\Delta \alpha \sum \limits _{j=0}^{2L}d_j w(\alpha _j) \frac{1}{(\Delta t)^{\alpha _j}}\mu _0^{\alpha _j},\) we know [6]

$$\begin{aligned} \chi =\frac{1}{O(\Delta t|\ln \Delta t|)}>0. \end{aligned}$$

Next summing up n from 1 to m, and adding a term \(\chi \Vert u_h^0\Vert ^2\) on both sides in 4.3, we obtain

$$\begin{aligned}&\sum \limits _{n=1}^{m}\frac{\rho }{2}\Vert u_h^n\Vert ^2+\sum \limits _{n=1}^{m}\left( \Vert p_h^n\Vert ^2+\tau \sum \limits _{j=1}^{N}\left[ p_h^n\right] ^2_{j-\frac{1}{2}}\right) \nonumber \\&\quad \ +\Delta \alpha \sum \limits _{j=0}^{2L}d_j w(\alpha _j) \frac{1}{(\Delta t)^{\alpha _j}}\sum \limits _{n=0}^{m}\sum \limits _{k=0}^{n}\left( \mu _k^{\alpha _j}\right) \int _{\Omega }u_h^{n-k}u_h^n\mathrm{d}x\nonumber \\&\le \chi \Vert u_h^0\Vert ^2+\frac{1}{2\rho }\sum \limits _{n=1}^{m}\Vert f^n\Vert ^2. \end{aligned}$$
(4.4)

In virtue of Lemma 2.4, we get

$$\begin{aligned}&\frac{\rho \Delta t}{2}\sum \limits _{n=1}^{m}\Vert u_h^n\Vert ^2+\Delta t\sum \limits _{n=1}^{m}\left( \Vert p_h^n\Vert ^2+\tau \sum \limits _{j=1}^{N}\left[ p_h^n\right] ^2_{j-\frac{1}{2}}\right) \\&\quad \le \chi \Delta t\Vert u_h^0\Vert ^2+\frac{\Delta t}{2\rho }\sum \limits _{n=1}^{m}\Vert f^n\Vert ^2,~~~1\le m\le M, \end{aligned}$$

where \(\chi \Delta t=\frac{1}{O(|\ln \Delta t|)}\le 1.\)

This finishes the proof of the stability result. \(\square \)

Theorem 4.2

Let \(u(x,t_n)\) be the exact solution of problem (1.1) at time \(t=t_n\), \(u_h^n\) be the numerical solution of fully discrete LDG scheme (3.3), for any positive integer m, there exists a constant C such that

$$\begin{aligned} \sum \limits _{n=1}^{m}\Vert u(\cdot ,t_n)-u_h^n\Vert \le C(h^{k+\frac{1}{2}}+(\Delta t)^2+\Delta \alpha ^4),~~~1\le m\le M. \end{aligned}$$

Proof

Denote

$$\begin{aligned}&e_u^n=u\left( x,t_n\right) -u_h^n=\mathcal {P}e_u^n-\left( \mathcal {P}u\left( x,t_n\right) -u\left( x,t_n\right) \right) ,\nonumber \\&e_p^n=p\left( x,t_n\right) -p_h^n=\mathcal {P^+}e_p^n-\left( \mathcal {P^+}p\left( x,t_n\right) -p\left( x,t_n\right) \right) . \end{aligned}$$
(4.5)

Taking fluxes (3.4), we can obtain the error equation:

$$\begin{aligned}&\rho \int _{\Omega }e_u^nv\mathrm{d}x+\Delta \alpha \sum \limits _{j=0}^{2L}d_j w(\alpha _j) \frac{1}{(\Delta t)^{\alpha _j}}\sum \limits _{k=0}^{n}\left( \mu _k^{\alpha _j}\right) \int _{\Omega }e_u^{n-k}v\mathrm{d}x\nonumber \\&\qquad \ +\int _{\Omega }e_p^nv_x\mathrm{d}x-\sum \limits _{j=1}^{N}\left( \left( \left( e_p^n\right) ^+v^-\right) _{j+\frac{1}{2}}-\left( \left( e_p^n\right) ^+v^+\right) _{j-\frac{1}{2}}\right) +\int _{\Omega }r^n v\mathrm{d}x\nonumber \\&\qquad \ +\int _{\Omega }e_p^n\xi \mathrm{d}x+\int _{\Omega }e_u^n\xi _x\mathrm{d}x-\sum \limits _{j=1}^{N}\left( \left( \left( e_u^n\right) ^-\xi ^-\right) _{j+\frac{1}{2}}-\left( \left( e_u^n\right) ^-\xi ^+\right) _{j-\frac{1}{2}}\right) \nonumber \\&\qquad \ +\tau \sum \limits _{j=1}^{N}\left[ p_h^n\right] [\xi ]_{j-\frac{1}{2}}\nonumber \\&\quad \ =0. \end{aligned}$$
(4.6)

By virtue of (4.5), error Eq. (4.6) can be written as follows:

$$\begin{aligned}&\rho \int _{\Omega }\mathcal {P}e_u^n v\mathrm{d}x+\int _{\Omega }\mathcal {P^+}e_p^nv_x\mathrm{d}x -\sum \limits _{j=1}^{N}\left( \left( \left( \mathcal {P^+}e_p^n\right) ^+v^-\right) _{j+\frac{1}{2}}-\left( \left( \mathcal {P^+}e_p^n\right) ^+v^+\right) _{j-\frac{1}{2}}\right) \nonumber \\&\qquad \ +\int _{\Omega }\mathcal {P^+}e_p^n\xi \mathrm{d}x+\int _{\Omega }\mathcal {P}e_u^n\xi _x\mathrm{d}x-\sum \limits _{j=1}^{N}\left( \left( \left( \mathcal {P}e_u^n\right) ^-\xi ^-\right) _{j+\frac{1}{2}}-\left( \left( \mathcal {P}e_u^n\right) ^-\xi ^+\right) _{j-\frac{1}{2}}\right) \nonumber \\&\qquad \ +\int _{\Omega }r^n v\mathrm{d}x+\tau \sum \limits _{j=1}^{N}\left[ \mathcal {P^+}e_p^n\right] [\xi ]_{j-\frac{1}{2}}\nonumber \\&\quad \ =\Delta \alpha \sum \limits _{j=0}^{2L}d_j w(\alpha _j) \frac{1}{(\Delta t)^{\alpha _j}}\sum \limits _{k=0}^{n}\left( -\mu _k^{\alpha _j}\right) \int _{\Omega }\mathcal {P}e_u^{n-k}v\mathrm{d}x \nonumber \\&\qquad \ -\Delta \alpha \sum \limits _{j=0}^{2L}d_j w(\alpha _j) \frac{1}{(\Delta t)^{\alpha _j}}\sum \limits _{k=0}^{n}\left( -\mu _k^{\alpha _j}\right) \int _{\Omega }\left( \mathcal {P}u\left( x,t_{n-k}\right) -u\left( x,t_{n-k}\right) \right) v\mathrm{d}x\nonumber \\&\qquad \ +\int _{\Omega }\left( \mathcal {P^+}p(x,t_n)-p(x,t_n)\right) v_x\mathrm{d}x-\sum \limits _{j=1}^{N}\left( \left( (\mathcal {P^+}p(x,t_n)-p(x,t_n)\right) ^+v^-\right) _{j+\frac{1}{2}}\nonumber \\&\qquad \ -\left( \left( \left( \mathcal {P^+}p(x,t_n)-p(x,t_n)\right) ^+v^+\right) _{j-\frac{1}{2}}\right) +\rho \int _{\Omega }\left( \mathcal {P}u(x,t_n)-u(x,t_n)\right) v\mathrm{d}x \nonumber \\&\qquad \ +\int _{\Omega }\left( \mathcal {P^+}p\left( x,t_n\right) -p\left( x,t_n\right) \right) \xi \mathrm{d}x+\int _{\Omega }\left( \mathcal {P}u\left( x,t_n\right) -u\left( x,t_n\right) \right) \xi _x\mathrm{d}x\nonumber \\&\qquad \ -\sum \limits _{j=1}^{N}\left( \left( \left( \mathcal {P}u\left( x,t_n\right) -u\left( x,t_n\right) \right) ^-\xi ^-\right) _{j+\frac{1}{2}}-\left( \left( \mathcal {P}u\left( x,t_n\right) -u\left( x,t_n\right) \right) ^-\xi ^+\right) _{j-\frac{1}{2}}\right) \nonumber \\&\qquad \ +\tau \sum \limits _{j=1}^{N}\left[ \mathcal {P^+}p(x,t_n)-p(x,t_n)\right] [\xi ]_{j-\frac{1}{2}} \end{aligned}$$
(4.7)

Let \(v=\mathcal {P}e_u^n, \xi =\mathcal {P^+}e_p^n\) in (4.7), and by the application of properties (2.1)–(2.2), we can obtain the following inequality easily

$$\begin{aligned}&\rho \Vert \mathcal {P}e_u^n\Vert ^2+\Vert \mathcal {P^+}e_p^n\Vert ^2 +\tau \sum \limits _{j=1}^{N}\left[ \mathcal {P^+}e_p^n\right] ^2_{j-\frac{1}{2}}\\&\qquad \ +\Delta \alpha \sum \limits _{j=0}^{2L}d_j w(\alpha _j) \frac{1}{(\Delta t)^{\alpha _j}}\sum \limits _{k=0}^{n}\left( \mu _k^{\alpha _j}\right) \Vert \mathcal {P}e_u^{n-k}\Vert \Vert \mathcal {P}e_u^n\Vert \\&\quad \ \le \Vert \mathcal {P^+}p(x,t_n)-p(x,t_n)\Vert \Vert \mathcal {P^+}e_p^n\Vert +\Vert r^n\Vert \Vert \mathcal {P}e_u^n\Vert \\&\qquad \ +\sum \limits _{j=1}^{N}\left( \mathcal {P}u(x,t_n)-u(x,t_n)\right) ^-\left[ \mathcal {P^+}e_p^n\right] _{j-\frac{1}{2}}\\&\qquad \ +\tau \sum \limits _{j=1}^{N}\left[ \mathcal {P^+}p(x,t_n)-p(x,t_n)\right] \left[ \mathcal {P^+}e_p^n\right] _{j-\frac{1}{2}} \end{aligned}$$

Noticing the fact that

$$\begin{aligned} \phi \varphi \le \varepsilon \phi ^2+\frac{1}{4\varepsilon }\varphi ^2, \end{aligned}$$

using the Höld’s inequality, choosing a small enough \(\varepsilon \le \tau \), we have

$$\begin{aligned}&\rho \Vert \mathcal {P}e_u^n\Vert ^2+\Vert \mathcal {P^+}e_p^n\Vert ^2+\Delta \alpha \sum \limits _{j=0}^{2L}d_j w(\alpha _j) \frac{1}{(\Delta t)^{\alpha _j}}\sum \limits _{k=0}^{n}\left( \mu _k^{\alpha _j}\right) \Vert \mathcal {P}e_u^{n-k}\Vert \Vert \mathcal {P}e_u^n\Vert \\&\quad \ \le \Vert \mathcal {P^+}p(x,t_n)-p(x,t_n)\Vert ^2+\frac{1}{\rho }\Vert r^n\Vert ^2 +\frac{1}{\varepsilon }\sum \limits _{j=1}^{N}\left( \left( \mathcal {P}u(x,t_n)-u(x,t_n)\right) ^-\right) ^2_{j-\frac{1}{2}}\\&\qquad \ +\frac{\tau ^2}{\varepsilon }\sum \limits _{j=1}^{N}\left[ \mathcal {P^+}p(x,t_n)-p(x,t_n)\right] ^2_{j-\frac{1}{2}} \end{aligned}$$

Notice

$$\begin{aligned} \Vert r^n\Vert \le C\left( (\Delta t)^2+\Delta \alpha ^4\right) , \end{aligned}$$

summing up n from 1 to m, using Lemma 2.4 and interpolating property (2.4), we have

$$\begin{aligned} \sum \limits _{n=1}^{m}\Vert \mathcal {P}e_u^n\Vert \le C\left( h^{k+\frac{1}{2}}+(\Delta t)^2+\Delta \alpha ^4\right) ,~~~1\le m\le M. \end{aligned}$$

From the triangle inequality, Theorem 4.2 follows. \(\square \)

Remark

We can find that a \(L^2\)-error estimate of half an order lower \(O\left( h^{k+\frac{1}{2}}\right) \) in space has been proved; however, the optimal error estimate will be obtained in the numerical experiments.

5 Numerical Examples

In this section, in order to verify numerical accuracy of the proposed method and the correctness of analysis, numerical experiments will be carried out.

Example In (1.1), taking \(\Omega =[0,1]\), \(T=0.5, w(\alpha )=\Gamma (p+1-\alpha ), \rho =1\), and

$$\begin{aligned} f(x,t)=\left[ \frac{2^p\Gamma (p+1)(t^p-t^{p-1})}{\ln t}+4\pi ^2(2t)^p+(2t)^p\right] \sin (2\pi x), \end{aligned}$$
(5.1)

where \(p>0\). Then the exact solution of the example is

$$\begin{aligned} u(x,t)=(2t)^p \sin (2\pi x). \end{aligned}$$

Firstly, to confirm the spatial accuracy, we take the fixed and sufficiently small step sizes \(\Delta t\) and \(\Delta \alpha \), and the varying \(h=1/5, 1/10, 1/15, 1/20,\), respectively, and the numerical errors and order of convergence in \(L^2\)-norm and \(L^\infty \)-norm are listed in Tables 1, 2, 3 and 4. From the tables one can find that the errors attain \((k+1)\)-th order of accuracy for piecewise \(P^k\) polynomials.

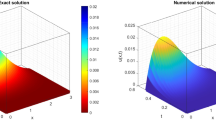
Secondly, the numerical accuracy of scheme (3.3) in time variable is computed. Take the fixed and sufficiently small h and \(\Delta \alpha \). From Table 5 and Fig. 1 we can find that the second order of convergence of scheme (3.3) in time variable is verified.

Table 1 \(L^2\) and \(L^\infty \) errors and convergence orders of scheme (3.3) in space with \(p=5, \Delta \alpha =\frac{1}{200}, \Delta t=\frac{1}{1000}\)
Full size table
Table 2 \(L^2\) and \(L^\infty \) errors and convergence orders of scheme (3.3) in space with \(p=4, \Delta \alpha =\frac{1}{200}, \Delta t=\frac{1}{1000}\)
Full size table
Table 3 \(L^2\) and \(L^\infty \) errors and convergence orders of scheme (3.3) in space with \(p=3, \Delta \alpha =\frac{1}{200}, \Delta t=\frac{1}{1000}\)
Full size table
Table 4 \(L^2\) and \(L^\infty \) errors and convergence orders of scheme (3.3) in space with \(p=2, \Delta \alpha =\frac{1}{200}, \Delta t=\frac{1}{1000}\)
Full size table
Table 5 \(L^2\) and \(L^\infty \) errors and convergence orders of scheme (3.3) in time with \(p=1, \Delta \alpha =\frac{1}{200}, h=\frac{1}{200}\). Piecewise \(P^2\) polynomials are used
Full size table
Fig. 1
figure 1

Temporal accuracy test using piecewise \(P^2\) polynomials for different p. \(\Delta \alpha =\frac{1}{200}, N=200\)

Full size image

6 Conclusion

We have proposed and analyzed a fully discrete LDG method for the distributed-order time-fractional reaction–diffusion equation in this paper. Based on the weighted and shifted Gr\(\ddot{u}\)nwald formula for discretizing the time-fractional derivative, we develop a fully discrete scheme to solve problem (1.1) and prove that the method is unconditionally stable and convergent with order \(O\left( h^{k+\frac{1}{2}}+(\Delta t)^2+\Delta \alpha ^4\right) \). Numerical example is computed to show the convergence order and excellent numerical performance of proposed method. It is noted that the method proposed in this paper could be extended to solve the problems on a rectangular or cubical domain, but the computation is very huge. In future we want to try our best to solve this problem.