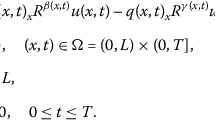Finite Difference/Finite Element Methods for Distributed-Order Time Fractional Diffusion Equations

Abstract

In this paper, a class of distributed-order time fractional diffusion equations (DOFDEs) on bounded domains is considered. By L1 method in temporal direction, a semi-discrete variational formulation of DOFDEs is obtained firstly. The stability and convergence of this semi-discrete scheme are discussed, and the corresponding fully discrete finite element scheme is investigated. To improve the convergence rate in time, the weighted and shifted Grünwald difference method is used. By this method, another finite element scheme for DOFDEs is obtained, and the corresponding stability and convergence are considered. And then, as a supplement, a higher order finite difference scheme of the Caputo fractional derivative is developed. By this scheme, an approach is suggested to improve the time convergence rate of our methods. Finally, some numerical examples are given for verification of our theoretical analysis.

1 Introduction

As is known to all, diffusion model is a fundamental mathematical model for evolution of probability densities. Based on the Brownian motion, it describes the particles distributing in a normal bell-shaped pattern. However, during the recent years, some experts find that it cannot afford to illustrate the transport process called anomalous diffusion in fractal media. In order to overcome this shortcoming, the fractional diffusion model with single time fractional derivative has been developed, and it is popular rapidly [1, 2]. Recently, the two-term time fractional diffusion equation is discussed, and then the multi-term time fractional diffusion equation is developed [3,4,5]. To solve these equations, numerous numerical methods have been devised. The finite difference method is one of the most popular methods for fractional diffusion equations [6, 7]. At the same time, some other numerical methods such as the finite element method and spectral method are also employed [8,9,10,11,12].

Although the single-term and multi-term time fractional diffusion models have wide applications, for the non-Markovian process which is non self-similar and exhibits a continuous distribution of time-scales, the above models are too difficult to simulate it. Thus the distributed-order fractional diffusion model is introduced [13]. In fact, it is discovered that an important application of distributed-order fractional diffusion equation is to model ultraslow diffusion, where a plume of particles spreads at a logarithmic rate [14]. In this paper, we consider the distributed-order fractional diffusion equations (DOFDEs)

$$\begin{aligned} \mathcal {D}^\omega _t u(X,t)=Au(X,t)+F(X,t),\quad (X,t)\in \Omega \times (0,T], \end{aligned}$$

(1)

where A is an operator, $\mathcal {D}^\omega _t$ is a distributed-order derivative, and

$$\begin{aligned} u(X,0)=\phi (X),\quad u(X,t)|_{\partial \Omega }=0. \end{aligned}$$

(2)

If $\Omega \in \mathbb {R}$, then

$$\begin{aligned} A=K_x\dfrac{\partial ^2}{\partial x^2},\quad K_x>0,\quad F(X,t)=f(x,t). \end{aligned}$$

(3)

If $\Omega \in \mathbb {R}^2$, then

$$\begin{aligned} A=K_x\frac{\partial ^2}{\partial x^2}+K_y\frac{\partial ^2}{\partial y^2},\quad K_x,K_y>0,\quad F(X,t)=f(x,y,t). \end{aligned}$$

(4)

The distributed-order fractional derivative $\mathcal {D}^\omega _t u(X,t)$ is defined as

$$\begin{aligned} \mathcal {D}^\omega _t u(X,t)=\int \limits _0^1\omega (\alpha ){_0^CD_t^\alpha }u(X,t)d\alpha \end{aligned}$$

with the Caputo fractional derivative

$$\begin{aligned} {_0^CD_t^\alpha }u(X,t)= \begin{array}{ll} {\left\{ \begin{array}{ll} \dfrac{1}{\Gamma (1-\alpha )}\displaystyle \int \limits _0^t(t-s)^{-\alpha }\dfrac{\partial u(X,s)}{\partial s}ds,&{}\quad \alpha \in (0,1),\\ \dfrac{\partial ^\alpha u(X,t)}{\partial t^\alpha },&{}\quad \alpha =0,1, \end{array}\right. } \end{array} \end{aligned}$$

and $\omega (\alpha )\ge 0,\int \limits _0^1\omega (\alpha )d\alpha =C_0>0$, moreover there exists the constant $0<\bar{\alpha }\le 1$ such that $\omega (\alpha )\equiv 0$ for $\forall \alpha \in (\bar{\alpha },1]$ and for $\forall \alpha \in [0,\bar{\alpha }]$.

During these years, some theoretical studies of distributed-order fractional diffusion equations have been done. In Ref. [15], Atanackovic, Pilipovic and Zorica discussed the Cauchy problems of DOFDEs by means of the theory of an abstract Volterra equation. And then they consider the above problem via Laplace and Fourier transformations [16]. Meerschaert et al. [17] provided an explicit strong solutions and stochastic analogues for DOFDEs on bounded domains. Gorenflo et al. [18] expressed a fundamental solution of the Cauchy problems of DOFDEs as probability density. Ansari and Moradi [19] investigated the exact solutions of some models of DOFDEs by Fox H functions. Li et al. [20] studied the asymptotic behavior of the solutions of DOFDEs. Jia et al. [21] discussed the well-posedness of the Cauchy problems of the abstract DOFDEs by functional calculus technique.

Generally speaking, the exact solutions to DOFDEs are rarely available in practice. Thus it is very necessary to develop some efficient numerical methods to enable the successful use of the model (1)–(4). In Ref. [22], Hu et al. considered the finite difference method for DOFDEs. Then Ye et al. [23] developed an implicit difference scheme for DOFDEs with the Riesz space fractional derivative. Ye et al. [24] discussed the compact difference scheme for DOFDEs on bounded domains and investigated the stability and convergence. Alikhanov [25] considered the finite difference method for multi-term variable-distributed order diffusion equation and obtained a prior estimate for the corresponding difference scheme. In Ref. [26], Morgado and Rebelo employed the implicit finite difference method to solve the distributed order time-fractional reaction–diffusion equation with a nonlinear source term and discussed the stability and convergence of the numerical scheme. In Ref. [27, 28], Gao and Sun considered two-dimensional DOFDEs and treated them by alternating direction implicit (ADI) difference schemes. In order to improve convergence rate, they also developed the ADI compact difference scheme and used the extrapolation technique. In Ref. [29], by the classical numerical quadrature formulas, Li and Wu approximate the DOFDEs by a multi-term time fractional diffusion equation and solve it via the reproducing kernel method.

As everyone knows, the finite element method is an important numerical method. However, to the best of our knowledge, only very few articles discussed the numerical solution of DOFDEs by using finite element method. In Ref. [30], Jin et al. developed two fully discrete finite element schemes based on Laplace transform and convolution quadratures, and some results of exponential convergence and first-order convergence are obtained respectively. Although [30] provided the effective methods to solve DOFDEs, we believe that it is still worth to develop more direct and convenient methods like finite difference/finite element method.

In this paper, we consider the finite difference/finite element methods to solve DOFDEs on bounded domains and develop three useful numerical schemes. For the first scheme, we treat the Caputo fractional derivative by using L1 method. This scheme is very easy to use and require low smoothness in temporal direction. However, the disadvantage of this scheme is low convergence rate in time. To overcome this problem, if u(X, t) meet high smoothness in temporal direction and $\phi (X)=0$ in (2), then we can obtain the second numerical scheme by using the weighted and shifted Grünwald difference method (WSGD) [33]. For this scheme, the two-order convergence rate is achieved in time. We know that the high convergence rate can reduce computation cost and improve the accuracy of numerical results. Therefore we develop a new approach to obtain higher convergence rate in time when $\bar{\alpha }<d\ (d\approx 0.373866584107526)$. For the obtained numerical schemes, we discuss the stabilities and convergences.

The rest of the paper is organized as follows. In Sect. 2, we will develop the numerical scheme for DOFDEs with L1 method in temporal direction and finite element method in spatial direction. Then the stability and convergence of the obtained scheme will be discussed. In Sect. 3, in order to improve the convergence rate in time, we will treat the Caputo fractional derivative by the WSGD method and establish another finite difference/finite element scheme for DOFDEs. The corresponding stability and convergence will be investigated. In Sect. 4, we will develop an approach to make our schemes for DOFDEs to be of higher convergence rate in time by a novel discrete scheme of the Caputo fractional derivative. It will be a complement to the above numerical schemes. In Sect. 5, we will show some numerical examples and demonstrate the correctness of our theoretical analysis. In Sect. 6, we will give a brief conclusion.

2 Numerical Scheme I for DOFDEs

In order to develop the finite element schemes of DOFDEs and discuss the corresponding stabilities and convergences, we give some useful notations firstly. In the following sections, we define $(f,g):=\int _\Omega fgd\Omega ,\Vert f\Vert _0:=(f,f)^{1/2}$, and denote the Sobolev norm $\Vert f\Vert _{H^k(\Omega )}$ by $\Vert f\Vert _k$. We also let $C,C_i,(i=1,2,\ldots )$ denote some constant numbers and may be different in different situations. And then let $\varDelta t=T/N$ be the time step with $t_n=n\varDelta t$.

To discretize the integral $\int _0^1g(\alpha )d\alpha$, we use the modified compound trapezoid formula. If $g(\alpha )\equiv 0$ for $\forall \alpha \in (\bar{\alpha },1]$ and for $\forall \alpha \in [0,\bar{\alpha }]$, moreover $g(\alpha )\in C^2[0,\bar{\alpha }]$, then it is obvious that

$$\begin{aligned} \displaystyle \int \limits _0^1g(\alpha )d\alpha =J^T_{\alpha }g(\alpha )+O(\varDelta \alpha ^2), \end{aligned}$$

(5)

where

$$\begin{aligned} J^T_{\alpha }g(\alpha ):=\varDelta \alpha \left( \dfrac{g(\alpha _0)}{2}+ \displaystyle \sum \limits _{j=1}^{L-1}g(\alpha _j)+\dfrac{g(\alpha _L)}{2}\right) +O(\varDelta \alpha ^2), \end{aligned}$$

and $\varDelta \alpha =\bar{\alpha }/L,\ \alpha _0=\varDelta \alpha ^2,\ \alpha _L=\bar{\alpha }-\varDelta \alpha ^2,\quad \alpha _j=j\varDelta \alpha , j=1,2,\ldots ,L-1.$

To discrete the Caputo fractional derivative, we use L1 method [31]. If $\Vert \frac{\partial ^2 u(X,t)}{\partial t^2}\Vert _0$ is a bounded function on t, then

$$\begin{aligned} {_0^CD_t^\alpha }u(X,t_n)=\nabla _t^\alpha u(X,t_n)+O(\varDelta t^{2-\alpha }),\ 0<\alpha \le 1, \end{aligned}$$

(6)

where

$$\begin{aligned} \nabla _t^\alpha u(X,t_n):=\dfrac{\varDelta t^{-\alpha }}{\Gamma (2-\alpha )}\displaystyle \sum \limits _{j=0}^{n}b^\alpha _{n,j}u(X,t_{n-j}), \end{aligned}$$

and $b^\alpha _{n,0}=1,b^\alpha _{n,n}=-n^{1-\alpha }+(n-1)^{1-\alpha }, b^\alpha _{n,j}=(j+1)^{1-\alpha }-2j^{1-\alpha }+(j-1)^{1-\alpha },j=1,2,\ldots ,n-1.$

Let $u^n$ be the numerical solution of $u(X,t_n)$, by (5)–(6) we can obtain the semi-discrete variational formulation of problem (1)–(4): for each $n\ (n=1,2,\ldots ,N)$, find $u^n\in H^1_0(\Omega )$ such that

$$\begin{aligned} \left( J^T_{\alpha }(\omega (\alpha )\nabla _t^\alpha u^n),v\right) +B(u^n,v)=(F^n,v),\quad \forall v\in H_0^1(\Omega ), \end{aligned}$$

(7)

where $u^0:=\phi (X),F^n:=F(X,t_n)$. For bilinear form B(u, v), if $\Omega \in \mathbb {R}$, then

$$\begin{aligned} B(u,v):=K_x(u_x,v_x); \end{aligned}$$

(8)

and if $\Omega \in \mathbb {R}^2$, then

$$\begin{aligned} B(u,v):=K_x(u_x,v_x)+K_y(u_y,v_y). \end{aligned}$$

(9)

It is easy to know that the bilinear form is symmetrical, continuous and coercive, i.e., there exist constants $C_1,C_2$ such that

$$\begin{aligned} B(u,v)\le C_1\Vert u\Vert _1\cdot \Vert v\Vert _1,\quad B(u,u)\ge C_2\Vert u\Vert _1^2. \end{aligned}$$

(10)

Now we discuss the stability and convergence of semi-discrete scheme (7).

Theorem 1

The semi-discrete variational formulation (7) is unconditionally stable.

Proof

Suppose that $w^n$ is another solution of (7), and let $z^n=u^n-w^n$. Then

$$\begin{aligned} \left( J^T_{\alpha }(\omega (\alpha )\nabla _t^\alpha z^n),v\right) +B(z^n,v)=0. \end{aligned}$$

Taking $v=z^n$, by (10) we have

$$\begin{aligned} \left( J^T_{\alpha }(\omega (\alpha )\nabla _t^\alpha z^n),z^n\right) \le 0, \end{aligned}$$

i.e.,

$$\begin{aligned} \left( \varDelta \alpha \left( \dfrac{\omega (\alpha _0)\nabla _t^{\alpha _0} z^n}{2}+\sum \limits _{j=1}^{L-1}\omega (\alpha _j)\nabla _t^{\alpha _j} z^n+\dfrac{\omega (\alpha _L)\nabla _t^{\alpha _L} z^n}{2}\right) ,z^n\right) \le 0. \end{aligned}$$

(11)

If we denote

$$\begin{aligned} \mu _2=\dfrac{\omega (\alpha _0)\varDelta t^{-\alpha _0}}{2\Gamma (2-\alpha _0)}+\displaystyle \sum \limits _{j=1}^{L-1}\dfrac{\omega (\alpha _j)\varDelta t^{-\alpha _j}}{\Gamma (2-\alpha _j)}+\dfrac{\omega (\alpha _L)\varDelta t^{-\alpha _L}}{2\Gamma (2-\alpha _L)}, \end{aligned}$$

(12)

then (11) gives

$$\begin{aligned} \mu _2\Vert z^n\Vert ^2_0\le & {} -\dfrac{\omega (\alpha _0)\varDelta t^{-\alpha _0}}{2\Gamma (2-\alpha _0)}\displaystyle \sum \limits _{k=1}^nb_{n,k}^{\alpha _0}(z^{n-k},z^n)\\&\quad -\displaystyle \sum \limits _{j=1}^{L-1}\dfrac{\omega (\alpha _j)\varDelta t^{-\alpha _j}}{\Gamma (2-\alpha _j)}\displaystyle \sum \limits _{k=1}^nb_{n,k}^{\alpha _j}(z^{n-k},z^n) -\dfrac{\omega (\alpha _L)\varDelta t^{-\alpha _L}}{2\Gamma (2-\alpha _L)}\displaystyle \sum \limits _{k=1}^nb_{n,k}^{\alpha _L}(z^{n-k},z^n). \end{aligned}$$

By $-b^{\alpha _j}_{n,k}\ge 0,k\ge 1$ and the Cauchy–Schwarz inequality, we obtain

$$\begin{aligned} \mu _2\Vert z^n\Vert _0\le & {} -\dfrac{\omega (\alpha _0)\varDelta t^{-\alpha _0}}{2\Gamma (2-\alpha _0)} \displaystyle \sum \limits _{k=1}^nb_{n,k}^{\alpha _0}\Vert z^{n-k}\Vert _0\\&\quad -\,\displaystyle \sum \limits _{j=1}^{L-1}\dfrac{\omega (\alpha _j)\varDelta t^{-\alpha _j}}{\Gamma (2-\alpha _j)}\displaystyle \sum \limits _{k=1}^nb_{n,k}^{\alpha _j} \Vert z^{n-k}\Vert _0 -\dfrac{\omega (\alpha _L)\varDelta t^{-\alpha _L}}{2\Gamma (2-\alpha _L)}\displaystyle \sum \limits _{k=1}^nb_{n,k}^{\alpha _L}\Vert z^{n-k}\Vert _0. \end{aligned}$$

Since $-\sum \nolimits _{k=1}^nb_{n,k}^{\alpha _j}=1,j=0,1,\ldots ,L$, the mathematical induction leads to $\Vert z^n\Vert _0\le \Vert z^0\Vert _0$. Hence the semi-discrete scheme (7) is unconditionally stable. $\square$

Next we consider the convergence of semi-discrete scheme (7).

Theorem 2

Assume that u(X, t) is the exact solution to (1)–(4) with $\omega (\alpha ),{_0^CD_t^\alpha u(X_i,t)|_{t=t_n}}\in C^2[0,\bar{\alpha }]$ and $u_{tt}\in L^\infty (0,T;L^2(\Omega ))$. Then the numerical solution $u^n$ to (7) satisfies

$$\begin{aligned} \Vert u(X,t_n)-u^n\Vert _0\le C(\varDelta \alpha ^2+\varDelta t^{2-\bar{\alpha }+\varDelta \alpha ^2}), \end{aligned}$$

where $X_i\in \Omega$.

Proof

Since $\omega (\alpha ),{_0^CD_t^\alpha u(X_i,t)|_{t=t_n}} \in C^2[0,\bar{\alpha }]$ and $u_{tt}\in L^\infty (0,T;L^2(\Omega ))$, by [27, 31] it is easy to know

$$\begin{aligned} \left( J^T_{\alpha }\left( \omega (\alpha )\nabla _t^\alpha u(X,t_n)\right) ,v\right) +B\left( u(X,t_n),v\right) =(F^n,v)+(R_1^n,v),\ \forall v\in H_0^1(\Omega ), \end{aligned}$$

(13)

where

$$\begin{aligned} \Vert R_1^n\Vert _0\le \left\| J^T_{\alpha }\left( \omega (\alpha )\nabla _t^\alpha u(X,t_n)\right) -\int _0^1\left( \omega (\alpha ){_0^CD_t^\alpha } u(X,t)|_{t=t_n}\right) d\alpha \right\| _0\le C(\varDelta \alpha ^2+\varDelta t^{2-\alpha _L}). \end{aligned}$$

Let $\varepsilon ^n=u(X,t_n)-u^n$ and take $v=\varepsilon ^n$. Then by (7) and (13) we have

$$\begin{aligned} \left( \varDelta \alpha \left( \dfrac{\omega (\alpha _0)\nabla _t^{\alpha _0} \varepsilon ^n}{2}+\displaystyle \sum \limits _{j=1}^{L-1}\omega (\alpha _j) \nabla _t^{\alpha _j} \varepsilon ^n+\frac{\omega (\alpha _L)\nabla _t^{\alpha _L} \varepsilon ^n}{2}\right) ,\varepsilon ^n\right) \le (R_1^n,\varepsilon ^n). \end{aligned}$$

(14)

By (12) and $\Vert \varepsilon ^0\Vert _0=0$, (14) gives

$$\begin{aligned} \begin{aligned} \varDelta \alpha \mu _2\Vert \varepsilon ^n\Vert _0\le&-\varDelta \alpha \left( \dfrac{\omega (\alpha _0)\varDelta t^{-\alpha _0}}{2\Gamma (2-\alpha _0)}\displaystyle \sum \limits _{k=1}^{n-1}b_k^{\alpha _0}\Vert \varepsilon ^{n-k}\Vert _0+\displaystyle \sum \limits _{j=1}^{L-1}\dfrac{\omega (\alpha _j)\varDelta t^{-\alpha _j}}{\Gamma (2-\alpha _j)}\right. \\&\quad \left. \times \,\displaystyle \sum \limits _{k=1}^{n-1}b_k^{\alpha _j}\Vert \varepsilon ^{n-k}\Vert _0+\dfrac{\omega (\alpha _L)\varDelta t^{-\alpha _L}}{2\Gamma (2-\alpha _L)}\displaystyle \sum \limits _{k=1}^{n-1}b_k^{\alpha _L}\Vert \varepsilon ^{n-k}\Vert _0\right) +\Vert R_1^n\Vert _0. \end{aligned} \end{aligned}$$

(15)

Let

$$\begin{aligned} \mu _1^i=\dfrac{\omega (\alpha _0)\varDelta t^{-\alpha _0}i^{-\alpha _0}}{2\Gamma (1-\alpha _0)} +\displaystyle \sum \limits _{j=1}^{L-1}\dfrac{\omega (\alpha _j)\varDelta t^{-\alpha _j}i^{-\alpha _j}}{\Gamma (1-\alpha _j)}+\dfrac{\omega (\alpha _L)\varDelta t^{-\alpha _L}i^{-\alpha _L}}{2\Gamma (1-\alpha _L)}. \end{aligned}$$

(16)

By (15)–(16) we get

$$\begin{aligned} \varDelta \alpha \mu _1^1\Vert \varepsilon ^1\Vert _0\le \varDelta \alpha \mu _2\Vert \varepsilon ^1\Vert _0\le \Vert R_1^1\Vert _0, \end{aligned}$$

i.e.,

$$\begin{aligned} \Vert \varepsilon ^1\Vert _0\le \dfrac{1}{\varDelta \alpha \mu _1^1} \max \limits _{1\le n\le N}\Vert R_1^n\Vert _0. \end{aligned}$$

Now we suppose that

$$\begin{aligned} \Vert \varepsilon ^i\Vert _0\le \dfrac{1}{\varDelta \alpha \mu _1^i} \max \limits _{1\le n\le N}\Vert R_1^n\Vert _0 \end{aligned}$$

(17)

holds for $i\le p$. Let $n=p+1$. It follows from ${-}\sum \nolimits _{k=1}^nb_{n,k}^{\alpha _j}=1$ and (17) that (15) yields

$$\begin{aligned}&\varDelta \alpha \mu _2\Vert \varepsilon ^{p+1}\Vert _0\\&\quad \le -\varDelta \alpha \left( \dfrac{\omega (\alpha _0)\varDelta t^{-\alpha _0}}{2\Gamma (2-\alpha _0)}\displaystyle \sum \limits _{k=1}^{p}b_{p+1,k}^{\alpha _0} +\displaystyle \sum \limits _{j=1}^{L-1}\dfrac{\omega (\alpha _j)\varDelta t^{-\alpha _j}}{\Gamma (2-\alpha _j)}\sum \limits _{k=1}^{p}b_{p+1,k}^{\alpha _j}\right. \\&\qquad \left. +\,\dfrac{\omega (\alpha _L)\varDelta t^{-\alpha _L}}{2\Gamma (2-\alpha _L)} \displaystyle \sum \limits _{k=1}^{p}b_{p+1,k}^{\alpha _L}\right) \dfrac{1}{\varDelta \alpha \mu _1^p}\max \limits _{1\le n\le N}\Vert R_1^n\Vert _0 +\max \limits _{1\le n\le N}\Vert R_1^n\Vert _0\\&\quad \le \varDelta \alpha \left( \dfrac{\omega (\alpha _0)\varDelta t^{-\alpha _0}}{2\Gamma (2-\alpha _0)}\left( 1+b_{p+1,p+1}^{\alpha _0}\right) +\displaystyle \sum \limits _{j=1}^{L-1}\dfrac{\omega (\alpha _j)\varDelta t^{-\alpha _j}}{\Gamma (2-\alpha _j)}\left( 1+b_{p+1,p+1}^{\alpha _j}\right) \right. \\&\qquad \left. +\,\dfrac{\omega (\alpha _L)\varDelta t^{-\alpha _L}}{2\Gamma (2-\alpha _L)}\left( 1+b_{p+1,p+1}^{\alpha _L}\right) \right) \dfrac{1}{\varDelta \alpha \mu _1^{p+1}}\max \limits _{1\le n\le N}\Vert R_1^n\Vert _0 +\max \limits _{1\le n\le N}\Vert R_1^n\Vert _0. \end{aligned}$$

Hence we have

$$\begin{aligned} \begin{aligned}&\varDelta \alpha \mu _2\Vert \varepsilon ^{p+1}\Vert _0 \le \dfrac{\mu _2}{\mu _1^{p+1}}\max \limits _{1\le n\le N}\left\| R_1^n\right\| _0 +\left( \dfrac{\omega (\alpha _0)\varDelta t^{-\alpha _0}}{2\Gamma (2-\alpha _0)} b_{p+1,p+1}^{\alpha _0} +\displaystyle \sum \limits _{j=1}^{L-1}\dfrac{\omega (\alpha _j)\varDelta t^{-\alpha _j}}{\Gamma (2-\alpha _j)}\right. \\&\qquad \left. \times \, b_{p+1,p+1}^{\alpha _j}+\dfrac{\omega (\alpha _L) \varDelta t^{-\alpha _L}}{2\Gamma (2-\alpha _L)}b_{p+1,p+1}^{\alpha _L}\right) \dfrac{1}{\mu _1^{p+1}}\max \limits _{1\le n\le N}\left\| R_1^n\right\| _0+ \max \limits _{1\le n\le N}\left\| R_1^n\right\| _0. \end{aligned} \end{aligned}$$

(18)

Since

$$\begin{aligned} b_{p+1,p+1}^{\alpha _j}=-\left( (p+1)^{1-\alpha _j}-p^{1-\alpha _j}\right) \le -(1-\alpha _j)(p+1)^{-\alpha _j}, \end{aligned}$$

it is easy to show that (18) yields

$$\begin{aligned} \varDelta \alpha \mu _2\left\| \varepsilon ^{p+1}\right\| _0\le \dfrac{\mu _2 }{\mu _1^{p+1}}\max \limits _{1\le n\le N}\left\| R_1^n\right\| _0. \end{aligned}$$

Therefore the mathematical induction leads to

$$\begin{aligned} \left\| \varepsilon ^{p+1}\right\| _0\le \dfrac{1}{\varDelta \alpha \mu _1^{p+1}}\max \limits _{1\le n\le N}\left\| R_1^n\right\| _0. \end{aligned}$$

(19)

Note that $\varDelta t^{-\alpha _j}(p+1)^{-\alpha _j}\ge T^{-\alpha _j}$. It is obvious that

$$\begin{aligned} \varDelta \alpha \mu _1^{p+1}= & {} \varDelta \alpha \left[ \dfrac{\omega (\alpha _0)\varDelta t^{-\alpha _0}(p+1)^{-\alpha _0}}{2\Gamma (1-\alpha _0)} +\displaystyle \sum \limits _{j=1}^{L-1}\dfrac{\omega (\alpha _j)\varDelta t^{-\alpha _j}(p+1)^{-\alpha _j}}{\Gamma (1-\alpha _j)}+\dfrac{\omega (\alpha _L) \varDelta t^{-\alpha _L}(p+1)^{-\alpha _L}}{2\Gamma (1-\alpha _L)}\right] \\\ge & {} \dfrac{\varDelta \alpha }{2}\left[ \dfrac{\omega (\alpha _0)}{T^{\alpha _0} \Gamma (1-\alpha _0)}+\displaystyle \sum \limits _{j=1}^{L-1}\dfrac{\omega (\alpha _j)}{T^{\alpha _j}\Gamma (1-\alpha _j)}+\dfrac{\omega (\alpha _L)}{T^{\alpha _L} \Gamma (1-\alpha _L)}\right] \rightarrow \dfrac{1}{2}\displaystyle \int \limits _0^1 \dfrac{\omega (\alpha )(1-\alpha )}{T^\alpha \Gamma (2-\alpha )}d\alpha . \end{aligned}$$

Since $\omega (\alpha )\ge 0,\omega (\alpha )\in C^2[0,\bar{\alpha }]$, it is easy to know that there exists a positive constant C such that $\varDelta \alpha \mu _1^{p+1}\ge C$. Moreover, from $\alpha _L=\bar{\alpha }-\varDelta \alpha ^2$, we obtain

$$\begin{aligned} \Vert \varepsilon ^{p+1}\Vert _0\le C(\varDelta \alpha ^2+\varDelta t^{2-\alpha _L}) \le C(\varDelta \alpha ^2+\varDelta t^{2-\bar{\alpha }+\varDelta \alpha ^2}). \end{aligned}$$

$\square$

Next we consider the corresponding fully discrete finite element scheme. First we divide $\Omega$ into a number of subregions. Suppose that $S_h$ denotes a quasi-uniform partition on $\Omega$ with maximum grid parameter h. Then we define $X_h^K$ as the finite element space on $S_h$ with the basis functions of piecewise polynomials of order K as follows

$$\begin{aligned} X_h^K:=\{w_h\in H_0^1(\Omega )\cap C(\bar{\Omega }),w_h|_E=P_K(E),E\in S_h\}. \end{aligned}$$

(20)

Assume that $u_h^n\in X_h^K$ is an approximation of $u(X,t_n)$. Next we define the fully discrete finite element scheme of (7): for each $n\ (n=1,2,\ldots ,N)$, find $u_h^n\in X_h^K$ satisfying

$$\begin{aligned} \left( J_{\alpha }^T\omega (\alpha )\nabla _t^\alpha u_h^n,v_h\right) +B(u_h^n,v_h)=(F^n,v_h),\quad \forall v_h\in X_h^K, \end{aligned}$$

(21)

where $u^0_h\in X_h^K$ is a suitable approximation of u(X, 0).

For the finite element space $X_h^K$, we define a projection operator $P_h:H_0^1(\Omega )\rightarrow X_h^K$ such that $w\in H_0^1(\Omega )$ satisfies

$$\begin{aligned} B(P_hw,v_h)=B(w,v_h),\quad \forall v_h\in X_h^K. \end{aligned}$$

(22)

Then $P_h$ satisfies the following property [32].

Lemma 1

If $w\in H^s(\Omega )\cap H^1_0(\Omega ),1<s\le K+1$, then

$$\begin{aligned} \Vert P_hw-w\Vert _0\le Ch^s\Vert w\Vert _s. \end{aligned}$$

Now, we discuss the convergence of fully discrete finite element scheme (21).

Theorem 3

Assume that u(X, t) is the exact solution to (1)–(4) with $\omega (\alpha ),{_0^CD_t^\alpha u(X_i,t)}|_{t=t_n}\in C^2[0,\bar{\alpha }]$ and $u_{tt},{_0^CD_t^\alpha u}\in L^\infty (0,T;H^{K+1}(\Omega ))$. Then the numerical solution $u^n_h$ to (21) satisfies

$$\begin{aligned} \Vert u(X,t_n)-u^n_h\Vert _0\le C(\varDelta \alpha ^2+\varDelta t^{2-\bar{\alpha }+\varDelta \alpha ^2}+h^{K+1}). \end{aligned}$$

Proof

For the exact solution u(X, t) of problem (1)–(4), it is obvious that

$$\begin{aligned} \left( \int _0^1 \omega (\alpha ){_0^CD_t^\alpha u(X,t)|_{t=t_n}} d\alpha ,v_h\right) +B\left( u(X,t_n),v_h\right) =(F^n,v_h),\ \forall v_h\in X_h^K. \end{aligned}$$

(23)

Taking $\rho ^n=u(X,t_n)-P_h u(X,t_n), \theta ^n=P_hu(X,t_n)-u_h^n$, and subtracting (21) from (23), by (22) we have

$$\begin{aligned} \left( J_{\alpha }^T\left( \omega (\alpha )\nabla _t^\alpha \theta ^n\right) ,v_h\right) +B(\theta ^n,v_h)=-\left( J_{\alpha }^T\left( \omega (\alpha )\nabla _t^\alpha \rho ^n\right) ,v_h\right) -(r_1^n,v_h), \end{aligned}$$

(24)

where $r_1^n=\int _0^1 \omega (\alpha ){_0^CD_t^\alpha u(X,t)|_{t=t_n}} d\alpha -J_{\alpha }^T\left( \omega (\alpha )\nabla _t^\alpha u(X,t_n)\right) .$

By taking $v_h=\theta ^n$, it follows from (10) and (12) that (24) gives

$$\begin{aligned}&\varDelta \alpha \mu _2\Vert \theta ^n\Vert ^2_0\le -\varDelta \alpha \left( \dfrac{\omega (\alpha _0)\varDelta t^{-\alpha _0}}{2\Gamma (2-\alpha _0)}\displaystyle \sum \limits _{k=1}^nb_{n,k}^{\alpha _0} \theta ^{n-k}+\displaystyle \sum \limits _{j=1}^{L-1}\dfrac{\omega (\alpha _j)\varDelta t^{-\alpha _j}}{\Gamma (2-\alpha _j)}\displaystyle \sum \limits _{k=1}^nb_{n,k}^{\alpha _j} \theta ^{n-k}\right. \\&\quad \left. +\,\dfrac{\omega (\alpha _L)\varDelta t^{-\alpha _L}}{2\Gamma (2-\alpha _L)} \displaystyle \sum \limits _{k=1}^nb_{n,k}^{\alpha _L}\theta ^{n-k},\theta ^n\right) -(J_{\alpha }^T\omega (\alpha )\nabla _t^\alpha \rho ^n,\theta ^n)-(r_1^n,\theta ^n). \end{aligned}$$

By the Cauchy–Schwarz inequality, we obtain

$$\begin{aligned} \begin{aligned} \varDelta \alpha \mu _2\Vert \theta ^n\Vert _0\le&-\varDelta \alpha \left( \dfrac{\omega (\alpha _0)\varDelta t^{-\alpha _0}}{2\Gamma (2-\alpha _0)}\displaystyle \sum \limits _{k=1}^nb_{n,k}^{\alpha _0}\Vert \theta ^{n-k}\Vert _0+\displaystyle \sum \limits _{j=1}^{L-1}\dfrac{\omega (\alpha _j)\varDelta t^{-\alpha _j}}{\Gamma (2-\alpha _j)}\right. \\&\quad \left. \times \,\displaystyle \sum \limits _{k=1}^nb_{n,k}^{\alpha _j}\Vert \theta ^{n-k}\Vert _0 +\dfrac{\omega (\alpha _L)\varDelta t^{-\alpha _L}}{2\Gamma (2-\alpha _L)} \displaystyle \sum \limits _{k=1}^nb_{n,k}^{\alpha _L}\Vert \theta ^{n-k}\Vert _0\right) \\&\quad +\,\Vert J_{\alpha }^T\omega (\alpha )\nabla _t^\alpha \rho ^n\Vert _0+\Vert r_1^n\Vert _0. \end{aligned} \end{aligned}$$

(25)

Since $\omega (\alpha ),{_0^CD_t^\alpha u(X_i,t)}|_{t=t_n}\in C^2[0,\bar{\alpha }]$, and $u_{tt},{_0^CD_t^\alpha u}\in L^\infty (0,T;H^{K+1}(\Omega ))$, it is clear that

$$\begin{aligned} \left\| r_1^n\right\| _0\le C\left( \varDelta \alpha ^2+\varDelta t^{2-\bar{\alpha }+\varDelta \alpha ^2}\right) ,\quad \left\| J_{\alpha }^T(\omega (\alpha )\nabla _t^\alpha \rho ^n)\right\| _0\le C\left( h^{K+1}+\varDelta t^{2-\bar{\alpha }+\varDelta \alpha ^2}h^{K+1}\right) . \end{aligned}$$

Without loss of generality, we assume that $\Vert \theta ^0\Vert _0=0$. By a similar proof process to Theorem 2, (25) yields

$$\begin{aligned} \left\| \theta ^n\right\| _0\le C\left( \varDelta \alpha ^2+\varDelta t^{2-\bar{\alpha }+\varDelta \alpha ^2}+h^{K+1}\right) . \end{aligned}$$

Therefore, by Lemma 1 we obtain

$$\begin{aligned} \left\| u(X,t_n)-u^n_h\right\| _0\le C\left( \varDelta \alpha ^2+\varDelta t^{2-\bar{\alpha }+\varDelta \alpha ^2}+h^{K+1}\right) . \end{aligned}$$

$\square$

3 Numerical Scheme II for DOFDEs

For the above numerical scheme, we find that the convergence rate is low in time in comparison with the convergence rate in space. Therefore, in order to improve the convergence rate in time direction, it is necessary to develop some new methods. In this section, we suppose that $\phi (X)=0$ in (2) and the higher smoothness on u(X, t) in temporal direction is satisfied.

First we consider the integral $\int _0^1 g(\alpha )d\alpha$. If $g(\alpha )\equiv 0,\forall \alpha \in (\bar{\alpha },1]$ and , moreover $g(\alpha )\in C^4[0,\bar{\alpha }]$, then we discretize the integral by the modified compound Simpson formula

$$\begin{aligned} \int \limits _0^1g(\alpha )d\alpha =J^S_\alpha g(\alpha )+O(\varDelta \alpha ^4), \end{aligned}$$

(26)

where

$$\begin{aligned} J^S_\alpha g(\alpha ):=\dfrac{\varDelta \alpha }{3}\left( g(\alpha _0)+2 \sum \limits _{j=1}^{L-1}g(\alpha _{2j})+4\sum \limits _{j=1}^{L} g(\alpha _{2j-1})+g(\alpha _{2L})\right) \end{aligned}$$

and $\varDelta \alpha =\bar{\alpha }/(2L),\alpha _0=\varDelta \alpha ^4,\alpha _{2L}=\bar{\alpha }-\varDelta \alpha ^4,\alpha _j=j\varDelta \alpha ,j=1,2,\ldots ,2L-1.$

For the Caputo fractional derivative, we use the WSGD formula [33]. Define the space $\varphi ^{2+\alpha }(\mathbb {R})$ as

$$\begin{aligned} \varphi ^{2+\alpha }(\mathbb {R}):=\left\{ f|f\in L^1(\mathbb {R}), {_{-\infty } D_t^{2+\alpha }}f\in L^1(\mathbb {R}), and \int \limits _{-\infty }^{+\infty }|\omega |^{2+\alpha }|\mathcal {F}(\omega )|d\omega <+\infty \right\} , \end{aligned}$$

where $\mathcal {F}(\omega )$ is the Fourier transform of f(t), and ${_{-\infty } D_t^{2+\alpha }}$ is the Riemann–Liouville fractional derivative. Next we give a definition called as Condition $A^\alpha$.

Definition 1

For $w(t)\in [0,T]$ with $w(0)=0$, we let $\bar{w}(t)$ denote the extension of w(t) and satisfy

$$\begin{aligned}\bar{w}(t)= \begin{array}{ll} {\left\{ \begin{array}{ll} 0,&{}\quad t<0,\\ w(t),&{}\quad 0\le t\le T,\\ h(t),&{}\quad t< T\le 2T,\\ 0,&{}\quad t>2T. \end{array}\right. } \end{array} \end{aligned}$$

If there exists $\bar{w}(t)\in \varphi ^{2+\alpha }(\mathbb {R})$, then we call that w(t) satisfies the Condition $A^\alpha$.

For the Condition $A^\alpha$, more details can be find in [28]. By Ref.  [28, 33], we have the following theorem.

Theorem 4

If $w(t)\in [0,T]$ and satisfies the Condition $A^\alpha$, then

$$\begin{aligned} \begin{array}{lll} {_0^CD_t^\alpha }w(t)|_{t=t_n}=\varDelta _t^\alpha w(t_n)+O(\varDelta t^2), \end{array} \end{aligned}$$

(27)

where

$$\begin{aligned} \varDelta _t^\alpha w(t_n):=\varDelta t^{-\alpha }\displaystyle \sum \limits _{k=0}^{n}\lambda _k^\alpha w(t_{n-k}),\quad \lambda _0^\alpha =\left( 1+\dfrac{\alpha }{2}\right) g_0^\alpha ,\quad \lambda _k^\alpha =\left( 1+\dfrac{\alpha }{2}\right) g_k^\alpha -\dfrac{\alpha }{2}g_{k-1}^\alpha , \end{aligned}$$

and $g_k=(-1)^k\frac{\Gamma (\alpha +1)}{\Gamma (k+1)\Gamma (\alpha -l+1)},k=0,1,\ldots .$

By (26) and (27), we can develop another semi-discrete variational formulation of problem (1)–(4). Let $u^n$ be the numerical solution of $u(X,t_n)$ to (1)–(4): for each $n\ (n=1,2,\ldots ,N)$, find $u^n\in H_0^1(\Omega )$ such that

$$\begin{aligned} (J_{\alpha }^S(\omega (\alpha )\varDelta _t^\alpha u^n),v)+B(u^n,v)=(F^n,v),\quad \forall v\in H_0^1(\Omega ), \end{aligned}$$

(28)

where $u^0=0,F^n:=F(X,t_n)$, and the bilinear form B(u, v) is defined by (8)–(9).

For the above numerical scheme, we will discuss the stability and convergence. First we introduce the following lemma.

Lemma 2

[28, 34] The coefficients $\{\lambda _k^\alpha \}$ defined in Theorem 4 with vector $(v_0,v_1,\ldots ,v_m)$ satisfy

$$\begin{aligned} \sum \limits _{n=0}^m\left( \sum \limits _{k=0}^n \lambda _k^\alpha v_{n-k}\right) v_n\ge 0. \end{aligned}$$

By Lemma 2, we can obtain the stability and convergence of semi-discrete scheme (28).

Theorem 5

The semi-discrete scheme (28) is unconditionally stable.

Proof

Assume that $w^n$ is another solution of semi-discrete scheme (28). Let $z^n=u^n-w^n$. Then

$$\begin{aligned} \left( J_{\alpha }^S(\omega (\alpha )\varDelta _t^\alpha z^n),v\right) +B(z^n,v)=0. \end{aligned}$$

Taking $v=z^n$, by (10) we have

$$\begin{aligned} \left( J_{\alpha }^S(\omega (\alpha )\varDelta _t^\alpha z^n),z^n\right) +C_2\Vert z^n\Vert ^2_1\le 0. \end{aligned}$$

For the above inequality, summing it from $n=1$ to m, we obtain

$$\begin{aligned} \begin{aligned}&\dfrac{\varDelta \alpha }{3}\displaystyle \sum \limits _{n=1}^m \left( \omega (\alpha _0)\varDelta t^{-\alpha _0}\displaystyle \sum \limits _{k=0}^n \lambda ^{\alpha _0}_{k} z^{n-k}+2\displaystyle \sum \limits _{j=1}^{L-1} \omega (\alpha _{2j})\varDelta t^{-\alpha _{2j}}\displaystyle \sum \limits _{k=0}^n \lambda ^{\alpha _{2j}}_{k}z^{n-k}\right. \\&\quad \quad +\,\left. 4\displaystyle \sum \limits _{j=1}^{L}\omega (\alpha _{2j-1})\varDelta t^{-\alpha _{2j-1}}\displaystyle \sum \limits _{k=0}^n \lambda ^{\alpha _{2j-1}}_{k}z^{n-k}+\omega (\alpha _{2L})\varDelta t^{-\alpha _{2L}}\right. \\&\quad \quad \left. \times \,\displaystyle \sum \limits _{k=0}^n \lambda ^{\alpha _{2L}}_{k}z^{n-k},z^n\right) +C_2 \displaystyle \sum \limits _{n=1}^m\Vert z^n\Vert _1^2\le 0. \end{aligned} \end{aligned}$$

(29)

Let

$$\begin{aligned} \begin{aligned} \mu =&\dfrac{\varDelta \alpha }{3}\left( \omega (\alpha _0)\varDelta t^{-\alpha _0}\lambda ^{\alpha _0}_{0} +2\displaystyle \sum \limits _{j=1}^{L-1}\omega (\alpha _{2j})\varDelta t^{-\alpha _{2j}} \lambda ^{\alpha _{2j}}_{0}\right. \\&\quad \left. +\,4\displaystyle \sum \limits _{j=1}^{L}\omega (\alpha _{2j-1})\varDelta t^{-\alpha _{2j-1}}\lambda ^{\alpha _{2j-1}}_{0}+\omega (\alpha _{2L})\varDelta t^{-\alpha _{2L}}\lambda ^{\alpha _{2L}}_{0}\right) . \end{aligned} \end{aligned}$$

(30)

Then (29) yields

$$\begin{aligned}&\dfrac{\varDelta \alpha }{3}\displaystyle \sum \limits _{n=0}^m\left( \omega (\alpha _0)\varDelta t^{-\alpha _0}\displaystyle \sum \limits _{k=0}^n \lambda ^{\alpha _0}_{k} z^{n-k}+2\displaystyle \sum \limits _{j=1}^{L-1}\omega (\alpha _{2j})\varDelta t^{-\alpha _{2j}}\displaystyle \sum \limits _{k=0}^n \lambda ^{\alpha _{2j}}_{k}z^{n-k}\right. \\&\quad \quad +\,\left. 4\displaystyle \sum \limits _{j=1}^{L}\omega (\alpha _{2j-1})\varDelta t^{-\alpha _{2j-1}}\displaystyle \sum \limits _{k=0}^n \lambda ^{\alpha _{2j-1}}_{k}z^{n-k}+\omega (\alpha _{2L})\varDelta t^{-\alpha _{2L}}\right. \\&\quad \quad \left. \times \,\displaystyle \sum \limits _{k=0}^n \lambda ^{\alpha _{2L}}_{k}z^{n-k},z^n\right) +C_2 \displaystyle \sum \limits _{n=1}^m\Vert z^n\Vert _1^2\le \mu \Vert z^0\Vert _0^2. \end{aligned}$$

By Lemma 2 we have

$$\begin{aligned} C_2\sum \limits _{n=1}^m\Vert z^n\Vert _1^2\le \mu \Vert z^0\Vert _0^2. \end{aligned}$$

Since $\varDelta t^{\alpha _{2L}}\mu$ is bounded and $\varDelta t^{1-\alpha _{2L}}\le T^{1-\alpha _{2L}}$, we obtain

$$\begin{aligned} \varDelta t\sum \limits _{n=1}^m\Vert z^n\Vert _1^2\le C\varDelta t^{\alpha _{2L}}\sum \limits _{n=1}^m\Vert z^n\Vert _1^2 \le C\Vert z^0\Vert _0^2. \end{aligned}$$

$\square$

Theorem 6

Assume that u(X, t) is the exact solution to (1)–(4) with $\omega (\alpha ),{_0^CD_t^\alpha u(X_i,t)}|_{t=t_n}\in C^4[0,\bar{\alpha }]$ and $\Vert u\Vert _0$ satisfying the Condition $A^{\bar{\alpha }-\varDelta \alpha ^4}$. Then the numerical solution $u^n$ to (28) satisfies

$$\begin{aligned} \varDelta t\sum \limits _{n=1}^m\Vert u(X,t_n)-u^n\Vert _1\le C(\varDelta \alpha ^4+\varDelta t^2),\ m=1,2,\ldots ,N. \end{aligned}$$

Proof

Let $\varepsilon ^n=u(X,t_n)-u^n$. By (28) we have

$$\begin{aligned} \left( J_{\alpha }^S(\omega (\alpha )\varDelta _t^\alpha \varepsilon ^n),v\right) +B(\varepsilon ^n,v)=(R_2^n,v), \end{aligned}$$

and it is easy to know that

$$\begin{aligned} \Vert R_2^n\Vert _0\le \left\| \int _0^1\omega (\alpha ){_0^CD_t^\alpha } u(X,t)|_{t=t_n}d\alpha -J_{\alpha }^S\left( \omega (\alpha )\varDelta _t^\alpha u(X,t_n)\right) \right\| _0\le C(\varDelta \alpha ^4+\varDelta t^2). \end{aligned}$$

Since $\Vert \varepsilon ^n\Vert _0^2\le C_0\Vert \varepsilon ^n\Vert _1^2$, taking $v=\varepsilon ^n$ and $C=C_2/C_0$ yields

$$\begin{aligned}&\left( J_{\alpha }^S\left( \omega (\alpha )\varDelta _t^\alpha \varepsilon ^n\right) ,\varepsilon ^n\right) +C_2\Vert \varepsilon ^n\Vert _1^2\le \Vert R_2^n\Vert _0\Vert \varepsilon ^n\Vert _0\\&\quad \le \,\dfrac{1}{2 C}\left\| R_2^n\right\| _0^2+\dfrac{C_2}{2}\Vert \varepsilon ^n\Vert _1^2. \end{aligned}$$

Therefore we obtain

$$\begin{aligned} \left( J_{\alpha }^S\left( \omega (\alpha )\varDelta _t^\alpha \varepsilon ^n\right) ,\varepsilon ^n\right) +\dfrac{C_2}{2}\Vert \varepsilon ^n\Vert _1^2\le \dfrac{1}{2 C}\Vert R_2^n\Vert _0^2. \end{aligned}$$

(31)

Summing (31) from $n=1$ to m, we have

$$\begin{aligned} \sum \limits _{n=1}^m\left( J_{\alpha }^S\left( \omega (\alpha )\varDelta _t^\alpha \varepsilon ^n\right) ,\varepsilon ^n\right) +\dfrac{C_2}{2}\sum \limits _{n=1}^m\left\| \varepsilon ^n\right\| _1^2\le \dfrac{1}{2C}\sum \limits _{n=1}^m\left\| R_2^n\right\| _0^2. \end{aligned}$$

(32)

By $(\varepsilon ^0,\varepsilon ^0)=0$, and Lemma 2, it is easy to know

$$\begin{aligned} \sum \limits _{n=1}^m\left( J_{\alpha }^S\left( \omega (\alpha )\varDelta _t^\alpha \varepsilon ^n\right) ,\varepsilon ^n\right) \ge 0. \end{aligned}$$

Hence, by (32) we have

$$\begin{aligned} \left( \displaystyle \sum \limits _{n=1}^m\Vert \varepsilon ^n\Vert _1\right) ^2\le m\displaystyle \sum \limits _{n=1}^m\Vert \varepsilon ^n\Vert _1^2 \le \dfrac{m}{CC_2}\displaystyle \sum \limits _{n=1}^m\Vert R_2^n\Vert _0^2\le \dfrac{m^2}{CC_2}\left( \varDelta \alpha ^4+\varDelta t^2\right) ^2. \end{aligned}$$

Since $\varDelta tm\le T$, we obtain

$$\begin{aligned} \varDelta t\sum \limits _{n=1}^m\Vert \varepsilon ^n\Vert _1\le C\left( \varDelta \alpha ^4+\varDelta t^2\right) . \end{aligned}$$

$\square$

Now we develop the corresponding fully discrete scheme. Assume that $u^n_h\in X_h^K$ is the approximation of $u(X,t_n)$. We define the fully discrete finite element scheme of (28): for each $n\ (n=1,2,\ldots ,N)$, find $u_h^n\in X_h^K$ satisfying

$$\begin{aligned} \left( J_{\alpha }^S(\omega (\alpha )\varDelta _t^\alpha u_h^n),v_h\right) +B(u_h^n,v_h)=(F^n,v_h),\quad \forall v_h\in X_h^K, \end{aligned}$$

(33)

where $u^0_h\in X_h^K$ is a suitable approximation of u(X, 0).

Theorem 7

Assume that u(X, t) is the exact solution to (1)–(4) with $\omega (\alpha ),{_0^CD_t^\alpha u(X_i,t)}|_{t=t_n}\in C^4[0,\bar{\alpha }]$ and $\Vert u\Vert _{0},\Vert u\Vert _{K+1}$ satisfying the Condition $A^{\bar{\alpha }-\varDelta \alpha ^4}$. Then the numerical solution $u^n_h$ to (33) satisfies

$$\begin{aligned} \varDelta t\sum \limits _{n=1}^m\Vert u(X,t_n)-u_h^n\Vert _0\le C(\varDelta \alpha ^4+\varDelta t^2+h^{K+1}),\quad m=1,2,\ldots ,N. \end{aligned}$$

Proof

Suppose that u(X, t) is the exact solution of (1)–(4). Then we have

$$\begin{aligned} (J_{\alpha }^S\omega (\alpha )\varDelta _t^\alpha u(X,t_n),v_h)+B(u(X,t_n),v_h)=(F^n,v_h)+(r_2^n,v_h),\quad \forall v_h\in X_h^K, \end{aligned}$$

(34)

where

$$\begin{aligned} r_2^n=J_{\alpha }^S(\omega (\alpha )\varDelta _t^\alpha u(X,t_n))-\int _0^1\omega (\alpha ){_0^CD_t^\alpha } u(X,t)|_{t=t_n}d\alpha . \end{aligned}$$

Subtracting (33) from (34), and taking $\rho ^n=u(t_n)-P_hu(t_n), \theta ^n=P_hu(t_n)-u_h^n$, by (22) we obtain

$$\begin{aligned} \left( J_{\alpha }^S(\omega (\alpha )\varDelta _t^\alpha \theta ^n),v_h\right) +B(\theta ^n,v_h)=-\left( J_{\alpha }^S(\omega (\alpha )\varDelta _t^\alpha \rho ^n),v_h\right) +(r_2^n,v_h). \end{aligned}$$

(35)

Since $\sum \nolimits _{n=0}^m\left( J_{\alpha }^S\left( \omega (\alpha )\varDelta _t^\alpha \theta ^n\right) ,\theta ^n\right) \ge 0$ and $\Vert \theta ^0\Vert _0=0$, taking $v_h=\theta ^n$ and summing (35) from $n=1$ to m yield

$$\begin{aligned} \displaystyle \sum \limits _{n=1}^m\Vert \theta ^n\Vert _1^2\le & {} -\displaystyle \sum \limits _{n=1}^m\left( J_{\alpha }^S\left( \omega (\alpha )\varDelta _t^\alpha \rho ^n\right) , \theta ^n\right) +\displaystyle \sum \limits _{n=1}^m(r_2^n,\theta ^n)\\\le & {} \displaystyle \sum \limits _{n=1}^m\left( \Vert J_{\alpha }^S\left( \omega (\alpha ) \varDelta _t^\alpha \rho ^n\right) \Vert _0+\Vert r_2^n\Vert _0\right) \Vert \theta ^n\Vert _0\\\le & {} \left( \displaystyle \sum \limits _{n=1}^m\left( \Vert J_{\alpha }^S \left( \omega (\alpha )\varDelta _t^\alpha \rho ^n\right) \Vert _0+\Vert r_2^n\Vert _0\right) ^2 \right) ^{\frac{1}{2}}\left( \displaystyle \sum \limits _{n=1}^m \Vert \theta ^n\Vert ^2_0\right) ^{\frac{1}{2}}. \end{aligned}$$

Note that $\Vert \theta ^n\Vert _0^2\le C\Vert \theta ^n\Vert _1^2$ and

$$\begin{aligned} \left\| J_{\alpha }^S\left( \omega (\alpha )\varDelta _t^\alpha \rho ^n\right) \right\| _0+\left\| r_2^n\right\| _0\le & {} C\left\{ \left\| \int _0^1\omega (\alpha ){_0^CD_t^\alpha }\rho ^nd\alpha \right\| _0 +\varDelta \alpha ^4+\varDelta t^2\right\} \\\le & {} C\left\{ \varDelta \alpha ^4+\varDelta t^2+h^{K+1}\right\} . \end{aligned}$$

Therefore we have

$$\begin{aligned} \displaystyle \sum \limits _{n=1}^m\Vert \theta ^n\Vert _1\le & {} \sqrt{m} \left( \displaystyle \sum \limits _{n=1}^m\Vert \theta ^n\Vert _1^2\right) ^{\frac{1}{2}}\\\le & {} \sqrt{m}\left( \displaystyle \sum \limits _{n=1}^m\left( \left\| \int _0^1\omega (\alpha ){_0^CD_t^\alpha }\rho ^nd\alpha \right\| _0 +\Vert r_2^n\Vert _0\right) ^2\right) ^{\frac{1}{2}}\\\le & {} Cm\left\{ \varDelta \alpha ^4+\varDelta t^2+h^{K+1}\right\} . \end{aligned}$$

Since $m\varDelta t\le T$, the above inequality gives

$$\begin{aligned} \varDelta t\sum \limits _{n=1}^m\Vert \theta ^n\Vert _1\le C\left\{ \varDelta \alpha ^4 +\varDelta t^2+h^{K+1}\right\} . \end{aligned}$$

Furthermore we obtain

$$\begin{aligned} \varDelta t\displaystyle \sum \limits _{n=1}^m\left\| u(X,t_n)-u_h^n\right\| _0\le & {} C\varDelta t\displaystyle \sum \limits _{n=1}^m\left( \left\| \rho ^n\right\| _0+\left\| \theta ^n\right\| _1\right) \\\le & {} C\left( \varDelta \alpha ^4+\varDelta t^2+h^{K+1}\right) . \end{aligned}$$

$\square$

4 An Approach to Improving Convergence Rate in Time

In the above section, we have obtained the effective numerical scheme for DOFDEs with high order convergence rate in time. In this section, we will introduce a novel discrete scheme of the Caputo fractional derivative. By this discrete scheme, if $\bar{\alpha }<d \ (d\approx 0.373866584107526)$, then we can develop a new numerical scheme for DOFDEs. This will be an important supplement for finite difference/finite element method to solve DOFDEs with higher convergence rate in time.

For the Caputo fractional derivative $_0^CD_t^\alpha f(t)$, we suppose that $f(t_0),f(t_{1/2}),f(t_1),f(t_2)$ and $f(t_3)$ are known. Let $L_{f,0}^1$ denote the linear Lagrange function of f(t) on $[t_0,t_1]$, and $L_{f,i}^2$ denote the quadratic Lagrange function of f(t) on $[t_{i-1},t_{i+1}],i\ge 1$. For $n\ge 4$, we have

$$\begin{aligned}&{_0^CD_t^\alpha }f(t)|_{t=t_n}\\&\quad =\displaystyle \int \limits _{t_0}^{t_1}\dfrac{(t_n-\tau )^{-\alpha }}{\Gamma (1-\alpha )}f'(\tau )d\tau +\displaystyle \sum \limits _{j=1}^{n-1} \displaystyle \int \limits _{t_{j}}^{t_{j+1}}\dfrac{(t_n-\tau )^{-\alpha }}{\Gamma (1-\alpha )}f'(\tau )d\tau \\&\quad =\displaystyle \int \limits _{t_0}^{t_1}\dfrac{(t_n-\tau )^{-\alpha }}{\Gamma (1-\alpha )}{L^1_{f,0}}'(\tau )d\tau +\displaystyle \sum \limits _{j=1}^{n-1} \displaystyle \int \limits _{t_{j}}^{t_{j+1}}\dfrac{(t_n-\tau )^{-\alpha }}{\Gamma (1-\alpha )}{L^2_{f,j}}'(\tau )d\tau +R^n_C,\quad n\ge 4, \end{aligned}$$

where

$$\begin{aligned} R^n_C= & {} \displaystyle \int \limits _{t_0}^{t_1}\dfrac{(t_n-\tau )^{-\alpha }}{\Gamma (1-\alpha )}\left( f'(\tau )-{L^1_{f,0}}'(\tau )\right) d\tau +\displaystyle \sum \limits _{j=1}^{n-1}\displaystyle \int \limits _{t_{j}}^{t_{j+1}} \dfrac{(t_n-\tau )^{-\alpha }}{\Gamma (1-\alpha )}\left( f'(\tau )-{L^2_{f,j}}'(\tau ) \right) d\tau \\= & {} -\displaystyle \int \limits _{t_0}^{t_1}\dfrac{\alpha (t_n-\tau )^{-\alpha -1}}{\Gamma (1-\alpha )}\left( f(\tau )-{L^1_{f,0}}(\tau )\right) d\tau -\displaystyle \sum \limits _{j=1}^{n-1}\displaystyle \int \limits _{t_{j}}^{t_{j+1}} \dfrac{\alpha (t_n-\tau )^{-\alpha -1}}{\Gamma (1-\alpha )}\left( f(\tau )-{L^2_{f,j}} (\tau )\right) d\tau . \end{aligned}$$

Therefore it is easy to know

$$\begin{aligned}&{_0^CD_t^\alpha }f(t)|_{t=t_n}\\&\quad =\left[ \left( \dfrac{-3t_{n}^{1-\alpha }-t_{n-1}^{1-\alpha }}{\varDelta t\Gamma (2-\alpha )}+\dfrac{4t_{n}^{2-\alpha }-4t_{n-1}^{2-\alpha }}{\varDelta t^2\Gamma (3-\alpha )}\right) f(t_0)+\left( \dfrac{4t_{n}^{1-\alpha } +4t_{n-1}^{1-\alpha }}{\varDelta t\Gamma (2-\alpha )}-\dfrac{8t_{n}^{2-\alpha } -8t_{n-1}^{2-\alpha }}{\varDelta t^2\Gamma (3-\alpha )}\right) f(t_{1/2})\right. \\&\qquad \left. +\,\left( \dfrac{-t_{n}^{1-\alpha }-3t_{n-1}^{1-\alpha }}{\varDelta t^2\Gamma (2-\alpha )}+\dfrac{4t_{n}^{2-\alpha }-4t_{n-1}^{2-\alpha }}{\varDelta t^2\Gamma (3-\alpha )}\right) f(t_1)\right] +\displaystyle \sum \limits _{j=1}^{n-1}\left[ \left( \dfrac{-t_{n-j}^{1-\alpha } -t_{n-j-1}^{1-\alpha }}{2\varDelta t\Gamma (2-\alpha )}+\dfrac{t_{n-j}^{2-\alpha } -t_{n-j-1}^{2-\alpha }}{\varDelta t^2\Gamma (3-\alpha )}\right) f(t_{j-1)}\right. \\&\qquad \left. -\,2\left( \dfrac{-t_{n-j-1}^{1-\alpha }}{\varDelta t\Gamma (2-\alpha )} +\dfrac{t_{n-j}^{2-\alpha }-t_{n-j-1}^{2-\alpha }}{\varDelta t^2\Gamma (3-\alpha )}\right) f(t_j)+\left( \dfrac{t_{n-j}^{1-\alpha }-3t_{n-j-1}^{1-\alpha }}{2\varDelta t^2 \Gamma (2-\alpha )}+\dfrac{t_{n-j}^{2-\alpha }-t_{n-j-1}^{2-\alpha }}{\varDelta t^2 \Gamma (3-\alpha )}\right) f(t_{j+1})\right] +R_C^n. \end{aligned}$$

Furthermore we obtain

$$\begin{aligned} {_0^CD_t^\alpha }f(t)|_{t=t_n}=\bar{\varDelta }_t^\alpha f(t_n)+R_C^n,\ n\ge 4, \end{aligned}$$

(36)

where $\bar{\varDelta }_t^\alpha f(t_n):=\displaystyle \sum \nolimits _{k=0}^n\gamma _k^\alpha f(t_{n-k})+\gamma _{n-1/2}^\alpha f(t_{1/2})$ and

$$\begin{aligned} \gamma _0^\alpha= & {} \dfrac{t_1^{1-\alpha }}{2\varDelta t\Gamma (2-\alpha )} +\dfrac{t_1^{2-\alpha }}{\varDelta t^2\Gamma (3-\alpha )},\gamma _1^\alpha =\dfrac{t_2^{1-\alpha }-3t_1^{1-\alpha }}{2\varDelta t\Gamma (2-\alpha )} +\dfrac{t_2^{2-\alpha }-3t_1^{2-\alpha }}{\varDelta t^2\Gamma (3-\alpha )},\\ \gamma _2^\alpha= & {} \dfrac{t_3^{1-\alpha }-3t_2^{1-\alpha }+3t_1^{1-\alpha }}{2\varDelta t\Gamma (2-\alpha )}+\dfrac{t_3^{2-\alpha }-3t_2^{2-\alpha }+3t_1^{2-\alpha }}{\varDelta t^2\Gamma (3-\alpha )},\\ \gamma _{n-1}^\alpha= & {} \dfrac{-2t_n^{1-\alpha }-6t_{n-1}^{1-\alpha } +3t_{n-2}^{1-\alpha }-t_{n-3}^{1-\alpha }}{2\varDelta t\Gamma (2-\alpha )} +\dfrac{4t_n^{2-\alpha }-6t_{n-1}^{2-\alpha }+3t_{n-2}^{2-\alpha } -t_{n-3}^{2-\alpha }}{\varDelta t^2\Gamma (3-\alpha )},\\ \gamma _{n-1/2}^\alpha= & {} \dfrac{4t_n^{1-\alpha }+4t_{n-1}^{1-\alpha }}{\varDelta t\Gamma (2-\alpha )}-\dfrac{8t_n^{2-\alpha }-8t_{n-1}^{2-\alpha }}{\varDelta t^2\Gamma (3-\alpha )},\gamma _{n}^\alpha =\dfrac{-6t_n^{1-\alpha } -3t_{n-1}^{1-\alpha }-t_{n-2}^{1-\alpha }}{2\varDelta t\Gamma (2-\alpha )} \\+ & {} \dfrac{4t_n^{2-\alpha }-3t_n^{2-\alpha }-t_{n-1}^{2-\alpha }}{\varDelta t^2\Gamma (3-\alpha )},\\ \gamma _{n-j}^\alpha= & {} \dfrac{t_{n-j+1}^{1-\alpha }-3t_{n-j}^{1-\alpha } +3t_{n-j-1}^{1-\alpha }-t_{n-j-2}^{1-\alpha }}{2\varDelta t\Gamma (2-\alpha )} +\dfrac{t_{n-j+1}^{2-\alpha }-3t_{n-j}^{2-\alpha }+3t_{n-j-1}^{2-\alpha } -t_{n-j-2}^{2-\alpha }}{\varDelta t^2\Gamma (3-\alpha )},\\ j= & {} 2,3,\ldots ,n-3. \end{aligned}$$

We note that

$$\begin{aligned} |f(t)-{L^2_{f,j}}(t)|\le C|f'''(\xi _j)|\varDelta t^3,\ t,\xi _0\in (t_{0},t_{1}),\ and\ t,\xi _j\in (t_{j-1},t_{j+1}),\quad j\ge 1, \end{aligned}$$

thus it is clear that

$$\begin{aligned} |R^n_C|\le C\varDelta t^{3-\alpha }. \end{aligned}$$

To implement the approximation (36), we need to know the initial values $f(t_{1/2}),f(t_1),f(t_2)$ and $f(t_3)$. For convenience, we let N be an even number. Suppose that time step $\varDelta t=T/N$ and $t_k=k\varDelta t$. Then we will employ the scheme (6) to compute $_0^CD_t^\alpha f(t)$ with time step $\varDelta t_1:=\varDelta t/N$ on time domain $[t_0,t_3]$. By this way, we can obtain the numerical solutions of $f(t_{1/2}),f(t_1),f(t_2),f(t_3)$ with convergence rate $4-2\alpha$. Another way is to use the Richarson extrapolation method [35]. We compute the numerical solutions of $f(t_{1/2}),f(t_1),f(t_2),f(t_3)$ by scheme (6) with time step $\varDelta t_1:=\varDelta t/2$ and $\varDelta t_2:=\varDelta t/4$ respectively. Then the Richarson extrapolation technique will give the numerical solutions of $f(t_{1/2}),f(t_1),f(t_2),f(t_3)$ with high convergence rate.

Similar to Sects. 2 and 3, we can use (36) to develop a finite difference/finite element scheme with higher order in time for DOFDEs. Assume that $u^n_h\in X_h^K$ is the approximation of $u(X,t_n)$. Then we define the fully discrete finite element scheme: for each $n\ (n=4,5,\ldots ,N)$, find $u_h^n\in X_h^K$ satisfying

$$\begin{aligned} (J_{\alpha }^S\omega (\alpha )\bar{\varDelta }_t^\alpha u_h^n,v_h)+B(u_h^n,v_h)=(F^n,v_h),\quad \forall v_h\in X_h^K, \end{aligned}$$

(37)

where $F^n:=F(X,t_n)$, the bilinear form B(u, v) is defined by (8)–(9), $u^0_h\in X_h^K$ is a suitable approximation of u(X, 0). For scheme (21), the initial values $u^{1/2}_h, u^1_h, u^2_h, u^3_h$ can be obtained by the above similar method. If $\alpha <d\ (d\approx 0.373866584107526)$, then it is easy to check that the coefficient $\gamma _j^\alpha \le 0,j=1,2,\ldots ,n$. Therefore, by the similar discussion to Sect. 2, the numerical scheme (37) is unconditionally stable, and the convergence rate will be $O(\varDelta \alpha ^4+\varDelta t^{3-\bar{\alpha }+\varDelta \alpha ^4}+h^{K+1})$ based on L2-norm.

5 Numerical Experiments

In this section, we will give some numerical examples to prove the correctness of our theoretical analysis proposed in the above sections. Here we choose the finite element space $X^1_h$ defined in (20) with linear Lagrange polynomials. In the first example, we will solve DOFDEs on one-dimensional domain by the obtained numerical schemes and show some numerical results in Tables 1, 2, 3, and 4. In the second example, the DOFDEs on two-dimensional domains will be solved, and some numerical results will be shown in Tables 5, 6, 7, and 8.

Example 1

Consider the one-dimensional distributed-order fractional diffusion equations

$$\begin{aligned} \mathcal {D}^\omega _t u(x,t)=2\frac{\partial ^2 u}{\partial x^2}+f(x,t),\ (x,t)\in (0,0.5)\times (0,0.5]. \end{aligned}$$

Case 1 Suppose that $\omega (\alpha )=\Gamma (5-\alpha ),u(x,0)=0,u(0,t)=u(0.5,t)=0$ and

$$\begin{aligned} f(x,t)=10^2(24t^4-24t^3)/\ln (t)\sin 2\pi x+8\pi ^2\cdot 10^2t^4\sin 2\pi x. \end{aligned}$$

Then the exact solution is $u(x,t)=10^2t^4\sin 2\pi x$.

Case 2 Suppose that $\omega (\alpha )= \begin{array}{ll} {\left\{ \begin{array}{ll} \Gamma (4-\alpha ),&{}\quad 0\le \alpha \le 0.3\\ 0, &{}\quad else \end{array}\right. } \end{array}$, $u(x,0)=\sin 2\pi x,u(0,t)=u(0.5,t)=0$ and

$$\begin{aligned} f(x,t)=10^4(6t^3-6t^{2.7})/\ln (t)\sin 2\pi x+8\pi ^2(10^4t^3+1)\sin 2\pi x. \end{aligned}$$

Then the exact solution is $u(x,t)=(10^4t^3+1)\sin 2\pi x$.

Here we choose linear Lagrange piecewise polynomials in $X_h^1$. In Tables 1 and 2, we show the errors and convergence rates on scheme (21) and scheme (33) for Case 1 with different space and time steps, respectively. In Tables 3 and 4, we list the errors and convergence rates on scheme (21) and scheme (37) for Case 2 with different space and time steps, respectively. By Tables 1, 2, 3, and 4, we can show that the obtained results are consistent with our theoretical analysis.

Table 1 Errors and convergence rates for Example 1 on Case 1 with different spatial steps

Table 2 Errors and convergence rates for Example 1 on Case 1 with different temporal steps

Table 3 Errors and convergence rates for Example 1 on Case 2 with different spatial steps

Table 4 Errors and convergence rates for Example 1 on Case 2 with different temporal steps

Example 2

Consider the two-dimensional distributed-order fractional diffusion equations

$$\begin{aligned} \mathcal {D}^\omega _t u(x,y,t)=2\frac{\partial ^2 u}{\partial x^2}+3\frac{\partial ^2 u}{\partial y^2}+f(x,y,t),\ (x,y,t)\in \Omega \times (0,0.5]. \end{aligned}$$

Case 1 Suppose that $\Omega =(0,1)\times (0,1),\omega (\alpha )=\Gamma (5-\alpha ), u(x,y,0)=0,u(x,y,t)|_{\partial \Omega }=0$ and

$$\begin{aligned} f(x,y,t)=10(24t^4-24t^3)/\ln (t)\sin \pi x\sin \pi y+5\pi ^2\cdot 10t^4\sin \pi x\sin \pi y. \end{aligned}$$

Then the exact solution is $u(x,y,t)=10t^4\sin \pi x\sin \pi y$.

Case 2 Suppose that $\Omega =(0,0.1)\times (0,0.1),\omega (\alpha )= {\left\{ \begin{array}{ll} \Gamma (4-\alpha ),0\le \alpha \le 0.36\\ 0, else \end{array}\right. }$, $u(x,y,0)=\sin 10\pi x\sin 10\pi y,$ $u(x,y,t)|_{\partial \Omega }=0$ and

$$\begin{aligned} f(x,y,t)=60(t^3-t^{2.64})/\ln (t)\sin 10\pi x\sin 10\pi y + 500\pi ^2(10t^3+1)\sin 10\pi x\sin 10\pi y. \end{aligned}$$

Then the exact solution is $u(x,y,t)=(10t^3+1)\sin 10\pi x\sin 10\pi y$.

Here we choose linear Lagrange piecewise polynomials in $X_h^1$. In Tables 5 and 6, we show the errors and convergence rates on scheme (21) and scheme (33) for Case 1 with different space steps and time steps, respectively. In Tables 7 and 8, we give the errors and convergence rates on scheme (21) and scheme (37) for Case 2 with different space steps and time steps, respectively. By these tables, the correctness of our theoretical analysis is verified.

Table 5 Errors and convergence rates for Example 2 on Case 1 with different spatial steps

Table 6 Errors and convergence rates for Example 2 on Case 1 with different temporal steps

Table 7 Errors and convergence rates for Example 2 on Case 2 with different spatial steps

Table 8 Errors and convergence rates for Example 2 on Case 2 with different temporal steps

6 Conclusions

In this paper, we consider the finite difference/finite element methods for problem (1)–(4). Two unconditionally stable numerical schemes are developed. The first numerical scheme is developed with low smoothness requirements on u(X, t) in temporal direction. However, the convergence rate of this scheme is low in time. In order to improve the convergence, if u(X, t) satisfies the high smoothness condition in temporal direction and $u(X,0)=0$, then we develop the second numerical scheme with convergence rate 2 in time. As a supplement, if $\bar{\alpha }<d\ (d\approx 0.373866584107526)$ in problem (1)–(4), then a new approach is presented to improve further the time convergence rate of our methods by introducing a novel discrete scheme of the Caputo fractional derivative. To discuss the stabilities and convergences of these numerical schemes, the mathematical induction is used in the first numerical scheme, and the coefficient property of the WSGD method is considered in the second numerical scheme. Finally, we give some numerical examples to show the validity of numerical schemes and verify the correctness of our theoretical analysis. We believe that these work will enrich the finite difference/finite element methods for DOFDEs.