Introduction

Shape memory alloys (SMAs) are a special class of intermetallic alloys that can recover large, seemingly permanent, strains—an order of magnitude greater than those in traditional intermetallic alloys—when subjected to appropriate thermomechanical inputs. A reversible, diffusionless, solid-to-solid, phase transformation between the material’s high-temperature, high-symmetry austenite and low-temperature, low-symmetry martensite crystalline phases is the physical mechanism behind this phenomenon. Two key behaviors result from this transformation—the shape memory effect (SME) and pseudoelasticity. The former refers to the ability of the material to recover transformation strains via heating from a deformed shape in martensite to a remembered, austenitic one while the latter is associated with the large, hysteretic stress–strain excursions experienced by SMAs at a sufficiently high temperature [1].

Since their discovery in the 1960s, SMAs have been predominantly used in pseudoelastic biomedical devices (such as endovascular stents, dental appliances, orthopedic implants and surgical instruments) [2–5]. However, in today’s technological landscape, there is a growing importance of SMAs for commercial applications involving high power output solid-state actuators in non-biomedical applications such as aeronautics and transportation. Solid-state SMA actuators are capable of performing significant amount of mechanical work when subjected to temperature changes, usually via joule heating. The work output per unit volume of SMA-based actuators exceeds that of other electromagnetic or thermal actuators (such as piezoelectric or thermopneumatic) and are therefore a desirable alternative when large actuation forces and a small volume are required and thermodynamic efficiency is not important [1, 6–8]. Some of the notable engineering applications that make use of SMA actuators in the aerospace industry are the Smart Wing Program by a collaboration of DARPA, AFRL, and Northrop Grumman [9], NASA’s Smart Aircraft and Marine Propulsion System demonstration (SAMPSON) [10], and the Boeing variable geometry chevron [11].

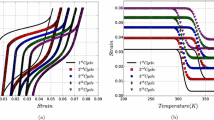
Reliable and safe design of SMA actuators requires understanding of the fracture properties of SMAs and the potential impact of macroscopic cracks on their functional and structural response. Owing to their unique thermomechanical properties, fracture response of SMAs is more complex than that of traditional structural metals and metallic alloys due to the reversibility of phase transformation, detwinning and reorientation of martensitic variants, the possibility of dislocation and transformation-induced plasticity, and the strong thermomechanical coupling [12]. Although there is a considerable body of theoretical and experimental work dedicated to address the problem of fracture and crack growth in SMAs subjected to mechanical loading at nominally isothermal conditions [13–33], there is a dearth of literature related to the fracture behavior of SMAs under combined thermomechanical loading. As recently observed, notched NiTi SMA specimens may fail during cooling, under a constant applied tensile load that is lower than the isothermal strength at the beginning of coolingFootnote 1. For the U-shaped notched specimens tested, failure by the formation of an unstable crack during cooling was observed for bias load levels as low as 60 % of the isothermal bias load needed for failure at the beginning of cooling (Fig. 1). This is an intriguing response that from an energetic point of view may seem in disagreement with the general view of dissipative processes resulting in an enhancement of fracture toughness. As a first attempt to understand this characteristic SMA response, Baxevanis et al. [12, 34] numerically investigated the effect of thermomechanically induced phase transformation on the driving force for crack growth in an infinite center-cracked SMA plate during thermal cycling under plane-strain, mode-I, constant applied loading. This thermomechanical loading path (referred to as isobaric) is an idealization of typical loading paths that utilize SMAs as actuators. Motivated by experimental [16, 22] and analytical findings [28, 29], the authors argued that in most SMA material systems the length scale of the nonlinear deformation zone surrounding the crack tip should be small enough to ensure the validity of (i) an analysis of the fracture response of SMAs on the basis of a constitutive law that does not account for plastic deformation, and (ii) a single parameter for characterizing the fracture toughness of martensite forming at the crack tip, i.e., the crack-tip energy release rate. A significant increase in the crack-tip energy release rate was found during cooling, almost an order of magnitude greater than that due to the isothermal mechanical loading applied before cooling. Thus, it is plausible that the crack-tip energy release rate may reach the material-specific critical value during cooling under a constant mechanical load and initiate crack growth, in accordance with the experimentally observed response described above.

Fig. 1
figure 1

Strain in the direction of the tensile applied loading (vertical to the axes of the notches) at the end of the isothermal loading (60 % of the isothermal strength at that temperature) and just before the formation of an unstable crack under the same bias load at a lower temperature, higher than the martensitic-finish temperature. Taken from [12]

Full size image

In this paper, the authors build upon the aforementioned work and investigate crack growth in SMAs under thermal actuation for the same prototype problem of infinite center-cracked SMA plate under plane-strain, mode-I, constant applied loading. Specifically, it is examined whether the interplay between the increase in the driving force for crack growth due to large scale phase transformation and the shielding effect of the transformed material left in the wake of the growing crack results in stable crack growth. Moreover, the near-tip mechanical fields and fracture toughness are investigated and their sensitivity to phase transformation metrics and bias load levels is reported.

The paper is organized as follows. In "Material Model" section, the constitutive material model used to simulate the thermomechanical behavior of SMAs is briefly reviewed. In "Problem Formulation" section, the boundary value problem is formulated and the solution methodology using the finite element method and VCCT is outlined. In "Numerical Results" section, first, a brief review of the key results reported in [12, 34] is presented to draw a connection between those results that refer to static cracks and the crack growth results discussed in detail later on in the same section. Finally, some of the key findings of this work are summarized and concluded in "Conclusions" section.

Material Model

The proposed model relies on the unified model for polycrystalline SMAs proposed by Boyd and Lagoudas [35, 36]. It is developed within the framework of continuum thermodynamics and adopts the classical rate-independent small-strain flow theory for the evolution equations of the transformation strains.

Within the context of isotropic elastic response, the increments of the strain tensor components, \({\mathrm{d}}\varepsilon _{ij}\), are given as

$$\begin{aligned} {\mathrm{d}}\varepsilon _{ij} = S_{ijkl} {\mathrm{d}}\sigma _{kl} + {\mathrm{d}} S_{ijkl} \sigma _{kl} + {\mathrm{d}}{\varepsilon }^t_{ij}, \end{aligned}$$
(1)

where \(\sigma _{ij}\), \(\varepsilon _{ij}^t\) are the Cartensian components of the stress tensor and of the transformation strain tensor, respectively, and \({S}_{ijkl}\) are the components of the ‘current’ compliance tensor. The thermoelastic strains are an order of magnitude smaller than the transformations strains, and thus neglected. Throughout this paper, standard Einstein notation is used with summation over repeated indices assumed. The ‘current’ compliance tensor varies with the martensite volume fraction \(\xi\) as \(S_{ijkl}=(1-\xi ) S^{\mathrm{A}}_{ijkl} + \xi S^{\mathrm{M}}_{ijkl}\), where \(S^{\mathrm{A}}_{ijkl}\) and \(S^{\mathrm{M}}_{ijkl}\) are the components of the compliance tensor of austenite and martensite, respectively. The assumption of elastic isotropy for both the austenitic and martensitic phases reads as \(S^{\alpha }_{ijkl}=\frac{1+\nu _{\alpha }}{2E_{\alpha }}(\delta _{il}\delta _{jk}+\delta _{ik}\delta _{jl})-\frac{\nu _{\alpha }}{E_{\alpha }}\delta _{ij}\delta _{kl}\), where the index \(\alpha\) stands for A in the case of austenite and for M in the case of martensite. \(E_{\alpha }\), \(\nu _{\alpha }\) denote the Young’s modulus and Poisson’s ratio of the two phases, respectively, and \(\delta _{ij}\) is Kronecker’s delta. The above approximation of the ‘current’ compliance tensor is considered sufficient although more accurate approximations on the basis, for example, of the self-consistent or the Mori–Tanaka methods, could be used instead.

An evolution equation of the transformation strain is defined so that it is related to the evolution of martensite volume fraction \(\xi\),

$$\begin{aligned} {\mathrm{d}}{\varepsilon }^{t}_{ij}= \Lambda _{ij} {\mathrm{d}}\xi , \ \ \Lambda _{ij}= {\left\{ \begin{array}{ll} \Lambda ^{\mathrm{fwd}}_{ij}, \; {\mathrm{d}}\xi >0, \\ \Lambda ^{\mathrm{rev}}_{ij}, \; {\mathrm{d}}\xi <0, \end{array}\right. } \end{aligned}$$
(2)

where, \(\Lambda _{ij}\), the components of the direction tensor, are defined as

$$\begin{aligned} \Lambda ^{\mathrm{fwd}}_{ij}= \frac{3}{2}\frac{H^{\mathrm{cur}}}{\bar{\sigma }} s_{ij}, \ \ \Lambda ^{\mathrm{rev}}_{ij}= \frac{\varepsilon ^t_{ij}}{\xi }. \end{aligned}$$
(3)

Here, \(H^{\mathrm{cur}}\) is the uniaxial transformation strain magnitude for complete transformation, \(\bar{\sigma }=\sqrt{\frac{3}{2}s_{ij}s_{ij}}\) is the Mises equivalent stress and \(s_{ij}=\sigma _{ij}-\sigma _{kk}\delta _{ij}/3\) are the stress deviator components. During forward transformation, the transformation strain is oriented by the direction of the deviatoric stress, which motivates the selected \(J_2\) form of the direction tensor. During reverse phase transformation, it is assumed that the direction and magnitude of the transformation strain recovery are governed by the average orientation of the martensite at transformation reversal (the cessation of forward transformation, be it partial or full). This definition allows to return to a zero transformation strain for every state with a null martensite volume fraction. \(H^{\mathrm{cur}}\) is a function of the stress state since most SMA materials do not exhibit a constant maximum attainable transformation strain at all stress levels. A saturated value of maximum attainable transformation strain, \(H_{\mathrm{sat}}\), is reached at a high stress level, which is dependent on the SMA material as well as the processing conditions for a polycrystalline material, resulting in different crystallographic and morphological textures, for example. Following this observation, the maximum transformation strain \(H^{\mathrm{cur}}\) is represented by the following decaying exponential function

$$\begin{aligned} H^{\mathrm{cur}}(\bar{\sigma })=H_{\mathrm{sat}}\left( 1-e^{-k\bar{\sigma }}\right) , \end{aligned}$$
(4)

where the parameter k controls the rate at which \(H^{\mathrm{cur}}\) exponentially evolves from 0 to \(H_{\mathrm{sat}}\).

During transformation, the stress tensor components should remain on the transformation surface

$$\begin{aligned} \Phi =0, \; \; \Phi = {\left\{ \begin{array}{ll} \Phi ^{\mathrm{fwd}}=\pi ^{\mathrm{fwd}}- Y_0,\; d\xi >0, \\ \Phi ^{\mathrm{rev}}=-\pi ^{\mathrm{rev}}- Y_0,\; d\xi <0, \end{array}\right. } \end{aligned}$$
(5)

with \(\pi ^{\mathrm{fwd}}\), \(\pi ^{\mathrm{rev}}\) being the thermodynamic driving forces for forward and reverse transformation, respectively, and \(Y_0\) is the critical value of the thermodynamic force to both initiate and sustain forward and reverse phase transformation. The thermodynamic driving force for forward transformation is written as

$$\begin{aligned} \pi ^{\mathrm{fwd}}=\sigma _{ij}\Lambda ^{\mathrm{fwd}}_{ij}+\frac{1}{2}{\Delta S_{ijkl}}\sigma _{ij}\sigma _{kl}+\rho \Delta s_0 T -\rho \Delta u_0 - f^{\mathrm{fwd}}, \end{aligned}$$
(6)

where

$$\begin{aligned} f^{\mathrm{fwd}}=\frac{1}{2}\alpha _1\left[ 1+ \xi ^{n_1}-(1-\xi )^{n_2}\right] + \alpha _3, \end{aligned}$$
(7)

and for reverse transformation

$$\begin{aligned} \pi ^{\mathrm{rev}}=\sigma _{ij}\Lambda ^{\mathrm{rev}}_{ij}+\frac{1}{2}{\Delta S_{ijkl}}\sigma _{ij}\sigma _{kl}+\rho \Delta s_0 T -\rho \Delta u_0 - f^{\mathrm{rev}}, \end{aligned}$$
(8)

where

$$\begin{aligned} f^{\mathrm{rev}}=\frac{1}{2}\alpha _2\left[ 1+ \xi ^{n_3}-(1-\xi )^{n_4}\right] - \alpha _3. \end{aligned}$$
(9)

\(f^{\mathrm{fwd}}\) and \(f^{\mathrm{rev}}\) are functions describing the transformation hardening behavior during forward and reverse phase transformation, respectively. \(s_0\) and \(u_0\) are the specific entropy and internal energy, respectively, \(\rho\) is the density, \(\Delta\) denotes the difference in property between the martensitic and the austenitic states, \(\alpha _i\) \((i=1,2,3)\) and \(n_i\) \((i=1,2,3,4)\) are coefficients that assume real number values.

Given these constitutive relations, the following model parameters must be calibrated: (i) the elastic parameters of martensite and austenite, (ii) parameters contained in the functional form of the maximum transformation strain \(H^{\mathrm{cur}}(\bar{\sigma })\), and (iii) six model parameters (\(\rho \Delta s_0\), \(\rho \Delta u_0\), \(\alpha _1\), \(\alpha _2\), \(\alpha _3\), \(Y_0\)) that are characteristic of the martensitic transformation. The common material properties that are used to calibrate the model are \(E_{\mathrm{A}}\), \(E_{\mathrm{M}}\), \(\nu _{\mathrm{A}}\), \(\nu _{\mathrm{M}}\), \(H_{\mathrm{sat}}\), \(M_{\mathrm{s}}\), \(M_{\mathrm{f}}\), \(A_{\mathrm{s}}\), \(A_{\mathrm{f}}\), \(C_{\mathrm{M}}\), and \(C_{\mathrm{A}}\). \(M_{\mathrm{s}}\), \(M_{\mathrm{f}}\), \(A_{\mathrm{s}}\) and \(A_{\mathrm{f}}\) are the martensitic-start, martensitic-finish, austenitic-start, and austenitic-finish temperatures at zero load, respectively, and \(C_M\) and \(C_{\rm A}\) are the forward and reverse transformation slopes in the stress–temperature phase diagram, respectively (Fig. 2). The elastic constants can be calculated directly from isothermal stress–strain curves where loads are applied at temperatures outside the transformation regions. The parameters for \(H^{\mathrm{cur}}(\bar{\sigma })\) can be calibrated directly from isobaric material testing, where the value of k in particular is chosen to best fit the experimental trend. The remaining six parameters are calibrated by considering the conditions under which forward transformation begins and ends in the stress–temperature space [1]. The exponents \(n_i\) \((i=1,2,3,4)\) do not have an associated material property but are directly chosen to best fit the two corners of the forward transformation plots.

Fig. 2
figure 2

Stress–temperature phase diagram. Cooling at constant applied load

Full size image

Problem Formulation

In this section, the boundary value problem of mode-I crack growth in an infinite center-cracked SMA plate subjected to thermal cycling under plane strain constant applied loading is described.

The SMA plate is subjected to far-field in-plane uniform uniaxial tensile load, in the direction normal the crack line as shown in Fig. 3. The load is applied at a nominal temperature higher than the austenitic-finish temperature, \(A_{\mathrm{f}}\), and a region of transformed material is formed near the crack tip. Small scale transformation conditions prevail, according to which the size of the transformation zone is small compared to the crack length 2 a, by applying a load resulting in uniaxial tensile stress at infinity, \(\sigma _{\infty }\), that is sufficiently smaller than the stress required for initiation of martensitic transformation, \(\sigma ^{M_{\mathrm{s}}}\), at the given temperature. Maintaining the tensile load at the boundary constant, the entire cracked SMA specimen is then subjected to thermal cycling, i.e., alternate cooling and heating between the high temperature at which the mechanical load is applied and a low temperature that is smaller than \(M_{\rm f}\) (to ensure that the bulk of the specimen completely transforms between pure austenite and martensite). The cooling and heating rates are assumed to be sufficiently slow with respect to the time rate of heat transfer by conduction in order to discard any effects of local temperature gradients arising from latent heat of phase transformation and to maintain a uniform temperature field throughout the specimen.

Fig. 3
figure 3

Boundary value problem for an infinite center-cracked SMA plate in initial austenite phase subjected to a constant far-field uniaxial tensile loading and thermal cycling. Martensite regions are shown in red color and austenite ones in blue (Color figure online)

Full size image

Due to symmetry of the problem, the analysis is restricted to one-quarter of the plate. A system of co-ordinates \((x_1, x_2)\) is chosen such that the origin lies at the center of the crack and the \(x_1\)-axis is extending along the line of the crack while the \(x_2\)-axis is aligned in the direction of loading. A finite element mesh of 8-node, isoparametric quadrilateral elements is constructed in ABAQUS to represent the center-cracked SMA specimen with a finer mesh density in the crack growth path in front of the crack-tip. The VCCT capability of ABAQUS, which is an extension of the classical crack-closure technique based on Irwin’s crack closure integral [37–40], is employed to calculate the crack-tip energy release rate.

Within this model for fracture of SMAs, dimensional analysis and manipulation of the constitutive law dictate that the normalized stresses, \(\sigma _{ij}/\sigma _{\infty }\), strains, \(\varepsilon _{ij}/H_{\mathrm{sat}}\), and temperature, \(C_{\mathrm{M}}(T-M_{\mathrm{s}})/\sigma _{\infty }\) will be dependent on the following dimensionless parameters:

$$\begin{aligned}&\frac{E_{\mathrm{A}}H_{\mathrm{sat}}}{\sigma _{\infty }}, \; k\sigma _{\infty }, \; \frac{C_{\mathrm{M}}(A_{\mathrm{s}}-M_{\mathrm{s}})}{\sigma _{\infty }},\; \frac{C_{\mathrm{M}}(A_{\mathrm{f}}-A_{\mathrm{s}})}{\sigma _{\infty }},\; \frac{C_{\mathrm{M}}(M_{\mathrm{s}}-M_{\mathrm{f}})}{\sigma _{\infty }}, \; \frac{C_{\mathrm{M}}}{C_{\mathrm{A}}},\nonumber \\&\frac{E_{\mathrm{M}}}{E_{\mathrm{A}}}, \; \nu _{\mathrm{M}},\frac{\nu _{\mathrm{M}}}{\nu _{\mathrm{A}}}, \end{aligned}$$
(10)

which, under the convention of tensile stresses being positive, are subject to the following inequalities

$$\begin{aligned} \frac{C_{\mathrm{M}}(A_{\mathrm{f}}-A_{\mathrm{s}})}{\sigma _{\infty }} \ge 0 \ \ {\text {and}} \ \ \frac{C_{\mathrm{M}}(M_{\mathrm{s}}-M_{\mathrm{f}})}{\sigma _{\infty }} \ge 0, \end{aligned}$$

since \(M_{\mathrm{f}} \le M_{\mathrm{s}}\), \(A_{\mathrm{s}} \le A_{\mathrm{f}}\). Note that, in what follows, the Poisson’s ratios of the two phases are assumed equal, i.e., \(\nu _{\mathrm{A}}=\nu _{\mathrm{M}}=\nu\), which is the case for most SMA material systems.

Numerical Results

Before presenting results pertaining to crack advance, a brief description of the numerical findings regarding the mechanical fields near the crack tip and the driving force for crack growth in static cracks, obtained in [12, 34], is given.

Fig. 4
figure 4

Normalized energy release rate, \(G_I/G_{\infty }\), versus normalized temperature, \(C_{\rm M}(T-M_{\rm s})/\sigma _{\infty }\), and martensite volume fraction, \(\xi\), during cooling. The martensite volume fraction distribution during heating is similar to the one during cooling for the same values of \(G_I/G_{\infty }\)

Full size image

Brief Review of the Mechanical Fields and Driving Force for Crack Growth Prior to Crack Advance

As shown in Baxevanis et al. [12, 34], prior to crack growth, the incremental response of the material inside the fully transformed zone surrounding the crack tip is linear elastic at all times, and the fields are characterized by a crack-tip energy release rate, \(G_{I}\). During cooling, the thermomechanically induced “global” scale phase transformation, i.e., transformation extending to infinity, results in stress redistribution near the crack that substantially increases the crack-tip energy release rate, an order of magnitude for some material systems. The evolution of normalized crack-tip energy release rate, \(G_I/{G}_{\infty }\), during a thermal cycle is shown in Fig. 4 for the parameter values given in Table 1 under the assumption that the critical crack-tip energy release rate value required for crack growth is never reached, where \(G_{\infty }\) represents the energy release rate resulting from the applied mechanical load prior to thermal cycling. \(G_I/{G}_{\infty }\) first increases during cooling, reaches a peak, and then decreases before attaining a constant value at temperature \(T=M_{\rm f}\), at which the entire SMA specimen has fully transformed into martensite. During heating, the energy release rate starts increasing at \(T=A_{\rm s}\), which marks the beginning of reverse phase transformation behind the crack tip, reaches a peak, and decreases before attaining a constant value. As discussed in Baxevanis et al. [12, 34], the increase of the energy release rate during cooling should be attributed to “global” phase transformation occurring in a fan ahead of the crack tip where the transformation strains have an anti-shielding effect, whereas the subsequent decrease once the peak is reached is attributed to phase transformation occurring in regions behind the crack tip. Similar arguments can explain the evolution of energy release rate during heating.

Table 1 Dimensionless parameter values used for the numerical results except if stated otherwise
Full size table

Stable Crack Growth

In what follows, the ratio \(G_{\mathrm{crit}}/G_{\infty }\) is chosen such that during cooling the crack-tip energy release rate, \(G_{I}\), reaches the critical value, \(G_{\mathrm{crit}}\), and initiates crack growth. The most important result, explained in detail below, is that stable crack growth is observed, i.e., further cooling is needed to maintain crack growth.

Martensitic Transformation and Near-Tip Stress Field During Crack Growth

Prior to presenting results for the toughness enhancement associated with stable crack growth, some features of the crack-tip mechanical fields are now presented.

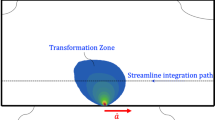
The transformation region depicted by the martensitic volume fraction close to the crack tip at initiation of crack growth and during crack advance are shown in Fig. 5 for an applied load level such that \(G_{\mathrm{crit}}/{G}_{\infty }=2\). The chosen system of co-ordinates \((x_1, x_2)\) is normalized with the initial half crack length, a, where origin represents the center of the crack and \((x_1,0)=(1,0)\) represents the initial location of the crack tip. Fig. 5a shows the region of stress-induced martensite (red color) at the initiation of crack growth, surrounded by a region of partially transformed material and the rest of the specimen in untransformed austenitic phase (blue color). As the crack advances, unloading takes place in the wake of the growing crack; however, no reverse phase transformation is observed due to further cooling required to drive crack growth (Fig. 5b) (see the phase diagram in Fig. 2).

Fig. 5
figure 5

Martensite volume fraction distribution, \(\xi\), near the crack tip

Full size image

The material points in front of the crack tip experience non-proportional loading due to the “global” transformation interfering with the boundary conditions, as depicted in Fig. 6, in which the stress triaxiality ratio \(T=\bar{\sigma }/\sigma _m\) (\(\sigma _m\) denotes the mean normal stress) distribution is plotted at the initiation of crack growth and during crack advance. However, at the vicinity of the crack-tip, inside the region of fully transformed material, the stress field at all times is equivalent to the asymptotic K-field of an isotropic elastic material. During crack advance, the stress intensity factor \(K=K_{\mathrm{crit}}\) is related to the critical crack-tip energy release rate through \(G_{\mathrm{crit}}=(1-\nu _{\mathrm{M}}^2)K_{\mathrm{crit}}^2/E_M\), as it can be seen in Fig. 7, in which the angular dependence of the SMA stress field close to the crack tip during crack growth is compared to the angular dependence of the stress field for an isotropic linear elastic solid. Moreover, the numerical results suggest that close to the crack tip the stresses have a \(1/\sqrt{r}\) radial asymptotic behavior during thermal cycling. These results, apart from justifying the assumption of a single parameter being capable of describing the mechanical fields close to the crack tip, validate the VCCT in calculating that parameter.

Fig. 6
figure 6

Stress triaxiality ratio, \(T=\bar{\sigma }/\sigma _m\), where \(\bar{\sigma }\) is the von Mises stress and \(\sigma _m\) is the mean normal stress

Full size image
Fig. 7
figure 7

Angular distribution of stresses close to the crack tip during crack growth. The markers are the numerical results for the SMA material and the solid lines are numerical results for an elastic material with the properties of martensite. The \(1/\sqrt{r}\) radial dependence has been accounted for within the normalization

Full size image

Toughness Enhancement Associated with Crack Advance

Stable crack growth arises due to stress redistribution caused by the transformation deformations left in the wake of the growing crack that shields the crack [12, 34], and it is therefore necessary to continue cooling the material in order to maintain a critical stress field at the advancing crack tip. Eventually, once the crack advances a distance comparable to its initial length, the increment of the loading parameter, i.e., temperature, needed to achieve a given increment of growth diminishes and the crack approaches nominally steady-state growth at a constant temperature (Fig. 8). This transformation toughening response is quite similar to the one observed in pseudoelastic SMAs or other dissipative materials in which cracks grow in an initially stable manner under increasing mechanical load (or, depending on the loading arrangement, load-point displacement) until critical conditions are attained. The normalized temperature–crack advance response in Fig. 8 should therefore be considered indicative of toughness enhancement for the loading paths considered here, similarly to the R-curve response of dissipative materials under isothermal loading.

Fig. 8
figure 8

Normalized temperature, \(C_{\mathrm{M}} (T-M_{\mathrm{S}})/\sigma _{\infty }\), versus normalized crack growth, \(\delta a/a\), for \(G_{\mathrm{crit}}/G_{\infty } = 2\)

Full size image

Influence of Phase Transformation Metrics and Bias Load on Crack Growth

Next, the dependence of actuation-induced transformation toughening on non-dimensional transformations metrics, defined in Eq. (10), and bias load is presented.

Fig. 9
figure 9

Normalized temperature, \(C_{\mathrm{M}}(T-M_{\mathrm{s}})/\sigma _{\infty }\), versus normalized crack growth, \(\delta a/a\)

Full size image

In Fig. 9a, the normalized temperature, \(C_{\mathrm{M}}(T-M_{\mathrm{s}})/\sigma _{\infty }\), is plotted against normalized crack growth, \(\delta a/a\), for a range of values for the relative maximum transformation strain \(E_AH_{\mathrm{sat}}/\sigma _{\infty }\). Larger relative transformation strains imply larger transformation strains left in the wake of the growing crack and more energy being dissipated by the transformed material, which in turn implies that more cooling is required from the initiation of crack growth for steady-state conditions to be met. The effect of \({C_{\mathrm{M}}(M_{\mathrm{s}}-M_{\mathrm{f}})}/{\sigma _{\infty }}\) on the transformation toughening is presented in Fig. 9b. Higher \(C_{\mathrm{M}}(M_{\mathrm{s}}-M_{\mathrm{f}})/{\sigma _{\infty }}\)-values require higher temperature differentials to reach given levels of martensite volume fraction during forward transformation (which is interpreted as transformation hardening) and result in lower crack-tip energy release rate values in static cracks during thermal cycling [34]. Therefore, for higher \(C_{\mathrm{M}}(M_{\mathrm{s}}-M_{\mathrm{f}})/{\sigma _{\infty }}\)-values more cooling is required for attaining steady-state growth conditions.

Table 2 Parameter values used for the numerical results presented in Fig. 10
Full size table

Since most of the non-dimensional parameters listed in Eq. 10 depend on the in-plane uniform uniaxial tensile stress at infinity, \(\sigma _{\infty }\), and therefore are not material parameters, the influence of the bias load on the crack growth kinetics is examined for dimensional parameters chosen so as to conform with those of an NiTi material system and yield quantitative results on the crack growth response expected for this specific material during actuation.

The influence of the stable crack growth response is depicted in Fig. 10 for different values of applied load, \(\sigma _{\infty }\), resulting in \(G_{\mathrm{crit}}/G_{\infty }\) equal to 3.25, 3.75, and 3.9. For \(G_{\mathrm{crit}}/G_{\infty }=3.25\), the response is similar to that of Fig. 8, in the sense that steady-state crack growth conditions are met during cooling in the first thermal cycle. For sufficiently high values of \(G_{\mathrm{crit}}/G_{\infty }\) (= 3.75 and 3.9), i.e., sufficiently small bias loads, however, the material is capable of sustaining multiple cooling/heating cycles before crack growth reaches nominally steady-state conditions. In these cases, the increment of temperature needed to attain a given increment of crack advance initially gets smaller, until transformation starts taking place in a fan behind the crack tip shielding the crack and increasing the required temperature change for attaining a given increment of crack advance. Once the whole material is transformed, crack growth ceases. During heating, i.e., increasing values of \(C_{\mathrm{M}} (T-M_{\mathrm{S}})/\sigma _{\infty }\), the crack also advances as the shielding effect of transformation behind the crack tip is lost [note that the peak in the energy release rate during heating is usually higher than the corresponding peak during cooling for stationary cracks (Fig. 4)]. Crack growth in subsequent cycles results from the increase in crack length from the previous cycles since for larger cracks the crack-tip energy release rate is closer to the critical value.

Fig. 10
figure 10

Normalized temperature, \(C_{\mathrm{M}} (T-M_{\mathrm{S}})/\sigma _{\infty }\), vs. normalized crack growth, \(\delta a/a\), for varying bias loads, \(G_{\mathrm{crit}}/G_{\infty }\). The parameters values used are those of Table 2

Full size image

Conclusions

Finite element calculations are carried out in an attempt to understand crack growth in SMA actuators. The prototype problem of an infinite center-cracked SMA plate subjected to thermal cycling under plane strain, mode I, constant applied loading is employed in the analysis. The crack is assumed to propagate when the crack-tip energy release rate reaches a material-specific critical value. In all cases, the applied loads are sufficiently low so that the crack-tip energy release rate prior to thermal cycling is less than the critical value but sufficiently high so that the critical value is reached during the first thermal cycle. Stable crack growth is observed associated with the crack shielding effect of the transformed material left in the wake of the growing crack. This toughening effect is sensitive to the transformation metrics and applied load levels. The smaller the bias load levels are, more thermal cycles are required for the crack to attain steady-state growth conditions.

A geometry dependence of crack growth resistance is expected as the outer boundaries exert an influence on the crack-tip deformation state whenever they are reached by the transformation zone at sufficiently low temperatures. Therefore, the present study should be extended to crack configurations beyond that of the infinite center-crack problem. It should be also extended to actuation loading paths beyond the isobaric ones in an effort to fill the gap between the test and working conditions.