Analytical Investigation on CNT Based Maxwell Nano-fluid with Cattaneo–Christov Heat Flux Due to Thermal Radiation

Abstract

At first, we derive a series form solution of the coupled highly nonlinear equations, which includes various conditions. Then, via the method of directly defined inverse mapping with the series form solution firstly reported in this paper, we can obtain theoretical and approximate analytical analysis about the transfer of heat as well as the magnetohydrodynamic flow of Maxwell nanofluid by the influence of convective heating with effects of thermal radiation. In the energy equation, heat flux model is adopted to develop the equations for viscoelastic relaxation over boundary layer flow. For this investigation, we considered base liquid as engine oil and other forms of carbon nanotubes such as single walled nanotubes and multi-walled nanotubes. Suitable similarity transformations are applied for transformation of given boundary layer flow equations. Results are compared numerically by Keller–Box method. It is found that for both singled and multi-walled carbon nanotube based nanofluids the thermal relaxation time and temperature function are inversely proportional. More interestingly it is noted that for the two types of nanofluids, fluid relaxation parameter exactly coordinates with heat transfer rate as well as skin friction investigated. Also shown that the base functions of solutions are highly convergence.

Introduction

The attention on electrically conducting fluid with magnetic field is of greater importance in many applications of engineering industries such as power generation, metals purification process, hardening, MHD pumps etc. The process of cooling of stretched sheets or filaments are through a quiescent fluid and the quality and characters of the final product depends upon the rate of cooling in various processes. The cooling rate can be governed by drawing such strips or filaments into the fluid, which leads to get the final product with desired characteristics. The magnetic field can produce a significant amount of Lorentz force in the presence of a magnetization force and electric current. It is prominent that the impact of hall current is very essential in the presence of a strong magnetic field. Besides, in a low-density ionized gas the conductivity normal to the magnetic field is decreased by free growth of electrons and ions with or without magnetic field. Gupta [1] examined the impact of Hall effects of the hydromagnetic flow over flat plate. Hayat et al. [2] reported the effects of Hall current and heat transfer on the rotating flow through a porous medium. Saleem and Aziz [3] investigated the hydromagnetic flow over a stretching surface in the presence of Hall current. Aziz and Nabil [4] studied the effects of Hall current on hydromagnetic mixed convection flow past an exponentially stretching surface. Pal [5] considered thermal radiation effects on the unsteady flow of viscous fluid past a permeable stretching surface with Hall current. Gangadhar et al. [6] studied the effects of Newtonian heating about MHD flow concerning micro polar nanofluid over permeable stretching/shrinking sheet.

Nanotechnology has impacted the world of science, technology, medical sciences, engineering significantly and remarkably influencing future technologies and solutions. Suspending nano particles in the base fluid not only enhances the thermal properties of the fluids but also affects the velocity of the fluids. Researchers have been used various of models to study the different thermal and physical properties of nanofluids. One of the pioneering models are presented by Choi [7, 8] and Hamilton and Crosser model [9]. Buongiorno [10] incorporated both Brownian motion and thermophoresis in his model. The above-mentioned models focus only the spherical or rotational elliptical nature of the nanoparticles [11]. In regard to Maxwell’s theory [12], Xue recommended a model that includes the rotational elliptical nanotubes and it considers large axial ratio and the space distribution on CNTs. CNTs is opening doors to many technological and industrial area that involve heat transfer, such as fast cooling of chips, ultra-capacitors, electrochemical supercapacitor, etc. [13,14,15].

Types of carbon nanotubes are categorized as, single-walled carbon nanotubes and multi-walled carbon nanotubes. Murshed et al. [16] found that the carbon nanotubes increase the thermal conductivity six times that of the base fluid. Ganesh Kumar et al. [17] deliberated the impact of non-linear radiation of viscoelastic nanofluid flow over elongating sheet. Khan et al. [18] analyzed about transfer of heat resolution of CNT founded nanofluids by the consequences of slip of velocity through non-parallel walls. Recently, various aspects of magnetic force, heat generation, shape effects, radiation, etc. on nanoparticles were studied by [19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59].

The analysis of heat transfer plays a very crucial role in nature and almost in all industrial sectors. The phenomena of heat transfer are clearly explained in Fourier’s law of heat conduction [60]. Though, the main flaw of the Fourier’s laws is the principle of causality. By employing the thermal relaxation time in the Fourier’s model leads to a finite heat distribution rate [61]. Besides, Maxwell–Cattaneo model is improved significantly when time derivative is considered by Christov [62]. Tibullo and Zampoli [63] obtained uniqueness result for Cattaneo–Christov heat conduction model. Fluid flow and heat transfer with Cattaneo–Christov heat flux model is examined by Han et al. [64]. Flow of Maxwell fluid over a linear stretching sheet with the Cattaneo–Christov heat flux is reported by Mustafa [65]. The detailed discussions of the flow over a stretching sheet with variable thickness with Cattaneo–Christov heat flux model are available in the literature [66,67,68]. Oyelakin et al. [69] explored the Catteneo–Christov heat flux phenomenon by past nanofluid flow as well as transfer of heat resolution on vertical cone inside porous medium. Farooq et al. [70] examined the dissection of heat as well as mass flux phenomenon by Cattaneo–Christov over compressed flow contain inside porous medium along with changeable mass distribute. Prabir Kumar et al. [71] studied the influence of Cattaneo–Christov heat flux on the boundary layer flow past a stretching sheet.

In the highest degree of perception, no one at any time endeavor to investigate about MHD flow concerning CNT engine oil through non-linear enlarging surface by means of heat flux model by Cattaneo–Christov with MDDIM [72]. Outcome of convective heating as well as thermal radiations are made of use in equation of energy. The governing PDEs are transformed as extremely non-linear ODEs. Owing to non-linearly as well as outline essence of the question, an accurate resolution is different. A catalogue of counterpart co-efficient among the activity factors as well as the physical measures of observation of this model estimated to appraise the link between the flow as well as temperature are pictured through charts and graphs.

Recently, Liao [72] has been developed the new technique MDDIM and analyzed the various types of nonlinear problems. The nonlinear system of differential equations with convective heat transfer on a porous flat plate was studied by Baxter et al. [73]. After that Dewasurendra et al. [74] has been analyzed the coupled systems of nonlinear differential equations of nanofluid flow problem with mass and heat transfer effects by MDDIM.

To the best of authors’ knowledge this governing equations has not been examined with MDDIM before and the reported results are new. All the obtained outcomes from the above approximate analytic and numerical procedures are displayed through graphs and tables to discuss various resulting parameters.

Mathematical Formulation

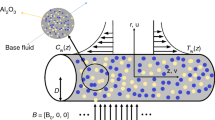
For our study we considered a two-dimensional flow which is steady, viscous and magnetohydrodynamic upper convective viscoelastic Maxwell nanofluid having both single and multi-walled carbon nanotubes on a vertical sheet. The base fluid for this investigation is viscous engine oil. In the coordinate frame y-axis is fixed along the plane and x-axis is upright to it which is shown in Fig. 1. The nanofluid moves in positive y-direction with velocity u_w′ = a′x^m, where ‘a′’ indicates the constant of stretching rate and ‘m’ denotes the stretching index may not be an integer. The fluid flow is considered as laminar and applied magnetic field of intensity $\tilde{B}(x) = \tilde{B}_{0} x^{{\frac{m - 1}{2}}}$ is perpendicular to the sheet. Moreover, it is assumed that outward applied electric field is very small hence we have negligible magnetic Reynolds numbers. Correspondingly, it is noted that magnetic flux inside is considerably small with outward magnetic flux. There is a constant temperature T_w inside the boundary layer whereas T_∞ outside it. The equations governing the flow are given below (see Kundu et al. [71]):

$$ \frac{{\partial u^{\prime}}}{\partial x} + \frac{{\partial v^{\prime}}}{\partial y} = 0 $$

(1)

$$ \begin{aligned} & u^{\prime}\frac{{\partial u^{\prime}}}{\partial x} + v^{\prime}\frac{{\partial u^{\prime}}}{\partial y} + \lambda_{1} \left( {u^{\prime 2} \frac{{\partial^{2} u^{\prime}}}{{\partial x^{2} }} + v^{\prime 2} \frac{{\partial^{2} u^{\prime}}}{{\partial y^{2} }} + 2u^{\prime}v^{\prime}\frac{{\partial^{2} u^{\prime}}}{\partial x\partial y}} \right) \\ & \quad = \frac{1}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho }_{nf} }}\left( {\mu^{\prime}_{nf} \frac{{\partial^{2} u^{\prime}}}{{\partial y^{2} }} + g\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } \beta } \right)_{nf} \left( {T - T_{\infty } } \right) - \sigma \tilde{B}^{2} \left( x \right)u^{\prime}} \right) \\ \end{aligned} $$

(2)

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } C_{p} \left( {u^{\prime}\frac{{\partial u^{\prime}}}{\partial x} + v^{\prime}\frac{\partial T}{\partial y}} \right) = - \nabla \cdot \hat{q} - \frac{{\partial q_{r} }}{\partial y} $$

(3)

where u′ is the x portion of velocity, v′ is the y portion of velocity. The third term of expression (2) represents the convective part of the Maxwell fluid and λ₁ is the relaxation of the time for velocity, $\hat{q}$ is the heat flux. $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho }_{nf}$ is the effective density of the nanofluid, μ_nf′ is the effective dynamic viscosity of nanofluid, β is the thermal expansion coefficient regarding to the volume, σ is the electrical conductivity, g is the gravitational force, C_p is the specific heat at constant pressure. We have,

$$ \hat{q} + \lambda_{2} \left[ {\frac{{\partial \hat{q}}}{\partial t} + \bar{V} \cdot \nabla \hat{q} - \hat{q} \cdot \nabla \bar{V} + \left( {\nabla \cdot \bar{V}} \right)\hat{q}} \right] = - \tilde{K}_{f} \nabla T - \frac{{\partial q_{r} }}{\partial y} $$

(4)

Here $\bar{V}$ is the velocity vector and λ₂ is the relaxation of time of heat flux, $\tilde{K}_{nf}$ is the thermal conductivity of the nanofluid. For incompressible fluids Eq. (4) becomes

$$ \hat{q} + \lambda_{2} \left[ {\frac{{\partial \hat{q}}}{\partial t} + \bar{V} \cdot \nabla \hat{q} - \hat{q} \cdot \nabla \bar{V}} \right] = - \tilde{K}_{\text{f}} \nabla T - \frac{{\partial q_{\text{r}} }}{\partial y} $$

(5)

Eliminating $\hat{q}$, we get:

$$ \begin{aligned} & u^{\prime}\frac{\partial T}{\partial x} + v^{\prime}\frac{\partial T}{\partial y} + \lambda_{2} \left( {u^{\prime}\frac{{\partial u^{\prime}}}{\partial x}\frac{\partial T}{\partial x} + v^{\prime}\frac{{\partial v^{\prime}}}{\partial y}\frac{\partial T}{\partial y} + u^{\prime}\frac{{\partial u^{\prime}}}{\partial x}\frac{\partial T}{\partial y} + v^{\prime}\frac{{\partial u^{\prime}}}{\partial y}\frac{\partial T}{\partial x}} \right. \\ & \quad \left. { + 2u^{\prime}v^{\prime}\frac{{\partial^{2} T}}{\partial x\partial y} + u^{\prime 2} \frac{{\partial^{2} T}}{{\partial x^{2} }} + v^{\prime 2} \frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) = \bar{\alpha }_{nf} \frac{{\partial^{2} T}}{{\partial y^{2} }} - \frac{{\partial q_{r} }}{\partial y} \\ \end{aligned} $$

(6)

Here $\bar{\alpha }_{nf}$ is the thermal diffusivity of the nanofluid.

Fig. 1

Flow configuration and coordinate system

The Rosseland diffusion approximation of radiation heat flux q_r is given by

$$ q_{r} \, = \, - \frac{{4\sigma_{s} }}{{3k_{e} }}\frac{{\partial T^{4} }}{\partial y} $$

(7)

where σ_s is the Stefan–Bolzmann constant and k_e is the mean absorption coefficient. If the temperature differences are significantly small, then Eq. (7) can be linearized by expanding T⁴ into the Taylor series about T_∞ which, after neglecting higher order terms, takes the form

$$ T^{4} = 4T_{\infty }^{3} T - 3T_{\infty }^{4} $$

(8)

Using Eqs. (7) and (8), Eq. (6) reduces to

$$ \begin{aligned} & u^{\prime}\frac{\partial T}{\partial x} + v^{\prime}\frac{\partial T}{\partial y} + \lambda_{2} \left( {u^{\prime}\frac{{\partial u^{\prime}}}{\partial x}\frac{\partial T}{\partial x} + v^{\prime}\frac{{\partial v^{\prime}}}{\partial y}\frac{\partial T}{\partial y} + u^{\prime}\frac{{\partial u^{\prime}}}{\partial x}\frac{\partial T}{\partial y}} \right. \\ & \quad \quad \left. { + v^{\prime}\frac{{\partial u^{\prime}}}{\partial y}\frac{\partial T}{\partial x} + 2u^{\prime}v^{\prime}\frac{{\partial^{2} T}}{\partial x\partial y} + u^{\prime 2} \frac{{\partial^{2} T}}{{\partial x^{2} }} + v^{\prime 2} \frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) \\ & \quad = \bar{\alpha }_{nf} \frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{16\sigma_{s} T_{\infty }^{3} }}{{3k_{e} \rho C_{p} }}\frac{{\partial^{2} T}}{{\partial y^{2} }} \\ \end{aligned} $$

(9)

Maxwell’s relation for thermal conductivity is

$$ \bar{\alpha }_{nf} = \frac{{\tilde{K}_{nf} }}{{\tilde{K}_{f} }} = 1 + \frac{{3\left( {\bar{\alpha }_{nf} - 1} \right)\varphi }}{{\left( {\bar{\alpha }_{nf} + 2} \right)\left( {\bar{\alpha }_{nf} - 1} \right)\varphi }} $$

(10)

Here φ is the volume fraction of nanoparticles.

Jeffery model for thermal conductivity is

$$ \frac{{\tilde{K}_{nf} }}{{\tilde{K}_{f} }} = 1 + 3\bar{\lambda }\varphi + \left( {3\bar{\lambda }^{2} + \frac{{3\bar{\lambda }^{2} }}{4} + \frac{{9\bar{\lambda }^{3} }}{16}\frac{{\bar{\alpha }_{nf} + 2}}{{2\bar{\alpha }_{nf} + 3}} + \cdots } \right)\varphi^{2} $$

(11)

Here $\bar{\lambda } = \frac{{\bar{\alpha }_{nf} - 1}}{{\bar{\alpha }_{nf} + 2}}$. The results of the two models coincide when the concentration is low.

Thermal conductivity is expressed by Hamilton and Crosser model as

$$ \frac{{\tilde{K}_{nf} }}{{\tilde{K}_{f} }} = \frac{{\bar{\alpha }_{nf} + \left( {n^{\prime} - 1} \right) - \left( {n^{\prime} - 1} \right)\left( {1 - \bar{\alpha }_{nf} } \right)\varphi }}{{\bar{\alpha }_{nf} + \left( {n^{\prime} - 1} \right) + \left( {1 - \bar{\alpha }_{nf} } \right)\varphi }} $$

(12)

Here n′ is the shape feature of nanoparticle which is of the form of $n^{\prime} = \frac{3}{{\varphi^{\omega } }}$. Where ‘ω’ takes values between 1 and 2. If φ = 1 then the shape of the nanoparticle is spherical and for φ = 0.5 it is cylindrical in shape. Xue [11] observed that these models work well when the shapes of nanoparticle either spherical or elliptical with low eccentricity also be observed that it can’t explain the effect of CNTs like thermal conductivity distribution. To overcome this again Xue [11] suggested a model

$$ \frac{{\tilde{K}_{nf} }}{{\tilde{K}_{f} }} = \frac{{1 - \varphi + 2\varphi \frac{{\tilde{K}_{CNT} }}{{\tilde{K}_{CNT} - \tilde{K}_{f} }}\ln \frac{{\tilde{K}_{CNT} + \tilde{K}_{f} }}{{2\tilde{K}_{f} }}}}{{1 - \varphi + 2\varphi \frac{{\tilde{K}_{f} }}{{\tilde{K}_{CNT} - \tilde{K}_{f} }}\ln \frac{{\tilde{K}_{CNT} + \tilde{K}_{f} }}{{2\tilde{K}_{f} }}}} $$

(13)

Here, $\tilde{K}_{CNT}$ is thermal conductivity of the CNTs. The thermo-physical characteristics of the CNT-engine oil of nanofluid are estimated with the help of the following expressions and Table 1.

Table 1 Thermo-physical properties (see Kundu et al. [71])

The expression of dynamic viscosity of the nanofluid is given by

$$ \mu^{\prime}_{nf} = \frac{{\mu^{\prime}_{f} }}{{\left( {1 - \varphi } \right)^{2.5} }} $$

(14)

Here μ_f′ is the effective viscosity of the base fluid i.e. engine oil. φ is the volume fraction of the CNTs which are both SWCNTs and MWCNTs. If $\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } C_{p} } \right)_{nf}$ is the effective heat capacity, then $\bar{\alpha }_{nf}$ is given by

$$ \begin{aligned} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho }_{nf} & = \left( {1 - \varphi } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho }_{f} + \varphi \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho }_{CNT} ,\,\,\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } C_{p} } \right)_{nf} = \left( {1 - \varphi } \right)\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } C_{p} } \right)_{f} + \varphi \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } C_{p} } \right)_{CNT} , \\ \bar{\alpha }_{nf} & = \frac{{\tilde{K}_{nf} }}{{\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } C_{p} } \right)_{nf} }},\,\,\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } \beta } \right)_{nf} = \left( {1 - \varphi } \right)\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } \beta } \right)_{f} + \varphi \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } \beta } \right)_{CNT} \\ \end{aligned} $$

(15)

In the above equation $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho }_{CNT}$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho }_{f}$ are the density of CNTs and base fluid, respectively, and $\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } C_{p} } \right)_{CNT}$, $\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } C_{p} } \right)_{f}$ are the heat capacity of CNTs and base fluid, respectively. β_CNT, β_f are the thermal expansion co-efficient of CNTs as well as base fluid.

Boundary Conditions

Boundary conditions of the above system is considered as

$$ \begin{aligned} u^{\prime} & = u^{\prime}_{w} + u^{\prime}_{s} ,\,\,\,v^{\prime} = 0,\,\,\,T = \dot{T}_{w} + T_{s} ,\,\,\,{\text{at}}\,\,\,\,y = 0\,\, \\ & \quad \,u^{\prime} \to 0,\,\,\,T \to T_{\infty } ,\,\,\,\,{\text{as}}\,\,\,\,y \to \infty \\ \end{aligned} $$

(16)

u_s′ is the velocity slip which is proportional locally to the shear stress at the wall, i.e. $u^{\prime}_{s} = \dot{l}_{1} \frac{{\partial u^{\prime}}}{\partial y}$, where $\dot{l}_{1}$ shows momentum slip parameter and expressed as $\dot{l}_{1} = l_{1} x^{{ - \frac{m - 1}{2}}} .$ Furthermore, the slip temperature near solid boundary indicated as $T_{s} = \dot{l}_{2} \frac{\partial T}{\partial y}$, and $\dot{l}_{2} = l_{2} x^{{ - \frac{m - 1}{2}}}$ is called as the thermal slip parameter. If no slippage case then $\dot{l}_{1} = \dot{l}_{2} = 0$.

Non-dimensionalization

Arrange the stream function $\bar{\psi }$ such that fulfilling the expression of continuity interpreted as $u^{\prime} = \frac{{\partial \bar{\psi }}}{\partial y}$ as well as $v^{\prime} = - \frac{{\partial \bar{\psi }}}{\partial x}.$ Then the expressions (2), (9) and the corresponding boundary conditions (16) are modified as follows

$$ \begin{aligned} & \frac{{\partial \bar{\psi }}}{\partial y}\frac{{\partial^{2} \bar{\psi }}}{\partial x\partial y} - \frac{{\partial \bar{\psi }}}{\partial x}\frac{{\partial^{2} \bar{\psi }}}{{\partial y^{2} }} + \lambda_{1} \left( {\left( {\frac{{\partial \bar{\psi }}}{\partial y}} \right)^{2} \frac{{\partial^{3} \bar{\psi }}}{{\partial x^{2} \partial y}} + \left( {\frac{{\partial \bar{\psi }}}{\partial x}} \right)^{2} \frac{{\partial^{3} \bar{\psi }}}{{\partial y^{3} }} - 2\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\psi } }}{\partial y}\frac{{\partial \bar{\psi }}}{\partial x}\frac{{\partial^{3} \bar{\psi }}}{{\partial x\partial y^{2} }}} \right) \\ & \quad = \frac{1}{{\left( {1 - \varphi + \varphi \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho }_{CNT} }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho }_{f} }}} \right)}}\left( {\frac{{\nu_{f} }}{{\left( {1 - \varphi } \right)^{2.5} }}\frac{{\partial^{3} \bar{\psi }}}{{\partial y^{3} }} + \left( {1 - \varphi + \varphi \frac{{\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } \beta } \right)_{CNT} }}{{\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } \beta } \right)_{f} }}} \right)\frac{{\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } \beta } \right)_{f} }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho }_{f} }}g\left( {T - T_{\infty } } \right) - \frac{{\sigma \tilde{B}^{2} \left( x \right)}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho }_{f} }}\frac{{\partial \bar{\psi }}}{\partial y}} \right) \\ \end{aligned} $$

(17)

$$ \begin{aligned} & \frac{{\partial \bar{\psi }}}{\partial y}\frac{\partial T}{\partial x} - \frac{{\partial \bar{\psi }}}{\partial x}\frac{\partial T}{\partial y} + \lambda_{2} \left( {\frac{{\partial \bar{\psi }}}{\partial y}\frac{{\partial^{2} \bar{\psi }}}{\partial x\partial y}\frac{\partial T}{\partial x} + \frac{{\partial \bar{\psi }}}{\partial x}\frac{{\partial^{2} \bar{\psi }}}{\partial x\partial y}\frac{\partial T}{\partial y} - \frac{{\partial \bar{\psi }}}{\partial y}\frac{{\partial^{2} \bar{\psi }}}{{\partial x^{2} }}\frac{\partial T}{\partial y}} \right. \\ & \quad \quad \left. { - \frac{{\partial \bar{\psi }}}{\partial x}\frac{{\partial^{2} \bar{\psi }}}{{\partial y^{2} }}\frac{\partial T}{\partial x} - 2\frac{{\partial \bar{\psi }}}{\partial y}\frac{{\partial \bar{\psi }}}{\partial x}\frac{{\partial^{2} T}}{\partial x\partial y} + \left( {\frac{{\partial \bar{\psi }}}{\partial y}} \right)^{2} \frac{{\partial^{2} T}}{{\partial x^{2} }} + \left( {\frac{{\partial \bar{\psi }}}{\partial x}} \right)^{2} \frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) \\ & \quad = \frac{{\tilde{K}_{nf} }}{{\left( {1 - \varphi } \right)\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } C_{p} } \right)_{f} + \varphi \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } C_{p} } \right)_{CNT} }}\frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{16\sigma_{s} T_{\infty }^{3} }}{{3k_{e} \rho C_{p} }}\frac{{\partial^{2} T}}{{\partial y^{2} }} \\ \end{aligned} $$

(18)

With boundary conditions

$$ \begin{aligned} \frac{{\partial \bar{\psi }}}{\partial y} & = a^{\prime}x^{m} + l_{2}^{'} \frac{{\partial^{2} \bar{\psi }}}{{\partial y^{2} }},\,\,\,\frac{{\partial \bar{\psi }}}{\partial x} = 0,\,\,T = \dot{T}_{w} + l_{2}^{'} \frac{\partial T}{\partial y},\,\,\,{\text{at}}\,\,y = 0, \\ & \quad \frac{{\partial \bar{\psi }}}{\partial y} \to 0,\,\,\,T \to T_{\infty } \,\,\,{\text{as}}\,\,\,y \to \infty \\ \end{aligned} $$

(19)

Furthermore, originating the local similarity transformation like

$$ \eta = y\sqrt {\frac{{a^{\prime}x^{m - 1} }}{{\nu_{f} }}} ,\,\,\,\bar{\psi } = \sqrt {a^{\prime}x^{m + 1} \nu^{\prime}_{f} } f\left( \eta \right),\,\,\,\theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{\dot{T}_{w} - T_{\infty } }} $$

(20)

Hence

$$ u^{\prime} = a^{\prime}x^{m} f^{\prime}\left( \eta \right),\,\,\,v^{\prime} = - \frac{1}{2}\sqrt {a^{\prime}\nu_{\text{f}} x^{m - 1} } \left\{ {\left( {m + 1} \right)f\left( \eta \right) + \left( {m - 1} \right)\eta f'\left( \eta \right)} \right\} $$

(21)

Substitute the expression (17) into the expressions (14)–(16), we can obtain

$$ \begin{aligned} & f^{\prime\prime\prime} + \left( {1 - \varphi } \right)^{2.5} \left[ {\left( {1 - \varphi + \varphi \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho }_{CNT} }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho }_{f} }}} \right)\left( {\frac{m + 1}{2}ff^{\prime\prime} - mf^{\prime 2} } \right.} \right. \\ & \quad \left. { - \alpha \left\{ \begin{aligned} m\left( {m - 1} \right)f^{\prime 3} - \frac{{m^{2} - 1}}{4}\eta f^{\prime 2} f^{\prime\prime} \hfill \\ + \frac{{\left( {m + 1} \right)^{2} }}{4}f^{2} f^{\prime\prime\prime} - \frac{{\left( {m + 1} \right)\left( {3m - 1} \right)}}{2}ff^{\prime}f^{\prime\prime\prime} \hfill \\ \end{aligned} \right\}} \right) \\ & \quad \left. { - M^{2} f^{\prime} + \left( {1 - \varphi + \varphi \frac{{\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } \beta } \right)_{CNT} }}{{\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } \beta } \right)_{f} }}} \right)\bar{\lambda }\theta } \right] = 0 \\ \end{aligned} $$

(22)

$$ \begin{aligned} & \left( {1 + Nr} \right)\frac{1}{\Pr }\frac{{\tilde{K}_{nf} }}{{\tilde{K}_{f} }}\theta^{\prime\prime} + \left\{ {1 - \varphi + \varphi \frac{{\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } C_{p} } \right)_{CNT} }}{{\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } C_{p} } \right)_{f} }}} \right\} \\ & \quad \times \left[ \begin{array}{l} \frac{m + 1}{2}f\theta^{\prime} - 2mf^{\prime}\theta - \gamma \hfill \\ \left\{ \begin{array}{l} \left( {6m^{2} - 2m} \right)\theta f^{\prime} + \frac{{\left( {3 - 9m} \right)\left( {m + 1} \right)}}{4}ff^{\prime}\theta^{\prime} \hfill \\ - m\left( {m + 1} \right)\theta ff^{\prime\prime} + \frac{{\left( {m + 1} \right)^{2} }}{4}f^{2} \theta^{\prime\prime} \hfill \\ \end{array} \right\} \hfill \\ \end{array} \right] = 0 \\ \end{aligned} $$

(23)

The appropriate boundary conditions are

$$ \begin{aligned} f\left( 0 \right) & = 0,\,\,\,f^{\prime}\left( 0 \right) = 1 + \xi f^{\prime\prime}\left( 0 \right),\,\,\,\theta \left( 0 \right) = 1 + \zeta \theta^{\prime}\left( 0 \right),\,\,\,{\text{at}}\,\,\eta = 0 \\ f^{\prime}\left( \eta \right) & = 0,\,\,\theta \left( \eta \right) = 0,\,\,\,{\text{as}}\,\,\,\eta \to \infty \\ \end{aligned} $$

(24)

In the above equations η represents similarity variable; f(η) denotes the non-dimensional stream function; θ(η) denotes the non-dimensional temperature; $\bar{\lambda } = \frac{{Gr_{x} }}{{\text{Re}_{x}^{2} }}$ denotes thermal buoyancy factor that is proportion of local Reynolds number as well as local Grashof number explicated with $\text{Re}_{x} = \frac{{u^{\prime}_{w} }}{{v^{\prime}_{f} }}$, $Gr_{x} = \frac{{\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } \beta } \right)_{f} \left( {\dot{T}_{w} - T_{\infty } } \right)x^{3} }}{{\bar{v}_{f}^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho }_{f} }}$ respectively. $M = \tilde{B}_{0} \sqrt {\frac{\sigma }{{a\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho }_{f} }}}$ is the external magnetic flux factor. When $\bar{\lambda }$ greater than zero it supports the flow and for less than zero it obstruct the flow.

If $\bar{\lambda }$ is equal to zero it express position of forced convection. If $\bar{\lambda }$ is very much larger than 1, the force of buoyancy will be prevalent. Therefore, mixed convective flow procreates when $\bar{\lambda } = 0\left( 1 \right)$; $\bar{\alpha } = \bar{\lambda }_{1} a^{\prime}x^{m - 1}$ and $\gamma = \bar{\lambda }_{2} a^{\prime}x^{m - 1}$ illustrates fluid relaxation duration as well as thermal relaxation duration respectively. $\Pr = \frac{{\mu^{\prime}_{f} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } C_{p} } \right)_{f} }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho }_{f} \tilde{K}_{f} }}$ is the Prandtl number. Furthermore, the slip momentum factor is designated by $\xi = l_{1} \sqrt {\frac{{a^{\prime}}}{{\nu_{f} }}}$ and thermal slip factor is denoted as $\zeta = l_{2} \sqrt {\frac{{a^{\prime}}}{{\nu_{f} }}}$, $Nr = \frac{{16\sigma_{e} T_{\infty }^{3} }}{{3k_{e} k}}$ is the radiation parameter.

Physical Quantities of Interest

Physical quantities assign in current research are co-efficient of skin friction C_fx and the Nusselt number Nu_x are expressed as

$$ C_{fx} = \frac{{\mu^{\prime}_{nf} }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho }_{f} \bar{u}_{w}^{2} }}\left( {\frac{\partial u}{\partial y}} \right)_{y = 0} = \frac{1}{{\left( {1 - \varphi } \right)^{2.5} }}\text{Re}_{x}^{{ - \frac{1}{2}}} f^{\prime\prime}\left( 0 \right) $$

(25)

$$ Nu_{x} = - \frac{{x\tilde{K}_{nf} }}{{\tilde{K}_{f} \left( {T_{w} - T_{\infty } } \right)}}\left( {\frac{\partial T}{\partial y}} \right)_{y = 0} + q_{ry = 0} = - \text{Re}_{x}^{{ - \frac{1}{2}}} \frac{{\tilde{K}_{nf} }}{{\tilde{K}_{f} }}(1 + Nr)\theta^{\prime\prime}\left( 0 \right) $$

(26)

Now, degraded skin friction as well as degraded Nusselt number will be defined as

$$ C_{fx} = C_{fx} \text{Re}_{x}^{{\frac{1}{2}}} = \frac{1}{{\left( {1 - \varphi } \right)^{2.5} }}f^{\prime\prime}\left( 0 \right) $$

(27)

$$ Nu_{x} = Nu_{x} \text{Re}_{x}^{{ - \frac{1}{2}}} = - \frac{{\tilde{K}_{nf} }}{{\tilde{K}_{f} }}(1 + Nr)\theta^{\prime}\left( 0 \right) $$

(28)

Numerical Experiment

Put

$$ \begin{aligned} B_{ 1} & = \left( { 1 - \varphi } \right)^{ 2. 5} ,\,\,\,B_{2} = \left( {1 - \varphi + \varphi \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho }_{CNT} }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho }_{f} }}} \right),\,\,\,\,B_{3} = \left( {1 - \varphi + \varphi \frac{{(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } \beta )_{CNT} }}{{(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } \beta )_{f} }}} \right), \\ B_{4} & = \left( {1 + Nr} \right)\frac{1}{{P_{r} }}\frac{{\tilde{K}_{n} f}}{{\tilde{K}_{f} }},\,\,\,\,B_{5} = \left( {1 - \chi + \chi \frac{{(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } C_{p} )_{CNT} }}{{(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } C_{p} )_{f} }}} \right). \\ \end{aligned} $$

$$ \begin{aligned} n_{1} & = \frac{m + 1}{2},\,\,\,n_{2} = m(m - 1),\,\,\,n_{3} = \frac{{m^{2} - 1}}{4},\,\,\,n_{4} = \frac{{(m + 1)^{2} }}{2},\,\,\, \\ n_{5} & = \frac{(m + 1)(3m - 1)}{2},\,\,\,n_{ 6} = 6m^{ 2} - 2m,\,\,\,n_{7} = \frac{(3 - 9m)(m + 1)}{4}. \\ \end{aligned} $$

Now Eqs. (19)–(20) become,

$$ \begin{aligned} & f^{\prime\prime\prime} + B_{1} (B_{2} n_{1} ff^{\prime\prime} - mf^{{{\prime }2}} - \bar{\alpha }\{ n_{2} f^{{{\prime }3}} - n_{3} \eta f^{{{\prime }2}} f^{\prime\prime} \\ & \quad + n_{4} f^{2} f^{\prime\prime\prime} - n_{5} ff^{\prime}f^{\prime\prime}\} ) - Mf^{\prime} + B_{3} \bar{\lambda }\theta = 0 \\ \end{aligned} $$

(29)

$$ B_{4} \theta^{\prime\prime} + B_{5} \left\{ {n_{1} f\theta^{\prime} - 2mf^{\prime}\theta - \gamma \left( {n_{6} \theta f^{\prime} + n_{7} ff^{\prime}\theta^{\prime} - n_{8} \theta ff^{\prime\prime} + n_{4} f^{2} \theta^{\prime\prime}} \right)} \right\} = 0 $$

(30)

Again put

$$ f\prime = q,\,\,\,f\prime \prime = q\prime = r,\,\,\,f\prime \prime \prime = r\prime = s;\,\,\,\,\theta \prime = p,\,\,\,\theta \prime \prime = p\prime . $$

Now the Eqs. (26)–(27) will become

$$ r' + B_{1} \left( {B_{2} n_{1} fr - mq^{2} - \bar{\alpha }\left\{ {n_{2} q^{3} - n_{3} \eta q^{2} r + n_{4} f^{2} s - n_{5} fqr} \right\} - Mq + B_{3} \bar{\lambda }\theta } \right) = 0 $$

(31)

$$ B_{4} p' + B_{4} \left[ {n_{1} fp - 2mq\theta - r\left( {n_{6} \theta q + n_{7} fqP - n_{8} \theta fr + n_{4} f^{2} p'} \right)} \right] = 0 $$

(32)

$$ f_{j}^{i} - f_{j - 1}^{i} = \frac{{h_{j} }}{2}\left( {q_{j} + q_{j - 1} } \right) $$

(33)

$$ q_{j}^{i} - q_{j - 1}^{i} = \frac{{h_{j} }}{2}\left( {r_{j} + r_{j - 1} } \right) $$

(34)

$$ \theta_{j}^{i} - \theta_{j - 1}^{i} = \frac{{h_{j} }}{2}\left( {p_{j} + p_{j - 1} } \right) $$

(35)

$$ \begin{aligned} & \left( {r_{j}^{i} - r_{j - 1}^{i} } \right) + B_{1} h_{j} \left[ {B_{2} n_{1} f_{{j - \frac{1}{2}}}^{i} r_{{j - \frac{1}{2}}}^{i} - m\left( {q_{{j - \frac{1}{2}}}^{i} } \right)^{2} - \bar{\alpha }\left\{ {n_{2} \left( {q_{{j - \frac{1}{2}}}^{i} } \right)^{3} } \right.} \right. \\ & \quad \left. {\left. { - n_{3} \eta \left( {q_{{j - \frac{1}{2}}}^{i} } \right)^{2} \left( {r_{{j - \frac{1}{2}}}^{i} } \right) + n_{4} \left( {f_{{j - \frac{1}{2}}}^{i} } \right)^{2} \left( {s_{{j - \frac{1}{2}}}^{i} } \right) - n_{5} f_{{j - \frac{1}{2}}}^{i} q_{{j - \frac{1}{2}}}^{i} r_{{j - \frac{1}{2}}}^{i} } \right\}} \right] \\ & \quad - M\left( {q_{{j - \frac{1}{2}}}^{i} } \right) + B_{3} \bar{\lambda }\left( {\theta_{{j - \frac{1}{2}}}^{i} } \right) = M_{{j - \frac{1}{2}}} \\ \end{aligned} $$

(36)

$$ \begin{aligned} & B_{4} \left( {P_{j}^{i} - P_{{j - \frac{1}{2}}}^{i} } \right) + B_{5} h_{j} \left[ {n_{1} f_{{j - \frac{1}{2}}}^{i} P_{{j - \frac{1}{2}}}^{i} - 2m\left( {q_{{j - \frac{1}{2}}}^{i} \theta_{{j - \frac{1}{2}}}^{i} } \right)} \right. \\ & \quad \left. { - r\left\{ {n_{6} \theta_{{j - \frac{1}{2}}}^{i} q_{{j - \frac{1}{2}}}^{i} + n_{7} f_{{j - \frac{1}{2}}}^{i} q_{{j - \frac{1}{2}}}^{i} P_{{j - \frac{1}{2}}}^{i} - n_{8} \theta_{{j - \frac{1}{2}}}^{i} f_{{j - \frac{1}{2}}}^{i} r_{{j - \frac{1}{2}}}^{i} + n_{4} \left( {f_{{j - \frac{1}{2}}}^{i} } \right)^{2} } \right\}} \right] \\ & \,\quad \frac{{\left( {p_{j}^{i} - p_{{j - \frac{1}{2}}}^{i} } \right)}}{{h_{j} }} = L_{{j - \frac{1}{2}}} \\ \end{aligned} $$

(37)

Here

$$ \begin{aligned} M_{{j - \frac{1}{2}}} & = - \left( {r_{j}^{i - 1} - r_{j - 1}^{i - 1} } \right) + B_{1} h_{j} \left[ {B_{2} n_{2} \left( {f_{{j - \frac{1}{2}}}^{i - 1} r_{{j - \frac{1}{2}}}^{i - 1} } \right) - m\left( {q_{{j - \frac{1}{2}}}^{i - 1} } \right)^{2} } \right. \\ & \quad - \bar{\alpha }\left\{ {n_{2} \left( {q_{{j - \frac{1}{2}}}^{i - 1} } \right)^{3} - n_{3} \eta \left( {q_{{j - \frac{1}{2}}}^{i - 1} } \right)^{2} r_{{j - \frac{1}{2}}}^{i - 1} + n_{4} \left( {f_{{j - \frac{1}{2}}}^{i - 1} } \right)^{2} s_{{j - \frac{1}{2}}}^{i - 1} } \right. \\ & \quad \left. {\left. { - n_{5} f_{{j - \frac{1}{2}}}^{i - 1} q_{{j - \frac{1}{2}}}^{i - 1} r_{{j - \frac{1}{2}}}^{i - 1} } \right\}} \right] - Mq_{{j - \frac{1}{2}}}^{i - 1} + B_{3} \bar{\lambda }\theta_{{j - \frac{1}{2}}}^{i - 1} \\ \end{aligned} $$

(38)

$$ \begin{aligned} L_{{j - \frac{1}{2}}} & = - B_{4} \left( {p_{j}^{i - 1} - p_{j - 1}^{i - 1} } \right) - B_{5} h_{j} \left[ {n_{1} f_{{j - \frac{1}{2}}}^{i - 1} } \right.p_{{j - \frac{1}{2}}}^{i - 1} - 2m\left( {q_{{j - \frac{1}{2}}}^{i - 1} \theta_{{j - \frac{1}{2}}}^{i - 1} } \right)^{{}} \\ & \quad + r\left\{ {n_{6} \left( {q_{{j - \frac{1}{2}}}^{i - 1} \theta_{{j - \frac{1}{2}}}^{i - 1} } \right)^{3} + n_{7} f_{{j - \frac{1}{2}}}^{i - 1} q_{{j - \frac{1}{2}}}^{i - 1} p_{{j - \frac{1}{2}}}^{i - 1} } \right. \\ & \quad - \left. {\left. {n_{5} \theta_{{j - \frac{1}{2}}}^{i - 1} f_{{j - \frac{1}{2}}}^{i - 1} r_{{j - \frac{1}{2}}}^{i - 1} + n_{4} \left( {f_{{j - \frac{1}{2}}}^{i - 1} } \right)^{2} \left( {\frac{{p_{j}^{i - 1} - p_{j - 1}^{i - 1} }}{{h_{j} }}} \right)} \right\}} \right] \\ \end{aligned} $$

(39)

$$ e_{1} \delta r_{j} + e_{2} \delta r_{j - 1} + e_{3} \delta q_{j} + e_{4} \delta q_{j - 1} + e_{5} \delta f_{j} + e_{6} \delta f_{j - 1} = \left( {b_{5} } \right)_{j} $$

(40)

$$ \left( {e_{1} } \right)_{j} = 1 + \frac{{B_{1} B_{2} h_{j} n_{1} }}{2}f_{{j - \frac{1}{2}}}^{i} - \frac{{B_{1} h_{j} }}{2}\left( {q_{{j - \frac{1}{2}}}^{i} } \right)^{2} \bar{\alpha }n_{3} \eta $$

(41)

$$ \left( {e_{2} } \right)_{j} = - 1 + \frac{{B_{1} B_{2} h_{j} n_{1} }}{2}f_{{j - \frac{1}{2}}}^{i} - \frac{{B_{1} h_{j} }}{2}\left( {q_{{j - \frac{1}{2}}}^{i} } \right)^{2} \bar{\alpha }n_{3} \eta $$

(42)

$$ \begin{aligned} \left( {e_{3} } \right)_{j} & = \frac{{B_{1} h_{j} m}}{2}q_{{j - \frac{1}{2}}}^{i} - \frac{{B_{1} h_{j} \bar{\alpha }n_{2} }}{2}\left( {q_{{j - \frac{1}{2}}}^{i} } \right)^{2} + \frac{{B_{1} h_{j} n_{3} \bar{\alpha }\eta }}{2}\left( {q_{{j - \frac{1}{2}}}^{i} } \right)\left( {r_{{j - \frac{1}{2}}}^{i} } \right) \\ & \quad + \frac{{B_{1} h_{j} \bar{\alpha }n_{5} f_{{j - \frac{1}{2}}}^{i} r_{{j - \frac{1}{2}}}^{i} }}{2} - M \\ \end{aligned} $$

$$ \left( {e_{4} } \right)_{j} = \left( {e_{3} } \right)_{j} $$

(43)

$$ \left( {e_{5} } \right)_{j} = 1 + \frac{{B_{1} h_{j} n_{1} }}{2}r_{{j - \frac{1}{2}}}^{i} - \frac{{B_{1} h_{j} }}{2}\bar{\alpha }n_{4} \eta f_{{j - \frac{1}{2}}}^{i} s_{{j - \frac{1}{2}}}^{i} , $$

(44)

$$ \left( {e_{6} } \right)_{j} = \left( {e_{5} } \right)_{j} ; $$

(45)

$$ \left( {\delta f_{j} - \delta f_{j - 1} } \right) - \frac{{h_{j} }}{2}\left( {q_{j} + q_{j - 1} } \right) = \left( {b_{1} } \right)_{j} $$

(46)

$$ \left( {\delta q_{j} - \delta q_{j - 1} } \right) - \frac{{h_{j} }}{2}\left( {r_{j} + r_{j - 1} } \right) = \left( {b_{2} } \right)_{j} $$

(47)

$$ \left( {\delta r_{j} - \delta r_{j - 1} } \right) - \frac{{h_{j} }}{2}\left( {s_{j} + s_{j - 1} } \right) = \left( {b_{3} } \right)_{j} $$

(48)

$$ \left( {\delta \theta_{j} - \delta \theta_{j - 1} } \right) - \frac{{h_{j} }}{2}\left( {p_{j} + p_{j - 1} } \right) = \left( {b_{4} } \right)_{j} $$

(49)

$$ \left( {g_{1} } \right)_{j} = B_{4} + \frac{{B_{5} h_{j} n_{1} }}{2}f_{{j - \frac{1}{2}}}^{i} + \frac{{B_{5} h_{j} \gamma n_{7} }}{2}f_{{j - \frac{1}{2}}}^{i} q_{{j - \frac{1}{2}}}^{i} - B_{5} \gamma n_{4} \left( {f_{{j - \frac{1}{2}}}^{i} } \right)^{2} $$

(50)

$$ \left( {g_{2} } \right)_{j} = - B_{4} + \frac{{B_{5} h_{j} n_{1} }}{2}f_{{j - \frac{1}{2}}}^{i} + \frac{{B_{5} h_{j} \gamma n_{7} }}{2}f_{{j - \frac{1}{2}}}^{i} q_{{j - \frac{1}{2}}}^{i} - B_{5} \gamma n_{4} \left( {f_{{j - \frac{1}{2}}}^{i} } \right)^{2} $$

(51)

$$ \left( {g_{3} } \right)_{j} = - mB_{5} h_{j} \theta_{{j - \frac{1}{2}}}^{{}} - \frac{{B_{5} h_{j} \gamma n_{6} }}{2}\theta_{{j - \frac{1}{2}}}^{{}} - B_{5} h_{j} \gamma n_{7} f_{{j - \frac{1}{2}}}^{i} p_{{j - \frac{1}{2}}}^{i} $$

(52)

$$ \left( {g_{4} } \right)_{j} = \left( {g_{3} } \right)_{j} $$

(53)

$$ \begin{aligned} \left( {g_{5} } \right)_{j} & = \frac{{B_{5} h_{j} n_{1} }}{2}p_{{j - \frac{1}{2}}}^{i} - \frac{{B_{5} h_{j} \gamma n_{7} }}{2}q_{{j - \frac{1}{2}}}^{i} p_{{j - \frac{1}{2}}}^{i} \\ & \quad + \frac{{B_{5} h_{j} n_{8} \gamma }}{2}\theta_{{j - \frac{1}{2}}}^{i} r_{{j - \frac{1}{2}}}^{i} + \frac{{B_{5} h_{j} n_{4} }}{2}f_{{j - \frac{1}{2}}}^{i} \left( {p_{{j - \frac{1}{2}}}^{i} } \right) \\ \end{aligned} $$

(54)

$$ \left( {g_{6} } \right)_{j} = \left( {g_{5} } \right)_{j} $$

(55)

$$ \begin{aligned} \left( {b_{5} } \right)_{j} & = B_{1} h_{j} n_{4} \left( {f_{{j - \frac{1}{2}}}^{i} } \right)^{2} \left( {s_{{j - \frac{1}{2}}}^{i} } \right) + B_{1} h_{j} n_{2} \bar{\alpha }\left( {q_{{j - \frac{1}{2}}}^{i} } \right)^{3} \\ & \quad + B_{3} \bar{\lambda }\theta_{{j - \frac{1}{2}}}^{i} + M_{{j - \frac{1}{2}}} \\ \end{aligned} $$

(56)

$$ \left( {b_{6} } \right)_{j} = B_{5} h_{j} n_{8} \theta_{{j - \frac{1}{2}}} f_{{j - \frac{1}{2}}} r_{{j - \frac{1}{2}}} + L_{{j - \frac{1}{2}}} $$

(57)

$$ A\delta = B $$

(58)

where,

$$ A = \left[ {\begin{array}{*{20}c} {E_{1} } & {C_{1} } & \cdots & \cdots & \cdots & \cdots \\ {D_{1} } & {E_{2} } & \cdots & \cdots & \cdots & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \cdots & \cdots & \cdots & \cdots & {D_{J} } & {E_{J} } \\ \end{array} } \right]\,\,\delta = \left[ {\begin{array}{*{20}c} {\delta_{1} } \\ {\delta_{2} } \\ \vdots \\ \vdots \\ {\delta_{J} } \\ \end{array} } \right]\,\,B = \left[ {\begin{array}{*{20}c} {b_{1} } \\ {b_{2} } \\ \vdots \\ \vdots \\ {b_{j} } \\ \end{array} } \right] $$

$$ E_{1} = \left[ {\begin{array}{*{20}c} 0 & 0 & 1 & 0 & 0 \\ {\frac{{ - h_{1} }}{2}} & 0 & 0 & {\frac{{ - h_{1} }}{2}} & 0 \\ 0 & {\frac{{ - h_{1} }}{2}} & 0 & 0 & {\frac{{ - h_{1} }}{2}} \\ {e_{2} } & 0 & {e_{5} } & {e_{1} } & 0 \\ 0 & {g_{2} } & {g_{5} } & 0 & {g_{1} } \\ \end{array} } \right] $$

(59)

$$ C = \left[ {\begin{array}{*{20}c} {\frac{{ - h_{1} }}{2}} & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ {e_{3} } & 0 & 0 & 0 & 0 \\ {g_{3} } & 0 & 0 & 0 & 0 \\ \end{array} } \right] $$

(60)

$$ D = \left[ {\begin{array}{*{20}c} 0 & 0 & { - 1} & 0 & 0 \\ 0 & 0 & 0 & {\frac{{ - h_{2} }}{2}} & 0 \\ 0 & 0 & 0 & 0 & {\frac{{ - h_{2} }}{2}} \\ 0 & 0 & {e_{6} } & {e_{2} } & 0 \\ 0 & 0 & {g_{6} } & 0 & {g_{2} } \\ \end{array} } \right] $$

(61)

$$ E_{2} = \left[ {\begin{array}{*{20}c} {\frac{{ - h_{2} }}{2}} & 0 & 1 & 0 & 0 \\ { - 1} & 0 & 0 & {\frac{{ - h_{2} }}{2}} & 0 \\ 0 & { - 1} & 0 & 0 & {\frac{{ - h_{2} }}{2}} \\ {e_{4} } & 0 & {e_{5} } & {e_{1} } & 0 \\ {g_{4} } & 0 & {g_{5} } & 0 & {g_{1} } \\ \end{array} } \right] $$

(62)

The method used to solve (58) is the block elimination tri-diagonal method. The convergence criterion is set as 0.0001.

Solution of the Problem by MDDIM

For more details of MDDIM, Liao [72] was introduced this technique for finding an approximate analytical solution to highly nonlinear differential equations. The method of MDDIM is used for obtaining the approximate analytical solution of (22)–(23) with (24). We assume the set of an infinite number of base functions that are linearly independent variables areas;

$$ M_{\infty } = \left\{ {1,\,e^{ - \eta \delta } ,\,e^{ - 2\eta \delta } ,\,e^{ - 3\eta \delta } , \ldots } \right\}. $$

(63)

We have considered the base functions as;

$$ X = \sum\limits_{j = 0}^{\infty } {\left\{ {\sigma_{j} e^{ - j\eta \delta } /\sigma_{j} \varepsilon {\mkern 1mu} \Re } \right\}} . $$

(64)

Here X is the solution and base space for f(η) and θ(η).

Consider first two terms of M_∞ as

$$ M_{2} = \left\{ { 1, e^{ - \eta \delta } } \right\}. $$

(65)

Next, form the space of functions taking their linear combinations

$$ M* = \left\{ {\sigma_{0} + \sigma_{1} e^{ - \eta \delta } /\sigma_{0} ,\sigma_{1} \varepsilon \,\Re } \right\} . $$

(66)

Take primary solutions as ξ(η) belongs to M*  have the following form

$$ \xi (\eta ) = \sum\limits_{j = 0}^{1} {\left\{ {\sigma_{j} e^{ - \eta \delta } } \right\}} . $$

(67)

Write,

$$ \hat{A} = \left\{ {e^{ - 2\eta \delta } ,\,e^{ - 3\eta \delta } ,\, \ldots } \right\}, $$

(68)

and we define $\hat{X}$ as follows:

$$ \hat{X} = \sum\limits_{j = 2}^{\infty } {\left\{ {\sigma_{j} e^{ - j\eta \delta } /\sigma_{j} \varepsilon {\mkern 1mu} \Re } \right\}} . $$

(69)

Therefore, we get the functions as: $X = \hat{X}UM^{*}$.

Define base function as

$$ M_{R} = \left\{ {\mu_{1} (\eta ),\,\mu_{2} (\eta ),\,\mu_{3} (\eta ), \ldots } \right\} $$

(70)

The linear combinations of base function from Eq. (6), we defined as;

$$ S = \sum\limits_{j = 1}^{\infty } {\left\{ {a_{j} \mu_{j} (\eta )/a_{j} \varepsilon {\mkern 1mu} \Re } \right\}} . $$

(71)

Define inversely defined mapping for the solution of f as follows;

$$ {\text{Define}}\,\,{\text{ J}}:{\text{S}}\, \to \,{\text{X}}\,\,{\text{ by}}\,\,\,J\left[ {e^{ - j\eta \delta } } \right] = \frac{{e^{ - j\eta \delta } }}{{Aj^{3} + j}}. $$

(72)

where δ and A, are parameters.

Define inversely defined mapping for the solution of θ as follows;

$$ {\text{Define }}\,{\text{J}}:{\text{S}} \to {\text{X }}\,{\text{by}}\,\,\,J\left[ {e^{ - j\eta \delta } } \right] = \frac{{e^{ - j\eta \delta } }}{Aj + j}. $$

(73)

In the present problem, analysis of MDDIM, from Eq. (24), we choose the initial guesses as follows;

$$ f_{0} \left( \eta \right) = \xi \left( { 1 {-} e^{ - \eta } } \right) + \eta ,\,\,\,{\text{and}}\,\,\,\theta_{0} \left( \eta \right) = \left( { 1 - \xi } \right)e^{ - \eta } . $$

(74)

The objective of the proposed analysis that is MDDIM is that choosing appropriate initial profiles which sustaining the initial conditions of the current study; choose directly defined inverse mappings for the solutions, which simplifies the evaluation process analytically. From the governing equations of the present study we can write the nonlinear operator directly. In MDDIM process, we obtain a set of nonlinear differential equations which are called deformation equations and these have to solve. We assumed the set of base functions, initial guesses and directly defined inverse mappings for the solution analysis. Using computational software’s MAPLE and MATHEMATICA, the governing equations are reformulated, and the series solutions computed. Since the MDDIM is explained in detail in [72,73,74], the method of solution procedure not presented here for the sake of brevity.

Verification of Code

An analogy in sketch among current results with that of Li et al. [68], to demonstrate preciseness of the method we executed. Table 2 displayed the determine values of co- efficient of skin friction f″ (0), as well as Nusselt number θ′ (0), for dissimilar values of ξ and λ in non-existence of single walled as well as multi walled carbon nano tubes concentration (φ = 0) along thermal radiation (Nr = 0), convective heating as well (Bi → ∞). Every one comfortably authenticates out of Table 2, that the data explained analytically and numerically acquired by the current techniques and that of Li et al. [68] are in excellent concord accordingly support the employ of the current code owing to present model.

Table 2 Comparison of MDDIM and KBM results with that of Li et al. [68] at f″(0) and − θ′ (0) for various ξ and λ with $m = 0.1,\,\bar{\alpha } = 0.4,\,\gamma = 0.3,\,M = 3.0,\,Pr = 1.0,\,Nr = 0,\,Bi \to \infty$

Results and Discussion

In the present part, the foremost aim is to examine the transformation of temperature, non-dimensional velocity, coefficient of skin friction, and Nusselt number, by the impact of changeable factors through MDDIM and KBM. Approximate analytical results and Numerical computations outcomes are shown in the Tables 2 and 3 and graphically presented in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12 to discuss various resulting parameters which are involved the problem. This comparison shows a decent agreement between present approximate analytical results and previous published work. Furthermore, the outcomes demonstrate that the MDDIM and KBM are very efficient and adequately powerful for use of solving fluid flow problems. Physical and thermal characteristics of base fluid are displayed in Table 1. These characteristics are accustomed to investigate the developments appearing in temperature and velocity profiles exposed to fluctuation in dissimilar factors. To carry out the computerized imitation, the fundamental measures of the factors are cautiously calculated as $\bar{\alpha } = 0.5$, φ = 0.2, M = 0.5, $\bar{\lambda } = 0.1$, m = 0.1, γ = 0.2, Pr = 0.7, B_i = 0.1, ξ = 0.1, and N_r = 0.5 except particularize.

Table 3 Effects of different parameters on C_fx and $Nu_{x}$ when Pr =0.7, Bi =0.1, λ = 0.1 and m = 0.1 by MDDIM

Fig. 2

The MDDIM solutions of dimensionless velocity distribution f′ (ς) for different values of M

Fig. 3

The MDDIM solutions of dimensionless temperature distribution θ(ς) for different values of M

Fig. 4

The MDDIM solutions of dimensionless velocity distribution f′ (ς) for different values of χ

Fig. 5

The MDDIM solutions of dimensionless temperature distribution θ(ς) for different values of χ

Fig. 6

The MDDIM solutions of dimensionless velocity distribution f′ (ς) for different values of ξ

Fig. 7

The MDDIM solutions of dimensionless temperature distribution θ(ς) for different values of ξ

Fig. 8

The MDDIM solutions of dimensionless velocity distribution f′ (ς) for different values of $\bar{\alpha }$

Fig. 9

The MDDIM solutions of dimensionless temperature distribution θ(ς) for different values of γ

Fig. 10

The MDDIM solutions of dimensionless temperature distribution θ(ς) for different values of Nr

Fig. 11

The MDDIM solutions of dimensionless temperature distribution θ(ς) for different values of Bi

Fig. 12

The MDDIM solutions of dimensionless temperature distribution θ(ς) for different values of Pr

From Table 2, it is noticed that for SWCNT and MWCNT nanofluids deviations in the co-efficient of skin friction and local Nusselt number for different factors. Table 3 declare that if ‘M’ rises from 0 to 0.5 significantly improve the values of C_fx for SWCNT nano fluid is increased by 46% and MWCNT nanofluid decreased by 3.89% additionally almost equal changes in measures of M, Nu_x, is raised by 44% for SWCNT nanofluid and decreased by 3.73% for MWCNT nanofluid. The relaxation factor α of the fluid changes between 0.0 and 0.5 the cut down C_fx and Nu_x for SWCNT is magnified by 1.02% and 1.11%, but the corresponding order of $\bar{\alpha }$, the enlargement of skin friction as well as the heat transport rate is decreased by 0.23% and 2.26% for MWCNT nanofluids. Get out of Table 3, it points that γ acquires from 0.0 to 0.5; $C_{fx}$ procure highly less fall of 0.09% and 1.25% concerning SWCNT as well as MWCNT founded nanofluids. That means friction among the layers of solid as well as fluid hike up as a result the velocity falling off. Furthermore it is acknowledged out of Table 3 that by the identical enlargement of $\gamma$, Nu_x against SWCNT nanofluid subsided by and concerning MWCNT nano fluid is declined by 0.03% and 1.23%. Ascertained that ξ ranks out of 0.0–1.0, the co-efficient of skin friction against SWCNT as well as MWCNT founded nano fluid declined through 45% and 3.43% respectively. Merely Nu_x for the equivalent cut down through 46% and 1.21%.

A crucial remark established in Table 3 is such as φ ranks concerning 0.01–0.2, C_fx against SWCNT as well as MWCNT nano fluid reduced through 51.4% and 75.3%. Furthermore, SWCNT as well as MWCNT nanofluid is declined through, 58% and 77% respectively against the equal class of φ, Nu_x. That means the lessening rate of transfer of heat concerning SWCNT founded nanofluid is more outstanding than MWCNT nanofluid. Furthermore it is ascertained that as φ truly complement by C_fx for two kinds of nano particles, merely the opposite result is prevailed against Nu_x. It is observed from Table 3 that, we perceived when Nr changes from 0.0 to 2.0 C_fx concerning SWCNT as well as MWCNT founded nanofluid prevails a decrease of 2.97% and 12.8%. Further Nu_x correspondingly declined through 2.8% and 12.68%.

Figures 2 and 3 displayed diagrammatically about the influence of magnetic factor ‘M’ on temperature also on velocity as well. Magnetic field which acts tangentially over fluid flow resistance creates which named as Lorentz force. The same force makes the fluid slow down like elongating sheet. The velocity profile of fluid reduces but temperature distribution amplifies by enhancing the magnetic factor. Also reveals that the magnetic field acts tangentially, resists transport phenomenon. Out of Fig. 2 it is meritorious that correlated to multi-walled carbon nano tube fluid the swiftness of single walled carbon nano tube disintegrates quickly with M, because of greater density measures for SWCNTs. Even temperature values also grater for MWCNT’s wherewith SWCNT’s. Principal consideration backside of this is grater thermal conductivity.

Figures 4 and 5 describe about the development of distribution of temperature as well as non-dimensional velocity by using solid nano particle volume proportion χ. Figure 4 designate that besides the progressive measures of φ, velocity profile advances, accordingly the momentum boundary layer increases notably. Also, it’s remarkable that MNCNT nanofluid velocity pick up quick development besides SWCNT nano fluid. Figure 5 is manifested by escalating the measures of φ, when the liquids temperature is reduced. Additionally, multi-walled carbon nano tubes have marginally greater values of temperature correlated to carbon nano tubes having single walled. As thermal expansion of SWCNTs is lower than MWCNT’s which in Table 1 is already examined.

The deviations in temperature and velocity because of proper growth in slip factor are shown in Figs. 6 and 7. Thickness of momentum boundary layer goes down in existence of SWCNT as well as MWCNT together. This prodigy taken place approximately by virtue of actuality such as ξ growth that is true slip increases as a result it accomplishes to a negligible quantity of diffusion by reason of elongated surface of the liquid. Nevertheless, smaller the fluid’s momentum, the friction among the layers of fluid and CNTs magnifies, turned out the temperature rises. The same information earlier said was displayed in Fig. 7 clearly.

Figure 8 manifest the influence of relaxation factor $\bar{\alpha }$ of a fluid on velocity profile during SWCNT plus MWCNT nano particles presence. The earlier figure conceals surprising reflection that, from outward, it explains velocity profile not notably interrupt by $\bar{\alpha }$, if browse carefully means when φ < 1 it appears the velocity falls.

Aforementioned one occurs as a result of the actuality that $\bar{\alpha }$ illustrate the relaxation time of fluid generally familiar as Deborah number, that performance significant work as an account of viscoelastic materials. When $\bar{\alpha }$ < 1 such as the memory duration is lesser then deformation duration α is proportion among the relaxation time and time of deformation. Consequently, the fluid designates as absolutely viscous. If $\bar{\alpha }$ > 1, fluid resembles as elastically solid. Hence, base liquid as engine oil that considered as merely viscous in nature. Therefore, we presume $\bar{\alpha }$ < 1 as in our study. Like $\bar{\alpha }$ growth, the viscosity amplifies consequently momentum of fluid declines. Hence, in association of CNTs of both types the thickness of momentum boundary layer is falling function of $\bar{\alpha }$.

Figure 9 exhibits the influence of thermal relaxation time (γ) over temperature distribution. Thermal relaxation factor is determined like slow response of heat flux. When n = 0 the determined heat flux model, is changed towards Fourier’s law. By progressive measures of γ, the thickness of thermal boundary layer goes down and also the rate of reduction is grater for MWCNT nano fluid in both cases. This peculiarity is noticed due to the reality that, SWCNTs thermal conductivity is greater from MWCNTs. Henceforth for SWCNT nano fluid transfer of disintegrate quickly when delay reaction of heat flux amplifies. By multiplying thermal radiation factor Nr, a flourishing in distribution of temperature is detected from Fig. 10 about SWCNT and MWCNT nano fluids as well. Because furtherance in radiation factor inferred reduce in Rosseland radiation absorptive. Therefore, variance of heat flux radiation q_r enhances such that co-efficient of absorption is reduced. Thus, transferred of heat radiation rate of the fluid rises accordingly temperature of fluid grows.

The MDDIM solutions of dimensionless temperature distribution θ(ς) for different values of Biot number Bi displayed in the Fig. 11. The better convention contributes to the peak surface temperatures that significantly magnifies the temperature and the thicknesses of thermal boundary layer increased.

In Fig. 12 we embellished the fluctuations of temperature beside Prandtl number during both CNTS. Note that, Pr = 0.7 is representing the air. We also ascertained that rise in the Prandtl number reduces in the temperature of fluid actually it defines that for greater Prandtl number thermal boundary layer gets delicate. Prandtl number indicates, momentum distribute as well as thermal distribute ratio. Therefore, Prandtl number utilizes to enhance the cooling rate in convective flows.

Conclusions

In this present article, we analyzed the effects of thermal radiation over CNT-engine oil-based Maxwell-nano fluid with heat flux model by Cattaneo–Christov, through a non-linear elongated surface. SWCNT and MWCNT are considered as nano particles because of their greater thermal conductivity as well as thermal expansion.

Observed points from the current examination are listed below:

• 1. In the presence of magnetic field velocities as well as temperatures are changed in the opposite manner.

• 2. Velocity as well as temperature of SWCNT lower than that of MWCNT.

• 3. For both SWCNT as well as MWCNT on enhancing the values of Nr and Bi temperature raised considerably.

• 4. The values of skin friction co-efficient, Nusselt number are more concerning MWCNT than those of SWCNTs.

The outcomes demonstrate that the MDDIM is efficient and adequately powerful for use of solving many fluid flow problems. This model contributes advanced characteristics which gives inspiration for further investigations.