Introduction

Fluids have diverse rheological characteristics. Therefore, it is not possible to study the rheological behaviors of fluids using one rheological stress–strain relation. For example, the Newtonian rheological model exhibits only viscosity-related rheology and its use for non-Newtonian fluids leads to erroneous results or provides inaccurate information about the flow and related phenomena (heat, mass transfer, etc.). Hence, non-Newtonian stress–strain relations have been proposed by the researchers. These stress–strain models include graded fluids and viscoelastic fluid models. Graded fluids are further divided into second grade [1], third grade [2], and fourth grade [3], whereas viscoelastic fluids are also categorized into Maxwell fluid [4], Jeffrey fluid [5], and Oldroyd fluids [6]. Here in this study, we are considering Maxwell Fluid. Various studies are available on this fluid. For example, Hayat et al. [7] investigated the unsteady flow of a Maxwell fluid in between two side walls caused by a rapidly moved sheet. Vieru et al. [8] expanded the investigation of the fractional Maxwell model for flow in between two perpendicular sidewalls of a plate. Wang and Hayat [9] investigated Maxwell’s fluid flow in a porous media Tan and Masuoka [10] investigated the linear convective stability of a Maxwell fluid layer in porous media. Ramesh and Gireesha [11] studied the effect of a heat source/sink on the behavior of a Maxwell nanofluid.

Controlling energy losses and improving the thermal performance of the working fluid are both important. For the enhancement of thermal performance, several techniques are in practice. The dispersion of nanoparticles solid particles in a fluid is a relatively new and effective approach. As a result of the higher thermal conductivity reflective of fluids in this suspension of nanosized solid particles, the effective thermal conductivity of the suspension rises, and it behaves like a good heat conductor. The working fluid’s thermal performance eventually improves. This remarkable feature of suspension has attracted the attention of researchers who want to understand more about the influence of nanoparticle suspension on fluid thermal performance. It is now a scientific fact that if many types of nanoparticles are dispersed in a fluid, optimal heat transfer may be accomplished. Hybrid nanoparticles are made up of many types of nanoparticles. The sole of hybrid nanoparticles on the thermal enhancement of fluids has recently attracted a lot of attention. Many researchers worked on hybrid nanofluids assuming different nanoparticles on heat and mass transfer. For example, Suresh et al.[12] examined the effect of \({\text{Al}}_{{\text{2}}} {\text{O}}_{{\text{3}}} - {\text{Cu/H}}_{{\text{2}}} {\text{O}}\) on heat transfer. Baghbanzadeha et al. [13] investigated the manufacture of spherical silica/multi-wall CNT hybrid nanoparticles of associated nanofluids. The effects of \({\text{Al}}_{{\text{2}}} {\text{O}}_{{\text{3}}} - {\text{Cu/H}}_{{\text{2}}} {\text{O}}\) on heat transfer and flow properties in the turbulent flow regime were investigated by Takabi and Shokouhmand [14]. Hayat and Nadeem [15] discussed the challenge of a hybrid nanofluid consisting of \({\text{Al}}_{{\text{2}}} {\text{O}}_{{\text{3}}} - {\text{CuO/H}}_{{\text{2}}} {\text{O}}\) rotational flow. Hayat et al. [16] analyzed the rotating flow of Ag – CuO/water with radiation and partial slip boundary effects. Subhani and Nadeem [17] worked on the topic of micropolar flow through an exponentially stretched surface in a hybrid nanofluid. Yousefi et al. [18] investigated the dynamics of stagnation point flow toward a wavy cylinder in a titania–copper hybrid nanofluid.

Most nanomodels, such as those of Buongiorno [19, 20], Nield, and Kuznetsov [21, 22], took Brownian diffusion and thermophoresis into account when modeling the transport equations. However, Tiwari and Das [23] proposed a mathematical nanofluid model that considers the solid volume fraction of nanoparticles when analyzing the behavior of nanofluids. However, this model ignored the effect of nanoparticles diameter on the fluid’s thermal properties. Correlations among the thermophysical properties of hybrid nanoparticle and fluid [23,24,25,26,27,28,29] are

$$\begin{aligned} \frac{{\mu _{{{\text{hnf}}}} }}{{\mu _{{\text{f}}} }} = & \frac{1}{{(1 - \varphi _{2} )^{{2.5}} (1 - \varphi _{1} )^{{2.5}} }}, \\ \frac{{\tilde{K}_{{{\text{hnf}}}} }}{{\tilde{K}_{{{\text{bf}}}} }} = & \frac{{ - 2\varphi _{2} \tilde{K}_{{{\text{bf}}}} + \tilde{K}_{{{\text{s}}_{2} }} + 2\tilde{K}_{{{\text{bf}}}} + 2\varphi _{2} \tilde{K}_{{{\text{s}}_{2} }} }}{{ - \varphi _{2} \tilde{K}_{{{\text{s}}_{2} }} + 2\tilde{K}_{{{\text{bf}}}} + \varphi _{2} \tilde{K}_{{{\text{bf}}}} + \tilde{K}_{{{\text{s}}_{2} }} }}, \\ \end{aligned}$$
(1)
$$\frac{{\tilde{K}_{{{\text{bf}}}} }}{{\tilde{K}_{{\text{f}}} }} = \frac{{ - 2\varphi _{1} \tilde{K}_{{\text{f}}} + 2\tilde{K}_{{\text{f}}} + 2\varphi _{1} \tilde{K}_{{{\text{s}}_{1} }} + \tilde{K}_{{{\text{s}}_{1} }} }}{{ - \varphi _{1} \tilde{K}_{{{\text{s}}_{1} }} + 2\tilde{K}_{{\text{f}}} + \varphi _{1} \tilde{K}_{{\text{f}}} + \tilde{K}_{{{\text{s}}_{1} }} }},$$
(2)
$$\begin{aligned} \frac{{\tilde{\sigma }_{{{\text{bf}}}} }}{{\tilde{\sigma }_{{\text{f}}} }} = & \frac{{ - 2\varphi _{1} \tilde{\sigma }_{{\text{f}}} + 2\sigma _{{\text{f}}} + \tilde{\sigma }_{{{\text{s}}_{1} }} + 2\varphi _{1} \tilde{\sigma }_{{{\text{s}}_{1} }} }}{{\varphi _{1} \tilde{\sigma }_{{\text{f}}} + 2\sigma _{{\text{f}}} + \tilde{\sigma }_{{{\text{s}}_{1} }} - \varphi _{1} \tilde{\sigma }_{{{\text{s}}_{1} }} )}}, \\ \frac{{\tilde{\sigma }_{{{\text{hnf}}}} }}{{\tilde{\sigma }_{{{\text{bf}}}} }} = & \frac{{ - 2\varphi _{2} \tilde{\sigma }_{{{\text{bf}}}} + 2\tilde{\sigma }_{{{\text{bf}}}} + \tilde{\sigma }_{{{\text{s}}_{2} }} + 2\varphi _{2} \tilde{\sigma }_{{{\text{s}}_{2} }} )}}{{\varphi _{2} \tilde{\sigma }_{{{\text{bf}}}} + 2\tilde{\sigma }_{{{\text{bf}}}} + \tilde{\sigma }_{{{\text{s}}_{2} }} - \varphi _{2} \tilde{\sigma }_{{{\text{s}}_{2} }} )}}, \\ \end{aligned}$$
(3)
$$\begin{aligned} \frac{{D_{{{\text{hnf}}}}^{*} }}{{D_{{\text{f}}}^{*} }} = & (1 - \varphi _{2} )^{{ - 1}} (1 - \varphi _{1} )^{{ - 1}} , \\ \rho _{{{\text{hnf}}}} = & \varphi _{2} \rho _{{{\text{s}}_{2} }} + \left\{ {\rho _{{\text{f}}} - \varphi _{1} \rho _{{\text{f}}} + \varphi _{1} \rho _{{{\text{s}}_{1} }} } \right\}(1 - \varphi _{2} ), \\ \end{aligned}$$
(4)
$$\left( {\rho c_\text{p} } \right)_{{{\text{hnf}}}} = \varphi _{2} \left( {\rho c_{{\text{p}}} } \right)_{{{\text{s}}_{2} }} + \left\{ {\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} - \varphi _{1} \left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} + \varphi _{1} \left( {\rho c_{{\text{p}}} } \right)_{{{\text{s}}_{1} }} } \right\}(1 - \varphi _{2} ),$$
(5)

Heat and mass transfer have numerical applications. These applications include heat exchangers and other devices used for heat transfer enhancement, drilling out oil and related products and their transportation to refineries, filling solutions through pipes, enhanced oil recovery, geothermal reservoirs, drying of porous solids, thermal and cooling systems, refrigerations, thermal insulation, and underground species transport. Given the modern applications stated above, several investigations have been published on heat and mass transfer in Newtonian and non-Newtonian fluids. The geometry of the physical model has a significant influence on the kinetics of chemical reactions, the augmentation of heat and mass, and the rate of heat and mass. Pipes are used in engineering applications involving heat and mass transmission. Circular pipes are the most prevalent type of these pipes. As a result, numerous scholars have talked about heat and mass inflow across circular pipes. For example, Rehman and Nadeem [30] studied micropolar nanofluid boundary layer flow across a vertical cylinder with mixed convection. Wang [31] explored the steady continuous two-dimensional flow of viscous fluid in an external stretching cylinder. The suction effect of a heat transfer flow passing through a stretched cylinder was investigated by Ishak et al. [32]. Gorla et al. [33] investigated the heat transfer flow of nanostructures with a melting boundary condition on the stretched cylinder surface. Rasekh et al. [34] looked at how nanoparticles transport heat over a stretched cylinder. They discovered that the rate of heat transmission in the boundary layer is influenced by thermophoresis and Brownian motion forces. Norfifah et al. [35] investigated the flow of heat via a stretched cylinder with arbitrary surface heat flux.

Entropy generation is the process during which some amount of thermal energy becomes unavailable for any mechanical work. Process of thermal energy being unavailable for the mechanical system is referred to as entropy generation, and these energy losses are referred to as entropy. For efficient thermal systems, this type of loss of energy must be minimized. To do this, complete understanding of the thermal system and entropy must be acquainted. The priority of investigators working in the field of thermal system is to reduce energy losses. Thus, minimization of entropy generation is the prime objective of the thermal system to be efficient. For this reason, entropy generation has been studied much. Some relevant literature is being cited and described here. For example, Bejan [36] was the first to work on entropy generation minimization. Several studies have been published as a result of his research on entropy generation. However, several recent studies are detailed here. Oliveski et al. [37] worked on entropy generation for natural convection and concluded that the irreversibility coefficient is inversely related to the Bejan number, which is proportional to the Rayleigh number. Sohail et al. [38] investigated changing thermal conductivity and heat conductance in MHD Casson fluid across a nonlinear bidirectional stretching surface with entropy generation. In this study, they conclude that the system’s molecular stability decreases as a result of the increased Joule heating phenomena. Bhatti et al. [39] studied the impact of a magnetic field on the entropy generation with nanoparticles in heat and mass transport. In the presence of MHD, Omid Mahian et al. [40] examined the entropy of two vertical cylinders under different conditions. Bassam Abu-Hijleh et al. [41,42,43,44] investigated the entropy heat generation across a horizontal cylinder. Many researchers have published their research on the impact of stretching a cylinder on entropy generation [45,46,47,48,49,50]. For example, Butt et al. [45] examined the effects of entropy generation on a stretching surface embedded in a porous medium in viscous flow. PDEs were converted to ODEs using similarity transformations, and then, the equations were solved numerically (using bvp4c) to demonstrate that the entropy effects were enhanced by the presence of a magnetic field, a porous medium, and viscous dissipation effects. Butt and Ali [46] examine heat transfer in MHD with entropy generation. The governing equations were numerically solved, and the findings were compared to the previous research. Acharya et al. [47] worked on a permeable stretched cylinder that was passed over by a radiative couple stress fluid. The spectral quasi-linearization method is used to address ODEs.

This study aims to investigate the influence of heat and mass transfer in Maxwell fluid in the presence of hybrid copper (Cu), and aluminum oxide Al2O3 nanoparticles, magnetic field, and entropy generation over a heat stretchable cylinder by using the finite element method (FEM) [51,52,53,54,55,56,57,58,59,60,61]. According to the literature, no research on Maxwell hybrid nanofluid in the presence of entropy generation on a stretching cylinder has been done yet. This void is filled by the current inquiry. This article is divided into 5 sections. “Introduction” section is a review of published work on key research. “Mathematical models and development of problem” section includes physical and geometrical models. “Numerical methodology” section provides an overview of the numerical approach. “Results and discussion” section contains the results based on the results and discussion section. “Entropy generation” Section contains the final remarks.

Mathematical models and development of problem

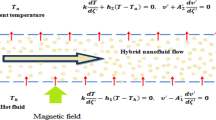
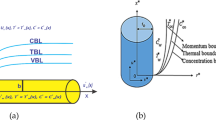
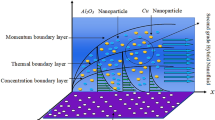
We have considered heat and mass transfer of two-dimensional MHD flow of an incompressible, steady, engine oil-based Maxwell hybrid nanofluid containing copper (Cu) and aluminum oxide Al2O3 nanoparticles through a horizontal stretched cylinder with radius D and wall velocity \(V_{\text{w}}\left( z\right) =cz/l\). The surface of the cylinder is kept at the non-uniform wall temperature \(T_{\text{w}}=T_{\infty }+T_{0}\left({z}/l\right) ^\text{n}\), and the ambient temperature is \(T_{\infty }\) with \(T_{\text{w}} >T_{\infty }\). Fluid flows along the horizontal direction in the z-axis, and the r-axis is along the vertical direction, respectively. The fluid stream along the radial direction was subjected to be a homogeneous magnetic field with magnitude \(B_{0}\). The optimization of entropy is investigated. Figure 1 shows a schematic representation.

Fig. 1
figure 1

Physical and coordinate system

Full size image

The basic equations are approximated through boundary layer approximations; we get

$$\begin{aligned} \frac{\partial \left( ru\right) }{\partial r}+\frac{\partial \left( rv\right) }{\partial z}=0, \end{aligned}$$
(6)
$$\begin{gathered} u\frac{{\partial v}}{{\partial r}} + v\frac{{\partial v}}{{\partial z}} + \lambda _{1} \left( {u^{2} \frac{{\partial ^{2} v}}{{\partial r^{2} }} + v^{2} \frac{{\partial ^{2} v}}{{\partial z^{2} }} + 2uv\frac{{\partial ^{2} v}}{{\partial r\partial z}}} \right) \hfill \\ \quad = - \left( {\frac{\sigma }{\rho }} \right)_{{{\text{hnf}}}} B_{0}^{2} \left[ {v + \lambda _{1} u\frac{{\partial v}}{{\partial r}}} \right] + \left( {\frac{\mu }{\rho }} \right)_{{{\text{hnf}}}} \left( {\frac{{\partial ^{2} v}}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial v}}{{\partial r}}} \right), \hfill \\ \end{gathered}$$
(7)
$$\begin{aligned} \frac{{\partial T}}{{\partial r}} + v\frac{{\partial T}}{{\partial z}} = & \left( {\frac{1}{r}\frac{{\partial T}}{{\partial r}} + \frac{{\partial ^{2} T}}{{\partial r^{2} }}} \right)\left( {\frac{{\tilde{K}}}{{\rho c_{{\text{p}}} }}} \right)_{{{\text{hnf}}}} \\ & + \left( {\frac{\mu }{{\rho c_{{\text{p}}} }}} \right)_{{{\text{hnf}}}} \left( {\frac{{\partial u}}{{\partial r}}} \right)^{2} + \left( {\frac{\sigma }{{\rho c_{{\text{p}}} }}} \right)_{{{\text{hnf}}}} B_{0}^{2} v^{2} , \\ \end{aligned}$$
(8)
$$\begin{aligned} u\frac{\partial C}{\partial r}+v\frac{\partial C}{\partial z}=D_{\text{hnf}}^{*}\left( \frac{\partial ^{2}C}{\partial r^{2}}+\frac{1}{r}\frac{\partial C}{\partial r}\right) , \end{aligned}$$
(9)

where [u, 0, v] is the velocity field.

Boundary conditions of the given problem are stated below

$$\begin{aligned} v = & V_{{\text{w}}} (z) = \frac{{cz}}{l},\;u = 0,\;T = T_{{\text{w}}} \left( z \right) = T_{\infty } + T_{0} \left( {\frac{z}{l}} \right)^\text{n} , \\ C = & C_{{\text{w}}} \left( z \right) = C_{\infty } + C_{0} \left( {\frac{z}{l}} \right)^\text{n} \;{\text{at}}\;r = D,\;v \to 0,\;T \longrightarrow T_{\infty } ,\;C \longrightarrow C_{\infty } ,\;{\text{as}}\;r \to \infty . \\ \end{aligned}$$
(10)

Similarity transformation

$$\begin{aligned} u = & - \left( r \right)^{{ - 1}} \frac{{\partial \psi }}{{\partial z}},\;v = \left( r \right)^{{ - 1}} \frac{{\partial \psi }}{{\partial r}}, \\ \psi (x,z) = & \sqrt {\frac{{\nu _{{\text{f}}} c}}{l}z} Df(\eta ), \\ \theta (\eta ) = & \frac{{T - T_{\infty } }}{{T_{{\text{w}}} - T_{\infty } }},\;\phi (\eta ) = \frac{{C - C_{\infty } }}{{C_{{\text{w}}} - C_{\infty } }}, \\ \eta = & \frac{{r^{2} - D^{2} }}{{2D}}\sqrt {\left( {\frac{c}{{\nu _{{\text{f}}} l}}} \right)} , \\ \end{aligned}$$
(11)

normalized form of Eqs. (6)–(10) are

$$\begin{gathered} \left( {1 + 2\alpha \eta } \right)^{2} \left( {\frac{{\left( \rho \right)_{{\text{f}}} }}{{\left( \rho \right)_{{{\text{hnf}}}} }}} \right)\left( {\frac{{\mu _{{{\text{hnf}}}} }}{{\mu _{{\text{f}}} }}} \right)f^{{\prime \prime \prime }} + 2\left( {\frac{{\mu _{{{\text{hnf}}}} }}{{\mu _{{\text{f}}} }}} \right)\left( {1 + 2\alpha \eta } \right)\left( {\frac{{\left( \rho \right)_{{\text{f}}} }}{{\left( \rho \right)_{{{\text{hnf}}}} }}} \right)\alpha f^{{\prime \prime }} - \alpha {\text{Def}}^{2} f^{{\prime \prime }} \hfill \\ \quad \quad - \left( {1 + 2\alpha \eta } \right)De\left( {f^{2} f^{{\prime \prime \prime }} - 2\left( {1 + 2\alpha \eta } \right)f^{\prime } ff^{{\prime \prime }} } \right)\left( {\frac{{\left( {\rho c_{p} } \right)_{{\text{f}}} }}{{\left( {\rho c_{p} } \right)_{{{\text{hnf}}}} }}} \right)\left( {\frac{{\mu _{{{\text{hnf}}}} }}{{\mu _{{\text{f}}} }}} \right){\text{Pr}}\;{\text{Ec}}\left( {f^{{\prime \prime }} } \right)^{2} \hfill \\ \quad \quad + \left( {1 + 2\alpha \eta } \right)\left[ { - \left( {f^{\prime } } \right)^{2} + ff^{{\prime \prime }} - \left( {\frac{{\left( {\rho c_{p} } \right)_{{\text{f}}} }}{{\left( {\rho c_{p} } \right)_{{{\text{hnf}}}} }}} \right)\left( {{\text{Ha}}} \right)^{2} \left( {\frac{{\tilde{\sigma }_{{{\text{hnf}}}} }}{{\tilde{\sigma }_{{\text{f}}} }}} \right)(f^{\prime }-Deff^{\prime\prime }) } \right] \hfill \\ \quad = 0,\;f(0) = 0,\;{\text{ }}f^{\prime } (0) = 1,\;{\text{ }}f^{\prime } \left( \infty \right) \to 0, \hfill \\ \end{gathered}$$
(12)
$$\begin{gathered} \hfill \left( {1 + 2\alpha \eta } \right)\left( {\frac{{\tilde{K}_{{{\text{hnf}}}} }}{{\tilde{K}_{{\text{f}}} }}} \right)\left( {\frac{{\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{{\text{hnf}}}} }}} \right)\theta ^{{\prime \prime }} + 2\left( {\frac{{\tilde{K}_{{{\text{hnf}}}} }}{{\tilde{K}_{{\text{f}}} }}} \right)\left( {\frac{{\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{{\text{hnf}}}} }}} \right)\alpha \theta ^{\prime } + \Pr f\theta ^{\prime } \\ \hfill \quad + \left( {\frac{{\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{{\text{hnf}}}} }}} \right){\text{Ec}}\Pr \left( {\frac{{\tilde{\sigma }_{{{\text{hnf}}}} }}{{\tilde{\sigma }_{{\text{f}}} }}} \right){\text{Ha}}^{2} f^{{\prime 2}} - n\Pr f^{\prime } \theta = 0,\;\theta (0) = 1,\;\theta \left( \infty \right) \to 0, \\ \end{gathered}$$
(13)
$$\begin{gathered} \left( {1 + 2\alpha \eta } \right)\left( {\frac{{D_{{{\text{hnf}}}}^{*} }}{{D_{{\text{f}}}^{*} }}} \right)\phi ^{{\prime \prime }} + 2\left( {\frac{{D_{{{\text{hnf}}}}^{*} }}{{D_{{\text{f}}}^{*} }}} \right)\alpha \phi ^{\prime } + {\text{Sc}}f\phi ^{\prime } \hfill \\ \quad - n{\text{Sc}}f^{\prime } \phi = 0,\;\phi (0) = 1,\;\phi \left( \infty \right) \to 0, \hfill \\ \end{gathered}$$
(14)

Parameters are expressed by

$$\begin{aligned} \Pr = & \left( {\frac{{\mu c_{{\text{p}}} }}{{\tilde{K}}}} \right)_{{\text{f}}} ,\;{\text{Ec}} = \frac{{U_{{\text{w}}}^{2} }}{{\left( {T_{{\text{w}}} - T_{\infty } } \right)\left( {c_{{\text{p}}} } \right)_{{\text{f}}} }}, \\ {\text{De}} = & \frac{{\lambda _{1} c}}{l},\;\alpha = \frac{{r^{2} }}{{D^{2} }},\;{\text{Sc}} = \frac{{\nu _{{\text{f}}} }}{{D_{{\text{f}}}^{*} }},\;\left( {{\text{Ha}}} \right)^{2} = \frac{{\tilde{\sigma }_{{\text{f}}} B_{0}^{2} l}}{{\rho _{{\text{f}}} c}}. \\ \end{aligned}$$
(15)

Dimensionless wall shear stress is given by

$$\begin{aligned} C_{\text{f}}=\frac{\mu _{\text{hnf}}\left. \frac{\partial v}{\partial r}\right| _{r=D} }{\rho _{\text{f}}(V_{\text{w}})^{2}}=\frac{1}{\sqrt{{\text {Re}}}}\left( \frac{\mu _{\text{hnf}}}{\mu _{\text{f}}}\right) f^{\prime \prime }(0), \end{aligned}$$
(16)

Normalized wall heat flux and wall mass flux are

$$\begin{aligned} {\text{Nu}} = & \frac{{ - z\tilde{K}_{{{\text{hnf}}}} \left. {\frac{{\partial T}}{{\partial r}}} \right|_{{r = D}} }}{{\tilde{K}_{{\text{f}}} (T_{{\text{w}}} - T_{\infty } )}} = - \frac{{\tilde{K}_{{{\text{hnf}}}} }}{{\tilde{K}_{{\text{f}}} }}\sqrt {{\text{Re}}} \theta ^{\prime } (0),~\; \\ {\text{Sh}} = & \frac{{ - zD_{{{\text{hnf}}}}^{*} \left. {\frac{{\partial C}}{{\partial r}}} \right|_{{r = D}} }}{{D_{{\text{f}}}^{*} (C_{{\text{w}}} - C_{\infty } )}} = - \frac{{D_{{{\text{hnf}}}}^{*} }}{{D_{{\text{f}}}^{*} }}\sqrt {{\text{Re}}} \phi ^{\prime } (0), \\ \end{aligned}$$
(17)

where \({\text {Re}}=\left( cz^{2}/l\nu _{\text{f}}\right)\).

Thermophysical properties of nanoparticles and base fluid are given in Table 1.

Table 1 Values of thermophysical properties [61–64]
Full size table

Numerical methodology

The finite element method (FEM) is applied to the coupled nonlinear problems Eqs. (12)–(14). The set of nonlinear equations is stated in their suitable residuals form and then converted into weak form. The Galerkin approximation is used to approximate the weak form by selecting suitable linear shape functions. The stiffness matrix elements are developed and calculated over typical elements. The assembly process is completed, and these algebraic equations are linearized by the Picard linearization approach. The iterative procedure is used to solve the given system of linear equations and linearized. The computer code is developed, and its accuracy is validated by comparing the computed results with Majeed [65] published work [by considering \(Ha^{2}=\varphi _{1}=\varphi _{2}=0\) in Eq. (12)]. This validation is shown in Table 2.

Table 2 Validation of results when \(Ha^{2}=\varphi _{1} =\varphi _{2}=0.\)
Full size table

Results and discussion

The parametric analysis is used to study the transport of a fluid mixture (a mixture of biofluid engine oil, Cu, and Al2O3), and the findings are presented in Figs. 2−9. A nanofluid is a mixture of engine oil and copper, whereas a hybrid Maxwell nanofluid is a mixture of copper, aluminum oxide, and engine oil. Dashed curves are for velocity, temperature, and concentration profiles for hybrid Maxwell nanofluid and dotted curves represent the velocity, temperature, and concentration profiles for Maxwell nanofluid.

Figure 2 depicts the effect of curvature parameter \(\left( \alpha \right)\) on the velocity profile as \(\alpha\) is the radial variable divided by the diameter of the circular pipe. As a result, increasing the value means decreasing the diameter. Simulations have shown that as \(\alpha\) increases, velocity profile for both Maxwell nanofluid (Cu/engine oil) and hybrid Maxwell nanofluid (Al2O3–Cu/engine oil) increased, but hybrid Maxwell nanofluid shows greater increment as compared with Maxwell nanofluid. Thus, an increase in the curvature parameter plays a significant role in accelerating the fluid motion.

Fig. 2
figure 2

Variation of curvature parameter on velocity profile

Full size image

The Deborah number (De) measures the fluid’s elastic behavior, and the fluid’s elastic nature causes it to resist or seek to avoid momentum changes induced by boundaries (here, in this case, longitudinal movement of the cylinder). The numerical simulations against various values of De are recorded in Fig. 3. The recorded results show that velocity of hybrid Maxwell nanofluid (Al2O3–Cu/engine oil) and Maxwell nanofluid (Cu/engine oil) decreases due to an increase in De. It is clear that Cu/engine oil is more elastic than Al2O3–Cu/engine oil. Cu/engine oil has a narrower viscosity area than Al2O3–Cu/engine oil. In Fig. 3, it is also worth noting that the velocity profiles for Newtonian fluids have greater values than those for non-Newtonian fluids (viscoelastic fluid).

Fig. 3
figure 3

Variation of fluid parameter on velocity profile

Full size image

The Hartmann number \(\left( Ha^{2}\right)\) is the product of electric current due to the change in magnetic flux caused by the fluid–magnetic interaction. The fluid–magnetic interaction produces the Lorentz force (a magnetic force operating in the opposite direction of fluid particle motion). Figure 4 predicts the behavior of Lorentz force on the movement of particles of Al2O3–Cu/engine oil and Cu/engine oil. Thus, by changing the intensity of the magnetic field, momentum boundary layer thickness can be controlled (see Fig. 4).

Fig. 4
figure 4

Variation of magnetic parameter on velocity profile

Full size image

The influence of the Prandtl number \(\left( \Pr \right)\) on the temperature profile is shown in Fig. 5. A rise in Prandtl number is caused by a reduction in thermal diffusivity. Furthermore, heat conduction is proportional to diffusivity. As a result, a rise in \(\Pr\) compromises heat conduction. Numerical experiments provide the same prediction (see Fig. 5).

Fig. 5
figure 5

Variation of Prandtl number on temperature profile

Full size image

Temperature profile shows an increasing trend as the curvature parameter \(\left( \alpha \right)\) increased as shown in Fig. 6. Temperature profiles for both types of nanofluids, Maxwell nanofluid (Cu/engine oil) and hybrid Maxwell nanofluid (Al2O3–Cu/engine oil), exhibit a rising tendency when \(\alpha\) is increased. This rising tendency is due to an increase in the corrective transfer of heat in fluid, which occurs when the velocity of the fluid increases as a function of the curvature parameter.

Fig. 6
figure 6

Variation of curvature parameter on temperature profile

Full size image

In the energy equation, the Hartmann number \((Ha^{2})\) is also the coefficient of the component that occurs due to the consideration of Ohmic dissipation effects, and an increase in \(Ha^{2}\) corresponds to an increase in magnetic field strength. Thus, the amount of electrical energy is proportional to the change of intensity of the magnetic field. Due to the increase in the intensity of the magnetic field, Ohmic dissipation process increases gradually as shown in Fig. 7. The profiles shown in Fig. 7 also show that Ohmic dissipation in hybrid Maxwell nanofluid (Al2O3–Cu/engine oil) takes place faster than that in Maxwell nanofluid (Cu/engine oil).

Fig. 7
figure 7

Variation of magnetic parameter on temperature profile

Full size image

Figure 8 demonstrates the effect of the curvature parameter \((\alpha )\) on the concentration field as the curvature parameter increases the concentration of both types of nanofluids Maxwell nanofluid (Cu/engine oil) and hybrid Maxwell nanofluid Al2O3–Cu/engine oil) increases. The increase in fluid concentration near the wall is because of the increase in velocity of both nanofluids by increasing \(\alpha\). As a result, a drop in velocity suggests a decrease in solute convective transport. As a result, the concentration field exhibits a decreasing tendency relative to the \(\alpha\).

Fig. 8
figure 8

Variation of curvature parameter on concentration profile

Full size image

Figure 9 shows the effect of Schmidt number (Sc) on the concentration of Maxwell nanofluid and hybrid Maxwell nanofluid. By increasing Sc, a decreasing trend is observed for both cases.

Fig. 9
figure 9

Variation of Schmidt number on concentration profile

Full size image

In Tables 3 and 4, we examine the numerical results for hybrid Maxwell nanofluid (Al2O3–Cu) and Maxwell nanofluid (Al2O3) against different values of the different parameters for wall shear stress, wall heat flux, and wall mass flux, respectively. The wall shear stress is examined versus the curvature of the cylinder in Table 3 for the case of hybrid Maxwell nanofluid. The curvature parameter has shown an increasing trend in the shear stress. It is also noted wall shear stress for Al2O3–Cu/engine oil fluid has a greater magnitude than those for Al2O3/engine oil fluid. Similar behavior of Hartmann number on wall shear stress and wall heat flux is noticed. Hartmann number is responsible for an increase in the behavior of wall shear stress and wall heat flux. The wall heat flux is examined versus the Deborah number, the curvature of the cylinder, and Hartmann number in Table 4, for the case of Maxwell nanofluid. The curvature of the cylinder and Hartmann number have shown an increasing trend in the wall shear stress and wall heat flux. Deborah number shows a decreasing trend in wall heat and mass flux. It is also noted that wall heat flux for Al2O3–Cu/engine oil fluid has a greater magnitude than those for Al2O3/engine oil.

Table 3 Numerical values of normalized wall shear stress and normalized wall heat and mass fluxes for Al2O3–Cu/engine oil
Full size table
Table 4 Numerical values of normalized wall shear stress, and normalized wall heat and mass fluxes for Cu/engine oil
Full size table

Entropy generation

For a Newtonian fluid across a hyperbolic stretching cylinder, the local volumetric rate of entropy generation EG is defined as:

$$\begin{aligned} E_{\text{G}}=\frac{K_{\text{hnf}}}{T_{\infty }^{2}}\left( \frac{\partial T}{\partial r}\right) ^{2}+\frac{\mu _{\text{hnf}}}{T_{\infty }}\left( \frac{\partial v}{\partial r}\right) ^{2}+\frac{\sigma _{\text{hnf}}B_{0}^{2}}{T_{\infty }}v^{2}. \end{aligned}$$
(18)

The entropy effects due to heat transfer are expressed by the first component on the R.H.S, while the entropy effects due to fluid friction and Joule heating are represented by the remaining component. After using similarity transformation, we get

$$\begin{aligned} E_{{\text{G}}} = & \frac{{K_{{{\text{hnf}}}} r^{2} c\left( {T_{{\text{w}}} - T_{\infty } } \right)^{2} }}{{T_{\infty }^{2} \nu _{{\text{f}}} lR^{{*2}} }}\left( {\theta ^{\prime } } \right)^{2} + \nu _{{{\text{hnf}}}} \left[ {\frac{{r^{2} c^{3} z^{2} \rho _{{\text{f}}} }}{{T_{\infty } R^{{*2}} l^{3} }}} \right]\left( {f^{{\prime \prime }} } \right)^{2} \\ & + \frac{{\sigma _{{{\text{hnf}}}} B_{0}^{2} }}{{T_{\infty } }}\left[ {\frac{{\left( {cz} \right)^{2} }}{{l^{2} }}} \right]\left( {f^{\prime } } \right)^{2} \\ \end{aligned}$$
(19)

The above equation can be written as

$$\begin{aligned} N_{{\text{S}}} = & \frac{{T_{\infty }^{2} l^{2} E_{{\text{G}}} }}{{K_{{\text{f}}} \left( {T_{{\text{w}}} - T_{\infty } } \right)^{2} }} = \left( {\frac{{K_{{{\text{hnf}}}} }}{{K_{{\text{f}}} }}} \right)\left( {1 + 2\alpha \eta } \right){\text{Re}}\left( {\theta ^{\prime } } \right)^{2} \\ & + \frac{{\mu _{{{\text{hnf}}}} }}{{\mu _{{\text{f}}} }}\left( {{\text{Br}}\Omega {\text{Re}}\left( {1 + 2\alpha \eta } \right)} \right)\left( {f^{{\prime \prime }} } \right)^{2} \\ & + \frac{{\sigma _{{{\text{hnf}}}} }}{{\sigma _{{\text{f}}} }}\left[ {\left( {Ha} \right)^{2} {\text{BrRe}}\Omega } \right]\left( {f^{\prime } } \right)^{2} , \\ \end{aligned}$$
(20)

where \({\text{Br}}\left( { = \mu _{{\text{f}}} c^{2} z^{2} /K_{{\text{f}}} \left( {T_{{\text{w}}} - T_{\infty } } \right)} \right),\) NS Re and \(\Omega \left( =T_{\infty }/\left( T_{\text{w}}-T_{\infty }\right) \right)\).

Figures 10−12 display the effect of Br, De,  and n on entropy generation. All of these entropy generating factors have an increasing impact on entropy profiles. The Brinkman number controls the comparative significance of viscous effects, and it can be shown that when Br rises, entropy rises as well (see Fig. 10). Same as when De and n increase, accelerated behavior can be seen in the entropy profile as shown in Figs. 11 and 12.

Fig. 10
figure 10

Variation of Brinkman number on entropy generation

Full size image
Fig. 11
figure 11

Variation of fluid parameter on entropy generation

Full size image
Fig. 12
figure 12

Variation of time index on entropy generation

Full size image

Conclusion

In this study, the MHD flow over elongating pipe with Maxwell hybrid nanofluid has been studied numerically. FEM is used to solve the system of equations derived from  governing laws. The following key points of the study are

  1. 1.

    The Deborah number is the measure of the elasticity of the fluid and elasticity is the characteristics of the fluid due to which fluid avoids or tries to avoid momentum changes. Therefore, Deborah number has shown a decreasing behavior on the motion of the particles of both mono–nanoengine oil and hybrid nanoengine oil.

  2. 2.

    With increasing, \(\mathrm{{Ha}}^{2}\), and \(\alpha\) the system heat up, but rising Prandtl number values have the reverse effect.

  3. 3.

    When the magnetic field intensity is increased, the Ohmic dissipation increases as well.

  4. 4.

    Entropy generation is boosted up when n, De, and Br are raised.