Modelling of a Three Dimensional Thermoelastic Half Space with Three Phase Lags using Memory Dependent Derivative

Abstract

A mathematical model for a three dimensional isotropic half-space has been formulated to inspect lagging behaviours due to the presence of phase lags in context of memory dependent derivative, as an extension of several existing thermoelastic models like- Green-Naghdi-III, Lord Shulman, and Fourier’s Law etc. The analytical and procedural work has been done in integral transform domain preceded by eigenvalue approach to find the solution from the governing equations. Numerical computations and graphical representation of distribution of non-dimensional stress components, temperature with the effect of three phase lag, kernel function and time-delay has been performed with the help of the efficient mathematical software.

Introduction

The concept of finite propagation of wave was replaced by the infinite speed phenomena of thermal disturbance as proposed by Biot [1] to transform the Fourier’s Law of heat conduction into diffusion equation. The revolution of generalized thermoelasticity can be classified in five generalizations as described by Hetnarski and Ignaczak [2].

First Generalization

As an extended thermoelasticity theory (ETE), Lord and Shulman [3] introduced one relaxation time parameter in generalized thermoelasticity by replacing the Fourier’s Law of heat conduction

$$ q = \kappa \,\Delta T $$

(1)

with Maxwell–Cattaneo law. Generally problems on generalized thermoelasticity (coupled or uncoupled) was solved with the help of potential functions mechanism. But according to Dhaliwal and Sherief [4] and Sherief and Anwar [5], convergent solution is not always possible using potential functions to solve problems having physical or field variables like –displacement, stress, strain, temperature. As an alternative process to solve problems with classical heat conduction equation

$$ \,\,q + \tau_{q} \tfrac{\partial q}{\partial t} = - k\nabla \theta $$

(2)

($\kappa$ = thermal conductivity of material, $\tau_{q}$ = build-up time and q = heat flux), Single Phase Lag (SPL) model was proposed by Ozisik and Tzou [6].

Second Generalization

Green-Lindsay [7] proposed temperature-rate dependent theory (TRDTE) with two relaxation times as parameters in coupled thermoelasticity theory.

Third Generalization

In this generalization, Hetnarski and Ignaczak [8] introduced the concept of Low-Temperature coupled thermoelasticity for non-linear model of heat conduction. Chimmelli and Kosinski [9] studied that this model can predict the behaviour of wave-like thermal signals.

Fourth Generalization

Green-Naghdi [10] proposed G-N theory with the concept of thermoelasticity theory without energy dissipation known as Green-Naghdi-II model. In this model the classical Fourier’s law is modified by the temperature rate gradient. In G-N-III model, damped thermoelastic waves [11] and general concept of energy dissipation [12] have been discussed.

Fifth Generalization

Dual Phase Lag (DPL) model is introduced as the fifth generalization thermoelasticity theory proposed by Chandrasekhariah [13] and Tzou [14]. Tzou considered the generalized heat conduction equation describing the lagging behaviour imposed on the thermoelastic solid introducing DPL to both of the temperature gradient and the heat flux vector. To avoid finiteness of $\tau_{q}$ in SPL model due to heat-flux, Tzou [15] introduced the concept of DPL with the following heat conduction equation:

$$ q + \tau_{q} \tfrac{\partial q}{\partial t} = - k(1 + \tau_{\theta } \,\tfrac{\partial }{\partial t})\nabla \theta $$

(3)

with two time parameters $\tau_{q} ,\tau_{\theta }$ where $\tau_{q}$ = heat flux time lag and $\tau_{\theta }$ = temperature gradient time lag. Depending upon the relation between $\tau_{q}$ and $\tau_{\theta }$, different model has been specified as follows:

• (i) Classical Fourier’s Law when $\tau_{q} = \tau_{\theta } ,$ not necessary equals to zero.

• (ii) Biot theory or Dipole Coupled Theory (DCT) when $\tau_{q} = \tau_{\theta } = 0$.

• (iii) Cattaneo-Vernotte (CV) model when $\tau_{q} > 0,\tau_{\theta } = 0$ and

• (iv) Lord-Shulman (LS) model when $\tau_{q} = \tau ,\tau_{\theta } = 0$.

As a new generalization thermoelasticity, Roy Choudhury [16] discussed the concept of Three Phase Lag Model [3PHL] introducing three time parameters $\tau_{q} ,\tau_{T} ,\tau_{\nu }$ where $\tau_{q}$ = heat flux time lag,$\tau_{T}$ = temperature gradient time lag and $\tau_{v}$ = thermal displacement gradient time lag satisfying the inequality $0 \le \tau_{\nu } \le \tau_{T} \prec \tau_{q}$.To discuss the lagging behaviour, using $\vec{\nabla }v$, $\vec{q}$ and $\vec{\nabla }T$ as thermal displacement gradient, heat flux vector and temperature gradient respectively, the constitutive equation of generalised heat conduction can be written as

$$ \vec{q}(P,t + \tau_{q} ) = - [\kappa^{*} \,\vec{\nabla }v(P,t + \tau_{v} ) + \kappa \,\vec{\nabla }T(P,t + \tau_{T} )] $$

(4)

where $P\left( {\vec{r}} \right)$ is the point where material volume located at time $(t + \tau_{v} )$ and $(t + \tau_{T} )$ together with heat flux flow at different instant of $\tau_{q}$ for a finite time t > 0.

Taking Taylor’s series expansion from the above mentioned equation, we have

$$ \vec{q} + \tau_{q} \frac{{\partial \vec{q}}}{\partial t} = - [\kappa^{*} \,\vec{\nabla }v + \kappa \,\tau_{T} \,\frac{\partial }{\partial t}\vec{\nabla }\theta + \tau_{v}^{*} \,\vec{\nabla }\theta ] $$

(5)

where $\tau_{v}^{*} \, = \kappa + \kappa^{*} \tau_{v} \,\,\,\,and\,\,\dot{v} = \theta$.

Now depending upon different values of $\tau_{q} ,\tau_{T} ,\tau_{v}$ and $\kappa^{*}$, different theory can be classified as below-

• (i) Classical Fourier’s Law :$\kappa^{*}$ = 0, $\tau_{q} = \tau_{T}$

• (ii) Lord-Shulman (L-S) Theory: $\kappa^{*}$ = 0,$\tau_{q} = \tau \,\,and\,\,\tau_{T} = 0$, where $\tau$ is the relaxation time.

• (iii) Green-Naghdi-III (G-N-III) theory: $\tau_{q} = 0,\tau_{T} = 0\,\,and\,\,\tau_{v} = 0\,$

Neglecting the terms above the 2^nd order of $\tau_{q}$ in Taylor’s expansion and then eliminating $- div\,\vec{q}$, the generalized heat conduction Eq. (4) reduced to

$$ \begin{aligned} \kappa^{*} \nabla^{2\,} \,\dot{\theta } + k\,\tau_{T} \nabla^{2\,} \,\ddot{\theta } + \tau_{v}^{*} \nabla^{2\,} \,\dot{\theta } \hfill \\ = \left( {1 + \tau_{q} \frac{\partial }{\partial t} + \frac{{\partial^{2} }}{{\partial t^{2} }}\frac{1}{2}\tau_{q}^{2} } \right)F(x_{1} ,x_{2} ,x_{3} ,t) \hfill \\ \end{aligned} $$

(6)

where,$F(x_{1} ,x_{2} ,x_{3} ,t) = \left( {\rho \,C_{E} \dot{\theta } + \gamma \,T_{0} \,\dot{e}} \right)$ and $\rho ,\,C_{E} ,\gamma ,\,T_{0}$ and e denote density, specific heat conduction, material constant, reference temperature and dilation respectively.

To provide easier procedure to avoid analytical and simulation complexity in both DPL and 3PHL model, the Memory Dependent Derivative (MDD) concept has been introduced using $K(t - \xi )$ as the kernel function with ω (> 0) as time delay where $\xi$ is any real number arbitrarily chosen.

In context of MDD, we have introduced the generalized heat conduction equation as-

$$ \begin{aligned} \kappa^{*} \left( {1 + \tfrac{{\tau_{\theta } }}{1!}D_{\omega } } \right)\theta_{,ij} + k\,\tau_{T} \left( {1 + \tfrac{{\tau_{\theta } }}{1!}D_{\omega } } \right)\ddot{\theta }_{,ij} + \tau_{v}^{*} \left( {1 + \tfrac{{\tau_{\theta } }}{1!}D_{\omega } } \right)\dot{\theta }_{,ij} \hfill \\ = \left( {1 + \tfrac{{\tau_{q} }}{1!}D_{\omega } + \tfrac{{\tau_{q}^{2} }}{2!}D_{\omega }^{2} } \right)\left( {\rho \,C_{E} \dot{\theta } + \gamma \,T_{0} \,\dot{e}} \right) \hfill \\ \end{aligned} $$

where the integral form of a common derivative of a first order function is defined by Wang and Li [17] as $\,\,\,\,\,D_{\omega } f(t) = \tfrac{1}{\omega }\int_{t - \omega }^{t} {K(t - \xi )f^{\prime}\left( \xi \right)} \,d\xi$.

In context of MDD, the kernel function,$K(t - \xi$) is defined as follows-

$$ \begin{aligned} K(t - \xi ) = 1 - \frac{{2p_{2} }}{\omega }(t - \xi ) + \frac{{p_{1}^{2} }}{{\omega^{2} }}(t - \xi )^{2} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left\{ \begin{aligned} 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,when\,\,\,p_{1} = 0,\,p_{2} = 0; \hfill \\ 1 - \frac{(t - \xi )}{\omega }\,\,\,\,\,when\,p_{1} = 0,p_{2} = \frac{1}{2}; \hfill \\ 1 - (t - \xi )\,\,\,\,\,\,when\,p_{1} = 0,p_{2} = \frac{\omega }{2}; \hfill \\ \left( {1 - \frac{t - \xi }{\omega }} \right)^{2} \,when\,p_{1} = p_{2} = 1 \hfill \\ \end{aligned} \right. \hfill \\ \end{aligned} $$

Using convolution theorem of the Laplace transform, kernel function,$K(t - \xi )$ is defined by $L\left\{ {\omega \,D_{\omega } f(t)} \right\} = \int_{t - \omega }^{t} {K(t - \xi )f^{\prime}\left( \xi \right)} \,d\xi = F(s).G(s)$ where $F(s) = L\left\{ {f(t)} \right\}$ and $G(s) = \left[ {1 - \tfrac{{2p_{2} }}{\omega s} + \tfrac{{2p_{1}^{2} }}{{\omega^{2} s^{2} }}} \right] - e^{ - \omega s} \left[ {(1 - 2p_{2} + p_{1}^{2} ) + \tfrac{{2(p_{1}^{2} - p_{2}^{2} )}}{\omega s} + \tfrac{{2p_{1}^{2} }}{{\omega^{2} s^{2} }}} \right]$.

Further, Ezzat et al. [23], Abbas [29] discussed fractional order thermoelasticity in context of three phase lags. Again Sarkar [24] and Abbas [25] [28] [30] studied the thermoelastic infinite medium for spherical and cylindrical cavity respectively with MDD. Atwa and Sarkar [26] also studied a problem related to magneto-thermoelasticity for a perfectly conducting medium in context of MDD. In a semiconducting medium photothermal effect has been analysed by Lofty and Sarkar [27].Prior to this Abbas et al. [31] studies the non-leaner thermoelasticity where as finite element method has been used by Abbas et al. [32] to discuss generalised thermoelasticity under ramp-type heating.

In our current work, the method of Laplace inversion and double Fourier inversion are applied to obtain the specific and accurate numerical solution for stress distribution, temperature distribution and to enquire the lagging behaviour imposed on the physical variable against space variables for a three dimensional isotropic half space.

Formulation of the Model

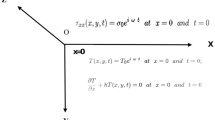
We consider a three dimensional homogeneous isotropic thermoelastic half space lying in the region $R = \left\{ {\left( {x_{1} ,x_{2} ,x_{3} } \right)\,:x_{1} \ge 0, - \infty \le x_{2} \le \infty , - \infty \le x_{3} \le \infty } \right\}$ as in Fig. 1.

Fig. 1

Schematic diagram of the problem

Equation of motion:

$$ \rho \,\ddot{u}_{i} = \left( {\lambda + 2\mu } \right)u_{j,ij} + \mu \,u_{i,jj} - \gamma \left( {1 + \nu D_{\omega } } \right)\theta_{,i} $$

(7)

Heat conduction equation:

$$ \begin{aligned} \kappa^{*} \left( {1 + \tfrac{{\tau_{\theta } }}{1!}D_{\omega } } \right)\theta_{,ij} + k\,\tau_{T} \left( {1 + \tfrac{{\tau_{\theta } }}{1!}D_{\omega } } \right)\ddot{\theta }_{,ij} + \tau_{v}^{*} \left( {1 + \tfrac{{\tau_{\theta } }}{1!}D_{\omega } } \right)\dot{\theta }_{,ij} \hfill \\ = \left( {1 + \tfrac{{\tau_{q} }}{1!}D_{\omega } + \tfrac{{\tau_{q}^{2} }}{2!}D_{\omega }^{2} } \right)\left( {\rho \,C_{E} \dot{\theta } + \gamma \,T_{0} \,\dot{e}} \right) \hfill \\ \end{aligned} $$

(8)

Constitutive Stress–strain equation:

$$ \sigma_{ij} = \lambda \,e_{kk} \,\,\delta_{ij} + 2\,\mu \,\,e_{ij} - \gamma \,\delta_{ij} (1 + \nu \,D_{\omega } )\,\theta \,\,\delta_{ij} $$

(9)

Considering $F(x_{1} ,x_{2} ,x_{3} ,t) = \rho C_{E} \dot{\theta } + \gamma T_{0} \dot{e}$ the heat conduction Eq. (8) reduces to

$$ \begin{aligned} \kappa^{*} \left( {1 + \tfrac{{\tau_{\theta } }}{\omega }\,\,\omega D_{\omega } } \right)\theta_{,ij} + k\,\tau_{T} \left( {1 + \tfrac{{\tau_{\theta } }}{\omega }\,\,\omega D_{\omega } } \right)\ddot{\theta }_{,ij} \hfill \\ + \tau_{v}^{*} \left( {1 + \tfrac{{\tau_{\theta } }}{\omega }\,\,\omega D_{\omega } } \right)\dot{\theta }_{,ij} = \left( {1 + \tfrac{{\tau_{q} }}{\omega }\,\,\omega D_{\omega } + \tfrac{{\tau_{q}^{2} }}{2\omega }\,\,wD_{\omega }^{2} } \right)F \hfill \\ \end{aligned} $$

(10)

Introducing the non-dimension variables$\begin{aligned} &\left( {x^{\prime}_{1} ,x^{\prime}_{2} ,x^{\prime}_{3} ,u^{\prime}_{1} ,u^{\prime}_{2} ,u^{\prime}_{3} } \right) = c_{0} \eta \left( {x_{1} ,x_{2} ,x_{3} ,u_{1} ,u_{2} ,u_{3} } \right),\,\, \hfill \\ &\theta^{\prime} = \tfrac{\gamma }{\lambda + 2\mu }\theta ,\,\,(\nu ',t^{\prime}) = c_{0}^{2} \eta (\nu ,t),\,\sigma^{\prime}_{ij} = \tfrac{1}{\lambda + 2\mu }\sigma_{ij} \hfill \\ \end{aligned}$ and dropping primes for convenient, the Eqs. (7), (8) and (10) reduces to

$$ \begin{aligned} u_{1,tt} &= u_{{1,x_{1} x_{1} }} + \varepsilon_{1} \,\left( {u_{{2,x_{1} x_{2} }} + u_{{3,x_{1} x_{3} }} } \right) \hfill \\ &\quad + \varepsilon_{2} \,\,\left( {u_{{1,x_{2} x_{2} }} + u_{{1,x_{3} x_{3} }} } \right) - \theta_{{,x_{1} }} - \varepsilon_{3} \tfrac{\nu }{\omega }\int\limits_{t - \omega }^{t} {K(t,\xi )} \,\,\theta_{{,\xi x_{1} }} \,d\xi , \hfill \\ &u_{2,tt} = u_{{2,x_{2} x_{2} }} + \varepsilon_{1} \,\left( {u_{{1,x_{1} x_{2} }} + u_{{3,x_{2} x_{3} }} } \right) \hfill \\ &\, + \varepsilon_{2} \,\,\left( {u_{{2,x_{1} x_{1} }} + u_{{2,x_{3} x_{3} }} } \right) - \theta_{{,x_{2} }} - \varepsilon_{3} \tfrac{\nu }{\omega }\int\limits_{t - \omega }^{t} {K(t,\xi )} \,\,\theta_{{,\xi x_{2} }} \,d\xi , \hfill \\ u_{3,tt} &= u_{{3,x_{3} x_{3} }} + \varepsilon_{1} \,\left( {u_{{1,x_{1} x_{3} }} + u_{{2,x_{2} x_{3} }} } \right) \hfill \\ &\quad + \varepsilon_{2} \,\,\left( {u_{{3,x_{1} x_{1} }} + u_{{3,x_{2} x_{2} }} } \right) - \theta_{{,x_{3} }} - \varepsilon_{3} \tfrac{\nu }{\omega }\int\limits_{t - \omega }^{t} {K(t,\xi )} \,\,\theta_{{,\xi x_{3} }} \,d\xi \hfill \\ \end{aligned} $$

(11)

$$ \begin{aligned} &\theta_{{,x_{1} \,x_{1} }} + \theta_{{,x_{2} \,x_{2} }} + \theta_{{,x_{3} \,x_{3} }} + \frac{{\tau_{\theta } }}{\omega }\left( \begin{subarray}{l} \int\limits_{t - \omega }^{t} {K(t,\xi )} \,\,\theta_{{,\xi \,x_{1\,} x_{1} }} \,d\xi + \\ \int\limits_{t - \omega }^{t} {K(t,\xi )} \,\,\theta_{{,\xi \,\,x_{2} \,x_{2} }} d\xi + \int\limits_{t - \omega }^{t} {K(t,\xi )} \,\,\theta_{{,\xi \,_{3} \,x_{3} }} \,d\xi \end{subarray} \right) \hfill \\& \,\, + \varepsilon_{6} \left( {\left( {\theta_{{,x_{1} \,x_{1} }} + \theta_{{,x_{2} \,x_{2} }} + \theta_{{,x_{3} \,x_{3} }} } \right)_{,tt} \, + \frac{{\tau_{\theta } }}{\omega }\left( \begin{subarray}{l} \int\limits_{t - \omega }^{t} {K(t,\xi )} \,\,\theta_{{,\xi \,\,\xi \,\,\xi \,\,x_{1\,} x_{1} \,}} \,d\xi \\ + \int\limits_{t - \omega }^{t} {K(t,\xi )} \,\,\theta_{{,\xi \,\,\xi \,\,\xi \,\,x_{2} \,x_{2} }} d\xi + \int\limits_{t - \omega }^{t} {K(t,\xi )} \,\,\theta_{{,\xi \,\,\xi \,\,\xi \,\,x_{3} \,x_{3} }} \,d\xi \end{subarray} \right)} \right) \hfill \\ & + \varepsilon_{7} \left( {\left( {\theta_{{,x_{1} \,x_{1} }} + \theta_{{,x_{2} \,x_{2} }} + \theta_{{,x_{3} \,x_{3} }} } \right)_{,t} \, + \frac{{\tau_{\theta } }}{\omega }\left( \begin{subarray}{l} \int\limits_{t - \omega }^{t} {K(t,\xi )} \,\,\theta_{{,\xi \,\,\,\xi \,\,x_{1\,} x_{1} \,}} \,d\xi \\ + \int\limits_{t - \omega }^{t} {K(t,\xi )} \,\,\theta_{{,\xi \,\,\xi \,\,x_{2} \,x_{2} }} d\xi + \int\limits_{t - \omega }^{t} {K(t,\xi )} \,\,\theta_{{,\xi \,\,\xi \,\,x_{3} \,x_{3} }} \,d\xi \end{subarray} \right)} \right) \hfill \\ \end{aligned} $$

$$ \, = \varepsilon_{8} \left( \begin{subarray}{l} \theta_{,t} + \left( {u_{{1,x_{1} \,t}} + u_{{2,x_{2} \,t}} + u_{{3,x_{3} \,t}} } \right)_{,tt} \, \\ + \frac{{\tau_{q} }}{\omega }\left( {\int\limits_{t - \omega }^{t} {K(t,\xi )} \,\,\theta_{,\xi \,\,\xi \,\,\,} \,d\xi + \varepsilon_{5} \left( \begin{subarray}{l} \int\limits_{t - \omega }^{t} {K(t,\xi )} \,\,u_{{1,\xi \,\,\xi \,\,\,x_{1} }} d\xi \\ + \int\limits_{t - \omega }^{t} {K(t,\xi )} \,\,u_{{2,\xi \,\,\xi \,\,\,x_{2} }} d\xi + \int\limits_{t - \omega }^{t} {K(t,\xi )} \,\,u_{{3,\xi \,\,\xi \,\,x_{3} }} \,d\xi \end{subarray} \right)} \right) \\ + \frac{{\tau_{q}^{2} }}{2\omega }\left( {\int\limits_{t - \omega }^{t} {K(t,\xi )} \,\,\theta_{,\xi \,\,\xi \,\,\xi \,\,\,} \,d\xi + \varepsilon_{5} \left( \begin{subarray}{l} \int\limits_{t - \omega }^{t} {K(t,\xi )} \,\,u_{{1,\xi \,\,\xi \,\,\xi \,\,\,\,x_{1} }} d\xi \\ + \int\limits_{t - \omega }^{t} {K(t,\xi )} \,\,u_{{2,\xi \,\,\xi \,\,\xi \,\,\,\,x_{2} }} d\xi + \int\limits_{t - \omega }^{t} {K(t,\xi )} \,\,u_{{3,\xi \,\,\xi \,\,\,\xi \,\,x_{3} }} \,d\xi \end{subarray} \right)} \right) \end{subarray} \right) $$

(12)

$$ \begin{aligned} &\sigma_{11} = u_{{1,x_{1} }} + \varepsilon_{4} \left( {u_{{2,x_{2} }} + u_{{3,x_{3} }} } \right) - \theta - \varepsilon_{3} \frac{\nu }{\omega }\int\limits_{t - \omega }^{t} {K(t,\xi )} \,\,\theta_{,\xi \,\,} \,d\xi , \hfill \\ &\sigma_{22} = u_{{2,x_{2} }} + \varepsilon_{4} \left( {u_{{1,x_{1} }} + u_{{3,x_{3} }} } \right) - \theta - \varepsilon_{3} \frac{\nu }{\omega }\int\limits_{t - \omega }^{t} {K(t,\xi )} \,\,\theta_{,\xi \,\,} \,d\xi , \hfill \\& \sigma_{33} = u_{{3,x_{3} }} + \varepsilon_{4} \left( {u_{{1,x_{1} }} + u_{{2,x_{2} }} } \right) - \theta - \varepsilon_{3} \frac{\nu }{\omega }\int\limits_{t - \omega }^{t} {K(t,\xi )} \,\,\theta_{,\xi \,\,} \,d\xi , \hfill \\& \sigma_{12} = \varepsilon_{2} \left( {u_{{1,x_{2} }} + u_{{2,x_{1} }} } \right), \hfill \\& \sigma_{13} = \varepsilon_{2} \left( {u_{{1,x_{3} }} + u_{{3,x_{1} }} } \right), \hfill \\& \sigma_{12} = \varepsilon_{2} \left( {u_{{2,x_{3} }} + u_{{3,x_{2} }} } \right) \hfill \\ \end{aligned} $$

(13)

Method of Solution: Vector–Matrix Method

Applying Laplace and Fourier transform defined by $L\left\{ {f(x,y,t)} \right\} = \bar{g}(x,y,s) = \int_{0}^{\infty } {e^{ - st} } f(x,y,t)\,dt,\,\,\text{Re} (s) > 0$ and $F\left\{ {f(x,y,t)} \right\} = \bar{f}^{*} (x,q,s) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{ - \infty }^{\infty } {e^{ - iqy} \bar{f}(x,y,s)\,dy}$ respectively and eliminating “-”, “*” Eqs. (11) (12), (13) reduces to

$$ \begin{aligned} U_{1}^{\prime \prime } = A_{11} U_{1} + A_{12} U_{2}^{\prime } + A_{13} U_{3}^{\prime } + A_{14} \varTheta^{\prime}, \hfill \\ U_{2}^{\prime \prime } = B_{11} U_{2} + B_{12} U_{3} + B_{13} \varTheta + B_{14} U_{1}^{\prime } , \hfill \\ U_{3}^{\prime \prime } = C_{11} U_{2} + C_{12} U_{3} + C_{13} \varTheta + C_{14} U_{1}^{\prime } \hfill \\ \end{aligned} $$

(14)

$$ \varTheta^{\prime \prime } = D_{11} U_{2} + D_{12} U_{3} + D_{13} \varTheta + D_{14} U_{1}^{\prime } $$

(15)

$$ \begin{aligned} &\sigma_{11} = U_{1}^{\prime } + \beta_{1} U_{2} + \beta_{2} U_{3} + \beta_{3} \varTheta , \hfill \\ &\sigma_{22} = \varepsilon_{4} U_{1}^{\prime } + \beta_{4} U_{2} + \beta_{2} U_{3} + \beta_{3} \varTheta , \hfill \\ &\sigma_{33} = \varepsilon_{4} U_{1}^{\prime } + \beta_{1} U_{2} + \beta_{5} U_{3} + \beta_{3} \varTheta , \hfill \\& \sigma_{12} = \beta_{6} U_{1} + \varepsilon_{2} U_{2}^{\prime } , \hfill \\ &\sigma_{13} = \beta_{7} U_{1} + \varepsilon_{2} U_{3}^{\prime } , \hfill \\ &\sigma_{23} = \beta_{7} U_{2} + \beta_{6} U_{3} \hfill \\ \end{aligned} $$

(16)

where, $\varepsilon_{i} \,,i = 1,2,..,13\,\,\,and\,\,\beta_{i} \,,i = 1,2,..7$ are mentioned in appendix and “′”, “″” represent the 1^st and 2^nd derivatives with respect to x₁.

The Eqs. (14) and (15) reduces to the following vector matrix differential equation as Ghosh et al. [18], [33] -

$$ \frac{{{\mathbf{d}}\underrightarrow v}}{{{\mathbf{d}}x_{1} }} = {\mathbf{A}}\underrightarrow v $$

(17)

where, $\underrightarrow v = \left[ {U_{1} \,U_{2} \,U_{3} \,\,\varTheta \,\,U_{1}^{\prime } \,U_{2}^{\prime } \,U_{3}^{\prime } \,\,\varTheta^{\prime}} \right]^{T}$ and A is given in the appendix.

The roots of the characteristic equation $\left| {A - \lambda \,I} \right| = 0$ are $\lambda = \pm \lambda_{i}$(i = 1, 2, 3, 4) which are known as eigenvalue of the matrix A.

Let $\underrightarrow X\,\left( \lambda \right) = \left[ {\begin{array}{*{20}c} {d_{1} } & {d_{2} } & {d_{3} } & {d_{4} } & {\lambda d_{1} } & {\lambda d_{2} } & {\lambda d_{3} } & {\lambda d_{4} } \\ \end{array} } \right]^{T}$ be the eigenvector corresponding to the eigenvalue λ of the matrix A.

The solution of the Eq. (17) is given by

$$ {\vec{\mathbf{v}}} = \sum\limits_{i = 1}^{6} {X_{i} y_{i} } $$

(18)

where $y_{i} = A_{i} e^{{\lambda_{i} x}} \,$ and A_i are arbitrarily constants to be determined by using boundary conditions.

Thus we obtain the displacement components and temperature as follows:

$$ \begin{aligned} U_{1} = \sum\limits_{j = 1}^{4} A_{j} x_{1j} \,e^{{\lambda_{j} x_{1} }} ,U_{2} = \sum\limits_{j = 1}^{4} A_{j} x_{2j} e^{{\lambda_{j} x_{1} }} , \hfill \\ U_{3} = \sum\limits_{j = 1}^{4} A_{j} x_{3j} e^{{\lambda_{j} x_{1} }} \,and\,\varTheta = \sum\limits_{j = 1}^{4} A_{j} x_{4j} e^{{\lambda_{j} x_{1}^{{}} }} \hfill \\ \end{aligned} $$

(19)

Using Eq. (19) in Eq. (16), we obtain the stress components as below-

$$ \begin{aligned} \sigma_{11} = \sum\limits_{i = 1}^{4} {A_{i} } \,R_{1i} (x_{1} )\,\,,\sigma_{22} = \sum\limits_{i = 1}^{4} {A_{i} } \,R_{2i} (x_{1} )\,\,,\sigma_{33} = \sum\limits_{i = 1}^{4} {A_{i} } \,R_{3i} (x_{1} )\,\,, \hfill \\ \sigma_{12} = \sum\limits_{i = 1}^{4} {A_{i} } \,R_{4i} (x_{1} )\,\,,\sigma_{13} = \sum\limits_{i = 1}^{4} {A_{i} } \,R_{5i} (x_{1} )\,\,,\sigma_{23} = \sum\limits_{i = 1}^{4} {A_{i} } \,R_{6i} (x_{1} )\,\,,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ and\,\,\,\,\,\,\theta = \sum\limits_{i = 1}^{4} {A_{i} } \,R_{7i} (x_{1} )\,\,,R_{ji} (j = 1,2,..,7 \, and \, i = 1,2,..4) \, are \, given \, in \, the \, appendix. \hfill \\ \end{aligned} $$

(20)

Initial And Boundary Conditions

In our problem, we consider following initial conditions $u_{1} = u_{2} = u_{3} = \theta = \dot{u}_{1} = \dot{u}_{2} = \dot{u}_{3} = \dot{\theta } = 0$.

For the determination of A_i, we consider the following boundary conditions-

$$ \begin{aligned} &{Mechanical} \, {boundary} \, {conditions:} \hfill \\ &\sigma_{11} \left( {0,x_{2} ,x_{3} ,t} \right) = 0,\,\,\sigma_{12} \left( {0,x_{2} ,x_{3} ,t} \right) = 0,\,\,\sigma_{13} \left( {0,x_{2} ,x_{3} ,t} \right) = 0,\,\, \hfill \\ &Thermal \, boundary \, {condition:} \hfill \\ &\theta \left( {0,x_{2} ,x_{3} ,t} \right) = r,\,\,\,\,\,\,where\,\,r\,\,is \, a \, cons\tan ts. \hfill \\ \end{aligned} $$

(21)

Applying Laplace and double Fourier transformation, the Eq. (21) becomes

$$ \begin{aligned} \sigma_{11} \left( {0,\psi_{2} ,\psi_{3} ,s} \right) = 0,\,\,\sigma_{12} \left( {0,\psi_{2} ,\psi_{3} ,s} \right) = 0,\,\,\sigma_{13} \left( {0,\psi_{2} ,\psi_{3} ,s} \right) = 0\,\, \hfill \\ \,\,and\,\,\,\theta \left( {0,\psi_{2} ,\psi_{3} ,s} \right) = r^{*} ,\,\,\,\,\,\,where\,\,r^{*} \,\, = - \tfrac{2}{\pi }\tfrac{{\theta_{0} }}{s}\tfrac{{\sin \,[\psi_{2} g]}}{{\psi_{2} }}\tfrac{{\sin \,[\psi_{3} g]}}{{\psi_{3} }} \hfill \\ \end{aligned} $$

(22)

Using above boundary conditions (22) in Eqs. (19) and (20) a set of linear simultaneous equations are obtained as follows-

$$ \sum\limits_{j = 1}^{4} {A_{j} l_{1j} } = 0,\sum\limits_{j = 1}^{4} {A_{j} l_{4j} (x)} = 0,\sum\limits_{j = 1}^{4} {A_{j} l_{5j} (x)} = 0,\sum\limits_{j = 1}^{4} {A_{j} l_{7j} } = r^{*} $$

(23)

where l_ij (i = 1,2,..,7) and j = 1,2,3,4 are given in the appendix.

Applying Crammer’s rule in the above mentioned equations we obtain the values of arbitrary constants, A_i(i = 1,2,3,4) as $A_{i} = \frac{{D_{i} }}{\Delta }$ where D_i and Δ are given in the appendix.

Numerical

To avoid complexity of the inversion of Laplace–Fourier transform in space–time domain, an efficient computer programme has been developed for numerical computation of physical variables like stress, strain, temperature by using Method of Bellman et al. [19], where we have taken the roots(t_i) of Legendre Polynomial of degree 7 as the seven values of time (t = t_i, i = 1…7, where t₁ = 0.025775, t₂ = 0.138382, t₃ = 0.352509, t₄ = 0.693147, t₅ = 1.21376, t₆ = 2.04612 and t₇ = 3.67119). Also Inverse Fourier Transforms are calculated numerically by infinite integral using seven point Gaussian quadrature formulas for different values of x₂ and x₃. Numerical computations and distribution of physical variable to inspect the influence of time parameter (t), phase lag variables, space variable(x), time-delay (ω) have been analyzed. The numerical values (in SI unit) of constants for silicon are considered as follows: $\begin{aligned} \kappa = 386.0,\kappa^{*} = 200.0,C_{E} = 1.4 \times 10^{3} ,\lambda = 7.76 \times 10^{10} , \hfill \\ \mu = 3.86 \times 10^{10} ,\rho = 8954.0,T_{0} = 293.0,\nu = 0.33,\gamma = 210 \times 10^{4} , \hfill \\ \tau_{\theta } = 0.01,\tau_{q} = 0.2,\tau_{T} = 0.15,\tau_{v} = 0.05,c_{0} = 2200 \hfill \\ \end{aligned}$

Graphical Analysis

For fixed time delay (ω = 0.04) with the kernel function, $K(t,\xi ) = \left[ {1 - (t - \xi )/\omega } \right]^{2} ,p_{1} = 0.5,p_{2} = 0.7$ at $t = t_{5} ,and\,t = t_{7}$ $t = t_{1} ,t = t_{3} ,$ at fixed $x_{2} = 1.5\,\,and\,\,x_{3} = 1.7$.

Figure 2 depicts the non-dimensional numerical distribution of the normal stress, $\sigma_{11}$ for different values of x₁. Initially the numerical value of $\sigma_{11}$ is zero. At $t = t_{1} \,\,and\,\,t = t_{3}$,$\sigma_{11}$ is positive indicating extensional stress while at $t = t_{5} \,\,and\,\,t = t_{7}$, it is negative stress up to x₁ = 0.3, then a tendency to show a positive or extensive stress before vanishing to zero.

Fig. 2

Distribution of $\sigma_{11}$ versus $x_{1}$ at different time

Figure 3 and 4 represent the characteristic curves of non-dimensional stress components ($\sigma_{12} \,and\,\sigma_{13}$) along x₁-axis. The numerical value increase from zero and then become steady after gaining maximum value at $x_{1} = 0.25$.A gradual decrease in the rate of increment of both $\sigma_{12} \,and\,\sigma_{13}$ are marked from $t_{5} \to t_{3} \to t_{7}$ with a very low rate observed at $t = t_{1}$.

Fig. 3

Distribution of $\sigma_{12} \,\,vs.\,\,x_{1}$ at different time

Fig. 4

Distribution of $\sigma_{13}$ versus $x_{1}$ at different time

Figure 5 shows the characteristics behaviour of $\sigma_{22}$ along $x_{1}$-axis. The non-dimensional numerical values of this stress component increase gradually and thereafter decrease attaining maximum value in the region $0.1 \le x_{1} \le 0.2$ before vanishing at x₁ = 0.4.Afterwards, an alternate small negative and positive stress values appear with increasing $x_{1}$.

Fig. 5

Distribution of $\sigma_{22}$ versus $x_{1}$ at different time

For fixed time delay (ω = 0.04) with the kernel function,$K(t,\xi ) = \left[ {1 - (t - \xi )/\omega } \right]^{2} ,p_{1} = 0.5,p_{2} = 0.7$ at $t = t_{2} ,t = t_{4} \,$ and $t = t_{6}$ at fixed $x_{2} = 1.5$ and $x_{3} = 1.7$.

Figure 6 represents the numerical distribution of the non-dimensional stress component ($\sigma_{23}$) along $x_{1}$-axis. The non-dimensional numerical value of $\sigma_{23}$ have been observed at x₁ = 0.6 showing oscillating characteristics. Maximum shearing stress have been seen near the middle plane of the plate while from $t = t_{2} \,\,to\,\,\,t = t_{6}$, a sharp decrease in numerical values of shearing stress is noted.

Fig. 6

Distribution of $\sigma_{23}$ versus $x_{1}$ at different time

Figure 7 exhibits the characteristic representation of the stress component ($\sigma_{33}$) for different values of x₁ at different time $t = t_{1} ,t = t_{3} ,t = t_{5} ,and\,t = t_{7}$ for fixed time delay (ω = 0.04). At different time, $\sigma_{33} \,\,\,$ gradually decreases having least value in $\,\,0.1 \le x_{1} \le 0.2$ and maximum value at $\,x_{1} = 0.5$. Finally $\,\,\,\,\sigma_{33} \,\,\, \to 0\,\,as\,\,x_{1} \to \infty \,\,.$

Fig. 7

Distribution of $\,\sigma_{33}$ versus $x_{1}$ at different time

Figure 8 is about the temperature distribution along $\,x_{1}$-axis for different numerical values of kernel function ($k(t,\xi )$) for fixed ω = 0.04. The characteristic curves depict that the numerical values of temperature gradually increase and after certain time at $\,\,\,\,x_{1} = 0.6$ and onwards become steady.

Fig. 8

Temperature distribution versus $x_{1}$ for diff. values of $k(t,\xi ).$

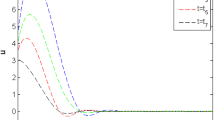
Figure 9 represents the numerical characteristics of temperature for different values of time-delays. The characteristic curves become steady after increasing gradually from zero. The maximum value of temperature is noted at $\,\,\,\,x_{1} = 0.6$ which becomes steady up to $\,\,\,\,x_{1} = 1.0$.

Fig. 9

Temperature distribution versus $x_{1}$ for diff. value of $\omega$

Figure 10 represent the phase lag effect on temperature distribution. For both the G-N-III and L-S model the temperature gradually increases from zero for $t = t_{1} ,t = t_{3}$.

Fig. 10

Temperature distribution versus $x_{1}$ for different PHL model

Figure 11 characterises the distribution of temperature along x₁ –axis for $\tau_{\theta } = 0.01,\tau_{q} = 0.2,$$\tau_{T} = 0.15$,$\tau_{v} = 0.05$ as the effect of three phase lags in this model on temperature at different time $t = t_{2} ,t = t_{4} ,t = t_{6}$.The non-dimensional numerical value of temperature increase gradually with a maximum value at $\,\,\,\,x_{1} = 0.6$ for fixed time delay (ω = 0.04) with kernel function, $K(t,\xi ) = \left[ {1 - (t - \xi )/\omega } \right]^{2} ,p_{1} = 0.5,p_{2} = 0.7$.

Fig. 11

Temperature distribution versus $x_{1}$ at diff time

Application

The concept of half space has a great impact in engineering science. We know the boundary conditions are preserved on the conducting boundary surface which is also known as image plane or symmetry plane. But when the same dielectric medium removes and replaces the conducting medium in upper half space the three dimensional medium becomes homogeneous, linear and isotropic in various electrostatic field. It is also notable that field calculation for lower half space has no significant physical meaning as temperature distribution is calculated based on upper half field distribution. In thermoelasticity, a finite speed propagation of thermal signal is considered as thermodynamic theories are generally based on the wave-like (or hyperbolic-type) heat conduction equation. This phenomenon of generalized thermoelasticity attracts the researchers.

Unambiguous numerical results and inherent procedural complexities using both Integral order and Fractional order Calculus to solve problems in generalized thermoelasticity leads the researchers to opt for the new generation technique like 3PHL model using MDD. This model in association with Kernel function and time delay in context of MDD can produce convergent and specific solution for the generalized heat conduction equation. This model provides specific and moderate solution for field variables with respect to space variables in different field of thermoelasticity in Engineering and Mechanical sciences like-construction engineering, visco-elasticity, nuclear reactor design, etc. together with earthquake science, geophysics. Use of Integral transform in MDD and the different phase lag variables in conventional heat conduction equation this model depicts more accurate and convenient continuous numerical results to calculate damage tolerance, thermal durability of an elastic material and help to inspect lagging behaviour on filed variables.

Application of the Infinite Half Space Model to Explain the Coding of Oceanic Lithosphere/Plate

The dashed line indicates the approximation as a plate of constant thickness (based on Mc Kenzie et al. [20] and Sclater et al. [21].

Evaluation of heat flow through the earth especially along the tectonically active plate margins is a continuous process throughout the history of the earth. The maximum heat flux is observed along the mid-oceanic-ridge [M.O.R.] areas. Thus the application of three dimensional mathematical- model, specially related to heat flux, has a significant correlation with natural heat fluxes through the oceanic lithosphere along the M.O.R.

Considering different boundary-layered models, the plate models better explain the observed thermal data above the oceanic or continental lithosphere and evaluate the thermal structure of the earth as determined by the seismic wave propagation studies. The huge amount of heat flux in the M.O.R. is found to be distributed at great distances from the ridge axis and sufficiently large vertical ocean depths over the oceanic lithosphere [Fig. 12a, b]. A two-layered model of the oceanic lithosphere has been considered. The upper layer is an elastic rigid rock layer with a mechanically defined lower boundary, above which conduction of heat is thought to be the main process of heat transfer. Apart from the uniform heat source, several evidences of heat sources are suggested like the radiogenic heat in the upper lithosphere, shearing heat at the lower surface of the lithosphere, reheating of old lithosphere due to intrusion of hot mantle plumes at hotspots and heat transfer due to small scale convection currents in the lower lithosphere. Thus the convecting asthenosphere into the lithosphere is thought to attribute the heat transfer model, consequently giving a thinner lithosphere [Fig. 13a, b] than in the half-space models. Structural variation between the oceanic and continental crusts derived from dispersion of seismic waves is highly compatible with the thermal model of an elastic and rigid mechanical layer underlain by a convecting thermal boundary layer extending to about 150 km.

Fig. 12

a predicted thermal structure in the coding plate (as Turcotte and Schubert [22]). b vertical heat flow is narrow columns that move away from ridge crest showing symmetrical behavior on both sides

Fig. 13

Schematic Diagram of lithospheric plate structre beneth oceans

The mathematical calculations show that there is a gradual increase in temperatures which becomes steady as the source of heat moves along x₁ for different variables like Kernel function, time, time delay and phase lag. A similar behaviour of a high heat flux is observed as the hot mantle material along with the added effects of other heat sources move upward along the ridge axis and a gradual cooling of successive older rocks away from the ridge crest [Fig. 13a].

Movement of heat sources along the x₁ for different variables resulting a high initial extensive and compressive normal stresses appears to be due to excessive applied forces generated by the upward movement of hot mantle material and simultaneous release of pressure. While the convective currents below the rigid plates appear to cause the shearing stresses at slightly later times.

Conclusion

In our present work, studying various applications on mechanical engineering, applied mathematics,industrial, geophysical sectors and geothermal structure of the earth we have analysed the different generalized heat conduction equations and different phase lag models to introduce a new model for a three dimensional isotropic half space in context of MDD with three different phase lags. According to our work we have reached to the following conclusion that

• (i) The 3PHL model is more efficient relative to other existing well-known theories of thermoelasticity.

• (ii) The 3PHL model acts like a general or standard one from which other thermoelastic models can be specified as different special cases.

• (iii) The kernel function with its different values and time delay parameter has significant influence in the characteristic representation of distribution of components of field variables with respect to space variables. The kernel function together with time delay parameter shows instantaneous change rate for heat conduction depending upon previous state.

• (iv) The time variable and time delay parameter in MDD is capable to judge and is able to predict accurately and specifically the behavioural characteristics of the possible field variables.

• (v) Use of Integral transforms used in MDD, provide more accurate, specific and continuous numerical results compared to other thermoelastic models like fractional order or integral order derivative.

• (vi) We are capable to measure significant differences in the distribution of field variables with respect to different models –Fourier’s law model, L-S model, G-N-III model with 3PHL model.

• (vii) We conclude finally that Figs. 1, 2, 3, 10 satisfied the boundary conditions and the rest of the figures(Figs. 4, 5, 6, 7, 8, 9) satisfied the numerical results according to our analytical problem.

Appendix

$$ A = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ {M_{51} } & {M_{52} } & {M_{53} } & {M_{54} } & {M_{55} } & {M_{56} } & {M_{57} } & {M_{58} } \\ {M_{61} } & {M_{62} } & {M_{63} } & {M_{64} } & {M_{65} } & {M_{66} } & {M_{67} } & {M_{68} } \\ {M_{71} } & {M_{72} } & {M_{73} } & {M_{74} } & {M_{75} } & {M_{76} } & {M_{77} } & {M_{78} } \\ {M_{81} } & {M_{82} } & {M_{83} } & {M_{84} } & {M_{85} } & {M_{86} } & {M_{87} } & {M_{88} } \\ \end{array} } \right] $$

$$ \underrightarrow v = \left[ {U_{1} \,U_{2} \,U_{3} \,\,\varTheta \,\,U_{1}^{\prime } \,U_{2}^{\prime } \,U_{3}^{\prime } \,\,\varTheta^{\prime}} \right]^{T} $$

$$ \begin{aligned} &M_{51} = A_{11} ,M_{52} = 0,M_{53} = 0,M_{54} = 0,M_{55} = 0, \hfill \\ &M_{56} = A_{12} ,M_{57} = A_{13} ,M_{58} = A_{14} , \hfill \\ &M_{61} = 0,\,\,M_{62} = B_{11} ,\,M_{63} = B_{12} ,\,M_{64} = B_{13} \,,M_{65} = B_{14} ,M_{66} = 0,\,\,\,M_{67} = 0\,,\,\,\,\,\,M_{68} = 0 \hfill \\ &M_{71} = 0,\,\,M_{72} = C_{11} ,\,M_{73} = C_{12} ,\,M_{74} = C_{13} ,\,M_{75} = C_{14} ,M_{76} = 0,\,\,M_{77} = 0\,,\,\,\,M_{78} = 0 \hfill \\ &M_{81} = 0,\,\,M_{82} = D_{11} ,\,M_{83} = D_{12} ,\,M_{84} = D_{13} ,\,M_{85} = D_{14} ,M_{86} = 0,\,M_{87} = 0\,,\,\,M_{88} = 0 \hfill \\ \end{aligned} $$

$$ \begin{aligned} A_{11} = s^{2} + \varepsilon_{3} \left( {\psi_{2}^{2} + \psi_{3}^{2} } \right), \hfill \\ A_{12} = - i\,\varepsilon_{1} \,\psi_{2} , \hfill \\ A_{13} = - i\,\varepsilon_{1} \,\psi_{3} , \hfill \\ A_{14} = 1 + \frac{{\varepsilon_{3} \,\nu \,G}}{\omega }, \hfill \\ \end{aligned} $$

$$ \begin{aligned} B_{11} = \frac{{s^{2} + \psi_{2}^{2} }}{{\varepsilon_{3} }}, \hfill \\ B_{12} = \frac{{\varepsilon_{1} \,\psi_{2\,} \psi_{3} }}{{\varepsilon_{3} }} \hfill \\ B_{13} = \frac{{i\,\psi_{2} }}{{\varepsilon_{3} }}\left( {1 + \frac{{\varepsilon_{3} \,\nu \,G}}{\omega }} \right), \hfill \\ B_{14} = - \frac{{i\,\varepsilon_{1} \,\psi_{2} }}{{\varepsilon_{3} }}, \hfill \\ \end{aligned} $$

$$ \begin{aligned} C_{11} = \frac{{\varepsilon_{1} \,\psi_{2\,} \psi_{3} }}{{\varepsilon_{3} }}, \hfill \\ C_{12} = \frac{{s^{2} + \psi_{3}^{2} + \varepsilon_{3} \psi_{2}^{2} }}{{\varepsilon_{3} }}, \hfill \\ C_{13} = \frac{{i\,\psi_{3} }}{{\varepsilon_{3} }}\left( {1 + \frac{{\varepsilon_{3} \,\nu \,G}}{\omega }} \right), \hfill \\ C_{14} = - \frac{{i\,\varepsilon_{1} \,\psi_{3} }}{{\varepsilon_{3} }}, \hfill \\ \end{aligned} $$

$$ \begin{aligned} D_{11} = \frac{{\varepsilon_{12} }}{{\varepsilon_{9} }},\,\, \hfill \\ D_{12} = \frac{{\varepsilon_{13} \,}}{{\varepsilon_{9} }},\,\,\, \hfill \\ D_{13} = \frac{{\varepsilon_{10} \,}}{{\varepsilon_{9} }},\,\, \hfill \\ D_{14} = \frac{{\varepsilon_{14} \,}}{{\varepsilon_{9} }}\,\, \hfill \\ \end{aligned} $$

$$ \begin{aligned} \beta_{1} = i\,\varepsilon_{4} \,\psi_{2} \hfill \\ \beta_{2} = i\,\varepsilon_{4} \,\psi_{3} \hfill \\ \beta_{3} = - \left( {1 + \frac{{\varepsilon_{3} \,\nu \,G}}{\omega }} \right), \hfill \\ \beta_{4} = i\,\psi_{2} , \hfill \\ \beta_{5} = i\,\psi_{3} , \hfill \\ \beta_{6} = i\,\varepsilon_{2} \,\psi_{2} , \hfill \\ \beta_{7} = i\,\varepsilon_{2} \,\psi_{3} , \hfill \\ \end{aligned} $$

$$ \begin{aligned} \varepsilon_{1} = \frac{\lambda + \mu }{\lambda + 2\mu };\varepsilon_{2} = \frac{\mu }{\lambda + 2\mu };\varepsilon_{3} = \frac{1}{{c_{0} \eta^{2} }};\,\,\varepsilon_{4} = \frac{\lambda }{\lambda + 2\mu }; \hfill \\ \varepsilon_{5} = \frac{{T_{0} \,\gamma^{2} }}{{k\,\,\eta \,\,\left( {\lambda + 2\mu } \right)}};\,\,\varepsilon_{6} = \frac{{k\,c_{0}^{4} \,\eta^{2} \,\tau_{T} }}{{k\,^{*} }};\,\,\,\varepsilon_{7} = \frac{{c_{0} \,\eta \,\,\tau_{v}^{*} }}{{k\,^{*} }};\,\,\, \hfill \\ \varepsilon_{8} = \frac{k}{{k\,^{*} }};\,\,\varepsilon_{9} = \left( {1 + \frac{{\tau_{\theta } \,\,G}}{\omega }} \right)\left( {1 + \varepsilon_{6} \,s^{2} + + \varepsilon_{7} \,s} \right);\,\,\, \hfill \\ \end{aligned} $$

$$ \begin{aligned} \varepsilon_{10} = \varepsilon_{8} \left( {s + \frac{{\tau_{q} \,s\,G}}{\omega } + \frac{{\tau_{q}^{2} \,s^{2} \,G}}{2\,\omega }} \right) + \varepsilon_{9} \left( {\psi_{2}^{2} + \psi_{3}^{2} } \right);\,\, \hfill \\ \varepsilon_{11} = \varepsilon_{5} \,\varepsilon_{8} \left( {s + \frac{{\tau_{q} \,s\,G}}{\omega } + \frac{{\tau_{q}^{2} \,s^{2} \,G}}{2\,\omega }} \right); \hfill \\ \end{aligned} $$

$$ \begin{aligned} \varepsilon_{12} = i\,\psi_{2\,} \varepsilon_{5} \,\varepsilon_{8} \left( {s + \frac{{\tau_{q} \,s\,G}}{\omega } + \frac{{\tau_{q}^{2} \,s^{2} \,G}}{2\,\omega }} \right);\,\,\, \hfill \\ \varepsilon_{13} = i\,\psi_{3\,} \varepsilon_{5} \,\varepsilon_{8} \left( {s + \frac{{\tau_{q} \,s\,G}}{\omega } + \frac{{\tau_{q}^{2} \,s^{2} \,G}}{2\,\omega }} \right); \hfill \\ \end{aligned} $$

$\begin{aligned} & d_{1} = (h_{24} h_{13} - h_{14} h_{23} )(h_{22} h_{33} - h_{32} h_{23} ) - (h_{34} h_{23} - h_{24} h_{33} )(h_{12} h_{23} - h_{22} h_{13} ), \\ & d_{2} = (h_{34} h_{23} - h_{24} h_{33} )(h_{11} h_{23} - h_{21} h_{13} ) - (h_{24} h_{13} - h_{14} h_{23} )(h_{21} h_{33} - h_{31} h_{23} ), \\ & d_{3} = (h_{12} h_{21} - h_{11} h_{22} )(h_{21} h_{34} - h_{31} h_{24} ) - (h_{22} h_{31} - h_{21} h_{32} )(h_{11} h_{24} - h_{14} h_{21} ), \\ & d_{4} = (h_{11} h_{23} - h_{21} h_{13} )(h_{22} h_{33} - h_{32} h_{23} ) - (h_{12} h_{23} - h_{22} h_{13} )(h_{21} h_{33} - h_{31} h_{23} ), \\ \end{aligned}$,

$$ \begin{aligned} h_{11} = M_{51} - \lambda^{2} \,\,,h_{12} = \lambda M_{56} \,\,,h_{13} = \lambda M_{57} \,\,,h_{14} = \lambda M_{58} \hfill \\ h_{21} = M_{65} \,\,,h_{22} = M_{62} \, - \lambda^{2} \,,h_{23} = M_{63} \,\,,h_{24} = M_{64} \hfill \\ h_{31} = \lambda M_{75} \,,h_{32} = M_{72} \,\,,h_{33} = M_{73} \, - \lambda^{2} \,,h_{34} = \lambda M_{74} \hfill \\ h_{41} = \lambda M_{85} \,\,,h_{42} = M_{82} \,\,,h_{43} = M_{83} \,\,,h_{44} = M_{84} - \lambda^{2} \hfill \\ \end{aligned} $$

$$ R_{1i} = \left( { - \lambda_{i} \,d_{1i} + \sum\limits_{k = 1}^{3} {\beta_{k} \,d_{(k + 1)i} } } \right)e^{{ - \lambda_{i} x_{1} }} ,,i = 1(1)4 $$

$$ R_{2i} = \left( { - \lambda_{i} \,\,\varepsilon_{4} \,d_{1i} + \beta_{4} \,d_{2i} + \beta_{2} \,d_{3i} + \beta_{3} \,d_{4i} } \right)e^{{ - \lambda_{i} x_{1} }} ,i = 1(1)4 $$

$$ R_{3i} = \left( { - \lambda_{1} \,\varepsilon_{4} \,d_{1i} + \beta_{1} \,d_{2i} + \beta_{5} \,d_{3i} + \beta_{3} \,d_{4i} } \right)e^{{ - \lambda_{i} x_{1} }} ;,i = 1(1)4 $$

$$ R_{4i} = \left( {\beta_{6} \,d_{1i} - \varepsilon_{2} \,\lambda_{i} \,d_{2i} } \right)e^{{ - \lambda_{i} x_{1} }} ,i = 1(1)4 $$

$$ R_{5i} = \left( {\beta_{7} \,d_{1i} - \varepsilon_{2} \,\lambda_{i} \,d_{3i} } \right)e^{{ - \lambda_{i} x_{1} }} ,i = 1(1)4 $$

$$ R_{6i} = \left( {\beta_{7} \,d_{2i} + \beta_{6} \,d_{3i} } \right)e^{{ - \lambda_{i} x_{1} }} ,i = 1(1)4 $$

$$ R_{7i} = d_{4i} \,e^{{ - \lambda_{i} x_{1} }} i = 1(1)4 $$

$$ \begin{aligned} l_{1j} = R_{1j} (0),\,\,\,\,l_{4j} = R_{4j} (0),\,\,\,\,l_{5j} = R_{5j} ,\,\, \hfill \\ \,l\,_{7j} = R_{7j} (0),\,\,\,\,where\,j = 1,2,3,4 \hfill \\ \end{aligned} $$

$$ and\,\,A_{i} = \frac{{D_{i} }}{\Delta }\,,i = 1,2,3,4 $$

$$ \begin{aligned} D_{1} = \left[ {\begin{array}{*{20}c} 0 & {l_{12} } & {l_{13} } & {l_{14} } \\ 0 & {l_{42} } & {l_{43} } & {l_{44} } \\ 0 & {l_{52} } & {l_{53} } & {l_{54} } \\ {r^{*} } & {l_{72} } & {l_{73} } & {l_{74} } \\ \end{array} } \right],D_{2} = \left[ {\begin{array}{*{20}c} {l_{11} } & 0 & {l_{13} } & {l_{14} } \\ {l_{41} } & 0 & {l_{43} } & {l_{44} } \\ {l_{51} } & 0 & {l_{53} } & {l_{54} } \\ {l_{71} } & {r^{*} } & {l_{73} } & {l_{74} } \\ \end{array} } \right], \hfill \\ D_{3} = \left[ {\begin{array}{*{20}c} {l_{11} } & {l_{12} } & 0 & {l_{14} } \\ {l_{41} } & {l_{42} } & 0 & {l_{44} } \\ {l_{51} } & {l_{52} } & 0 & {l_{54} } \\ {l_{71} } & {l_{72} } & {r^{*} } & {l_{74} } \\ \end{array} } \right],D_{4} = \left[ {\begin{array}{*{20}c} {l_{11} } & {l_{12} } & {l_{13} } & 0 \\ {l_{41} } & {l_{42} } & {l_{43} } & 0 \\ {l_{51} } & {l_{52} } & {l_{53} } & 0 \\ {l_{71} } & {l_{72} } & {l_{73} } & {r^{*} } \\ \end{array} } \right],\Delta = \left[ {\begin{array}{*{20}c} {l_{11} } & {l_{12} } & {l_{13} } & {l_{14} } \\ {l_{41} } & {l_{42} } & {l_{43} } & {l_{44} } \\ {l_{51} } & {l_{52} } & {l_{53} } & {l_{54} } \\ {l_{71} } & {l_{72} } & {l_{73} } & {l_{74} } \\ \end{array} } \right] \hfill \\ \end{aligned} $$