Modeling of a homogeneous isotropic half space in the context of multi-phase lag coupled thermoelasticity

Abstract

A two-dimensional multi-phase lag model in the context of generalized thermoelasticity is established for an isotropic half-space medium. A vector-matrix differential equation is obtained from the governing equations using normal mode analysis. The eigenvalue approach is applied to obtain the solutions. The temperature-dependent displacements, stresses, strains are calculated numerically and represented graphically to show the accuracy of the solution under mechanical and thermal loads.

1 Introduction

The modified coupled stress-strain theory has become popular in Nano-systems to study strain, displacement, vibration, buckling, bending, etc., in the engineering structures like beams, plates and shells. The modified theory of coupled stress has been introduced by Yang et al. (2002). The theory of generalized thermoelasticity was introduced to remove the finiteness of the heat equation in the conventional classical thermoelasticity (CTE) theory. The generalized thermoelasticity theory has become acceptable to the different engineering fields as well as to the researcher as it is capable of avoiding the finiteness of heat propagation.

In the history of generalized thermoelasticity, Lord and Shulman (1967) introduced a one-relaxation time parameter in the conventional heat conduction equation to modify classical Fourier law (CFL), which is also known as the first generalization theory of thermoelasticity. In the second generalization theory, Green and Lindsay (1972) proposed temperature rate dependent theory (TRDTE) by introducing two relaxation time parameters in the coupled theory of thermoelasticity. In the third generalization, Hetnarski and Ignaczak (1996) proposed the non-linear model introducing the concept of coupled thermoelasticity with low temperature. Green and Naghdi (1991, 1992, 1993) proposed three thermoelastic models known as Green-Naghdi type-I, type-II and type-III, respectively. Type-I is considered similar to the classical theory of thermoelasticity. Type-II model provides the idea of non-dissipation of energy associated with zero production rate of entropy. Type-III Green-Naghdi model is associated with type-I and type-II together with the study of energy dissipation and damped thermoelastic waves. Later on, Tzou (1995, 1999) and Chandrasekhariah (1998) discussed the Dual Phase Lag (DPL) model to inspect the lagging behavior in the thermoelastic medium. Again, Roy Choudhuri (2007) discussed the concept of the Three Phase Lag Model [TPL], introducing three-time parameters in the conventional heat conduction equation. Ghosh et al. (2019), Ghosh and Lahiri (2020), Quintanilla and Racke (2008) found the solutions of the heat equation in the theory of TPL heat conduction in their recent research work. Also, Zenkour (2018) proposed a refined two-temperature multi-phase-lag (RPL) model for a generalized thermoelastic medium consisting of both the heat flux vector and the temperature gradient. In their work, Sardar et al. (2022) studied a three-dimensional coupled thermoelasticity for an anisotropic half-space using multi-phase lag gradients. Zenkour (2018) also studied the thermomechanical effects of microbeams using refined multiphase-lag theory. In association, Alharbi et al. (2022) studied a multi-phase-lag model to investigate the influence of variable thermal conductivity with initial stress on a fibre-reinforced thermoelastic material in the magnetic field.

In our recent study, we investigated the effect of multi-phase lag variables on a two-dimensional thermoelastic isotropic medium.

2 Formulation of the problem

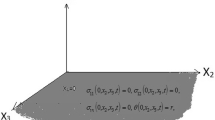
In the orthogonal co-ordinate system XOY, we consider a two dimensional isotropic half-space defined in the region $W=\{0\leq x < \infty, -\infty<y<\infty\}$ (as in Fig. 1) subject to traction free boundary $x=0$. Also, y-axis is considered vertically downwards, and the xy-plane is along the free surface of the half-space.

Fig. 1

Schematic diagram of the problem

3 Basic equations

Equation of motion:

For a homogeneous isotropic half-space, as in Ghosh et al. (2017), Zenkour (2018) and Eringen (1984), respectively, we consider the following governing equations.

$$ (\lambda +\mu )\frac{\partial e}{\partial x}+\mu \nabla ^{2}u- \frac{P}{2}\frac{\partial ^{2}u}{\partial y^{2}}+\frac{P}{2} \frac{\partial ^{2}v}{\partial x\partial y}-\gamma \frac{\partial T}{\partial x}=\rho \Bigg[ \frac{\partial ^{2}u}{\partial t^{2}}-\Omega ^{2}u\Bigg] $$

(1)

$$ (\lambda +\mu )\frac{\partial e}{\partial y}+\mu \nabla ^{2}v+ \frac{P}{2}\frac{\partial ^{2}u}{\partial x\partial y}-\frac{P}{2} \frac{\partial ^{2}v}{\partial x^{2}}+\gamma \frac{\partial T}{\partial y}=\rho \Bigg[ \frac{\partial ^{2}v}{\partial t^{2}}-\Omega ^{2}v\Bigg] $$

(2)

The stress-displacement relation:

$$ \tau _{xx}=(\lambda +2\mu +P)\frac{\partial u}{\partial x}+(\lambda +P) \frac{\partial v}{\partial y}-\gamma T $$

(3)

$$ \tau _{yy}=(\lambda +2\mu +P)\frac{\partial v}{\partial y}+(\lambda +P) \frac{\partial u}{\partial x}-\gamma T $$

(4)

$$ \tau _{xy}=\Bigg(\mu -\frac{P}{2}\Bigg)\frac{\partial v}{\partial x}+ \Bigg(\mu +\frac{P}{2}\Bigg)\frac{\partial u}{\partial y} $$

(5)

Heat conduction equation (In context of multi-phase Lag):

$$\begin{aligned} &\Bigg(1+\sum _{n=1}^{N}\frac{\tau _{\theta}^{n}}{n!} \frac{\partial ^{n}}{\partial t^{n}}\Bigg)\Bigg(K_{11} \frac{\partial ^{2} T}{\partial x^{2}}+ K_{22} \frac{\partial ^{2} T}{\partial y^{2}}\Bigg) \\ &=\Bigg[\overline{R}+\tau _{0}\frac{\partial}{\partial t}+\sum _{n=1}^{N} \frac{\tau _{q}^{n+1}}{(n+1)!} \frac{\partial ^{n+1}}{\partial t^{n+1}}\Bigg] \Bigg[\rho C_{E} \frac{\partial ^{2}T}{\partial t^{2}}+(3\lambda +2\mu )\alpha _{0}T_{0} \frac{\partial ^{2}}{\partial t^{2}}\Bigg( \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\Bigg) \Bigg] \end{aligned}$$

(6)

where $\gamma =(3\lambda +2\mu )\alpha _{t}$, $\lambda +2\mu =\rho {c_{1}}^{2}$ and $e =\frac{\partial u}{\partial x}+ \frac{\partial v}{\partial y}$

4 Nomenclature

Column 1	Column 2
u, v: Displacement Components	e: Dilatation
T: Absolute thermodynamic temperature.	t: Time variable
$C_{E}$: Specific heat at constant strain	λ, μ: Lame’s Constant
$T_{0}$: Reference temperature	τ: Relaxation Time
$\tau _{q}$, $\tau _{\theta }$: Dual-phase-lag, $\tau _{0}$: thermal relaxation time	ρ : Density of the material
$K_{11}$, $K_{22}$ : Thermal conductivity	Ω: angular velocity in the domain W.
$\alpha _{t}$ : Coefficient of linear thermal expansion	P: Initial stress

5 Method of solution

5.1 Formulation of a vector-matrix differential equation

For the solution of equations (1)–(6), the physical quantities can be decomposed into the following form

$$ \textstyle\begin{array}{c@{\quad}c} t^{\prime}=\frac{C_{1}^{2}}{K_{1}}t,~~~(~ x^{\prime},~ y^{\prime})= \frac{C_{1}}{K_{1}}(x,y), & (u^{\prime}, v^{\prime})= \frac{c_{1}^{3}\rho}{K_{1}(3\lambda +2\mu )\alpha _{t}T_{0}}(u,v), \\ \tau _{0}^{\prime}=\frac{C_{1}^{2}}{K_{1}}\tau _{0}, & T^{\prime}= \frac{T}{T_{0}} \\ (\tau _{xx}^{\prime}, \tau _{yy}^{\prime}, \tau _{xx}^{\prime})= \frac{1}{(3\lambda +2\mu )\alpha _{t}T_{0}}(\tau _{xx}, \tau _{yy}, \tau _{xy}) & \Omega ^{\prime}=\frac{K_{1}}{C_{1}^{2}}\Omega ,K_{1}= \frac{K_{11}}{\rho C_{E}} , \\ \rho =\frac{\rho ^{\prime}}{\alpha T_{0}},c_{1}^{2}= \frac{\lambda +2\mu}{\rho} & (\tau _{q}^{\prime}, \tau _{\theta}^{ \prime})=\frac{C_{1}^{2}}{K_{1}}(\tau _{q},\tau _{\theta}) \end{array} $$

(7)

Introducing non-dimensional variables, we obtain from equations (1), (2) and (6) (omitting primes for convenience),

$$ \frac{\partial ^{2} u}{\partial x^{2}}+C_{11} \frac{\partial ^{2}v}{\partial x\partial y}+C_{12} \frac{\partial ^{2}u}{\partial y^{2}}-\frac{\partial T}{\partial x}= \frac{\partial ^{2} u}{\partial t^{2}}-\Omega ^{2}u $$

(8)

$$ \frac{\partial ^{2} v}{\partial y^{2}}+C_{21} \frac{\partial ^{2}v}{\partial x^{2}}+C_{22} \frac{\partial ^{2}u}{\partial x\partial y}+ \frac{\partial T}{\partial y}= \frac{\partial ^{2} v}{\partial t^{2}}- \Omega ^{2}v $$

(9)

$$\begin{aligned} &\frac{K_{11}}{\rho C_{E}c_{1}^{2}}\Bigg(1+\sum _{n=1}^{N} \frac{\tau _{\theta}^{n}}{n!}\frac{\partial ^{n}}{\partial t^{n}} \Bigg)\Bigg(\frac{\partial ^{2}T}{\partial x^{2}}+ \frac{K_{22}}{K_{11}}\frac{\partial ^{2}T}{\partial y^{2}}\Bigg) \\ &\quad =\Bigg(\overline{R}+\tau _{0}\frac{\partial}{\partial t}+\sum _{n=1}^{N} \frac{\tau _{q}^{n+1}}{(n+1)!} \frac{\partial ^{n+1}}{\partial t^{n+1}}\Bigg)\Bigg( \frac{\partial ^{2}T}{\partial t^{2}}+ \frac{\gamma ^{2}T_{0}}{\rho ^{2}c_{1}^{2}c_{E}} \frac{\partial ^{2}}{\partial t^{2}}\Bigg( \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\Bigg) \Bigg) \end{aligned}$$

(10)

After introducing non-dimensional variables, the stress-displacement relations (equations (3)–(5)) reduce to (omitting primes for convenience),

$$ \tau _{xx}=C_{41}\frac{\partial u}{\partial x}+C_{42} \frac{\partial v}{\partial y}-T $$

(11)

$$ \tau _{yy}=C_{41}\frac{\partial v}{\partial y}+C_{42} \frac{\partial u}{\partial x}-T $$

(12)

$$ \tau _{yy}=C_{51}\frac{\partial v}{\partial x}+C_{52} \frac{\partial u}{\partial y} $$

(13)

5.2 Normal mode analysis

To decompose the physical variables in terms of normal modes, as in Ghosh et al. (2018), we consider the following normal mode analysis

$$ (u,v,\tau _{xx}, \tau _{yy},\tau _{xy},T)(x,y,t)=(u^{\ast},v^{\ast}, \tau _{xx}^{\ast},\tau _{yy}^{\ast},\tau _{xy}^{\ast},T^{\ast})(x)e^{ \omega t+iay} $$

(14)

where $\omega$ is the angular frequency, a is the wave number along the x-axis, and $i = \sqrt{-1}$.

Introducing normal mode analysis to equation 8, 9 and 10, we obtain (omitting asterisks for convenience):

$$ \frac{d^{2}u}{dx^{2}}=M_{11}u+M_{12}v+M_{13}T+M_{14}\frac{du}{dx}+M_{15} \frac{dv}{dx}+M_{16}\frac{dT}{dx} $$

(15)

$$ \frac{d^{2}v}{dx^{2}}=M_{21}u+M_{22}v+M_{23}T+M_{24}\frac{du}{dx}+M_{25} \frac{dv}{dx}+M_{26}\frac{dT}{dx} $$

(16)

$$ \frac{d^{2}T}{dx^{2}}=M_{31}u+M_{32}v+M_{33}T+M_{34}\frac{du}{dx}+M_{35} \frac{dv}{dx}+M_{36}\frac{dT}{dx} $$

(17)

Introducing normal mode analysis to equations (11)–(13), we obtain the stress components as (omitting asterisks for convenience)

$$ \tau _{xx}=C_{41}\frac{du}{dx}+C_{42}~~ i a v-T $$

(18)

$$ \tau _{yy}=C_{41}~~ i a v +C_{42}\frac{du}{dx}-T $$

(19)

$$ \tau _{xy}=C_{51}\frac{dv}{dx}+C_{52}\quad i a u $$

(20)

where $M_{ij}$ ($i=1,2,3$ and $j= 1,2,..,6$) and $C_{ij}$ ($i=1,2,3,4,5$ and $j= 1,2$) are mentioned in the Appendix.

6 Solution of the vector-matrix differential equation

The equations (15)–(17) reduce to the compact form of vector-matrix differential equation as follows

$$ \frac{d}{dx}(\vec{v})=A\vec{v} $$

(21)

where $\vec{v}=\left ( \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} u & v & T & \frac{du}{dx} & \frac{dv}{dx} & \frac{dT}{dx} \end{array} \right )$, and A is given in the appendix.

For the solution of the vector-matrix differential equation (21), we apply the method of eigenvalue approach as in Ghosh and Lahiri (2018). The characteristic equation of matrix A is given by

$$ \begin{vmatrix} A-\lambda I \end{vmatrix} =0 $$

(22)

The roots of the characteristic equation (21) are $\lambda =\lambda _{i}$ ($i=1(1)6$), and the corresponding eigenvector $\mathbf{X}$ is given below

$$ \mathbf{X} =\left [\delta _{1} \quad \delta _{2} \quad \delta _{3} \quad \lambda \delta _{1} \quad \lambda \delta _{2} \quad \lambda \delta _{3} \quad \right ]^{T} $$

(23)

where

$$ \textstyle\begin{array}{c} {\delta _{1}=f_{11}f_{23}-f_{13}f_{22},} \\ {\delta _{2}=f_{13}f_{21}-f_{11}f_{23},} \\ {\delta _{3}=f_{11}f_{22}-f_{12}f_{21}} \end{array} $$

(24)

and $f_{ij}$ ($i, j=1,2,3$) are given in the Appendix.

The solution of the vector-matrix equation is given by

$$ \textstyle\begin{array}{c} { u=\sum _{i=1}^{3}A_{i}(\delta _{1})_{\lambda =-\lambda _{i}}e^{- \lambda _{i}x}} \\ {v=\sum _{i=1}^{3}A_{i}(\delta _{2})_{\lambda =-\lambda _{i}}e^{- \lambda _{i}x}} \\ {T=\sum _{i=1}^{3}A_{i}(\delta _{3})_{\lambda =-\lambda _{i}}e^{- \lambda _{i}x}} \end{array} $$

(25)

Thus the stress components are as follows

$$ \textstyle\begin{array}{c} {\tau _{xx}=\sum _{j=1}^{3} A_{j} R_{1j}(x),} \\ {\tau _{yy}=\sum _{j=1}^{3} A_{j} R_{2j}(x),} \\ {\tau _{xy}=\sum _{j=1}^{3} A_{j} R_{3j}(x),} \end{array} $$

(26)

where $R_{ij}$ $i,j=1,2,3$ are given in the appendix, and $A_{j}$, $j=1,2,3$ are to be obtained using the boundary conditions..

7 Boundary conditions

Due to the regularity condition of the solution at infinity, three terms containing exponentials of growing in nature in the space variables $x$ have been discarded, and the remaining arbitrary constants $A_{i}$, ($i=1,2,\ldots4$) are to be determined from the following boundary conditions.

7.1 Mechanical boundary

The boundary of the half-space $x=0$ has no traction elsewhere, i.e.,

$$ \tau _{xx} (x, y ,t)=\sigma _{0} e^{i \omega t} ~~at~~ x=0 ~~and~~ t=0; $$

(27)

7.2 The thermal boundary condition

$$ T (x, y ,t)=T_{0} e^{i \omega t} ~~at~~ x=0 ~~and~~ t=0; $$

(28)

$$ \frac{\partial T}{\partial x}+hT (x, y ,t)=0 ~~at~~ x=0 ~~and~~ t=0; $$

(29)

Applying the above boundary conditions in equations (25) and (26), we get the following simultaneous equations:

$$ \textstyle\begin{array}{c} {A_{1} S_{11}+ A_{2} S_{12}+A_{3} S_{13}=z_{1}} \\ {A_{1} S_{41}+ A_{2} S_{42}+A_{3} S_{43}=z_{2}} \\ {A_{1} S_{51}+ A_{2} S_{52}+A_{3} S_{53}=0} \end{array} $$

(30)

The arbitrary constants can be obtained by solving the above simultaneous equations where, $A_{i} =\frac{D_{i} }{ D }$, $i=1,2,3$, $D,D_{i}$: $i=1,2,3$, $S_{ij}$: $i,j=1,2,3$ and $z_{i}$: $i=1,2$, which are given in the Appendix.

8 Numerical analysis

Numerical analysis and computation have been done using the mechanical and thermal conditions mentioned in equations (27)–(29) to study the characteristic behaviors of the physical constants with respect to space variables in triclinic half-space. The numerical values (in SI units) of constants are taken as in Eringen (1984), Zenkour (2018):

$$\textstyle\begin{array}{l@{\quad }l@{\quad }l} \lambda =9.4 \times \, 10^{10}~\mbox{N}/\mbox{m}^{2} , & \mu =4.0 \times \, 10^{10}~\mbox{kg}/\mbox{ms}^{2} , & \rho =1.7\times 10^{3}~\mbox{kg}/\mbox{m}^{3} , \\ a=2.0,\ b=0.5,\ T_{0} =293, & K,\alpha _{T} =7.4033 \times 10^{-7} & K^{-1},\ t=0.3s,\ \sigma _{0} =200.0 , \\ K_{11}=113 \times 10^{-4}~\mbox{N}/\mbox{m}^{2} , & K_{22}=117 \times 10^{-4}~\mbox{N}/\mbox{m}^{2} , & C_{E} =1.4\times 10^{3}~\mbox{J}/(\mbox{kgk}), \\ \gamma =210\times 10^{4} ,\ \Omega =0.5,& k=348,\ \Omega =0.5, & E_{T}=0.0016,\ \omega =2.0 \end{array} $$

9 Geometrical representation and analysis

The expressions for displacements, stress, and temperature are very complex, and we prefer to develop an efficient computer program for numerical computations. We now depict some graphs to illustrate the problem.

10 Concluding remarks

Figure 2, 3 and 4 depict the characteristic behavior of the different stress components $\tau _{xx}$, $\tau _{xy}$, and $\tau _{yy}$, respectively, along the $x$-axis with respect to the space variable ($x$) in different times (t=0.1, t=0.4, t=0.7). Also, Fig. 5, 6 and 7 represent the space variation of non-dimensional displacement components (u and v) and temperature ($T$) along the x-direction for different times mentioned in the legend.

Fig. 2

Distribution of $\tau _{xx}$ vs. x for different t at y =0.7

Fig. 3

Distribution of $\tau _{xy}$ vs. x for different t at y =0.7

Fig. 4

Distribution of $\tau _{yy}$ vs. x for different t at y =0.7

Fig. 5

Distribution of temperature (T) vs. x for different t at y =0.7

Fig. 6

Distribution of displacement component (u) vs. x for different t at y =0.7

Fig. 7

Distribution of displacement component (v) vs. x for different t at y =0.7

Figure 8, 9, 10 and 11 are pointing out the three-dimensional variations of different stress components $\tau _{xx}$, $\tau _{xy}$, $\tau _{yy}$ and temperature ($T$), respectively, with respect to the space variable($x$ and $y$) in a particular time span (t=0.3).

Fig. 8

Normal stress component, $\tau _{xx}$ as a function of x and y at time t=0.3

Fig. 9

Shearing tress, $\tau _{xy}$ as a function of x and y at time t=0.3

Fig. 10

Normal stress component, $\tau _{yy}$ as a function of x and y at time t=0.3

Fig. 11

Representation of temperature ( $T$ ) as a function of x and y at time t=0.3

Also, Fig. 12, 13 are about the three-dimensional depiction of the two elementary displacement components ($u$ and $v$) w.r.t $x$ and $y$ for the fixed time (t=0.3).

Fig. 12

Displacement field (u) as a function of x and y at time t=0.3

Fig. 13

Displacement field (v) as a function of x and y at time t=0.3

11 Significance and applications

The Dual Phase Lag (DPL) model by Tzou, Chandrasekhariah and Three Phase Lag (TPL) by Roy Choudhury have been extended here using the refined technics known as the multi-phase lag model. In our work, the multi-phase lag concept is studied and verified successfully using the prominent mechanical and thermal boundary conditions associated with governing equations. The two- and three-dimensional variations of the different stress components, strain components and temperature curves have been represented graphically.

The tabular data in Fig. 14 represents the compact variations of the numerical value of different stress components, temperature and displacement components in the context of different thermoelastic models compared to the multi-phase lag model. From the data table, it is possible to differentiate the effect of different phase lag models and multi-phase lags on different physical variables.

Fig. 14

Data table

Appendix 1

$$\begin{aligned} M_{11}=&aC_{12}+\omega ^{2}-\Omega ^{2},\quad M_{12}=M_{13}=M_{14}=0,\quad M_{15}=-iaC_{11},\quad M_{16}=1, \\ M_{21}=& M_{25}=M_{26}=0,\quad M_{22}= \frac{a^{2}+\omega ^{2}+\Omega ^{2}}{C_{21}},\quad M_{23}=- \frac{ia}{C_{21}},\quad M_{24}=-\frac{iaC_{22}}{C_{21}}, \\ M_{31}=&M_{35}=M_{36}=0,\quad M_{32}=ia \frac{\gamma ^{2}T_{0}}{\rho ^{2}C_{1}^{2}C_{E}}, \\ M_{33}=&a^{2}\frac{K_{22}}{K_{11}}+ \frac{\omega ^{2}\Bigg(\overline{R}+\tau _{0}\omega +\sum _{n=1}^{N}\frac{\tau _{q}^{n+1}}{(n+1)!}\omega ^{n+1}\Bigg)}{\frac{K_{11}}{\rho C_{E}C_{1}^{2}}\Bigg(1+\sum _{n=1}^{N}\frac{\tau _{\theta}^{n}}{n!}\omega ^{n}\Bigg)}, \, \\ M_{34}=& \frac{\gamma ^{2}T_{0}}{\rho ^{2}C_{1}^{2}C_{E}} \frac{\omega ^{2}\Bigg(\overline{R}+\tau _{0}\omega +\sum _{n=1}^{N}\frac{\tau _{q}^{n+1}}{(n+1)!}\omega ^{n+1}\Bigg)}{\frac{K_{11}}{\rho C_{E}C_{1}^{2}}\Bigg(1+\sum _{n=1}^{N}\frac{\tau _{\theta}^{n}}{n!}\omega ^{n}\Bigg)}\\ C_{11}=&C_{22}=\frac{\lambda +\mu +\frac{P}{2}}{\lambda +2\mu},\quad C_{12}=C_{21}= \frac{\mu -\frac{P}{2}}{\lambda +2\mu}\\ C_{41}=&\frac{\lambda +2\mu +\rho}{\rho c_{1}^{2}},\quad C_{42}= \frac{\lambda +P}{\rho c_{1}^{2}},\quad C_{51}= \frac{\mu -\frac{P}{2}}{\rho c_{1}^{2}},\quad c_{52}= \frac{\mu +\frac{P}{2}}{\rho c_{1}^{2}}\\ A=&\left ( \textstyle\begin{array}{c@{\quad}c} L_{11} & L_{12} \\ L_{21} & L_{22} \end{array}\displaystyle \right ) \qquad L_{11}=\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\displaystyle \right ) \qquad L_{12}=\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\displaystyle \right ) \\ L_{21}=&\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c} M_{11} & M_{12} & M_{13} \\ M_{21} & M_{22} & M_{23} \\ M_{31} & M_{32} & M_{33} \end{array}\displaystyle \right ) \qquad L_{22}=\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c} M_{14} & M_{15} & M_{16} \\ M_{24} & M_{25} & M_{26} \\ M_{34} & M_{35} & M_{36} \end{array}\displaystyle \right ) \end{aligned}$$

$$\begin{aligned} \textstyle\begin{array}{c@{\quad}c@{\quad}c} f_{11}=M_{11}+\lambda M_{14}-\lambda ^{2} & f_{21}=M_{21}+\lambda M_{24} & f_{31}=M_{31}+\lambda M_{34} \\ f_{12}=M_{12}+\lambda M_{15} & f_{22}=M_{22}+\lambda M_{25}-\lambda ^{2} & f_{32}=M_{32}+\lambda M_{35} \\ f_{13}=M_{13}+\lambda M_{16} & f_{23}=M_{23}+\lambda M_{26} & f_{33}=M_{33}+ \lambda M_{36}-\lambda ^{2} \end{array}\displaystyle \end{aligned}$$

$$\begin{aligned} R_{1i}(x) =& [-C_{41}\lambda _{i}(delta_{1})_{\lambda =\lambda _{i}}+iaC_{42}( \delta _{2})_{\lambda =-\lambda _{i}}-(\delta _{3})_{\lambda = \lambda _{i}}]e^{-\lambda _{i}x},\ i=1,2,3 \\ R_{2i}(x) = &[iaC_{41}(\delta _{2})_{\lambda =-\lambda _{i}}-C_{42} \lambda _{1}(\delta _{1})_{\lambda =-\lambda _{i}}-(\delta _{3})_{ \lambda =-\lambda _{i}}]e^{-\lambda _{i}x},\ i=1,2,3 \\ R_{3i}(x) = &[-C_{51}\lambda _{i}(\delta _{2})_{\lambda =-\lambda _{i}}+iaC_{52}( \delta _{1})_{\lambda =-\lambda _{i}}]e^{-\lambda _{i}x},\ i=1,2,3 \end{aligned}$$

$$\begin{aligned} z_{1} &= \sigma _{0}e^{i\omega t} \\ z_{2}& = T_{0}e^{i\omega t} \end{aligned}$$

$$\begin{aligned} S_{ij} =& R_{ij}(0),\quad i=1,4,\quad j=1,2,3 \\ S_{5k} =& R_{5k}(x),\quad k=1,2,3 \end{aligned}$$

$$D_{1}= \begin{vmatrix} z_{1} & S_{12} & S_{13} \\ z_{2} & S_{42} & S_{43} \\ 0 & S_{52} & S_{53} \end{vmatrix} \quad D_{2}= \begin{vmatrix} S_{11} & z_{1} & S_{13} \\ S_{41} & z_{2} & S_{43} \\ S_{51} & 0 & S_{53} \end{vmatrix} $$

$$D_{3}= \begin{vmatrix} S_{11} & S_{12} & z_{1} \\ S_{41} & S_{42} & z_{2} \\ S_{51} & S_{52} & 0 \end{vmatrix} \quad D= \begin{vmatrix} S_{11} & S_{12} & S_{13} \\ S_{41} & S_{42} & S_{43} \\ S_{51} & S_{52} & S_{53} \end{vmatrix} $$