Steady Viscous Flow Around a Permeable Spheroidal Particle

Abstract

Stokes incompressible viscous fluid flow through a permeable spheroidal particle which is a bit deformed from the shape of a sphere is studied and solved analytically. It consists of two regions, porous region which obeys Darcy’s law and liquid region in which Stokes approximation is used. Boundary conditions used at the interface are mass conservation, balance of normal stress, and Beavers–Joseph–Saffman–Jones condition. Expression for drag which acts on the spheroid is obtained and well known results are deduced in the limiting cases. Variation of drag coefficient with various parameters like deformation, slip, permeability, no slip are shown by graphs.

Introduction

Fluid flow past a permeable particle of varying shapes like sphere, cylinder, spheroid or disordered geometry has always been a topic of interest because of its application in the field of sciences. Permeable membrane is a biological or synthetic material containing tiny pores that allows only small particles like water molecules and ions to pass through it. Movement of particle under semipermeable membrane generally occurs from areas having high concentration to the areas having low concentration which is basically known as diffusion. Plants and animals are mainly composed up of cells. Common example of semipermeable membrane can be seen in plants and animals through a process known as osmosis. Some examples of flow past permeable particle includes flow through porous fluidized beds or dense layer of permeable particle in catalyst reactors, fall of snowflakes, flow of a liquid or gaseous mixture whose composition is analysed in the chromatography column, sedimentation of flakes during coagulation treatment of water, deposition of blood clots in medical tests etc. In the case of capillary-porous particle structure, the kinematics of mass transfer processes occurring in fluid-solid dispersed systems depends greatly on the convective fluid transport in the porous due to the macroscopic motion of the continuous medium.

Problem considering the flow through porous particle have been generally modelled using Stokes version of Navier–Stokes equation for the flow in the outer region and Darcy’s law [1] or Brinkman [2] for flow in the porous region. A number of articles related to the flow past porous bodies of various shape like sphere, cylinder, spheroid, approximate sphere have been published. A few of them are pointed out here related to the present topic. Long back in 1962, Leonov [3] investigated the slow stationary axisymmetric stream of an incompressible fluid about a porous sphere presenting the typical form of the streamline pattern. Later, Joseph and Tao [4] discussed the stationary porous sphere immersed in a uniform streaming viscous fluid. They concluded that drag acting on a permeable sphere is similar to the drag force on an impermeable sphere with reduced radius. They used the continuity of normal component of velocity, pressure and no tangential velocity at the interface of the porous-fluid medium. Sutherland and Tan [5] worked on finding the sedimentation of a porous sphere by using Darcy’s law for flow in porous region. Review article of Neale and Epstein [6] shows the summary of low Reynolds number flow relative to permeable spheres. In their work they have compared results of several authors. Jones [7] considered low Reynolds number flow past a spherical shell by using modified Beaver–Joseph slip condition. With the aim of studying flow with finite but low Reynolds number, Feng and Michaelides [8] considered the motion of a permeable sphere. Jager and Mikelic [9] on their work discussed about the interface boundary condition of Beavers, Joseph, and Saffman. Creeping flow past and within a permeable spheroid was considered by Vainshtein et al. [10]. Creeping viscous fluid flow past a porous approximate spherical shell was handled by Srinivasacharya [11] by using Darcy law for flow in porous media. They considered continuity of normal velocity, continuity of pressure along with Beavers–Joseph [12] slip condition. Coupling of Stokes–Darcy equation for the flow through porous media, where Beaver-Joseph-Saffman boundary conditions are used as the interface condition was reported by Urquiza et al. [13]. Shapovalov [14] investigated the flow of a viscous fluid through a partially permeable spherical particle. He used the same boundary conditions as in [4] and derived the similar expressions for the flow parameters and the drag coefficient. Cao et al. [15] investigated the coupled Stokes–Darcy model by using Beavers–Joseph slip boundary condition at the interface. Vereshchagin and Dolgushev [16] analysed the viscous incompressible low velocity flow past a hollow porous sphere by using both slip (Beavers–Joseph) and no slip boundary conditions separately.

Recently, Prakash et al. [17] examined the flow past an assemblage of porous particles. Prakash and Raja Shekhar [18] investigated the dynamic permeability of an assembly of permeable porous particles by using Saffman boundary condition [19]. Saad [20] investigated the problem of Stokes flow past an assemblage of axisymmetric porous spheroidal particle by using cell models. Chen [21] focused on extracting fluid from a porous media governed by Darcy law through a slender permeable prolate-spheroid. The effective permeability of a porous medium for spherical and spheroidal vug with fracture inclusion was discussed by Rasoulzadeh and Kuchuk [22] by using the Beaver-Joseph-Saffman boundary condition proposed by Jones. Recently, Tiwari et al. [23] worked on the flow problem considering non-homogeneous porous cylindrical particle modelled using Beaver-Joseph slip boundary condition. By considering Saffman’s boundary condition, Khabthani et al. [24] analysed lubricating motion of a sphere towards a thin porous slab. Lai et al. [25] studied simple projection technique for the coupled Navier–Stokes and Darcy flows by using Beaver–Joseph–Saffman condition.

In present paper, we have concentrated on viscous flow past a permeable spheroid, which is a slightly deformed sphere and have calculated the hydrodynamic drag force acting on the permeable spheroidal particle. The flow considered here is axially symmetric in nature. Stream function and the component of pressure for the regions outside and inside the permeable spheroidal particle are obtained. Variation of drag experienced by the particle versus permeability parameter, slip coefficient and deformation parameter are shown graphically. Deduction cases leads to some well known previous results.

Problem Formulation

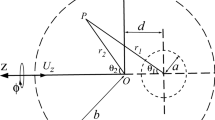
Consider the steady viscous fluid flow through a permeable spheroid which is kept fixed in a uniform stream having velocity U ( See Fig. 1). Outside region I and inner porous region II are represented here by i,where $i=1,2$.

Fig. 1

: Geometry of fluid flow through permeable spheroid

Flow equation for region I which obeys Stokes equation are

$$\begin{aligned} {\nabla }\cdot {\mathbf {q}^{(1)}}= & {} 0 \end{aligned}$$

(1)

$$\begin{aligned} {\nabla }p^{(1)}+\mu \nabla \times \nabla \times \mathbf {q}^{(1)}= & {} 0 \end{aligned}$$

(2)

where $\mathbf {q}^{(1)}$ and $p^{(1)}$ are velocity and pressure in the liquid region, and $\mu$ the coefficient of viscosity of the fluid.

Flow equation for region II that obeys Darcy’s law are

$$\begin{aligned} {\nabla }\cdot {\mathbf {q}^{(2)}}= & {} 0 \end{aligned}$$

(3)

$$\begin{aligned} {\nabla }p^{(2)}+\frac{\mu }{k} \mathbf {q}^{(2)}= & {} 0 \end{aligned}$$

(4)

where $\mathbf {q}^{(2)}$ and $p^{(2)}$ are velocity and pressure in porous region, k the permeability of porous medium.

We introduce the non-dimensional variables for converting the flow governing equations to dimensionless form as,

$$\begin{aligned} {r}=a{\tilde{r}}, \mathbf {q}^{(i)}=U\tilde{\mathbf {q}}^{(i)},{\nabla }=\frac{\tilde{{\nabla }}}{a},p^{(i)}=\frac{\mu U}{a}{\tilde{p}}^{(i)} \end{aligned}$$

(5)

Substituting them in Eqs. (1) to (2) and then dropping the tildes, we get

$$\begin{aligned} {\nabla }\cdot {\mathbf {q}^{(1)}}= & {} 0 \end{aligned}$$

(6)

$$\begin{aligned} {\nabla }p^{(1)}+\nabla \times \nabla \times \mathbf {q}^{(1)}= & {} 0 \end{aligned}$$

(7)

$$\begin{aligned} {\nabla }\cdot \mathbf {q}^{(2)}= & {} 0 \end{aligned}$$

(8)

$$\begin{aligned} {\nabla }p^{(2)}+\alpha ^{2} \mathbf {q}^{(2)}= & {} 0 \end{aligned}$$

(9)

where $\displaystyle {\alpha ^2=\frac{a^2}{k}}$.

Let $(r,\theta ,\phi )$ be the spherical polar co-ordinate system. Consider fluid flow is axially symmetric in nature, thus all the quantities considered for the flow doesn’t depends on $\phi$. Here, velocity vectors are denoted by

$$\begin{aligned} \mathbf {q}^{(i)}=q_{r}^{(i)}(r,\theta )\mathbf {e}_{r}+q_{\theta }^{(i)}(r,\theta )\mathbf {e}_{\theta },\,\,i=1,2 \end{aligned}$$

(10)

Consider $r=a\left[ 1+f(\theta )\right]$ as the surface of the spheroid [26]. Orthogonality relations of Gegenbauer functions $\vartheta _{m}(\zeta )$, $\zeta =\cos \theta$ allow us, under general circumstances, to assume the expansion $f{(\theta )} =\sum _{m=2}^{\infty }\alpha _{m}\vartheta _m{(\zeta )}$ where the Gegenbauer function is related to the Legendre function $P_{n}{(\zeta )}$ by the relation

$$\begin{aligned} \vartheta _{n}{(\zeta )} = \frac{P_{n-2}{(\zeta )}-P_{n}{(\zeta )}}{2n-1},\quad n\ge {2} \end{aligned}$$

(11)

So, the spheroidal surface will be $r= a[1+\alpha _{m}\vartheta _m{(\zeta )}]$. Coefficients $\alpha _{m}$ are assumed to be sufficiently small so that we can neglect their squares and higher powers [26]. Subsequently, we have $(r/a)^y\approx {1+y\alpha _{m}\vartheta _{m}{(\zeta )}}$ where y is positive or negative.

Consider $\psi ^{(i)}$; $i=1,2$ to be Stokes stream functions for inner and outer spheroidal region, respectively.

Components of velocity in relation to stream function are

$$\begin{aligned} q_{r}^{(i)}=\frac{1}{r^2}\frac{\partial {\psi ^{(i)}}}{\partial \zeta },q_{\theta }^{(i)}=\frac{1}{r\sqrt{1-\zeta ^{2}}}\frac{\partial \psi ^{(i)}}{\partial {r}};\,\,i=1,2 \end{aligned}$$

(12)

Elimination of terms containing pressure $p^{(1)}$ and $p^{(2)}$ from Eqs. (7) and (9), we get the equation below for the stream function

$$\begin{aligned} E^4\psi ^{(1)}= & {} 0, \end{aligned}$$

(13)

$$\begin{aligned} E^2\psi ^{(2)}= & {} 0. \end{aligned}$$

(14)

where $\displaystyle {E^{2}=\frac{\partial ^{2}}{\partial {r^{2}}}+\frac{1-\zeta ^{2}}{r^{2}}\frac{\partial ^{2}}{\partial {\zeta ^{2}}}}$

Boundary Condition

In order to find the flow velocity components inside and outside the permeable spheroid, appropriate boundary conditions are required to be chosen. At the clear fluid-permeable interface, we consider continuity of normal components of velocity, Shear force is proportional to the tangential component of the fluid velocity, which is called the Beavers–Joseph–Saffman–Jones condition [7, 12, 19, 22] and a jump condition for pressures i.e., normal stress in the clear fluid is equal to pressure in the permeable region [22, 23].

Boundary conditions at spheroidal surface are

$$\begin{aligned} (\mathbf {q}^{(1)}-\mathbf {q}^{(2)})\cdot \mathbf {n}= & {} 0 , \end{aligned}$$

(15)

$$\begin{aligned} \mathbf {n}\cdot \tau ^{\,(1)}\cdot \mathbf {s}= & {} \frac{\mu }{\lambda \sqrt{k}}\mathbf {q}^{(1)}\cdot \mathbf {s} , \end{aligned}$$

(16)

$$\begin{aligned} \mathbf {n}\cdot \tau ^{\,(1)}\cdot \mathbf {n}= & {} -\mathbf {p}^{\,(2)}. \end{aligned}$$

(17)

where $\lambda$ is the non-dimensional BJS slip coefficient and it depends on the characteristics of the porous medium. The range of $\lambda$ is between 0.25 and 10 [19, 23, 27]. $\tau ^{\,(1)}$ is the stress tensor for viscous fluid. If $\lambda =0$, and the permeability is very low then the problem reduces to the flow past a semipermeable particle.

Also, $\mathbf {n}=\mathbf {e}_r-\alpha _{m}\sqrt{1-\zeta ^{2}}P_{m-1}{(\zeta )}\mathbf {e}_\theta ,$ and $\mathbf {s}$ are a unit normal vector and an arbitrary tangential vector at the spheroidal surface $r=a[1+\alpha _{m}\vartheta _m{(\zeta )}]$.

Boundary conditions at infinity ($r\rightarrow \infty$) for the external flow are written as $q_{r}^{(1)}=-U\cos \theta$ and $q_{\theta }^{(1)}=U\sin \theta$.

Substituting the above values of $\mathbf {n}$ and $\mathbf {s}$ in Eqs. (15) to (17), we get the boundary conditions in non-dimensional form as

$$\begin{aligned} {q}_r^{(1)}-{q}_r^{(2)}= & {} ({q}_\theta ^{(1)}-{q}_\theta ^{(2)})\alpha _{m}\sqrt{1-\zeta ^{2}}P_{m-1}{(\zeta )}, \end{aligned}$$

(18)

$$\begin{aligned} \tau _{r\theta }^{\,(1)}+\alpha _{m}\sqrt{1-\zeta ^{2}} P_{m-1}{(\zeta )}\left( \tau _{rr}^{\,(1)}-\tau _{\theta \theta }^{\,(1)}\right)= & {} \frac{\alpha }{\lambda }\left( {q}_\theta ^{(1)}+{q}_r^{(1)}\alpha _{m}\sqrt{1-\zeta ^{2}}P_{m-1}{(\zeta )}\right) ,\qquad \quad \end{aligned}$$

(19)

$$\begin{aligned} \tau _{rr}^{\,(1)}-2\alpha _{m}\tau _{r\theta }^{\,(1)}\sqrt{1-\zeta ^{2}} P_{m-1}{(\zeta )}= & {} -{p}^{(2)}. \end{aligned}$$

(20)

The boundary conditions in relation to stream function $\psi ^{(i)}$;  $i=1,2$ at the spheroidal surface are

$$\begin{aligned}&\left( \frac{\partial \psi ^{(1)}}{\partial \zeta }-\frac{\partial \psi ^{(2)}}{\partial \zeta }\right) =r\alpha _{m}P_{m-1}{(\zeta )}\left( \frac{\partial \psi ^{(1)}}{\partial {r}}-\frac{\partial \psi ^{(2)}}{\partial {r}}\right) , \end{aligned}$$

(21)

$$\begin{aligned}&\left[ 2r\frac{\partial }{\partial {r}}\left( \frac{1}{r}\frac{\partial \psi ^{(1)}}{\partial {r}}\right) -E^2\psi ^{\,(1)}\right. \nonumber \\&\qquad +\left. 2\alpha _{m}\vartheta _2{(\zeta )}P_{m-1}{(\zeta )}\left( 4\frac{\partial ^2\psi ^{(1)}}{\partial r\partial \zeta }-\frac{6}{r^2}\frac{\partial \psi ^{(1)}}{\partial \zeta }+\frac{P_{1}{(\zeta )}}{r\vartheta _2{(\zeta )} }\frac{\partial \psi ^{(1)}}{\partial {r}}\right) \right] \nonumber \\&\quad =\frac{\alpha }{\lambda }\left( \frac{\partial \psi ^{(1)}}{\partial {r}}+\frac{1}{r}(1-\zeta ^{2})\alpha _{m}P_{m-1}{(\zeta )}\frac{\partial \psi ^{(1)}}{\partial \zeta }\right) , \end{aligned}$$

(22)

$$\begin{aligned}&-{p}^{(1)}-\frac{2}{r^2}\left[ \frac{2}{r}\frac{\partial \psi ^{(1)}}{\partial \zeta }-\frac{\partial ^2\psi ^{(1)}}{\partial r\partial \zeta }\right] -\frac{2\alpha _{m}P_{m-1}{(\zeta )}}{r}\left[ 2r\frac{\partial }{\partial {r}}\left( \frac{1}{r}\frac{\partial \psi ^{(1)}}{\partial r}\right) -E^2\psi ^{\,(1)}\right] =-{p}^{(2)}.\nonumber \\ \end{aligned}$$

(23)

Solution of the Problem

Solution for region I and region II obtained by solving Eqs. (13) and (14) are given as

$$\begin{aligned} \psi ^{(1)}= & {} \left[ r^2+\frac{a_2}{r}+b_2 r\right] \vartheta _2{(\zeta )}+\sum _{n=3}^\infty \left[ A_nr^{-n+1}+B_nr^{-n+3}\right] \vartheta _n{(\zeta )} \end{aligned}$$

(24)

$$\begin{aligned} \psi ^{(2)}= & {} \left[ c_2r^2+\frac{d_2}{r}\right] \vartheta _2{(\zeta )}+\sum _{n=3}^\infty [C_nr^{n}+D_nr^{-n+1}]\vartheta _n{(\zeta )} \end{aligned}$$

(25)

Expression of pressure in region I and II are given below

$$\begin{aligned} p^{(1)}= & {} -\frac{b_2}{r^2}P_1{(\zeta )} +\sum _{n=3}^\infty \left[ \left( \frac{6-4n}{n}\right) B_nr^{-n}\right] P_{n-1}{(\zeta )} \end{aligned}$$

(26)

$$\begin{aligned} p^{(2)}= & {} \alpha ^2\left[ \left( c_2r-\frac{d_2}{2r^2}\right) P_1{(\zeta )} +\sum _{n=3}^\infty \left[ C_n\frac{r^{n-1}}{n-1}-\frac{D_nr^{-n}}{n}\right] P_{n-1}{(\zeta )}\right] \end{aligned}$$

(27)

Since at the center of the permeable spheroid the pressure is limited, so ($p^{(2)}< \infty$ at $r=0$); thus the value of $d_{2}=0$.

The Eqs .(25) and (27) reduces to

$$\begin{aligned} \psi ^{(2)}= & {} c_2r^2\vartheta _2{(\zeta )}+\sum _{n=3}^\infty C_nr^{n}\vartheta _n{(\zeta )} \end{aligned}$$

(28)

$$\begin{aligned} p^{(2)}= & {} \alpha ^2\left[ c_2 rP_1{(\zeta )} +\sum _{n=3}^\infty C_n\frac{r^{n-1}}{n-1}P_{n-1}{(\zeta )}\right] \end{aligned}$$

(29)

Now, the solution which corresponds to the boundary $r=1+\alpha _{m}\vartheta _{m}{(\zeta )}$ are first identified. By comparing the Eqs . (24) and (28) with that obtained in the problem of flow of viscous incompressible fluid through a permeable sphere, we see that the terms involving $A_n$, $B_n$ and $C_n$ for the value of $n>2$ are extra and they doesn’t exist for the case of a permeable sphere. Here, we have considered the case of a spheroid which is a slightly deformed sphere. Thus, the flow through this geometry is not expected to be much different from that of a flow through a permeable sphere [14]. For the solution of the case

$$\begin{aligned} r=1+\sum _{m=2}^{\infty }\alpha _{m}\vartheta _{m}{(\zeta )}, \end{aligned}$$

(30)

We adopt the same idea for every m and evaluate the stream functions in both the regions.

Application to a Permeable Spheroid

As an application of the above analysis, we consider the case of flow past a permeable prolate and oblate spheroid. In Cartesian coordinate system, spheroidal surface is represented as

$$\begin{aligned} \frac{x^2+y^2}{c^2}+\frac{z^2}{c^2{(1-\varepsilon )^2}}=1 \end{aligned}$$

(31)

where the radius of the equator is c and $\varepsilon$ is very small so that we can neglect its squares and higher powers. Equation of the spheroidal surface (31) in polar form is $r=a[1+2\varepsilon \vartheta _{2}{(\zeta )}]$ with $a=c(1-\varepsilon )$. When $0<\varepsilon \le 1$, the considered spheroid is oblate, and for $\varepsilon <0$, it is a prolate spheroid. In case with $\varepsilon =0$, it resembles with the equation of the sphere with radius c. Above results are applicable for the case, when $m=2$; $\alpha _{m}=2\varepsilon$. Therefore, the equation for the stream functions are

$$\begin{aligned} \psi ^{(1)}= & {} \left[ r^2+\frac{a_2+A_2}{r}+(b_2+B_2) r\right] \vartheta _2{(\zeta )}+\left[ \frac{A_4}{r^{3}}+\frac{B_4}{r}\right] \vartheta _4{(\zeta )}, \end{aligned}$$

(32)

$$\begin{aligned} \psi ^{(2)}= & {} (c_2+C_2)r^2\vartheta _2{(\zeta )}+C_4r^{4}\vartheta _4{(\zeta )}. \end{aligned}$$

(33)

Drag Force Acting on the Body

Drag force which acts on spheroidal particle due to the flow of viscous fluid in outer region can be evaluated by taking use of the formula

$$\begin{aligned} F_D=\int _{S}{(\mathbf {n}\cdot \tau ^{(1)})\cdot \mathbf {k}}dS \end{aligned}$$

(34)

where $\mathbf {n}=\mathbf {e}_r-\varepsilon \sin {2\theta } \mathbf {e}_{\theta }$; $dS=2\pi a^2(1+2\varepsilon \sin ^{2}\theta )\sin \theta d\theta$; $\mathbf {k}$ is the unit vector acting in the z direction and integrating over the surface of the body $r=1+\varepsilon \sin ^{2}\theta$.

$$\begin{aligned} F_D=4\pi \mu Ua(b_2+B_2) \end{aligned}$$

(35)

Substituting the values of $b_2$ and $B_2$ along with $a=c(1-\varepsilon )$ and $\alpha =\beta (1-\varepsilon )$ [20], we obtain

$$\begin{aligned} F_D=-4\pi \mu U c\left[ \frac{6 {{\beta }^{2}} \lambda +3 {{\beta }^{3}}+12 \beta }{\left( 6 {{\beta }^{2}}+18\right) \lambda +2 {{\beta }^{3}}+9 \beta }+\varepsilon \varDelta \right] \end{aligned}$$

(36)

where

$$\begin{aligned} \varDelta= & {} \left[ \frac{3 \beta \, \left( 12 \beta \, \left( {{\beta }^{2}}-15\right) \, {{\lambda }^{2}}-12 \left( {{\beta }^{4}}+19 {{\beta }^{2}}+36\right) \lambda -\beta \, \left( {{\beta }^{2}}+12\right) \, \left( 2 {{\beta }^{2}}+5\right) \right) }{5{\left( 6 {{\beta }^{2}} \lambda +18 \lambda +2 {{\beta }^{3}}+9 \beta \right) ^{2}}}\right] \nonumber \\ \end{aligned}$$

(37)

$\displaystyle {\beta =\frac{c}{\sqrt{k}}}$.

Some Special Results

First case If $\lambda =0$, it reduces to the semipermeable spheroid and the drag is

$$\begin{aligned} F_D=6\pi \mu U c\left[ \frac{2\left( \left( {{\beta }^{2}}+12\right) \, \left( 2 {{\beta }^{2}}+5\right) \varepsilon -5 \left( {{\beta }^{2}}+4\right) \, \left( 2 {{\beta }^{2}}+9\right) \right) }{5{{\left( 2 {{\beta }^{2}}+9\right) }^{2}}}\right] \end{aligned}$$

(38)

Second case If the deformation parameter $\varepsilon =0$, it reduces to permeable sphere and the drag is

$$\begin{aligned} F_D=-6\pi \mu U c\left[ \frac{2\beta (2 {{\beta }} \lambda + {{\beta }^{2}}+4) }{\left( 6 {{\beta }^{2}}+18\right) \lambda +\beta (2 {{\beta }^{2}}+9)}\right] \end{aligned}$$

(39)

Third case If the deformation parameter $\varepsilon =0$ and $\lambda =0$, it reduces to semipermeable sphere and the drag is

$$\begin{aligned} F_D=-6\pi \mu U c\left[ \frac{2 {{\beta }^{2}}+8}{2 {{\beta }^{2}}+9}\right] \end{aligned}$$

(40)

Fourth case If $\beta \rightarrow \infty$ ( permeability $k=0$), it behaves as a solid spheroid and the drag is

$$\begin{aligned} F_D=-6\pi \mu U c\left[ 1-\frac{\varepsilon }{5}\right] \end{aligned}$$

(41)

which is same as the classical stokes drag past a solid spheroid [26]

Fifth case If both $\varepsilon =0$ and $\beta \rightarrow \infty$ i.e., permeability $k=0$, it behaves as solid sphere and the drag is

$$\begin{aligned} F_D=-6\pi \mu Uc \end{aligned}$$

(42)

which is the renowned classical expression for Stokes drag past a solid sphere [26].

Fourth case For the case with $\beta \rightarrow 0$ ( infinite permeability $k\rightarrow \infty$), we have

$$\begin{aligned} F_D=0 \end{aligned}$$

(43)

which indicates the absence of drag.

Sedimentation Velocity

We can calculate the sedimentation or terminal velocity $U_\infty$ by using the formula for drag given by Eq. (36). The drag force is equated to the excess of the gravity acting on the spheroid above its buoyancy given as

$$\begin{aligned} \frac{4}{3}\pi c^3g(1-\varepsilon )(\rho _m-\rho )=-4\pi \mu U c\left[ \frac{6 {{\beta }^{2}} \lambda +3 {{\beta }^{3}}+12 \beta }{\left( 6 {{\beta }^{2}}+18\right) \lambda +2 {{\beta }^{3}}+9 \beta }+\varepsilon \varDelta \right] \end{aligned}$$

(44)

where spheroidal mean density is denoted as $\rho _m$.

Thus we have terminal velocity as

$$\begin{aligned} U_\infty =-\frac{c^2g(\rho _m-\rho )}{3\mu }\left[ \frac{\left( {\left( 6 {{\beta }^{2}}+18\right) \lambda +2 {{\beta }^{3}}+9 \beta }\right) (1-\varepsilon )}{6 {{\beta }^{2}} \lambda +3 {{\beta }^{3}}+12 \beta +\varepsilon \varDelta \left( \left( 6 {{\beta }^{2}}+18\right) \lambda +2 {{\beta }^{3}}+9 \beta \right) }\right] \end{aligned}$$

(45)

In case of sphere ($\varepsilon =0$), we get the terminal velocity as

$$\begin{aligned} U_\infty =-\frac{c^2g(\rho _m-\rho )}{9\mu }\left[ \frac{\left( 6 {{\beta }^{2}}+18\right) \lambda +2 {{\beta }^{3}}+9 \beta }{2 {{\beta }^{2}} \lambda + {{\beta }^{3}}+4 \beta }\right] \end{aligned}$$

(46)

and if $\lambda =0$ in Eq. (46), we have the terminal velocity for semipermeable sphere as

$$\begin{aligned} U_\infty =-\frac{2c^2g(\rho _m-\rho )}{9\mu }\left[ \frac{2 {{\beta }^{2}}+9 }{ {2{\beta }^{2}}+8}\right] \end{aligned}$$

(47)

Graphical Representation

Variation of drag coefficient $\displaystyle {D_N=\frac{F_D}{-6\pi \mu U c}}$ with permeability parameter $\left( \displaystyle {k_{1}=\frac{1}{\beta ^2}}\right)$ for varying deformation parameter $\varepsilon$, slip coefficient $\lambda$ are shown in Figs. 2 to 4. Figure 2 and 3 illustrates the variation of drag with changing permeability and deformation. It is observed that the drag coefficient decreases monotonically with the increasing permeability. As the deformation parameter increases, there is a decrease in drag coefficient. We observed that the drag on permeable sphere ($\varepsilon =0$) is lower than that of the drag on permeable prolate spheroid ($\varepsilon =-0.1,-0.3$) and greater than that of the drag on permeable oblate spheroid ($\varepsilon =0.1,0.3$). In case of permeable particle, we observed the same. From Figure 4, the variation of drag coefficient with slip parameter $\lambda$ for varying deformation $\varepsilon$ is recognised. It is well noticed that drag coefficient decreases monotonically with increasing slip. However, $D_N$ is relatively higher for prolate spheroid.

Fig. 2

Representation of drag coefficient versus permeability for varying deformation parameter $\varepsilon$ with fixed slip coefficient $\lambda =3$

Fig. 3

Representation of drag coefficient versus permeability for varying deformation parameter $\varepsilon$ with fixed slip $\lambda =0$ (Semipermeable case)

Fig. 4

Representation of drag coefficient versus slip coefficient for varying deformation parameter $\varepsilon$ with permeability $k_1=0.05$

Conclusions

The steady creeping flow of viscous fluid with incompressible nature past a permeable spheroidal particle governed by Darcy law has been investigated using BJSJ condition. An analytical solution of the problem with the governing equations for the flow inside and outside the particle has been obtained. An explicit expression for drag force acting on the spheroidal particle is presented and well known results are deduced in reduction case. The effect of permeability, deformation and slip parameter on the flow are discussed. Obtained results are exhibited in graphically. The drag coefficient is found to be a decreasing function of permeability, deformation and slip parameter.

Appendix

On applying the Eqs. (21) to (23) upto first order of $\alpha _{m}$, we obtain the following equations

$$\begin{aligned}&\left( 1+a_2+b_2-c_2\right) P_1{(\zeta )}+\alpha _{m}(2-a_2+b_2-2c_2)[\vartheta _{m}{(\zeta )}P_1{(\zeta )}+\vartheta _{2}{(\zeta )}P_{m-1}{(\zeta )}] \nonumber \\&\quad +\sum _{n=3}^{\infty }(A_n+B_n-C_n)P_{n-1}{(\zeta )}=0 \end{aligned}$$

(48)

$$\begin{aligned}&\left( (6\lambda +\alpha )a_2-\alpha b_2-2\alpha \right) \vartheta _{2}{(\zeta )}+\alpha _{m}\vartheta _2{(\zeta )}\left[ -((18\lambda + 2\alpha )a_2+2\alpha )\vartheta _{m}{(\zeta )}\right. \nonumber \\&\quad +\left. \left( (18\lambda +2\alpha )a_2+(6\lambda +2\alpha )2b_2+2\alpha \right) P_{1}{(\zeta )}P_{m-1}{(\zeta )}\right] \nonumber \\&\quad -\sum _{n=3}^{\infty }[\left( 2(1-n^2)\lambda +\alpha (1-n)\right) A_n+\left( 2n(2-n)\lambda +\alpha (3-n)\right) B_n]\vartheta _{n}{(\zeta )}=0\qquad \end{aligned}$$

(49)

$$\begin{aligned}&(6a_2+3b_2+\alpha ^2c_2)P_1{(\zeta )}+\alpha _{m}[-12a_2-6b_2+\alpha ^2c_2]\vartheta _{m}{(\zeta )}P_1{(\zeta )}\nonumber \\&\quad -12a_2\alpha _{m}[\vartheta _{2}{(\zeta )}P_{m-1}{(\zeta )}+\vartheta _{m}{(\zeta )}P_{1}{(\zeta )}] \nonumber \\&\quad +\sum _{n=3}^{\infty }\left[ 2(n+1)A_n+\frac{2(n^2+n-3)}{n}B_n+\frac{\alpha ^2}{n-1}C_n\right] P_{n-1}{(\zeta )}=0 \end{aligned}$$

(50)

Solving the leading terms of Eqs. (48) to (50), we get the values of $a_2$,  $b_2$, and $c_2$ as

$$\begin{aligned} a_2= & {} \frac{\alpha ({{\alpha }^{2}}+6) }{6\left( {{\alpha }^{2}}+3\right) \lambda +\alpha (2 {{\alpha }^{2}}+9) } \end{aligned}$$

(51)

$$\begin{aligned} b_2= & {} -\frac{3\alpha (2 {{\alpha }} \lambda +{{\alpha }^{2}}+4) }{6\left( {{\alpha }^{2}}+3\right) \lambda +\alpha (2 {{\alpha }^{2}}+9) } \end{aligned}$$

(52)

$$\begin{aligned} c_2= & {} \frac{3(6 \lambda +\alpha ) }{6\left( {{\alpha }^{2}}+3\right) \lambda +\alpha (2 {{\alpha }^{2}}+9) } \end{aligned}$$

(53)

In order to calculate other arbitrary constants $A_n$, $B_n$,  and $C_n$,we require the following identities

$$\begin{aligned} \vartheta _{m}{(\zeta )}\vartheta _{2}{(\zeta )}= & {} -\frac{(m-2)(m-3)}{2(2m-1)(2m-3)}\vartheta _{m-2}{(\zeta )}\nonumber \\&+\frac{m(m-1)}{(2m+1)(2m-3)}\vartheta _{m}{(\zeta )} \nonumber \\&-\frac{(m+1)(m+2)}{2(2m-1)(2m+1)}\vartheta _{m+2}{(\zeta )} \end{aligned}$$

(54)

$$\begin{aligned} \vartheta _{m}{(\zeta )}P_1{(\zeta )}+P_{m-1}{(\zeta )}\vartheta _{2}{(\zeta )}= & {} -\frac{(m-2)(m-3)}{2(2m-1)(2m-3)}P_{m-3}{(\zeta )}\nonumber \\&+\frac{m(m-1)}{(2m+1)(2m-3)}P_{m-1}{(\zeta )}\nonumber \\&-\frac{(m+1)(m+2)}{2(2m-1)(2m+1)}P_{m+1}{(\zeta )} \end{aligned}$$

(55)

$$\begin{aligned} P_{1}{(\zeta )}\vartheta _{2}{(\zeta )}P_{m-1}{(\zeta )}= & {} -\frac{(m-1)(m-2)(m-3)}{2(2m-1)(2m-3)}\vartheta _{m-2}{(\zeta )}\nonumber \\&+\frac{m(m-1)}{2(2m+1)(2m-3)}\vartheta _{m}{(\zeta )}\nonumber \\&+\frac{m(m+1)(m+2)}{2(2m-1)(2m+1)}\vartheta _{m+2}{(\zeta )} \end{aligned}$$

(56)

$$\begin{aligned} \vartheta _{m}{(\zeta )}P_1{(\zeta )}= & {} \frac{(m-2)}{(2m-1)(2m-3)}P_{m-3}{(\zeta )}\nonumber \\&+\frac{1}{(2m+1)(2m-3)}P_{m-1}{(\zeta )}\nonumber \\&-\frac{(m+1)}{(2m-1)(2m+1)}P_{m+1}{(\zeta )} \end{aligned}$$

(57)

By taking the use of these identities in Eqs (43) to (45) we see that the values of $A_n$, $B_n$ and $C_n$ $=0$ for $n\ne m-2,m,m+2$ and for $n=m-2,m,m+2$ we have the following expressions

$$\begin{aligned}&A_n+B_n-C_n+\xi _1 {{\overline{a}}}_n=0 \end{aligned}$$

(58)

$$\begin{aligned}&\left( 2(1-n^2)\lambda +\alpha (1-n)\right) A_n+\left( 2n(2-n)\lambda +\alpha (3-n)\right) B_n+\xi _2 {{\overline{a}}}_n+\xi _3 {{\overline{b}}}_n=0\qquad \end{aligned}$$

(59)

$$\begin{aligned}&2(n+1)A_n+\frac{2(n^2+n-3)}{n}B_n+\frac{\alpha ^2}{n-1}C_n+\xi _4 {{\overline{c}}}_n+\xi _5 {{\overline{a}}}_n=0 \end{aligned}$$

(60)

where

$$\begin{aligned}&\xi _1=2-a_2+b_2-2c_2 \\&\xi _2=-(18\lambda + 2\alpha )a_2-2\alpha \\&\xi _3=(18\lambda +2\alpha )a_2+(6\lambda +2\alpha )2b_2+2\alpha \\&\xi _4=-12a_2-6b_2+\alpha ^2 c_2 \\&\xi _5=-12a_2 \end{aligned}$$

and

$$\begin{aligned} {{\overline{a}}}_n= & {} \frac{n(n-1)\alpha _{n}}{(2n+1)(2n-3)} \end{aligned}$$

(61)

$$\begin{aligned} {{\overline{b}}}_n= & {} \frac{n(n-1)\alpha _{n}}{2(2n+1)(2n-3)} \end{aligned}$$

(62)

$$\begin{aligned} {{\overline{c}}}_n= & {} \frac{\alpha _{n}}{(2n+1)(2n-3)} \end{aligned}$$

(63)

The expression for $B_2$ is

$$\begin{aligned} B_2=-\frac{6\alpha \varepsilon \, \left( 36 \alpha \, \left( {{\alpha }^{2}}+5\right) \, {{\lambda }^{2}}+12 \left( 2 {{\alpha }^{4}}+13 {{\alpha }^{2}}+12\right) \lambda +\alpha \, \left( 4 {{\alpha }^{4}}+33 {{\alpha }^{2}}+60\right) \right) }{5{{\left( 6 {{\alpha }^{2}} \lambda +18 \lambda +2 {{\alpha }^{3}}+9 \alpha \right) }^{2}}} \end{aligned}$$

(64)