1 Introduction

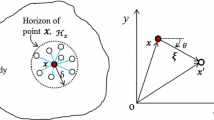
Carbonate formations, particularly naturally fractured ones, usually have connected and nonconnected fractures, matrix (host porous media of inclusions), and connected and nonconnected vugs. A vug is a cavity, inclusion, or void pore, which is larger compared with the intergranular pore size, and created by rock dissolution (diagenesis). Vugs normally have almost infinite permeability and are normally elongated in one direction in the horizontal plane. Some vugs can have irregular shapes, but can still be roughly approximated by spheroids. As shown in Fig. 1, several vugs can be connected with each other, referred to as touching vugs (Lucia 1999), and create wormholes without many branches. Fractures are mechanical breaks in rocks and create discontinuities with a displacement across surfaces or narrow zones (Committee on Fracture Characterization and Fluid Flow 1996). Unlike vugs, fractures normally have planar shapes, with much smaller apertures than their vertical height and lateral length. Connected vugs are created by further rock dissolution and fracturing and can also be enlarged by additional dissolution.

Fig. 1
figure 1

Connected and isolated vugs, and fractures

Full size image

Here, we focus on microfractures, and short (less than a few tens of meters) secondary and tertiary fractures, which are assumed to be discrete or only locally continuous and not continuous or discrete primary (major) fractures or any long fractures (more than a few tens of meters). Fractures and vugs are embedded in the matrix; thus, they contribute to the effective matrix permeability and porosity. If vugs and/or secondary and tertiary open fractures are directly connected to the major fractures, then they must be a part of the fracture system, for which Kuchuk et al. (2015) presented the modeling details of such fracture systems.

In most carbonate formations, vug sizes vary from a few \(\upmu \hbox {m}\) to thousands of \(\upmu \hbox {m}\) (Arns et al. 2005), while fracture apertures vary from 0.001 to 10 mm (Bertels et al. 2001; Detwiler et al. 2001; Keller et al. 1999). Thus, fracture-intersecting vugs do not make any observable change in the fracture conductivity, although they may enhance fracture conductivities for low-conductivity fractures. Naturally fractured formations might contain many faults and thousands of fractures with different apertures, conductivities, lengths, orientations, sizes, and spacings and may well have a power-law distribution of these properties (Aarseth et al. 1997; Belfield and Sovich 1994; Braester 2005; Nurmi et al. 1995). This condition implies that naturally fractured formations might contain hundreds or thousands of primary fractures, and possibly thousands or millions of small vertical and near-vertical fractures. Consequently, it is important to obtain the effective permeability of the matrix with thousands or millions small discrete and/or only locally continuous fractures.

In this paper, we deal with four possible vug/fracture systems: isolated vugs, connected vugs, fractures, and dissolution-enlarged fractures, as shown in Fig. 1. For a given rock volume, all or any combination of these vug/fracture systems might occur. Although the geometry of the majority of vugs can be described by a spherical shape, a wide range of vugs have elongated shapes, which cannot be described by a spherical shape. Spheroidal shapes (axis-symmetric ellipsoids) are very suitable choices for describing a variety of vug geometries. These shapes can cover geometries with an aspect ratio close to 1, spherical geometry, as well as elongated, needle-like shapes with a large aspect ratio. Isolated vugs will be treated as being spherical or spheroidal in shape, whereas vugs will be treated as elongated spheroidal shapes and fractures will be treated as vertical spheroidal disks. Therefore, the spheroidal geometry will provide us sufficient flexibility to work with a wide variety of vugs and fracture shapes. A spheroid is reduced to a sphere when the focal length of the spheroid approaches zero. A prolate spheroid degenerates to a long rod when the focal length of the spheroid approaches infinity, and it represents the connected vug geometry (a tunnel geometry). An oblate spheroid degenerates to a flat spheroidal disk that can approximate the fracture geometry. We use the term vug to address both vug and microfracture inclusions.

The spatial resolution of petrophysical logs and cores is still very limited for a good quality description of vuggy and fractured media. Standard sampling methods such as thin sections, core plugs, and even whole core are perhaps, for most cases, too small to measure the effective permeability of a vuggy and/or fractured medium. In particular, the standard Hassler core plugs are too small to measure the effective permeability.

Mostly numerical methods have been widely used to investigate fluid flow in porous media with vugs (Arbogast and Brunson 2007; Arbogast et al. 2004; Arbogast and Gomez 2009; Moctezuma-Berthier et al. 2002, 2004; Wieck et al. 1995; Zhao and Valliappan 1994), where a coupled system of equations of flow including Stokes flow (Stokes’ law) in the vugs and Darcy’s law in the matrix is solved by use of finite element or finite volume method. Asymptotic solution to this problem through the homogenization technique was obtained for the case of binary medium where a vug is periodically repeated through the porous matrix (Arbogast and Lehr 2006; Bouchelaghem 2011a, b). At the fine scale, the Stokes flow in the vug was coupled to the Darcy’s law in the matrix. A macroscopic Darcy’s law governing fluid flow in the macroscale porous medium was obtained. The cell problem, resulting in the macroscale effective permeability, was solved numerically for several vug shapes by Arbogast and Lehr (2006). Analytical solutions for the cell problem of a similar case for spheroidal vugs was obtained by Bouchelaghem (2011a, b). Another similar upscaling approach was presented by Popov et al. (2009) in which the Stokes–Brinkman equation rather than the Darcy–Stokes equation was used at the fine scale to compute the upscaled effective permeability of fractured karst carbonate reservoirs based on homogenization theory. The Stokes–Brinkman equations can be reduced to either the Stokes or the Darcy equations by appropriate choice of parameters to avoid the explicit formulation of the boundary conditions at the fluid–matrix interfaces.

The exact analytical solution for fluid flow in porous media including a single circular or slightly deformed circular-shaped vug was obtained by Raja Sekhar and Sano (2000) and Raja Sekhar and Sano (2003). Markov et al. (2010) developed an analytical solution for the fluid flow and effective permeability of a vuggy porous media, including circular and spherical vugs. Happel and Brenner (1983), using the separation of variables method, obtained for the first time an analytical solution for Stokes flow past a spheroidal vugs. Fitts (1991) obtained an analytical solution for fluid flow in the vuggy porous domain containing porous inclusions in the shape of prolate or oblate spheroids.

The objective of this paper is to derive the effective permeability of a porous medium, including spherical- and/or spheroidal-shaped vug and/or fracture inclusions. For this purpose, an incompressible, steady-state, single-phase Darcian flow in the matrix medium is coupled with Stokes flow inside the spheroidal vug. Then, analytic solutions for the Stokes flow inside the spheroid are derived as a set of semi-separable solutions in terms of the ellipsoidal coordinates (Charalambopoulos and Dassios 2002; Dassios 2007; Dassios et al. 1994, 2004; Iyengar and Radhika 2011, 2015; Radhika and Iyengar 2010). The fluid flow field in the matrix medium is coupled with the Stokes flow in the vug through a no-jump condition on normal velocities, jump on pressures, and the generalized Beavers–Joseph–Saffman condition given by Beavers and Joseph (1967) and Jones (1973) on the matrix and vug or fracture interface. The equivalent permeability of the vug or fracture is obtained by substituting it with a porous vug having the same external matrix pressure field. The effective permeability of the ensemble of the system is obtained by using the volume averaging of the pressure field and velocity over the domain (Rubin and Gómez-Hernández 1990). The effect of shape, spatial distribution, and volume concentration of vugs on the effective permeability is investigated.

Fig. 2
figure 2

Schematic of the fluid flow through a vuggy inclusion located at the center of the matrix cell

Full size image

2 Mathematical Formulation of the Problem

A steady-state axis-symmetric flow of an incompressible fluid is assumed in a porous medium, in which the fluid-filled vuggy inclusions of different sizes and shapes are scattered throughout. The matrix domain is exposed to an external uniform pressure gradient. The size of a matrix cell is assumed to be sufficiently large compared with the vug size; therefore, in the far field the pressure field remains unaffected by the presence of vuggy inclusions. We begin our analysis with the case of only one vuggy inclusion, \(\varOmega _\mathrm{v}\), located at the center of a relatively large matrix cell \(\varOmega _\mathrm{m}\) as shown in Fig. 2. The origin of the coordinate system is located at the center of the vug. The external uniform pressure gradient is assumed to be in the x direction of the elongated axis of the vug, denoted by the Cartesian coordinates (x, y, z).

In the matrix domain, the conservation of mass and Darcy’s law can be expressed as

$$\begin{aligned} \nabla .~\mathbf {u}_\mathrm{m}= & {} 0,\quad \text {in }\varOmega _\mathrm{m}, \end{aligned}$$
(1)
$$\begin{aligned} \mathbf {u}_\mathrm{m}= & {} -\dfrac{k_\mathrm{m} }{\mu }\nabla {p_\mathrm{m}},\quad \text {in }\varOmega _\mathrm{m}, \end{aligned}$$
(2)

where \(\mathbf {u}_\mathrm{m}=(u_\mathrm{m}, v_\mathrm{m})\), \(p_\mathrm{m}\), \(k_\mathrm{m}\) , and \(\mu \) denote the velocity vector, the pressure, the permeability, and the fluid viscosity in the matrix domain, respectively. In general, the subscript m refers to the matrix domain variables and properties. The fluid is assumed to be the same in the matrix and vuggy domains. The pressure field for the matrix domain from Eqs. 1 and 2 can be written as

$$\begin{aligned} \nabla ^2 p_\mathrm{m}=0 ,\quad \text {in }\varOmega _\mathrm{m}. \end{aligned}$$
(3)

In a general orthogonal curvilinear coordinate system \((\chi _1,\chi _2,\chi _3)\) with \((\mathbf e _{\chi _1},\mathbf e _{\chi _2},\mathbf e _{\chi _3})\) as the base vectors and \((h_1,h_2,h_3)\) as the corresponding scale factors, the del and Laplacian operator are as follows

$$\begin{aligned} \nabla= & {} \dfrac{1}{h_1}\dfrac{\partial }{\partial \chi _1}{} \mathbf e _{\chi _1}+ \dfrac{1}{h_2}\dfrac{\partial }{\partial \chi _2}{} \mathbf e _{\chi _2}+ \dfrac{1}{h_3}\dfrac{\partial }{\partial \chi _3}{} \mathbf e _{\chi _3}, \end{aligned}$$
(4)
$$\begin{aligned} \nabla ^2= & {} \dfrac{1}{h_1h_2 h_3}\bigg [ \dfrac{\partial }{\partial \chi _1} \left( \dfrac{h_2h_3}{h_1} \dfrac{\partial }{\partial \chi _1} \right) + \dfrac{\partial }{\partial \chi _2} \left( \dfrac{h_1h_3}{h_2} \dfrac{\partial }{\partial \chi _2} \right) \bigg ]. \end{aligned}$$
(5)

For the axis-symmetric fluid flow, where \(\dfrac{\partial }{\partial \chi _3}=0\), the stream function \( \varPsi _\mathrm{m}\) in the matrix domain is introduced as

$$\begin{aligned} u_\mathrm{m}= & {} \dfrac{1}{h_2h_3}\dfrac{\partial \varPsi _\mathrm{m}}{\partial \chi _2},\quad \text {in }\varOmega _\mathrm{m}, \nonumber \\ v_\mathrm{m}= & {} -\dfrac{1}{h_1h_3}\dfrac{\partial \varPsi _\mathrm{m}}{\partial \chi _1},\quad \text {in }\varOmega _\mathrm{m}. \end{aligned}$$
(6)

Inside the vug, the fluid flow is assumed to be laminar and happening at small Reynolds number with negligible inertial forces. This means that Stokes flow takes place inside the vug, for which the steady-state mass and momentum balance equations can be written as

$$\begin{aligned}&\nabla .\mathbf {u}_\mathrm{v}=0,\quad \text {in }\varOmega _\mathrm{v}, \end{aligned}$$
(7)
$$\begin{aligned}&\nabla {p_\mathrm{v}}+\mu \nabla \times \nabla \times \mathbf {u}_\mathrm{v}=0,\quad \text {in }\varOmega _\mathrm{v}, \end{aligned}$$
(8)

where, \(\mathbf {u}_\mathrm{v}=(u_\mathrm{v}, v_\mathrm{v})\) and \(p_\mathrm{v}\) denote the velocity vector and the pressure inside the vug inclusion, respectively. We introduce the stream function \(\varPsi _\mathrm{v}\) inside the vug as

$$\begin{aligned} u_\mathrm{v}= & {} \dfrac{1}{h_2h_3}\dfrac{\partial \varPsi _\mathrm{v}}{\partial \chi _2},\quad \text {in }\varOmega _\mathrm{v},\nonumber \\ v_\mathrm{v}= & {} -\dfrac{1}{h_1h_3}\dfrac{\partial \varPsi _\mathrm{v}}{\partial \chi _1},\quad \text {in }\varOmega _\mathrm{v}. \end{aligned}$$
(9)

Obtaining the curl of Eq. 8, together with some mathematical manipulations, the stream function in the Stokes domain satisfies the following equation

$$\begin{aligned} E^4\varPsi _\mathrm{v}=E^2(E^2\varPsi _\mathrm{v})=0,\quad \text {in }\varOmega _\mathrm{v}, \end{aligned}$$
(10)

where the differential operator \(E^2\) is given by

$$\begin{aligned} E^2=\dfrac{h_3}{h_1h_2}\bigg [ \dfrac{\partial }{\partial \chi _1} \left( \dfrac{h_2}{h_1h_3} \dfrac{\partial }{\partial \chi _1} \right) +\dfrac{\partial }{\partial \chi _2} \left( \dfrac{h_1}{h_2h_3} \dfrac{\partial }{\partial \chi _2} \right) \bigg ]. \end{aligned}$$
(11)

Using this notation, Eq. 8 can be written as

$$\begin{aligned}&-\dfrac{1}{h_1}\dfrac{\partial p_\mathrm{v}}{\partial \chi _1}+\dfrac{\mu }{h_2h_3} \dfrac{\partial }{\partial \chi _2}\left( E^2\varPsi _\mathrm{v}\right) =0,\quad \text {in }\varOmega _\mathrm{v},\nonumber \\&\quad -\dfrac{1}{h_2}\dfrac{\partial p_\mathrm{v}}{\partial \chi _2}-\dfrac{\mu }{h_1h_3} \dfrac{\partial }{\partial \chi _1}\left( E^2\varPsi _\mathrm{v}\right) =0,\quad \text {in }\varOmega _\mathrm{v}. \end{aligned}$$
(12)

In the orthogonal curvilinear coordinate system, the differential operators \(\nabla ^2\) and \(E^2\) remain separable with respect to the spatial coordinates. The problem is closed with the following set of regularity conditions and the boundary condition on the interface of the vug and matrix domains.

Bounded Velocity Inside the Vug

$$\begin{aligned}&\lim _{r\rightarrow 0}|\varPsi _\mathrm{v}(\chi _1,\chi _2,\chi _3)|<\infty , \end{aligned}$$
(13)
$$\begin{aligned}&\lim _{r\rightarrow 0}| u_\mathrm{v} |<\infty ,\quad \lim _{r\rightarrow 0}| v_\mathrm{v} |<\infty , \end{aligned}$$
(14)

where r is the distance of any point inside the vug from the origin of coordinate system.

Regularity of Pressure Field at Infinity

$$\begin{aligned} \lim _{x\rightarrow \infty }p_\mathrm{m}=|\nabla (p_\mathrm{m})_{\infty }|x. \end{aligned}$$
(15)

\(\nabla (p_\mathrm{m})_{\infty }\) is the uniform pressure gradient in the matrix in x-direction at infinity and is not perturbed due to presence of the inclusion.

Continuity of the Normal Velocities on the Interface This condition guarantees the conservation of mass between porous matrix and the vug.

$$\begin{aligned} \mathbf {u}_\mathrm{v}.\mathbf {n}=\mathbf {u}_\mathrm{m}.\mathbf {n} , \quad \text {on } \varGamma _{m,v}, \end{aligned}$$
(16)

where \(\mathbf {n}\) is the unit normal to the interface and \(\varGamma _{m,v}\) is the interface of the matrix cell and the vug as shown in Fig. 2.

Pressure Jump on the Interface This condition represents the balance of two driving forces in the normal direction along the interface, the kinematic pressure in the matrix and the normal component of the normal stress in the vug.

$$\begin{aligned} -p_\mathrm{m}=-p_\mathrm{v}+ 2\mu ~ \mathbf {n}.\epsilon .\mathbf {n},\quad \text {on } \varGamma _{m,v}, \end{aligned}$$
(17)

where \(\epsilon =\dfrac{1}{2}\left( \nabla \mathbf {u}_\mathrm{v}+\nabla \mathbf {u}_\mathrm{v}^T\right) \) is the rate of strain tensor given in the orthogonal coordinate system as

$$\begin{aligned}&\epsilon _{\chi _1,\chi _1} =\dfrac{1}{h_1}\dfrac{\partial u_\mathrm{v}}{\partial \chi _1} +\dfrac{v_\mathrm{v}}{h_1h_2}\dfrac{\partial h_1}{\partial \chi _2}, \end{aligned}$$
(18)
$$\begin{aligned}&\epsilon _{\chi _2 ,\chi _1} =\epsilon _{\chi _1 ,\chi _2}=\dfrac{h_2}{h_1}\dfrac{\partial }{\partial \chi _1}\left( \dfrac{v_\mathrm{v}}{h_2}\right) + \dfrac{h_1}{h_2}\dfrac{\partial }{\partial \chi _2}\left( \dfrac{u_\mathrm{v}}{h_1}\right) . \end{aligned}$$
(19)

Slip Condition for Tangential Velocities on the Interface This condition addresses the important issue of how the porous media affect the flow at the interface. Beavers and Joseph (1967) showed experimentally that a free fluid in contact with a porous medium flows faster than a fluid in contact with a solid surface. This observation is taken into account by imposing a slip boundary condition on the interface of the matrix and free fluid contact. Later, Saffman (1971) showed that this slip is independent from the tangential velocity in the porous domain.

In the current work, we use the generalized form of Beavers–Joseph–Saffman slip boundary condition proposed by Jones (1973). Thus, for complicated interface geometries other than the plane interface, the generalized form of the slip boundary condition can be expressed as

$$\begin{aligned} \mathbf {n}.\epsilon .\varvec{\tau _i}=\dfrac{\lambda }{\sqrt{\varvec{\tau _i}.k_\mathrm{m} .\varvec{\tau _i}}}\mathbf {u}_\mathrm{v}.\varvec{\tau _i},\quad i=1,2 \quad \text {on }\varGamma _{m,v}, \end{aligned}$$
(20)

where \(\lambda \) is an empirical coefficient, \(k_\mathrm{m}\) is the permeability of the matrix domain, and \(\varvec{\tau _i}\) is the tangential unit vector to the interface (Fig. 2). Note that for axis-symmetric problems, \(i=1\) in the slip boundary condition.

3 Spheroidal Vug

Stream function in the vug domain and pore pressure in the host homogeneous porous media can be analytically solved for certain geometries. Knowing these two functions, the other characteristics of flow can be determined in the ensemble of the domain. In this study, we present analytic solutions for vugs of prolate spheroidal shapes. The analytic solution for oblate spheroid can be easily obtained using the same methodology.

Fig. 3
figure 3

Spheroidal coordinates and a schematic of a spheroidal vug in the matrix

Full size image

Let us consider one prolate spheroidal fluid-filled vuggy inclusion \(\varOmega _\mathrm{v}\) located in the homogeneous matrix medium \(\varOmega _\mathrm{m}\) with major axis a in the x-direction and minor axis b in the y, z directions with \(a>b\) as shown in Fig. 3.

We employ the prolate spheroidal coordinate system \((\xi ,\eta ,\phi )\) with unit normal vectors \((\mathbf {e}_\xi , \mathbf {e}_\eta , \mathbf {e}_\phi )\), which is related to the Cartesian coordinate system through

$$\begin{aligned} \begin{aligned} x&=c \cosh \xi ~\cos \eta ,\\ y&=c \sinh \xi ~\sin \eta ~\sin \phi , \\ z&=c \sinh \xi ~\sin \eta ~\cos \phi , \\ \end{aligned} \end{aligned}$$
(21)

with

$$\begin{aligned} 0\le \xi <\infty ,\quad 0\le \eta \le \pi ,\quad 0\le \phi \le 2\pi , \end{aligned}$$
(22)

and the focal length of the spheroid c as

$$\begin{aligned} c=\sqrt{a^2-b^2}, \end{aligned}$$
(23)

For the sake of the notational convenience, the following change of variables is introduced

$$\begin{aligned} s=\cosh \xi ,\quad t=\cos \eta , \end{aligned}$$
(24)

and then,

$$\begin{aligned} \begin{aligned} x&=cst,\\ y&=c \sqrt{s^2-1} \sqrt{1-t^2}\sin \phi ,\\ z&=c \sqrt{s^2-1} \sqrt{1-t^2}\cos \phi .\\ \end{aligned} \end{aligned}$$
(25)

The coordinates of any point inside of the spheroidal vug is given by

$$\begin{aligned} \varOmega _\mathrm{v}=\{(s,t,\phi ): 1\le s\le s_o,\quad -1\le t\le 1, \quad 0\le \phi \le 2\pi \}, \end{aligned}$$
(26)

with \(s_o=a/c,\) which defines the prolate spheroid of semi-axes a, b. One can see that use of the spheroidal coordinate system facilitates the definition of the boundary condition on the contact of vug and porous media in terms of the boundary condition on \(s=s_o\). Besides, the \(E^2\) and \(\nabla ^2\) operators remain separable with respect to the spheroidal coordinate system variables.

The prolate spheroidal coordinate scale factors are as follows

$$\begin{aligned} h_1=h_2=c\sqrt{s^2-t^2}, \quad h_3=c\sqrt{s^2-1}\sqrt{1-t^2}. \end{aligned}$$
(27)

Using \((s,t,\phi )\) as the new coordinate variables leads to the following differential equation

$$\begin{aligned} \begin{aligned} \dfrac{\partial }{\partial \xi }=\sqrt{s^2-1}\dfrac{\partial }{\partial s},\quad \dfrac{\partial }{\partial \eta }=-\sqrt{1-t^2}\dfrac{\partial }{\partial t}. \end{aligned} \end{aligned}$$
(28)

3.1 Fluid Flow Inside the Spheroidal Vug

We apply the same method introduced by Dassios et al. (1994) to solve the axis-symmetric Stokes flow in the spheroidal coordinate system. Inside the spheroidal vug, the Stokes stream function should satisfy Eq. 10, where the differential operator \(E^2\) in the spheroidal coordinate system is given as

$$\begin{aligned} E^2=\dfrac{1}{c^2(s^2-t^2)}\left[ (s^2-1){\partial ^2 \over \partial s^2}+(1-t^2)\dfrac{\partial ^2 }{\partial t^2}\right] . \end{aligned}$$
(29)

We define the kernel of \(E^2\) denoted by \({\text {KerE}}^2\) as ensemble of all functions f that f satisfies \(E^2f=0\). Similarly, if a function f satisfies \(E^4f=0\), it belongs to the kernel of \(E^4\) denoted by \({\text {KerE}}^4\). We introduce the following series expansion for the stream function \(\varPsi _\mathrm{v}\) decomposed into two parts, the part already in \({\text {KerE}}^2\) and the part not in \({\text {KerE}}^2\), but still in \({\text {KerE}}^4\); thus, resulting in

$$\begin{aligned} \varPsi _\mathrm{v}(s,t)= c^2\varPhi (s,t) + c^2\varTheta (s,t),\quad \text {in }\varOmega _\mathrm{v}. \end{aligned}$$
(30)

\(\varTheta (s,t)\) belongs to the \({\text {KerE}}^2\) which gives

$$\begin{aligned} E^2\varTheta =0. \end{aligned}$$
(31)

\(\varTheta (s,t)\) is a trivial solution for \({\text {KerE}}^4\). \(\varPhi (s,t)\) represents the remainder of the functions in \({\text {KerE}}^4\) which do not belong to \({\text {KerE}}^2\)

$$\begin{aligned} E^2\varPhi \ne 0,\quad E^4\varPhi =0. \end{aligned}$$
(32)

The coefficient \(c^2\) preceding either of the terms on the right-hand side of Eq. 30 is for additional formulation convenience. In the following subsections, we define \(\varTheta \) and \(\varPhi \) separately.

Functions in \({KerE}^2\)

Using the technique of separation of variables, it becomes possible to verify that \(\varTheta (s,t)\in {\text {KerE}}^2\) can be expressed in the form of a series as

$$\begin{aligned} \varTheta (s,t)=\sum _{i=1}^{4}\sum _{n=0}^{\infty }a_{i,n}\varTheta _{i,n}(s,t), \end{aligned}$$
(33)

where \(a_{i,n}\) are the constants to be defined and \(\varTheta _{i,n}\) is given by

$$\begin{aligned} \varTheta _{1,n}(s)= & {} G_n(s)G_n(t), \end{aligned}$$
(34a)
$$\begin{aligned} \varTheta _{2,n}(s)= & {} G_n(s)H_n(t),\end{aligned}$$
(34b)
$$\begin{aligned} \varTheta _{3,n}(s)= & {} H_n(s)G_n(t), \end{aligned}$$
(34c)
$$\begin{aligned} \varTheta _{4,n}(s)= & {} H_n(s)H_n(t), \end{aligned}$$
(34d)

where \(G_n\) and \(H_n\) are the Gegenbauer polynomials of first and second kind and of degree \(-\frac{1}{2}\), which is given in “Appendix 1.”

Functions in \({KerE}^{4}\)

We look for the functions \(\varPhi (s,t)\) with \(E^2\varPhi \in {\text {KerE}}^2\), and then \(\varPhi \in {\text {KerE}}^4\). Let us introduce the following series expansion for \(\varPhi (s,t)\) as

$$\begin{aligned} \varPhi (s,t)=\sum _{i=1}^{4}\sum _{n=0}^{\infty }\varPhi _{i,n}(s,t). \end{aligned}$$
(35)

Then, the stream function inside the vug will be rewritten as

$$\begin{aligned} \varPsi _\mathrm{v}(s,t)=\sum _{i=1}^{4}(\varPsi _\mathrm{v})_i(s,t)=c^2\sum _{i=1}^{4}\sum _{n=0}^{\infty }\varPhi _{i,n}(s,t)+ c^2\sum _{i=1}^{4}\sum _{n=0}^{\infty }\varTheta _{i,n}(s,t). \end{aligned}$$
(36)

The functions \(\varPhi _{i,n}(s,t)\) are defined so that

$$\begin{aligned} E^2\varPhi _{i,n}(s,t)= C_{i,n}\varTheta _{i,n}(s,t),\quad \text {in }\varOmega _\mathrm{v}, \end{aligned}$$
(37)

for \(i=1,\ldots ,4,\quad n=0,1,2,\ldots \), where \(C_{i,n}\) is the constant to be defined later. One can deduce from the previous equations that

$$\begin{aligned} E^4\varPhi _{i,n}(s,t)=E^2\left( E^2\varPhi _{i,n}(s,t)\right) =C_{i,n}E^2\varTheta _{i,n}(s,t)=0. \end{aligned}$$
(38)

Let us study Eq. 37 for \(i=1\)

$$\begin{aligned} \bigg [(s^2-1){\partial ^2 \over \partial s^2}+(1-t^2)\dfrac{\partial ^2 }{\partial t^2} \bigg ]\varPhi _{1,n}(s,t)= c^2~C_{1,n}(s^2-t^2)G_{n}(s)G_{n}(t). \end{aligned}$$
(39)

In general, the equation in the form of

$$\begin{aligned} \bigg [(s^2-1){\partial ^2 \over \partial s^2}+(1-t^2)\dfrac{\partial ^2 }{\partial t^2} \bigg ]U(s,t)=f_\mathrm{m}(s)g_n(t), \end{aligned}$$
(40)

where \(f_\mathrm{m}\) and \(g_n\) are the Gegenbauer polynomials of the first or second kind and of order n and m, with \(n\ne m\) and \(n+m\ne 1\), has a particular solution defined in terms of a separable function as

$$\begin{aligned} U_{n,m}(s,t)=\dfrac{f_\mathrm{m}(s)g_n(t)}{(n-m)(n+m-1)}. \end{aligned}$$
(41)

Using relations given by Eqs. 85 and 86 in “Appendix 1,” the terms including \(s^2\) and \(t^2\) on the right-hand side (RHS) of Eq. 39 are absorbed into Gegenbauer polynomials. Consequently, the solution of Eq. 39 is

$$\begin{aligned} \varPhi _{1,n}(s,t)= & {} c^2~C_{1,n}\bigg (\dfrac{-\alpha _n}{2(2n-1)} G_{n-2}(s)+\dfrac{ \beta _n}{2(2n+1)} G_{n+2}(s)\bigg )G_n(t) \nonumber \\&- c^2~C_{1,n}G_n(s)\bigg (\dfrac{\alpha _n}{2(2n-1)} G_{n-2}(t)- \dfrac{\beta _n}{2(2n+1)} G_{n+2}(t)\bigg ), \end{aligned}$$
(42)

where \(\alpha _n,\beta _n,\gamma _n\) for \(n\ge 4\) are given by Eq. 87 in “Appendix 1.” As long as we just use the terms including Gegenbauer polynomials of first kind, one can redefine \(\alpha _n,\beta _n,\gamma _n\) for \(n<4\), as

$$\begin{aligned} \begin{aligned}&\alpha _0=\alpha _1=\alpha _2=\alpha _3=0,\\&\gamma _0=1,\quad \gamma _1=1,\quad \gamma _2=\dfrac{1}{5},\quad \gamma _3=\dfrac{3}{7},\\&\beta _0=-2,\quad \beta _1=2,\quad \beta _2=\dfrac{4}{5},\quad \beta _3=\dfrac{4}{7}. \end{aligned} \end{aligned}$$
(43)

Note that \(\varPhi _{1,n}\) only includes the particular solution to nonhomogeneous Eq. 37 and the solution to the homogeneous problem will be included in \(\varTheta _{1,n}\). Therefore, \((\varPsi _\mathrm{v})_{1}\) includes the complete set of the solution as follows

$$\begin{aligned} (\varPsi _\mathrm{v})_{1}(s,t)=c^2 \sum _{n=0}^{\infty } \varPhi _{1,n}(s,t)+c^2\sum _{n=0}^{\infty } a_{1,n}\varTheta _{1,n}(s,t), \end{aligned}$$
(44)

which can be written as

$$\begin{aligned} (\varPsi _\mathrm{v})_{1}(s,t)=c^2~\sum _{n=1}^{\infty }g_{1,n}(s)G_{n}(t), \end{aligned}$$
(45)

with

$$\begin{aligned} g_{1,n}= & {} a_{1,n}G_n(s)+c^2 \bigg (\dfrac{\beta _{n-2}C_{1,n-2}}{2(2n-3)}-\dfrac{\alpha _n C_{1,n}}{2(2n-1)}\bigg ) G_{n-2}(s) \nonumber \\&+\,c^2\bigg (\dfrac{\beta _n C_{1,n} }{2(2n+1)}-\dfrac{\alpha _{n+2}C_{1,n+2}}{2(2n+3)} \bigg )G_{n+2}(s). \end{aligned}$$
(46)

Applying the same procedure for \(\varPhi _{2,n}(s,t),\varPhi _{3,n}(s,t),\varPhi _{4,n}(s,t)\) in Eq. 37, and associating the terms including Gegenbauer polynomials of t of the same order, the complete set of solutions for Stokes stream function can be determined. In our work, the general solution for Stokes stream function can be simplified using the following assumptions:

  • The solution has to be bounded on the axis of symmetry; thus, i is limited to \(i=1,3\) in Eq. 36 regarding to the definition of \(\varTheta _{i,n}\) given in Eq. 34.

  • The solution has symmetry with respect to t and then only the even n values are used, \(n=2k\).

  • The solution has to be bounded inside the spheroidal vug when \(s\rightarrow 1\) and then i is limited to \(i=1\), regarding to the definition of \(\varTheta _{i,n}\) given in Eq. 34.

Eventually, the stream function inside the spheroidal vug is given as

$$\begin{aligned} \varPsi _\mathrm{v}(s,t)=c^2~\sum _{k=1}^{\infty }g_{1,2k}(s)G_{2k}(t). \end{aligned}$$
(47)

Note that none of the individual terms in Eq. 47 satisfies \(E^4\varPsi _\mathrm{v}(s,t)=0\), but the sum of all the other terms do. This condition can be investigated using the method for developing the solution.

Once the stream function in the vug is defined, we can determine the pressure field inside the vug using Eqs. 12 and 28 as follows

$$\begin{aligned} \begin{aligned} (s^2-1){\partial p_\mathrm{v}\over \partial s}=-\dfrac{\mu }{c\rho }\dfrac{\partial }{\partial t}\left( E^2\varPsi _\mathrm{v} \right) ,\\ (1-t^2)\dfrac{\partial p_\mathrm{v}}{\partial t}=\dfrac{\mu }{c\rho }~{\partial \over \partial s}\left( E^2\varPsi _\mathrm{v}\right) , \end{aligned} \end{aligned}$$
(48)

and the pressure field inside the spheroidal vug is given as

$$\begin{aligned} p_\mathrm{v}(s,t)=-\sum _{k=1}^{\infty } \dfrac{\mu ~c}{ 2k(2k-1)} ~ C_{1,2k}P_{2k-1}(s)P_{2k-1}(t). \end{aligned}$$
(49)

\(P_{n}(t)\) is the Legendre polynomial of first kind and order n.

3.2 Fluid Flow in the Matrix Domain Outside the Spheroidal Vug

The host porous media pressure field outside the vug should satisfy the Laplacian equation given by Eq. 3, with the Laplacian differential operator given for the spheroidal coordinate system as

$$\begin{aligned} \nabla ^2=\dfrac{1}{c^2(s^2-t^2)}\bigg [(s^2-1){\partial ^2 \over \partial s^2}+ (1-t^2)\dfrac{\partial ^2 }{\partial t^2}+2s{\partial \over \partial s}-2t\dfrac{\partial }{\partial t} \bigg ]. \end{aligned}$$
(50)

Considering the regularity of the far field pressure in Eq. 15 as

$$\begin{aligned} \lim _{s\rightarrow \infty }p_\mathrm{m}(s,t)=|\nabla (p_\mathrm{m})_{\infty }|cst, \end{aligned}$$
(51)

the pressure field outside the spheroidal vug is given by

$$\begin{aligned} p_\mathrm{m}(s,t)=\sum _{k=1}^{\infty }c~F_{2k-1}(s)P_{2k-1}(t), \end{aligned}$$
(52)

with

$$\begin{aligned} F_{2k-1}(s)=|\nabla (p_\mathrm{m})_{\infty }|~s~\delta _{1,{2k-1}}+A_{2k} Q_{2k-1}(s), \end{aligned}$$
(53)

where \(\delta _{1,{2k-1}}\) is the Kronecker delta function, \(Q_n(s)\) is the Legendre polynomial of second kind and order n, and \(A_{2k}\) are the coefficients to be determined later. As the pressure field has to be odd with respect to the axis of symmetry, only odd terms are included in this solution. Note that

$$\begin{aligned} \lim _{s\rightarrow \infty }\dfrac{Q_{2k-1}(s)P_{2k-1}(t)}{cst}=0. \end{aligned}$$
(54)

The stream function in Darcy’s domain is obtained through the definition of the velocity field using Eq. 6 as

$$\begin{aligned} (s^2-1)~{\partial p_\mathrm{m}\over \partial s}= & {} -\dfrac{\mu }{k_\mathrm{m} c\rho }~\dfrac{\partial \varPsi _\mathrm{m}}{\partial t},\nonumber \\ (1-t^2)~\dfrac{\partial p_\mathrm{m}}{\partial t}= & {} \dfrac{\mu }{k_\mathrm{m} c\rho }~{\partial \varPsi _\mathrm{m}\over \partial s}. \end{aligned}$$
(55)

The stream function outside the spheroidal vug is given by

$$\begin{aligned} \varPsi _\mathrm{m}(s,t)= -\dfrac{c^2 k_\mathrm{m} }{\mu }\dfrac{(s^2-1)(1-t^2)}{{2k}({2k-1})} F'_{2k-1}(s) P'_{2k-1}(t), \end{aligned}$$
(56)

where \('\) denotes derivative. It can be shown that

$$\begin{aligned} \lim _{x\rightarrow \infty }\varPsi _\mathrm{m}=\dfrac{1}{2}U_{\infty }r^2, \end{aligned}$$
(57)

where \(r^2=c^2(s^2-1)(1-t^2)\) and \(U_{\infty }=-\frac{k_\mathrm{m} }{\mu }|\nabla (p_\mathrm{m})_{\infty }|\).

3.3 Coupling Matrix and Stokes Domains

The undetermined coefficients of the stream function in the vug and the pressure field in host porous media can be determined by imposing the boundary conditions given in Eqs. 16, 17 and 20. The condition given by Eq. 16 in the spheroidal coordinates is as follows

$$\begin{aligned} \dfrac{\partial \varPsi _\mathrm{v}}{\partial t}=\dfrac{\partial \varPsi _\mathrm{m}}{\partial t}, \quad \text {on}\quad s=s_o, \end{aligned}$$
(58)

which after associating the coefficients of the same t-dependent functions yields

$$\begin{aligned} g_{1,2k}(s_o)=-\dfrac{k_\mathrm{m} }{2k(2k-1)\mu }(s_o^2-1)F_{2k}'(s_o). \end{aligned}$$
(59)

The generalized Beavers–Joseph–Saffman condition described in Eq. 20, with the tangential component of the rate of the strain tensor \(\epsilon _{\xi \eta }=\epsilon _{\eta \xi }\) given as

$$\begin{aligned} \epsilon _{\xi \eta }= & {} \dfrac{1}{c^3}\left[ \sqrt{\dfrac{(s^2-1)}{(1-t^2)}} \left( \dfrac{-2s}{(s^2-t^2)^2} {\partial \varPsi _\mathrm{v}\over \partial s} +\dfrac{1}{(s^2-t^2)}{\partial ^2 \varPsi _\mathrm{v}\over \partial s^2} \right) \right. \\&\left. -\sqrt{\dfrac{(1-t^2)}{(s^2-1)}} \left( \dfrac{2t}{(s^2-t^2)^2} \dfrac{\partial \varPsi _\mathrm{v}}{\partial t} +\dfrac{1}{(s^2-t^2)}\dfrac{\partial ^2 \varPsi _\mathrm{v}}{\partial t^2} \right) \right] , \end{aligned}$$

reduces to

$$\begin{aligned}&\left( -2s {\partial \varPsi _\mathrm{v}\over \partial s} +(s^2-t^2){\partial ^2 \varPsi _\mathrm{v}\over \partial s^2} \right) - \left( 2t \dfrac{\partial \varPsi _\mathrm{v}}{\partial t} +(s^2-t^2)\dfrac{\partial ^2 \varPsi _\mathrm{v}}{\partial t^2} \right) \nonumber \\&\quad = \dfrac{c\lambda }{\sqrt{k_\mathrm{m} }} \sqrt{s^2-1}{(s^2-t^2)}^{\frac{3}{2}}{\partial \varPsi _\mathrm{v}\over \partial s}, \text {on }s=s_o. \end{aligned}$$
(60)

Replacing the Stokes stream function from Eq. 47 yields the following equation

$$\begin{aligned}&\sum _{k=1}^{\infty } -\dfrac{2s_o(s_o^2-1)}{2k(2k-1)}g'_{1,2k}(s_o) P'_{2k-1}(t) \nonumber \\&\quad + \bigg [\dfrac{s_o^2-1}{2k(2k-1)}g''_{1,2k}(s_o) +g_{1,2k}(s_o)\bigg ](s_o^2-t^2) P'_{2k-1}(t) \nonumber \\&\quad +2 g_{1,2k}(s_o)t~P_{2k-1}(t) = \sum _{k=1}^{\infty } \dfrac{\lambda c}{\sqrt{k_\mathrm{m} }} \dfrac{ \sqrt{s_o^2-1}}{2k(2k-1)}g'_{1,2k}(s_o)(s_o^2-t^2)^\frac{3}{2} P'_{2k-1}(t). \end{aligned}$$
(61)

It is complicated to separate the coefficients of \(P_{2k-1}(t)\) or \(P'_{2k-1}(t)\) for Eq. 61 in order to equalize the coefficients of the same terms. We rewrite all the terms in the form of Legendre polynomial expansion series. For computational purposes, this is a good technique for working with nonsimilar terms. Using the Legendre series expansion as shown in “Appendix 2,” all of the terms in Eq. 61 are expressed in terms of \(P_{2n}(t)\), and we can equalize the similar terms.

The pressure jump condition given by Eq. 17 in the spheroidal coordinate system with

$$\begin{aligned} \epsilon _{\xi \xi }= \dfrac{1}{c^3 (s^2-t^2)}\bigg (\dfrac{\partial ^2\varPsi _\mathrm{v}}{\partial s \partial t}+\dfrac{t}{s^2-t^2}{\partial \varPsi _\mathrm{v}\over \partial s} - \dfrac{s(2s^2-1-t^2)}{(s^2-t^2)(s^2-1)}\dfrac{\partial \varPsi _\mathrm{v}}{\partial t}\bigg ), \end{aligned}$$
(62)

and is given as

$$\begin{aligned}&\sum _{k=1}^{\infty }\dfrac{c^2}{2}\bigg ( C_{1,2k}P_{2k-1}(s_o)+ F_{2k-1}(s)/\mu \bigg )(s_o^2-t^2)^2P_{2k-1}(t) \nonumber \\&\quad = \sum _{k=1}^{\infty }g'_{1,2k}(s_o)(s_o^2-t^2)P_{2k-1}(t)\nonumber \\&\qquad -\sum _{k=1}^{\infty }g'_{1,2k}(s_o)t~G_{2k}(t) -\sum _{k=1}^{\infty }g_{1,2k}(s_o)\dfrac{s_o(2s_o^2-1-t^2)}{s_o^2-1}P_{2k-1}(t). \end{aligned}$$
(63)

We rewrite all of the terms in the form of the Legendre polynomial series expansion and equalize the similar terms. For the sake of computational ease, we replace the infinite sum \(\sum _{k=1}^{\infty }\) with finite sum \(\sum _{k=1}^{N}\) with \(N\ge 1\). Having 3N equations given by Eqs. 59, 61, and 63, we can obtain 3N unknowns \(C_{1,2k}, a_{1,2k}, A_{2k}\) by solving an algebraic linear system of equations.

In “Appendix 5,” it is shown that when the spheroidal semi-focal distance tends to zero the flow problem reduces to problem of flow in porous domain with spherical vugs which is expected to be so.

Fig. 4
figure 4

Streamline and pressure field in a porous medium, including vuggy inclusion \(b/a=1\). a Streamline. b Pressure field

Full size image
Fig. 5
figure 5

Streamlines in the matrix medium with a permeability of \(k_\mathrm{m} =0.001\) mD through a spheroidal vug of \(b/a=1\) for several Beavers–Joseph coefficients. a \(\lambda =5\). b \(\lambda =2\). c \(\lambda =0.2\). d \(\lambda =0.1\)

Full size image
Fig. 6
figure 6

Fluid flow in the matrix medium with a permeability of \(k_\mathrm{m} =0.001\) mD through spheroidal vugs with various aspect ratios. The local corrugations are due to very close numerical precision of stream function values. a \(b/a=0.75\). b \(b/a=0.5\). c \(b/a=0.25\)

Full size image
Fig. 7
figure 7

Streamlines for a matrix domain with a permeability of \(k_\mathrm{m} =0.001\) mD with spheroidal vugs scattered through with the Beavers–Joseph coefficient \(\lambda =0.1\)

Full size image

Figure 4 shows the pressure field and streamlines in a matrix cell, including a spheroidal vug with aspect ratio equal to 1. The streamlines in the area near the vug tend to pass through the fluid-filled vug, which has less resistance through which to pass. The pressure remains constant inside the vug, which means negligible pressure drop occurs in the vug.

The effect of the Beavers–Joseph–Saffman coefficient on the flow is shown in Fig. 5. As \(\frac{\sqrt{k_\mathrm{m} }}{\lambda }\) becomes larger, the streamlines are no longer continuous on the interface of the matrix and vug domains, and the tangential component of the velocity in the vug domain becomes much more significant. Because the tangential component of the velocity on the interface on the matrix side is negligible, the inflow and outflow to and from the matrix domain is normal to the interface.

Figure 6 shows the flow field for different aspect ratios of the vuggy inclusion. As shown, the fluid in the matrix domain tends to pass through the vug. Inside the vug, the streamline tends to be a straight line in the general direction of the flow close to the longitudinal axis of the vug.

Figure 7 shows an example of fluid flow in a matrix cell, including randomly distributed vugs with various aspect ratios. The objective here is to develop a method for determining the effective permeability of such a domain. In the next section, we will determine the equivalent permeability of a single spheroidal vug.

4 Equivalent Permeability of a Single Spheroidal Vug

The equivalent permeability of a fluid-filled prolate spheroidal vug \(\varOmega _\mathrm{v}\) in a porous matrix \(\varOmega _\mathrm{m}\) will be determined in this section. We assume that the spheroidal vug can be replaced by a porous inclusion that creates the same flow field exterior to the vug. We determine the flow properties of this porous inclusion notably its permeability which can be considered as the equivalent permeability of the vug. The permeability of a porous inclusion \((\varOmega _\mathrm{m})_\mathrm{in}\) of same size as the fluid-filled vug which generates the same pressure field in the matrix domain will be obtained. The pressure inside the porous spheroidal inclusion should satisfy the Laplacian equation. We apply the method of separation of variables to the Laplacian equation. In fact, we assume that the solution to the Laplacian equation in the spheroidal coordinate system can be found in terms of multiplication of two sets of pure functions of s , t the independent variables of the spheroidal coordinate system. Considering the condition of bounded pressure at the center of inclusion, the pressure inside the porous spheroidal inclusion is given as

$$\begin{aligned} (p_\mathrm{m})_\mathrm{in}=c~\sum _{k=1}^\infty D_{2k}P_{2k-1}(s)P_{2k-1}(t),\quad \text {in }(\varOmega _\mathrm{m})_\mathrm{in} \end{aligned}$$
(64)

where \((p_\mathrm{m})_\mathrm{in}\) represents the pressure in the porous spheroidal inclusion. This means that the first approximation of the stream function inside the porous inclusion is a straight line, which is a result of using Darcy’s law for describing the fluid flow inside the inclusion.

The boundary condition for coupling a porous inclusion and the matrix medium is the no-jump boundary condition for the pressures and the normal fluxes on the interface given as

$$\begin{aligned}&p_\mathrm{m}=(p_\mathrm{m})_\mathrm{in},\quad \text {on } s=s_o, \end{aligned}$$
(65)
$$\begin{aligned}&\dfrac{k_\mathrm{m} }{\mu }{\partial p_\mathrm{m}\over \partial s}=\dfrac{(k_\mathrm{m})_\mathrm{in}}{\mu }{\partial (p_\mathrm{m})_\mathrm{in}\over \partial s},\quad \text {on } s=s_o, \end{aligned}$$
(66)

where \(p_\mathrm{m}\) is given in Eq. 52, and \((k_\mathrm{m})_\mathrm{in}\) is the permeability of the porous inclusion which is the equivalent permeability of the spheroidal vug that is determined. After associating the coefficient of terms \(P_{2k-1}(t)\), we determine the undetermined coefficients of pressure in the porous inclusion as

$$\begin{aligned} D_{2k}=\dfrac{F_{2k-1}(s_o)}{P_{2k-1}(s_o)}. \end{aligned}$$
(67)

Finally, the equivalent permeability of a prolate spheroidal vug with outer spheroid \(s_o\) located in a homogeneous matrix of permeability \(k_\mathrm{m}\) is given as

$$\begin{aligned} (k_\mathrm{m} )_\mathrm{in}=k_\mathrm{m} \dfrac{\sum _{k=1}^\infty F'_{2k-1}(s_o)}{\sum _{k=1}^\infty \dfrac{F_{2k-1}(s_o)}{P_{2k-1}(s_o)} P'_{2k-1}(s_o)}. \end{aligned}$$
(68)

Note that this is the component of the permeability tensor in the direction of the larger semi-axis of prolate spheroid.

Fig. 8
figure 8

Effect of aspect ratio and the Beavers–Joseph–Saffman coefficient on the equivalent permeability of a spheroidal vug for \(k_\mathrm{m} =0.001 mD\)

Full size image

In Fig. 8, the equivalent permeability for a spheroidal vug is plotted for various aspect ratios. The highest permeability is for the spherical vug when the aspect ratio b / a is equal to 1. For a fix value of a, as the vug becomes more elongated, its volume fraction reduces and, respectively, the equivalent permeability reduces. For low aspect ratios, i.e., in the case of this figure for \(b/a<0.1\) the medium can be assumed as a homogeneous medium. In other words, nonconnected narrow fractures can be ignored.

The effect of Beavers–Joseph–Saffman boundary condition on the equivalent permeability of the spheroidal vug is shown in Fig.8. For larger values of the Beavers–Joseph–Saffman coefficient \(\lambda \), as the streamlines on the interface are semi-continuous, the equivalent permeability of the vug is higher than the case of lower values of \(\lambda \), where a rotation zone appears inside the vug due to the inclination of the streamlines.

Fig. 9
figure 9

Effect of the matrix permeability on the equivalent permeability of a spheroidal vug for \(\lambda =1\)

Full size image

Figure 9 shows that the equivalent permeability of a spheroidal vug located in a higher permeable matrix is less than the equivalent permeability of the same vug placed in a lower permeable matrix. The higher permeable host media reduces the effect of presence of vugs.

Figure 9, illustrates the role of the host matrix permeability on the equivalent permeability of a spheroidal vug. The equivalent permeability of a spheroidal vug placed in a high permeable matrix is less than the equivalent permeability of the same vug placed in a low permeable host matrix. The more permeable the host matrix is the role of the vug is less significant.

5 Effective Permeability of the Matrix Medium Including Spheroidal Vugs

Previously, we substituted the fluid-filled vug with its equivalent porous inclusion having an equivalent permeability, but greater than the permeability of the host matrix. Now, the matrix domain under consideration consists of a set of locally homogeneous porous regions. The effective permeability of the entire nonhomogeneous porous domain is desired.

The effective medium theory provides the effective permeability for a binary medium, where all the inhomogeneities are identical in shape, orientation, size, and physical properties. The effective medium theory is based on analyzing the perturbation of one single inhomogeneity located at the center of porous matrix and superposition of the remaining inhomogeneities effect, assuming they can be considered to be at the center and have no interference with other inhomogeneities.

Three formulas widely used in the field of effective medium theory are the Maxwell formula, the self-consistent (or symmetric Bruggeman) formula and the differential or asymmetric (Bruggeman 1935) formula. The Maxwell formula is widely used of the three equations. The Maxwell formula for the effective permeability of a binary domain including porous spheroidal inclusions is given as

$$\begin{aligned} (k)_\mathrm{eff}=k_\mathrm{m} + \dfrac{\omega ((k_\mathrm{m} )_\mathrm{in}-k_\mathrm{m} )}{1+d_{i}(1-\omega )((k_\mathrm{m} )_\mathrm{in}-k_\mathrm{m} )/k_\mathrm{m} }, \end{aligned}$$
(69)

where \(k_\mathrm{eff}\) is the effective permeability of the entire porous medium, \(\omega \) is the volume fraction of inclusions, \(k_\mathrm{m}\) is the permeability of the host matrix, \((k_\mathrm{m})_\mathrm{in}\) is the equivalent permeability of one inclusion, and \(d_i\) is the depolarization coefficient for a given direction. In general, the Maxwell formula provides reasonable results for isotropic assemblages of nonoverlapping inclusions in binary media.

Another method for determining the effective permeability of a nonhomogeneous porous medium is by upscaling through the direct solution of the steady-state problem. In this method, the equivalent permeability tensor for an arbitrary nonhomogeneous upscaling cell is calculated from the solution of the steady-state flow equation in a domain that corresponds to the upscaling cell itself. The equivalent permeability tensor is computed in such a way that Darcy’s law between the volume averages of the small-scale fluxes and field-scale volumetric fluxes and gradients is satisfied (Rubin and Gómez-Hernández 1990), i.e.,

$$\begin{aligned} -k_\mathrm{eff}=\dfrac{-\langle k\nabla p\rangle }{\langle \nabla p\rangle }, \end{aligned}$$
(70)

where k is the local permeability, and the angular brackets imply the volume integral defined as

$$\begin{aligned} \langle f \rangle =\int _{V}fdv. \end{aligned}$$
(71)

Let us determine the effective permeability of a spherical porous cell of radius \(\rho _1\), including one spherical fluid-filled vug of radius \(\rho _o<\rho _1\) located at the center of a matrix volume. The pressure field \((p_\mathrm{m})_\mathrm{in,s}\) inside the vug’s equivalent spherical porous inclusion and the pressure field \((p_\mathrm{m})_{s}\) outside the spherical vug in the matrix are given in “Appendix 4” in Eqs. 105, 115 as

$$\begin{aligned} (p_\mathrm{m})_{\mathrm{in},\mathrm{s}}= & {} D_\mathrm{in}\rho \cos \theta ,\quad 0\le \rho \le \rho _o,\nonumber \\ (p_\mathrm{m})_{s}= & {} \left( \dfrac{D}{\rho ^2}+|\nabla (p_\mathrm{m})_{\infty }|\right) \cos \theta ,\quad \rho _o\le \rho \le \rho _1, \end{aligned}$$
(72)

where \(D, D_\mathrm{in}\) are coefficients to be determined later. The volume average of the pressure field in the entire domain is expressed as the sum of volume average of pressure in the porous inclusion and in the matrix written as

$$\begin{aligned} \left\langle {\partial p\over \partial x}\right\rangle = \left\langle {\partial (p_\mathrm{m})_{\mathrm{in},\mathrm{s}}\over \partial x}\right\rangle _\mathrm{in}+\left\langle {\partial (p_\mathrm{m})_{s}\over \partial x}\right\rangle _{m}. \end{aligned}$$
(73)

In the spherical coordinates, the volume integral is given by

$$\begin{aligned} \langle f \rangle = \int _0^{2\pi }\int _0^{\pi }\int _0^{\rho _o} f(\rho ,\theta ,\phi )\rho ^2\sin \theta d\rho d\theta d\phi . \end{aligned}$$
(74)

Because \(x=\rho \cos \theta \), the pressure gradient in the x direction is given as

$$\begin{aligned} {\partial (p_\mathrm{m})_{\mathrm{in},\mathrm{s}}\over \partial x}= & {} D_\mathrm{in}, \nonumber \\ {\partial (p_\mathrm{m})_{s}\over \partial x}= & {} \dfrac{\partial (p_\mathrm{m})_{s}}{\partial \rho }\dfrac{1}{\cos \theta }- \dfrac{\partial (p_\mathrm{m})_{s}}{\partial \theta }\dfrac{1}{\rho ^2\sin \theta }=-\dfrac{D}{\rho ^3}+|\nabla (p_\mathrm{m})_{\infty }|. \end{aligned}$$
(75)

Substituting this equation in Eq. 70 and performing the volume average of the steady-state solution yield the effective permeability of the porous volume, including one spherical vug in the center given by

$$\begin{aligned} k_\mathrm{eff}=k_\mathrm{m} +\dfrac{\omega ((k_\mathrm{m} )_{\mathrm{in},\mathrm{s}}-k_\mathrm{m} )}{-\dfrac{\omega ((k_\mathrm{m} )_{\mathrm{in},\mathrm{s}}-k_\mathrm{m} )}{k_\mathrm{m} }\ln \dfrac{\rho _o}{\rho _1}+1+\dfrac{1}{3}\dfrac{(k_\mathrm{m} )_{\mathrm{in},\mathrm{s}}-k_\mathrm{m} }{k_\mathrm{m} }(1-\omega )}, \end{aligned}$$
(76)

with \((k_\mathrm{m} )_{\mathrm{in},\mathrm{s}}\) given in Eq. 118. This equation is equivalent to Maxwell’s formula given in Eq. 69 if \(\dfrac{\rho _o}{\rho _1}\sim 1\). As one can see, using Maxwell’s formula would result in overestimating the effective permeability.

Fig. 10
figure 10

Normalized effective permeability of the porous domain, including spheroidal vugs versus \(\omega \) as vug volume fractions and n as number of vugs

Full size image
Fig. 11
figure 11

Effective permeability of a vuggy porous domain for a fixed-volume fraction of vugs \(\omega =0.0049\) and various aspect ratios versus number of vugs with \(\lambda =1, k_\mathrm{m} =0.001\) mD

Full size image
Fig. 12
figure 12

Effective permeability of a vuggy porous domain with several spheroidal vugs randomly distributed in domain and with random aspect ratios for \(\lambda =1, k_\mathrm{m} =0.001\) mD

Full size image
Fig. 13
figure 13

Example of pressure field for a random distribution of vugs

Full size image

Using the pressure averaging approach for obtaining effective permeability as given in Eq. 70 for a spheroidal vug, one can use the pressure field that has already been obtained in the previous sections to determine the effective permeability. Note that in the spheroidal coordinate system, the volume integral is given as

$$\begin{aligned} \langle f\rangle =\int _0^{2\pi }\int _{-1}^{1}\int _1^{s} f(s,t,\phi )c^3(s^2-t^2) ds~dt~d\phi , \end{aligned}$$
(77)

and

$$\begin{aligned} {\partial f\over \partial x}={\partial f\over \partial s}\dfrac{1}{ct}+{\partial f\over \partial s}\dfrac{1}{cs}. \end{aligned}$$
(78)

Figure 10 shows the normalized effective permeability of porous matrix including spherical and spheroidal vugs with various sizes. It can be seen that Maxwell method results in overestimating the effective permeability. Also, the effective permeability increases as the volume fraction of vugs increases. The elongated vugs result in more effective permeability, for the same volume fraction of vugs.

In Fig. 11, the effective permeability of a vuggy porous domain for a fixed-volume fraction of vugs is plotted vs. various numbers of vugs as well as for various aspect ratios. It can be seen that for the same volume fraction of vugs, the narrower the vugs are, the higher the effective permeability is. One vug enhances effective permeability more than several vugs with the same volume fraction, but the effect of the increase in number of vugs is not very significant. The small fluctuation in the results might be because of numerical error during calculating the volume integral.

The pressure field at the extents of the matrix domain is assumed to be uniform and unperturbed by the presence of the vugs; that is why the spatial position of the vugs has no significant effect on the effective permeability of the ensemble of domain.

The effective permeability of several cases of random distribution and various sizes of spheroidal vugs within a matrix medium is shown in Fig. 12. Overall, we can state that the parameter having the largest impact on the effective permeability is the volume fraction of the vugs. For a fixed-volume fraction, the less the number of vugs is, the higher the effective permeability will be. Examples of pressure field of some of the cases the authors considered are shown in Fig. 13.

6 Conclusions

The analytical solutions for the problem of the axis-symmetric flow of an incompressible fluid in a porous matrix including spherical and spheroidal vugs have been presented. Darcian flow in the matrix was coupled with Stokes flow in the vug through a no-jump condition of normal velocities, jump on pressures, and generalized Beavers–Joseph–Saffman condition, on the interface of the matrix and vug. The generalized form of the Beavers–Joseph–Saffman boundary condition allowed us to consider even very small sizes of vugs. The equivalent permeability of the vug was obtained by substituting it with a porous vug having the same external matrix pressure field. The developed solution reduces to the solution for spherical vugs when the focal length of the spheroid approaches zero.

In general, the equivalent permeability of the vug and the effective permeability of the entire domain are directly proportional to the volume fraction of the vug. The bigger the vugs volume is, the higher the effective permeability of the ensemble of the domain will be. For a fixed spheroidal major axis length, when the aspect ratio (the ratio of major spheroid axis to the minor spheroid axis) approaches one, the spheroid becomes a sphere, the volume fraction increases, and as a result, the equivalent permeability of the vug reaches its maximum. In contrary, for a given volume fraction, the minimum equivalent permeability is related to the minimum (unit) aspect ratio, that is when the vug becomes a sphere. The spatial position of the vugs has negligible effect on the effective permeability of the ensemble domain. Different spatial arrangement of one same set of vugs of various sizes does not change the effective permeability of the medium. This is a result of the regularization conditions at infinity that we imposed on the problem. For a fixed aspect ratio and same total vug volume fraction, increasing the number of vugs can reduce the effective permeability; however, the effect is not very significant. This is somehow a trivial result; a single big vug placed at the center of the porous domain enhances the effective permeability more compared to the case when the same vug volume is divided to smaller vugs spread out in the porous domain. The interaction of the streamlines through the passages between the vugs reduces a little bit the effective permeability. The difference is negligible.