A Single Item Inventory Model with Variable Production Rate and Defective Items

Abstract

In this present work, a single item production–inventory model is considered. The rate of production is considered as variable. Here the production of defective items also considered. Since some defective items are being produced, corresponding to that a damage rate is applied. It is assumed that there is a demand for both defective and non-defective items. Thus, two types of demand have been considered here. It is considered that the production rate is a monotonically decreasing function. An efficiency cost has also been applied to fulfill the customers’ demand. Under these circumstances, a profit function is constructed for the manufacturer. Finally, the proposed model is discussed considering some numerical data.

Introduction

Many mathematical models are developed on inventory of any production system. In any production–inventory system, the product of a firm depends upon the various production factors. These factors are raw material supplies, various costs, number of labours, production facilities, firm size, machine repairs etc. Considering all those factors in mind, there are several research works on production–inventory systems. This type of production–inventory models are evaluated by Economic Production Quantity (EPQ) modelling. This method is the extension of Economic Order Quantity (EOQ) modelling. Economic order quantity (EOQ) is the order quantity that minimizes the total holding costs and ordering costs. It is one of the oldest classical production scheduling models. The framework used to determine this order quantity is also known as Wilson EOQ Model, Wilson Formula or Andler Formula. The model was developed by Harris [1], but R.H. Wilson, a consultant who applied it extensively, and K. Andler are given credit for their in-depth analysis. The extension of this model is EPQ modelling, which is developed by E.W. Taft in 1918. EPQ model depends on demands, selling price and different costs. EPQ model is used when (i) parts of products will be produced and demand is dependent and (ii) compute how much to make at one time (production lot size). Baker and Urban [4] presented a deterministic inventory system with an inventory level dependent demand rate. Mandal and Phaujdar [5] developed an inventory model for deteriorating items and stock dependent consumption rate. Sajadifar and Mavaji [2] introduced an inventory model with demand dependent replenishment rate for damageable item and shortage. Palanivel and Uthayakumar [3] presented a production–inventory model with variable production cost and probabilistic deterioration. Samanta and Roy [6] introduced a production–inventory model with deteriorating items and shortages. El-Gohary et al. [10] introduced a model using optimal control to adjust the production rate of a deteriorating inventory system. Singh and Sharma [7] presented an integrated model with variable production and demand rate under inflation. Mukhopadhyay and Goswami [11] introduced an economic production quantity (EPQ) model for three type imperfect items with rework and learning in setup. Manna et al. established [8] an EOQ model with ramp type demand rate, time dependent deterioration rate, unit production cost and shortages. Teng and Chang [9] presented an economic production quantity models for deteriorating items with price and stock dependent demand. Chiu et al. [12] developed an economic production quantity model with the steady production rate of scrap items. Chiu et al. [12] presented a simplified approach to the multi-item economic production quantity model with scrap, rework, and multi-delivery. Patra and Mondal [13] established a model of risk analysis in a production–inventory model with fuzzy demand, variable production rate and production time dependent selling price. Considering this model without fuzzy demand, in this present work, our aim is to develop a production model with variable production rate including an efficiency cost. In their work they had not considered the defective items in their proposed model. Now in any production system production of a defective item is a common fact. So our aim is to include the effect of defective item in that production system.

The present paper is organized as follows: In section “The Mathematical Model” the notations, assumptions and mathematical formulation of the proposed model has been discussed. In section “Numerical Results and Discussion” the model has been illustrated with numerical results and in section “Conclusion” the conclusion is followed.

The Mathematical Model

Notations

• (i) $D_1$ : customer’s demand rate for good items

• (ii) $D_2$ : customer’s demand rate for defective items

• (iii) $C_0$ : manufacturer’s setup cost

• (iv) K : production rate per unit time

• (v) $I_{1}$ : stock of the production for good items

• (vi) $I_{2}$ : stock of the production for defective items

• (vii) T : total business period

• (viii) p : manufacturer’s selling price per item

• (ix) $\lambda$ : inverse efficiency (decision variable)

• (x) $C_{p_0}$ : production cost per unit item

• (xi) $C_h$ : holding cost per unit item per unit time

• (xii) REV : total revenue

• (xiii) STC : total set up cost

• (xiv) PDC : total production cost

• (xv) EFC : efficiency cost

• (xvi) HDC : total holding cost

• (xvii) TP : total profit

• (xviii) $C_{p_1}$ : rate of efficiency cost

• (xix) $t_1$ : duration of constant production

• (xx) $t_2$ : total production period

• (xxi) $Q_1$ : inventory level at time $t_1$ for good items

• (xxii) $Q_2$ : inventory level at time $t_2$ for good items

• (xxiii) $Q_3$ : inventory level at time $t_2$ for defective items

• (xxiv) $\theta$ : defective rate

Assumptions

Under the following assumptions the proposed production–inventory model has been developed.

• (i) The production system has been considered for a single item.

• (ii) Shortages are not allowed in this proposed inventory model.

• (iii) Defective items are considered with a constant rate $\theta$.

• (iv) The total business period (T) is considered as constant.

• (v) The production rate has been considered as a variable. Initially the production rate will be the constant as all the factors associated with the system are in well and good conditions. With the increase of time there will be some insufficiency in the system so the production gradually decreases. Now there will be shortages in the fulfilment of meeting customers’ demand as the production decreases. No manufacturer wants to face such type of situations so there is a need of increase the efficiencies of all the factors. To increase the efficiencies an extra cost has been included which is known as efficiency cost, denoted by EFC.

• (vi) As the production rate is variable as discussed in the above assumption and the total business period (T) is fixed, then to fulfil the total customers’ demand during the business period T, some efficiencies (E) of different factors in the system must be increased for more production. Considering this fact in the production–inventory system, production rate, K, which is taken as a function of a new variable $\lambda$ known as inverse efficiency, is proposed as follows:

  $$\begin{aligned} K=\left\{ \begin{array}{ll} K_0,&{}\text{ for }\quad \,0\le t\le t_1 \nonumber \\ K_0e^{-\lambda (t-t_1)},&{} \text{ for } \quad t_1\le t\le t_2 \end{array} \right. \end{aligned}$$

  where $\lambda =\frac{1}{E}$.

• (vii) The production will be stopped after a certain time $t_2$ in such a way that the system gives the optimum profit satisfying the customer’s total demand during the business period.

• (viii) In this paper, the selling price of a good quality item as well as defective quality item is considered as constant.

• (ix) The demand of good quality item ($D_1$) and defective quality item ($D_2$) has been considered also as constant.

Mathematical Formulation of the Proposed System

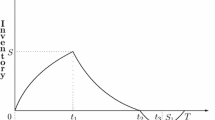
A production system produced a single item which starts at the time $t=0$. Initially its production rate is constant $K_0$. This rate of production is continued upto the time $t_1$. At that time the inventory level of good quality item reaches $Q_1$. Then the production rate K decreases as per the assumption (vi) and the production stops at the time $t_2$. Therefore, the inventory built up during the period $[0,t_2]$ achieving the customers’ demand $D_1$ and during the period $[t_2,T]$ the inventory is gradually declined and it depletes at the end of business period $t=T$ due to customers’ consumption. Now, let $I_1(t)$ be the inventory level of good quality item at any time t. In this proposed system the differential equation of $I_1(t)$ according to the assumptions described above, can be expressed mathematically as follows:

$$\begin{aligned} \frac{dI_1(t)}{dt}=\left\{ \begin{array}{lll} K_0-D_1-\theta &{} \text{ when } \quad 0\le t\le t_1\\ K_0e^{-\lambda (t-t_1)}-D_1-\theta &{} \text{ when } \quad t_1\le t\le t_2 \\ -D_1 &{} \text{ when } \quad t_2\le t\le T \end{array} \right. \end{aligned}$$

(1)

with the boundary conditions

$$\begin{aligned} I_1(0) =0,\,\, I_1(t_1)=Q_1,\,\, I_1(t_2)=Q_2,\,\, I_1(T)=0 \end{aligned}$$

(2)

Here it is considered that the defective quality items also have some demand. Since there is the production upto time time $t_2$ and the production rate of defective quality item is $\theta$ so its inventory built at time $t_2$ is $Q_3$. After then the inventory gradually declines upto time T and finished at time T. Now, if $I_2(t)$ be the inventory level of defective quality item at the time t in such a system then the differential equation of $I_2(t)$ according to the assumptions described above, can be expressed mathematically as follows:

$$\begin{aligned} \frac{dI_2(t)}{dt}=\left\{ \begin{array}{ll} \displaystyle \theta -D_2 &{} \text{ when } \quad 0\le t\le t_2\\ -D_2 &{} \text{ when } \quad t_2\le t\le T \end{array} \right. \end{aligned}$$

(3)

with the boundary conditions

$$\begin{aligned} I_2(0) =0,\,\, I_2(t_2)=Q_3,\,\, I_2(T)=0 \end{aligned}$$

(4)

A graphical representation of this inventory system is depicted in Fig. 1.

Fig. 1

Graphical representation of the proposed model

Now, integrating the differential Eq. (1) for the interval [0, t] where $t\in [0,t_1]$ it is obtained that

$$\begin{aligned}&\int _{0}^{t}dI_1=\int _{0}^{t}(K_0-D_1-\theta )dt\nonumber \\&\quad {or},\quad I_1(t)-I_1(0)=(K_0-D_1-\theta )t\mid _{0}^{t}\\&\quad or,\quad I_1(t)=(K_0-D_1-\theta )t\nonumber \end{aligned}$$

(5)

Using boundary condition $I(t_1)=Q_1$ we have,

$$\begin{aligned} Q_1=(K_0-D_1-\theta )t_1 \end{aligned}$$

(6)

Again, integrating the differential Eq. (1) for the interval $[t_1,t]$ where $t\in [t_1,t_2]$ it is obtained that

$$\begin{aligned}&\int _{t_1}^{t}dI_1=\int _{t_1}^{t}(K_0e^{-\lambda (t-t_1)}-D_1-\theta )dt\nonumber \\&\quad or,\quad I_1(t)-I_1(t_1)=\left[ -\frac{K_0e^{\lambda t_1}}{\lambda }e^{-\lambda t}-D_1t-t\theta \right] \mid _{t_1}^{t}\nonumber \\&\quad or,\quad I_1(t)=Q_1-\frac{K_0e^{\lambda t_1}}{\lambda }(e^{-\lambda t}-e^{-\lambda t_1})-D_1(t-t_1)-\theta (t-t_1) \end{aligned}$$

(7)

Using boundary condition $I_1(t_2)=Q_2$ we have,

$$\begin{aligned} Q_2=Q_1-\frac{K_0e^{\lambda t_1}}{\lambda }(e^{-\lambda t_2}-e^{-\lambda t_1})-D_1(t_2-t_1)-\theta (t_2-t_1) \end{aligned}$$

(8)

Also, integrating the differential Eq. (1) for the interval $[t_2,t]$ where $t\in [t_2,T]$ it is obtained that

$$\begin{aligned}&\int _{t_2}^{t}dI_1=\int _{t_2}^{t}-D_1dt\nonumber \\&\quad or,\quad I_1(t)-I_1(t_2)=-D_1(t-t_2)\nonumber \\&\quad or,\quad I_1(t)=Q_2-D_1(t-t_2) \end{aligned}$$

(9)

Using boundary condition $I(T)=0$ we have,

$$\begin{aligned} Q_2-D_1(T-t_2)=0 \end{aligned}$$

(10)

Now, integrating the differential Eq. (3) for the interval [0, t] where $t\in [0,t_2]$ it is obtained that

$$\begin{aligned}&\int _{0}^{t}dI_2=\int _{0}^{t}(\theta -D_2)dt\nonumber \\&\quad or,I_2(t)-I_2(0)=(\theta -D_2)t\mid _{0}^{t}\nonumber \\&\quad or,I_2(t)=(\theta -D_2)t \end{aligned}$$

(11)

Using boundary condition $I_2(t_2)=Q_3$ we have,

$$\begin{aligned} Q_3=(\theta -D_2)t_2 \end{aligned}$$

(12)

Also, integrating the differential Eq. (3) for the interval $[t_2,t]$ where $t\in [t_2,T]$ it is obtained that

$$\begin{aligned}&\int _{t_2}^{t}dI_2=\int _{t_2}^{t}-D_2dt\nonumber \\&\quad or,I_2(t)-I_2(t_2)=-D_2(t-t_2)\nonumber \\&\quad or,I_2(t)=Q_3-D_2(t-t_2) \end{aligned}$$

(13)

Using boundary condition $I(T)=0$ we have,

$$\begin{aligned} Q_3-D_2(T-t_2)=0 \end{aligned}$$

(14)

Now the different costs associated with the proposed production–inventory system are production cost (PDC), setup cost (STC), holding cost (HDC) and efficiency cost (EFC). All these cost are calculated as follows.

Total production cost PDC is given by

$$\begin{aligned} PDC= & {} C_{p_0}\left[ \int _{0}^{t_1}K_0dt+\int _{t_1}^{t_2}K_0e^{-\lambda (t-t_1)}\right] \nonumber \\= & {} C_{p_0}\left[ K_0t_1-\frac{K_0(e^{\lambda (t_1-t_2)}-1)}{\lambda }\right] \end{aligned}$$

(15)

Total holding cost HDC is obtained as follows

$$\begin{aligned}&HDC=C_h\left[ \int _{0}^{T}I_1(t)dt+\int _{0}^{T}I_2(t)dt\right] \nonumber \\&\quad =C_h\left[ \int _{0}^{t_1}(K_0-D_1-\theta )t dt\right. \nonumber \\&\qquad +\int _{t_1}^{t_2}\left\{ Q_1-\frac{K_0e^{\lambda t_1}}{\lambda }e^{-\lambda t}+\frac{K_0}{\lambda }-D_1(t-t_1)-\theta (t-t_1)\right\} dt\nonumber \\&\qquad \left. +\int _{t_2}^{T}\{Q_2-D_1(t-t_2)\}dt+\int _{0}^{t_2}(\theta -D_2)tdt+\int _{t_2}^{T}\{Q_3-D_2(t-t_2)\}dt\right] \nonumber \\&\quad =C_h\left[ \frac{K_0T}{\lambda }-\frac{K_0(e^{\lambda (t_1-t_2)}T}{\lambda }-\frac{D_1T^2}{2}-\frac{D_2T^2}{2}\right. \nonumber \\&\qquad +K_0Tt_1-\frac{D_1t_1^2}{2}+\frac{K_0t_1^2}{2}-\frac{K_0t_2}{\lambda }+\frac{e^{\lambda (t_1-t_2)}K_0t_2}{\lambda }-K_0t_1t_2+\frac{D_1t_2^2}{2}\nonumber \\&\qquad \left. +\frac{t_2^2\theta }{2}+\frac{2K_0(e^{\lambda (t_1-t_2)}-1-(1+t_1\lambda )(t_1-t_2)\lambda +(t_1-t_2)(t_1+t_2)(D_1+\theta )\lambda ^2)}{2\lambda ^2}\right] \nonumber \\ \end{aligned}$$

(16)

Total setup cost STC is given by the following

$$\begin{aligned} STC=C_{0} \end{aligned}$$

(17)

and the Efficiency cost EFC is calculated as follows

$$\begin{aligned} EFC= & {} C_{p_1}\int _{t_1}^{t_2}K_0e^{-\lambda (t-t_1)}dt\nonumber \\= & {} \frac{C_{p_1}K_0e^{\lambda t_1}}{\lambda }(e^{-\lambda t_1}-e^{-\lambda t_2}) \end{aligned}$$

(18)

Now the total Revenue REV, obtained by selling good items to the customers at the rate of $p_0$ per item and by selling damage items to the customers at the rate of $p_1$ per item is given by

$$\begin{aligned} REV= & {} \int _{0}^{t_1}(K_0-\theta )p_0dt+\int _{t_1}^{t_2}\{K_0e^{-\lambda (t-t_1)}-\theta \}p_0dt+\int _{0}^{t_2}p_1\theta dt\nonumber \\= & {} (K_0-\theta )p_0t_1+(K_0p_0)e^{\lambda t_1}\int _{t_1}^{t_2}e^{-\lambda t}dt-\int _{t_1}^{t_2}(p_0\theta ) dt+p_1t_2\theta \nonumber \\= & {} (K_0-\theta )p_0t_1-\frac{(K_0p_0)e^{\lambda t_1}}{\lambda }(e^{-\lambda t_2}-e^{-\lambda t_1})-p_0(t_2-t_1)\theta +p_1t_2\theta \nonumber \\ \end{aligned}$$

(19)

Therefore for any demands $D_1$ and $D_2$ the total profit TP in the production–inventory system is given by

$$\begin{aligned}&TP(\lambda ,t_2)=REV-PDC-STC-HDC-EFC\nonumber \\&i.e,TP(\lambda ,t_2)=(K_0-\theta )p_0t_1-\frac{(K_0p_0)e^{\lambda t_1}}{\lambda }(e^{-\lambda t_2}-e^{-\lambda t_1})-p_0(t_2-t_1)\theta +p_1t_2\theta \nonumber \\&\quad -\,C_{p_0}\left[ K_0t_1-\frac{K_0(e^{\lambda (t_1-t_2)}{-}1)}{\lambda }\right] {-}C_{0}-C_h\left[ \frac{K_0T}{\lambda }-\frac{K_0(e^{\lambda (t_1-t_2)}T}{\lambda }-\frac{D_1T^2}{2}-\frac{D_2T^2}{2}\right. \nonumber \\&\quad +\,K_0Tt_1-\frac{D_1t_1^2}{2}+\frac{K_0t_1^2}{2}-\frac{K_0t_2}{\lambda }+\frac{e^{\lambda (t_1-t_2)}K_0t_2}{\lambda }-K_0t_1t_2+\frac{D_1t_2^2}{2}\nonumber \\&\quad \left. +\,\frac{t_2^2\theta }{2}+\frac{2K_0(e^{\lambda (t_1-t_2)}-1-(1+t_1\lambda )(t_1-t_2)\lambda +(t_1-t_2)(t_1+t_2)(D_1+\theta )\lambda ^2)}{2\lambda ^2}\right] \nonumber \\&\quad -\,\frac{C_{p_1}K_0e^{\lambda t_1}}{\lambda }(e^{-\lambda t_1}-e^{-\lambda t_2}) \end{aligned}$$

(20)

which is the required deterministic profit function for deterministic demand $D_1$ and $D_2$. Our aim is to find the maximum profit for the manufacturer. The function is highly non linear so the problem has been discussed numerically in the next section.

Numerical Results and Discussion

The proposed model has been discussed with some numerical results. For this purpose some initial values are taken as follows:

$K_0=200; p_0=30; p_1=25; C_{P_0}=20; C_{P_1}=5;T=1; C_0=90; C_h=5; t_1=0.2; D_1=100; D_2=35; \theta =45;$

Considering these initial values it is seen that the maximum profit for the proposed model is 558.8 where the inverse efficiency is 0.7017 and production stop time is 0.777.

Now, a sensitivity analysis has been considered with different demands of the good quality items as well as defective quality items. Firstly the demand of the defective quality items are considered as constant and the demand of the good quality items are different. The other initial conditions are given as follows and the results has been shown in Table 1.

$K_0=200; p_0=30; p_1=25; C_{P_0}=20; C_{P_1}=5;T=1; C_0=90; C_h=5; t_1=0.2; D_2=35; \theta =45;$

Table 1 Maximum profit corresponding to different demand of $D_1$

Now from Table 1 it is observed that for the different demands of $D_1$ between 100 and 110, the total maximum profits in the system lie between 558.8 and 621.7. which is gradually increasing with the increase of demand of the good item and which is obvious with real life phenomenon. The graphical representation is given in Fig. 2.

Fig. 2

Change of profit with change of demand of good items

Now, the demand of the good quality items are considered as constant and the demand of the defective quality items are different. The other initial conditions are given as follows and the results has been shown in Table 2.

$K_0=200; p_0=30; p_1=25; C_{P_0}=20; C_{P_1}=5;T=1; C_0=90; C_h=5; t_1=0.2; D_1=100; \theta =45;$

Table 2 Maximum profit corresponding to different demand of $D_2$

Fig. 3

Change of profit with change of demand of defective items

Table 3 Maximum profit corresponding to different demand of $D_1$ and $D_2$

Now from Table 2 it is observed that for the different demands of $D_2$ between 35 and 45, the total maximum profits in the system lie between 558.8 and 514.5. Which is gradually decreasing with the increase of demand of the defective items and which is also obvious with real life phenomenon. The graphical representation is given in Fig. 3.

Also, let, $K_0=1000; p_0=30; p_1=25; C_{P_0}=20; D1=500; D2=200; C_{P_1}=5;T=1; C_0=90; C_h=5; t_1=0.2; \theta =250;$

Considering these initial values it is seen that the maximum profit for the proposed model is 3192.8 where the inverse efficiency is 0.6273 and production stop time is 0.8000.

Now a sensitivity analysis also has been shown for different demand of good quality item as well as defective quality item for the proposed production–inventory system considering the other initial values are same as given above, which are given by Table 3.

Now from Table 3 it is observed that for the different demands of $D_1$ between 500 to 510 and $D_2$ between 200 to 210, the total maximum profits in the system lie between 3192.8 and 3264.6, which is gradually increasing with the increase of demand of the good items the defective items and which is obvious with real life phenomenon. The graphical representation is given in Fig. 4.

Fig. 4

Change of profit with change of demand of good items and defective items

Conclusion

In this present paper, a single item production–inventory model has been presented. Instead of constant production rate a variable production rate has been considered. Due to some fault in the system, the production of defective items are common. So the production of defective items have been introduced here. It is also considered that good quality item as well as defective quality item has some demand. An efficiency cost also has been included to fulfil the customers’ demand. Considering all those phenomenon the profit function has been maximized for the manufacturer with some numerical results.