Inventory system with defective products and investment opportunity for reducing defective proportion

Abstract

This paper proposes a production-inventory model with defective items. The model incorporates additional investment opportunity on quality improvement for reducing the proportion of defective products. Defective proportion depends upon production rate and the amount of this additional investment on quality improvement. Shortages are allowed and are fully backlogged. Only a random proportion of defective items can be resold at a highly discounted price and rest are to be disposed. Demand rate is assumed to be dependent on selling price. Unit cost is assumed to be a decreasing function of production rate. Profit maximization criterion is used to develop the model. The model jointly determines the optimum values of additional investment, selling price, production rate, production cycle, and production period. Concavity of the expected average net profit is proved. An iteration-based simple algorithm is provided to solve the developed model. The model is illustrated by a numerical example. A sensitivity analysis has been performed.

1 Introduction

Traditional inventory models assume that all the items produced through a production process are of good quality/perfect. But in many manufacturing systems this assumption is not valid as some defective items often exist due to the imperfect production process. The proportion of defectives depends upon several factors, such as: quality of raw materials, skills of operators, proper maintenance, use of advance technology in the production system etc. Many researchers have made significant efforts to analyze inventory systems with defective products and imperfect production processes under various realistic situations. The first contributions which addressed the situation of imperfect production process are by Porteas (1986) and Rosenblatt and Lee (1986). Porteas (1986) analyzed a manufacturing system where the process shifts to an ‘out of control’ state at random with a given probability each time another unit is produced. Rosenblatt and Lee (1986) developed an inventory model assuming that the time between ‘in control’ and ‘out of control’ states is random and exponentially distributed. The system produces defective product during ‘out of control’ state. These defective items can be reworked with an additional cost. Their contributions encouraged many other researchers to investigate production systems with defective product. Kim and Hong (1999) generalized the model of Rosenblatt and Lee (1986) assuming arbitrary distribution of elapsed time until the process shifts. Their model does not consider shortages. Chung and Hou (2003) extended the work of Kim and Hong (1999) by incorporating shortages. Salameh and Jaber (2000) studied a joint lot sizing and inspection policy EOQ model where a random proportion of units produced are defective. Many other researchers have contributed significantly in this field of research (e.g. Hayek and Salameh 2001; Goyal and Cardenas-Barron 2002; Chiu 2003; Papachristos and Konstantaras 2006; Eroglu and Ozdemir 2007; Wee et al. 2007; Lo et al. 2007; Ben-Daya et al. 2008; Mondal et al. 2009; Sana 2010; Datta 2010; Khan et al. 2011; Datta 2013; Hsu and Hsu 2013; Uthayakumar and Palanivel 2014; Sarkar et al. 2014; Dey and Giri 2014; Sivashankari and Panayappan 2014; Lai et al. 2015; Mandal and Giri 2015). Their models addressed various realistic situations with imperfect product/process. Recently, Lai et al. (2015) developed an inventory system where they incorporated a quality improvement cost to reduce the defective proportion. They studied a two-echelon inventory system. Their model assumes a constant production rate of the vendor and a constant demand rate of the buyer. Their model does not consider shortages. Mandal and Giri (2015) developed a model with investment opportunity for quality improvement. Their model assumes constant production rate. Datta (2010)’s model assumes that the defective fraction is an increasing function and unit cost is a decreasing function of production rate. He assumes the production rate can be set at any level within machine limits. His model does not consider shortages. Quality improvement investment opportunity is also not incorporated in his model. Mondal et al. (2009) studied an inventory system with advertisement cost and selling price dependent demand rate, variable production rate. They assume that the defective proportion increases with production rate. They developed the model without incorporating investment opportunity on quality improvement and without shortages. Datta (2013) developed an inventory system with quality and price dependent demand rate where a proportion of items produced are defective. He assumed that only a fraction of defective items are repairable.

In this paper, the author proposes a generalized production-inventory model with the following features:

• (a) production rate can be set at any level within machine limits;

• (b) additional investment opportunity on quality improvement is available for reducing defective proportion;

• (c) defective fraction depends on production rate and on the additional investment amount for quality improvement;

• (d) demand rate is a decreasing function of selling price;

• (e) unit cost is a decreasing function of production rate;

• (f) a random proportion of defective items can be sold at highly discounted price and the rest will be disposed.

To justify the importance of the proposed model, a comparison of this model with some of the related published works is shown in Table 1.

Table 1 Comparison of the present model with some of the related published works

The proposed model jointly determines the optimum values of production rate, selling price, additional investment amount, production cycle, production period which maximize the expected value of average net profit per unit time. Concavity of expected average net profit is proved. A user-friendly solution algorithm is provided. The model is illustrated by a numerical example. A sensitivity analysis has been performed.

2 Assumptions and notations

2.1 Assumptions

• (a) Time horizon is infinite.

• (b) Lead time is negligible.

• (c) Demand rate is assumed to be a linearly decreasing function of the selling price.

• (d) Production rate is finite and can be set at a particular level within the specified limits of the production system.

• (e) Unit cost is a decreasing function of production rate. This assumption is true because of the known fact that mass production reduces unit cost.

• (f) A fraction of items produced are defective. This fraction is an increasing function of production rate and can be reduced by investing on advanced technology, better quality raw materials, providing training to operators for improving efficiency etc. Quality improvement initiative may require some initial activities, like inspection/quality testing of raw materials, inviting quotation for modernising the production process. The cost involved in inspection, inviting quotation etc. does not depend upon the lot size. It incurs a fixed cost in a production run which is analogous to setup/ordering cost. Hence, a part of this additional investment is constant. The other part of investment is dependent part which is proportional to the production quantity. Investment on raw materials, labor cost etc. come under this dependent part. The fraction of defective items is a decreasing function of the dependent part of this additional investment. This model assumes that the fraction of defective items depends negative exponentially on the dependent part of additional investment.

• (g) The system has an automated inspection system which will inspect each produced unit whether it is perfect or defective, and then defective items will be immediately separated.

• (h) Defective units are not repairable. A random fraction of defective items are having minor defects which can be sold at a highly discounted price and will generate salvage value. The remaining defective items with major defects will be disposed. Selling of the items with minor defects and disposing off the items with major defects are outsourced to a third party service provider. The third party service provider takes care of stocking and selling/disposing of defective items. The manufacture pays some amount to the third party per unit disposed (disposal cost) for its service. The third party pays the manufacturer some amount (salvage value for manufacturer) for each item with minor defects.

• (i) Shortages are permitted and are fully backlogged.

2.2 Notations

• s: selling price of each unit of perfect product (a decision variable);

• $D(s){:}$ demand rate, taken in the linear form, $D(s) = \beta - ks$ where $\beta ,k > 0$ and $s < \frac{\beta }{k}$.

• P: production rate (a decision variable), which is flexible and can be set at any level in $P_{\hbox{min} } \le P \le P_{\hbox{max} }$ where $P_{\hbox{min} }$ and $P_{\hbox{max} }$ are the minimum and maximum limits respectively;

• x: the random fraction of defective products with minor defects which can be sold at discounted price $(0 \le x \le 1)$;

• $g(x){:}$ probability density function of x;

• $E(x){:}$ expectation of x;

• $C_{u} (P){:}$ unit cost for producing one unit of the item where $C_{u} (P) = m + \frac{n}{P}$ as in Datta (2010), $m,n > 0$;

• $C_{h}$: holding cost per unit per unit time;

• $C_{s}$: shortage cost per unit per unit time;

• $C_{d}$: disposal cost per unit for disposing defective items with major defect;

• $C_{v}$: salvage value generated from each unit of sold defective items with minor defect;

• $C_{1}$: setup cost per production run;

• $z$: constant part of additional investment for reducing defective rate;

• $w_{m}$: maximum amount of additional investment of dependent part which can be invested for each unit of production (a decision variable);

• $w$: actual investment amount of dependent part per unit of production ($0 \le w \le w_{m}$), a decision variable;

• $f(P,w){:}$ fraction(proportion) of defective items produced, where $f(P,w) = k_{1} \exp ( - vw)P^{{k_{2} }}$, $v > 0$ is a shape parameter and $k_{1} ,k_{2} \in (0,1)$ (v, k ₁ and k ₂ are constants);

• $C_{0} {:}$ sum of setup cost and constant part of additional investment. It can be expressed as $C_{0} = C_{1} + z\,.\,H(w)$ where $H(w)$ is unit step function defined by $H(w) = \left\{ {\begin{array}{*{20}c} {0\quad {\text{for}}\;w \le 0} \\ {1\quad {\text{for}}\;w > 0} \\ \end{array} } \right.$.

• If no investment is made on quality improvement for reducing defective rate, then $w = 0$ and $C_{0} = C_{1}$;

• $t_{1}$: time at which initial backlog is cleared;

• $t_{2}$: time at which the production stops;

• $t_{3}$: time at which shortages start to accumulate;

• T: length of the production cycle;

• $S_{1} {:}$ maximum backorder quantity;

• $S_{2} {:}$ maximum inventory level;

• $A = (1 - f)P$: rate of production of perfect items, $A - D(s) > 0$;

• $Pf$: rate of production of defective items;

• $I(t)$: stock (inventory) level for perfect(good) items at time t;

• ANR: average net revenue per unit time in a production cycle;

• $\varPi (S{}_{1},S_{2} ,s,P,w)$: Expected value of ANR;

• $\varPi_{(.)} {:}$ partial derivative of $\varPi$ with respect to (.).

3 Mathematical formulation

The system consists of identical production cycles over infinite time horizon. One of such cycles is chosen for analysis. Cycle starts at $t = 0$ when production starts and ends at $t = T$ when the production of next cycle starts. It is assumed that each cycle starts with previous cycle’s backlog and end with backlog of same quantity. Ending backlog is cleared in the next production cycle.

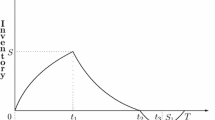
A graphical representation of the system for perfect items is shown in Fig. 1.

Fig. 1

Pictorial representation of the system for perfect items

Production starts at $t = 0$ with initial inventory level $- S_{1}$. Here $S_{1}$ is the previous cycle’s backorder quantity. Inventory level gradually increases at the rate of $A - D(s)$ per unit time from its initial level $- S_{1} .$ Backlog is completely cleared at time $t = t_{1}$ when the sock level reaches zero level. During $[t_{1} ,t_{2} ]$ stock level increases at the same rate $A - D(s)$ and reaches the level $S_{2}$ at $t = t_{2} .$ Production stops at time $t = t_{2} .$ From time $t = t_{2}$, till the end of the cycle, stock level depletes due to demand at the rate $D(s)$ per unit time, and reaches zero level at time $t = t_{3} .$ Backlogged shortages start to accumulate from time $t = t_{3}$ and continue till the end of the cycle $t = T$. The accumulated backorder quantity at $t = T$ is $S_{1} .$ This backlog quantity will be cleared in the next cycle.

The differential equations which represent the proposed system are:

$$\frac{dI(t)}{dt} = \left\{ {\begin{array}{*{20}l} {A - D(s)} \hfill & {0 \le t \le t_{2} } \hfill \\ { - D(s)} \hfill & {t_{2} \le t \le T} \hfill \\ \end{array} } \right.$$

(1)

with the boundary conditions $I(0) = - S_{1} ,\;I(t_{1} ) = 0,\;I(t_{2} ) = S_{2} ,\;I(t_{3} ) = 0\;{\text{and}}\;I(T) = - S_{1} .$

Using the conditions $I(0) = - S_{1} \;{\text{and}}\;I(t_{2} ) = S_{2} ,$ the solutions of the system of Eqs. (1) are obtained as:

$$I(t) = \{ A - D(s)\} t - S_{1} ,\;\;0 \le t \le t_{2}$$

(2)

$$I(t) = S_{2} - D(s)(t - t_{2} ),\;\;t_{2} \le t \le T$$

(3)

Using $I(t_{1} ) = 0\;{\text{and}}\;I(t_{2} ) = S_{2}$ in Eq. (2), we get

$$t_{1} = \frac{{S_{1} }}{A - D(s)}\quad {\text{and}}\quad t_{2} = \frac{{S_{1} + S_{2} }}{A - D(s)}$$

(4)

Using $I(t_{3} ) = 0\quad {\text{and}}\quad I(T) = - S_{1}$ in Eq. (3), we get

$$t_{3} = t_{2} + \frac{{S_{2} }}{D(s)} = \frac{{S_{1} D(s) + AS_{2} }}{{\{ A - D(s)\} D(s)}}\quad {\text{and}}\quad T = t_{2} + \frac{{S_{1} + S_{2} }}{D(s)} = \frac{{A(S_{1} + S_{2} )}}{{\{ A - D(s)\} D(s)}}$$

(5)

3.1 Cost calculation during the cycle $0 \le t \le T$

$${\text{Setup cost }} = C_{1} ;$$

$${\text{Unit cost }} = C_{u} (P)Pt_{2} = \frac{{C_{u} (P)(S_{1} + S_{2} )P}}{A - D(s)};$$

$$\begin{aligned} & {\text{Additional cost}}\left( {\text{amount invested}} \right){\text{ on quality improvement to reduce defective rate}} \\ & \quad = z\,.\,H(w) + Pwt_{2} = z\,.\,H(w) + \frac{{(S_{1} + S_{2} )wP}}{A - D(s)}; \\ \end{aligned}$$

$${\text{Disposal cost }} = (1 - x)C_{d} f(P,w)Pt_{2} = \frac{{(1 - x)C_{d} f(P,w)(S_{1} + S_{2} )P}}{A - D(s)};$$

$${\text{Salvage value }} = xC_{v} f(P,w)Pt_{2} = \frac{{xC_{v} f(P,w)(S_{1} + S_{2} )P}}{A - D(s)};$$

$${\text{Holding cost }} = C_{h} \left\{ {\int_{{t_{1} }}^{{t_{3} }} {I(t)dt} } \right\} = \frac{{C_{h} AS_{2}^{2} }}{{2\{ A - D(s)\} D(s)}};$$

$${\text{Shortage cost }} = - C_{s} \left\{ {\int_{0}^{{t_{1} }} {I(t)dt} + \int_{{t_{3} }}^{T} {I(t)dt} } \right\} = \frac{{C_{s} AS_{1}^{2} }}{{2\{ A - D(s)\} D(s)}};$$

$${\text{Gross revenue by selling the perfect items }} = At_{2} s = \frac{{As(S_{1} + S_{2} )}}{A - D(s)}.$$

Hence the average net revenue per unit time is

$$\begin{aligned} ANR(S_{1} ,S_{2} ,s,w,P;x) = & \frac{1}{T}({\text{Gross revenue}} + {\text{salvage value}} - {\text{setup cost}} - {\text{unit cost}} - {\text{additional cost}} \\&- {\text{unit cost}} - {\text{additional cost}}\\ & - {\text{disposal cost}} - {\text{holding cost}} - {\text{shartages cost)}} \\ = &\, sD(s) - \frac{{\{ C_{u} (P) + w + ((1 - x)C_{d} - xC_{v} )f(P,w)\} PD(s)}}{A} \\ & - \frac{{AC_{h} S_{2}^{2} + AC_{s} S_{1}^{2} + 2C_{0} D(s)\{ A - D(s)\} }}{{2A(S_{1} + S_{2} )}} \\ \end{aligned}$$

Expected value of the average net revenue ANR is:

$$\begin{aligned} \varPi (S_{1} ,S_{2} ,s,w,P) = & \int_{0}^{1} {ANR(S_{1} ,S_{2} ,s,w,P;x)} \,g(x)dx \\ = &\, sD(s) - \frac{{\{ C_{u} (P) + w + ((1 - E(x))C_{d} - E(x)C_{v} )f(P,w)\} PD(s)}}{A} \\ & - \frac{{AC_{h} S_{2}^{2} + AC_{s} S_{1}^{2} + 2C_{0} D(s)\{ A - D(s)\} }}{{2A(S_{1} + S_{2} )}} \\ \end{aligned}$$

(6)

Theorem 1

For a given set of values of $s,w\,\,{\text{and}}\,\,P$, $\varPi$ is strictly concave in the variables $S{}_{1}{\text{ and }}S_{2} .$

Proof

From Eq. (6), we obtain

$$\varPi_{{S_{1} }} = \frac{{ - AC_{s} S_{1}^{2} - 2AC_{s} S_{1} S_{2} + AC_{h} S_{2}^{2} + 2C_{0} \{ A - D(s)\} D(s)}}{{2A(S_{1} + S_{2} )^{2} }};$$

(7)

$$\varPi_{{S_{2} }} = \frac{{ - AC_{h} S_{2}^{2} - 2AC_{h} S_{1} S_{2} + AC_{s} S_{1}^{2} + 2C_{0} \{ A - D(s)\} D(s)}}{{2A(S_{1} + S_{2} )^{2} }};$$

(8)

$$\varPi_{{S_{1} S_{1} }} = - \frac{{A(C_{h} + C_{s} )S_{2}^{2} + 2C_{0} \{ A - D(s)\} D(s)}}{{A(S_{1} + S_{2} )^{3} }} < 0;$$

(9)

$$\varPi_{{S_{2} S_{2} }} = - \frac{{A(C_{h} + C_{s} )S_{1}^{2} + 2C_{0} \{ A - D(s)\} D(s)}}{{A(S_{1} + S_{2} )^{3} }} < 0;$$

$$\varPi_{{S_{1} S_{2} }} = \frac{{A(C_{h} + C_{s} )S_{1} S_{2} - 2C_{0} \{ A - D(s)\} D(s)}}{{A(S_{1} + S_{2} )^{3} }}.$$

Hence,

$$\varPi_{{S_{1} S_{1} }} .\varPi_{{S_{2} S_{2} }} - \varPi_{{S_{1} S_{2} }}^{2} = \frac{{2C_{0} \{ A - D(s)\} D(s)(C_{h} + C_{s} )}}{{A(S_{1} + S_{2} )^{4} }}\; > 0.$$

(10)

$\varPi_{{S_{1} S_{1} }} \, < 0,\varPi_{{S_{2} S_{2} }} < 0{\text{ and }}\varPi_{{S_{1} S_{1} }} \varPi_{{S_{2} S_{2} }} - \varPi_{{S_{1} S_{2} }}^{2} > 0$ imply that $\varPi$ is strictly concave in $S{}_{1}{\text{ and }}S_{2} .$□

Theorem 2

For a given set of values of $w\;{\text{and}}\;P$, $\varPi$ is concave in the variables $s,S{}_{1}{\text{and}}\,S_{2}$ , provided $S{}_{1} + S_{2} > \frac{{C_{0} kA}}{{4\{ A - D(s)\} D(s)}}.$

Proof

From Eq. (6), we obtain

$$\varPi_{s} = \beta - 2ks + \{ C_{u} (P) + w + ((1 - E(x))C_{d} - E(x)C_{v} )f(P,w)\} .\frac{kP}{A} - \frac{{C_{0} k}}{{A(S_{1} + S_{2} )}}(2\beta - A - 2ks);$$

(11)

$$\varPi_{ss} = - 2k + \frac{{2k^{2} C_{0} }}{{A(S_{1} + S_{2} )}} = - 2k\left( {1 - \frac{{C_{0} k}}{{A(S_{1} + S_{2} )}}} \right)$$

(12)

$$\varPi_{{S_{1} s}} = \varPi_{{S_{2} s}} = \frac{{C_{0} k\{ - A + 2D(s)\} }}{{A(S_{1} + S_{2} )^{2} }}.$$

Hessian matrix is:

$$H = \left( {\begin{array}{*{20}c} {\varPi_{{S_{1} S_{1} }} } & {\varPi_{{S_{1} S_{2} }} } & {\varPi_{{S_{1} s}} } \\ {\varPi_{{S_{2} S_{1} }} } & {\varPi_{{S_{2} S_{2} }} } & {\varPi_{{S_{2} s}} } \\ {\varPi_{{sS_{1} }} } & {\varPi_{{sS_{2} }} } & {\varPi_{ss} } \\ \end{array} } \right)$$

If the hessian H is negative definite, then $\varPi$ is strictly concave in $s,S{}_{1}{\text{and}}\,S_{2}$.

Let $M_{1} ,M_{2} ,M_{3}$ be leading principal minors of H. Then,

$$M_{1} = (\varPi_{{S_{1} S_{1} }} ),\;M_{2} = \left( {\begin{array}{*{20}c} {\varPi_{{S_{1} S_{1} }} } & {\varPi_{{S_{1} S_{2} }} } \\ {\varPi_{{S_{1} S_{2} }} } & {\varPi_{{S_{2} S_{2} }} } \\ \end{array} } \right)\quad {\text{and}}\quad M_{3} = \left( {\begin{array}{*{20}c} {\varPi_{{S_{1} S_{1} }} } & {\varPi_{{S_{1} S_{2} }} } & {\varPi_{{S_{1} s}} } \\ {\varPi_{{S_{2} S_{1} }} } & {\varPi_{{S_{2} S_{2} }} } & {\varPi_{{S_{2} s}} } \\ {\varPi_{{sS_{1} }} } & {\varPi_{{sS_{2} }} } & {\varPi_{ss} } \\ \end{array} } \right)$$

H is negative definite only if $\det (M_{1} ) < 0,\;\det (M_{2} ) > 0\;{\text{and }}\det (M_{3} ) < 0.$

We obtain,

$$det(M_{1} ) = \varPi_{{S_{1} S_{1} }} < 0,\quad \det (M_{2} ) = \varPi_{{S_{1} S_{1} }} .\varPi_{{S_{2} S_{2} }} - \varPi_{{S_{1} S_{2} }}^{2} \; > 0,$$

by (9) and (10).

After simplification, we obtain

$$\det (M_{3} ) = \frac{{C_{0} k(C_{h} + C_{s} )}}{{A^{2} (S_{1} + S_{2} )^{5} }}\left[ { - 4A\{ A - D(s)\} D(s)(S_{1} + S_{2} ) + 4C_{0} k\{ A - D(s)\} D(s) + \,C_{0} k(2D(s) - A)^{2} } \right]$$

$$\det (M_{3} ) < 0\quad {\text{only if}}\quad S_{1} + S_{2} > \frac{{C_{0} kA}}{{4\{ A - D(s)\} D(s)}}.$$

Thus, for $S_{1} + S_{2} > \frac{{C_{0} kA}}{{4\{ A - D(s)\} D(s)}}$, H is negative definite and hence $\varPi$ is strictly concave in $s,S{}_{1}{\text{and}}\,S_{2}$.□

The proposed model reduces to the following optimization problem:

$$\begin{aligned} & {\text{Maximize}}\,\varPi (S_{1} ,S_{2} ,s,w,P) \\ & {\text{subject to}}\,\left[ {\begin{array}{l} {P_{\hbox{min} } \le P \le P_{\hbox{max} } ,\;} \\ {A - D(s) > 0,\;} \\ {0 \le w \le w_{m} ,s,S_{1} ,S_{2} \ge 0.} \\ \end{array} } \right. \\ \end{aligned}$$

(13)

4 Solution procedure

For given values of the model parameters, the optimizing problem (13) can be solved by any standard optimization software. But, the author has proposed a very efficient algorithm using 3-phase iterative formulae to solve the problem. Iterative formulae converge very fast. The advantage of using this proposed algorithm is that it does not require prior knowledge of any software.

4.1 Construction of the iterative formulae

For given values of the decision variables $P{\text{ and }}w,$ the extreme points can be obtained by solving the following equations:

$$\varPi_{{S_{1} }} = 0,\varPi_{{S_{2} }} = 0{\text{ and }}\varPi_{s} = 0.$$

By $\varPi_{{S_{1} }} = 0$, we obtain the following iterative formula

$$S_{1}^{(n)} = - S_{2}^{(n)} + \sqrt {\left( {1 + \frac{{C_{h} }}{{C_{s} }}} \right)(S_{2}^{(n)} )^{2} + \frac{{2C_{0} D(s^{(n)} )}}{{AC_{s} }}\{ A - D(s^{(n)} )\} }$$

(14)

Similarly, using the remaining two equations $\varPi_{s} = 0{\text{ and }}\varPi_{{S_{2} }} = 0,$ we obtain the following two iterative formulae:

$$s^{(n + 1)} = \left[ {\beta + (C_{u} (P) + w + ((1 - E(x))C_{d} - E(x)C_{v} )f)\frac{kP}{A} + \frac{{C_{0} k(A - 2\beta )}}{{A(S_{1}^{(n)} + S_{2}^{(n)} )}}} \right] \div \left[ {2k\left( {1 - \frac{{C_{0} k}}{{A(S_{1}^{(n)} + S_{2}^{(n)} )}}} \right)} \right]$$

(15)

$$S_{2}^{(n + 1)} = - S_{1}^{(n)} + \sqrt {\left( {1 + \frac{{C_{s} }}{{C_{h} }}} \right)(S_{1}^{(n)} )^{2} + \frac{{2C_{0} D(s^{(n + 1)} )}}{{AC_{h} }}\{ A - D(s^{(n + 1)} )\} }$$

(16)

where $n = 0,1,2, \ldots$.

Initial approximations for $s$ and $S_{2}$ can be taken as $s^{(0)} = \frac{\beta }{2k}$ and $S_{2}^{(0)} = \sqrt {\frac{{2C_{0} D(s^{(0)} )}}{{C_{h} }}}$ respectively.

4.2 Solution algorithm

• Step 1 Initialize the model parameters C ₁ , C _h , C _s , C _d , C _v , x, $\beta$, k, k ₁ , k ₂, m, n, v, w _m , z, $P_{\hbox{min} }$, $P_{\hbox{max} }$.

• Step 2 Define the step-sizes g for P and h for w;

• Step 3 Set w = 0;

• Step 4 p-opt = P _min, s-opt = 0, S ₁-opt = 0, S ₂-opt = 0, w-opt = 0, $\varPi$-opt = $\varPi$ = 0.

• Step 5 Set $P = P_{\hbox{min} }$.

• Step 6 Set P-best = P _min and s-best = S ₁-best = S ₂-best = $\varPi$-best = 0.

• Step 7 Calculate f, A, C _u, C ₀.

• Step 8 Set initial approximations of s and S ₂ as $s^{(0)} = \frac{\beta }{2k},$ $S_{2}^{(0)} = \sqrt {\frac{{2C_{0} D(s^{(0)} )}}{{C_{h} }}}$.

• Step 9 Use Eqs. (14), (15) and (16) repeatedly until s, S ₁, S ₂ become stable.

• Step 10 Calculate $\varPi$ using Eq. (6).

• Step 11 If $\varPi$-best < $\varPi$, then step 12. Else step 13.

• Step 12 Reset P-best = P, s-best = s, S ₁-best = S ₁, S ₂-best = S ₂, w-best = w, $\varPi$-best = $\varPi$.

• Step 13 Set P = P + g.

• Step 14 If P > P _max, then step 15. Else step 7.

• Step 15 If $\varPi$-opt < $\varPi$-best, then step 16. Else step 17.

• Step 16 Reset P-opt = P-best, s-opt = s-best, S ₁ -opt = S ₁ -best, S ₂-opt = S ₂-best, w-opt = w-best, $\varPi$-opt = $\varPi$-best.

• Step 17 w = w + h.

• Step 18 If w > w _m, then step 19. Else step 5.

• Step 19 Print the values of P-opt, s-opt, S ₁-opt, S ₂-opt, w-opt, $\varPi$-opt.

• Step 20 Stop.

5 Numerical example

Example

To illustrate the developed model, an inventory system is considered with the following data: $D(s) = (1200 - 4s){\text{ units/week}},f = 0.1\exp ( - 0.1w)P^{0.2} ,C_{u} = \$ (30 + \frac{10000}{P}),C_{1} = \$ 100,$ $C_{h} = \$ 20,$ $C_{s} = \$ 15,$ $C_{d} = \$ 2,C_{v} = \$ 5,z = \$ 200,w_{m} = \$ 15{\text{ /unit}},P_{\hbox{min} } = 1000{\text{ units/week}},$ $P_{\hbox{max} } = 10000{\text{ units/week}},v = 0.1.$ The random fraction x is assumed to be beta distributed with parameters $a = 5,b = 3$. We obtain, $E(x) = \frac{a}{a + b} = 0.625.$

Using the proposed algorithm, the following optimal solution is obtained: $S_{1}^{*} = 98.7420,S_{2}^{*} = 74.0565,s^{*} = \$ 176.66,P^{*} = 4568,w^{*} = \$ 9.80,\varPi^{*} = \$ 59998.78 / {\text{week}}$. Optimum production cycle = $T^{*} =$ 0.4051 week = 2.84 days (‘*’ indicates optimal value).

Production period = 0.055 week = 0.385 day.

If no additional investment is made for reducing defective proportion, the expected average net profit would be $\varPi^{*} = \$ 55774.31$. Hence, additional investment increases the profit by 7.57 %.

The graph of $\varPi^{*}$ against production rate (P) and against investment (w) are shown in Figs. 2 and 3 respectively. It is clearly evident from graphs that $\varPi^{*}$ is a concave in P, and also in w.

Fig. 2

Pattern of expected average net profit for changes in P

Fig. 3

Pattern of expected average net profit for changes in w

6 Sensitivity analysis

In this section, the following two types of sensitivity analyses have been performed:

• (a) The effects of changes of defective fraction reducing parameter v on optimum production rate $P^{*}$ and $\varPi^{*}$.

• (b) The effects of the additional investment cost parameter w on $\varPi^{*}$ for different values of v.

Both v and w are decreased and increased up to 60 % from its original/optimal value. Results are presented in Table 2.

Table 2 Sensitivity analysis

Following characteristics of the system are observed from sensitivity analysis:

• $P^{*}$ increases when v increases;

• $P^{*}$ is highly sensitive to the changes in v;

• $\varPi^{*}$ is comparatively less sensitive for the changes in v;

• $\varPi^{*}$ is more sensitive for negative changes of v than positive changes;

• $\varPi^{*}$ is almost insensitive to the changes in w from its optimum value for smaller values of v. However, $\varPi^{*}$ becomes more sensitive to the changes in w from its optimum value for higher values of v.

• $\varPi^{*}$ is more sensitive for negative changes of w than positive changes.

7 Special case

In this section, as a special case, we derive the optimum value of the maximum inventory level (S ₂) of the classical inventory model with constant demand, finite replenishment rate and without shortages. It may be noted that the results of classical inventory model is based on cost minimization model. Though the developed model is profit maximization model, for constant demand it gives the same results as in cost minimization model. Take k = 0, f = 0. This implies demand rate $D = \beta$, a constant and all items are perfect. Here $A = (1 - f)P = P$, finite replenishment rate. If shortages are not allowed, then $S_{1} = 0$ which can be obtained from Eq. (14) by taking limit as $C_{s} \to \infty$. Substituting $S_{1} = 0$ in Eq. (16), we obtain $S_{2}^{*} = \sqrt {\frac{{2C_{0} \beta }}{{C_{h} }}\left( {1 - \frac{\beta }{P}} \right)}$, optimum value of maximum inventory level. This formula agrees with corresponding formula of basic EOQ model with finite replenishment rate and without shortages. Taking limit of $S_{2}^{*}$ as $P \to \infty$, we obtain $S_{2}^{*} = \sqrt {\frac{{2C_{0} \beta }}{{C_{h} }}}$. This is the classical economic lot size formula. This verifies the correctness of the developed model.

8 Concluding remarks

In this paper, the author has developed a production-inventory system with defective items incorporating additional investment opportunity on raw material and production process for reducing the proportion of defectives. It jointly determines optimum values of production rate, selling price, additional investment which maximizes the expected average net profit. The model also considers that only a random proportion of defective items can be resold at highly discounted price and the remaining items are to be disposed. Numerical example shows that additional investment can increase the expected average net profit. The demand parameters $\beta \;{\text{and}}\;k$ can be easily estimated by linear regression using historical data. The defective proportion parameters $v,k_{1} ,k_{2}$ can be estimated by linear regression after taking a logarithmic transformation. This model can be extended further by incorporating inflationary effects on the costs, partially backlogged shortages.