Application of Bipolar Fuzzy Sets in Planar Graphs

Abstract

A bipolar fuzzy set is a generalization of a fuzzy set. In this paper, we apply the concept of bipolar fuzzy sets to multigraphs and planar graphs. We introduce the notions of bipolar fuzzy multigraphs, bipolar fuzzy planar graphs, bipolar fuzzy dual graphs, and investigate some of their interesting properties. We also study isomorphism between bipolar fuzzy planar graphs.

Introduction

Graph theory is now a very important research area due to its wide applications. There are many practical applications with a graph structure in which crossing between edges is a nuisance including design problems for circuits, subways and utility lines. Crossing of two connections normally means that the communication lines must be run at different heights. This is not a big issue for electrical wires, but it creates extra expenses for some types of lines. Circuits, in particular, are easier to manufacture if their connections can be constructed in fewer layers. These applications are designed by the concept of planar graphs. Circuits where crossing of lines is necessary, can not be represented by planar graphs. Numerous computational challenges can be solved by means of cuts of planar graph. In the city planning, subway tunnels, pipelines, metro lines are essential in twenty-first century. Due to crossing, there is a chance for an accident. Also, the cost of crossing of routes in underground is high. But, underground routes reduce the traffic jam. In a city planning, routes without crossing is perfect for safety. But due to lack of space, crossing of such lines is allowed. It is easy to observe that the crossing between one congested and one non-congested route is better than the crossing between two congested routes. The term “congested” has no definite meaning. We generally use “congested”, “very congested”, “highly congested” routes, etc. These terms are called linguistic terms and they have some membership values. A congested route may be referred as strong route and low congested route may be called as weak route. Thus crossing between strong route and weak route is more safe than the crossing between two strong routes. That is, crossing between strong route and weak route may be allowed in city planning with certain amount of safety. The terms strong route and weak route lead strong edge and weak edge of a fuzzy graph, respectively. And the permission of crossing between strong and weak edges leads to the concept of fuzzy planar graph [1, 17, 20].

In 1994, Zhang [28] initiated the concept of bipolar fuzzy sets as a generalization of fuzzy sets [26]. Bipolar fuzzy sets are an extension of fuzzy sets [26] whose membership degree range is $[-1, 1]$. In a bipolar fuzzy set, the membership degree 0 of an element means that the element is irrelevant to the corresponding property, the membership degree (0, 1] of an element indicates that the element somewhat satisfies the property, and the membership degree $[-1,0)$ of an element indicates that the element somewhat satisfies the implicit counter-property. Although bipolar fuzzy sets and intuitionistic fuzzy sets look similar to each other, they are essentially different sets. In many domains, it is important to be able to deal with bipolar information. It is noted that positive information represents what is granted to be possible, while negative information represents what is considered to be impossible. This domain has recently motivated new research in several directions. In particular, fuzzy and possibilistic formalisms for bipolar information have been proposed [11], because when we deal with spatial information in image processing or in spatial reasoning applications, this bipolarity also occurs. For instance, when we assess the position of an object in a space, we may have positive information expressed as a set of possible places and negative information expressed as a set of impossible places.

Fuzzy graph theory is finding an increasing number of applications in modeling real time systems where the level of information inherent in the system varies with different levels of precision. Fuzzy models are becoming useful because of their aim in reducing the differences between the traditional numerical models used in engineering and sciences and the symbolic models used in expert systems. Kaufmann’s initial definition of a fuzzy graph [13] was based on Zadeh’s fuzzy relations [27]. Rosenfeld [19] introduced the fuzzy analogue of several basic graph-theoretic concepts including bridges, cut-nodes, connectedness, trees and cycles. Bhattacharya [9] gave some remarks on fuzzy graphs, and Sunitha and Vijayakumar [23] characterized fuzzy trees. Akram et al. [2–6] has introduced many concepts, including bipolar fuzzy graphs, regular bipolar fuzzy graphs, bipolar fuzzy hypergraphs and metric aspects of bipolar fuzzy graphs. Abdul-Jabbar et al. [1] introduced the concept of a fuzzy dual graph and discussed some of its interesting properties. Recently, Samanta et al. [17, 20] introduced and investigated the concept of fuzzy planar graphs and studied several properties. For some applications readers may look in [24, 29]. In this article, we apply the concept of bipolar fuzzy sets to multigraphs and planar graphs. We introduce the notions of bipolar fuzzy multigraphs, bipolar fuzzy planar graphs, bipolar fuzzy dual graphs, and investigate some of their interesting properties. We also study isomorphism between bipolar fuzzy planar graphs.

We have used standard definitions and terminologies in this paper. For other notations,terminologies and applications not mentioned in the paper, the readers are referred to [7, 8, 10, 12, 14–16, 18, 21, 22].

Preliminaries

In this section, we review some elementary concepts whose understanding is necessary fully benefit from this paper.

Let X be a nonempty set. A fuzzy set [26] A drawn from X is defined as $A = \{\langle x {:}\; \mu _A(x) \rangle {:}\; x \in X\}$, where $\mu {:}\; X \rightarrow [0,1]$ is the membership function of the fuzzy set A. A fuzzy binary relation [27] on X is a fuzzy subset $\mu$ on $X \times X$. By a fuzzy relation, we mean a fuzzy binary relation given by $\mu {:}\; X \times X \rightarrow [0, 1]$. A fuzzy graph [13] $G =(V,\sigma ,\mu )$ is a non-empty set V together with a pair of functions $\sigma {:}\;V\rightarrow [0, 1]$ and $\mu {:}\;V \times V \rightarrow [0,1]$ such that for all $x, y\in V, \mu (x,y) \le \min (\sigma (x),\sigma (y))$, where $\sigma (x)$ and $\mu (x,y)$ represent the membership values of the vertex x and of the edge (x, y) in G, respectively. A loop at a vertex x in a fuzzy graph is represented by $\mu (x,x)\ne 0$. An edge is non-trivial if $\mu (x,y) \ne 0$. Let G be a fuzzy graph and for a certain geometric representation, the graph has only one crossing between two fuzzy edges $((w,x),\mu (w,x))$ and $((y,z),\mu (y,z))$. If $\mu (w,x)=1$ and $\mu (y,z)=0$, then we say that the fuzzy graph has no crossing. Similarly, if $\mu (w,x)$ has value near to 1 and $\mu (y, z)$ has value near to 0, the crossing will not be important for the planarity. If $\mu (y, z)$ has value near to 1 and $\mu (w,x)$ has value near to 1, then the crossing becomes very important for the planarity.

Let X be a nonempty set. A fuzzy multiset [25] A drawn from X is characterized by a function, ‘count membership’ of A denoted by $CM_A$ such that $CM_A {:}\; X \rightarrow Q$, where Q is the set of all crisp multisets drawn from the unit interval [0, 1]. Then for any $x \in X$, the value $CM_A(x)$ is a crisp multiset drawn from [0, 1]. For each $x \in X$, the membership sequence is defined as the decreasingly ordered sequence of elements in $CM_A(x)$. It is denoted by $(\mu ^1_A(x), \mu ^2_A(x), \mu ^3_A(x), \ldots , \mu ^p_A(x))$ where $\mu ^1_A(x) \ge \mu ^2_A(x) \ge \mu ^3_A(x)\ge \ldots \ge \mu ^p_A(x).$

Let V be a non-empty set and $\sigma {:}\;V\rightarrow [0,1]$ be a mapping and let $\mu =\{(x, y), \mu (x,y)_j,j=1,2,\ldots ,p_{x y}|(x,y)\in V\times V\}$ be a fuzzy multi-set of $V\times V$ such that $\mu (x,y)_j\le \min \{\sigma (x),\sigma (y)\}$ for all $j=1,2,\ldots ,p_{xy}$, where $p_{xy}=\max \{j|\mu (x,y)_j\ne 0\}$. Then $G=(V,\sigma , \mu )$ is denoted as fuzzy multigraph [17] where $\sigma (x)$ and $\mu (x,y)_j$ represent the membership value of the vertex x and the membership value of the edge (x, y) in G, respectively.

Definition 1

[28] Let X be a nonempty set. A bipolar fuzzy set B in X is an object having the form

$$\begin{aligned} B =\left\{ \left( x,\,\mu ^P_B (x),\,\mu ^N_B (x)\right) \,|\,x\in X\right\} \end{aligned}$$

where $\mu ^P_B {:}\;X\rightarrow [0,\,1]$ and $\mu ^N_B {:}\;X\rightarrow [-1,\,0]$ are mappings.

We use the positive membership degree $\mu ^P_B (x)$ to denote the satisfaction degree of an element x to the property corresponding to a bipolar fuzzy set B, and the negative membership degree $\mu ^N_B(x)$ to denote the satisfaction degree of an element x to some implicit counter-property corresponding to a bipolar fuzzy set B. If $\mu ^P_B(x)\not =0$ and $\mu ^N_B(x)=0$, it is the situation that x is regarded as having only positive satisfaction for B. If $\mu ^P_B (x)=0$ and $\mu ^N_B (x)\not =0$, it is the situation that x does not satisfy the property of B but somewhat satisfies the counter property of B. It is possible for an element x to be such that $\mu ^P_B(x)\not =0$ and $\mu ^N_B(x)\not =0$ when the membership function of the property overlaps that of its counter property over some portion of X.

For the sake of simplicity, we shall use the symbol $B =(\mu ^P_B ,\,\mu ^N_B )$ for the bipolar fuzzy set

$$\begin{aligned} B =\left\{ \left( x,\,\mu ^P_B (x),\,\mu ^N_B (x)\right) \,|\,x\in X\right\} . \end{aligned}$$

Definition 2

[28] Let X be a nonempty set. Then we call a mapping $A=(\mu ^P_A, \mu ^N_A){:}\; X \times X \rightarrow [0, 1] \times [-1,0]$ a bipolar fuzzy relation on X such that $\mu ^P_A(x, y) \in [0, 1]$ and $\mu ^N_A(x, y) \in [-1, 0]$.

Definition 3

[2] A bipolar fuzzy graph $G = (V, A, B)$ is a non-empty set V together with a pair of functions $A=(\mu ^P_A, \mu ^N_A){:}\;V\rightarrow [0, 1]\times [-1, 0]$ and $B=(\mu ^P_B, \mu ^N_B){:}\;V\times V\rightarrow [0, 1]\times [-1, 0]$ such that for all $x, y\in V$,

$$\begin{aligned} \mu ^P_B(x, y)\le \min \left( \mu ^P_A(x), \mu ^P_A(y)\right) ~~~\mathrm{and}~~~\mu ^N_{B}(x, y)\ge \max \left( \mu ^N_A(x), \mu ^N_A(y)\right) . \end{aligned}$$

Notice that $\mu ^P_B(x, y)>0, \mu ^N_B(x, y) <0$ for $(x, y) \in V \times V, \mu ^P_B(x, y)= \mu ^N_B(x, y)=0$ for $(x, y) \not \in V \times V$, and B is symmetric relation.

We now give definition of bipolar fuzzy multisets.

Definition 4

Let X be a nonempty set. A Bipolar Fuzzy Multiset (BFMS) A drawn from X is characterized by two functions: ‘count positive membership’ of $A (CM_A)$ and ‘count negative membership’ of $A(CN_A)$ given by $CM_A {:}\; X \rightarrow Q_1$ and $CN_A {:}\; X \rightarrow Q_2$ where $Q_1$ and $Q_2$ are the sets of all crisp multisets drawn from the intervals [0, 1] and $[-1, 0]$ , respectively, the positive membership sequence is defined as a $((\mu ^1)^P_A(x), (\mu ^2)^P_A(x), (\mu ^3)^P_A(x), \ldots , (\mu ^m)^P_A(x))$ and the negative membership sequence will be denoted by $((\mu ^1)^N_A(x), (\mu ^2)^N_A(x), (\mu ^3)^N_A(x), \ldots , (\mu ^m)^N_A(x))$. A BFMS A is denoted by

$$\begin{aligned}&\Big \{\Big \langle x{:}\; \left( (\mu ^1)^P_A(x), (\mu ^2)^P_A(x), \ldots , (\mu ^m)^P_A(x)\right) ,\\&\quad \left( (\mu ^1)^N_A(x), (\mu ^2)^N_A(x), \ldots , (\mu ^m)^N_A(x)\right) \Big \rangle {:}\; x \in X \Big \}. \end{aligned}$$

Bipolar Fuzzy Planar Graphs

We first introduce the notion of a bipolar fuzzy multigraph using the concept of a bipolar fuzzy multiset.

Definition 5

Let $A=(\mu ^P_A, \mu ^N_A)$ be a bipolar fuzzy set on V and let

$$\begin{aligned} B=\left\{ \left( xy, \mu ^P_B(xy)_i, \mu ^N_B(xy)_i\right) ,\quad i=1,2,\ldots ,m|xy\in V\times V\right\} \end{aligned}$$

be a bipolar fuzzy multiset of $V\times V$ such that

$$\begin{aligned} \mu ^P_B(xy)_i\le & {} \min \left\{ \mu ^P_A(x),\mu ^P_A(y)\right\} ,\\ \mu ^N_B(xy)_i\ge & {} \max \left\{ \mu ^N_A(x),\mu ^N_A(y)\right\} \end{aligned}$$

for all $i=1,2,\ldots ,m$. Then G is called a bipolar fuzzy multigraph.

Note that there may be more than one edge between the vertices x and $y.\; \mu ^P_B(xy)_i, \mu ^N_B(xy)_i$ represent the positive membership value and negative membership value of the edge xy in G, respectively. m denotes the number of edges between the vertices. In bipolar fuzzy multigraph G, B is said to be bipolar fuzzy multiedge set. $\mu ^{P}_A(xy)_i=0=\mu ^{N}_A(xy)_i$ for all $xy \in V \times V -E, 0 \le \mu ^{P}_A(xy)_i \le 1, -1 \le \mu ^{N}_A(xy)_i \le 0$.

Example 1

Consider a multigraph $G^*=(V, E)$ such that $V=\{a, b, c, d\}, E= \{ab, ab, ab, bc, bd\}$. Let $A=(\mu ^P_A, \mu ^N_A)$ be a bipolar fuzzy set of V and let $B=(\mu ^P_B, \mu ^N_B)$ be a bipolar fuzzy multiedge set of $V \times V$ defined by

By routine computations, it is easy to see from Fig. 1 that it is a bipolar fuzzy multigraph.

Fig. 1

Bipolar fuzzy multigraph

Definition 6

Let $B=\{(xy, \mu ^P_B(xy)_i, \mu ^N_B(xy)_i), i=1,2,\ldots ,m|xy\in V\times V\}$ be a bipolar fuzzy multiedge set in bipolar fuzzy multigraph G. The degree of a vertex $x\in V$ is denoted by deg(x) and is defined by $\deg (x)=\left( \sum \nolimits ^{m}_{i=1}\mu ^P_B(xy)_i, \sum \nolimits ^{m}_{i=1}\mu ^N_B(xy)_i\right)$ for all $y\in V$.

Example 2

In Example 1, degree of the vertices a, b, c, d are $\deg (a)=(0.5,-0.4), \deg (b)=(0.9,-0.9), \deg (c)=(0.3,-0.3), \deg (d)=(0.1,-0.2)$.

Definition 7

Let $B=\{(xy, \mu ^P_B(xy)_i, \mu ^N_B(xy)_i), i=1,2,\ldots ,m|xy\in V\times V\}$ be a bipolar fuzzy multiedge set in bipolar fuzzy multigraph G. A multiedge xy of G is strong if $\frac{1}{2}\min \{\mu ^P_A(x),\mu ^P_A(y)\}\le \mu ^P_B(xy)_i, \frac{1}{2}\max \{\mu ^N_A(x),\mu ^N_A(y)\}\le \mu ^N_B(xy)_i$ for all $i=1,2,\ldots ,m$.

Definition 8

Let $B=\{(xy, \mu ^P_B(xy)_i, \mu ^N_B(xy)_i), i=1,2,\ldots ,m|xy\in V\times V\}$ be a bipolar fuzzy multiedge set in bipolar fuzzy multigraph G. An bipolar fuzzy multigraph G is complete if $\min \{\mu ^P_A(x),\mu ^P_A(y)\}= \mu ^P_B(xy)_i, \max \{\mu ^N_A(x),\mu ^N_A(y)\}= \mu ^N_B(xy)_i$ for all $i=1,2,\ldots ,m$ and for all $x,y\in V$.

Example 3

Consider a bipolar fuzzy multigraph G as shown in Fig. 2.

By routine computations, it is easy to see from Fig. 2 that it is a bipolar fuzzy complete multigraph.

Fig. 2

Bipolar fuzzy complete multigraph

Definition 9

Strength of the bipolar fuzzy edge ab can be measured by the value

$$\begin{aligned} I_{ab}=(M_{ab}, N_{ab})=\left( \frac{\mu ^P_B(ab)_i }{\min \left( \mu ^P_A(a),\mu ^P_A(b)\right) }, \frac{\mu ^N_B(ab)_i }{\max \left( \mu ^N_A(a),\mu ^N_A(b)\right) }\right) . \end{aligned}$$

Definition 10

Let G be a bipolar fuzzy multigraph. An edge ab is said to be a bipolar fuzzy strong if $M_{ab}\ge 0.5$ or $N_{ab}\le 0.5$, otherwise weak.

Definition 11

Let G be a bipolar fuzzy multigraph and let B contains two edges $(ab,\mu ^P_B(ab)_i, \mu ^N_B(ab)_i )$ and $(cd, \mu ^P_B(cd)_j, \mu ^N_B(cd)_j )$ which are intersected at a point P, where i and j are fixed integers. We define the intersecting value at the point P by

$$\begin{aligned} \mathcal {I}_P=(M_P, N_P)=\left( \frac{M_{ab}+M_{cd}}{2}, \frac{N_{ab}+N_{cd}}{2} \right) . \end{aligned}$$

If the number of point of intersections in a bipolar fuzzy multigraph increases, planarity decreases. Thus for bipolar fuzzy multigraph, $\mathcal {I}_P$ is inversely proportional to the planarity. We now introduce the concept of a bipolar fuzzy planar graph.

Definition 12

Let G be a bipolar fuzzy multigraph and let $P_1,P_2,\ldots ,P_z$ be the points of intersections between the edges for a certain geometrical representation, G is said to be a bipolar fuzzy planar graph with bipolar fuzzy planarity value $f=(f^P, f^N)$, where

$$\begin{aligned} f=(f^P, f^N)=\left( \frac{1}{1+\{M_{P_1}+M_{P_2}+\ldots +M_{P_z}\}}, \frac{-1}{1+\{N_{P_1}+N_{P_2}+\ldots +N_{P_z}\}} \right) . \end{aligned}$$

Clearly, $f=(f^P, f^N)$ is bounded and $0<f^P\le 1, f^N$ is $-1\le f^N< 0$. If there is no point of intersection for a certain geometrical representation of a bipolar fuzzy planar graph, then its bipolar fuzzy planarity value is $(1, -1)$. In this case, the underlying crisp graph of this bipolar fuzzy graph is the crisp planar graph. If $f^P$ decreases and $f^N$ increases, then the number of points of intersection between the edges increases and decreases, respectively, and the nature of planarity decreases and decreases, respectively. We conclude that every bipolar fuzzy graph is a bipolar fuzzy planar graph with certain bipolar fuzzy planarity value.

Example 4

Consider a multigraph $G^*=(V, E)$ such that $V=\{a, b, c, d, e\}$,

$$\begin{aligned} E= \{ab, ac, ad, ad, bc, bd, cd, ce, ae, de, be \}. \end{aligned}$$

Let $A=(\mu ^P_A, \mu ^N_A)$ be a bipolar fuzzy of V and let $B=(\mu ^P_B, \mu ^N_B)$ be a bipolar fuzzy multiedge set of $V \times V$ defined by

The bipolar fuzzy multigraph as shown in Fig. 3 has two point of intersections $P_1$ and $P_2. P_1$ is a point between the edges $(ad,0.2,-0.1 )$ and $(bc,0.2,-0.1 )$ and $P_2$ is between $(ad,0.3,-0.1)$ and $(bc,0.2, -0.1)$. For the edge $(ad,0.2, -0.1), I_{ad}=(0.4, 1)$, For the edge $(ad,0.3, -0.1), I_{ad}=(0.6, 0.5 )$ and for the edge $(bc,0.2, -0.1), I_{bc}=(0.67, 1 )$. For the first point of intersection $P_1$, intersecting value $\mathcal {I}_{P_1}$ is (0.53, 0.75 ) and that for the second point of intersection $P_2,\mathcal {I}_{P_2}= (0.63, 0.75 )$. Therefore, the bipolar fuzzy planarity value for the bipolar fuzzy multigraph shown in Fig. 3 is $(0.46,- 0.4)$.

Fig. 3

Bipolar fuzzy planar graph

Bipolar fuzzy planarity value for the bipolar fuzzy complete multigraph is calculated from the following theorem.

Theorem 1

Let G be a bipolar fuzzy complete multigraph. The bipolar fuzzy planarity value, $f=(f^P, f^N)$ of G is given by $f^P=\frac{1}{1+n_p}$ and $f^N=\frac{-1}{1+n_p}$, where $n_p$ is the number of point of intersections between the edges in G.

Definition 13

An bipolar fuzzy planar graph G is called strong bipolar fuzzy planar graph if the bipolar fuzzy planarity value $f=(f^P, f^N)$ of the graph is $f^P \ge 0.5, f^N\le -0.5$.

Theorem 2

Let G be a strong bipolar fuzzy planar graph. The number of point of intersections between strong edges in G is at most one.

Proof

Let G be a strong bipolar fuzzy planar graph. Assume that G has at least two point of intersections $P_1$ and $P_2$ between two strong edges in G. For any strong edge $(ab, \mu ^P_B(ab)_i, \mu ^N_B(ab)_i )$,

$$\begin{aligned} \mu ^P_B(ab)_i\ge \frac{1}{2}\min \left\{ \mu ^P_A(a),\mu ^P_A(b)\right\} , \mu ^N_B(ab)_i\le \frac{1}{2}\max \left\{ \mu ^N_A(a),\mu ^N_A(b)\right\} . \end{aligned}$$

This shows that $M_{ab}\ge 0.5$ or $N_{ab}\le 0.5$. Thus for two intersecting strong edges $(ab, \mu ^P_B(ab)_i, \mu ^N_B(ab)_i )$ and $(cd, \mu ^P_B(cd)_j, \mu ^N_B(cd)_j )$,

$$\begin{aligned} \frac{M_{ab}+M_{cd}}{2}\ge 0.5,~\frac{N_{ab}+N_{cd}}{2}\le 0.5, \end{aligned}$$

that is, $M_{P_1}\ge 0.5 , N_{P_1}\le 0.5$. Similarly, $M_{P_2}\ge 0.5, N_{P_2}\le 0.5$. This implies that $1+M_{P_1}+M_{P_2}\ge 2, 1+N_{P_1}+N_{P_2}\le 2$. Therefore, $f^P=\frac{1}{1+M_{P_1}+M_{P_2}}\le 0.5, f^N=\frac{-1}{1+N_{P_1}+N_{P_2}}\ge -0.5$. It contradicts the fact that the bipolar fuzzy graph is a strong bipolar fuzzy planar graph. Thus number of point of intersections between strong edges can not be two. Obviously, if the number of point of intersections of strong bipolar fuzzy edges increases, the bipolar fuzzy planarity value decreases. Similarly, if the number of point of intersection of strong edges is one, then the bipolar fuzzy planarity value $f^P<0.5, f^N>-0.5$. Any bipolar fuzzy planar graph without any crossing between edges is a strong bipolar fuzzy planar graph. Thus, we conclude that the maximum number of point of intersections between the strong edges in G is one. $\square$

Theorem 3

Let G be a bipolar fuzzy planar graph with bipolar fuzzy planarity value $f=(f^P, f^N)$. If $f^P\ge 0.67, f^N\le - 0.67, G$ do not contain any point of intersection between two strong edges.

Definition 14

Let G be a bipolar fuzzy planar graph and $B=\{(xy, \mu ^P_B(xy)_i, \mu ^N_B(xy)_i),i=1,2,\ldots ,m|\,xy\in V\times V\}$. A bipolar fuzzy face of G is a region, bounded by the set of bipolar fuzzy edges $E^\prime \subset E$, of a geometric representation of G. The positive membership and negative values of the bipolar fuzzy face are:

$$\begin{aligned}&\min \left\{ \frac{\mu ^P_B(xy)_i}{\min \{\mu ^P_A(x),\mu ^P_A(y)\}},\quad i=1,2,\ldots ,m|\,xy\in E^\prime \right\} ,\\&\max \left\{ \frac{\mu ^N_B(xy)_i}{\max \{\mu ^N_A(x),\mu ^N_A(y)\}},\quad i=1,2,\ldots ,m|\,xy\in E^\prime \right\} . \end{aligned}$$

Definition 15

A bipolar fuzzy face is called strong bipolar fuzzy face if its positive membership value is greater than 0.5 or negative membership value is greater than $-0.5$, and weak face otherwise. Every bipolar fuzzy planar graph has an infinite region which is called outer bipolar fuzzy face. Other faces are called inner bipolar fuzzy faces.

Example 5

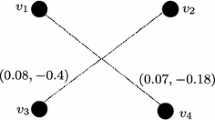
Consider a bipolar fuzzy planar graph as shown in Fig. 4. The bipolar fuzzy planar graph has the following faces:

• bipolar fuzzy face $F_1$ is bounded by the edges $(v_1v_2,0.5, -0.1),(v_2v_3,0.6, -0.1),(v_1v_3,0.5, -0.1)$.

• outer bipolar fuzzy face $F_2$ surrounded by edges $(v_1v_3, 0.5, -0.1), (v_1v_4, 0.5, -0.1), (v_2v_4, 0.6, -0.1), (v_2v_3, 0.6,-0.1)$,

• bipolar fuzzy face $F_3$ is bounded by the edges $(v_1v_2,0.5, -0.1),(v_2v_4,0.6, -0.1),(v_1v_4,0.5, -0.1).$

Clearly, the positive membership value and negative membership value of a bipolar fuzzy face $F_1$ are 0.833 and $-0.333$, respectively. The positive membership value and negative membership value of a bipolar fuzzy face $F_3$ are also 0.833 and -0.333, respectively. Thus $F_1$ and $F_3$ are strong bipolar fuzzy faces.

Fig. 4

Faces in bipolar fuzzy planar graph

We now introduce dual of bipolar fuzzy planar graph. In bipolar fuzzy dual graph, vertices are corresponding to the strong bipolar fuzzy faces of the bipolar fuzzy planar graph and each bipolar fuzzy edge between two vertices is corresponding to each edge in the boundary between two faces of bipolar fuzzy planar graph. The formal definition is given below.

Definition 16

Let G be a bipolar fuzzy planar graph and let

$$\begin{aligned} B=\left\{ \left( xy, \mu ^P_B(xy)_i, \mu ^N_B(xy)_i \right) ,\quad i=1,2,\ldots ,m|xy\in V\times V\right\} . \end{aligned}$$

Let $F_1, F_2, \ldots , F_k$ be the strong bipolar fuzzy faces of G. The bipolar fuzzy dual graph of G is a bipolar fuzzy planar graph $G^\prime =(V^\prime ,A^\prime , B^\prime )$, where $V^\prime =\{x_i, i=1, 2, \ldots , k\}$, and the vertex $x_i$ of $G^\prime$ is considered for the face $F_i$ of G. The positive membership and negative membership values of vertices are given by the mapping $A^\prime =(\mu ^P_{A^\prime }, \mu ^N_{A^\prime }){:}\;V^\prime \rightarrow [0,1]\times [-1, 0]$ such that $\mu ^P_{A^\prime }(x_i)=\max \{\mu ^P_{B^\prime }(uv)_i,i=1,2,\ldots ,p|uv$ is an edge of the boundary of the strong bipolar fuzzy face $F_i$}, $\mu ^N_{A^\prime }(x_i)=\min \{\mu ^N_{B^\prime }(uv)_i,i=1,2,\ldots ,p|uv$ is an edge of the boundary of the strong bipolar fuzzy face $F_i$}.

There may exist more than one common edges between two faces $F_i$ and $F_j$ of G. Thus there may be more than one edges between two vertices $x_i$ and $x_j$ in bipolar fuzzy dual graph $G^\prime$. Let $(\mu ^P)^l_B(x_ix_j)$ denote the positive membership value of the lth edge between $x_i$ and $x_j$, and $(\mu ^N)^1_B(x_ix_j)$ denote the negative positive membership value of the lth edge between $x_i$ and $x_j$. The positive membership and negative membership values of the bipolar fuzzy edges of the bipolar fuzzy dual graph are given by $\mu ^P_{B^\prime }(x_ix_j)_l=(\mu ^P)^l_B(uv)_j, \mu ^N_{B^\prime }(x_ix_j)_l=(\mu ^N)^l_B(uv)_j$ where $(uv)_l$ is an edge in the boundary between two strong bipolar fuzzy faces $F_i$ and $F_j$ and $l=1,2,\ldots ,s$, where s is the number of common edges in the boundary between $F_i$ and $F_j$ or the number of edges between $x_i$ and $x_j$. If there be any strong pendant edge in the bipolar fuzzy planar graph, then there will be a self loop in $G^\prime$ corresponding to this pendant edge. The edge positive membership and negative membership value of the self loop is equal to the positive membership and negative membership value of the pendant edge. Bipolar fuzzy dual graph of bipolar fuzzy planar graph does not contain point of intersection of edges for a certain representation, so it is bipolar fuzzy planar graph with planarity value $(1, -1)$. Thus the bipolar fuzzy face of bipolar fuzzy dual graph can be similarly described as in bipolar fuzzy planar graphs.

Example 6

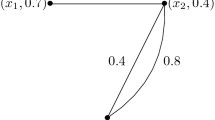
Consider a bipolar fuzzy planar graph $G=(V, A, B)$ as shown in Fig. 5 such that $V=\{a,b,c,d\}, A=(a, 0.6, -0.2 ), (b, 0.7, -0.2 ), (c, 0.8, -0.2), (d, 0.9, -0.1 ),$ and $B=\{(ab, 0.5, -0.01 ),(ac, 0.4, -0.01), (ad, 0.55, -0.01 ), (bc, 0.45, -0.01 ), (bc, 0.6, -0.01 ), (cd, 0.7, -0.01 )\}.$

The bipolar fuzzy planar graph has the following faces:

• bipolar fuzzy face $F_1$ is bounded by $(ab, 0.5, -0.01),(ac, 0.4, -0.01 ),(bc, 0.45, -0.01 )$,

• bipolar fuzzy face $F_2$ is bounded by $(ad, 0.55, -0.01),(cd, 0.7, -0.01), (ac, 0.4,-0.01 )$,

• bipolar fuzzy face $F_3$ is bounded by $(bc, 0.45, -0.01),(bc,0.6, -0.01 )$ and

• outer bipolar fuzzy face $F_4$ is surrounded by $(ab, 0.5, -0.01),(bc, 0.6, -0.01 ),(cd, 0.7,-0.01), (ad, 0.55, -0.01 )$.

Routine calculations show that all faces are strong bipolar fuzzy faces. For each strong bipolar fuzzy face, we consider a vertex for the bipolar fuzzy dual graph. So the vertex set $V^\prime =\{x_1, x_2, x_3, x_4\}$, where the vertex $x_i$ is taken corresponding to the strong bipolar fuzzy face $F_i, i=1,2,3,4.$ Thus

$$\begin{aligned} \mu ^P_{A^\prime }(x_1)= & {} \max \{0.5, 0.4, 0.45 \}=0.5, \mu ^P_{A^\prime }(x_2)=\max \{0.55,0.7,0.4\}=0.7,\\ \mu ^N_{A^\prime }(x_1)= & {} \min \{-0.01, -0.01, -0.01\}=-0.01,\\ \mu ^N_{A^\prime }(x_2)= & {} \min \{-0.01, -0.01,-0.01\}=-0.01,\\ \mu ^P_{A^\prime }(x_3)= & {} \max \{0.45,0.6\}=0.6,\mu ^P_{A^\prime }(x_4)=\max \{0.5,0.6,0.7,0.55\}=0.7,\\ (mu^N_A)^\prime (x_3)= & {} \min \{-0.01, -0.01\}=-0.01,\\ (\mu ^N_{A^\prime }(x_4)= & {} \min \{-0.01, -0.01, -0.01, -0.01\}=-0.01. \end{aligned}$$

There are two common edges ad and cd between the faces $F_2$ and $F_4$ in G. Hence between the vertices $x_2$ and $x_4$, there exist two edges in the bipolar fuzzy dual graph of G. Membership and negative positive membership values of these edges are given by

$$\begin{aligned} \mu ^P_{B^\prime }(x_2x_4)= & {} \mu ^P_B(cd)=0.7, \mu ^P_{B^\prime }(x_2x_4)=\mu ^P_{B}(ad)=0.55,\\ \mu ^N_{B^\prime }(x_2x_4)= & {} \mu ^N_B(cd)=-0.01, \mu ^N_{B^\prime }(x_2x_4)=\mu ^N_B(ad)=-0.01. \end{aligned}$$

The positive membership and negative positive membership values of other edges of the bipolar fuzzy dual graph are calculated as

$$\begin{aligned} \mu ^P_{B^\prime }(x_1x_3)= & {} \mu ^P_B(bc)=0.45, \mu ^P_{B^\prime }(x_1x_2)=\mu ^P_B(ac)=0.4,\\ \mu ^P_{B^\prime }(x_1x_4)= & {} \mu ^P_B(ab)=0.5, \mu ^P_{B^\prime }(x_3x_4)=(\mu ^P_B)^\prime (bc)=0.6,\\ (\mu ^N_B)^\prime (x_1x_3)= & {} \mu ^P_B(bc)=-0.01, \mu ^N_{B^\prime }(x_1x_2)=\mu ^N_B(ac)=-0.01,\\ \mu ^N_{B^\prime }(x_1x_4)= & {} \mu ^N_B(ab)=-0.01, (\mu ^N_B)^\prime (x_3x_4)=\mu ^N_B(bc)=-0.01. \end{aligned}$$

Thus the edge set of bipolar fuzzy dual graph is

$$\begin{aligned}&B^\prime =\{(x_1x_3,0.45,-0.01 ), (x_1x_2,0.4, -0.01 ),\\&\quad (x_1x_4,0.5, -0.01 ), (x_3x_4, 0.6, -0.01), (x_2x_4,0.7, -0.01 ), (x_2x_4, 0.55, -0.01)\}. \end{aligned}$$

In Fig. 5, the bipolar fuzzy dual graph $G^\prime =(V^\prime , A^\prime , B^\prime )$ of G is drawn by dotted line.

Fig. 5

Bipolar fuzzy dual graph

Weak edges in planar graphs are not considered for any calculation in bipolar fuzzy dual graphs. We state the following Theorems without their proofs.

Theorem 4

Let G be a bipolar fuzzy planar graph whose number of vertices, number of bipolar fuzzy edges and number of strong faces are denoted by n, p, m, respectively. Let $G^\prime$ be the bipolar fuzzy dual graph of G. Then:

• (i) the number of vertices of $G^\prime$ is equal to m,

• (ii) number of edges of $G^\prime$ is equal to p,

• (iii) number of bipolar fuzzy faces of $G^\prime$ is equal to n.

Theorem 5

Let $G=(V, A, B)$ be a bipolar fuzzy planar graph without weak edges and the bipolar fuzzy dual graph of G be $G^\prime =(V^\prime , A^\prime , B^\prime )$. The positive membership and negative membership values of bipolar fuzzy edges of $G^\prime$ are equal to positive membership and negative membership values of the bipolar fuzzy edges of G.

We now study isomorphism between bipolar fuzzy planar graphs.

Definition 17

[2] Let $G_1$ and $G_2$ be bipolar fuzzy graphs. An isomorphism $f{:}\;G_1 \rightarrow G_2$ is a bijective mapping $f{:}\;V_1 \rightarrow V_2$ which satisfies the following conditions:

• (c) $\mu ^P_{A_1}(x_1)= \mu ^P_{A_2}(f(x_1)), \mu ^N_{A_1}(x_1)= \mu ^N_{A_2}(f(x_1))$,

• (d) $\mu ^P_{B_1}(x_1y_1)= \mu ^P_{B_2}(f(x_1)f(y_1)), \mu ^N_{B_1}(x_1y_1) = \mu ^N_{B_2}(f(x_1)f(y_1))$

for all $x_1 \in V_1, x_1y_1 \in E_1$.

Definition 18

[2] Let $G_1$ and $G_2$ be bipolar fuzzy graphs. Then, a weak isomorphism $f{:}\;G_1 \rightarrow G_2$ is a bijective mapping $f{:}\;V_1 \rightarrow V_2$ which satisfies the following conditions:

• (e) f is homomorphism,

• (f) $\mu ^P_{A_1}(x_1)= \mu ^P_{A_2}(f(x_1)), \mu ^N_{A_1}(x_1)= \mu ^N_{A_2}(f(x_1)),$

for all $x_1 \in V_1$.

Definition 19

[2] Let $G_1$ and $G_2$ be the bipolar fuzzy graphs. A co-weak isomorphism $f{:}\;G_1 \rightarrow G_2$ is a bijective mapping $f{:}\;V_1 \rightarrow V_2$ which satisfies

• (g) f is homomorphism,

• (h) $\mu ^P_{B_1}(x_1y_1)= \mu ^P_{B_2}(f(x_1)f(y_1)), \mu ^N_{B_1}(x_1y_1) = \mu ^N_{B_2}(f(x_1)f(y_1))$

for all $x_1y_1 \in V_1$.

It is known that isomorphism between bipolar fuzzy graphs is an equivalence relation. If there is an isomorphism between two bipolar fuzzy graphs such that one is a bipolar fuzzy planar graph, then the other will be bipolar fuzzy graph. We state the following result without its proof.

Theorem 6

Let G be a bipolar fuzzy planar graph and let H be a bipolar fuzzy graph. If there exists an isomorphism $f{:}\;G \rightarrow H , H$ can be drawn as bipolar fuzzy planar graph with same planarity value of G.

Two bipolar fuzzy planar graphs with same number of vertices may be isomorphic. But, the relations between bipolar fuzzy planarity values of two bipolar fuzzy planar graphs may have the following relations:

Theorem 7

Let $G_1$ and $G_2$ be two isomorphic bipolar fuzzy graphs with bipolar fuzzy planarity values $f_1$ and $f_2$, respectively. Then $f_1 = f_2$.

Theorem 8

Let $G_1$ and $G_2$ be two weak isomorphic bipolar fuzzy graphs with bipolar fuzzy planarity values $f_1$ and $f_2$, respectively. $f_1 = f_2$ if the edge positive membership and negative membership values of corresponding intersecting edges are same.

Theorem 9

Let $G_1$ and $G_2$ be two co-weak isomorphic bipolar fuzzy graphs with bipolar fuzzy planarity values $f_1$ and $f_2$, respectively. $f_1 = f_2$ if the minimum of positive membership values and maximum of negative membership values of the end vertices of corresponding intersecting edges are same.

Conclusions

Graph theoretical concepts are widely used to study and model various applications in different areas including automata theory, operations research, economics, and transportation. However, in many cases, some aspects of a graph-theoretic problem may be vague or uncertain. It is natural to deal with the vagueness and uncertainty using the methods of fuzzy sets. Since bipolar fuzzy set has shown advantages in handling vagueness and uncertainty than fuzzy set, we have applied the concept of bipolar fuzzy sets to multigraphs and planar graphs in this paper. The natural extension of this research work is application of bipolar fuzzy planar graphs in the area of applied soft computing including neural networks, decision making and geographical information systems.