Certain Types of Product Bipolar Fuzzy Graphs

Abstract

Recently, bipolar fuzzy graph is a vastly growing research area as it is the generalization of the fuzzy graphs. In this paper, at first the concepts of regular and totally regular product bipolar fuzzy graphs is introduced. Then necessary and sufficient conditions are established under which regular and totally regular product bipolar fuzzy graph becomes equivalent. The notion of product bipolar fuzzy line graph is introduced and investigated some of its properties. A necessary and sufficient condition is given for a product bipolar fuzzy graph to be isomorphic to its corresponding product bipolar fuzzy line graph. It is also examined when an isomorphism between two product bipolar fuzzy graphs follows from an isomorphism of their corresponding fuzzy line graphs.

Introduction

Presently, science and technology is featured with complex processes and phenomena for which complete information is not always available. For such cases, mathematical models are developed to handle various types of systems containing elements of uncertainty. A large number of these models is based on fuzzy sets. Graph theory has numerous applications to problems on computer science, electrical engineering, system analysis, operations research, economics, networking routing, transportation, etc. Considering the fuzzy relations between fuzzy sets, Rosenfeld [18] introduced the concept of fuzzy graphs in 1975 and later on he developed the structure of fuzzy graphs, obtaining analogous of several graph concepts. The concept of weak isomorphism, co-weak isomorphism and isomorphism between fuzzy graphs was introduced by Bhutani in [4]. The notion of fuzzy line graph was introduced by Mordeson in [13]. Mordeson and Nair [15] defined the complement of fuzzy graph and further studied by Sunitha and Kumar [21]. After that several researchers are working on fuzzy graphs. Samanta and Pal introduced several types of fuzzy graphs such as fuzzy planar graphs [29], fuzzy competition graphs [26, 27], fuzzy tolerance graphs [22], fuzzy threshold graphs [23], etc. Some related work on fuzzy graphs may be found on [3, 5, 11, 16, 17].

Zhang [32–34] introduced the concept of bipolar fuzzy sets as a generalization of fuzzy sets in 1994. The idea which lies behind such description is connected with the existence of “bipolar information” (i.e. positive information and negative information) about the given set. Positive information represents what is granted to be possible, while negative information represents what is considered to be impossible. The range of membership degree of a bipolar fuzzy set is $[-1,1]$. In a bipolar fuzzy set, the membership degree 0 of an element means that the element is irrelevant to the corresponding property, the membership degree (0, 1] of an element indicates that the element somewhat satisfies the property, and the membership degree $[-1,0)$ of an element indicates that the element somewhat satisfies the implicit counter-property.

In 2011, using the concepts of bipolar fuzzy sets, Akram [1] introduced the notion of bipolar fuzzy graphs and defined different operations on it. Using this definition of bipolar fuzzy graphs, many research is going on till date. Some more work on bipolar fuzzy graphs may be found on [2, 6, 24, 25, 28, 31]. Talebi and Rashmanlou [30] studied on complement and isomorphism on bipolar fuzzy graphs. Later on, Rashmanlou et al. [19, 20] studied bipolar fuzzy graphs and bipolar fuzzy graphs with categorical properties. Moreover, as a generalization of bipolar fuzzy graphs, Ghorai and Pal [7] introduced the notion of m-polar fuzzy graphs and defined different operations on it. Some more work on m-polar fuzzy graph may be found on [8, 9].

In this paper, the concepts of regular and totally regular product bipolar fuzzy graphs is introduced. Then necessary and sufficient condition is established under which regular and totally regular product bipolar fuzzy graph becomes equivalent. The notion of product bipolar fuzzy line graph is introduced and investigated some of its properties. A necessary and sufficient condition is given for a product bipolar fuzzy graph to be isomorphic to its corresponding product bipolar fuzzy line graph. It is also examined when an isomorphism between two product bipolar fuzzy graphs follows from an isomorphism of their corresponding fuzzy line graphs.

Preliminaries

In this section, we recall some definitions which are used throughout the paper. For further study see references [10, 12–15].

Definition 2.1

[10] A graph is an ordered pair $G^*=(V,E)$, where V is the set of vertices of $G^*$ and E is the set of all edges of $G^*$. Two vertices x and y in an undirected graph $G^*$ are said to be adjacent in $G^*$ if xy is an edge of $G^*$. A simple graph is an undirected graph that has no loops and not more than one edge between any two different vertices.

Definition 2.2

[10] A subgraph of a graph $G^*=(V,E)$ is a graph $H=(W,F)$, where $W\subseteq V$ and $F\subseteq E$.

We write $xy\in E$ to mean $(x,y)\in E$, and if $e=xy\in E$, we say x and y are adjacent. Formally, given a graph $G^*=(V,E)$, two vertices $x,y\in V$ are said to be neighbors or adjacent nodes, if $xy\in E$. The neighborhood of a vertex v in a graph $G^*$ is the induced subgraph of $G^*$ consisting of all vertices adjacent to v and all edges connecting two such vertices. The neighborhood of v is often denoted by N(v). The degree deg(v) of vertex v is the number of edges incident on v. The open neighborhood for a vertex v in a graph $G^*$ consists of all vertices adjacent to v but not including v, i.e. $N(v)=\{u\in V: uv\in E\}$. If v is included in N(v), then it is called closed neighborhood for v and is denoted by N[v], i.e. $N[v]=N(v)\cup \{v\}$. A regular graph is a graph where each vertex has the same open neighborhood degree. A complete graph is a simple graph in which every pair of distinct vertices has an edge.

An isomorphism $\phi$ of the graphs $G^*_1$ and $G^*_2$ is a bijection between the vertex sets of $G^*_1$ and $G^*_2$ such that any two vertices $v_1$ and $v_2$ of $G^*_1$ are adjacent in $G^*_1$ if and only if $\phi (v_1)$ and $\phi (v_2)$ are adjacent in $G^*_2$. If $G^*_1$ and $G^*_2$ are isomorphic, then we denote it by $G^*_1\cong G^*_2$.

The line graph $L(G^*)$ of a simple graph $G^*$ is a graph which represents the adjacentness between edges of $G^*$. For a graph $G^*$, its line graph $L(G^*)$ is a graph such that:

• (i) each vertex of $L(G^*)$ represents an edge of $G^*$, and

• (ii) two vertices of $L(G^*)$ are adjacent if and only if their corresponding edges have a common end point in $G^*$.

Let $G^*=(V,E)$ be a graph where $V=\{v_1,v_2,\ldots ,v_n\}$. Let $S_i=\{v_i,x_{i1},\ldots ,x_{iq_i}\}$ where $x_{ij}\in E$ and $x_{ij}$ has $v_i$ as a vertex, $j=1,2,\ldots ,q_i$; $i=1,2,\ldots ,n$. Let $S=\{S_1,S_2,\ldots ,S_n\}$. Let $T=\{S_iS_j: S_i,S_j\in S, S_i\cap S_j\ne \emptyset , i\ne j\}$. Then $P(S)=(S,T)$ is an intersection graph and $P(S)=G^*$. The line graph $L(G^*)$ of $G^*$, is by definition the intersection graph P(E). That is, $L(G^*)=(Z,W)$ where $Z=\{\{x\}\cup \{u_x,v_x\}: x\in E,u_x,v_x\in V, x=u_xv_x\}$ and $W=\{S_xS_y: S_x\cap S_y\ne \emptyset ,x,y\in E,x\ne y\}$ and $S_x=\{x\}\cup \{u_x,v_x\},\,x\in E$.

Definition 2.3

[32] Let X be a non-empty set. A bipolar fuzzy set B in X is an object having the form $B=\{(x,\mu ^{P}_{B}(x),\mu ^{N}_{B}(x)): x\in X\}$, where $\mu ^{P}_{B}:X\rightarrow [0,1]$ and $\mu ^{N}_{B}:X\rightarrow [-1,0]$ are mappings.

The membership degree $\mu ^{P}_{B}(x)$ denotes the satisfaction degree of an element x to the property corresponding to a bipolar fuzzy set B and the negative membership degree $\mu ^{N}_{B}(x)$ denotes the satisfaction degree of an element x to some implicit counter-property corresponding to a bipolar fuzzy set B. If $\mu ^{P}_{B}(x)\ne 0$ and $\mu ^{N}_{B}(x)=0$, it is the situation that x is regarded as having only positive satisfaction for B. If $\mu ^{P}_{B}(x)=0$ and $\mu ^{N}_{B}(x)\ne 0$, it is the situation that x does not satisfy the property of B, but somewhat satisfies the counter-property of B. It is possible for an element x to be such that $\mu ^{P}_{B}(x)\ne 0$ and $\mu ^{N}_{B}(x)\ne 0$ when the membership function of the property overlaps that of its counter-property over some portion of X. For the simplicity, we use the symbol $B=(\mu ^{P}_{B},\mu ^{N}_{B})$ for the bipolar fuzzy set $B=\{(x,\mu ^{P}_{B}(x),\mu ^{N}_{B}(x)): x\in X\}$.

Definition 2.4

[32] Let X be a non-empty set. Then we call a mapping $A=(\mu ^{P}_{A},\mu ^{N}_{A}):X\times X\rightarrow [0,1]\times [-1,0]$ a bipolar fuzzy relation on X such that $\mu ^{P}_{A}(x,y)\in [0,1]$ and $\mu ^{N}_{A}(x, y) \in [-1,0]$.

Definition 2.5

[32] Let $A=(\mu ^{P}_{A}, \mu ^{N}_{A})$ and $B=(\mu ^{P}_{B}, \mu ^{N}_{B})$ be bipolar fuzzy sets on a set X. If $A=(\mu ^{P}_{A}, \mu ^{N}_{A})$ is a bipolar fuzzy relation on a set X, then $A=(\mu ^{P}_{A}, \mu ^{N}_{A})$ is called a bipolar fuzzy relation on $B=(\mu ^{P}_{B}, \mu ^{N}_{B})$ if $\mu ^{P}_{A}(x,y) \le min(\mu ^{P}_{B}(x),\mu ^{P}_{B}(y))$ and $\mu ^{N}_{A}(x,y) \ge max(\mu ^{N}_{B}(x), \mu ^{N}_{B}(y))$ for all $x, y \in X$. A bipolar fuzzy relation A on X is called symmetric if $\mu ^{P}_{A}(x,y)=\mu ^{P}_{A}(y,x)$ and $\mu ^{N}_{A}(x,y)=\mu ^{N}_{A}(y,x)$ for all $x,y \in X$.

For a given set V, define an equivalence relation $\sim$ on $V\times V-\{(x,x): x\in V\}$ as follows: $(x_1,y_1)\sim (x_2,y_2)\Leftrightarrow$ either $(x_1,y_1)=(x_2,y_2)$ or $x_1=y_2$ and $y_1=x_2$. The quotient set obtained in this way is denoted by $\widetilde{V^2}$, and the equivalence class that contains the element (x, y) is denoted as xy or yx.

Regular Product Bipolar Fuzzy Graphs

Throughout the paper, $G^*$ represents be a crisp graph and G will be a product bipolar fuzzy graph.

Definition 3.1

A product bipolar fuzzy graph of a graph $G^*=(V,E)$ is a pair $G=(A,B)$ where $A=(\mu ^{P}_{A}, \mu ^{N}_{A})$ is an bipolar fuzzy set in V and $B=(\mu ^{P}_{B}, \mu ^{N}_{B})$ is a bipolar fuzzy relation on $\widetilde{V^2}$ such that $\mu ^{P}_{B}(xy)\le \mu ^{P}_{A}(x)\times \mu ^{P}_{A}(y),\,\mu ^{N}_{B}(xy)\ge -(\mu ^{N}_{A}(x)\times \mu ^{N}_{A}(y))$ for all $xy\in \widetilde{V^2}$ and $\mu ^{P}_{B}(xy)=\mu ^{N}_{B}(xy)=0$ for all $xy\in (\widetilde{V^2}-E)$.

Example 3.2

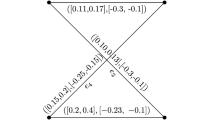
Let us consider the graph $G^*=(V,E)$ where $V=\{v_1,v_2,v_3,v_4\}$ and $E=\{v_1v_4,v_2v_3\}$. A product bipolar fuzzy graph G of $G^*$ is shown in Fig. 1.

Fig. 1

Product bipolar fuzzy graph G

Definition 3.3

A product bipolar fuzzy graph $G=(A,B)$ of $G^*=(V,E)$ is said to be strong if $\mu ^{P}_{B}(xy)=\mu ^{P}_{A}(x)\times \mu ^{P}_{A}(y)$ and $\mu ^{N}_{B}(xy)=-\mu ^{N}_{A}(x)\times \mu ^{N}_{A}(y)$ for all $xy\in E$.

The product bipolar fuzzy graph G in Fig. 1 is not strong.

Definition 3.4

Let $G=(A,B)$ be a product bipolar fuzzy graph of $G^*=(V,E)$. The open neighborhood degree of a vertex v in G is defined by $deg(v)=(deg^P(v),deg^N(v))$, where $deg^P(v)=\sum _{\begin{array}{c} u\ne v\\ uv\in E \end{array}}\mu ^{P}_{B}(uv)$ and $deg^N(v)=\sum _{\begin{array}{c} u\ne v\\ uv\in E \end{array}} \mu ^{N}_{B}(uv)$. If all the vertices of G have the same open neighborhood degree $(d_1,d_2)$, then G is called $(d_1,d_2)$-regular product bipolar fuzzy graph.

Definition 3.5

Let $G=(A,B)$ be a regular product bipolar fuzzy graph of $G^*=(V,E)$. The order of G is defined as $O(G)=(O^P(G),O^N(G))$ where $O^P(G)=\sum _{v\in V}\mu ^{P}_{A}(v)$ and $O^N(G)=\sum _{v\in V}\mu ^{N}_{A}(v)$. The size of G is defined as $S(G)=(S^P(G),S^N(G))$ where $S^P(G)=\sum _{uv\in E}\mu ^{P}_{B}(uv)$ and $S^N(G)=\sum _{uv\in E}\mu ^{N}_{B}(uv)$.

Definition 3.6

Let $G=(A,B)$ be a product bipolar fuzzy graph of $G^*=(V,E)$. The closed neighborhood degree of a vertex v is defined by $deg[v]=(deg^P[v],deg^N[v])$, where $deg^P[v]=deg^P(v)+\mu ^{P}_{A}(v)$ and $deg^N[v]=deg^N(v)+\mu ^{N}_{A}(v)$. If each vertex of G has the same closed neighborhood degree $(f_1,f_2)$, then G is called $(f_1,f_2)$-totally regular product bipolar fuzzy graph.

Next, it is shown with the examples that a product bipolar fuzzy graphs may be both regular and totally regular, neither totally regular nor regular and totally regular but not regular. In other words, there is no relation between regular and totally regular product bipolar fuzzy graphs.

Fig. 2

G is $(0.27,-0.06)$-regular and $(0.67,-0.26)$-totally regular product bipolar fuzzy graph

First of all we give an example of a product bipolar fuzzy graph which is both regular and totally regular (see Fig. 2).

Example 3.7

Let us consider the graph $G^*=(V,E)$ where $V=\{v_1,v_2,v_3,v_4\}$ and $E=\{v_1v_2,v_2v_4,v_3v_4,v_1v_3\}$ and consider the product bipolar fuzzy graph $G=(A,B)$ of $G^*$ (see Fig. 2). Here, $deg(v_1)=deg(v_2)=deg(v_3)=deg(v_4)=(0.27,-0.06)$ and $deg[v_1]=deg[v_2]=deg[v_3]=deg[v_4]=(0.67,-0.26)$. Hence, G is both $(0.27,-0.06)$-regular and $(0.67,-0.26)$-totally regular product bipolar fuzzy graph.

Now, we give an example of a product bipolar fuzzy graph which is neither regular nor totally regular (see Fig. 3).

Example 3.8

Let us consider a product bipolar fuzzy graph $G=(A,B)$ of $G^*=(V,E)$ where $V=\{v_1,v_2,v_3\}$ and $E=\{v_1v_2,v_1v_3\}$ (see Fig. 3). We have, $deg(v_1)=(0.27,-0.31), deg(v_2)=(0.15,-0.2), deg(v_3)=(0.12,-0.11)$ and $deg[v_1]=(0.57,-0.61), deg[v_2]=(0.75,-1), deg[v_3]=(0.62,-0.61)$. Hence, G is neither regular nor totally regular product bipolar fuzzy graph.

Fig. 3

G is neither regular nor totally regular product bipolar fuzzy graph

The following example shows that a product bipolar fuzzy graph may be totally regular but not regular (see Fig. 4).

Example 3.9

Consider the product bipolar fuzzy graph G given in Fig. 4. Since $deg(v_1)=deg(v_2)=(0.27,-0.06)\ne deg(v_3)=(0.24,-0.06)$ and $deg[v_1]=deg[v_2]=deg[v_3]=(0.67,-0.26)$, therefore G is $(0.67,-0.26)$-totally regular and but not regular product bipolar fuzzy graph.

Fig. 4

G is $(0.67,-0.26)$-totally regular but not regular product bipolar fuzzy graph

Similarly, we can give example of a product bipolar fuzzy graph which is regular but not totally regular (see Fig. 5).

Fig. 5

G is $(0.24,-0.06)$-regular but not totally regular product bipolar fuzzy graph

Next we have the following propositions.

Proposition 3.10

Let $G=(A,B)$ be a $(d_1,d_2)$-regular product bipolar fuzzy graph of $G^*=(V,E)$. Then $S(G)=\frac{n}{2}(d_1,d_2)$ where $\vert V \vert =n$.

Proof

Since G is $(d_1,d_2)$-regular, therefore we have $deg(v)=(d_1,d_2)$ for all $v\in V$.

This implies $deg^P(v)=\sum _{\begin{array}{c} u\ne v\\ uv\in E \end{array}}\mu ^{P}_{B}(uv)=d_1$ and $deg^N(v)=\sum _{\begin{array}{c} u\ne v\\ uv\in E \end{array}} \mu ^{N}_{B}(uv)=d_2$ for all $v\in V$.

Therefore, $\sum _{v\in V}\sum _{\begin{array}{c} u\ne v\\ uv\in E \end{array}}\mu ^{P}_{B}(uv)=\sum _{v\in V}d_1$

i.e $2\sum _{\begin{array}{c} u\ne v\\ uv\in E \end{array}}\mu ^{P}_{B}(uv)=nd_1$

i.e $2S^P(G)=nd_1$ i.e $S^P(G)=\frac{n}{2}d_1$.

Similarly, $\sum _{v\in V}\sum _{\begin{array}{c} u\ne v\\ uv\in E \end{array}}\mu ^{N}_{B}(uv)=\sum _{v\in V}d_1$

i.e $2\sum _{\begin{array}{c} u\ne v\\ uv\in E \end{array}}\mu ^{N}_{B}(uv)=nd_2$

i.e $2S^N(G)=nd_2$ i.e $S^N(G)=\frac{n}{2}d_2$.

Hence $S(G)=(\frac{n}{2}d_1,\frac{n}{2}d_2)=\frac{n}{2}(d_1,d_2)$. $\square$

Proposition 3.11

Let $G=(A,B)$ be a $(f_1,f_2)$-totally regular product bipolar fuzzy graph of $G^*=(V,E)$. Then $2S(G)+O(G)=n(f_1,f_2)$ where $\vert V \vert =n$.

Proof

Since G is $(f_1,f_2)$-totally regular, therefore we have $deg[v]=(f_1,f_2)$ for all $v\in V$.

This implies $deg^P[v]=f_1$ and $deg^N[v]=f_2$ for all $v\in V$.

Therefore, $deg^P(v)+\mu ^{P}_{A}(v)=f_1$ and $deg^N(v)+\mu ^{N}_{A}(v)=f_2$ for all $v\in V$.

Hence, $\sum _{v\in V}deg^P(v)+\sum _{v\in V}\mu ^{P}_{A}(v)=\sum _{v\in V}f_1$ and $\sum _{v\in V}deg^N(v)+\sum _{v\in V}\mu ^{N}_{A}(v) =\sum _{v\in V}f_2$

i.e $2S^P(G)+O^P(G)=nf_1$ and $2S^N(G)+O^N(G)=nf_2$.

That is, $2S(G)+O(G)=(2S^P(G)+O^P(G),2S^N(G)+O^N(G))=(nf_1,nf_2)=n(f_1,f_2)$. $\square$

Proposition 3.12

Let $G=(A,B)$ be a $(d_1,d_2)$-regular and $(f_1,f_2)$-totally regular product bipolar fuzzy graph of $G^*=(V,E)$. Then $O(G)=n(f_1-d_1,f_2-d_2)$ where $\vert V \vert =n$.

Proof

From Proposition 3.11, we have,

$$\begin{aligned} 2S(G)+O(G)=n(f_1,f_2) \end{aligned}$$

i.e $O(G)=n(f_1,f_2)-2S(G)=n(f_1,f_2)-2\frac{n}{2}(d_1,d_2)$ (by Proposition 3.10)

$=n(f_1-d_1,f_2-d_2)$. $\square$

Theorem 3.13

Let $G=(A,B)$ be a product bipolar fuzzy graph of $G^*=(V,E)$. Then $A=(\mu ^{P}_{A},\mu ^{N}_{A})$ is constant function if and only if the following are equivalent:

• (i) G is a $(d_1,d_2)$-regular bipolar fuzzy graph,

• (ii) G is a $(f_1,f_2)$-totally regular bipolar fuzzy graph.

Proof

Let us assume that $A=(\mu ^{P}_{A},\mu ^{N}_{A})$ is constant function. Therefore, let $\mu ^{P}_{A}(v)=a_1$ and $\mu ^{N}_{A}(v)=a_2$ for all $v\in V$, where $a_1\in [0,1 ]$ and $a_2\in [-1,0]$.

We will now show that the statements (i) and (ii) are equivalent.

$(i)\Rightarrow (ii){:}$ Let G be a $(d_1,d_2)$-regular product bipolar fuzzy graph. Therefore, $deg(v)=(deg^P(v),deg^N(v))=(d_1,d_2)$ for all $v\in V$.

Now, $deg[v]=(deg^P[v],deg^N[v])=(deg^P(v)+\mu ^{P}_{A}(v),deg^N(v)+\mu ^{N}_{A}(v))=(d_1+a_1,d_2+a_2)$ for all $v\in V$. Hence, G is $(d_1+a_1,d_2+a_2)$-totally regular product bipolar fuzzy graph.

$(ii)\Rightarrow (i){:}$ Let G be a $(f_1,f_2)$- totally regular product bipolar fuzzy graph.

Then $deg[v]=(deg^P[v],deg^N[v])=(f_1,f_2)$ for all $v\in V$.

That is, $deg^P(v)+\mu ^{P}_{A}(v)=f_1$ and $deg^N(v)+\mu ^{N}_{A}(v)=f_2$ for all $v\in V$,

or $deg^P(v)=f_1-a_1$ and $deg^N(v)=f_2-a_2$ for all $v\in V.$

Hence, G is $(f_1-a_1,f_2-a_2)$-regular product bipolar fuzzy graph.

Conversely let, (i) and (ii) are equivalent.

Suppose A is not constant function. This means there exist at least two vertices $u,v\in V$ such that $\mu ^{P}_{A}(u)\ne \mu ^{P}_{A}(v)$ and $\mu ^{N}_{A}(u)\ne \mu ^{N}_{A}(v)$.

Let G be a $(d_1,d_2)$-regular product bipolar fuzzy graph.

Then, $deg[u]=(deg^P(u)+\mu ^{P}_{A}(u),deg^N(u)+\mu ^{N}_{A}(u))=(d_1+\mu ^{P}_{A}(u),d_2+\mu ^{N}_{A}(u))$ and

$deg[v]=(deg^P(v)+\mu ^{P}_{A}(v),deg^N(v)+\mu ^{N}_{A}(v))=(d_1+\mu ^{P}_{A}(v),d_2+\mu ^{N}_{A}(v))$.

This shows that $deg[u]\ne deg[v]$ since $\mu ^{P}_{A}(u)\ne \mu ^{P}_{A}(v)$ and $\mu ^{N}_{A}(u)\ne \mu ^{N}_{A}(v)$.

Hence, G is not totally regular which is a contradiction to the assumption that (i) and (ii) are equivalent. Therefore, A must be constant.

In a similar way, we can show that if A is not constant function, then G totally regular does not imply that G is regular. This completes the proof. $\square$

Proposition 3.14

If a product bipolar fuzzy graph $G=(A,B)$ is both regular and totally regular, then $A=(\mu ^{P}_{A},\mu ^{N}_{A})$ is constant.

Proof

Let G be a $(d_1,d_2)$-regular and $(f_1,f_2)$-totally regular product bipolar fuzzy graph.

Now, $deg^P[v]=deg^P(v)+\mu ^{P}_{A}(v)=d_1+\mu ^{P}_{A}(v)=f_1$ and $deg^N[v]=deg^N(v)+\mu ^{N}_{A}(v)=d_2+\mu ^{N}_{A}(v)=f_2$ for all $v\in V$.

Hence, $\mu ^{P}_{A}(v)=f_1-d_1$ and $\mu ^{N}_{A}(v)=f_2-d_2$ for all $v\in V$. This shows that $A(v)=(\mu ^{P}_{A}(v),\mu ^{N}_{A}(v))=(f_1-d_1,f_2-d_2)$ for all $v\in V$ i.e A is constant. $\square$

Remark 3.15

The converse of the Proposition 3.14 is not true always. For example, consider the product bipolar fuzzy graph $G=(A,B)$ of $G^*=(V,E)$ where $V=\{v_1,v_2,v_3\}$ and $E=\{v_1v_2,v_2v_3,v_3v_1\}$ (see Fig. 6). Here, $A(v)=(\mu ^{P}_{A}(v),\mu ^{N}_{A}(v))=(0.4,-0.2)$ for all $v\in V$ i.e A is constant but G is neither regular nor totally regular.

Fig. 6

A is constant but G is neither regular nor totally regular

Theorem 3.16

Let $G=(A,B)$ be a product bipolar fuzzy graph of $G^*=(V,E)$ where $G^*$ is an odd cycle. Then G is regular product bipolar fuzzy graph of $G^*$ if and only if $B=(\mu ^{P}_{B},\mu ^{N}_{B})$ is constant.

Proof

Let G be a $(d_1,d_2)$-regular product bipolar fuzzy graph. Let $e_{1}, e_{2},\ldots , e_{2n+1}$ be the edges of $G^*$ such that $e_i=v_{i-1}v_i\in E,\,v_0,v_i\in V,\,i=1,2\ldots ,2n+1$ and $v_0=v_{2n+1}$.

Let $\mu ^{P}_{B}(e_1)=k_1$ and $\mu ^{N}_{B}(e_1)=k_2$ where $k_1\in [0,1]$ and $k_2\in [-1,0]$.

G is $(d_1,d_2)$-regular implies that $deg^P(v_1)=d_1$ and $deg^N(v_1)=d_2$.

This means, $deg^P(v_1)=\mu ^{P}_{B}(e_1)+\mu ^{P}_{B}(e_2)=d_1$ and $deg^N(v_1)=\mu ^{N}_{B}(e_1)+\mu ^{N}_{B}(e_2)=d_2$.

i.e. $k_1+\mu ^{P}_{B}(e_2)=d_1$ and $k_2+\mu ^{N}_{B}(e_2)=d_2$.

i.e. $\mu ^{P}_{B}(e_2)=d_1-k_1$ and $\mu ^{N}_{B}(e_2)=d_2-k_2$.

Again, $deg^P(v_2)=\mu ^{P}_{B}(e_2)+\mu ^{P}_{B}(e_3)=d_1$ and $deg^N(v_2)=\mu ^{N}_{B}(e_2)+\mu ^{N}_{B}(e_3)=d_2$.

This implies, $\mu ^{P}_{B}(e_3)=d_1-(d_1-k_1)=k_1$ and $\mu ^{N}_{B}(e_3)=d_2-(d_2-k_2)=k_2$, and so on.

Therefore, $\mu ^{P}_{B}(e_i)$ $=\left\{ \begin{array}{ccccc} k_1 &{}if&{}i&{}is&{}odd\\ (d_1-k_1) &{}if&{}i&{}is&{}even\\ \end{array}\right.$

and $\mu ^{N}_{B}(e_i)$ $=\left\{ \begin{array}{ccccc} k_2 &{}if&{}i&{}is&{}odd\\ (d_2-k_2) &{}if&{}i&{}is&{}even\\ \end{array}\right.$

Therefore, $\mu ^{P}_{B}(e_1)=\mu ^{P}_{B}(e_{2n+1})=k_1$ and $\mu ^{N}_{B}(e_1)=\mu ^{N}_{B}(e_{2n+1})=k_2$.

Sice $e_1$ and $e_{2n+1}$ are incident on the vertex $v_0$, and $deg(v_0)=(d_1,d_2)$, therefore we have, $\mu ^{P}_{B}(e_1)+\mu ^{P}_{B}(e_{2n+1})=d_1$ and $\mu ^{N}_{B}(e_1)+\mu ^{N}_{B}(e_{2n+1})=d_2$.

i.e $2k_1=d_1$ and $2k_2=d_2$.

i.e $k_1=\frac{d_1}{2}$ and $k_2=\frac{d_2}{2}$.

Therefore, $\mu ^{P}_{B}(e_i)=\frac{d_1}{2}$ and $\mu ^{N}_{B}(e_i)=\frac{d_2}{2}$ for all $i=1,2\ldots ,2n+1$. Hence B is constant.

Conversely, let B be a constant function. Let $B(uv)=(\mu ^{P}_{B}(uv),\mu ^{N}_{B}(uv))=(k_1,k_2)$ for all $uv\in E$, where $k_1\in [0,1]$ and $k_2\in [-1,0]$.

Then $deg(v)=(deg^P(v),deg^N(v))=(\sum _{\begin{array}{c} u\ne v\\ uv\in E \end{array}}\mu ^{P}_{B}(uv),\sum _{\begin{array}{c} u\ne v\\ uv\in E \end{array}}\mu ^{P}_{B}(uv))=(2k_1,2k_2)$ for all $v\in V$.

Consequently, G is $(2k_1,2k_2)$-regular product bipolar fuzzy graph. $\square$

Product Bipolar Fuzzy Line Graphs

In this section, first we define a product bipolar fuzzy intersection graph of a product bipolar fuzzy graph. Then we define the product bipolar fuzzy line graphs.

Definition 4.1

Let $P(S)=(S,T)$ be an intersection graph of a simple graph $G^*=(V,E)$. Let $G=(A,B)$ be a product bipolar fuzzy graph of $G^*$. We define a product bipolar fuzzy intersection graph $P(G)=(A_1,B_1)$ of P(S) as follows:

• (i) $A_1$ and $B_1$ are bipolar fuzzy subsets of S and T respectively,

• (ii) $\mu ^{P}_{A_1}(S_i)=\mu ^{P}_{A}(v_i),\,\mu ^{N}_{A_1}(S_i)=\mu ^{N}_{A}(v_i)$,

• (iii) $\mu ^{P}_{B_1}(S_iS_j)=\mu ^{P}_{B}(v_iv_j),\,\mu ^{N}_{B_1}(S_iS_j)=\mu ^{N}_{B}(v_iv_j)$ for all $S_i, S_j\in S,\,S_iS_j\in T$. In other words, any product bipolar fuzzy graph of P(S) is called a product bipolar fuzzy intersection graph.

The following Proposition is immediate.

Proposition 4.2

Let $G=(A,B)$ be a product bipolar fuzzy graph of $G^*=(V,E)$ and $P(G)=(A_1,B_1)$ be a product bipolar intersection graph of P(S). Then the following holds:

• (a) P(G) is a product bipolar fuzzy graph of P(S),

• (b) $G\cong P(G)$.

Proof

(a) Since $G=(A,B)$ is a product bipolar fuzzy graph we have by Definition 4.1,

$$\begin{aligned} \mu ^{P}_{B_1}(S_iS_j)= & {} \mu ^{P}_{B}(v_iv_j)\le \mu ^{P}_{A}(v_i)\times \mu ^{P}_{A}(v_j)=\mu ^{P}_{A_1}(S_i)\times \mu ^{P}_{A_1}(S_j)\hbox { and }\\ \mu ^{N}_{B_1}(S_iS_j)= & {} \mu ^{N}_{B}(v_iv_j)\ge -(\mu ^{N}_{A}(v_i)\times \mu ^{N}_{A}(v_j))=-(\mu ^{N}_{A_1}(S_i)\times \mu ^{N}_{A_1}(S_j)). \end{aligned}$$

Hence, P(G) is a product bipolar fuzzy graph.

(b) Let us define a mapping $\phi : V\rightarrow S$ by $\phi (v_i)=S_i$ for $i=1,2,\ldots ,n$. Then clearly $\phi$ is one to one mapping of V onto S.

Now $v_iv_j\in E$ if and only if $S_iS_j\in T$ and $T=\{\phi (v_i)\phi (v_j): v_iv_j\in E\}$.

Also, $\mu ^{P}_{A}(v_i)=\mu ^{P}_{A_1}(S_i)=\mu ^{P}_{A_1}(\phi (v_i))$ and $\mu ^{N}_{A}(v_i)=\mu ^{N}_{A_1}(S_i)=\mu ^{N}_{A_1}(\phi (v_i))$ for all $v_i\in V$,

$\mu ^{P}_{B}(v_iv_j)=\mu ^{P}_{B_1}(S_iS_j)=\mu ^{P}_{B}(\phi (v_i) \phi (v_j))$ and $\mu ^{N}_{B}(v_iv_j)=\mu ^{N}_{B_1}(S_iS_j)=\mu ^{N}_{B}(\phi (v_i) \phi (v_j))$ for all $v_iv_j\in E$.

Hence, $\phi$ is an isomorphism of G onto P(G), i.e $G\cong P(G)$. $\square$

This proposition shows that any product bipolar fuzzy graph is isomorphic to a product bipolar fuzzy intersection graph. Next, we define the product bipolar fuzzy line graph of a product bipolar fuzzy graph.

Definition 4.3

Let $L(G^*)=(Z,W)$ be a line graph of a simple graph $G^*=(V,E)$. Let $G=(A,B)$ be a product bipolar fuzzy graph of $G^*$. Then a product bipolar fuzzy line graph $L(G)=(A_1,B_1)$ of G is defined as follows:

• (i) $A_1$ and $B_1$ are bipolar fuzzy subsets of Z and W respectively,

• (ii) $\mu ^{P}_{A_1}(S_x)=\mu ^{P}_{B}(x)=\mu ^{P}_{B}(u_xv_x)$,

• (iii) $\mu ^{N}_{A_1}(S_x)=\mu ^{N}_{B}(x)=\mu ^{N}_{B}(u_xv_x)$,

• (iv) $\mu ^{P}_{B_1}(S_xS_y)=\mu ^{P}_{B}(x)\times \mu ^{P}_{B}(y)=\mu ^{P}_{B}(u_xv_x)\times \mu ^{P}_{B}(u_yv_y)$,

• (v) $\mu ^{N}_{B_1}(S_xS_y)=-(\mu ^{N}_{B}(x)\times \mu ^{N}_{B}(y))=-(\mu ^{N}_{B}(u_xv_x)\times \mu ^{N}_{B}(u_yv_y))$ for all $S_x, S_y\in Z$ and $S_xS_y\in W$.

Fig. 7

G is a product bipolar fuzzy graph

Example 4.4

Let us consider a graph $G^*=(V,E)$ where $V=\{v_1,v_2,v_3,v_4\}$ and $E=\{x_1=v_1v_2, x_2=v_2v_3, x_3=v_3v_4, x_4=v_4v_1\}$. Let $G=(A,B)$ be a product bipolar fuzzy graph of $G^*$ (see Fig. 7).

Now, consider a line graph $L(G^*)=(Z,W)$ such that $Z=\{S_{x_1}, S_{x_2}, S_{x_3}, S_{x_4}\}$ and $W=\{S_{x_1}S_{x_2}, S_{x_2}S_{x_3}, S_{x_3}S_{x_4}, S_{x_4}S_{x_1}\}$.

Let $A_1$ and $B_1$ be bipolar fuzzy subsets of Z and W respectively. Then by definition of product bipolar fuzzy line graph we have the following:

$$\begin{aligned}&\mu ^{P}_{A_1}(S_{x_1})=\mu ^{P}_{B}(x_1)=0.14, \mu ^{P}_{A_1}(S_{x_2})=\mu ^{P}_{B}(x_2)=0.18, \mu ^{P}_{A_1}(S_{x_3})=\mu ^{P}_{B}(x_3)=0.2,\\&\mu ^{P}_{A_1}(S_{x_4})=\mu ^{P}_{B}(x_4)=0.2, \mu ^{N}_{A_1}(S_{x_1})=\mu ^{N}_{B}(x_1)=-0.07, \mu ^{N}_{A_1}(S_{x_2})=\mu ^{N}_{B}(x_2)=-0.05,\\&\mu ^{N}_{A_1}(S_{x_3})=\mu ^{N}_{B}(x_3)=-0.14, \mu ^{N}_{A_1}(S_{x_4})=\mu ^{N}_{B}(x_4)=-0.18.\\&\mu ^{P}_{B_1}(S_{x_1}S_{x_2})=\mu ^{P}_{B}(x_1)\times \mu ^{P}_{B}(x_2)=0.14\times 0.18=0.0252, \mu ^{P}_{B_1}(S_{x_2}S_{x_3})=\mu ^{P}_{B}(x_2)\\&\quad \times \mu ^{P}_{B}(x_3)=0.18\times 0.2=0.036, \mu ^{P}_{B_1}(S_{x_3}S_{x_4})=\mu ^{P}_{B}(x_3)\times \mu ^{P}_{B}(x_4)=0.2\\&\quad \times 0.2=0.04, \mu ^{P}_{B_1}(S_{x_4}S_{x_1})=\mu ^{P}_{B}(x_4)\times \mu ^{P}_{B}(x_1)=0.2\\&\quad \times 0.14=0.028, \mu ^{N}_{B_1}(S_{x_1}S_{x_2})=-(\mu ^{N}_{B}(x_1)\times \mu ^{N}_{B}(x_2))=-(-0.07\\&\quad \times -0.05)=-0.0035,\mu ^{N}_{B_1}(S_{x_2}S_{x_3})=-(\mu ^{N}_{B}(x_2)\times \mu ^{N}_{B}(x_3))=-(-0.05\\&\quad \times -0.14)=-0.007,\mu ^{N}_{B_1}(S_{x_3}S_{x_4})=-(\mu ^{N}_{B}(x_3)\times \mu ^{N}_{B}(x_4))=-(-0.14\\&\quad \times -0.18)=-0.0252,\mu ^{N}_{B_1}(S_{x_4}S_{x_1})=-(\mu ^{N}_{B}(x_4)\\&\quad \times \mu ^{N}_{B}(x_1))=-(-0.18\times -0.07)=-0.0126. \end{aligned}$$

Hence, $L(G)=(A_1,B_1)$ is the product bipolar fuzzy line graph of G (see Fig. 8). It may be noted that L(G) is neither regular nor totally regular product bipolar fuzzy line graph.

Proposition 4.5

A product bipolar fuzzy line graph is a strong product bipolar fuzzy graph.

Proof

Follows from the Definition of product bipolar fuzzy line graph. $\square$

Proposition 4.6

If L(G) is a product bipolar fuzzy line graph of the product bipolar fuzzy graph G, then $L(G^*)$ is the line graph of $G^*$.

Fig. 8

The line graph L(G) of G

Proof

Since $G=(A,B)$ is a product bipolar fuzzy graph and $L(G)=(A_1,B_1)$ is a product bipolar fuzzy line graph, therefore $\mu ^{P}_{A_1}(S_{x})=\mu ^{P}_{B}(x)$ and $\mu ^{N}_{A_1}(S_{x})=\mu ^{N}_{B}(x)$ for all $x\in E$ and so $S_x\in Z$ $\Leftrightarrow x\in E$. Also, $\mu ^{P}_{B_1}(S_xS_y)=\mu ^{P}_{B}(x)\times \mu ^{P}_{B}(y)$ and $\mu ^{N}_{B_1}(S_xS_y)=-(\mu ^{N}_{B}(x)\times \mu ^{N}_{B}(y))$ for all $S_x, S_y\in Z$, and so $W=\{S_xS_y: S_x\cap S_y\ne \emptyset , x,y\in E, x\ne y\}$. This completes the proof. $\square$

Proposition 4.7

$L(G)=(A_1,B_1)$ is a product bipolar fuzzy line graph of some product bipolar fuzzy graph $G=(A,B)$ if and only if $\mu ^{P}_{B_1}(S_{x}S_{y})=\mu ^{P}_{A_1}(S_{x})\times \mu ^{P}_{A_1}(S_{y}))$ and $\mu ^{N}_{B_1}(S_{x}S_{y})=-(\mu ^{N}_{A_1}(S_{x})\times \mu ^{N}_{A_1}(S_{y}))$ for all $S_xS_y\in W$.

Proof

Suppose that $\mu ^{P}_{B_1}(S_{x}S_{y})=\mu ^{P}_{A_1}(S_{x})\times \mu ^{P}_{A_1}(S_{y}))$ and $\mu ^{N}_{B_1}(S_{x}S_{y})=-(\mu ^{N}_{A_1}(S_{x})\times \mu ^{N}_{A_1}(S_{y}))$ for all $S_xS_y\in W$.

Let us now define $\mu ^{P}_{A}(x)=\mu ^{P}_{A_1}(S_x)$ and $\mu ^{N}_{A}(x)=\mu ^{N}_{A_1}(S_x)$ for all $x\in E$.

Then, $\mu ^{P}_{B_1}(S_{x}S_{y})=\mu ^{P}_{A_1}(S_{x})\times \mu ^{P}_{A_1}(S_{y}))=\mu ^{P}_{A}(x)\times \mu ^{P}_{A}(y))$ and

$\mu ^{N}_{B_1}(S_{x}S_{y})=-(\mu ^{N}_{A_1}(S_{x})\times \mu ^{N}_{A_1}(S_{y}))=-(\mu ^{N}_{A}(x)\times \mu ^{N}_{A}(y))$.

A bipolar fuzzy set $A=(\mu ^{P}_{A},\mu ^{N}_{A})$ that yields that the property $\mu ^{P}_{B}(xy)\le \mu ^{P}_{A}(x)\times \mu ^{P}_{A}(y)$ and $\mu ^{N}_{B}(xy)\ge -(\mu ^{N}_{A}(x)\times \mu ^{N}_{A}(y))$ will suffice.

The converse part follows from the Definition 4.3. $\square$

Another characterization of product bipolar fuzzy line graphs of product bipolar fuzzy graph is given in the following proposition.

Proposition 4.8

$L(G)=(A_1,B_1)$ is a product bipolar fuzzy line graph of some product bipolar fuzzy graph if and only if $L(G^*)=(Z,W)$ is a line graph satisfying $\mu ^{P}_{B_1}(uv)=\mu ^{P}_{A_1}(u)\times \mu ^{P}_{A_1}(v)$ and $\mu ^{N}_{B_1}(uv)=-(\mu ^{N}_{A_1}(u)\times \mu ^{N}_{A_1}(v))$ for all $uv\in W$.

Proof

Follows from the Propositions 4.6 and 4.7. $\square$

Definition 4.9

Let $G_1=(A_1,B_1)$ and $G_2=(A_2,B_2)$ be two product bipolar fuzzy graphs of the graphs $G^*_1=(V_1,E_1)$ and $G^*_2=(V_2,E_2)$ respectively. A homomorphism between $G_1$ and $G_2$ is a mapping $\phi : V_1\rightarrow V_2$ such that

• (i) $\mu ^{P}_{A_1}(x)\le \mu ^{P}_{A_2}(\phi (x))$ and $\mu ^{N}_{A_1}(x)\ge \mu ^{N}_{A_2}(\phi (x))$ for all $x\in V_1$,

• (ii) $\mu ^{P}_{B_1}(xy)\le \mu ^{P}_{B_2}(\phi (x)\phi (y))$ and $\mu ^{N}_{B_1}(xy)\ge \mu ^{N}_{B_2}(\phi (x)\phi (y))$ for all $xy\in \widetilde{V^2_1}$.

A bijective homomorphism with the property that $\mu ^{P}_{A_1}(x)=\mu ^{P}_{A_2}(\phi (x))$ and $\mu ^{N}_{A_1}(x)=\mu ^{N}_{A_2}(\phi (x))$ for all $x\in V_1$ is called a (weak) vertex-isomorphism.

A bijective homomorphism with the property that $\mu ^{P}_{B_1}(xy)\le \mu ^{P}_{B_2}(\phi (x)\phi (y))$ and $\mu ^{N}_{B_1}(xy)\ge \mu ^{N}_{B_2}(\phi (x)\phi (y))$ for all $xy\in \widetilde{V^2_1}$, is called a (weak) line-isomorphism.

If $\phi$ is both (weak) vertex isomorphism and (weak) line-isomorphism, then $\phi$ is called a (weak) isomorphism of $G_1$ onto $G_2$. If $G_1$ is isomorphic to $G_2$, then we write $G_1\cong G_2$.

Proposition 4.10

$G_1=(A_1,B_1)$ and $G_2=(A_2,B_2)$ be two product bipolar fuzzy graphs of the graphs $G^*_1=(V_1,E_1)$ and $G^*_2=(V_2,E_2)$ respectively. If $\phi$ is a weak isomorphism $G_1$ onto $G_2$, then $\phi$ is an isomorphism of $G^*_1$ onto $G^*_2$.

Proof

Obvious. $\square$

Proposition 4.11

Let $L(G)=(A_1,B_1)$ be the product bipolar fuzzy line graph corresponding to the product bipolar fuzzy graph $G=(A,B)$ of $G^*=(V,E)$. Suppose that $G^*$ is connected. Then the following hold:

• (i) There exists a weak isomorphism of G onto L(G) if and only if $G^*$ is a cycle and for all $v\in V,\,x\in E,\,\mu ^{P}_{A}(v)=\mu ^{P}_{B}(x),\,\mu ^{N}_{A}(v)=\mu ^{N}_{B}(x)$, i.e. $A=(\mu ^{P}_{A},\mu ^{N}_{A})$ and $B=(\mu ^{P}_{B},\mu ^{N}_{B})$ are constant functions on V and E, respectively, taking on the same value.

• (ii) If $\phi$ is a weak isomorphism of G onto L(G), then $\phi$ is an isomorphism.

Proof

Suppose that $\phi$ is a weak isomorphism of G onto L(G). By Proposition 4.10, $\phi$ is an isomorphism of $G^*$ onto $L(G^*)$. By Proposition 4.6, $G^*$ is a cycle, [12, Theorem 8.2].

Let $V=\{v_1,v_2,\ldots ,v_n\}$ and $E=\{x_1=v_1v_2,x_2=v_2v_3,\ldots ,x_n=v_nv_1\}$, where $v_1v_2\ldots v_nv_1$ is a cycle. Let us define the bipolar fuzzy sets

$$\begin{aligned} \mu ^{P}_{A}(v_i)= & {} s_i,\,\mu ^{N}_{A}(v_i)=\acute{s_i}\hbox { and }\\ \mu ^{P}_{B}(v_iv_{i+1})= & {} t_i,\, \mu ^{P}_{B}(v_iv_{i+1})=\acute{t_i},\,i=1,2,\ldots ,n,\\ v_{n+1}= & {} v_1,\,s_i,t_i\in [0,1],\,\acute{s_i},\acute{t_i}\in [-1,0]. \end{aligned}$$

Then for $s_{n+1}=s_1,\,\acute{s}_{n+1}=\acute{s_1}$,

$$\begin{aligned} (a)\left\{ \begin{array}{c} t_i\le s_i\times s_{i+1}\\ \acute{t_i}\ge -\acute{s_i}\times \acute{s}_{i+1}, i=1,2,\ldots ,n.\\ \end{array}\right. \end{aligned}$$

Now, $Z=\{S_{x_1},S_{x_2}\ldots ,S_{x_n}\}$ and $W=\{S_{x_1}S_{x_2}\,S_{x_2}S_{x_3},\ldots ,S_{x_n}S_{x_1}\}$.

Also for $t_{n+1}=t_1$ and $\acute{t}_{n+1}=\acute{t_1}$,

$$\begin{aligned} \mu ^{P}_{A_1}(S_{x_i})= & {} \mu ^{P}_{B}(x_i)=\mu ^{P}_{B}(v_iv_{i+1})=t_i,\\ \mu ^{N}_{A_1}(S_{x_i})= & {} \mu ^{N}_{B}(x_i)=\mu ^{N}_{B}(v_iv_{i+1})=\acute{t_i} \hbox { and }\\ \mu ^{P}_{B_1}(S_{x_i}S_{x_{i+1}})= & {} \mu ^{P}_{B}(x_i)\times \mu ^{P}_{B}(x_{i+1})=t_i\times t_{i+1},\\ \mu ^{N}_{A_1}(S_{x_i}S_{x_{i+1}})= & {} -\mu ^{N}_{B}(x_i)\times \mu ^{N}_{B}(x_{i+1})=-\acute{t_i}\times \acute{t}_{i+1},\\&i=1,2\ldots ,n,\hbox { where }v_{n+1}=v_1,v_{n+2}=v_2. \end{aligned}$$

Since $\phi$ is an isomorphism of $G^*$ onto $L(G^*),\,\phi$ maps V one-to-one onto Z. Also $\phi$ preserves adjacency. Hence, $\phi$ induces a permutation $\pi$ of $\{1,2,\ldots ,n\}$ such that $\phi (v_i)=S_{x_{\pi (i)}}=S_{v_{\pi (i)}v_{\pi (i+1)}}$ and $x_i=v_iv_{i+1}\rightarrow \phi (v_i)\phi (v_{i+1})=S_{v_{\pi (i)} v_{\pi (i+1)}}S_{v_{\pi (i+1)}v_{\pi (i+2)}},\,i=1,2,\ldots ,(n-1)$.

Now, $s_i=\mu ^{P}_{A}(v_i)\le \mu ^{P}_{A_1}(\phi (v_i))=\mu ^{P}_{A_1} (S_{v_{\pi (i)}v_{\pi (i+1)}})=t_{\pi (i)}$,

$$\begin{aligned} \acute{s_i}= & {} \mu ^{N}_{A}(v_i)\ge \mu ^{N}_{A_1}(\phi (v_i))=\mu ^{N}_{A_1}(S_{v_{\pi (i)}v_{\pi (i+1)}})=\acute{t}_{\pi (i)},\\ t_i= & {} \mu ^{P}_{B}(v_iv_{i+1})\le \mu ^{P}_{B_1}(\phi (v_i)\phi (v_{i+1}))\\= & {} \mu ^{P}_{B_1}(S_{v_{\pi (i)}v_{\pi (i+1)}}S_{v_{\pi (i+1)}v_{\pi (i+2)}})\\= & {} \mu ^{P}_{B_1}(S_{v_{\pi (i)}v_{\pi (i+1)}})\times \mu ^{P}_{B_1}(S_{v_{\pi (i+1)}v_{\pi (i+2)}})=t_{\pi (i)}\times t_{\pi (i+1)},\\ \acute{t_i}= & {} \mu ^{N}_{B}(v_iv_{i+1})\le \mu ^{N}_{B_1}(\phi (v_i)\phi (v_{i+1}))\\= & {} \mu ^{N}_{B_1}(S_{v_{\pi (i)}v_{\pi (i+1)}}S_{v_{\pi (i+1)}v_{\pi (i+2)}})\\= & {} -\mu ^{N}_{B_1}(S_{v_{\pi (i)}v_{\pi (i+1)}})\times \mu ^{N}_{B_1}(S_{v_{\pi (i+1)}v_{\pi (i+2)}})\\= & {} -\acute{t}_{\pi (i)}\times \acute{t}_{\pi (i+1)} \hbox { for }i=1,2,\ldots ,n. \end{aligned}$$

That is, $s_i\le t_{\pi (i)},\,\acute{s_i}\ge \acute{t}_{\pi (i)}$ and

$$\begin{aligned} (b)\left\{ \begin{array}{l} t_i\le t_{\pi (i)}\times t_{\pi (i+1)}\\ \acute{t_i}\ge -\acute{t}_{\pi (i)}\times \acute{t}_{\pi (i+1)}, i=1,2,\ldots ,n.\\ \end{array}\right. \end{aligned}$$

By (b), we have $t_i\le t_{\pi (i)},\,\acute{t_i}\ge \acute{t}_{\pi (i)}$ for $i=1,2,\ldots ,n$ and so $t_{\pi (i)}\le t_{\pi (\pi (i))},\,\acute{t}_{\pi (i)}\ge \acute{t}_{\pi (\pi (i))}$ for $i=1,2,\ldots ,n$. Continuing, we have

$$\begin{aligned} t_i\le & {} t_{\pi (i)}\le \ldots \le t_{\pi ^j(i)}\le t_i, \end{aligned}$$

$\acute{t_i}\ge \acute{t}_{\pi (i)}\ge \ldots \ge \acute{t}_{\pi ^j(i)}\ge \acute{t_i}$ and so $t_i=t_{\pi (i)},\,\acute{t_i}=\acute{t}_{\pi (i)},\,i=1,2,\ldots ,n$, where $\pi ^{j+1}$ is the identity map. Again by (b), we have

$$\begin{aligned} t_i\le & {} t_{\pi (i)}=t_{i+1},\\ \acute{t_i}\ge & {} \acute{t}_{\pi (i+1)}=\acute{t}_{(i+1)},\, i=1,2,\ldots ,n\hbox { where }t_{n+1}=t_n,\, \acute{t}_{n+1}=\acute{t}_n. \end{aligned}$$

Hence by (a) and (b), we have $t_1=\ldots =t_n=s_1=\ldots s_n$,

$\acute{t_1}=\ldots =\acute{t_n}=\acute{s_1}=\ldots =\acute{s_n}$.

Thus we have not only proved the conclusion about A and B being constant functions, but also we have shown that (ii) holds.

Conversely, suppose that $G^*$ is a cycle and for all $v\in V,\,x\in E,\,\mu ^{P}_{A}(v)=\mu ^{P}_{B}(x),\,\mu ^{N}_{A}(v)=\mu ^{N}_{B}(x)$. By Proposition 4.6, $L(G^*)$ is the line graph of $G^*$. Since $G^*$ is a cycle, $G^*\cong L(G^*)$ by [12, Theorem 8.2]. This isomorphism induces an isomorphism of G onto L(G) since $\mu ^{P}_{A}(v)=\mu ^{P}_{B}(x),\,\mu ^{N}_{A}(v)=\mu ^{N}_{B}(x)$ for all $v\in V,\,x\in E$ and so $A=B=A_1=B_1$ on their respective domains. $\square$

Proposition 4.12

Let $G_1$ and $G_2$ be two product bipolar fuzzy graphs of the graphs $G^*_1=(V_1,E_1)$ and $G^*_2=(V_2,E_2)$ respectively, such that $G^*_1$ and $G^*_2$ is connected. Let $L(G_1)$ and $L(G_2)$ be the product bipolar fuzzy line graphs corresponding to $G_1$ and $G_2$ respectively. Suppose that it is not the case that one of $G^*_1$ and $G^*_2$ is complete graph $K_3$ and other is bipartite complete graph $K_{1,3}$. If $L(G_1)\cong L(G_2)$, then $G_1$ and $G_2$ are line isomorphic.

Proof

Since $L(G_1)\cong L(G_2)$, therefore by Proposition 4.10, $L(G^*_1)\cong L(G^*_2)$. Since $L(G^*_1)$ and $L(G^*_2)$ are the line graphs of $G^*_1$ and $G^*_2$, respectively, by Proposition 4.6, we have that $G^*_1\cong G^*_2$ by [12, Theorem 8.3].

Let $\psi$ be the isomorphism of $L(G_1)$ onto $L(G_2)$ and $\phi$ be the isomorphism of $G^*_1$ onto $G^*_2$.

Then $\mu ^{P}_{A_3}(S_x)=\mu ^{P}_{A_4}(\psi (S_x))=\mu ^{P}_{A_4}(S_{\phi (x)}),\,\mu ^{N}_{A_3}(S_x)=\mu ^{N}_{A_4}(\psi (S_x))=\mu ^{N}_{A_4}(S_{\phi (x)})$, where the latter equalities holds by the proof of [12, Theorem 8.3] and so $\mu ^{P}_{B_1}(x)=\mu ^{P}_{B_2}(\phi (x)),\,\mu ^{N}_{B_1}(x)=\mu ^{N}_{B_2}(\phi (x))$. Hence $G_1$ and $G_2$ are line isomorphic. $\square$

Conclusions

The theory of graph is an extremely useful tool in solving the combinatorial problems in different areas including algebra, number theory, geometry, topology, operation research, optimization, computer science, etc. Since researches or modelings on real world problems often involve bipolar information, therefore the study of bipolar fuzzy graphs is very significant. The bipolar fuzzy models gives more precision, flexibility, and comparability to the system as compared to the classical and fuzzy models. The concept of bipolar fuzzy graphs are applicable in different areas of engineering, computer science, computer networks, medical diagnosis etc. Therefore, we have studied the concept of regular and totally regular product bipolar fuzzy graphs and finally introduced product bipolar fuzzy line graphs and studied several important results of it. Our next plan is to extend our research work on regular and irregular m-polar fuzzy graphs, m-polar fuzzy intersection graphs, m-polar fuzzy interval graphs, m-polar fuzzy hypergraphs, etc.