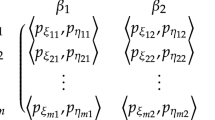1 Introduction

The bi-matrix games (BGs) are an important type of two person nonzero-sum non-cooperative games. Many researchers have studied the matrix games [1,2,3,4], BGs [5,6,7], fuzzy matrix games [8,9,10,11], fuzzy BGs, [12,13,14,15,16,17] and fuzzy optimization algorithm [18,19,20]. However, since some practical limitations such as resources and funds, not all (mixed) strategies are feasible for players or players have different preferences on the choice of certain strategies in most real game problems. It means that there are some restrictions or preferences for players in choosing strategies. Such kinds of non-cooperative games are called constrained games which are first introduced by Charnes [21, 22]. It proved out that constrained matrix games can get equilibrium solutions by solving a pair of dual linear programming models. Several papers are devoted to research the constrained matrix games [23] and fuzzy constrained matrix games [24, 25]. Different from the literature [23,24,25] on the matrix games, we focus on investigating the BGs. The BGs are remarkably different from the matrix games since the payoffs of BGs are not zero-sum. This means players have different objectives and can define their own payoffs based on their knowledge on the game and their respective goals. This leads to a great difference on research mechanism between BGs and the matrix games. So far as we know, there are only two papers about the constrained bi-matrix games (CBGs). Firouzbakht et al. [26] studied the CBGs with only one linear constraint on strategies of players. By a quadratic programming model, the Nash equilibrium solution is obtained. Meng and Zhan [27] proposed two methods for BGs with restrictions. But first of all, both methods need to find all vertices of the strategy sets of two players. This is often very difficult, especially when there are many strategies and many constraints on strategies for players. The method of CBGs proposed in this paper can overcome aforementioned shortcomings.

In fact, a universal and feasible method to solve CBGs has not been proposed yet. Additionally, in many real games, since information ambiguity and the complexity of the actual games, players often have some uncertainty in judging the situations. And players often allow a certain degree of flexibility on constraints. In this case, using fuzzy sets [28] to indicate the players’ payoffs in each situation is more realistic. The fuzzy set uses a single scale which is called the membership function to represent the degree of membership to the fuzzy set, while the degree of non-membership is equal to 1 minus the degree of membership. Since Zadeh [28] introduced the fuzzy set, several famous extensions and their fuzzy rules have been developed, such as intuitionistic fuzzy (IF) sets (IFSs) [15, 16, 29], type-2 fuzzy sets [30], fuzzy multisets [31], interval-valued fuzzy sets [32], and interval-valued IF sets [32]. Since the IFS consists of degrees of membership, non-membership, and indeterminacy by three functions. The uncertain information can be expressed more accurately and comprehensively by using IFSs. Therefore, the IFSs have widely studied and applied. The IF numbers (IFNs) [16] which are defined on the real number set are special kinds of IFSs. The IFNs can express more detail on ambiguous concepts and information than the fuzzy numbers. Then, it seems to be suitable for using IFNs to express the players’ degrees of flexibility on situations. Therefore, in this paper, the CBGs with payoffs expressed by IFNs are also studied. Such kinds of non-cooperative games are simply called intuitionistic fuzzy constrained bi-matrix games (IFCBGs). An effective method is proposed to obtain the equilibrium/optimal strategies (ESs) and equilibrium values (EVs) of the IFCBGs.

In summary, the main contributions of this paper have the following three aspects. (1) Considering that the players often have some constraints or preference on strategies and the payoffs of each situation are not exactly opposite, we investigate the CBGs. (2) Considering that the players often allow a certain degree of flexibility on constraints and the players often are not able to evaluate exactly the payoffs due to imprecision or lack of available information, we further study the IFCBGs. (3) We put forward practical and effective models and methods for the CBGs and IFCBGs.

This paper is organized as follows. Section 2 describes the CBG problems and gives the definition of the equilibrium solution (including ESs and EVs) which can be obtained by solving our proposed two linear programming models. Section 3 compares and analyzes the Rock-scissors-cloth game with and without constraints. In Sect. 4, two IF mathematical programming models are established to get equilibrium solutions of the IFCBGs. In Sect. 5, we use an example to verify rationality of the proposed models and method. Conclusion is given in Sect. 6.

2 Notation of the CBGs and Programming Models

In realistic game problems, players may have preferences in the choice of strategies. And due to the limitations of the real environments such as limited resources and insufficient funds, there are constraints on strategies for players. Therefore, it is important and necessary to study the BGs with constraints, i.e., CBGs.

There are players I and II, whose pure strategy sets are denoted by \( S_{1} = \{ \delta_{1} ,\delta_{2} , \ldots ,\delta_{m} \} \) and \( S_{2} = \{ \sigma_{1} ,\sigma_{2} , \ldots ,\sigma_{n} \} \), respectively. When player I chooses any pure strategy \( \delta_{i} \in S_{1} \) and player II chooses any pure strategy \( \sigma_{j} \in S_{2} \), i.e., at the situation \( (\delta_{i} ,\sigma_{j} ) \), the payoffs of the two players are expressed as \( a_{ij} \) and \( b_{ij} \), respectively. Then, the payoffs of the two players under all situations can be expressed as matrices \( {\mathbf{A}} = (a_{ij} )_{m \times n} \) and \( {\mathbf{B}} = (b_{ij} )_{m \times n} \), respectively. The vectors of mixed strategies are denoted as \( {\mathbf{x}} = (x_{1} ,x_{2} , \ldots ,x_{m} )^{\text{T}} \) and \( {\mathbf{y}} = (y_{1} ,y_{2} , \ldots ,y_{n} )^{\text{T}} \), where \( x_{i} { (}i = 1,2, \ldots ,m ) \) and \( y_{j} (j = 1,2, \ldots ,n ) { } \) are probabilities for two players choosing their pure strategies, respectively. And the mixed strategies \( x_{i} \, \) and \( y_{j} \) are affiliated with the sets of strategies (convex polyhedron) which are determined by some equations and inequalities. Let \( X = \{ {\mathbf{x}}|{\mathbf{E}}^{T} {\mathbf{x}} \ge {\mathbf{c}},{\mathbf{x}} \ge {\mathbf{0}}\} \) be player I’s strategy constrained set, where \( {\mathbf{c}} = (c_{1} ,c_{2} , \ldots ,c_{p} )^{\text{T}} \), \( {\mathbf{E}} = (e_{il} )_{m \times p} \), and \( p \) is a positive integer. Let \( Y = \{ {\mathbf{y}}|{\mathbf{Fy}} \ge {\mathbf{d}},{\mathbf{y}} \ge {\mathbf{0}}\} \) be player II’s strategy constrained set, where \( {\mathbf{d}} = (d_{1} ,d_{2} , \ldots ,d_{q} )^{\text{T}} \), \( {\mathbf{F}} = (f_{kj} )_{q \times n} \), and \( q \) is a positive integer.

The mixed strategy \( {\mathbf{x}} \) should satisfy \( \sum\limits_{i = 1}^{m} {x_{i} } = 1 \), which can be represented by \( \sum\limits_{i = 1}^{m} {x_{i} } \ge 1 \) and \( - \sum\limits_{i = 1}^{m} {x_{i} } \ge - 1 \). Thence, the system of inequalities \( {\mathbf{E}}^{T} {\mathbf{x}} \ge {\mathbf{c}} \) contains both \( \sum\limits_{i = 1}^{m} {x_{i} } \ge 1 \) and \( - \sum\limits_{i = 1}^{m} {x_{i} } \ge - 1 \). That is, \( {\mathbf{E}}^{T} {\mathbf{x}} \ge {\mathbf{c}} \) contains \( \sum\limits_{i = 1}^{m} {x_{i} = 1} \). Analogously, the player II’s mixed strategy \( {\mathbf{y}} \) should satisfy \( \sum\limits_{j = 1}^{n} {y_{j} = 1} \). And the constraint \( {\mathbf{Fy}} \ge {\mathbf{d}} \) contains \( \sum\limits_{j = 1}^{n} {y_{j} = 1} \).

Without loss of generality, assume that two players, respectively, choose optimal strategies from the constraint sets \( X \) and \( Y \) so as to maximize his/her own payoffs. Then, the expected payoffs of the two players are \( U = {\mathbf{x}}^{T} {\mathbf{Ay}} = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {x_{i} } } a_{ij} y_{j} \) and \( V = {\mathbf{x}}^{T} {\mathbf{By}} = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {x_{i} } } b_{ij} y_{j} \), respectively. Players often follow the decision principle of “taking the worst case and starting from the best.” Therefore, player I will choose strategy \( {\mathbf{x}}^{*} \in X \) that satisfies

$$ \mathop {\hbox{min} }\limits_{y \in Y} {\mathbf{x}}^{*T} {\mathbf{Ay}} = \mathop {\hbox{max} }\limits_{x \in X} \mathop {\hbox{min} }\limits_{y \in Y} {\mathbf{x}}^{T} {\mathbf{Ay}} . $$
(1)

Similarly, player II chooses strategy \( {\mathbf{y}}^{*} \in Y \) that satisfies

$$ \mathop {\hbox{min} }\limits_{{{\mathbf{x}} \in X}} {\mathbf{x}}^{T} {\mathbf{By}}^{*} = \mathop {\hbox{max} }\limits_{{{\mathbf{y}} \in Y}} \mathop {\hbox{min} }\limits_{{{\mathbf{x}} \in X}} {\mathbf{x}}^{T} {\mathbf{By}} . $$
(2)

In fact, if \( {\mathbf{B}} = - {\mathbf{A}} \), then the CBGs degenerate to constrained matrix games [23,24,25]. In other words, our proposed method for solving CBGs can also be applied to solve constrained matrix games.

Definition 1

[17] If \( ({\mathbf{x}}^{ * } ,{\mathbf{y}}^{ * } ) \in X \times Y \) satisfies the conditions as follows:

$$ {\mathbf{x}}^{*T} {\mathbf{Ay}}^{*} = \mathop {\hbox{min} }\limits_{y \in Y} {\mathbf{x}}^{*T} {\mathbf{Ay}} = \mathop {\hbox{max} }\limits_{x \in X} \mathop {\hbox{min} }\limits_{y \in Y} {\mathbf{x}}^{T} {\mathbf{Ay}} $$

and

$$ {\mathbf{x}}^{*T} {\mathbf{By}}^{*} = \mathop {\hbox{min} }\limits_{{{\mathbf{x}} \in X}} {\mathbf{x}}^{T} {\mathbf{By}}^{*} = \mathop {\hbox{max} }\limits_{{{\mathbf{y}} \in Y}} \mathop {\hbox{min} }\limits_{{{\mathbf{x}} \in X}} {\mathbf{x}}^{T} {\mathbf{By}} $$

for any mixed strategies \( {\mathbf{x}} \in X \) and \( {\mathbf{y}} \in Y \). Then, \( {\mathbf{x}}^{ * } \) and \( {\mathbf{y}}^{*} \) are called ESs, \( U^{*} = {\mathbf{x}}^{ * T} {\mathbf{Ay}}^{ * } \) and \( V^{*} = {\mathbf{x}}^{ * T} {\mathbf{By}}^{ * } \) are called EVs of the two players, respectively.

Theorem 1

If \( ({\mathbf{x}}^{ * } ,{\mathbf{z}}^{ * } ) \) and \( ({\mathbf{y}}^{ * } ,{\mathbf{s}}^{*} ) \) are feasible solutions of the two linear programming models as follows:

$$ \begin{aligned} & \hbox{max} \left\{ {{\mathbf{d}}^{T} {\mathbf{z}}} \right\} \\ & \left\{ \begin{array}{*{20}l} {\mathbf{F}}^{T} {\mathbf{z}} \le {\mathbf{A}}^{T} {\mathbf{x}} \hfill \\ {\mathbf{E}}^{T} {\mathbf{x}} \ge {\mathbf{c}} \hfill \\ {\mathbf{x}} \ge {\mathbf{0}} \hfill \\ {\mathbf{z}} \ge {\mathbf{0}} \hfill \\ \end{array} \right. \\ \end{aligned} $$
(3)

and

$$ \begin{aligned} & \hbox{max} \left\{ {{\mathbf{c}}^{T} {\mathbf{s}}} \right\} \\ & \left\{ \begin{array}{*{20}l} {\mathbf{Es}} \le {\mathbf{By}} \hfill \\ {\mathbf{Fy}} \ge {\mathbf{d}} \hfill \\ {\mathbf{y}} \ge {\mathbf{0}} \hfill \\ {\mathbf{s}} \ge {\mathbf{0}} \hfill \\ \end{array} \right. \\ \end{aligned} $$
(4)

respectively. Then, \( {\mathbf{x}}^{ * } \) and \( {\mathbf{y}}^{*} \) are ESs, \( U^{*} = {\mathbf{d}}^{T} {\mathbf{z}}^{*} = {\mathbf{x}}^{*T} {\mathbf{Ay}}^{*} \) and \( V^{*} = {\mathbf{c}}^{T} {\mathbf{s}}^{*} = {\mathbf{x}}^{*T} {\mathbf{By}}^{*} \) are EVs of players I and II, respectively.

Proof

Assume that the vector \( {\mathbf{x}} \)\( ({\mathbf{x}} \in X) \) of mixed strategies for player I is a given parameter. Then, \( \mathop {\hbox{min} }\limits_{{{\mathbf{y}} \in Y}} \{ {\mathbf{x}}^{T} {\mathbf{Ay}}\} \) is a function of \( {\mathbf{x}} \), i.e., the optimal solution of

$$ \begin{aligned} & \hbox{min} \left\{ {\left( {{\mathbf{x}}^{T} {\mathbf{A}}} \right){\mathbf{y}}} \right\} \\ & \left\{\begin{array}{*{20}l} {\mathbf{Fy}} \ge {\mathbf{d}} \hfill \\ {\mathbf{y}} \ge {\mathbf{0}} \hfill \\ \end{array} \right. \\ \end{aligned} $$
(5)

is a function of the parameter \( {\mathbf{x}} \in X \). Based on the dual programming theory, the dual programming model of Eq. (5) is

$$ \begin{aligned} & \hbox{max} \left\{ {{\mathbf{d}}^{T} {\mathbf{z}}} \right\} \\ & \left\{ \begin{array}{*{20}l} {\mathbf{F}}^{T} {\mathbf{z}} \le {\mathbf{A}}^{T} {\mathbf{x}} \hfill \\ {\mathbf{z}} \ge {\mathbf{0}} \hfill \\ \end{array} \right. \\ \end{aligned} $$
(6)

where \( {\mathbf{z}} = (z_{1} ,z_{2} , \ldots ,z_{q} )^{\text{T}} \) is a vector of the dual variables. And the objective values of Eqs. (5) and (6) are identical. Therefore, the ES \( {\mathbf{x}}^{*} \) and EV \( U^{*} \) of player I are equivalent to the optimal solution and optimal value of the linear programming model as follows:

$$ \begin{aligned} & \hbox{max} \left\{ {{\mathbf{d}}^{T} {\mathbf{z}}} \right\} \\ & \left\{ \begin{array}{*{20}l} {\mathbf{F}}^{T} {\mathbf{z}} \le {\mathbf{A}}^{T} {\mathbf{x}} \hfill \\ {\mathbf{E}}^{T} {\mathbf{x}} \ge {\mathbf{c}} \hfill \\ {\mathbf{x}} \ge {\mathbf{0}} \hfill \\ {\mathbf{z}} \ge {\mathbf{0}} \hfill \\ \end{array} \right. \\ \end{aligned} $$

which is just about Eq. (3).

Analogously, assume that the vector \( {\mathbf{y}} \)\( ({\mathbf{y}} \in Y) \) of mixed strategies for player II is a given parameter. Then, \( \mathop {\hbox{min} }\limits_{{{\mathbf{x}} \in X}} \{ {\mathbf{x}}^{T} {\mathbf{Ay}}\} \) is a function of \( {\mathbf{y}} \), i.e., the optimal solution of

$$ \begin{aligned} & \hbox{min} \{ {\mathbf{x}}^{T} ({\mathbf{By}})\} \\ & \left\{ \begin{array}{*{20}l} {\mathbf{E}}^{T} {\mathbf{x}} \ge {\mathbf{c}} \hfill \\ {\mathbf{x}} \ge {\mathbf{0}} \hfill \\ \end{array} \right. \\ \end{aligned} $$
(7)

is a function of the parameter \( {\mathbf{y}} \in Y \). The dual programming of Eq. (7) is obtained as follows:

$$ \begin{aligned} & \hbox{max} \left\{ {{\mathbf{c}}^{T} {\mathbf{s}}} \right\} \\ & \left\{ \begin{array}{*{20}l} {\mathbf{Es}} \le {\mathbf{By}} \hfill \\ {\mathbf{s}} \ge {\mathbf{0}} \hfill \\ \end{array} \right. \\ \end{aligned} $$
(8)

where \( {\mathbf{s}} = (s_{1} ,s_{2} , \ldots ,s_{p} )^{\text{T}} \) is a vector of the dual variables. And the objective values of Eqs. (7) and (8) are identical. Therefore, the ES \( {\mathbf{y}}^{*} \) and EV \( V^{*} \) of player II are equivalent to the optimal solution and optimal value of the linear programming as follows:

$$ \begin{aligned} & \hbox{max} \left\{ {{\mathbf{c}}^{T} {\mathbf{s}}} \right\} \\ & \left\{ \begin{array}{*{20}l} {\mathbf{Es}} \le {\mathbf{By}} \hfill \\ {\mathbf{Fy}} \ge {\mathbf{d}} \hfill \\ {\mathbf{y}} \ge {\mathbf{0}} \hfill \\ {\mathbf{s}} \ge {\mathbf{0}} \hfill \\ \end{array} \right. \\ \end{aligned} $$

which is just about Eq. (4). Thus, Theorem 1 has been proved.

It is proven that any BG has at least one Nash equilibrium solution in mixed strategy sense [33]. However, due to the fact that there are constraints on strategies of players for CBGs, the feasible domain of the player’s strategies may be an empty set when the constraints are too strict or too much. In turn, the CBGs may not have an equilibrium solution. Thus, we conclude that not all CBG problems have equilibrium solutions.

In this methodology, we can get the ESs and EVs of players for the CBGs by two linear programming models. Compared with the existing method [26, 27], the method proposed in this section is more effective in terms of breadth of applications and simplicity of calculation. The reason is as follows. The method [26] only studied the BGs with one linear constraint. The authors [27] established a nonlinear programming model for the CBGs, but they need to find all vertices of the strategy sets of two players, which is often a very difficult task.

3 A Numerical Example of the CBGs

In this section, Rock-scissors-cloth game [23] which is one of the classic BGs is taken as an example to show the validity of the method proposed in Sect. 2. The payoff matrices of the two players in the Rock-scissors-cloth game are as follows:

$$ {\mathbf{A}} = \left( {\begin{array}{*{20}c} 1 & 2 & 0 \\ 0 & 1 & 2 \\ 2 & 0 & 1 \\ \end{array} } \right),\quad {\mathbf{B}} = \left( {\begin{array}{*{20}c} 1 & 0 & 2 \\ 2 & 1 & 0 \\ 0 & 2 & 1 \\ \end{array} } \right) $$

The two players of the Rock-scissors-cloth game without constraints on strategies have only one equilibrium mixed strategy, i.e., \( {\mathbf{x}}^{*} = (x_{1} ,x_{2} ,x_{3} )^{\text{T}} = (1/3,1/3,1/3)^{\text{T}} \) and \( {\mathbf{y}}^{*} = (y_{1} ,y_{2} ,y_{3} )^{\text{T}} = (1/3,1/3,1/3)^{\text{T}} \). Now suppose that player I prefers rock. In this case, the Rock-scissors-cloth game becomes a CBG. Assuming that \( x_{1} \ge 0.5 \). Then, the two players’ strategy spaces are given as follows:

$$ X = \left\{ {\left( {x_{1} ,x_{2} ,x_{3} } \right)^{\text{T}} |x_{1} \ge 0.5,\;x_{1} + x_{2} + x_{3} = 1,\;x_{1} \ge 0,\;x_{2} \ge 0,\;x_{3} \ge 0} \right\} $$

and

$$ Y = \left\{ {\left( {y_{1} ,y_{2} ,y_{3} } \right)^{\text{T}} |y_{1} + y_{2} + y_{3} = 1,\;y_{1} \ge 0,\;y_{2} \ge 0,\;y_{3} \ge 0} \right\} $$

According to the proposed method in Sect. 2, Eqs. (3) and (4) can be rewritten as follows:

$$ \begin{aligned} & \hbox{max} \{ z_{1} - z_{2} \} \\ & \left\{ \begin{array}{*{20}l} z_{1} - z_{2} \le x_{1} + 2x_{3} \hfill \\ z_{1} - z_{2} \le 2x_{1} + x_{2} \hfill \\ z_{1} - z_{2} \le 2x_{2} + x_{3} \hfill \\ x_{1} \ge 0.5 \hfill \\ x_{1} + x_{2} + x_{3} = 1 \hfill \\ x_{1} ,x_{2} ,x_{3} ,z_{1} ,z_{2} \ge 0 \hfill \\ \end{array} \right. \\ \end{aligned} $$
(9)

and

$$ \begin{aligned} & \hbox{max} \{ 0.5s_{1} + s_{2} - s_{3} \} \\ & \left\{ \begin{array}{*{20}l} s_{1} + s_{2} - s_{3} \le y_{1} + 2y_{3} \hfill \\ s_{2} - s_{3} \le 2y_{1} + y_{2} \hfill \\ s_{2} - s_{3} \le 2y_{2} + y_{3} \hfill \\ y_{1} + y_{2} + y_{3} = 1 \hfill \\ y_{1} ,y_{2} ,y_{3} ,s_{1} ,s_{2} ,s_{3} \ge 0 \hfill \\ \end{array} \right. \\ \end{aligned} $$
(10)

respectively.

Lingo software is a simple tool for solving linear programming problems. Lingo has a built-in language for building optimized models that can easily express large-scale problems and uses Lingo’s efficient solver to quickly solve and analyze results. Lingo software requirements for computer hardware are inter i486 or higher processor, 16 MB or more memory and enough hard disk free space.

Using the simplex method through Lingo software to solve Eqs. (9) and (10), we get that the ESs and EVs of the two players are \( {\mathbf{x}}^{*} = (1/2,1/3,1/6)^{\text{T}} \), \( U^{*} = {\mathbf{d}}^{T} {\mathbf{z}}^{*} = 5/6 \), \( {\mathbf{y}}^{*} = (1/3,0,2/3)^{\text{T}} \), and \( V^{*} = {\mathbf{c}}^{T} {\mathbf{s}}^{*} = 7/6 \), respectively. This is to say, when player I prefers stone with the probability being greater than or equal to 0.5, the ESs of the Rock-scissors-cloth game are that the player I chooses rock, scissors, and cloth strategies with the probability of \( 1/2 \), \( 1/3 \), and \( 1/6 \), respectively, and the player II chooses stone, scissors, and cloth strategies with the probability of \( 1/3 \), \( 0 \), and \( 2/3 \), respectively. It is seen that this result is logically consistent with actual situation.

The solutions obtained by the proposed models and method for the Rock-scissors-cloth game with preference (or constraint) are consistent with the solutions [27] get by a bilinear programming model. However, the method [27] needs to find all vertices of the convex sets of \( X \) and \( Y \). This is often particularly difficult, especially for complicated CBGs. Obviously, our proposed models and method of the CBGs are more simple and effective.

4 IFCBGs

Generally, it is difficult for players to accurately estimate the payoffs of all situations. Describing the payoffs by real numbers is not consistent with practical problems. Therefore, in this section, we study the IFCBGs.

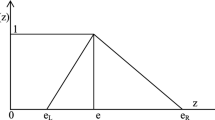
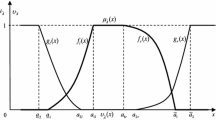
Assume that matrices \( {\tilde{\mathbf{A}}} = (\tilde{a}_{ij} )_{m \times n} \) and \( {\tilde{\mathbf{B}}} = (\tilde{b}_{ij} )_{m \times n} \) are payoffs of the two players, where \( \tilde{a}_{ij} = < (\underline{a}_{ij} ,a_{ij} ,\bar{a}_{ij} );w_{{a_{ij} }} ,u_{{a_{ij} }} > \) and \( \tilde{b}_{ij} = < (\underline{b}_{ij} ,b_{ij} ,\bar{b}_{ij} );w_{{b_{ij} }} ,u_{{b_{ij} }} > \) are IFNs. For easy calculation, assume that all \( \tilde{a}_{ij} \) and \( \tilde{b}_{ij} \) are TIFNs [34, 35]. Their membership functions and non-membership functions can be expressed as follows:

$$ \mu_{{\tilde{a}_{ij} }} (x) = \left\{ {\begin{array}{*{20}l} 0 \hfill & { (x < \underline{a}_{ij} )} \hfill \\ {(x - \underline{a}_{ij} )w_{{\tilde{a}_{ij} }} /(a_{ij} - \underline{a}_{ij} ) \, } \hfill & { (\underline{a}_{ij} \le x < a_{ij} )} \hfill \\ {w_{{\tilde{a}_{ij} }} } \hfill & { (x = a_{ij} )} \hfill \\ {(\bar{a}_{ij} - x)w_{{\tilde{a}_{ij} }} /(\bar{a}_{ij} - a_{ij} )} \hfill & { (a_{ij} < x \le \bar{a}_{ij} )} \hfill \\ 0 \hfill & { (x > \bar{a}_{ij} )} \hfill \\ \end{array} } \right. $$
(11)

and

$$ v_{{\tilde{a}_{ij} }} (x) = \left\{ {\begin{array}{*{20}l} 1 \hfill & { (x < \underline{a}_{ij} )} \hfill \\ {[a_{ij} - x + u_{{\tilde{a}_{ij} }} (x - \underline{a}_{ij} )]/(a_{ij} - \underline{a}_{ij} ) \, } \hfill & { (\underline{a}_{ij} \le x < a_{ij} )} \hfill \\ {u_{{\tilde{a}_{ij} }} } \hfill & { (x = a_{ij} )} \hfill \\ {[x - a_{ij} + u_{{\tilde{a}_{ij} }} (\bar{a}_{ij} - x)]/(\bar{a}_{ij} - a_{ij} ) \, } \hfill & { (a_{ij} < x \le \bar{a}_{ij} )} \hfill \\ 1 \hfill & { (x > \bar{a}_{ij} ) ,} \hfill \\ \end{array} } \right. $$
(12)

respectively, where \( w_{{\tilde{a}_{ij} }} \) and \( u_{{\tilde{a}_{ij} }} \) satisfy \( 0 \le w_{{\tilde{a}_{ij} }} \le 1 \), \( 0 \le u_{{\tilde{a}_{ij} }} \le 1 \), and \( 0 \le w_{{\tilde{a}_{ij} }} + u_{{\tilde{a}_{ij} }} \le 1 \).

Due to the fact that players often cannot accurately estimate the payoffs in each situation, the values of the IFCBGs are not strictly equal to \( {\mathbf{d}}^{T} {\mathbf{z}} \) in Eq. (6) and \( {\mathbf{c}}^{T} {\mathbf{s}} \) in Eq. (7). The players may allow some violations on the constraints \( {\mathbf{F}}^{T} {\mathbf{z}}\tilde{ \le }{\tilde{\mathbf{A}}}^{T} {\mathbf{x}} \) and \( {\mathbf{Es}}\tilde{ \le }{\tilde{\mathbf{B}}\mathbf{y}} \), where symbol “\( \tilde{ \le } \)” denotes a relaxed version of “\( \le \).” There is a double fuzziness that is fuzzy constraints and fuzzy payoffs. Therefore, the ESs \( {\mathbf{x}}^{*} \), \( {\mathbf{y}}^{*} \), and EVs \( U^{*} \), \( V^{*} \) of the IFCBGs are equal to the optimal solutions and optimal values of Eqs. (13) and (14) as follows:

$$ \begin{aligned} & \hbox{max} \left\{ {{\mathbf{d}}^{T} {\mathbf{z}}} \right\} \\ & \left\{ \begin{array}{*{20}l} {\mathbf{F}}^{T} {\mathbf{z}} - {\tilde{\mathbf{A}}}^{T} {\mathbf{x}} \le_{IF} (1 - t){\tilde{\mathbf{p}}} \hfill \\ {\mathbf{E}}^{T} {\mathbf{x}} \ge {\mathbf{c}} \hfill \\ {\mathbf{x}} \ge {\mathbf{0}} \hfill \\ {\mathbf{z}} \ge {\mathbf{0}} \hfill \\ \end{array} \right. \\ \end{aligned} $$
(13)

and

$$ \begin{aligned} & \hbox{max} \left\{ {{\mathbf{c}}^{T} {\mathbf{s}}} \right\} \\ & \left\{ \begin{array}{*{20}l} {\mathbf{Es}} - {\tilde{\mathbf{B}}\mathbf{y}} \le_{IF} (1 - t){\tilde{\mathbf{q}}} \hfill \\ {\mathbf{Fy}} \ge {\mathbf{d}} \hfill \\ {\mathbf{y}} \ge {\mathbf{0}} \hfill \\ {\mathbf{s}} \ge {\mathbf{0}} \hfill \\ \end{array} \right. \\ \end{aligned} $$
(14)

respectively, where \( {\tilde{\mathbf{p}}} = (\tilde{p}_{1} ,\tilde{p}_{2} , \ldots ,\tilde{p}_{n} )^{\text{T}} \), \( {\tilde{\mathbf{q}}} = (\tilde{q}_{1} ,\tilde{q}_{2} , \ldots ,\tilde{q}_{m} )^{\text{T}} \), and all elements of vectors \( {\tilde{\mathbf{p}}} \) and \( {\tilde{\mathbf{q}}} \) are TIFNs that are approximately equal to zero which express the maximum violations that the players may permit on constraints. The parameter \( t(0 \le t \le 1) \) is a real number. Symbol “\( \le_{IF} \)” is a relation for comparison of IFNs.

There are many ranking methods of IFNs [34,35,36,37,38]. In order to facilitate the application to the actual game problems, the mean-area ranking method is chosen to deal with the TIFNs in Eqs. (13) and (14). For any TIFN \( \tilde{a} = < (\underline{a} ,a,\bar{a});w_{a} ,u_{a} > \), the mean-area ranking method [34] is defined as follows:

$$ S_{\lambda } (\tilde{a}) = \left( { 2a + \underline{a} + \bar{a}} \right){{\left[ {\lambda w_{{\tilde{a}}} + (1 - \lambda )\left( {1 - u_{{\tilde{a}}} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {\lambda w_{{\tilde{a}}} + (1 - \lambda )\left( {1 - u_{{\tilde{a}}} } \right)} \right]} 4}} \right. \kern-0pt} 4} $$
(15)

where \( \lambda \in [0,1] \) is a weight. Then, by ranking index \( S_{\lambda } (\tilde{a}) \), the IF mathematical programming models (13) and (14) can be converted into the following mathematical programming:

$$ \begin{aligned} & \hbox{max} \left\{ {\varvec{d}^{T} \varvec{z}} \right\} \\ & \left\{ {\begin{array}{*{20}l} {\varvec{F}^{T} \varvec{z} - \varvec{S}_{\lambda } \left( {\tilde{\varvec{A}}} \right)^{T} \varvec{x} \le_{IF} (1 - t)\varvec{S}_{\lambda } \left( {\tilde{\varvec{p}}} \right)} \hfill \\ {\varvec{E}^{T} \varvec{x} \le c} \hfill \\ {\varvec{x} \ge {\mathbf{0}}} \hfill \\ {\varvec{z} \ge 0} \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(16)

and

$$ \begin{aligned} & \hbox{max} \left\{ {{\mathbf{c}}^{T} {\mathbf{s}}} \right\} \\ & \left\{ {\begin{array}{*{20}l} {{\mathbf{Es}} - {\mathbf{S}}_{\lambda } \left( {\tilde{\varvec{B}}} \right){\mathbf{y}} \le_{IF} (1 - t){\mathbf{S}}_{\lambda } \left( {\tilde{\varvec{q}}} \right)} \hfill \\ {{\mathbf{Fy}} \ge {\mathbf{d}}} \hfill \\ {{\mathbf{y}} \ge {\mathbf{0}}} \hfill \\ {{\mathbf{s}} \ge {\mathbf{0}}} \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(17)

respectively.

For a given \( \lambda \)\( (\lambda \in [0,1]) \), solving Eqs. (16) and (17), we can get optimal solutions \( ({\mathbf{x}}^{ * } (t),{\mathbf{z}}^{ * } (t)) \), \( ({\mathbf{y}}^{ * } (t),{\mathbf{s}}^{*} (t)) \), and optimal values \( {\mathbf{d}}^{T} {\mathbf{z}}^{*} (t) \), \( {\mathbf{c}}^{T} {\mathbf{s}}^{*} (t) \), respectively.

Theorem 2

If\( ({\mathbf{x}}^{ * } (t),{\mathbf{z}}^{ * } (t)) \)and\( ({\mathbf{y}}^{ * } (t),{\mathbf{s}}^{*} (t)) \)(\( \lambda \in [0,1] \)) are feasible solutions of Eqs. (16) and (17), respectively, then\( {\mathbf{x}}^{ * } (t) \)and\( {\mathbf{y}}^{ * } (t) \)are ESs,\( U^{*} (t) = {\mathbf{d}}^{T} {\mathbf{z}}^{*} (t) \)and\( V^{*} (t) = {\mathbf{c}}^{T} {\mathbf{s}}^{*} (t) \)are EVs of the two players for IFCBGs, respectively.

Proof

For the IFCBGs, there are two fuzziness: One is the violation on the constraints, and the other is the fuzzy payoffs. Then, based on fuzzy games and Eqs. (3) and (4) of the CBGs, we can obtain the ESs and EVs of the IFCBGs by the fuzzy programming models (i.e., Eqs. (13) and (14)). Next, we use one of the fuzzy optimization methods to transform the fuzzy optimization model into Eqs. (13) and (14) through the defuzzification function such as Eq. (15). Therefore, we can get the ESs and EVs of the IFCBGs by Eqs. (13) and (14) as described in Theorem 2.

5 A Numerical Example of the IFCBGs

There are two companies, which are called players I and II, respectively. For improving the competitiveness of companies, the two players have two strategies: introducing the senior talent \( \delta_{1} \) or \( \sigma_{1} \), introducing the advanced equipment \( \delta_{2} \) or \( \sigma_{2} \). When player I takes pure strategies \( \delta_{1} \) and \( \delta_{2} \), she/he needs to invest 7 million and 5 million dollars, respectively. Due to lack of funds, the player I can invest up to 6.5 million dollars. That is to say, the player I has a constraint condition: \( 7x_{1} + 5x_{2} \le 6.5 \) when choosing strategy. Similarly, the player II needs to invest 4 million and 6.5 million dollars when she/he takes pure strategies \( \sigma_{1} \) and \( \sigma_{2} \), respectively. However, due to lack of funds, the player II can invest up to 5.5 million dollars. Namely, the player II has a constraint condition: \( 4y_{1} + 6.5y_{2} \le 5.5 \) when selecting strategies. This is a typical IFCBG. According to the above description of the game, the constrained strategy sets of the two players are given as follows:

$$ X = \left\{ {{\mathbf{x}}|7x_{1} + 5x_{2} \le 6.5,x_{1} + x_{2} = 1,x_{1} \ge 0,x_{2} \ge 0} \right\} $$

and

$$ Y = \left\{ {{\mathbf{y}}|4y_{1} + 6.5y_{2} \le 5.5,y_{1} + y_{2} = 1,y_{1} \ge 0,y_{2} \ge 0} \right\}, $$

respectively. Due to the complexity of the market environment and the uncertainty of information, it is difficult for players to give accurate sales of products under each situation. Then, TIFNs are suitable for representing the uncertainty. The payoff matrices of players are given as follows:

$$ {\mathbf{A}} = \left( {\begin{array}{*{20}c} { < (5,6,8);0.8,0.1 > } & { < (2.5,4,6);0.4,0.3 > } \\ { < (2,4,5);0.5,0.4 > } & { < (4,5.5,7);0.6,0.2 > } \\ \end{array} } \right), $$

and

$$ {\mathbf{B}} = \left( {\begin{array}{*{20}c} { < (4,5.5,7);0.7,0.1 > } & { < (3,4,6);0.7,0.2 > } \\ { < (2.5,3.5,5);0.5,0.3 > } & { < (5,6,7);0.8,0.1 > } \\ \end{array} } \right) $$

where the element \( < (5,6,8);0.8,0.1 > \) in the matrix \( {\mathbf{A}} \) is the payoffs of player I under situation \( (\delta_{1} ,\sigma_{1} ) \). Other elements in the matrices \( {\mathbf{A}} \) and \( {\mathbf{B}} \) can make similar explanations.

According to the situation in the above actual example, we can get the coefficient matrices and vectors of the constraints as follows:

$$ {\mathbf{E}} = \left( {\begin{array}{*{20}c} { - 7} & 1 & { - 1} \\ { - 5} & 1 & { - 1} \\ \end{array} } \right),\quad {\mathbf{F}}^{T} = \left( {\begin{array}{*{20}c} { - 4} & 1 & { - 1} \\ { - 6.5} & 1 & { - 1} \\ \end{array} } \right) $$

and

$$ {\mathbf{c}} = ( - 6.5,1, - 1)^{\text{T}} ,\quad {\mathbf{d}} = ( - 5.5,1, - 1)^{\text{T}} $$

Let players choose \( \tilde{p}_{1} = \tilde{p}_{2} = < (0.19,0.2,0.21);0.6,0.2 > \) and \( \tilde{q}_{1} = \tilde{q}_{2} = < (0.05,0.1,0.15);0.7,0.1 > \), respectively.

According to Eq. (15), the defuzzification payoff matrices \( S_{\lambda } (A) \) and \( S_{\lambda } (B) \) can be obtained as follows:

$$ S_{\lambda } (A) = \left( {\begin{array}{*{20}c} {5.625 - 0.625\lambda } & {2.89 - 1.24\lambda } \\ {2.25 - 0.375\lambda } & {4.4 - 1.1\lambda } \\ \end{array} } \right), $$

and

$$ S_{\lambda } (B) = \left( {\begin{array}{*{20}c} {4.95 - 1.1\lambda } & {2.89 - 1.24\lambda } \\ {2.538 - 0.725\lambda } & {5.4 - 0.6\lambda } \\ \end{array} } \right) $$

Then, using Eqs. (16) and (17), we can construct the linear programming models with two parameters \( \lambda (\lambda \in [0,1]) \) and \( t(t \in [0,1]) \) as follows:

$$ \begin{aligned} & \hbox{max} \{ - 5.5z_{1} + z_{2} - z_{3} \} \\ & \left\{ \begin{array}{*{20}l} - 4z_{1} + z_{2} - z_{3} - (5.625 - 0.625\lambda )x_{1} - (2.25 - 0.375\lambda )x_{2} \le (0.16 - 0.04\lambda )(1 - t) \hfill \\ - 6.5z_{1} + z_{2} - z_{3} - (2.89 - 1.24\lambda )x_{1} - (4.4 - 1.1\lambda )x_{2} \le (0.16 - 0.04\lambda )(1 - t) \hfill \\ 7x_{1} + 5x_{2} \le 6.5 \hfill \\ x_{1} + x_{2} = 1 \hfill \\ x_{1} ,x_{2} ,z_{1} ,z_{2} ,z_{3} \ge 0 \hfill \\ \end{array} \right. \\ \end{aligned} $$
(18)

and

$$ \begin{aligned} & \hbox{max} \{ - 6.5s_{1} + s_{2} - s_{3} \} \\ & \left\{\begin{array}{*{20}l} - 7s_{1} + s_{2} - s_{3} - (4.95 - 1.1\lambda )y_{1} - (3.4 - 0.425\lambda )y_{2} \le (0.09 - 0.02\lambda )(1 - t) \hfill \\ - 5s_{1} + s_{2} - s_{3} - (2.538 - 0.725\lambda )y_{1} - (5.4 - 0.6\lambda )y_{2} \le (0.09 - 0.02\lambda )(1 - t) \hfill \\ 4y_{1} + 6.5y_{2} \le 5.5 \hfill \\ y_{1} + y_{2} = 1 \hfill \\ y_{1} ,y_{2} ,s_{1} ,s_{2} ,s_{3} \ge 0 \hfill \\ \end{array} \right. \\ \end{aligned} $$
(19)

respectively, where \( \lambda \) represents the players’ preference information about the membership degrees and non-membership degrees of TIFNs, \( t \) denotes the violation degrees that the players may permit on constraints.

For different values \( \lambda \) and \( t \), we can obtain the ESs and EVs of the two players through solving Eqs. (18) and (19), depicted as in Tables 1, 2, and 3.

Table 1 ESs and EVs of players I and II when \( \lambda = 0 \)
Full size table
Table 2 ESs and EVs of players I and II when \( \lambda = 0.5 \)
Full size table
Table 3 ESs and EVs of players I and II when \( \lambda = 1 \)
Full size table

It is easily seen from Table 1 that for the given values \( \lambda = 0 \) and \( t = 0 \), the ES and EV of player I are \( {\mathbf{x}}^{*} = (0.75,0.25)^{\text{T}} \) and \( U^{*} = {\mathbf{d}}^{T} {\mathbf{z}}^{*} = 4.033 \), respectively. And the ES and EV of player II are \( {\mathbf{y}}^{*} = (0.45,0.55)^{\text{T}} \) and \( V^{*} = {\mathbf{c}}^{T} {\mathbf{s}}^{*} = 4.193 \), respectively. The results indicate that for different values \( \lambda \) and \( t \), we can obtain different results. Therefore, it is necessary to consider the parameters.

6 Conclusions

We discussed CBGs which are kinds of BGs in which players have constraints or preferences on strategies. Two linear programming models for solving such kinds of CBGs are presented. We also researched IFCBGs. On this basis, two IF programming models are proposed to solve the kinds of IFCBGs. And numerical examples are used to illustrate the effectiveness of the models and method proposed in this paper. The main contributions of this paper are threefold. Firstly, we researched the BG problems with constraints. Secondly, we proposed an effective method for the CBGs. Compared with the existing work, the models and method proposed in this paper are more effective in terms of breadth of applications and simplicity of calculation. Thirdly, our paper is the first one to investigate the CBGs with IF information and give practicable models and method for IFCBGs.

Our models and method are direct and effective for the CBGs and IFCBGs. However, in this paper, the CBGs consider only linear constraints. In fact, in many realistic game problems, the players’ constraints on the strategies may be nonlinear. Then, the models may be more complicated. The convex optimization algorithm may be an effective method for the BGs with nonlinear constraints. It will be investigated on our future work. Additionally, multi-objective CBGs are also an important and a worthwhile research topic.