New Polynomial Lyapunov Functional Approach to Observer-Based Control for Polynomial Fuzzy Systems with Time Delay

Abstract

This paper presents a new Line-integral polynomial Lyapunov functional approach for observer-based control for a class of polynomial fuzzy systems with time delay and unmeasured state variables. To guarantee the global asymptotic stability and estimation error convergence, a design method is proposed. In this work we consider a Line-integral polynomial Lyapunov function in which the Lyapunov matrices are polynomial matrices depending not only of the estimated states but also of the estimated delayed states and we use the dual system to reduce the computational efforts. The design conditions are established in terms of Sum Of Squares (SOS) which can be numerically and symbolically solved via the recent developed SOSTOOLS and a Semi-Definite Program solver. Finally, numerical examples are proposed to show the validity and applicability of the proposed results .

1 Introduction

The well-known Takagi–Sugeno (T–S) fuzzy model is recognized as a powerful tool in approximating nonlinear systems. Since its introduction in 1985 [23], it has been attracting ever-increasing interest. The fuzzy model-based control methodology provides a natural, simple and effective design approach to complement other nonlinear control techniques (e.g [20]) that require special and rather involved knowledge.

On the other hand, time delay often occurs in many practical systems such as chemical processes, telecommunication, and mechanical systems, etc. As a consequence, T–S fuzzy model has been extended to tackle analysis and design problems of nonlinear systems with time delay. Lots of efforts have been made to develop updated stability analysis methods and various techniques have been obtained. The standard methods which use common Lyapunov-Krasovskii Functional, often lead to conservative results [10, 14, 30, 31]. Recently, different design techniques, aimed at reducing the conservatism, have been proposed. Thus, a result has been developed in [15] by applying the fuzzy function approach and the delay discretisation technique. The delay partitioning method, where the time delay is divided into several segments, has been proposed in [33]. It is shown in this work that the resulting conditions based on this technique are less conservatives when the number of partitions increases. More recently, less conservative result is given in [21] by using a novel integral inequality based on the Wirtinger inequality. In [32], the authors have studied stability of T–S fuzzy systems with time-delay by combining the fuzzy LKF with the Wirtinger-based integral inequality. We notice that all the results previously cited give sufficient conditions in terms of Linear Matrix Inequalities (LMIs) which can be easily solved using existing solvers such as the LMI Toolbox of Matlab software. Although the LMI-based approaches have received great interest and progress, the results obtained through LMIs are too conservative.

By the introduction of the Sum Of Squares (SOS) approach and numerical tools related to SOS programminga great interest has been given to analysis and design problems of polynomial nonlinear systems. SOS programming is considered as a powerful technique in automatic and control theory since it provides convex relaxations to solve optimization problems [16, 17].

Recently, the SOS approach is firstly considered to solve the polynomial fuzzy control system design problems [24, 29]. It is a completely different approach from the existing LMI approaches [5, 28]. SOS approach can supplied more relaxed results than the existing LMI approach, see [29] and [24].

Latest evolution in SOS programming techniques [4] make possible to state analysis design problems of polynomial control systems. For instance, novel robust fault detection design procedure for nonlinear systems has been developed in [6] via sum of squares decomposition. In [1], stability analysis of networked control systems is proposed. In [22], the problems of stability and stabilization are studied for polynomial fuzzy system with time varying delay. The SOS based local stabilization of polynomial fuzzy models with time delay has been investigated in [9] and the control design with saturation constraint for polynomial fuzzy systems with time delay is proposed in [7].

More latterly, numerous design of observer based control for polynomial fuzzy systems have been developed with a classical Lyapunov function in which the Lyapunov matrix is constant. For example, in [11] the problem of polynomial fuzzy observer design has been proposed via sum of squares approach. In [19, 26] and [25], a large class of free delay polynomial fuzzy models are proposed where state and control matrices are not dependent on unmeasurable states. Overall, there exists only very few literature works on SOS observer-based control designs for polynomial fuzzy systems with state delay. For example, we can cite [8], where the authors investigated the problem of observer-based control for nonlinear systems with time-varying delay, in which the Lyapunov matrix is constant.

In this paper, we introduce a new SOS based design method of the observer based control for polynomial fuzzy system with time delay. The framework gives key ideas to reduce the conservatism, get more relaxed results and reduce the computational efforts compared to work in [8]. The first key idea concerns the use of the dual system to reduce the computational efforts. The second key idea focuses on the analysis of the stability of the observer-based control system by using the newly proposed line-integral polynomial Lyapunov function, in which the polynomial Lyapunov matrix dependent in estimated states and the estimated delayed states. To the best of our knowledge, there are no works dealing with polynomial Lyapunov matrix depending on the same time on estimated states and estimated delayed states. The third key idea is that both the polynomial state matrices and the polynomial input matrices are depending not only on the estimated states but also on the estimated delayed system states. Furthermore, the polynomial delayed state matrices are depending on the estimated delayed system states. These ideas provide some added advantages of the relaxation. The stability of the control system is analysed using the newly proposed time-delay line-integral Lyapunov function, which provides more decision variables than the classical Lyapunov function. In addition, by introducing a novel integral inequality, we formulate the proposed stability conditions in terms of SOS. Two numerical examples are introduced. In the first example we compare our result with the result of [8] and we demonstrate that our approach improves the result in [8] for several main aspects. The second example is given to validity and illustrate the proposed approach.

The remainder paper is organized as follows. In Sect. 2, some preliminaries are proposed. Next in Sect. 3, the problem formulation of polynomial fuzzy models and the polynomial fuzzy observer-based are described. Section 4 presents a SOS design method for polynomial fuzzy controller and observer. In Sect. 5, numerical examples are given to demonstrate the effectiveness of the proposed method. Finally, Sect. 6 provides the conclusion.

2 Preliminaries

The following definitions and lemmas are helpful for next developments.

Definition 1

A polynomial Y(x(t)) is an SOS if there exists a set of polynomials $q_{i}(x(t)), i=1, \ldots ,s$ such that:

$$Y(x(t))=\sum _{i=1}^{s}q_{i}^2(x(t))$$

(1)

So if Y(x(t)) is SOS that signify $Y(x(t))>0,\,\forall x(t)$.

Definition 2

Let $x^{*}=0$ be an equilibrium of the autonomous system $\dot{x}(t)=g(x(t))$, if $V(x(t)):\mathbb {R}^{n}\rightarrow \mathbb {R}$ is a continuous scalar function satisfying the conditions as follows:

• (1) $V(0)=0$.

• (2) $V(x(t))>0$, $\forall x(t)\in \mathbb {R}^{n}\backslash 0^{n}$ (globally positive definite).

• (3) $\left\| {x(t)} \right\| \rightarrow \infty \Rightarrow V(x(t)) \rightarrow \infty$ (radially unbounded).

• (4) V(x(t)) is a continuously differentiable function.

  then, V(x(t)) is a Lyapunov function candidate to prove global asymptotic stability of the underlying system.

Lemma 1

[12] If the time derivative of the Lyapunov function candidate V(x(t)) of the autonomous system $\dot{x}(t)=g(x(t))$ is globally negative definite, i.e., $\dot{V}(x(t))<0$, $\forall x(t)\in \mathbb {R}^{n}\backslash 0^{n}$, then the equilibrium of the underlying system is proven to be globally asymptotically stable.

Lemma 2

[18] Let $g(\tilde{x}) = {\left[ {{g_1}(\tilde{x}), \ldots ,{g_n}(\tilde{x})} \right] ^T}$. A necessary and sufficient condition for $V(\tilde{x})$ to be a path-independent function is

$$\frac{{\partial {g_i}(\tilde{x})}}{{\partial {\tilde{x}_j}}} = \frac{{\partial {g_j}(\tilde{x})}}{{\partial {\tilde{x}_i}}}$$

(2)

for $i,\,j=1, \ldots ,n$.

3 Problem Formulation

Consider a nonlinear system with time delay represented by the following delayed Polynomial Fuzzy Model (PFM) with r plant rules.

Rule i $(i=1,2, \ldots ,r)$:

If $\theta _{1}(x(t))$ is $\mu _{i1}$ and $\ldots$ and $\theta _{p}(x(t))$ is $\mu _{ip}$ Then

$$\left\{ \begin{aligned} \dot{x}(t)&=A_{i}(x(t),x(t-\tau ))x(t)+A_{\tau _i}(x(t-\tau ))x(t-\tau )\\&\quad +\,B_{i}(x(t),x(t-\tau ))u(t)\\ y(t)&=C_{i} x(t)\\ x(t)&=\psi (t), t\in [-\tau ,0] \end{aligned} \right.$$

(3)

where $\theta _{j}(x(t)) (j=1,\ldots ,p)$ are the premise variables. Note that $\theta _{j}(x(t))$ are assumed to be independent of the states x(t) to be estimated. In other words, each $\theta _{j}(x(t))$ is a measurable time-varying quantity that may be measurable external variables, outputs and/or time. This has been also assumed in the existing works of the T–S fuzzy observer-based designs [27, 28]. $\mu _{ij}(i=1,\ldots ,r,j=1,\ldots ,p)$ are the fuzzy sets; $\psi (t)$ is a continuous vector-valued initial function on $\left[ {\begin{array}{ll} { - \tau }&0 \end{array}} \right]$; $x(t)\in \mathbb {R}^{n_x}$ is the state vector, $u(t)\in \mathbb {R}^{n_u}$ is the control input vector and $y(t)\in \mathbb {R}^{n_y}$ is the output vector. $A_i(x(t),x(t-\tau ))$ and $B_i(x(t),x(t-\tau ))$ are polynomial matrices in $(x(t),x(t-\tau ))$, $A_{\tau _i}(x(t-\tau )))$ are polynomial matrices in $x(t-\tau )$, $C_i$ are known constant real matrices. r is the number of IF-THEN rules. Delay $\tau$ is assumed to be known and constant.

Remark 1

We note that the state and control matrices not only depend on the system states but also on delayed system states. Hence, this class of nonlinear system is more general than the polynomial fuzzy systems that can be met in literature.

After deffuzzication process of model (3), the global system dynamics is given by the following equation :

$$\left\{ \begin{aligned} \dot{x}(t)&= \sum ^{r}_{i=1}h_{i}(\theta (x(t)))\{A_{i}(x(t),x(t-\tau ))x(t)\\ &\quad +\,A_{\tau _i}(x(t-\tau ))x(t-\tau )+B_{i}(x(t),x(t-\tau ))\\ & \qquad u(t)\}\\ y(t)&=\sum ^{r}_{i=1}h_{i}(\theta (x(t))) C_i x(t) \end{aligned} \right.$$

(4)

in which

$h_i(\theta (x(t))) = \frac{{\nu _i (\theta (x(t)))}}{{\sum \nolimits _{i = 1}^r {\nu _i (\theta (x(t)))} }}$, $\nu _{i}(\theta (x(t))) = \prod \limits _{j = 1}^p {\mu _{ij} (\theta _j (t))}$ is the membership function.

It is obvious that fuzzy weighting functions $h_i (\theta (x(t)))$ satisfy

$$\left\{ {\begin{array}{ll} {\sum \limits _{i = 1}^r {h_i (\theta (x(t)) = 1} } \\ {0 \le h_i (\theta (x(t))) \le 1} \\ \end{array}} \right.$$

(5)

In the sequel, for brevity time t is dropped. $h_i(\theta (x(t)))$ and $x(t-\tau )$ are respectively denoted by $h_i$ and $x_{\tau }$.

Usually, since the output vector can be measured by sensors in many real systems, we assume $C_1 = \cdots =C_r = C$ such that the polynomial fuzzy model can be rewritten as

$$\left\{ \begin{aligned}\dot{x}&= \sum ^{r}_{i=1}h_{i}\{A_{i}(x,x_{\tau })x+A_{\tau _i}(x_{\tau })x_{\tau }+B_{i}(x,x_{\tau })u\}\\ y&=C x \end{aligned} \right.$$

(6)

Let consider the following polynomial fuzzy observer based PDC (Parallel Distributed Compensation) controller:

$$\left\{ \begin{aligned} \dot{\widehat{x}} &= \sum ^{r}_{i=1}h_{i}\{A_{i}(\widehat{x},\widehat{x}_{\tau })\widehat{x}+A_{\tau _i}(\widehat{x}_{\tau })\widehat{x}_\tau +B_{i}(\widehat{x},\widehat{x}_{\tau })u\\ &\quad +\,L_{i}(\widehat{x})(y-\widehat{y})\}\\ \widehat{y}&=C\widehat{x}\\ u&=- \sum ^{r}_{i=1}h_{i}F_{i}(\widehat{x})\widehat{x} \end{aligned} \right.$$

(7)

where $\widehat{x}\in \mathbb {R}^{n_x}$ is the estimated state, $\widehat{y} \in \mathbb {R}^{n_y}$ is the estimated output vector, $L_{i}(\widehat{x})$ and $F_{i}(\widehat{x})$ are the polynomial observer gains and polynomial controller gains to be designed, respectively.

The augmented polynomial fuzzy model based observer control system is written as

$$\left\{\begin{aligned} \dot{\widetilde{x}}&= \sum ^{r}_{i=1}\sum ^{r}_{j=1}h_{i}h_{j}\{G_{ij}(x,x_{\tau },\widehat{x},\widehat{x}_{\tau })\widetilde{x}+M_{i}(x_{\tau },\widehat{x}_{\tau }) \widetilde{x}_{\tau }\}\\ \widetilde{x}&=\widetilde{\psi },t\in [-\tau ,0], \end{aligned} \right.$$

(8)

where

$$\begin{aligned} \widetilde{x}&= \left[ \begin{array}{c} \widehat{x}\\ x-\widehat{x} \end{array}\right] , \widetilde{x}_{\tau }= \left[ \begin{array}{c} \widehat{x}_{\tau }\\ x_{\tau }-\widehat{x}_{\tau } \end{array}\right] , \widetilde{\psi }= \left[ \begin{array}{c} \psi \\ \widehat{\psi } \end{array}\right] \\ G_{ij}(x,x_{\tau },\widehat{x},\widehat{x}_{\tau })&=\left[ \begin{array}{cc} G_{ij}^{11}(\widehat{x},\widehat{x}_{\tau })&{}G_{ij}^{12}(\widehat{x})\\ G_{ij}^{21}(x,x_{\tau },\widehat{x},\widehat{x}_{\tau })& G_{ij}^{22}(x,x_{\tau },\widehat{x} \end{array}\right] \\ G_{ij}^{11}(\widehat{x},\widehat{x}_{\tau })&= A_{i}(\widehat{x},\widehat{x}_{\tau })-B_{i}(\widehat{x},\widehat{x}_{\tau })F_{j}(\widehat{x})\\ G_{ij}^{12}(\widehat{x})&= L_{i}(\widehat{x})C\\ G_{ij}^{21}(x,x_{\tau },\widehat{x},\widehat{x}_{\tau })&= (A_{i}(x,x_{\tau })-A_{i}(\widehat{x},\widehat{x}_{\tau }))-(B_{i}(x,x_{\tau }) \\&\quad -B_{i}(\widehat{x},\widehat{x}_{\tau }))F_{j}(\widehat{x})\\ G_{ij}^{22}(x,x_{\tau },\widehat{x})&= A_{i}(x,x_{\tau })-L_{i}(\widehat{x})C\\ M_{i}(x_{\tau },\widehat{x}_{\tau })&= \left[ \begin{array}{cc} A_{\tau _i}(\widehat{x}_{\tau })& 0\\ A_{\tau _i}(x_{\tau })-A_{\tau _i}(\widehat{x}_{\tau }) & A_{\tau _i}(x_{\tau }) \end{array}\right] \end{aligned}$$

(9)

Lemma 3

There exist two orthogonal matrices $U\in \mathbb {R}^{n_y\times n_y}$ and $Z\in \mathbb {R}^{n_x\times n_x}$, such that

$$U^{T} C Z=\left[ \widetilde{C}\quad 0 \right]$$

(10)

where $\widetilde{C}=diag\big \{c_1,c_2,\ldots ,c_{n_y}\big \}$ and $c_i\ (i=1,\ldots ,n_y)$ are nonzero singular values of C.

Proof

Since $rank(C)=n_y$. $\square$

A new SOS framework will be presented in Sect. 4. The usefulness of the new SOS design framework will be demonstrated in design examples.

4 Main results

Before proceeding, knowing that the dual system of system (8) is asymptotically stable, if and only if system (8) is asymptotically stable, then we simply use the stability of the dual system.

The proposed line-integral polynomial Lyapunov function has the following form:

$$V(\widetilde{x})=V_{1}(\widehat{x},\widehat{x}_{\tau })+V_{2}(e_{x})+V_{3}(\widetilde{x})$$

(11)

where $V_{i}\in \textit{I}_{3}$ is a Lyapunov functional that is described as follows:

$$V_{1}(\widehat{x},\widehat{x}_{\tau })=2\int _{\varGamma } g(\psi ). {\hbox {d}\psi }$$

(12)

$$V_{2}(e_{x})= e_{x}^{T}P_{2}e_{x}$$

(13)

$${V_3}(\widetilde{x})= \int _{t - \tau }^t {{{\widetilde{x}}^T}(\alpha )S(\widetilde{x})\widetilde{x}(\alpha ){\hbox {d}\alpha }}$$

(14)

where $\varGamma$ is paths from the origin to $\widehat{x}$, $\psi \in \mathbb {R}^{n}$ is the dummy vector, ${\hbox {d}\psi }\in \mathbb {R}^{n}$ is an infinitesimal displacement vector, $e_{x}=x-\widehat{x}$ is the estimation error via the observer, $S(\widetilde{x})$ is symmetric positive definite matrix to be determined, $g(\psi )\in \mathbb {R}^{n}$ is vector function and has the following form

$$g(\widehat{x},\widehat{x}_{\tau })=\widetilde{P}_{1}(\widehat{x},\widehat{x}_{\tau })\widehat{x}$$

(15)

with $\widetilde{P}_{1}(\widehat{x},\widehat{x}_{\tau })\in \mathbb {R}^{n\times n}$ is a symmetric positive definite matrix such as

$$\begin{aligned} \widetilde{P}_{1}(\widehat{x},\widehat{x}_{\tau }) = \left[ {\begin{array}{cccc} {{d_{11}}(\widehat{x}_{1},\widehat{x}_{\tau _1})}&{{p_{12}}(\hat{x},\widehat{x}_{\tau })}& \cdots &{{p_{1n}}(\widehat{x},\widehat{x}_{\tau })}\\ {{p_{12}}(\widehat{x},\widehat{x}_{\tau })}&{{d_{22}}(\widehat{x}_{2},\widehat{x}_{\tau _2})}& \cdots &{{p_{2n}}(\widehat{x},\widehat{x}_{\tau })}\\ \vdots & \vdots & \ddots & \vdots \\ {{p_{1n}}(\widehat{x},\widehat{x}_{\tau })}&{{p_{2n}}(\widehat{x},\widehat{x}_{\tau })}& \cdots & {{d_{nn}}(\widehat{x}_{n},\widehat{x}_{\tau _n})} \end{array}} \right] \end{aligned}$$

where $p_{kl}(\widehat{x},\widehat{x}_{\tau })$ is written as

$${p_{kl}}(\widehat{x},\widehat{x}_{\tau }) = \sum \limits _{p = 1}^q {{C_p}(\widehat{x}_k^p\widehat{x}_l^p + } \widehat{x}_{\tau _k}^p\widehat{x}_{\tau _l}^p) + {p_{kl}}(\bar{x},{\bar{x}_\tau })$$

(16)

such that $\bar{x} \subseteq \widehat{x}$, $\bar{x}_{\tau } \subseteq \widehat{x}_{\tau }$, $\left\{ {{{\widehat{x}}_{\tau _k}},\left. {{{\widehat{x}}_{\tau _l}}} \right\} \cap } \right. \bar{x}_{\tau } = \emptyset$ and $\left\{ {{{\widehat{x}}_k},\left. {{{\widehat{x}}_l}} \right\} \cap } \right. \bar{x} = \emptyset$.

and $P_{2}\in \mathbb {R}^{n\times n}$ is a symmetric positive definite matrix and has the following form:

$$P_2= Z \widetilde{P}_2 Z^T$$

(17)

$$\widetilde{P}_2= \left[ \begin{array}{ll} \widetilde{P}_2^{11}&0 \\ 0&\widetilde{P}_2^{22} \end{array}\right]$$

(18)

The following lemma shows that proposed $V_{1}(\widehat{x},\widehat{x}_{\tau })$ is suitable polynomial Lyapunov candidate for (8)

Lemma 4

$V_{1}(\widehat{x},\widehat{x}_{\tau })$ is path-independent, positive definite and continuously differentiable.

Proof

A necessary and sufficient condition for $V_{1}(\widehat{x},\widehat{x}_{\tau })$ to be path-independent is

$$\frac{{\partial {g_i}(\widehat{x},\widehat{x}_{\tau })}}{{\partial {\widehat{x}_j}}} = \frac{{\partial {g_j}(\widehat{x},\widehat{x}_{\tau })}}{{\partial {\widehat{x}_i}}}\,\,\,\,\,\text{for}\, i,j=1,\ldots ,n.$$

(19)

where ${g_i}(\widehat{x},\widehat{x}_{\tau })$ is the ith row of the vector function $g(\widehat{x},\widehat{x}_{\tau })$ and $\widehat{x}_j$ is the jth element of column vector $\widehat{x}$. On the other hand expanding (15), the ith row of $g(\widehat{x},\widehat{x}_{\tau })$ becomes:

$${g_i}(\widehat{x},\widehat{x}_{\tau }) = {d_{ii}}({{\widehat{x}}_i},\widehat{x}_{\tau _{i}}){{\widehat{x}}_i} + \sum \limits _{k \ne i}^n {{p_{ik}}(\widehat{x},\widehat{x}_{\tau }){{\widehat{x}}_k}}$$

(20)

For $j\ne i$, taking a partial derivative with respect to $\widehat{x}_{j}$, we obtain:

$$\begin{aligned} \frac{{\partial {g_i}(\widehat{x},\widehat{x}_{\tau })}}{{\partial {{\widehat{x}}_j}}} &=\frac{{\partial {d_{ii}}(\widehat{x}_{i},\widehat{x}_{\tau _{i}})}}{{\partial {\widehat{x}_j}}}{\widehat{x}_i} + {p_{ij}}(\widehat{x},\widehat{x}_{\tau }) \\&\quad+\,\frac{{\partial {p_{ij}}(\widehat{x},\widehat{x}_{\tau })}}{{\partial {{\widehat{x}}_j}}}\,{\widehat{x}_j} \\ &={p_{ij}}(\widehat{x},\widehat{x}_{\tau })+p{C_p}\widehat{x}_i^p\widehat{x}_j^p,\,\,\,\,\,\,\, \forall \,1 \le i \le n \end{aligned}$$

(21)

Similarly

$$\frac{{\partial {g_j}(\widehat{x},\widehat{x}_{\tau })}}{{\partial {{\widehat{x}}_i}}} ={p_{ji}}(\widehat{x},\widehat{x}_{\tau })+p{C_p}\widehat{x}_j^p\widehat{x}_i^p,\,\,\,\,\,\,\, \forall \,1 \le j \le n$$

(22)

We already set $p_{ij}(\widehat{x},\widehat{x}_{\tau })=p_{ji}(\widehat{x},\widehat{x}_{\tau })$ for $1 \le i,j \le n$. This implies that (19) holds, and thus $V_{1}(\widehat{x},\widehat{x}_{\tau })$ is path-independent.

Moreover, considering Theorem 2 of [18], it can be easily proved that $V_{1}(\widehat{x},\widehat{x}_{\tau })$ is positive definite and continuously differentiable because $\widetilde{P}_{1}(\widehat{x},\widehat{x}_{\tau })$ is positive definite matrix. $\square$

Theorem 1

Consider polynomial fuzzy model (6) with observer based control (7). If there exist matrices $\widetilde{P}_1(\widehat{x},\widehat{x}_{\tau })$, $\widetilde{P}_2^{11}\in \mathbb {R}^{n_y\times n_y}$, $\widetilde{P}_2^{22}\in \mathbb {R}^{(n_x-n_y)\times (n_x-n_y)}$, $S_{1}(\widetilde{x})$, $S_{2}(\widetilde{x})$, $W_{j}^F(\widehat{x})$, $W_{j}^L(\widehat{x})$ such that the following SOS-based conditions are satisfied:

$$\begin{aligned}&v_1^T(\widetilde{P}_1(\widehat{x},\widehat{x}_{\tau })-\epsilon _{1}(\widehat{x},\widehat{x}_{\tau })I)v_1 \,\, is \,\, SOS \end{aligned}$$

(23)

$$\begin{aligned}&v_2^T(P_2-\epsilon _{2}I)v_2 \,\, is \,\, SOS \end{aligned}$$

(24)

$$\begin{aligned}&v_3^T(S_1(\widetilde{x})-\epsilon _{3}(\widetilde{x})I)v_3 \,\, is \,\, SOS\end{aligned}$$

(25)

$$\begin{aligned}v_3^T(S_2(\widetilde{x})-\epsilon _{3}(\widetilde{x})I)v_3 \,\, is \,\, SOS \end{aligned}$$

(26)

$$\begin{aligned}&\begin{array}{rl} -\,\widetilde{\eta }^T(\varUpsilon _{ij}(x,x_{\tau },\widehat{x},\widehat{x}_{\tau })+\varUpsilon _{ji}(x,x_{\tau },\widehat{x},\widehat{x}_{\tau })\\ +\,\epsilon _{4}(x,x_{\tau },\widehat{x},\widehat{x}_{\tau })I)\widetilde{\eta } \,\, is \,\, SOS\;\;\;\; \forall i \le j\\ \end{array} \end{aligned}$$

(27)

where

$$P_2= Z \widetilde{P}_2 Z^T$$

(28)

$$\widetilde{P}_2= \left[\begin{array}{ll} \widetilde{P}_2^{11}& 0 \\ 0& \widetilde{P}_2^{22} \end{array}\right]$$

(29)

$U\in \mathbb {R}^{n_y\times n_y}$, $Z\in \mathbb {R}^{n_x\times n_x}$ and $\widetilde{C}$ are given by applying lemma 3.

$$\begin{aligned} \varUpsilon _{ij}(x,x_{\tau},\widehat{x},\widehat{x}_{\tau })& = \left[\begin{array}{ll}\varUpsilon _{ij}^{1}(x,x_{\tau },\widehat{x},\widehat{x}_{\tau})& \varUpsilon _{ij}^{2}(x_{\tau },\widehat{x},\widehat{x}_{\tau}) \\ *& \varUpsilon _{ij}^{3}(\tilde{x}) \end{array}\right] \\\varUpsilon _{ij}^{1}(x,x_{\tau },\widehat{x},\widehat{x}_{\tau }) & = \left[\begin{array}{ll} \varUpsilon_{ij}^{11}(\widehat{x},\widehat{x}_{\tau })& \varUpsilon_{ij}^{12}(x,x_{\tau },\widehat{x},\widehat{x}_{\tau }) \\*& \varUpsilon _{ij}^{22}(x,x_{\tau},\widehat{x},\widehat{x}_{\tau }) \end{array}\right] \\ \varUpsilon_{ij}^{2}(x,x_{\tau },\widehat{x},\widehat{x}_{\tau })& =\left[\begin{array}{ll} \varUpsilon_{ij}^{13}(\widehat{x},\widehat{x}_{\tau })& \varUpsilon_{ij}^{14}(x_{\tau },\widehat{x},\widehat{x}_{\tau }) \\*& \varUpsilon _{ij}^{24}(x_{\tau },\widehat{x},\widehat{x}_{\tau}) \end{array}\right] \\ \varUpsilon _{ij}^{3}(\tilde{x}) & =\left[\begin{array}{ll} -S_1(\tilde{x})& 0 \\*& -\,S_2(\tilde{x}) \end{array}\right] \\ \varUpsilon_{ij}^{11}(\widehat{x},\widehat{x}_{\tau }) & = A_{i}(\widehat{x},\widehat{x}_{\tau})\widetilde{P}_1(\widehat{x},\widehat{x}_{\tau})-B_{i}(\widehat{x},\widehat{x}_{\tau })W^F_{j}(\widehat{x})\\& \quad +\,\widetilde{P}_1(\widehat{x},\widehat{x}_{\tau}) A_{i}(\widehat{x},\widehat{x}_{\tau })^T\\& \qquad -\,W^F_{j}(\widehat{x})^TB_{i}(\widehat{x},\widehat{x}_{\tau})^T+S_1(\tilde{x}) \\ \varUpsilon _{ij}^{12}(x,x_{\tau},\widehat{x},\widehat{x}_{\tau }) & = W_i^L(\widehat{x})C+\widetilde{P}_1(\widehat{x},\widehat{x}_{\tau})(A_{i}(x,x_{\tau }) \\& \quad -\,A_{i}(\widehat{x},\widehat{x}_{\tau}))^T-W_{j}^F(\widehat{x})^T(B_{i}(x,x_{\tau })\\& \qquad -\,B_{i}(\widehat{x},\widehat{x}_{\tau }))^T \\ \varUpsilon_{ij}^{13}(\widehat{x},\widehat{x}_{\tau }) & =\widetilde{P}_1(\widehat{x},\widehat{x}_{\tau })A_{\tau_i}(\widehat{x}_{\tau })^{T} \\ \varUpsilon _{ij}^{14}(x_{\tau},\widehat{x},\widehat{x}_{\tau }) & =\widetilde{P}_1(\widehat{x},\widehat{x}_{\tau })(A_{\tau _i}(x_{\tau})-A_{\tau _i}(\widehat{x}_{\tau }))^{T} \\ \varUpsilon_{ij}^{22}(x,x_{\tau },\widehat{x},\widehat{x}_{\tau }) & =A_{i}(x,x_{\tau })P_2-W_i^L(\widehat{x}) C \\&\quad +\, P_2A_{i}(x,x_{\tau })^T-C^T W_i^L(\widehat{x})^T \\& \qquad+\,S_2(\tilde{x})\\ \varUpsilon _{ij}^{24}(x_{\tau },\widehat{x},\widehat{x}_{\tau}) & = P_2(\widehat{x},\widehat{x}_{\tau })A_{\tau _i}(x_{\tau})^{T} \end{aligned}$$

(30)

$v_{1}$, $v_{2}$ and $v_{3}$ denote vectors that are independent of x, $x_{\tau }$, $\widehat{x}$ and $\widehat{x}_{\tau }$, and $\widetilde{\eta }$ denotes vectors dependent of x, $x_{\tau }$, $\widehat{x}$ and $\widehat{x}_{\tau }$. $\epsilon _{i}(x)$ is a slack variable (a radially unbounded positive definite polynomial) to keep the positivity of the SOS condition.

Then closed-loop polynomial fuzzy system (8) is asymptotically stable and polynomial controller and observer gains are given by:

$$F_i(\widehat{x})= W_i^F(\widehat{x})\widetilde{P}_1^{-1}(\widehat{x},\widehat{x}_{\tau })$$

(31)

$$L_i(\widehat{x})= W_i^L(\widehat{x}) U \widetilde{C} (\widetilde{P}_2^{11})^{-1} \widetilde{C}^{-1}U^T$$

(32)

Proof

Since the stability of the system implies the stabilization of its dual, we will be interested in the stability of the dual system, many papers [2, 3, 13] had investigated with the dual systems. So, we can deal with the stability of the dual system.

Deriving Lyapunov function (11), we obtain:

$$\begin{aligned} \dot{V}(\widetilde{x})& =2\frac{{\hbox{d}}}{{{\hbox {d}t}}}\int _0^t{{{\hat{x}}^T}{\tilde{P}_1}(\hat{x})\frac{{\hbox{d}\hat{x}}}{{{\hbox {d}t}}}} \,{\hbox {d}t} +\dot{e}_x^T{\tilde{P}_2}{e_x} + e_x^T{\tilde{P}_2}{\dot{e}_x}\\& \quad+{\widetilde{x}^T}S(\widetilde{x})\widetilde{x}-\widetilde{x}_\tau^TS(\widetilde{x}){\widetilde{x}_\tau } \\& =2\frac{\hbox{d}}{{{\hbox {d}t}}}\int _0^t{{{\hat{x}}^T}{\tilde{P}_1}(\hat{x})\,\dot{\hat{x}}\,{\hbox {d}t}} +\dot{e}_x^T{\tilde{P}_2}{e_x} + e_x^T{\tilde{P}_2}{\dot{e}_x}\\&\quad +{\widetilde{x}^T}S(\widetilde{x})\widetilde{x}-\widetilde{x}_\tau^TS(\widetilde{x}){\widetilde{x}_\tau } \\&=2{\widehat{x}^T}{\widetilde{P}_1}(\widehat{x},{\widehat{x}_\tau})\dot{\widehat{x}} + 2e_x^T{P_2}{\dot{e}_x} +{\widetilde{x}^T}S(\widetilde{x})\widetilde{x} \\&\quad-\widetilde{x}_\tau ^TS(\widetilde{x}){\widetilde{x}_\tau }\\&=2{\widetilde{x}^T}{\widetilde{P}}(\widehat{x},{\widehat{x}_\tau})\dot{\widetilde{x}}+{\widetilde{x}^T}S(\widetilde{x})\widetilde{x} -\widetilde{x}_\tau^TS(\widetilde{x}){\widetilde{x}_\tau } \end{aligned}$$

(33)

where

$$\begin{aligned} \widetilde{P}(\widehat{x},\widehat{x}_{\tau }) = \left[ {\begin{array}{ll} {{\widetilde{P}_1}(\widehat{x},\widehat{x}_{\tau })}&0\\ 0&{{P_2}} \end{array}} \right] and\,\, \widetilde{x}= \left[ \begin{array}{cc} \widehat{x}\\ e_{x} \end{array}\right] \end{aligned}$$

(34)

Changing $\dot{\widetilde{x}}$ by its expression of the dual system, function $\dot{V}(\widetilde{x})$ will be of the form:

$$\begin{aligned}&\begin{aligned} \dot{V}(\tilde{x})&=2\sum \limits _{i = 1}^r \sum \limits _{j = 1}^r {h_i}{h_j}{{\tilde{x}}^T}\tilde{P}(\hat{x},{{\hat{x}}_\tau })\big [G_{ij}^T(x,{x_\tau },\hat{x},{{\hat{x}}_\tau })\tilde{x} \\ & \quad +\,{M_i}^T({x_\tau },{{\hat{x}}_\tau }){{\tilde{x}}_\tau }\big ] + {\tilde{x}^T}S(\tilde{x})\tilde{x} - \tilde{x}_\tau ^TS(\tilde{x}){\tilde{x}_\tau } \end{aligned} \end{aligned}$$

(35)

The time derivative of $V(\tilde{x})$ satisfies

$$\begin{aligned} \begin{array}{rl} \dot{V}(\widetilde{x})=&{} \sum ^{r}_{i=1}h_{i}^{2} \widetilde{\eta }^{T} \varOmega _{ii}(x,x_{\tau },\widehat{x},\widehat{x}_{\tau }) \widetilde{\eta } +\sum ^{r}_{i=1}\sum ^{r}_{i<j}h_{i}h_{j}\widetilde{\eta }^{T}\\ {} &{}(\varOmega _{ij}(x,x_{\tau },\widehat{x},\widehat{x}_{\tau })+\varOmega _{ji}(x,x_{\tau },\widehat{x},\widehat{x}_{\tau })) \widetilde{\eta } \end{array} \end{aligned}$$

(36)

where $\widetilde{\eta }^{T}=[\widetilde{x}^{T},\widetilde{x}_{\tau }^{T}]^{T}$.

$$\begin{aligned} \varOmega _{ij}(x,x_{\tau },\widehat{x},\widehat{x}_{\tau }) & = \left[ \begin{array}{cc} \varOmega _{ij}^{11}(x,x_{\tau },\widehat{x},\widehat{x}_{\tau })&\varOmega _{ij}^{12}(x,x_{\tau },\widehat{x},\widehat{x}_{\tau })\\ *&-S(\widetilde{x}) \end{array}\right] \\ \varOmega _{ij}^{11}(x,x_{\tau },\widehat{x},\widehat{x}_{\tau })& = \widetilde{P}(\widehat{x},\widehat{x}_{\tau })G_{ij}^{T}(x,x_{\tau },\widehat{x},\widehat{x}_{\tau }) \\&+\,G_{ij}(x,x_{\tau },\widehat{x},\widehat{x}_{\tau }) \widetilde{P}(\widehat{x},\widehat{x}_{\tau })+S(\widetilde{x}) \\ \varOmega _{ij}^{12}(x,x_{\tau },\widehat{x},\widehat{x}_{\tau }) & = \widetilde{P}(\widehat{x},\widehat{x}_{\tau })M_{i}^{T}(x_{\tau },\widehat{x}_{\tau }) \end{aligned}$$

(37)

If the following conditions hold, $\dot{V}(\widetilde{x})<0$ at $\widetilde{x}\ne 0$

$$\begin{aligned} \begin{array}{rl} \varOmega _{ij}(x,x_{\tau },\widehat{x},\widehat{x}_{\tau })+\varOmega _{ji}(x,x_{\tau },\widehat{x},\widehat{x}_{\tau })\prec 0 \end{array} \end{aligned}$$

(38)

By applying Lemma 3 and taking into account that $P_2$ is in form of (28)–(29), we obtain

$$\begin{aligned} {L_i}(\hat{x})C{P_2}& = {L_i}(\hat{x})U\left[ {\begin{array}{cc} {\tilde{C}}&0 \end{array}} \right] {Z^T}Z\left[ {\begin{array}{cc} {\tilde{P}_2^{11}}& 0\\ 0& {\tilde{P}_2^{22}} \end{array}} \right] {Z^T} \\& = {L_i}(\hat{x})U\left[ {\begin{array}{cc} {\tilde{C}\tilde{P}_2^{11}}&0 \end{array}} \right] {Z^T} \\&= {L_i}(\hat{x})U\tilde{C}\tilde{P}_2^{11}{\tilde{C}^{ - 1}}{U^T}U\left[ {\begin{array}{cc} {\tilde{C}}&0 \end{array}} \right] {Z^T} \end{aligned}$$

Let $W_i^L(\widehat{x})=L_i(\widehat{x}) U \widetilde{C} \widetilde{P}_2^{11} \widetilde{C}^{-1} U^T$, we obtain:

$$\begin{aligned} L_i(\widehat{x}) C P_2=W_i^L(\widehat{x}) C \end{aligned}$$

(39)

Define

$$\begin{aligned} S(\widetilde{x}) = \left[ {\begin{array}{cc} {{S_1}(\widetilde{x})}&0\\ 0&{{S_2}(\widetilde{x})} \end{array}} \right] ,\,\,\,\,\, W_i^F(\widehat{x})=F_i(\widehat{x})\widetilde{P}_1(\widehat{x},\widehat{x}_{\tau }) \end{aligned}$$

(40)

Substituting (40) into (30), we obtain

$$\begin{aligned} \varUpsilon _{ij}(x,x_{\tau },\widehat{x},\widehat{x}_{\tau })+\varUpsilon _{ji}(x,x_{\tau },\widehat{x},\widehat{x}_{\tau })\prec 0 \end{aligned}$$

(41)

The SOS conditions in Theorem 1 imply (41), then, we have $\dot{V}(\widetilde{x})<0$. Therefore, dual system is asymptotically stable. $\square$

Remark 2

Thanks to equivalence principle between the closed loop systems and its dual, the polynomial fuzzy model based control system (8) is guaranteed to be asymptotically stable if the SOS-based conditions in Theorem 1 are satisfied.

Remark 3

Unlike the classical fuzzy Lyapunov function approach in [11, 25] in which the Lyapunov matrix is a constant matrix, our approach focuses on the analysis of the stability of the observer-based control system by using the newly polynomial fuzzy Lyapunov in which the polynomial Lyapunov matrix dependent on the estimated states and the estimated delayed states as well. Therefore, the proposed stability conditions are more relaxed than those obtained using the conventional Lyapunov function approaches even if the system doesn’t deal with the delay problem.

5 Illustrative Examples

To show the effectiveness of the developed approach and the less conservativeness of Theorem 1 using the new line-integral polynomial Lyapunov function, we present three numerical examples of the polynomial fuzzy system, where in the first one we compare our result with the result of algorithm 1 in [8].

5.1 Example 1

In the first example , we design an observer based control for polynomial fuzzy systems with time delay:

$$\left\{ \begin{aligned}\dot{x}&= \sum ^{2}_{i=1}h_{i}\{A_{i}(x,x_{\tau })x+A_{\tau _i}(x_{\tau })x_{\tau }+B_{i}(x,x_{\tau })u\}\\ y&=C x \end{aligned} \right.$$

(42)

where

$$\begin{aligned} A_{1}(x,x_{\tau }) &= \left[ \begin{array}{cc} 1 &{}-0.6x_{2}^{2}\\ -10 &{}-3-x_2^2 \end{array} \right] \\ A_{2}(x,x_{\tau }) & =\left[ \begin{array}{cc} -0.2172& -0.6x_{2}^{2}\\ -10&{} -3-x_2^2 \end{array} \right] \\ {B}_{1}(x,x_{\tau })& = {B}_{2}(x,x_{\tau })= \left[ \begin{array}{cc} 1\\ 0 \end{array} \right] , C= \left[ \begin{array}{cc} 1&0 \end{array} \right] \\ {A}_{\tau _1}(x_{\tau }) & = \left[ \begin{array}{cc} 0.1&{} 0\\ 0.1&{} 0 \end{array} \right] ,\,\,\, {A}_{\tau _2}(x_{\tau })= \left[ \begin{array}{cc} -0.1&{} 0\\ 0.1&{} 0 \end{array} \right] \end{aligned}$$

The membership functions are defined as

$$\begin{aligned} h_{1}=0.5(1-sin(x_{1})),\quad h_{2}=1-h_{1}. \end{aligned}$$

Remark 4

The goal is to find more relaxed result. For this, we propose to compare our result with the result presented in [8]. The proposed result is especially interesting from computational load point of view. Thus, the use the dual system allowed to introduce a vector dependent of x, $x_{\tau }$, $\hat{x}$ and $\hat{x}_{\tau }$. Consequently, we reduce not only the computational efforts but also the conservatism. Secondly, both polynomial state matrices $A_{i}$ and polynomial input matrices $B_{i}$ are depending on both the estimated system states and the estimated delayed system states. Finally, in our method we adopt a new Line-integral polynomial Lyapunov function in which the Lyapunov matrices $\widetilde{P}_1(\widehat{x},\widehat{x}_{\tau })$, $S_1(\widetilde{x})$ and $S_2(\widetilde{x})$ are not constant but polynomial matrices depending on the estimated states and the estimated delayed states. we can conclude that our approach improves the result in [8] for many main aspects.

The SOS conditions in algorithm 1 of [8] are infeasible if Lyapunov matrices $X_{1}$, $X_{2}$, $\widetilde{S}_{1}$ and $\widetilde{S}_{2}$ are constant matrices. However, our SOS conditions in Theorem 1 are feasible if we select $\widetilde{P}_1(\widehat{x},\widehat{x}_{\tau })$, $S_1(\widetilde{x})$ and $S_2(\widetilde{x})$ as polynomial matrices. Thus, the polynomial Lyapunov function in (11) with the polynomial Lyapunov matrices is more useful than the Lyapunov function in [8]. This shows the utility of our SOS based approach.

We choose $\epsilon _{1}(\widehat{x},\widehat{x}_{\tau })=\epsilon _{2}=\epsilon _{3}(\widetilde{x})=\epsilon _{4}(x,x_{\tau },\widehat{x},\widehat{x}_{\tau })=10^{-4}$, degree of $\widetilde{P}_1(\widehat{x},\widehat{x}_{\tau })$ is 2 in $\widehat{x}$ and $\widehat{x}_{\tau }$, degree of $P_2$ is 0, degrees of $S_1(\widetilde{x})$ and $S_2(\widetilde{x})$ are 2 in $\widehat{x}_{2}$ and the degrees of $W^F_{j}(\widehat{x})$ and $W^L_{j}(\widehat{x})$, $j=1,2$, are 2 in $\widehat{x}_{2}$.

By solving the SOS conditions in Theorem 1, we obtain the following solution:

$$\begin{aligned} \tilde{P}_1(\hat{x},\hat{x}_{\tau })= \left[ \begin{array}{cc} \tilde{P}_1^{11}(\hat{x},\hat{x}_{\tau })&{}\tilde{P}_1^{12}(\hat{x},\hat{x}_{\tau })\\ *&{} \tilde{P}_1^{22}(\hat{x},\hat{x}_{\tau }) \end{array} \right] \end{aligned}$$

(43)

where

$$\begin{aligned} \tilde{P}_1^{11}(\hat{x},\hat{x}_{\tau }) &= - 1.548e^{-8}\hat{x}_1^2 - 4.19e^{-16}\hat{x}_1 + 0.1525 \\ \tilde{P}_1^{12}(\hat{x},\hat{x}_{\tau })&= 9.742e^{-9}\hat{x}_1\hat{x}_2 - 3.631e^{-4} \\ \tilde{P}_1^{22}(\hat{x},\hat{x}_{\tau })& =1.641e^{-8}\hat{x}_2^2 - 8.292e^{-14}\hat{x}_2 + 8.439e^{-3} \\ P_2 &= \left[ \begin{array}{cc} 8.256e^{-3} & \quad 0 \\ *& \quad 2.54e^{-3} \end{array} \right] \end{aligned}$$

(44)

$$\begin{aligned} S_1(\hat{x}_{2})& =\left[ \begin{array}{cc} S_1^{11}(\hat{x}_{2})&{} S_1^{12}(\hat{x}_{2})\\ *&{} S_1^{22}(\hat{x}_{2}) \end{array} \right] \end{aligned}$$

(45)

with

$$\begin{aligned} S_1^{11}(\hat{x}_{2}) & = 0.9606\hat{x}_2^2 - 7.654e^{-11}\hat{x}_2 + 1.671 \\ S_1^{12}(\hat{x}_{2}) & = - 6.302e^{-6}\hat{x}_2^2 + 1.758e^{-11}\hat{x}_2 + 1.868e^{-3} \\ S_1^{22}(\hat{x}_{2}) & = 7.501e^{-3}\hat{x}_2^2 - 4.523e^{-13}\hat{x}_2 + 2.908e^{-2} \\ S_2(\hat{x}_{2})&= \left[ \begin{array}{cc} S_2^{11}(\hat{x}_{2})&{} S_2^{12}(\hat{x}_{2})\\ *& S_2^{22}(\hat{x}_{2}) \end{array} \right] \end{aligned}$$

(46)

where

$$\begin{aligned} S_2^{11}(\hat{x}_{2})&= 0.3048\hat{x}_2^2 + 3.826e^{-11}\hat{x}_2 + 0.6666 \\ S_2^{12}(\hat{x}_{2}) & = 1.664e^{-4}\hat{x}_2^2 + 3.03e^{-13}\hat{x}_2 + 6.769e^{-3} \\ S_2^{22}(\hat{x}_{2})& = 2.364e^{-3}\hat{x}_2^2 + 4.642e^{-14}\hat{x}_2 + 1.096e^{-2} \\ W_{1}^F(\hat{x}_{2})&= \left[ \begin{array}{cc} W_{1}^{F_{11}}(\hat{x}_{2})&W_{1}^{F_{12}}(\hat{x}_{2}) \end{array} \right] \end{aligned}$$

(47)

$$\begin{aligned} W_{1}^{F_{11}}(\hat{x}_{2})&= 1.099\hat{x}_2^2 - 4.515e^{-10}\hat{x}_2 + 2.492 \\ W_{1}^{F_{12}}(\hat{x}_{2})&= - 6.177e^{-3}\hat{x}_2^2 + 1.207e^{-11}\hat{x}_2 - 1.562 \\ W_{2}^F(\hat{x}_{2})&= \left[ \begin{array}{cc} W_{2}^{F_{11}}(\hat{x}_{2})&W_{2}^{F_{12}}(\hat{x}_{2}) \end{array} \right] \\ W_{2}^{F_{11}}(\hat{x}_{2}) &= 1.099\hat{x}_2^2 + 3.955e^{-10}\hat{x}_2 + 2.316 \\ W_{2}^{F_{12}}(\hat{x}_{2})&= - 6.174e^{-3}\hat{x}_2^2 + 4.995e^{-12}\hat{x}_2 - 1.562 \\ W_{1}^L(\hat{x}_{2})&= \left[ \begin{array}{cc} 0.323\hat{x}_2^2 - 8.703e^{-10}\hat{x}_2 + 1.852\\ - 3.817e^{-4}\hat{x}_2^2 + 7.848e^{-12}\hat{x}_2 - 6.829e^{-2} \end{array} \right] \\ W_{2}^L(\hat{x}_{2})&= \left[ \begin{array}{cc} 0.323\hat{x}_2^2 + 8.721e^{-10}\hat{x}_2 + 1.843\\ - 3.804e^{-4}\hat{x}_2^2 - 3.938e^{-12}\hat{x}_2 - 6.823e^{-2} \end{array} \right] \end{aligned}$$

(48)

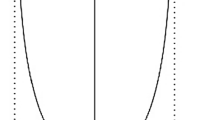
The simulation was carried out from the initial states, $x(0)=\left[6 \quad -1 \right] ^{T}$, $\hat{x}(0)=\left[1\quad -1.5 \right] ^{T}$ and a constant time delay $\tau =1$. Figure 1 shows the states of open-loop system (42). It is seen that unforced open-loop system (42) is unstable.

Fig. 1

Response of open-loop state system (42)

Figure 2 shows the evolution of state variables and their estimated values, for the same initial states as Fig. 1, by the polynomial controller and observer using Theorem 1. In fact, the controller guarantees the global asymptotic stability of the controlled system.

Fig. 2

Response of the state x(t) and its estimated

5.2 Example 2

Consider the following polynomial fuzzy model with time delay

$$\left\{ \begin{aligned}\dot{x} & = \sum ^{2}_{i=1}h_{i}\{A_{i}(x,x_{\tau })x+A_{\tau _i}(x_{\tau })x_{\tau }+B_{i}(x,x_{\tau })u\}\\ y & = C x \end{aligned} \right.$$

(49)

where

$$\begin{aligned} A_{1}(x,x_{\tau })& =\left[ \begin{array}{cc} 1 &{}-0.3x_{\tau _2}\\ -1.5 &{}-2-x_2^2 \end{array} \right] \\ A_{2}(x,x_{\tau })& =\left[ \begin{array}{cc} -0.2172&{} -0.3x_{\tau _2}\\ -1.5&{} -2-x_2^2 \end{array} \right] \\ {B}_{1}(x,x_{\tau })& ={B}_{2}(x,x_{\tau })= \left[ \begin{array}{cc} 1\\ 0 \end{array} \right] , C= \left[ \begin{array}{cc} 1&0 \end{array} \right] \\ {A}_{\tau _1}(x_{\tau })& =\left[ \begin{array}{cc} 0.1&{} 0\\ -0.1x_{\tau _1}&{} 0 \end{array} \right] ,\,\,\, {A}_{\tau _2}(x_{\tau })= \left[ \begin{array}{cc} 0.1&{} 0\\ 0.1&{} 0 \end{array} \right] \end{aligned}$$

The membership functions are the same as in example 1.

Figure 3 shows the behavior of the nonlinear system with $u = 0$. System (49) is unstable.

Fig. 3

Behaviors in $x_{1}(t)-x_{2}(t)$ plane (without feedback)

By solving the SOS conditions in Theorem 1, we obtain the following solution:

$$\begin{aligned} \tilde{P}_1(\hat{x},\hat{x}_{\tau })= \left[ \begin{array}{cc} \tilde{P}_1^{11}(\hat{x},\hat{x}_{\tau })&{}\tilde{P}_1^{12}(\hat{x},\hat{x}_{\tau })\\ *&{} \tilde{P}_1^{22}(\hat{x},\hat{x}_{\tau }) \end{array} \right] \end{aligned}$$

(50)

where

$$\begin{aligned} \tilde{P}_1^{11}(\hat{x},\hat{x}_{\tau })& =- 5.866e^{-9}\hat{x}_{1}^{2}+ 6.068e^{-9}\hat{x}_{1} + 0.02433 \\ \tilde{P}_1^{12}(\hat{x},\hat{x}_{\tau })& =-1.785e^{-11}\hat{x}_{\tau _{1}}\hat{x}_{\tau _{2}} + 1.503e^{-4} \\ \tilde{P}_1^{22}(\hat{x},\hat{x}_{\tau })& =7.022e^{-9}\hat{x}_{2}^2- 4.634e^{-10}\hat{x}_{2}+ 0.1746 \\ P_2& =\left[ \begin{array}{cc} 9.133e^{-4} &{}0\\ *&{} 5.512e^{-2} \end{array} \right] \end{aligned}$$

(51)

$$\begin{aligned} S_1(\hat{x}_{2})& =\left[ \begin{array}{cc} S_1^{11}(\hat{x}_{2})&{} S_1^{12}(\hat{x}_{2})\\ *&{}S_1^{22}(\hat{x}_{2}) \end{array} \right] \end{aligned}$$

(52)

$$\begin{aligned} S_1^{11}(\hat{x}_{2})& =0.837\hat{x}_{2}^2 - 7.171e^{-5}\hat{x}_{2} + 1.369 \\ S_1^{12}(\hat{x}_{2})& =3.678e^{-5}\hat{x}_{2}^2 + 7.542e^{-5}\hat{x}_{2} + 5.378e^{-4} \\ S_1^{22}(\hat{x}_{2})& =0.1601\hat{x}_{2}^2 + 6.012e^{-5}\hat{x}_{2} + 0.5299 \\ S_2(\hat{x}_{2})& =\left[ \begin{array}{cc} S_2^{11}(\hat{x}_{2})&{}S_2^{12}(\hat{x}_{2})\\ *&{} S_2^{22}(\hat{x}_{2}) \end{array} \right] \end{aligned}$$

(53)

$$\begin{aligned} S_2^{11}(\hat{x}_{2})& =0.2688\hat{x}_{2}^2 + 5.223e^{-5}\hat{x}_{2} + 0.5262 \\ S_2^{12}(\hat{x}_{2})& =1.47e^{-5}\hat{x}_{2}^2- 1.388e^{-6}\hat{x}_{2} - 6.827e^{-5} \\ S_2^{22}(\hat{x}_{2})& =5.722e^{-2}\hat{x}_{2}^2 - 8.123e^{-6}\hat{x}_{2} + 0.1935 \\ W_{1}^F(\hat{x}_{2})& =\left[ \begin{array}{cc} W_{1}^{F_{11}}(\hat{x}_{2})&W_{1}^{F_{12}}(\hat{x}_{2}) \end{array} \right] \end{aligned}$$

(54)

$$\begin{aligned} W_{1}^{F_{11}}(\hat{x}_{2})& =0.9624\hat{x}_{2}^2 + 2.982e^{-4}\hat{x}_{2} + 1.778 \\ W_{1}^{F_{12}}(\hat{x}_{2})& =2.528e^{-5}\hat{x}_{2}^2 + 7.81e^{-5}\hat{x}_{2} - 3.769e^{-2} \\ W_{2}^F(\hat{x}_{2})& =\left[ \begin{array}{cc} W_{2}^{F_{11}}(\hat{x}_{2})&W_{2}^{F_{12}}(\hat{x}_{2}) \end{array} \right] \\ W_{2}^{F_{11}}(\hat{x}_{2})& =0.9622\hat{x}_{2}^2 +2.316e^{-4}\hat{x}_{2} + 1.745 \\ W_{2}^{F_{12}}(\hat{x}_{2})& =1.923e^{-4}\hat{x}_{2}^2 + 6.547e^{-5}\hat{x}_{2} - 3.784e^{-2} \\ W_{1}^L(\hat{x}_{2})& =\left[ \begin{array}{cc} 0.2791\hat{x}_{2}^2 + 2.097e^{-5}\hat{x}_{2} + 1.386\\ - 3.894e^{-5}\hat{x}_{2}^2 +1.231e^{-5}\hat{x}_{2} - 1.444e^{-3} \end{array} \right] \\ W_{2}^L(\hat{x}_{2})& =\left[ \begin{array}{cc} 0.2792\hat{x}_{2}^2 - 6.175e^{-5}\hat{x}_{2} + 1.365\\ - 1.328e^{-5}\hat{x}_{2}^2 - 3.478e^{-6}\hat{x}_{2} -1.514e^{-3} \end{array} \right] \end{aligned}$$

(55)

Figure 4 shows control results, for several initial states, by the polynomial controller and observer using Theorem 1. In fact, the controller guarantees the global asymptotic stability of the controlled system.

Fig. 4

Behaviors in $x_{1}(t)-$ $x_{2}(t)$ plane (with feedback)

Figure 5 shows the evolution of state variables and their estimated values, from the initial states, $x(0)=\left[6 \quad -3 \right] ^{T}$, $\hat{x}(0)=\left[1 \quad -1 \right] ^{T}$ and a constant time delay $\tau =1.5$.

Fig. 5

Response of the state x(t) and its estimated

5.3 Example 3

Consider the following polynomial fuzzy model with time delay

$$\begin{aligned} \left\{ \begin{array}{l}\dot{x}= \sum ^{2}_{i=1}h_{i}\{A_{i}(x,x_{\tau })x+A_{\tau _i}(x_{\tau })x_{\tau }+B_{i}(x,x_{\tau })u\}\\ y=C x \end{array} \right. \end{aligned}$$

(56)

where

$$\begin{aligned} A_{1}(x,x_{\tau })& =\left[ \begin{array}{cc} x_{\tau _1} &{}5\\ -1 &{}-x_2^2 \end{array} \right] \\ A_{2}(x,x_{\tau })& =\left[ \begin{array}{cc} -0.2172x_{\tau _1}&{} 5\\ -1&{} -x_2^2 \end{array} \right] \\ {B}_{1}(x,x_{\tau })& ={B}_{2}(x,x_{\tau })= \left[ \begin{array}{cc} x_2^2+5\\ 0 \end{array} \right] , C= \left[ \begin{array}{cc} 1&0 \end{array} \right] \\ {A}_{\tau _1}(x_{\tau })& =\left[ \begin{array}{cc} 0.1&{} 0\\ -0.1x_{\tau _1}&{} 0 \end{array} \right] ,\,\,\, {A}_{\tau _2}(x_{\tau })= \left[ \begin{array}{cc} 0.1&{} 0\\ 0.1&{} 0 \end{array} \right] \end{aligned}$$

The membership functions are defined as

$$\begin{aligned} h_{1}=\dfrac{\sin (x_{1})+0.2172x_{1}}{1.2172x_{1}},\quad h_{2}=1-h_{1}. \end{aligned}$$

The membership functions of the polynomial fuzzy model have only $x_1$ that is measurable.

By solving the SOS conditions in Theorem 1, we obtain the following solution:

$$\begin{aligned} \tilde{P}_1(\hat{x},\hat{x}_{\tau })= \left[ \begin{array}{cc} \tilde{P}_1^{11}(\hat{x},\hat{x}_{\tau })&{}\tilde{P}_1^{12}(\hat{x},\hat{x}_{\tau })\\ *&{} \tilde{P}_1^{22}(\hat{x},\hat{x}_{\tau }) \end{array} \right] \end{aligned}$$

(57)

where

$$\begin{aligned} \tilde{P}_1^{11}(\hat{x},\hat{x}_{\tau })& =2.215e^{-8}\hat{x}_1^2 - 3.682e^{-7}\hat{x}_1 + 1.683e^{-5} \\ \tilde{P}_1^{12}(\hat{x},\hat{x}_{\tau })& =6.632e^{-15}\hat{x}_{\tau _1}\hat{x}_{\tau _2} + 6.745e^{-6} \\ \tilde{P}_1^{22}(\hat{x},\hat{x}_{\tau })& =6.737e^{-7}\hat{x}_2^2 - 4.797e^{-9}\hat{x}_2 + 6.685e^{-5} \\ P_2& =\left[ \begin{array}{cc} 3.82e^{-5} &{}0\\ *&{} 2.58e^{-5} \end{array} \right] \end{aligned}$$

(58)

$$\begin{aligned} S_1(\hat{x}_{2})& =\left[ \begin{array}{cc} S_1^{11}(\hat{x}_{2})&{} S_1^{12}(\hat{x}_{2})\\ *&{}S_1^{22}(\hat{x}_{2}) \end{array} \right] \end{aligned}$$

(59)

$$\begin{aligned} S_1^{11}(\hat{x}_{2})& =3.656e^{-5}\hat{x}_2^2 - 5.74e^{-9}\hat{x}_2 + 2.886e^{-5} \\ S_1^{12}(\hat{x}_{2})& =1.531e^{-5}\hat{x}_2^2 - 2.212e^{-7}\hat{x}_2 - 7.717e^{-7} \\ S_1^{22}(\hat{x}_{2})& =4.026e^{-5}\hat{x}_2^2 + 2.071e^{-8}\hat{x}_2 + 4.957e^{-6} \\ S_2(\hat{x}_{2})& =\left[ \begin{array}{cc} S_2^{11}(\hat{x}_{2})&{}S_2^{12}(\hat{x}_{2})\\ *&{} S_2^{22}(\hat{x}_{2}) \end{array} \right] \end{aligned}$$

(60)

$$\begin{aligned} S_2^{11}(\hat{x}_{2})& =6.759e^{-5}\hat{x}_2^2 - 1.579e^{-7}\hat{x}_2 + 7.352e^{-5} \\ S_2^{12}(\hat{x}_{2})& =3.792e^{-6}\hat{x}_2^2 - 4.133e^{-7}\hat{x}_2 - 4.793e^{-7} \\ S_2^{22}(\hat{x}_{2})& =3.077e^{-5}\hat{x}_2^2 + 2.2e^{-10}\hat{x}_2 - 4.631e^{-9} \\ W_{1}^F(\hat{x}_{2})& =\left[ \begin{array}{cc} W_{1}^{F_{11}}(\hat{x}_{2})&W_{1}^{F_{12}}(\hat{x}_{2}) \end{array} \right] \end{aligned}$$

(61)

$$\begin{aligned} W_{1}^{F_{11}}(\hat{x}_{2})& =1.86e^{-6}\hat{x}_2^2 + 4.041e^{-8}\hat{x}_2 + 5.549e^{-5} \\ W_{1}^{F_{12}}(\hat{x}_{2})& =- 1.393e^{-7}\hat{x}_2^2 + 3.552e^{-8}\hat{x}_2 + 7.184e^{-5} \\ W_{2}^F(\hat{x}_{2})& =\left[ \begin{array}{cc} W_{2}^{F_{11}}(\hat{x}_{2})&W_{2}^{F_{12}}(\hat{x}_{2}) \end{array} \right] \\ W_{2}^{F_{11}}(\hat{x}_{2})& =1.97e^{-6}\hat{x}_2^2 - 3.756e^{-8}\hat{x}_2 + 5.038e^{-5} \\ W_{2}^{F_{12}}(\hat{x}_{2})& =- 1.743e^{-7}\hat{x}_2^2 - 9.279e^{-8}\hat{x}_2 + 7.195e^{-5} \\ W_{1}^L(\hat{x}_{2})& =\left[ \begin{array}{cc} 1.313e^{-4}\hat{x}_2^2 - 2.257e^{-6}\hat{x}_2 + 7.73e^{-4}\\ 1.872e^{-5}\hat{x}_2^2 - 6.508e^{-7}\hat{x}_2 + 8.683e^{-5} \end{array} \right] \\ W_{2}^L(\hat{x}_{2})& =\left[ \begin{array}{cc} 1.277e^{-4}\hat{x}_2^2 - 1.336e^{-6}\hat{x}_2 + 6.92e^{-4}\\ 2.049e^{-5}\hat{x}_2^2 - 2.503e^{-7}\hat{x}_2 + 8.646e^{-5} \end{array} \right] \end{aligned}$$

(62)

Figure 6 shows control results, for several initial states, by the polynomial controller and observer using Theorem 1. In fact, the controller guarantees the global asymptotic stability of the controlled system.

Fig. 6

Behaviors in $x_{1}(t)-x_{2}(t)$ plane (with feedback)

Figure 7 shows the evolution of state variables and their estimated values, from the initial states, $x(0)=\left[0.3 \quad -8 \right] ^{T}$, $\hat{x}(0)=\left[-0.1 \quad 3\right] ^{T}$ and a constant time delay $\tau =4$. It can be found that the estimated state converges to the real state during the stabilizing control.

Fig. 7

Response of the state x(t) and its estimated

6 Conclusion

In this paper, we have presented a SOS based design approach of the observer and the controller for polynomial fuzzy system with time delay. We have proposed a polynomial fuzzy observer to estimate the states of the polynomial fuzzy system. A key feature of the SOS design conditions is the use of the dual system to reduce the computational efforts and a new Line-integral polynomial Lyapunov function in which the polynomial Lyapunov matrix is depending on the estimated states and estimated delayed states. In addition, all the design conditions are represented in terms of SOS and can symbolically and numerically be solved via the recent developed SOSTOOLS and an SDP solver. To illustrate the validity of the design approach, illustrative examples have been provided. This examples have shown the utility of our SOS approach for the polynomial fuzzy observer-based control design.

As a future work, the authors intend to derive SOS observer design conditions for polynomial fuzzy systems wiyh time delay considering unmeasurable premise variables.