1 Introduction

By applying the universal approximation property [1–4], amounts of adaptive fuzzy control schemes have been investigated and significant advances have been obtained in nonlinear systems [5–12]. In the past few decades, the combination of backstepping technique and fuzzy logic system for adaptive control of strict-feedback nonlinear systems got rapid development and research [8–13]. There is no doubt the controllers ensure all the signals which are bounded in [1–14]. However, all the aforementioned works do neglect the existence of nonsmooth nonlinearities, for instance, dead zone and backlash [14] which generally exist in a lot of practical systems.

As is well known, dead zone in many components of control systems is the crucial non-smooth nonlinearities in lots of industrial projects which have gravely deteriorated the system performance, on account of the characteristics of dead zone nonlinearity in actuators are poorly known. A typical dead zone example is dry friction in electromechanical systems [15]. Some scholars directly adopt the most straightforward approach to deal with dead zone nonlinearities by utilizing their inverses based on [16, 17]. Although the above method reduces difficult coefficient of the tracking deviation significantly, the model of dead zone is a simplification for physical properties.

To cope with discrete-time plants with unknown dead zone output, some scholars introduce a novel structure of controller. By [18] the new adaptive control schemes keep the closed-loop signal bounded even if the slopes of the dead zone are unequal. Recently, an adaptive fuzzy backstepping controller which does not construct the dead zone inverse is applied to solve the problem of the nonlinear systems with dead zone and dynamics, see [18, 19]. A novel smooth inverse model was proposed which compensates the impact of dead zone in controller design instead of applying traditional nonsmooth input models to describe output dead zone in [20, 21]. The large-scale nonlinear system and unified stochastic nonlinear interconnected systems have been discussed in depth by some researchers in [22, 23]. Nonlinear systems with dead zone input have been attracting a lot of attention in the adaptive fuzzy control community since few decades ago, numerous professors have dedicated endeavor to enhance the property of nonlinear systems with dead zone at the input in [24–28]. However, there are few research on the output nonlinearity. The recursive least squares (RLS) algorithm can be used to avoid constructing dead zone model in sensors, see [29].

By applying a Nussbaum function and an input-driven filter, the nonlinearity in the output mechanism is resolved in [30]. However, the schemes are not suitable for more universal systems. In addition, a novel smooth model is introduced to deal with dead zone in [31]. A number of gratifying results have been obtained to the above systems by applying the backstepping technique and the fuzzy logic systems (FLS); however, a few schemes are usable for working out pure-feedback control of nonlinear systems which represents a class of more ordinary systems [32]. It is shown that the mentioned pure-feedback control of nonlinear systems has no affine appearance of variables [33]. Other related research literatures on adaptive fuzzy output-feedback control, see [34–37].

In this paper, the tracking control issue of pure-feedback nonlinear systems with external disturbance and unknown dead zone output is researched. We will think about the adaptive control for nonlinear pure-feedback systems with uncertain nonlinearity and unknown dead zone output, which is a challenging and significant work. In this research, we have the following assumption. The virtual control signal and the actual control must be independent of the variables \(x_{i}\) in order to guarantee the controllers gainable. The primary contributions of this paper are that:

(1) The tracking control problem of pure-feedback nonlinear systems with external disturbance and unknown dead zone output is investigated, firstly. On account of the mean value theorem, the non-affine problem is solved.

(2) It is worth noticing that the pure-feedback systems synchronously take the external disturbance and unknown dead zone output into account, comparing with the now available results on pure-feedback issue. In addition, the adaptive fuzzy controller ensures all the signals are bounded in the closed-loop system and the system output converges to a small neighborhood of the initial signal.

The preparatory work is introduced, firstly. A new adaptive fuzzy control design is proposed in Sect. 3. In Sect. 4, the simulation examples are provided to prove the superiority of the scheme.

2 Problem Formulation and Preliminaries

The nonlinear pure-feedback system is given as:

$$\begin{aligned} \left\{ {{\begin{array}{*{20}c} \dot{x}_{i}\,=\,f_{i}(\bar{x}_{i},x_{i+1})+\psi _{i}(t),\ \ i=1,2,\ldots ,n-1 \\ \dot{x}_{n}\,=\,f_{n}(\bar{x}_{n},u)+\psi _{n}(t),\\ y\,=\,\chi (x_{1})\\ \end{array} }} \right. \end{aligned}$$
(2.1)

where \(\bar{x}_{i}=[x_{1},x_{2},\ldots ,x_{i}]\in R^{i}\) is called the state variable, and \(f_{i}(\cdot )\) are unknown smooth functions, \(\psi _{i}(t)\) is the unknown external disturbance, \(u\in R\) is called the input of the system , \(y\in R\) is called the output of the system which is the directly measurable variable. It is assumed that \(x_{1}(t)\) are immeasurable, but \(x_{2}(t),\ldots ,x_{n}(t)\) are measurable variables.

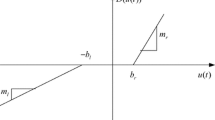
The unknown dead zone output \(\chi (x_{1})\) is considered as the following form:

$$\begin{aligned} y=\chi (x_{1})=\left\{ {{\begin{array}{*{20}c} \pi _{r}(x_{1}), &{}x_{1}\ge h_{r}&{}\\ 0, &{}h_{r}\le x_{1}\le h_{l}&{}\\ \pi _{l}(x_{1}), &{}x_{1}\le h_{l}&{} \end{array} }} \right. \end{aligned}$$
(2.2)

where the unknown parameters \(h_{r}\,<\,0\) and \(h_{l}\,>\,0\) and \(\pi _{r}(x_{1})\) and \(\pi _{l}(x_{1})\) are unknown nonlinear terms.

Remark 1

Literatures [29, 31–35] discussed the issue of adaptive control of nonlinear non-affine pure-feedback systems, which is more general than the previous systems.

Applying the mean value theorem (see [35]), the non-affine functions in (2.1) is rewritten as

$$\begin{aligned} f_{i}(\bar{x}_{i},x_{i+1})-f_{i}(\bar{x}_{i},x_{i+1}^{0})=v_{i}(\bar{x}_{i},\varsigma _{i})({x}_{i+1}-x_{i+1}^{0}), \ \ i=1,2,\ldots ,n \end{aligned}$$
(2.3)

where \((x_{1}^{0},x_{2}^{0},\ldots ,x_{n}^{0},u^{0})^{T}\) is an operating point of interest, \(x_{n+1}=u\), \(x_{n+1}^{0}=u^{0}\) and \(\varsigma _{i}\) is some point between \(x_{i+1}^{0}\) and \(x_{i+1}\). Substituting (2.3) into (2.1), the system dynamics have the following form:

$$\begin{aligned} \left\{ {{\begin{array}{*{20}c} \dot{x}_{i}\,=\,v_{i}(\bar{x}_{i},\varsigma _{i})({x}_{i+1}-x_{i+1}^{0})+f_{i}(\bar{x}_{i},x_{i+1}^{0})+\psi _{i}(t),\ \ i=1,2,\ldots ,n-1 \\ \dot{x}_{n}\,=\,v_{n}(\bar{x}_{n},\varsigma _{n})(u-u^{0})+f_{i}(\bar{x}_{n},u^{0})+\psi _{n}(t),\\ y\,=\,\chi (x_{1})\\ \end{array} }} \right. \end{aligned}$$
(2.4)

A fuzzy logic system is applied to approximate a continuous function f(x) on some compact set \(\Omega\) (see[20]). Adopt the singleton fuzzifier, the product inference, and the center-average defuzzifier to conclude the following fuzzy rules:

\(R^{i}\): If \(x_{1}\) is \({F}_{1}^{i}\) and \(\ldots\) and \(x_{n}\) is \({F}_{n}^{i}\). Then y is \(G^{i}\), \(i=1,2,\ldots ,N\).

\(\bar{x}_{n}=[x_{1},x_{2},\ldots ,x_{n}]\in R^{n}\) is the input of the fuzzy system and \(y\,\in \,R\) is the fuzzy system output, \({F}_{j}^{i}\) and \(G^{i}\) are the fuzzy sets in R. N is the amount of the rules. By the above discussion, it is not hard to obtain the output of the fuzzy system:

$$\begin{aligned} y(x)=\dfrac{{\sum }_{i\,=\,1}^{N}\Phi _{i}{\prod }_{j\,=\,1}^{n}\mu {F}_{j}^{i}(x_{j})}{{\sum }_{i\,=\,1}^{N}\left[ {\prod }_{j\,=\,1}^{n}\mu {F}_{j}^{i}(x_{j})\right] } \end{aligned}$$

where

$$\begin{aligned} \Phi _{i}\,=\,\max \limits _{y\in R}\mu G^{i}(y),\ \ \Phi \,=\,(\Phi _{1},\Phi _{2},\ldots ,\Phi _{N})^{T}. \end{aligned}$$

Let

$$\begin{aligned} G_{i}(x)\,=\,\dfrac{{\prod }_{j\,=\,1}^{n}\mu {F}_{j}^{i}(x_{j})}{{\sum }_{i\,=\,1}^{N}\left[ {\prod }_{j\,=\,1}^{n}\mu {F}_{j}^{i}(x_{j})\right] },\ \ G(x)\,=\,(G_{1}(x),G_{2}(x),\ldots ,G_{N}(x))^{T}, \end{aligned}$$

then

$$\begin{aligned} y(x)\,=\,\Phi ^{T}G(x). \end{aligned}$$

For the sake of proofing the main results, some lemmas and assumptions will be introduced.

Lemma 1

(see[5]): By applying FLS theory, we introduce a continuous function f(x) on a compact set \(\Omega\).

$$\begin{aligned} \sup \limits _{x\in \Omega }\left| f(x)-\Phi ^{T}P(x)\right| \le \varepsilon ,\ \ \forall \varepsilon \,>\,0. \end{aligned}$$

Lemma 2

(see[29]): We can find a smooth function \(\Gamma (\cdot )>0\) and an unknown term \(\Gamma _{0}\,\in \,R\) such that

$$\begin{aligned} \left| f_{1}(x_{1},x_{2}^{0})\right| \le \Gamma \left( |y|\right) +\Gamma _{0}. \end{aligned}$$

Remark 2

Due to \(x_{1}\) is not accessible for measurement, how to build the relationship between the unknown function \(f_{1}(x_{1}, x_{2}^{0})\) and the output y is a crux to construct a backstepping design method for (2.1). Because of Lemma 2, the difficulty of \(x_{1}\) unavailable is overcome. As a result, the following intermediate signal \(\alpha _{i}\) and the actual controlu are independent of the variable \(x_{1}\).

Assumption 1

(see[8]): The reference signal \(y_{0}\) has nth-order time derivatives which are continuous and bounded.

Assumption 2

(see[34]): The sign of \(v_{i}(\bar{x}_{i},x_{i+1})\) does not change. \(c_{m}\) and \(c_{M}\) are unknown constants such that

$$\begin{aligned} 0<c_{m}<\left| v_{i}(\bar{x}_{i},x_{i+1})\right|<c_{M}<\infty ,\ \ \forall (\bar{x}_{i},x_{i+1})\,\in \,R^{i}\,\times \,R, \ \ i\,=\,1,\ldots ,n, \end{aligned}$$

according to the needs of this thesis, it is further assumed that the signs \(v_{i}(\bar{x}_{i},x_{i+1})\ge c_{m}\). In addition, the constants \(c_{m}\) and \(c_{M}\) are unknown.

Assumption 3

(see[5]): It is assumed that there are known parameters \(\bar{p}_{i}(i\,=\,1,2,\ldots ,n)\), satisfying

$$\begin{aligned} \left| \psi _{i}(t)\right| \le \bar{p}_{i}. \end{aligned}$$

Assumption 4

(see[32]): It is assumed that there are unknown positive constants \(b_{M}\) such that

$$\begin{aligned} |\chi ^{'}(x_{1})|=|\dfrac{d\chi (z)}{dz}|_{z=x_{1}}|\le b_{M},\forall x_{1}\,\in \,R. \end{aligned}$$

For simplicity of our discussion, we give the following definitions.

Definition 1

(see[30]): \(H(\varphi )\) is a Nussbaum-type function such that:

$$\begin{aligned} \lim \limits _{a\,\rightarrow \,+\infty }\sup \dfrac{1}{a}\int _{0}^{a}H(\varphi )\mathrm {d}\varphi =+\infty ,\\ \lim \limits _{a\,\rightarrow \,-\infty }\inf \dfrac{1}{a}\int _{0}^{a}H(\varphi )\mathrm {d}\varphi =-\infty . \end{aligned}$$

We can list the functions which meet the definition, such as \(\varphi ^{2}\cos (\varphi )\), \(\varphi ^{2}\sin (\varphi )\), \(\exp (\varphi ^{2})\cos (\varphi )\).

Lemma 3

(see[31]): \(V(\cdot )\) and \(\varphi (\cdot )\) are the smooth functions, \(H(\cdot )\) is a smooth Nussbaum-type function. Then we have:

$$\begin{aligned} 0\le V(t)\le b_{0}+\int _{0}^{t}(q(x(\tau ))H(\varphi )+1)\dot{\varphi }e^{-b_{1}(t-\tau )}\mathrm {d}\tau ,\forall t\in [0,t_{f}), \end{aligned}$$
(2.5)

where \(b_{0}\) and \(b_{1}\,\ge \,0\) are suitable constant, \(q(x(\tau ))\) is a time-varying parameter that takes values in \(I\,=\,[l_{-},l_{+}]\) with \(0\not \in I\), V(t), \(\varphi (t)\), \(\int _{0}^{t}(q(x(\tau ))H(\varphi )+1)\dot{\varphi }\mathrm {d}\tau\) are bounded on \([0,t_{f})\).

3 The Design of Adaptive Fuzzy Control and Its Stability Analysis

In order to develop the n step backstepping approach, we make the following state transformation:

$$\begin{aligned} \omega _{1}&=y-y_{0},\nonumber \\ \omega _{i}&=x_{i}-\alpha _{i-1}, \ \ i\,=\,2,\ldots ,n, \end{aligned}$$
(3.1)

where \(\alpha _{i}\) is an intermediate control that is determined up to the ith step.

We define a constant before developing a backstepping-based design procedure,

$$\begin{aligned} \eta =\max \{\Vert \theta _{i}\Vert ^{2},\ \ i\,=\,0,1,2,\ldots ,n\}, \end{aligned}$$

\(\Vert \theta _{i}\Vert\) is unknown, so \(\eta\) is an unknown positive constant. \(\hat{\eta }\) is the estimate of \(\eta\), and \(\tilde{\eta }\,=\,\eta -\hat{\eta }\). According to the work in [8], it is straightforward to obtain that if \(\hat{\eta }(0)\,\ge \,0\), then \(\hat{\eta }(t)\,\ge \,0\), \(\,\forall t\,\ge \,0\).

Step 1: Think about the Lyapunov function candidate

$$\begin{aligned} V_{1}=\dfrac{\omega _{1}^{2}}{2}+\dfrac{\tilde{\eta }^{2}}{2r}, \end{aligned}$$
(3.2)

where r is a design parameter.

The time derivative of \(V_{1}\) is

$$\begin{aligned} \dot{V_{1}} \,=\, \omega _{1}\dot{\omega }_{1}-\dfrac{\tilde{\eta }}{r}\dot{\hat{\eta }}, \end{aligned}$$
(3.3)
$$\begin{aligned} \omega _{1}\dot{\omega }_{1}= & {} \omega _{1}\left[ \chi '(x_{1})(v_{1}(\bar{x}_{1},\varsigma _{1})({x}_{2}-x_{2}^{0}) +f_{1}(\bar{x}_{1},x_{2}^{0})+\psi _{1}(t))-\dot{y}_{o}\right] \nonumber \\= & {} \omega _{1}\left[ \rho _{1}\omega _{2}v_{1}(x_{1},\varsigma _{1})+\rho _{1}\alpha _{1}v_{1}(x_{1},\varsigma _{1}) -\rho _{1}x_{2}^{0}v_{1}(x_{1},\varsigma _{1})+\rho _{1}f_{1}(x_{1},x_{2}^{0}) +\rho _{1}\psi _{1}(t)-\dot{y}_{o}\right] , \end{aligned}$$
(3.4)

where \(\rho _{1}\,=\,\chi '(x_{1}), |\rho _{1}|\le b_{M}.\)

To deal with the issue that \(\rho _{1}\) is varying, the first virtual control law is constructed by introducing an even Nussbaum-type function \(H(\varphi )\).

$$\begin{aligned} \alpha _{1}\,=\,-H(\varphi )\bar{\alpha }_{1}, \end{aligned}$$
(3.5)

where \(\bar{\alpha }_{1}\) is the auxiliary virtual controller and \(H(\varphi )\) is a Nussbaum-type function such that

$$\begin{aligned} H(\varphi )\,=\,\varphi ^{2}\cos (\varphi ),\ \ \dot{\varphi }\,=\,-\gamma \bar{\alpha }_{1}\omega _{1}g_{1}, \end{aligned}$$

where \(\gamma >0\) is a parameter.

Through the forementioned discussion, we have

$$\begin{aligned} \omega _{1}\rho _{1}\alpha _{1}v_{1}(x_{1},\varsigma _{1})&=-\omega _{1}\rho _{1}H(\varphi )\bar{\alpha }_{1}v_{1}(x_{1},\varsigma _{1}) -\omega _{1}\bar{\alpha }_{1}v_{1}(x_{1},\varsigma _{1})+ \omega _{1}\bar{\alpha }_{1}v_{1}(x_{1},\varsigma _{1})\nonumber \\&=-\omega _{1}v_{1}(x_{1},\varsigma _{1})(\rho _{1}H(\varphi )+1)\bar{\alpha }_{1}+\omega _{1}v_{1}(x_{1},\varsigma _{1})\bar{\alpha }_{1}. \end{aligned}$$
(3.6)

By using Young’s inequality, Assumptions 3, 4 and Lemma 2, we can obtain the following inequalities:

$$\begin{aligned} \omega _{1}\rho _{1}\psi _{1}(t)&\le \dfrac{{b}_{M}^{2}{\bar{p}}_{1}^{2}{\omega }_{1}^{2}}{2{a}_{1}^{2}}+\dfrac{{a}_{1}^{2}}{2},\nonumber \\ \omega _{1}\rho _{1}f_{1}(x_{1},x_{2}^{0})&\le |\omega _{1}|(\Gamma (|y|)+\Gamma _{0}) \end{aligned}$$
(3.7)
$$\begin{aligned}&\le \dfrac{{b}_{M}^{2}\Gamma ^{2}(|y|){\omega }_{1}^{2}}{2{b}_{1}^{2}}+\dfrac{{b}_{M}^{2}{\Gamma }_{0}^{2}{\omega }_{1}^{2}}{2{b}_{1}^{2}}+{b}_{1}^{2}, \end{aligned}$$
(3.8)

where \(a_{1}\) and \(b_{1}\) are arbitrary positive constants.

Based on (3.6, 3.7, 3.8 and 3.4), one has

$$\begin{aligned} \omega _{1}\dot{\omega }_{1}\le \omega _{1}(\rho _{1}\omega _{2}v_{1}(x_{1},\varsigma _{1})+v_{1}(x_{1},\varsigma _{1})(\bar{\alpha }_{1}-x_{2}^{0})+\bar{l}_{1}) +\dfrac{1}{\gamma }(\rho _{1}H(\varphi )+1)\dot{\varphi }+\dfrac{{a}_{1}^{2}}{2}+{b}_{1}^{2}, \end{aligned}$$
(3.9)

where \(\bar{l}_{1}\,=\,\dfrac{{b}_{M}^{2}{\bar{p}}_{1}^{2}{\omega }_{1}^{2}}{2{a}_{1}^{2}}+ \dfrac{{b}_{M}^{2}\Gamma ^{2}(|y|){\omega }_{1}^{2}}{2{b}_{1}^{2}}+\dfrac{{b}_{M}^{2}{\Gamma }_{0}^{2}{\omega }_{1}^{2}}{2{b}_{1}^{2}}-\dot{y}_{o}\).

Because of Lemma 1, there is a fuzzy logic system \({\theta }_{1}^{T}G_{1}(X_{1})\) such that

$$\begin{aligned} \bar{l}_{1}\,=\,{\theta }_{1}^{T}G_{1}(X_{1})+\delta _{1}(X_{1}),\ \ |\delta _{1}(X_{1})|\le \varepsilon _{1},\ \ \forall \varepsilon _{1}>0, \end{aligned}$$

where \(X_{1}\,=\,(y,y_{o},\dot{y}_{o})\).

It can be shown that:

$$\begin{aligned} \omega _{1}\bar{l}_{1}\le \dfrac{\eta }{2{c}_{1}^{2}}\omega _{1}^{2}{G}_{1}^{T}(X_{1})G_{1}(X_{1})+\dfrac{{c}_{1}^{2}}{2}+\dfrac{{\omega }_{1}^{2}}{2}+\dfrac{{\varepsilon }_{1}^{2}}{2}, \end{aligned}$$
(3.10)

where \(c_{1}\) is a parameter.

Through the above discussion, we select the auxiliary virtual controller as follows:

$$\begin{aligned} \bar{\alpha }_{1}\,=\,-{c}_{M}^{-1}\left[ \left( h_{1}+\dfrac{1}{2}\right) \omega _{1}-\dfrac{\hat{\eta }}{2{c}_{1}^{2}}\omega _{1}{G}_{1}^{T}(X_{1})G_{1}(X_{1})\right] +x_{2}^{0}, \end{aligned}$$
(3.11)

where \(h_{1}\,>\,0\) is a design constant.

Substituting (3.10 and 3.11) into (3.9), we will obtain

$$\begin{aligned} \omega _{1}\dot{\omega }_{1}\le&-h_{1}{\omega }_{1}^{2}+\dfrac{\hat{\eta }}{2{c}_{1}^{2}}{\omega }_{1}^{2}{P}_{1}^{T}(X_{1})P_{1}(X_{1})+\omega _{1}\rho _{1}\omega _{2}c_{M}\nonumber \\&+\dfrac{1}{\gamma }(\rho _{1}H(\varphi )+1)\dot{\varphi }+\dfrac{{a}_{1}^{2}}{2}+{b}_{1}^{2}+\dfrac{{c}_{1}^{2}}{2}+\dfrac{{\varepsilon }_{1}^{2}}{2}. \end{aligned}$$
(3.12)

Combing (3.3) with (3.12), the time derivative of \(V_{1}\) has the following form:

$$\begin{aligned} \dot{V}_{1}\le \rho _{1}\omega _{1}\omega _{2}c_{M}-h_{1}{\omega }_{1}^{2}+\dfrac{1}{\gamma }\left( \rho _{1}H(\varphi )+1\right) \dot{\varphi }+\pi _{1} -\dfrac{\tilde{\eta }}{r}\left( \dot{\hat{\eta }}-\dfrac{r}{2{c}_{1}^{2}}{\omega }_{1}^{2}{G}_{1}^{T}(X_{1})G_{1}(X_{1})\right) , \end{aligned}$$
(3.13)

where \(\pi _{1}\,=\,\dfrac{{a}_{1}^{2}}{2}+{b}_{1}^{2}+\dfrac{{c}_{1}^{2}}{2}+\dfrac{{\varepsilon }_{1}^{2}}{2}\).

Step 2: Select the Lyapunov function candidate as

$$\begin{aligned} V_{2}\,=\,V_{1}+\dfrac{1}{2}{\omega }_{2}^{2}, \end{aligned}$$
(3.14)

Similarly to step 1, it is also easy to see that the time derivative of \(V_{2}\),

$$\begin{aligned} \dot{V}_{2}\,=\,\dot{V}_{1}+\omega _{2}(v_{2}(\bar{x}_{2},\varsigma _{2})\omega _{3}+v_{2}(\bar{x}_{2},\varsigma _{2})(\alpha _{2} -x_{3}^{0})\,+\,f_{2}(\bar{x}_{2},x_{3}^{0})+\psi _{2}(t)-\dot{\alpha }_{1}), \end{aligned}$$
(3.15)

where

$$\begin{aligned} \dot{\alpha }_{1}\,=\,\dfrac{\partial \alpha _{1}}{\partial y}\rho _{1}(v_{1}(\bar{x}_{1},\varsigma _{1})({x}_{2}-x_{2}^{0}) +f_{1}(\bar{x}_{1},x_{2}^{0})+\psi _{1}(t)) +\dfrac{\partial \alpha _{1}}{\partial \dot{y}_{o}}\ddot{y}_{o}-\dfrac{\partial \alpha _{1}}{\partial \varphi }\gamma \omega _{1}\bar{\alpha }_{1}v_{1}(x_{1},\varsigma _{1})+ \dfrac{\partial \alpha _{1}}{\partial \hat{\eta }}\dot{\hat{\eta }}. \end{aligned}$$
(3.16)

By applying Assumptions 2, 3 and 4, Lemma 2 and Young’s inequality, the following inequalities are viewed as :

$$\begin{aligned} -\omega _{2}\dfrac{\partial \alpha _{1}}{\partial y}\rho _{1}\psi _{1}(t)&\le \dfrac{{b}_{M}^{2}{\bar{p}}_{1}^{2}{\omega }_{2}^{2}}{2{a}_{2}^{2}}\left( \dfrac{\partial \alpha _{1}}{\partial y}\right) ^{2}+\dfrac{{a}_{2}^{2}}{2}, \end{aligned}$$
(3.17)
$$\begin{aligned} -\omega _{2}\dfrac{\partial \alpha _{1}}{\partial y}\rho _{1}f_{1}(x_{1},x_{2}^{0})&\le \dfrac{{b}_{M}^{2}\Gamma ^{2}(|y|){\omega }_{2}^{2}}{2{b}_{1}^{2}}\left( \dfrac{\partial \alpha _{1}}{\partial y}\right) ^{2} +\dfrac{{b}_{M}^{2}{\Gamma }_{0}^{2}{\omega }_{2}^{2}}{2{b}_{2}^{2}}\left( \dfrac{\partial \alpha _{1}}{\partial y}\right) ^{2}+{b}_{2}^{2}, \end{aligned}$$
(3.18)
$$\begin{aligned} \rho _{1}\omega _{1}\omega _{2}v_{1}(x_{1},\varsigma _{1})&\le \dfrac{{c}_{M}^{2}{b}_{M}^{2}{\omega }_{1}^{2}{\omega }_{2}^{2}}{2{k}_{0}^{2}}+\dfrac{{k}_{0}^{2}}{2}, \end{aligned}$$
(3.19)
$$\begin{aligned} -\omega _{2}\dfrac{\partial \alpha _{1}}{\partial y}\rho _{1}x_{2}v_{1}(x_{1},\varsigma _{1})&\le \dfrac{{b}_{M}^{2}{c}_{M}^{2}{\omega }_{2}^{2}{x}_{2}^{2}}{2{e}_{2}^{2}}\left( \dfrac{\partial \alpha _{1}}{\partial y}\right) ^{2}+\dfrac{{e}_{2}^{2}}{2}, \end{aligned}$$
(3.20)
$$\begin{aligned} \omega _{2}\dfrac{\partial \alpha _{1}}{\partial y}\rho _{1}x_{2}^{0}v_{1}(x_{1},\varsigma _{1})&\le \dfrac{{b}_{M}^{2}{c}_{M}^{2}{\omega }_{2}^{2}{{x}_{2}^{0}}^2}{2{m}_{2}^{2}}\left( \dfrac{\partial \alpha _{1}}{\partial y}\right) ^{2}+\dfrac{{m}_{2}^{2}}{2}, \end{aligned}$$
(3.21)

where \(a_{2}\), \(b_{2}\), \(k_{0}\), \(e_{2}\) and \(m_{2}\) are arbitrary positive constants.

Substituting (3.17, 3.18, 3.19, 3.20, 3.21) into (3.15) yields

$$\begin{aligned} \dot{V}_{2}\le&-h_{1}{\omega }_{1}^{2}+\dfrac{1}{\gamma }\left( \rho _{1}H(\varphi )+1\right) \dot{\varphi }+\pi _{1} -\dfrac{\tilde{\eta }}{r}\left( \dot{\hat{\eta }}-\dfrac{r}{2{c}_{1}^{2}}{\omega }_{1}^{2}{G}_{1}^{T}(X_{1})G_{1}(X_{1})\right) +\dfrac{{a}_{2}^{2}}{2}\nonumber \\&+{b}_{2}^{2}+\dfrac{{k}_{0}^{2}}{2}+\dfrac{{e}_{2}^{2}}{2}+\dfrac{{m}_{2}^{2}}{2}+\omega _{2}\left( \omega _{3}v_{2}(\bar{x}_{2},\varsigma _{2})+\alpha _{2}v_{2}(\bar{x}_{2},\varsigma _{2})+\bar{l}_{2}+\varphi _{2}(X_{2}) -\dfrac{\partial \alpha _{1}}{\partial \hat{\eta }}\dot{\hat{\eta }}\right) , \end{aligned}$$
(3.22)

where

$$\begin{aligned} \bar{l}_{2}=&-\varphi _{2}(X_{2})+\dfrac{{b}_{M}^{2}{\bar{p}}_{1}^{2}{\omega }_{2}}{2{a}_{2}^{2}}\left( \dfrac{\partial \alpha _{1}}{\partial y}\right) +\dfrac{{b}_{M}^{2}\Gamma ^{2}(|y|){\omega }_{2}}{2{b}_{1}^{2}}\left( \dfrac{\partial \alpha _{1}}{\partial y}\right) ^{2} +\dfrac{{b}_{M}^{2}{\Gamma }_{0}^{2}{\omega }_{2}}{2{b}_{2}^{2}}\left( \dfrac{\partial \alpha _{1}}{\partial y}\right) ^{2} +\dfrac{{c}_{M}^{2}{b}_{M}^{2}{\omega }_{1}^{2}{\omega }_{2}}{2{k}_{0}^{2}} -\dfrac{\partial \alpha _{1}}{\partial y_{o}}\dot{y}_{o}\\&+\dfrac{{b}_{M}^{2}{c}_{M}^{2}{\omega }_{2}^{2}{{x}_{2}^{0}}^2}{2{m}_{2}^{2}}\left( \dfrac{\partial \alpha _{1}}{\partial y}\right) ^{2}+\dfrac{{b}_{M}^{2}{c}_{M}^{2}{\omega }_{2}{x}_{2}^{2}}{2{e}_{2}^{2}}\left( \dfrac{\partial \alpha _{1}}{\partial y}\right) ^{2} -\dfrac{\partial \alpha _{1}}{\partial \dot{y}_{o}}\ddot{y}_{o}+\dfrac{\partial \alpha _{1}}{\partial \varphi }\gamma \omega _{1}\bar{\alpha }_{1}v_{1}(x_{1},\varsigma _{1})+f_{2}(\bar{x}_{2},x_{3}^{0})+\psi _{2}(t), \end{aligned}$$

with

$$\begin{aligned} \varphi _{2}(X_{2})=-h_{0}\hat{\eta }\dfrac{\partial \alpha _{1}}{\partial \hat{\eta }}-\omega _{2}\dfrac{r}{2c_{2}}\left| \omega _{2}\dfrac{\partial \alpha _{1}}{\partial \hat{\eta }}\right| +\dfrac{r}{2c_{2}}\dfrac{\partial \alpha _{1}}{\partial \hat{\eta }}{\omega }_{1}^{2}{G}_{1}^{T}(X_{1})G_{1}(X_{1}), \end{aligned}$$
(3.23)

where \(a_{0},c_{2}\) are positive design parameters.

Similarly to the discussion of (3.10), one has

$$\begin{aligned} \bar{l}_{2}={\theta }_{2}^{T}G_{2}(X_{2})+\delta _{2}(X_{2}),\ \ \left| \delta _{2}(X_{2})\right| \le \varepsilon _{2}, \end{aligned}$$
(3.24)

where \(X_{2}\,=\,(y,y_{o},\dot{y}_{o},\ddot{y}_{o},x_{2},\hat{\eta },\rho )\).

It is means that the following inequalities

$$\begin{aligned} \omega _{2}\bar{l}_{2}\le \dfrac{\eta }{2{c}_{2}^{2}}\omega _{2}^{2}{G}_{2}^{T}(X_{2})G_{2}(X_{2})+\dfrac{{c}_{2}^{2}}{2}+\dfrac{{\omega }_{2}^{2}}{2}+\dfrac{{\varepsilon }_{2}^{2}}{2}, \end{aligned}$$
(3.25)

can be obtained, where \(c_{2}\) is a parameter.

Similarly to (3.11), we have

$$\begin{aligned} \alpha _{2}(X_{2})\,=\,-{c}_{M}^{-1}\left[ \left( h_{2}+\dfrac{1}{2}\right) \omega _{2}-\dfrac{\hat{\eta }}{2{c}_{2}^{2}}\omega _{2}{G}_{2}^{T}(X_{2})G_{2}(X_{2})\right] +x_{3}^{0}, \end{aligned}$$
(3.26)

where \(h_{2}\) is a positive design constant.

Combing (3.15) and (3.23, 3.24, 3.25, 3.26) with (3.22), the time derivative of \(V_{2}\) has the following form:

$$\begin{aligned} \dot{V}_{2}\le&-\sum \limits _{i\,=\,1}^{2}h_{i}{\omega }_{i}^{2}+\omega _{2}\omega _{3}c_{M}+\dfrac{1}{\gamma }\left( \rho _{1}H(\varphi )+1\right) \dot{\varphi }+\omega _{2}\left( \varphi _{2}(X_{2})-\dfrac{\partial \alpha _{1}}{\partial \hat{\eta }}\dot{\hat{\eta }}\right) \nonumber \\&-\dfrac{\tilde{\eta }}{r}\left( \dot{\hat{\eta }} -\sum \limits _{i\,=\,1}^{2}\dfrac{r}{2{c}_{i}^{2}}{\omega }_{i}^{2}{G}_{i}^{T}(X_{i})G_{i}(X_{i})\right) +\pi _{2}, \end{aligned}$$
(3.27)

where \(\pi _{2}\,=\,\pi _{1}+\dfrac{{a}_{2}^{2}}{2}+{b}_{2}^{2}+\dfrac{{c}_{2}^{2}}{2}+\dfrac{{k}_{0}^{2}}{2}+\dfrac{{m}_{2}^{2}}{2}+\dfrac{{e}_{2}^{2}}{2}+\dfrac{{\varepsilon }_{2}^{2}}{2}\).

Step i  :  Select the Lyapunov function candidate as

$$\begin{aligned} V_{i}\,=\,V_{i-1}+\dfrac{1}{2}{\omega }_{i}^{2},(3\le i< n) \end{aligned}$$
(3.28)

similar to the discussion in Step 2, the time derivative of \(V_{i}\) is shown as the following form:

$$\begin{aligned} \dot{V}_{i}\,=\,\dot{V}_{i-1}+\omega _{i}\left( v_{i}(\bar{x}_{i},\varsigma _{i})\omega _{i+1}+v_{i}(\bar{x}_{i},\varsigma _{i})\left( \alpha _{i} -x_{i+1}^{0}\right) +f_{i}\left( \bar{x}_{i},x_{i+1}^{0}\right) +\psi _{i}(t)-\dot{\alpha }_{i-1}\right) \end{aligned}$$
(3.29)

where

$$\begin{aligned} \dot{\alpha }_{i-1}\,=\,&-\dfrac{\partial \alpha _{i-1}}{\partial \varphi }\gamma \omega _{1}\bar{\alpha }_{1}v_{1}(x,\varsigma _{1}) +\dfrac{\partial \alpha _{i-1}}{\partial \hat{\eta }}\dot{\hat{\eta }}+ \dfrac{\partial \alpha _{i-1}}{\partial y}\rho _{1}\left( v_{1}(x_{1},\varsigma _{1})(x_{2}-x_{2}^{0})+f_{1}(x_{1},x_{2}^{0})+\psi _{1}(t)\right) \nonumber \\&+\sum \limits _{j\,=\,2}^{i-1}\dfrac{\partial \alpha _{i-1}}{\partial x_{j}}\left( v_{j}(\bar{x}_{j},\varsigma _{j})(x_{j+1}-x_{j+1}^{0})+f_{j}(\bar{x}_{j},x_{j+1}^{0})+\psi _{j}(t)\right) +\sum \limits _{j\,=\,1}^{i}\dfrac{\partial \alpha _{i-1}}{\partial {y}_{o}^{j-1}}{y}_{o}^{j}. \end{aligned}$$
(3.30)

Similar to the analysis of (3.17, 3.18, 3.20) and (3.21), we can obtain the following inequalities:

$$\begin{aligned} -\omega _{i}\dfrac{\partial \alpha _{i-1}}{\partial y}\rho _{1}\psi _{1}(t)&\le \dfrac{{b}_{M}^{2}{\bar{p}}_{1}^{2}{\omega }_{i}^{2}}{2{a}_{i}^{2}}\left( \dfrac{\partial \alpha _{i-1}}{\partial y}\right) ^{2}+\dfrac{{a}_{i}^{2}}{2}, \end{aligned}$$
(3.31)
$$\begin{aligned} -\omega _{i}\dfrac{\partial \alpha _{i-1}}{\partial y}\rho _{1}f_{1}(x_{1},x_{2}^{0})&\le \dfrac{{b}_{M}^{2}\Gamma ^{2}(|y|){\omega }_{i}^{2}}{2{b}_{i}^{2}} \left( \dfrac{\partial \alpha _{i-1}}{\partial y}\right) ^{2} +\dfrac{{b}_{M}^{2}{\Gamma }_{0}^{2}{\omega }_{i}^{2}}{2{b}_{i}^{2}}\left( \dfrac{\partial \alpha _{i-1}}{\partial y}\right) ^{2}+{b}_{i}^{2}, \end{aligned}$$
(3.32)
$$\begin{aligned} -\omega _{i}\dfrac{\partial \alpha _{i-1}}{\partial y}\rho _{1}x_{2}v_{1}(x_{1},\varsigma _{1})&\le \dfrac{{b}_{M}^{2}{c}_{M}^{2}{\omega }_{i}^{2}{x}_{2}^{2}}{2{e}_{i}^{2}}\left( \dfrac{\partial \alpha _{i-1}}{\partial y}\right) ^{2}+\dfrac{{e}_{i}^{2}}{2}, \end{aligned}$$
(3.33)
$$\begin{aligned} \omega _{i}\dfrac{\partial \alpha _{i-1}}{\partial y}\rho _{1}x_{2}^{0}v_{1}(x_{1},\varsigma _{1})&\le \dfrac{{b}_{M}^{2}{c}_{M}^{2}{\omega }_{i}^{2}{x}_{2}^{2}}{2{m}_{i}^{2}}\left( \dfrac{\partial \alpha _{i-1}}{\partial y}\right) ^{2}+\dfrac{{m}_{i}^{2}}{2}, \end{aligned}$$
(3.34)

where \(a_{i}\), \(b_{i}\), \(e_{i}\) and \(m_{i}\) are arbitrary positive constants.

We take the same way in Step 2, then

$$\begin{aligned} \dot{V}_{i}\le&-\sum \limits _{j\,=\,1}^{i-1}h_{j}{\omega }_{j}^{2}+\dfrac{1}{\gamma }\left( \rho _{1}H(\varphi )+1\right) \dot{\varphi }+\pi _{i-1} -\dfrac{\tilde{\eta }}{r}\left( \dot{\hat{\eta }}-\sum \limits _{j\,=\,1}^{i-1}\dfrac{r}{2{c}_{j}^{2}}{\omega }_{j}^{2}{G}_{j}^{T}(X_{j})G_{j}(X_{1})\right) \nonumber \\&+\omega _{i}\left( \omega _{i+1}v_{i}(\bar{x}_{i},\varsigma _{i})+v_{i}(\bar{x}_{i},\varsigma _{i})(\alpha _{i}-x_{i+1}^{0})+\bar{l}_{i}+\varphi _{i}(X_{i}) -\dfrac{\partial \alpha _{i-1}}{\partial \hat{\eta }}\dot{\hat{\eta }}\right) \nonumber \\&+\dfrac{{a}_{i}^{2}}{2}+{b}_{i}^{2}+\dfrac{{m}_{i}^{2}}{2} +\dfrac{{e}_{i}^{2}}{2}, \end{aligned}$$
(3.35)

where

$$\begin{aligned} \bar{l}_{i}\,=\,&-\varphi _{i}(X_{i})+\dfrac{{b}_{M}^{2}{\bar{p}}_{1}^{2}{\omega }_{i}}{2{a}_{i}^{2}}\left( \dfrac{\partial \alpha _{i-1}}{\partial y}\right) +\dfrac{{b}_{M}^{2}\Gamma ^{2}(|y|){\omega }_{i}}{2{b}_{i}^{2}}\left( \dfrac{\partial \alpha _{i-1}}{\partial y}\right) ^{2} +\dfrac{{b}_{M}^{2}{\Gamma }_{0}^{2}{\omega }_{i}}{2{b}_{i}^{2}}\left( \dfrac{\partial \alpha _{i-1}}{\partial y}\right) ^{2}\\&+\dfrac{{b}_{M}^{2}{c}_{M}^{2}{\omega }_{i}{x}_{i}^{2}}{2{e}_{i}^{2}}\left( \dfrac{\partial \alpha _{i-1}}{\partial y}\right) ^{2} +\dfrac{{b}_{M}^{2}{c}_{M}^{2}{\omega }_{i}^{2}{x}_{2}^{2}}{2{m}_{i}^{2}}\left( \dfrac{\partial \alpha _{i-1}}{\partial y}\right) ^{2} -\sum \limits _{j\,=\,1}^{i}\dfrac{\partial \alpha _{i-1}}{\partial {y}_{o}^{(j-1)}}{y}_{o}^{(j)} +\dfrac{\partial \alpha _{i-1}}{\partial \varphi }\gamma \omega _{1}\bar{\alpha }_{1}v_{1}(x_{1},\varsigma _{1}) \\&+\sum \limits _{j\,=\,2}^{i-1}\dfrac{\partial \alpha _{i-1}}{\partial x_{j}}\left( v_{j}(\bar{x}_{j},\varsigma _{j})(x_{j+1}-x_{j+1}^{0})+f_{j}(\bar{x}_{j},x_{j+1}^{0})+\psi _{j}(t)\right) +\psi _{i}(t)+ f_{i}(\bar{x}_{i},x_{i+1}^{0})+\omega _{i}\omega _{i+1}v_{i}(\bar{x}_{i},\varsigma _{i}), \end{aligned}$$

with

$$\begin{aligned} \varphi _{i}(X_{i})\,=\,-h_{0}\hat{\eta }\dfrac{\partial \alpha _{i-1}}{\partial \hat{\eta }}-\sum \limits _{j\,=\,2}^{i}\omega _{i}\dfrac{r}{2c_{i}}\left| \omega _{j}\dfrac{\partial \alpha _{i-1}}{\partial \hat{\eta }}\right| +\sum \limits _{j\,=\,1}^{i-1}\dfrac{r}{2c_{i}}\dfrac{\partial \alpha _{i-1}}{\partial \hat{\eta }}{\omega }_{j}^{2}{G}_{j}^{T}(X_{j})G_{j}(X_{j}), \end{aligned}$$
(3.36)

where \(c_{i}\) are positive design parameters.

From (3.24), there is a fuzzy logic system \({\theta }_{i}^{T}G_{i}(X_{i})\); it satisfies

$$\begin{aligned} \bar{l}_{i}\,=\,{\theta }_{i}^{T}G_{i}(X_{i})+\delta _{i}(X_{i}),\ \ |\delta _{i}(X_{i})|\le \varepsilon _{i}, \end{aligned}$$
(3.37)

where \(X_{i}\,=\,(y,{\bar{y}}_{o}^{i},x_{2},\ldots ,x_{i},\hat{\eta },\rho )\).

We can prove

$$\begin{aligned} \omega _{i}\bar{l}_{i}\le \dfrac{\eta }{2{c}_{i}^{2}}\omega _{i}^{2}{G}_{i}^{T}(X_{i})G_{i}(X_{i})+\dfrac{{c}_{i}^{2}}{2}+\dfrac{{\omega }_{i}^{2}}{2}+\dfrac{{\varepsilon }_{i}^{2}}{2}, \end{aligned}$$
(3.38)

where \(c_{i}\) is a parameter.

Similarly to (3.11), we have

$$\begin{aligned} \alpha _{i}(X_{i})\,=\,-{c}_{M}^{-1}\{(h_{i}+\dfrac{1}{2})\omega _{i}-\dfrac{\hat{\eta }}{2{c}_{i}^{2}}\omega _{i}{G}_{i}^{T}(X_{i})G_{i}(X_{i})\}+x_{i+1}^{0}, \end{aligned}$$
(3.39)

where \(h_{i}>0\) is a design constant.

Combing (3.36, 3.37, 3.38, 3.39) with (3.35):

$$\begin{aligned} \dot{V}_{i}\le&-\sum \limits _{j\,=\,1}^{i}h_{j}{\omega }_{j}^{2}+\dfrac{1}{\gamma }(\rho _{1}H(\varphi )+1)\dot{\varphi } +\sum \limits _{j\,=\,2}^{i}\omega _{j}\left( \varphi _{j}(X_{j})-\dfrac{\partial \alpha _{j-1}}{\partial \hat{\eta }}\dot{\hat{\eta }}\right) \nonumber \\&-\dfrac{\tilde{\eta }}{r}\left( \dot{\hat{\eta }}-\sum \limits _{j\,=\,1}^{i}\dfrac{r}{2{c}_{j}^{2}}{\omega }_{j}^{2}{G}_{j}^{T}(X_{j})G_{j}(X_{j})\right) +\pi _{i}+\omega _{i}\omega _{i+1}c_{M}, \end{aligned}$$
(3.40)

where \(\pi _{i}\,=\,\pi _{i-1}+\dfrac{{a}_{i}^{2}}{2}+{b}_{i}^{2}+\dfrac{{c}_{i}^{2}}{2}+\dfrac{{e}_{i}^{2}}{2}+\dfrac{{m}_{i}^{2}}{2}+\dfrac{{\varepsilon }_{i}^{2}}{2}.\)

Step n: Select the Lyapunov function candidate as

$$\begin{aligned} V_{n}\,=\,V_{n-1}+\dfrac{1}{2}{\omega }_{n}^{2}. \end{aligned}$$
(3.41)

Similarly,

$$\begin{aligned} \dot{V}_{n}\,=\,\dot{V}_{n-1}+\omega _{n}\left( v_{n}(\bar{x}_{n},\varsigma _{n})(u-u^{0})\,+\,f_{i}(\bar{x}_{n},u^{0})+\psi _{n}(t)-\dot{\alpha }_{n-1}\right) \end{aligned}$$
(3.42)

where

$$\begin{aligned} \dot{\alpha }_{n-1}\,=\,&-\dfrac{\partial \alpha _{n-1}}{\partial \varphi }\gamma \omega _{1}\bar{\alpha }_{1}v_{1}(x,\varsigma _{1}) +\dfrac{\partial \alpha _{n-1}}{\partial \hat{\eta }}\dot{\hat{\eta }}+ \dfrac{\partial \alpha _{n-1}}{\partial y}\rho _{1}\left( v_{1}(x_{1},\varsigma _{1})(x_{2}-x_{2}^{0})+f_{1}(x_{1},x_{2}^{0})+\psi _{1}(t)\right) \nonumber \\&+\sum \limits _{i\,=\,2}^{n-1}\dfrac{\partial \alpha _{n-1}}{\partial x_{i}}\left( v_{i}(\bar{x}_{i},\varsigma _{i})(x_{i+1}-x_{i+1}^{0})+f_{i}(\bar{x}_{i},x_{i+1}^{0})+\psi _{i}(t)\right) +\sum \limits _{i\,=\,1}^{n}\dfrac{\partial \alpha _{n-1}}{\partial {y}_{o}^{i-1}}{y}_{o}^{i}. \end{aligned}$$
(3.43)

Based on the above discussion, taking (3.31, 3.32, 3.33, 3.34) with \(i\,=\,n\) into account that

$$\begin{aligned} -\omega _{n}\dfrac{\partial \alpha _{n-1}}{\partial y}\rho _{1}\psi _{1}(t)&\le \dfrac{{b}_{M}^{2}{\bar{p}}_{1}^{2}{\omega }_{n}^{2}}{2{a}_{n}^{2}}\left( \dfrac{\partial \alpha _{n-1}}{\partial y}\right) ^{2}+\dfrac{{a}_{n}^{2}}{2}, \end{aligned}$$
(3.44)
$$\begin{aligned} -\omega _{n}\dfrac{\partial \alpha _{n-1}}{\partial y}\rho _{1}f_{1}(x_{1},x_{2}^{0})&\le \dfrac{{b}_{M}^{2}\Gamma ^{2}(|y|){\omega }_{n}^{2}}{2{b}_{n}^{2}}\left( \dfrac{\partial \alpha _{n-1}}{\partial y}\right) ^{2} +\dfrac{{b}_{M}^{2}{\Gamma }_{0}^{2}{\omega }_{n}^{2}}{2{b}_{n}^{2}}\left( \dfrac{\partial \alpha _{n-1}}{\partial y}\right) ^{2}\,+\,{b}_{n}^{2}, \end{aligned}$$
(3.45)
$$\begin{aligned} -\omega _{n}\dfrac{\partial \alpha _{n-1}}{\partial y}\rho _{1}x_{2}v_{1}(x_{1},\varsigma _{1})&\le \dfrac{{b}_{M}^{2}{c}_{M}^{2}{\omega }_{n}^{2}{x}_{2}^{2}}{2{e}_{n}^{2}}\left( \dfrac{\partial \alpha _{n-1}}{\partial y}\right) ^{2}+\dfrac{{e}_{n}^{2}}{2}, \end{aligned}$$
(3.46)
$$\begin{aligned} \omega _{n}\dfrac{\partial \alpha _{n-1}}{\partial y}\rho _{1}x_{2}^{0}v_{1}(x_{1},\varsigma _{1})&\le \dfrac{{b}_{M}^{2}{c}_{M}^{2}{\omega }_{i}^{2}{x}_{2}^{2}}{2{m}_{n}^{2}}\left( \dfrac{\partial \alpha _{n-1}}{\partial y}\right) ^{2}+\dfrac{{m}_{n}^{2}}{2}, \end{aligned}$$
(3.47)

where \(a_{n}\), \(b_{n}\) \(e_{n}\) and \(m_{n}\) are arbitrary positive constants.

Substituting (3.44, 3.35, 3.36, 3.47) into (3.42), it yields

$$\begin{aligned} \dot{V}_{n}\le&-\sum \limits _{i\,=\,1}^{n-1}h_{i}{\omega }_{i}^{2}+\dfrac{1}{\gamma }(\rho _{1}H(\varphi )+1)\dot{\varphi }+\pi _{n-1} -\dfrac{\tilde{\eta }}{r}\left( \dot{\hat{\eta }}-\sum \limits _{i\,=\,1}^{n-1}\dfrac{r}{2{c}_{i}^{2}}{\omega }_{i}^{2}{G}_{i}^{T}(X_{i})G_{i}(X_{1})\right) \nonumber \\&+\dfrac{{a}_{n}^{2}}{2}+{b}_{n}^{2}+\dfrac{{e}_{n}^{2}}{2}+\dfrac{{m}_{n}^{2}}{2}+\omega _{n}\left( v_{n}(\bar{x}_{n},\varsigma _{n})(u-u^{0})+\bar{l}_{n}+\varphi _{n}(X_{n}) -\dfrac{\partial \alpha _{i-1}}{\partial \hat{\eta }}\dot{\hat{\eta }}\right) , \end{aligned}$$
(3.48)

where

$$\begin{aligned} \bar{l}_{n}=&-\varphi _{n}(X_{n})+\dfrac{{b}_{M}^{2}{\bar{p}}_{1}^{2}{\omega }_{n}}{2{a}_{i}^{2}}\left( \dfrac{\partial \alpha _{n-1}}{\partial y}\right) +\dfrac{{b}_{M}^{2}\Gamma ^{2}(|y|){\omega }_{n}}{2{b}_{i}^{2}}\left( \dfrac{\partial \alpha _{n-1}}{\partial y}\right) ^{2} +\dfrac{{b}_{M}^{2}{\Gamma }_{0}^{2}{\omega }_{n}}{2{b}_{i}^{2}}\left( \dfrac{\partial \alpha _{n-1}}{\partial y}\right) ^{2}\\&+\dfrac{{b}_{M}^{2}{c}_{M}^{2}{\omega }_{n}{x}_{i}^{2}}{2{e}_{n}^{2}}\left( \dfrac{\partial \alpha _{n-1}}{\partial y}\right) ^{2}+\dfrac{{b}_{M}^{2}{c}_{M}^{2}{\omega }_{i}^{2}{x}_{2}^{2}}{2{m}_{n}^{2}}\left( \dfrac{\partial \alpha _{n-1}}{\partial y}\right) ^{2} +\sum \limits _{i\,=\,2}^{n-1}\dfrac{\partial \alpha _{n-1}}{\partial x_{i}}\left( x_{i+1}v_{i}(\bar{x}_{i})+f_{i}(\bar{x}_{i})+\psi _{i}(t)\right) \\&-\sum \limits _{i\,=\,1}^{n}\dfrac{\partial \alpha _{n-1}}{\partial {y}_{o}^{(i-1)}}{y}_{o}^{(i)} +\dfrac{\partial \alpha _{n-1}}{\partial \varphi }\gamma \omega _{1}\bar{\alpha }_{1}v_{1}(x_{1},\varsigma _{1})+f_{n}(\bar{x}_{n},u_{0})+\psi _{n}(t), \end{aligned}$$

with

$$\begin{aligned} \varphi _{n}(X_{n})\,=\,-h_{0}\hat{\eta }\dfrac{\partial \alpha _{n-1}}{\partial \hat{\eta }}-\sum \limits _{i\,=\,2}^{n}\omega _{n}\dfrac{r}{2c_{n}}\left| \omega _{i}\dfrac{\partial \alpha _{n-1}}{\partial \hat{\eta }}\right| +\sum \limits _{i\,=\,1}^{n-1}\dfrac{r}{2c_{n}}\dfrac{\partial \alpha _{n-1}}{\partial \hat{\eta }}{\omega }_{i}^{2}{G}_{i}^{T}(X_{i})G_{i}(X_{i}), \end{aligned}$$
(3.49)

where \(c_{n}\) are positive design parameters.

Similarly, one has

$$\begin{aligned} \bar{l}_{n}\,=\,{\theta }_{n}^{T}G_{n}(X_{n})+\delta _{n}(X_{n}),\ \ |\delta _{n}(X_{n})|\le \varepsilon _{n},\ \ \varepsilon _{n}>0, \end{aligned}$$
(3.50)

where \(X_{n}\,=\,(y,{\bar{y}}_{o}^{(n)},x_{2},\ldots ,x_{n},\hat{\eta },\rho )\).

It is easy to show that

$$\begin{aligned} \omega _{n}\bar{l}_{n}\le \dfrac{\eta }{2{c}_{n}^{2}}\omega _{n}^{2}{G}_{n}^{T}(X_{n})G_{n}(X_{n})+\dfrac{{c}_{n}^{2}}{2}+\dfrac{{\omega }_{n}^{2}}{2}+\dfrac{{\varepsilon }_{n}^{2}}{2}, \end{aligned}$$
(3.51)

where \(c_{n}\) is a parameter.

The control law is selected as

$$\begin{aligned} u\,=\,-{c}_{M}^{-1}\left[ \left( h_{n}+\dfrac{1}{2}\right) \omega _{n}-\dfrac{\hat{\eta }}{2{c}_{n}^{2}}\omega _{n}{G}_{n}^{T}(X_{n})G_{n}(X_{n})\right] +u_{0}, \end{aligned}$$
(3.52)

where \(h_{n}\) is a positive design constant.

Together with (3.49, 3.50, 3.51, 3.52) and (3.48), the time derivative of \(V_{n}\) is shown as:

$$\begin{aligned} \dot{V}_{n}\le&-\sum \limits _{i\,=\,1}^{n}h_{i}{\omega }_{i}^{2}+\dfrac{1}{\gamma }\left( \rho _{1}H(\varphi )+1)\dot{\varphi }+\sum \limits _{i\,=\,2}^{n}\omega _{i}(\varphi _{i}(X_{i})-\dfrac{\partial \alpha _{i-1}}{\partial \hat{\eta }}\dot{\hat{\eta }}\right) \nonumber \\&-\dfrac{\tilde{\eta }}{r}\left( \dot{\hat{\eta }}-\sum \limits _{i\,=\,1}^{n}\dfrac{r}{2{c}_{i}^{2}}{\omega }_{i}^{2}{G}_{i}^{T}(X_{i})G_{i}(X_{i})\right) +\pi _{n}, \end{aligned}$$
(3.53)

where \(\pi _{n}\,=\,\pi _{n-1}+\dfrac{{a}_{n}^{2}}{2}+{b}_{n}^{2}+\dfrac{{c}_{n}^{2}}{2}+\dfrac{{e}_{n}^{2}}{2}+\dfrac{{m}_{n}^{2}}{2}+\dfrac{{\varepsilon }_{n}^{2}}{2}.\)

We employ the adaptive law as

$$\begin{aligned} \dot{\hat{\eta }}\,=\,\sum \limits _{i\,=\,1}^{n}\dfrac{r}{2{c}_{i}^{2}}{\omega }_{i}^{2}{G}_{i}^{T}(X_{i})G_{i}(X_{i})-h_{0}\hat{\eta },\ \ \hat{\eta }(0)\ge 0. \end{aligned}$$
(3.54)

By applying the work in [29], it can be shown that

$$\begin{aligned} \sum \limits _{i\,=\,2}^{n}\omega _{i}\left( \varphi _{i}(X_{i})-\dfrac{\partial \alpha _{i-1}}{\partial \hat{\eta }}\dot{\hat{\eta }}\right) \le 0. \end{aligned}$$
(3.55)

It is noted that

$$\begin{aligned} \tilde{\eta }\hat{\eta }\,=\,\tilde{\eta }(\eta -\tilde{\eta })\le -\dfrac{\tilde{\eta }^{2}}{2}+\dfrac{\eta ^{2}}{2}. \end{aligned}$$
(3.56)

Combing (3.53, 3.54, 3.55, 3.56), the time derivative of \(V_{n}\) satisfies

$$\begin{aligned} \dot{V}_{n}\le -\sum \limits _{i\,=\,1}^{n}h_{i}{\omega }_{i}^{2}+\dfrac{1}{\gamma }(\rho _{1}H(\varphi )+1)\dot{\varphi }+\pi _{n} -\dfrac{h_{0}}{2r}\tilde{\eta }^{2}+\dfrac{h_{0}}{2r}\eta ^{2}. \end{aligned}$$
(3.57)

Define

$$\begin{aligned} D&=min\{2h_{i},h_{0}\}>0, \ \ (1\le i\le n),\nonumber \\ \pi&=\pi _{n}+\dfrac{h_{0}}{2r}\eta ^{2}\nonumber \\&=\sum \limits _{i\,=\,1}^{n}\dfrac{{a}_{i}^{2}}{2}+\sum \limits _{i\,=\,1}^{n}{b}_{i}^{2}+\sum \limits _{i\,=\,1}^{n}\dfrac{{c}_{i}^{2}}{2} +\sum \limits _{i\,=\,1}^{n}\dfrac{{e}_{i}^{2}}{2}+\sum \limits _{i\,=\,2}^{n}\dfrac{{m}_{i}^{2}}{2}+\sum \limits _{i\,=\,1}^{n}\dfrac{{\varepsilon }_{i}^{2}}{2}+\dfrac{h_{0}}{2r}\eta ^{2}, \end{aligned}$$
(3.58)

then we get

$$\begin{aligned} \dot{V}_{n}\le -D{V}_{n}+\pi +\dfrac{1}{\gamma }(\rho _{1}H(\varphi )+1)\dot{\varphi }. \end{aligned}$$
(3.59)

With above discussions, then we present our contribution in this thesis.

Theorem 1

By applying the fuzzy logic systems and Assumptions 1, 2, 3 and 4, the unknown functions \(\bar{l}_{i}\) are approximated to some bounded term for the nonlinear system (2.4). By choosing the control law (3.52) and the intermediate virtual control (3.5, 3.11, 3.26, 3.39) and the adaptive law (3.50), it makes all the signals which are mentioned in this system be bounded. In addition, the tracking deviation \(\omega _{1}\,=\,y-y_{0}\) meets the following condition

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }S_{1}^{2}\le \dfrac{2\pi }{D}+\dfrac{2\sigma }{\gamma },\ \ 1\le i\le n, \end{aligned}$$
(3.60)

where D and \(\pi\) are defined in (3.58), and \(\sigma\) defined in (3.62).

Proof

Integrating (3.59) over [0,t], we can obtain the following inequality:

$$\begin{aligned} V_{n}(t)\le e^{-Dt}(V_{n}(0)-\dfrac{\pi }{D})+\dfrac{\pi }{D}+\dfrac{e^{-Dt}}{\gamma }\int _{0}^{t}(\rho _{1}H(\varphi )+1)\dot{\varphi } e^{Dt}\mathrm {d}\tau . \end{aligned}$$
(3.61)

\(V_{n}(t)\), \(\varphi (t)\) and \(\int _{0}^{t}(\rho _{1}H(\varphi )+1)\dot{\varphi }\mathrm {d}\tau\) are bounded in \([0,t_{f})\) by Lemma 3. In addition, \(\int _{0}^{t}(\rho _{1}H(\varphi )+1)\dot{\varphi } e^{-D(t-\tau )}\mathrm {d}\tau \le \int _{0}^{t}(\rho _{1}H(\varphi )+1)\dot{\varphi } \mathrm {d}\tau\), it is shown that \(\int _{0}^{t}(\rho _{1}H(\varphi )+1)\dot{\varphi } e^{-D(t-\tau )}\mathrm {d}\tau\) are bounded on \([0,t_{f})\).

Define

$$\begin{aligned} \sigma \,=\,\mathop {max} \limits _{t\in [0,t_{f})}\left| \int _{0}^{t}(\rho _{1}H(\varphi )+1)\dot{\varphi } e^{-D(t-\tau )}\mathrm {d}\tau \right| . \end{aligned}$$
(3.62)

By (3.60) and (3.61), we have \(\dfrac{\omega _{1}^{2}}{2}\le V_{n}(t)\le e^{-Dt}(V_{n}(0)-\dfrac{\pi }{D})+\dfrac{\pi }{D}+\dfrac{\sigma }{\gamma }\).

Because of \(D>0\), it is not hard to elicit that all the signals mentioned in this system are bounded. Therefore, when \(t\rightarrow +\infty\), (3.60) holds.

Remark 3

It is evident that the tracking deviation depends on \(a_{i}\), \(b_{i},c_{i},e_{i},h_{i}\), r, \(\gamma\) and unknown term \(\eta\) by the above analysis. It is guaranteed that the tracking deviation is in a small neighborhood of the origin. According to (3.57), increasing \(h_{i}\), r and \(\gamma\), meanwhile reducing \(a_{i}\), \(b_{i}\), \(c_{i}\) and \(e_{i}\), leads to a small tracking error.

4 Simulation Examples

The second-order nonlinear system is introduced to examine the availability of the proposed scheme.

$$\begin{aligned} \left\{ {{\begin{array}{*{20}c} \dot{x}_{1}\,=\,x_{2}\ln (10+{x}_{1}^{2})+{x}_{1}^2\sin x_{1}+0.01e^{-t}\cos t,\\ \dot{x}_{2}\,=\,u(1+e^{-{x}_{1}^{2}-{x}_{2}^{2}})+\dfrac{x_{1}x_{2}}{1+{x}_{1}^{2}+{x}_{2}^{2}}+0.5cos(2t),\\ y\,=\,\chi (x_{1}).\\ \end{array} }} \right. \end{aligned}$$
(4.1)

The dead zone \(\chi (x_{1})\) is seen as:

$$\begin{aligned} y=\chi (x_{1})=\left\{ {{\begin{array}{*{20}c} 1.5(x_{1}-0.25)^{1.34},&{}x_{1}\ge 0.25&{}\\ 0,&{}0.2< x_{1}<0.25&{}\\ 0.5(x_{1}+0.2)^{1.5},&{}x_{1}\le 0.2.&{} \end{array} }}\right. \end{aligned}$$
(4.2)

The reference signal is hypothesized as \(y_{r}\,=\,0.5\sin t+\sin (0.5t)\). Because (4.1) not only contains the nonlinear term \(f_{1}(\bar{x}_{1})\), \(f_{2}(\bar{x}_{1})\), \(g_{1}(\bar{x}_{1})\), \(g_{2}(\bar{x}_{2})\) and disturbance terms \(\psi _{1}(t)\), \(\psi _{2}(t)\), but also has the dead zone output \(y\,=\,\chi (x_{1})\) , the control schemes proposed earlier is very inappropriate to this system.

For the fuzzy control, we select the following membership functions:

$$\begin{aligned} \mu _{F_{i}^{1}(x)}&=\exp [-(x+2.5)^{2}],\ \ \mu _{F_{i}^{2}(x)}\,=\,\exp [-(x+1.5)^{2}],\nonumber \\ \mu _{F_{i}^{3}(x)}&=\exp [-(x+0.5)^{2}],\ \ \mu _{F_{i}^{4}(x)}\,=\,\exp [-(x-0.5)^{2}],\nonumber \\ \mu _{F_{i}^{5}(x)}&=\exp [-(x-1.5)^{2}],\ \ \mu _{F_{i}^{6}(x)}\,=\,\exp [-(x-4)^{2}]. \end{aligned}$$
(4.3)

Choose the intermediate virtual control functions (3.9), the actual control (3.47) and the parameter adaptive law (3.49) with \(c_{1}\,=\,3.4\), \(c_{2}\,=\,4.2\), \(h_{1}\,=\,30\), \(h_{2}\,=\,20\), \(k_{0}\,=\,5\), \(r=400\) and \(\gamma \,=\,40\) for Case 1 and \(c_{1}\,=\,1.2\), \(c_{2}\,=\,2.5\), \(h_{1}\,=\,40\), \(h_{2}\,=\,35\), \(k_{0}\,=\,5\), \(r=400\) and \(\gamma \,=\,40\) for Case 2. The initial conditions are chosen as \([x_{1}(0)\), \(x_{2}(0)\), \(\hat{\eta }(0)]\,=\,[0.1\), 0.2, 0].

The simulation consequences are revealed in Figs. 1, 2, 3 and 4, where Fig. 1 reveals the output y and the reference signal \(y_{r}\) for the Case 1, Fig. 2 displays the trajectories of the control u, Fig. 3 shows the trajectories of the parameter \(\hat{\eta }\), and Fig. 4 presents the trajectories of y and the reference signal \(y_{r}\) for the Case 2.

Fig. 1
figure 1

Trajectories of y(solid line) and \(y_{r}\)(dashed line) for Case 1

Full size image
Fig. 2
figure 2

Trajectories of control u for Case 1

Full size image
Fig. 3
figure 3

Trajectories of \(\hat{\eta }\) for Case 1

Full size image
Fig. 4
figure 4

Trajectories of y for Case 2

Full size image