Adaptive Fuzzy PI Output Feedback Control for a Class of Switched Nonlinear Systems with Unmodeled Dynamics and Dead-Zone Output

Abstract

In this paper, the problem of adaptive fuzzy proportional-integral output feedback tracking control is investigated for a class of uncertain switched nonlinear systems with dead-zone output, unknown control coefficients, and unmodeled dynamics. The unknown parameter of the dead-zone output is processed using adaptive estimation technique. A set of switched filters are developed to estimate unmeasurable states. Then, by combining fuzzy logic systems and backstepping technique, an adaptive output feedback PI tracking controller is developed, which has intuitive structure and a strong physical meaning. Finally, the boundedness of the tracking error and all signals in the closed-loop system is demonstrated via a multiple Lyapunov function. The effectiveness of the proposed scheme is confirmed through two examples.

1 Introduction

In recent decades, switched systems are investigated because they can be used to model many practical systems [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15], such as, robot control systems [16,17,18], flight systems [19, 20], and network systems [21,22,23,24]. It is well-known that switched systems consist of multiple subsystems and a switching rule. Because the stability of a subsystem does not determine the stability of the switched system, a variety of stability analysis tools are developed to analyze the stability of switched systems, such as common Lyapunov function, multiple Lyapunov function, and single Lyapunov function. Subsequently, a large number of research results are reported. For example, in [25], the tracking control problem is researched for switched nonlinear systems by adopting the common Lyapunov function. By designing a set of switched state observers to estimate the unknown states, an adaptive fuzzy output-feedback controller is constructed in [26] for nonstrict feedback switched nonlinear systems. In [27], the tracking control problem is investigated for switched nonlinear systems via dynamic surface control method. Recently, the adaptive neural tracking control problem for a class of nonlower triangular uncertain switched stochastic nonlinear pure feedback systems is studied in [28]. In [29], an adaptive nonlinear disturbance observer strategy is proposed for switched uncertain pure feedback nonlinear systems with mismatched external disturbances and arbitrary switching. However, the above literature does not take into account unmodeled dynamics.

Unmodeled dynamics is common in engineering environment owing to the wide existence of modeling errors and external disturbances. If the unmodeled dynamics are neglected, the closed-loop system performance will be destroyed [30]. Therefore, numerous studies are researched for switched nonlinear systems with unmodeled dynamics [31,32,33,34]. In [31], a novel robust adaptive stabilization control scheme is proposed by employing a small-gain approach. Two types of unmodeled dynamics, namely stable and unstable, are considered by constructing the multiple Lyapunov function in [32]. Aiming at time-delay systems, an adaptive fuzzy prescribed performance control scheme is introduced in [33]. An adaptive neural tracking controller is developed for interconnected switched systems in [34]. On the other hand, unknown control coefficients are one of the serious uncertainties in nonlinear systems. In [25], a tracking control scheme is developed for switched nonlinear systems with unknown control coefficients. The problem of output feedback bounded control is studied for a class of switched nonlinear uncertain systems in [35]. However, the aforementioned studies are restricted; they do not consider the influence of system constraints. System constraints, such as actuator saturation, state constraints, and dead-zone output. These constraints widely exist in practical engineering systems. Owing to the limitations in the physical properties of the components, the dead-zone as one of the nonsmooth nonlinearities often found in physical systems. The existing dead-zone may seriously affect the system performance. This inspires studies on the control problem of nonlinear systems with a dead-zone output. For instance, an adaptive fuzzy output feedback dynamic surface control scheme is developed for nonlinear systems in [36]. In [37], an adaptive tracking controller is designed for nonstrict feedback nonlinear systems with input saturation and unknown output dead-zone by introducing the Nussbaum-type function. In [38], the adaptive neural tracking control problem is studied for switched nonlinear systems with unknown backlash-like hysteresis and output dead-zone. Although good control performance is obtained in the aforementioned schemes, the effect of unmodeled dynamics is not considered and the controller is relatively complex.

PI control, as a control scheme with a simple and intuitive structure and strong physical significance, is popular in practical engineering applications. In the early days, a novel compensator identification scheme is proposed in [39] to address the problem of factory identification. Subsequently, for linear systems, a proportional-integral-differential (PID) gain self-tuning technique is proposed in [40]. In [41], a PI/PID control scheme is first developed for nonlinear systems. However, derivative control has an evident drawback, i.e., it is easy to introduce high-frequency noise. Therefore, many studies focus on PI control, which not only avoids the aforementioned defects, but also simplifies the controller structure and significantly reduces the calculation cost. In [42, 43], the intelligent PI (iPI) controllers are investigated for a class of flexible-link manipulator. For the purpose of addressing the tracking control problem for multiple-input-multiple-output (MIMO) nonlinear system with dead-zone input, a PI control scheme is designed in [44]. Aiming at non-affine systems with actuator and sensor faults, a PI controller is proposed to handle the tracking control problem in [45]. In [46], a PI structure controller is constructed by defining the generalized error at each step of the backstepping method. In recent years, a decentralized adaptive neural network PI tracking control scheme is proposed in [47] for interconnected nonlinear systems with input quantization and dynamic uncertainty. Note that the aforementioned studies on the problem of PI control does not involve switched systems, which inspires us to investigate the PI control problem of the switched nonlinear systems. To sum up, it is necessary to study the problem of PI control for switched nonlinear systems with unmodeled dynamics, unknown control coefficients, and dead-zone output. To solve this problem, three key points need to be addressed: (i) how to design a controller with a PI structure for switched nonlinear systems with unmodeled dynamics, unknown control coefficients, and dead-zone output? (ii) how to deal with unknown information of the dead-zone output and unknown control coefficient? (iii) how to compensate the nonlinear term caused by the construction of the virtual control law and controller at each step?

This paper addresses the problem of adaptive fuzzy PI output feedback control for a class of uncertain switched nonlinear systems with unmodeled dynamics, unknown control coefficients, and dead-zone output. An adaptive fuzzy PI output feedback controller is proposed by applying the backstepping method and FLSs. The boundedness of the tracking error and all signals in the closed-loop system are demonstrated via Lyapunov stability theory. The main contributions can be summarized as follows.

• An adaptive fuzzy PI controller for uncertain switched nonlinear systems with unmodeled dynamics, unknown control coefficients, and dead-zone output is proposed for the first time; this controller features an intuitive structure and a strong physical meaning.

• The difficulty of unknown parameter of the dead-zone is overcome by adaptive estimation.

• The properties of the hyperbolic tangent function and FLSs are flexibly employed to deal with the nonlinear terms generated by constructing the virtual control law and control law.

The remainder of this paper is organised as follows. Section 2 presents the problem formulation. In Sect. 3, the switched filters, adaptive fuzzy PI controller and stability analysis of the closed-loop systems are presented. Section 4 provides two examples that verify the effectiveness of the scheme. Section 5 concludes the paper.

2 Problem Formulation and Preliminaries

2.1 Problem Formulation

Consider the following switched nonlinear systems with unmodeled dynamics

$$\begin{aligned} {\dot{\varsigma }}= & \, q_{\sigma (t)}(\varsigma ,y,d(t)),\nonumber \\ {\dot{x}}_1= & \, h_{1}x_2+f_{1,\sigma (t)}(x_{1})+\Delta _{1,\sigma (t)}(\varsigma ,y,d(t)),\nonumber \\ {\dot{x}}_2= & \, h_{2}x_3+f_{2,\sigma (t)}(x_{1},x_{2})+\Delta _{2,\sigma (t)}(\varsigma ,y,d(t)),\nonumber \\&\vdots&\nonumber \\ {\dot{x}}_n= & \, h_{n}u+f_{n,\sigma (t)}(x_{1},x_{2},\ldots ,x_{n})+\Delta _{n,\sigma (t)}(\varsigma ,y,d(t)),\nonumber \\ y= & \, D(x_1), \end{aligned}$$

(1)

where $x=[x_1,x_2,\ldots ,x_n]^T\in {R^{n}}$ are the system states, u is the control input and $y=D(x_1)$ denotes the output with dead-zone, $\varsigma$ represents an unmodeled dynamic, and $h_{1},h_{2},\ldots ,h_{n}$ are positive constants that represents the unknown control coefficients. Besides, $\sigma (t):[0,+\infty )\rightarrow {{\mathcal {P}}=\{1,2,\ldots ,p\}}$ denotes the switching signal. For any $i=1,2,\ldots ,n$ and $k\in {\mathcal {P}}$, $f_{i,k}$ and $q_{k}(\varsigma ,y,d(t))$ are uncertain functions, and $\Delta _{i,k}(\varsigma ,y,d(t))$ represent unknown functions called non-parametric uncertainties, d(t) means an unknown disturbance.

In system (1), the dead-zone output y is represented as

$$ y=D(x_1)={\left\{ \begin{array}{ll} l(x_{1}-v),&{}x_{1}> v\\ 0,&{}-v\le x_{1}\le v\\ l(x_{1}+v),&{}x_{1}< -v,\end{array}\right. } $$

(2)

where $l> 0$ denotes the slope of the dead-zone and $v> 0$ represents the width parameter.

Similar to the treatment of the dead-zone output in [38], (2) can be approximated as

$$\begin{aligned} x_{1}=\frac{y}{l}+\frac{2v}{\pi }\arctan (ay), \end{aligned}$$

(3)

where a is a positive constant. Then

$$\begin{aligned} \frac{{\text{d}}x_{1}}{{\text{d}}y}=\frac{1}{l}+\frac{2v}{\pi }\frac{a}{1+(ay)^{2}}. \end{aligned}$$

(4)

We can further obtain ${\dot{y}}=\frac{{\text{d}}y}{{\text{d}}x_{1}}{\dot{x}}_{1}=\breve{\beta }{\dot{x}}_{1}$, $\frac{l\pi }{\pi +2val}\le \breve{\beta }=\frac{{\text{d}}y}{{\text{d}}x_{1}}< l$.

Remark 1

Note that (2) is a non-smooth model. The non-smooth dead-zone nonlinearity in (2) can be approximated by (3). As the parameter a increases, the model represented by (3) is closer to the system output (2), as shown in Fig. 1.

Fig. 1

Curves of y when $a=2$ and $a=20$

Remark 2

Define $h=h_{1}h_{2}\ldots h_{n}$. It is clear that $\breve{\beta }h$ is bounded. Consequently, there exist two positive constants ${\bar{\beta }}_{1}$ and ${\bar{\beta }}_{2}$ such that ${\bar{\beta }}_{1}< \breve{\beta }h< {\bar{\beta }}_{2}$.

Adaptive PI fuzzy output feedback tracking control problem: In this paper, an adaptive PI fuzzy output feedback tracking controller will be designed by the backstepping method for system (1), such that the system output y tracks the reference signal $y_{d}$ and all signals of the closed-loop system are bounded.

Assumption 1

$y_{d},{\dot{y}}_{d},\ldots ,y^{(n)}_{d}$ are smooth and bounded.

Assumption 2

[33] The subsystem ${\dot{\varsigma }}=q_{\sigma (t)}(\varsigma ,y,d(t))$ is input-to-state stable(ISS) with input y. An ISS-Lyapunov functon $V_{\varsigma }$ satisfies

$$ \beta _{1}(|\varsigma |)\le V_{\varsigma }(\varsigma )\le \beta _{2}(|\varsigma |), \frac{\partial V_{\varsigma }}{\partial \varsigma }{\dot{\varsigma }}\le -a_{0}V_{\varsigma }+n_{0}\gamma (|y|), $$

(5)

where $\beta _{1}$, $\beta _{2}$, $\gamma$ belong to class-${\mathcal {K}}_{\infty }$, $a_{0}$ and $n_{0}> 0$ are unknown positive constants, where $\gamma (s)=O(s^{2})$, and “O” denotes that there exist $m>0$ and $n>0$, for any $|s|<n$, such that $|\gamma (s)|\le m|s^{2}|$.

Assumption 3

[48] The nonlinear function $\Delta _{i,k}(\varsigma ,y,d(t))$ satisfies

$$\begin{aligned} |\Delta _{i,k}(\varsigma ,y,d(t))|\le w_{ik}\varphi _{i1}(|\varsigma |)+w_{ik}\varphi _{i2}(y), \end{aligned}$$

(6)

where $w_{ik}$ are unknown constants, $\varphi _{i1}(|\varsigma |)$, and $\varphi _{i2}(y)$ are smooth functions that satisfy $\varphi _{i1}(0)=0$, $\varphi _{i2}(0)=0$. Similar to [48], we can obtain $\varphi _{i2}(y)=y{\bar{\varphi }}_{i2}(y)$ (${\bar{\varphi }}_{i2}(y)$ is a smooth function) and the following property [33] holds

$$\begin{aligned} \lim _{t\rightarrow 0^{+}}\sup \frac{\varphi _{i,1}^{2}(|\varsigma |)}{V_{\varsigma }}< +\infty . \end{aligned}$$

(7)

Lemma 1

[49] f(X) is a continuous function defined on a compact set ${\mathcal {K}}$, and there exists FLSs $y=\Phi ^{T}S(X)$ such that

$$\begin{aligned} sup_{X\in {\mathcal {K}}}|f(X)-\Phi ^{T}S(X)|\le \varepsilon , \end{aligned}$$

(8)

where $\Phi$ represents the weight of the FLSs, S(X) is a basis function vector, and $\varepsilon > 0$ is a prescribed accuracy.

Lemma 2

[50] For any $1\le i\le n$, define the set as ${\mathcal {E}}_{\chi _{i}}=\{\chi _{i}|\;\Vert \chi _{i}\Vert < \imath \varpi _{i}\}$, where $\imath =0.8814$ and $\varpi _{i}>0.$ Then, if $\chi _{i}\not \in {\mathcal {E}}_{\chi _{i}}$, the inequality $[1-2\tanh ^{2}(\frac{\chi _{i}}{\varpi _{i}})]\le 0$ holds.

Remark 3

Note that many studies have been investigated on PI control for nonswitched nonlinear systems [47, 51]. However, in practical situations, switching behavior and unmodeled dynamics widely exist in many systems. Hence, it is important to study PI control for switched nonlinear systems with unmodeled dynamics.

Remark 4

From Lemma 1, we can conclude that the following conclusion: $f(\chi )=\Phi ^{T}S(X)+\vartheta$, where $\vartheta$ is a bounded function that satisfies $|\vartheta |\le \varepsilon$ and S(X) satisfies: $0< S(X)^{T}S(X)\le 1$.

3 Main Results

3.1 Design of Filters

To manage unknown control coefficients, the following variables are defined

$$\begin{aligned} \zeta _{i}=\frac{x_{i}}{h_{i}\ldots h_{n}}, \ f_{i,k}^{*}=\frac{f_{i,k}}{h_{i}\ldots h_{n}}, \ \Delta _{i,k}^{*}=\frac{\Delta _{i,k}}{h_{i}\ldots h_{n}}. \end{aligned}$$

Then we have

$$\begin{aligned} {\dot{\zeta }}_{1}= & {} \zeta _{2}+f_{1,k}^{*}+\Delta _{1,k}^{*},\nonumber \\ {\dot{\zeta }}_{2}= & {} \zeta _{3}+f_{2,k}^{*}+\Delta _{2,k}^{*},\nonumber \\&\cdots&\nonumber \\ {\dot{\zeta }}_{n}= & {} u+f_{n,k}^{*}+\Delta _{n,k}^{*}. \end{aligned}$$

(9)

Construct a set of filters as

$$\begin{aligned} \dot{{\hat{\zeta }}}_{1}= & {} {\hat{\zeta }}_{2}-\mu _{1,k}{\hat{\zeta }}_{1},\nonumber \\ \dot{{\hat{\zeta }}}_{2}= & {} {\hat{\zeta }}_{3}-\mu _{2,k}{\hat{\zeta }}_{1},\nonumber \\&\cdots&\nonumber \\ \dot{{\hat{\zeta }}}_{n}= & {} u-\mu _{n,k}{\hat{\zeta }}_{1}, \end{aligned}$$

(10)

where $\mu _{1,k}, \mu _{2,k},\ldots ,\mu _{n,k}$ are positive constants. Define the error variables as ${\tilde{\zeta }}_{i}=\zeta _{i}-{\hat{\zeta }}_{i}$. Combining (9) with (10) leads to

$$\begin{aligned} \dot{{\tilde{\zeta }}}=A_{k}{\tilde{\zeta }}+F^{*}_{k}+\Delta ^{*}_{k}+\frac{1}{h}U_{k}x_{1}, \end{aligned}$$

(11)

where $A_{k}=\begin{pmatrix}-\mu _{1,k}&{}&{}&{}\\ \vdots &{}I_{n-1}&{}\\ mu_{n,k}&{}\cdots &{}0\end{pmatrix}$, $F^{*}_{k}=\begin{pmatrix}f_{1,k}^{*}\\ \vdots \\ f_{n,k}^{*}\end{pmatrix}$, $\Delta ^{*}_{k}=\begin{pmatrix}\Delta _{1,k}^{*}\\ \vdots \\ \Delta _{n,k}^{*}\end{pmatrix}$, $U_{k}=\begin{pmatrix}\mu _{1,k}\\ \vdots \\ \mu _{n,k}\end{pmatrix}$.

Define $w^{*}=\max \{1,\frac{w_{i,k}}{h_{i}\cdots h_{n}},\frac{1}{h}\}$ and $e=\frac{1}{w^{*}}{\tilde{\zeta }}$. Then one has

$$\begin{aligned} {\dot{\varsigma }}= & \, q_{\sigma (t)}(\varsigma ,y),\nonumber \\ {\dot{e}}= & \, A_{k}e+\frac{1}{w^{*}}F^{*}_{k}+\frac{1}{w^{*}}\Delta ^{*}_{k}+\frac{1}{w^{*}}\frac{1}{h}U_{k}x_{1},\nonumber \\ {\dot{x}}_{1}= & \, h{\hat{\zeta }}_{2}+hw^{*}e_{2}+f_{1,k}^{*}+\Delta _{1,k}^{*},\nonumber \\ \dot{{\hat{\zeta }}}_{1}= & \, {\hat{\zeta }}_{2}-\mu _{1,k}{\hat{\zeta }}_{1},\nonumber \\ \dot{{\hat{\zeta }}}_{2}= & \, {\hat{\zeta }}_{3}-\mu _{2,k}{\hat{\zeta }}_{1},\nonumber \\&\cdots&\nonumber \\ \dot{{\hat{\zeta }}}_{n}= & \, u-\mu _{n,k}{\hat{\zeta }}_{1}. \end{aligned}$$

(12)

Choose the appropriate parameter $\mu _{i,k}$ such that $A_{k}$ is a Hurwitz matrix. Hence there exists a positive definite symmetric matrix $P_{k}$ such that

$$\begin{aligned} A_{k}^{T}P_{k}+P_{k}A_{k}=-2I. \end{aligned}$$

(13)

Choosing $V_{k}^{*}=e^{T}P_{k}e$ and calculating the derivative of ${V}_{k}^{*}$ yield

$$\begin{aligned} {\dot{V}}_{k}^{*}=-2e^{T}e+2e^{T}P_{k}\frac{1}{w^{*}}F^{*}_{k}+2e^{T}P_{k}\frac{1}{w^{*}}\Delta ^{*}_{k}+2e^{T}P_{k}\frac{1}{w^{*}}\frac{1}{h}U_{k}x_{1}. \end{aligned}$$

(14)

According to Remark 4, we obtain $F^{*}_{k}=\Phi _{0,k}^{T}S_{0,k}+\vartheta _{0,k}$, $\Phi _{0,k}=[\Phi _{01,k},\Phi _{02,k},\ldots ,\Phi _{0n,k}]$, $S_{0,k}$ is a basis function vector, $\vartheta _{0,k}=[\vartheta _{01,k},\vartheta _{02,k},\ldots ,\vartheta _{0n,k}]$, where $\Phi _{0i,k}$ are the weights, and $\vartheta _{0i,k}$ are bounded functions that satisfy $\Vert \vartheta _{0,k}\Vert \le \varepsilon _{0,k}$, where $\varepsilon _{0,k}$ is a positive constant. Then the following inequations is derived

$$\begin{aligned} 2e^{T}P_{k}\frac{1}{w^{*}}F^{*}_{k}= & \, 2e^{T}P_{k}\frac{1}{w^{*}}(\Phi _{0,k}^{T}S_{0}+\vartheta _{0,k})\nonumber \\= & \, 2e^{T}P_{k}\frac{1}{w^{*}}\Phi _{0,k}^{T}S_{0}+2e^{T}P_{k}\frac{1}{w^{*}}\vartheta _{0,k}\nonumber \\\le & \, \frac{1}{4}e^{T}e+8\Vert P_{k}\Vert ^{2}\frac{1}{{w^{*}}^{2}}(\theta +\varepsilon _{0,k}^{2}), \end{aligned}$$

(15)

$$\begin{aligned} 2e^{T}P_{k}\frac{1}{w^{*}}\Delta ^{*}_{k}\le & {} \frac{1}{4}e^{T}e+8\Vert P_{k}\Vert ^{2}\sum _{i=1}^{n}\varphi _{i,1}^{2}(|\varsigma |)+8\Vert P_{k}\Vert ^{2}\sum _{i=1}^{n}y^{2}{\bar{\varphi }}_{i,2}^{2}(y), \end{aligned}$$

(16)

$$\begin{aligned} 2e^{T}P_{k}\frac{1}{w^{*}}\frac{1}{h}U_{k}x_{1}= & {} 2e^{T}P_{k}\frac{1}{w^{*}}\frac{1}{h}U_{k}(\frac{y}{l}+\frac{2v}{\pi }\arctan (ay))\nonumber \\\le & {} \frac{1}{4}e^{T}e+8\Vert P_{k}\Vert ^{2}\Vert U_{k}\Vert ^{2}\frac{1}{l^{2}}y^{2}+8\Vert P_{k}\Vert ^{2}\Vert U_{k}\Vert ^{2}v^{2}, \end{aligned}$$

(17)

where $\theta =\max \{\Vert \Phi _{i,k}\Vert ^{2}: 0\le i\le n, k\in {\mathcal {P}}\}$, and $\Phi _{i,k}$ mean the weights of FLSs.

Combining (14), (15), (16) with (17) leads to

$$\begin{aligned} {\dot{V}}_{k}^{*}\le -e^{T}e+b_{k}y^{2}(\sum _{i=1}^{n}{\bar{\varphi }}_{i,2}^{2}(y)+1)+8\Vert P_{k}\Vert ^{2}\sum _{i=1}^{n}\varphi _{i,1}^{2}(|\varsigma |)+d_{0,k}, \end{aligned}$$

(18)

where $b_{k}=8\Vert P_{k}\Vert ^{2}\cdot \max \{1,\frac{1}{l^{2}}\Vert U_{k}\Vert ^{2}\}$, $d_{0,k}=8\Vert P_{k}\Vert ^{2}\frac{1}{{w^{*}}^{2}}(\theta +\varepsilon _{0,k}^{2})+8\Vert P_{k}\Vert ^{2}\Vert U_{k}\Vert ^{2}v^{2}$.

3.2 Controller Design

First, a set of coordinate transformations are defined:

$$\begin{aligned} r_{1}= & \, y-y_{d},\\ r_{2}= & \, {\hat{\zeta }}_{2}-\alpha _{1},\\&\,\vdots&\\ r_{n}= & \, {\hat{\zeta }}_{n}-\alpha _{n-1}, \end{aligned}$$

where $\alpha _{1},\ldots ,\alpha _{n-1}$ are the virtual control laws and the following generalized errors are further introduced:

$$\begin{aligned} \chi _{1}= & \, r_{1}+s_{1}\int _{0}^{t}r_{1} {\text{d}}\tau ,\\ \chi _{2}= & \, r_{2}+s_{2}\int _{0}^{t}r_{2} {\text{d}}\tau ,\\&\,\vdots&\\ \chi _{n}= & \, r_{n}+s_{n}\int _{0}^{t}r_{n} {\text{d}}\tau , \end{aligned}$$

where $s_{1},\ldots ,s_{n}$ are positive constants.

In this paper, the virtual control laws are constructed as

$$\begin{aligned} \alpha _{1}= & \, {\hat{\beta }}{\bar{\alpha }}_{1}, \end{aligned}$$

(19)

$$\begin{aligned} {\bar{\alpha }}_{1}= & {} -(g_{P_{1}}+{\triangle }g_{P_{1}}(\cdot ))r_{1}-(g_{I_{1}}+{\triangle }g_{I_{1}}(\cdot ))\int _{0}^{t}r_{1}{\text{d}}\tau , \end{aligned}$$

(20)

$$\begin{aligned} \alpha _{i}= & {} -(g_{P_{i}}+{\triangle }g_{P_{i}}(\cdot ))r_{i}-(g_{I_{i}}+{\triangle }g_{I_{i}}(\cdot ))\int _{0}^{t}r_{i}{\text{d}}\tau , \end{aligned}$$

(21)

for any $i=1,\ldots ,n-1$, $g_{P_{i}}=c_{i}$, $g_{I_{i}}=s_{i}g_{P_{i}}$, ${\Delta }g_{P_{i}}(\cdot )=\frac{{\hat{\theta }}}{2a_{i}^{2}}$, ${\Delta }g_{I_{i}}(\cdot )=s_{i}{\triangle }g_{P_{i}}(\cdot )$, ${\hat{\theta }}$ is the estimation of $\theta$, ${\hat{\beta }}$ is the estimation of $\beta$, where $\beta =\frac{1}{{\bar{\beta }}_{1}}$. $a_{i}$, $c_{i}$ are the positive constants.

The adaptive PI controller is designed as

$$\begin{aligned} u=-(g_{P_{n}}+{\triangle }g_{P_{n}}(\cdot ))r_{n}-(g_{I_{n}}+{\triangle }g_{I_{n}}(\cdot ))\int _{0}^{t}r_{n}{\text{d}}\tau , \end{aligned}$$

(22)

where $g_{P_{n}}=c_{n}$, $g_{I_{n}}=s_{n}g_{P_{n}}$, ${\Delta }g_{P_{n}}(\cdot )=\frac{{\hat{\theta }}}{2a_{n}^{2}}$, ${\Delta }g_{I_{n}}(\cdot )=s_{n}{\triangle }g_{P_{n}}(\cdot )$, $a_{n}$, $c_{n}$ are the positive constants.

The adaptive laws are designed as:

$$\begin{aligned} \dot{{\hat{\theta }}}= & {} \sum _{i=1}^{n}\frac{\jmath \chi _{i}^{2}}{2a_{i}^{2}}-\hbar {\hat{\theta }}, \end{aligned}$$

(23)

$$\begin{aligned} \dot{{\hat{\beta }}}= & {} Proj({\hat{\beta }}(t), \Xi ), \end{aligned}$$

(24)

$$\begin{aligned} Proj({\hat{\beta }}(t), \Xi )= & {} {\left\{ \begin{array}{ll} 0,&{}\hbox {if}\ {\hat{\beta }}={\hat{\beta }}_{\max }\wedge \Xi > 0\\ 0,&{}\hbox {if}\ {\hat{\beta }}={\hat{\beta }}_{\min }\wedge \Xi < 0\\ \Xi ,&{} \hbox {otherwise}\end{array}\right. }, \end{aligned}$$

(25)

where $\Xi =(c_{1}+\frac{{\hat{\theta }}}{2a_{1}^{2}})\chi _{1}^{2}-\imath {\hat{\beta }}$, $\jmath$, $\hbar$, $\imath$ are positive constants.

Remark 5

In [42, 43], the intelligent proportional-integral (iPI) controllers are proposed for flexible joint manipulator and the iPI controllers can obtain better disturbance and noise rejection performance. Compared with the proposed control scheme in this paper, some differences are listed as follows. First, the gains of the iPI controller in [42, 43] are constants while in this paper the gains of the proposed controller contains two parts: constant part and time-varying part. Second, the iPI controllers are designed for a second-system while in this paper we consider a n-order system and the generalized error is defined to derive the PI controller.

Remark 6

According to [52], we know the projection operator has two properties: (i) ${\hat{\beta }}_{\min }\le {\hat{\beta }}\le {\hat{\beta }}_{\max }$. (ii) ${\tilde{\beta }} Proj({\hat{\beta }}, \Xi )\ge {\tilde{\beta }}\Xi$.

Next, the PI controller is designed using the backstepping method.

Step 1: The first-order derivative $\chi _{1}$ is presented as

$$\begin{aligned} {\dot{\chi }}_{1}= & {} {\dot{r}}_{1}+s_{1}r_{1}\nonumber \\= & {} {\dot{y}}-{\dot{y}}_{d}+s_{1}(y-y_{d})\nonumber \\= & {} \breve{\beta }{\dot{x}}_{1}-{\dot{y}}_{d}+s_{1}(y-y_{d})\nonumber \\= & {} \breve{\beta }(h{\hat{\zeta }}_{2}+hw^{*}e_{2}+f_{1,k}^{*}+\Delta _{1,k}^{*})-{\dot{y}}_{d}+s_{1}(y-y_{d}). \end{aligned}$$

(26)

Choose the Lyapunov function as

$$\begin{aligned} V_{1}=\frac{1}{2}\chi _{1}^{2}. \end{aligned}$$

(27)

Computing the derivative of $V_{1}$ leads to

$$\begin{aligned} {\dot{V}}_{1}= & \, \chi _{1}{\dot{\chi }}_{1}\nonumber \\= & \, \chi _{1}(\breve{\beta }(h{\hat{\zeta }}_{2}+hw^{*}e_{2}+f_{1,k}^{*}+\Delta _{1,k}^{*})-{\dot{y}}_{d}+s_{1}(y-y_{d})). \end{aligned}$$

(28)

To structure $\alpha _{1}$, the nonlinear function is defined as follows

$$\begin{aligned} \Psi _{1,k}= & {} \frac{\chi _{1}}{2}+\frac{1}{2}\chi _{1}l^{2}h^{2}{w^{*}}^{2}+\breve{\beta } f_{1,k}^{*}+\frac{1}{4}l^{2}\chi _{1}w_{1{ k}}^{2}+\breve{\beta } w_{1{ k}}\varphi _{12}(y)-{\dot{y}}_{d}+s_{1}(y-y_{d})\nonumber \\&-\breve{\beta } hs_{2}\int _{0}^{t}r_{2}{\text{d}}\tau +\frac{2}{\chi _{1}}\tanh ^{2}\Big(\frac{\chi _{1}}{\varpi _{1}}\Big)\eta _{1,k}(y), \end{aligned}$$

(29)

where $\eta _{1,k}(y)=b_{k}y^{2}{\bar{\varphi }}_{12}^{2}(y)$.

Using FLSs, we have

$$\begin{aligned} \Psi _{1,k}=\Phi _{1,k}^{T}S_{1,k}+\vartheta _{1,k}, \end{aligned}$$

(30)

where $\Phi _{1,k}$ denotes the weight of the FLSs $\Psi _{1,k}$ , $S(X)_{1,k}$ is a basis function vector, and $\vartheta _{1,k}$ is a bounded function that satisfies $|\vartheta _{1,k}|\le \varepsilon _{1,k}$, where $\varepsilon _{1,k}$ is a positive constant.

Then one has

$$\begin{aligned} {\dot{V}}_{1}\le & {} \chi _{1}(\breve{\beta } h{\hat{\zeta }}_{2}+\Psi _{1,k}-\frac{\chi _{1}}{2}+\breve{\beta } hw^{*}e_{2}-\frac{1}{2}\chi _{1}l^{2}h^{2}{w^{*}}^{2}+\breve{\beta }\Delta _{1,k}^{*}-\frac{1}{4}l^{2}\chi _{1}w_{1k}^{2}\nonumber \\&-\breve{\beta } w_{1k}\varphi _{12}(y)+\breve{\beta } hs_{2}\int _{0}^{t}r_{2}{\text{d}}\tau -\frac{2}{\chi _{1}}\tanh ^{2}\Big(\frac{\chi _{1}}{\varpi _{1}}\Big)\eta _{1,k}(y)). \end{aligned}$$

(31)

Using Youngs inequality and Assumption 3 leads to

$$\begin{aligned} \chi _{1}\breve{\beta } hw^{*}e_{2}\le & {} \frac{1}{2}\chi _{1}^{2}l^{2}h^{2}{w^{*}}^{2}+\frac{1}{2}e^{T}e, \end{aligned}$$

(32)

$$\begin{aligned} \chi _{1}\breve{\beta }\Delta _{1,k}^{*}\le & {} \chi _{1}\breve{\beta }w_{1k}\varphi _{11}(|\varsigma |)+\chi _{1}\breve{\beta }w_{1k}\varphi _{12}(y)\nonumber \\\le & {} \frac{1}{4}\chi _{1}^{2}l^{2}w_{1k}^{2}+\varphi _{11}^{2}(|\varsigma |)+\chi _{1}\breve{\beta }w_{1k}\varphi _{12}(y), \end{aligned}$$

(33)

Substituting (32) and (33) into (31),we have

$$\begin{aligned} {\dot{V}}_{1}\le & {} \chi _{1}\breve{\beta } h(\alpha _{1}+\chi _{2})+\chi _{1}\Psi _{1,k}-\frac{\chi _{1}^{2}}{2}+\frac{1}{2}e^{T}e+\varphi _{11}^{2}(|\varsigma |)-2\tanh ^{2}(\frac{\chi _{1}}{\varpi _{1}})\eta _{1,k}(y)\nonumber \\\le & {} \chi _{1}\breve{\beta } h\alpha _{1}+\breve{\beta } h\chi _{1}\chi _{2}+\frac{\chi _{1}^{2}\theta }{2a_{1}^{2}}+\frac{a_{1}^{2}+\varepsilon _{1,k}^{2}}{2}+\frac{1}{2}e^{T}e\nonumber \\&+\varphi _{11}^{2}(|\varsigma |)-2\tanh ^{2}\Big(\frac{\chi _{1}}{\varpi _{1}}\Big)\eta _{1,k}(y). \end{aligned}$$

(34)

Substituting the $\alpha _{1}$ into (34) yields

$$\begin{aligned} {\dot{V}}_{1}\le & {} -{\bar{\beta }}_{1}\chi _{1}^{2}{\hat{\beta }}\Big(c_{1}+\frac{{\hat{\theta }}}{2a_{1}^{2}}\Big)+\breve{\beta } h\chi _{1}\chi _{2}+\frac{\chi _{1}^{2}\theta }{2a_{1}^{2}}+\frac{a_{1}^{2}+\varepsilon _{1,k}^{2}}{2}+\frac{1}{2}e^{T}e+\varphi _{11}^{2}(|\varsigma |)-2\tanh ^{2}\Big(\frac{\chi _{1}}{\varpi _{1}}\Big)\eta _{1,k}(y)\nonumber \\= & {} \frac{{\tilde{\beta }}\chi _{1}^{2}}{\beta }\Big(c_{1}+\frac{{\hat{\theta }}}{2a_{1}^{2}}\Big)+\frac{\chi _{1}^{2}{\tilde{\theta }}}{2a_{1}^{2}}+\frac{1}{2}e^{T}e+\varphi _{11}^{2}(|\varsigma |)-c_{1}\chi _{1}^{2}+\frac{a_{1}^{2}+\varepsilon _{1,k}^{2}}{2}+\breve{\beta } h\chi _{1}\chi _{2}\nonumber \\&-2\tanh ^{2}\Big(\frac{\chi _{1}}{\varpi _{1}}\Big)\eta _{1,k}(y). \end{aligned}$$

(35)

Step 2: By computing the derivative of $\chi _{2}$, we can obtain

$$\begin{aligned} {\dot{\chi }}_{2}= & \, {\dot{r}}_{2}+s_{2}r_{2}\nonumber \\= & \, \dot{{\hat{\zeta }}}_{2}-{\dot{\alpha }}_{1}+s_{2}({\hat{\zeta }}_{2}-\alpha _{1})\nonumber \\= & \, {\hat{\zeta }}_{3}-\mu _{2,k}{\hat{\zeta }}_{1}-{\dot{\alpha }}_{1}+s_{2}({\hat{\zeta }}_{2}-\alpha _{1}). \end{aligned}$$

(36)

Select Lyapunov function as

$$\begin{aligned} V_{2}=V_{1}+\frac{1}{2}\chi _{2}^{2}. \end{aligned}$$

(37)

The derivative of $V_{2}$ is

$$\begin{aligned} {\dot{V}}_{2}={\dot{V}}_{1}+\chi _{2}({\hat{\zeta }}_{3}-\mu _{2,k}{\hat{\zeta }}_{1}-{\dot{\alpha }}_{1}+s_{2}({\hat{\zeta }}_{2}-\alpha _{1})). \end{aligned}$$

(38)

The nonlinear function $\Psi _{2,k}$ is defined as

$$\begin{aligned} \Psi _{2,k}=\frac{\chi _{2}}{2}-\mu _{2,k}{\hat{\zeta }}_{1}-{\dot{\alpha }}_{1}+s_{2}({\hat{\zeta }}_{2}-\alpha _{1})-s_{3}\int _{0}^{t}r_{3} {\text{d}}\tau +\breve{\beta } h\chi _{1}+\frac{2}{\chi _{2}}\tanh ^{2}(\frac{\chi _{2}}{\varpi _{2}})\eta _{2,k}(y), \end{aligned}$$

(39)

where $\eta _{2,k}(y)=b_{k}y^{2}{\bar{\varphi }}_{22}^{2}(y),$ which is estimated by FLSs

$$\begin{aligned} \Psi _{2,k}=\Phi _{2,k}^{T}S_{2,k}+\vartheta _{2,k}, \end{aligned}$$

(40)

where $\Phi _{2,k}$ is weight of FLSs $\Psi _{2,k}$ , $S(X)_{2,k}$ is a basis function vector, $\vartheta _{2,k}$ is a bounded function satisfies $|\vartheta _{2,k}|\le \varepsilon _{2,k}$, $\varepsilon _{2,k}$ is a positive constant.

Similar to step 1, we have

$$\begin{aligned} {\dot{V}}_{2}= & {} {\dot{V}}_{1}+\chi _{2}({\hat{\zeta }}_{3}-\mu _{2,k}{\hat{\zeta }}_{1}-{\dot{\alpha }}_{1}+s_{2}({\hat{\zeta }}_{2}-\alpha _{1}))\nonumber \\= & {} {\dot{V}}_{1}+\chi _{2}({\hat{\zeta }}_{3}+\Psi _{2,k}-\frac{\chi _{2}}{2}+s_{3}\int _{0}^{t}r_{3} {\text{d}}\tau -\breve{\beta } h\chi _{1}-\frac{2}{\chi _{2}}\tanh ^{2}\Big(\frac{\chi _{2}}{\varpi _{2}}\Big)\eta _{2,k}(y))\nonumber \\\le & {} {\dot{V}}_{1}+\chi _{2}\alpha _{2}+\chi _{2}\chi _{3}+\frac{\chi _{2}^{2}\theta }{2a_{2}^{2}}+\frac{a_{2}^{2}+\varepsilon _{2,k}^{2}}{2}-\breve{\beta } h\chi _{1}\chi _{2}-2\tanh ^{2}\Big(\frac{\chi _{2}}{\varpi _{2}}\Big)\eta _{2,k}(y). \end{aligned}$$

(41)

Substituting $\alpha _{2}$ into (41) leads to

$$\begin{aligned} {\dot{V}}_{2}\le & {} {\dot{V}}_{1}+\chi _{2}\chi _{3}+\frac{\chi _{2}^{2}{\tilde{\theta }}}{2a_{2}^{2}}-c_{2}\chi _{2}^{2}+\frac{a_{2}^{2}+\varepsilon _{2,k}^{2}}{2}-\breve{\beta } h\chi _{1}\chi _{2}-2\tanh ^{2}\Big(\frac{\chi _{2}}{\varpi _{2}}\Big)\eta _{2,k}(y)\nonumber \\\le & {} \frac{{\tilde{\beta }}\chi _{1}^{2}}{\beta }\Big(c_{1}+\frac{{\hat{\theta }}}{2a_{1}^{2}}\Big)+\frac{1}{2}e^{T}e+\varphi _{11}^{2}(|\varsigma |)+\chi _{2}\chi _{3}\nonumber \\&+\sum _{j=1}^{2}\Big\{\frac{\chi _{j}^{2}{\tilde{\theta }}}{2a_{j}^{2}}-c_{j}\chi _{j}^{2}+\frac{a_{j}^{2}+\varepsilon _{j,k}^{2}}{2}-2\tanh ^{2}\Big(\frac{\chi _{j}}{\varpi _{j}}\Big)\eta _{j,k}(y)\Big\}. \end{aligned}$$

(42)

Step i($3\le i\le n-1$): By calculating the derivative of ${\chi }_{i}$, one has

$$\begin{aligned} {\dot{\chi }}_{i}= & \, {\dot{r}}_{i}+s_{i}r_{i}\nonumber \\= & \, \dot{{\hat{\zeta }}}_{i}-{\dot{\alpha }}_{i-1}+s_{i}({\hat{\zeta }}_{i}-\alpha _{i-1})\nonumber \\= & \, {\hat{\zeta }}_{i+1}-\mu _{i,k}{\hat{\zeta }}_{1}-{\dot{\alpha }}_{i-1}+s_{i}({\hat{\zeta }}_{i}-\alpha _{i-1}). \end{aligned}$$

(43)

Through the previous analysis, the derivative of $V_{i-1}$ is expressed as:

$$\begin{aligned} {\dot{V}}_{i-1}\le & {} \frac{{\tilde{\beta }}\chi _{1}^{2}}{\beta }\Big(c_{1}+\frac{{\hat{\theta }}}{2a_{1}^{2}}\Big)+\frac{1}{2}e^{T}e+\varphi _{11}^{2}(|\varsigma |)+\chi _{i-1}\chi _{i}\nonumber \\&+\sum _{j=1}^{i-1}\Big\{\frac{\chi _{j}^{2}{\tilde{\theta }}}{2a_{j}^{2}}-c_{j}\chi _{j}^{2}+\frac{a_{j}^{2}+\varepsilon _{j,k}^{2}}{2}-2\tanh ^{2}\Big(\frac{\chi _{j}}{\varpi _{j}}\Big)\eta _{j,k}(y)\Big\}. \end{aligned}$$

(44)

The Lyapunov function of step i can be selected as

$$\begin{aligned} V_{i}=V_{i-1}+\frac{1}{2}\chi _{i}^{2}. \end{aligned}$$

(45)

The derivative of $V_{i}$ is

$$\begin{aligned} {\dot{V}}_{i}= & \, {\dot{V}}_{i-1}+\chi _{i}{\dot{\chi }}_{i}\nonumber \\= & \, {\dot{V}}_{i-1}+\chi _{i}({\hat{\zeta }}_{i+1}-\mu _{i,k}{\hat{\zeta }}_{1}-{\dot{\alpha }}_{i-1}+s_{i}({\hat{\zeta }}_{i}-\alpha _{i-1})). \end{aligned}$$

(46)

The nonlinear function $\Psi _{i,k}$ is defined as

$$\begin{aligned} \Psi _{i,k}=\frac{\chi _{i}}{2}-\mu _{i,k}{\hat{\zeta }}_{1}-{\dot{\alpha }}_{i-1}+s_{i}({\hat{\zeta }}_{i}-\alpha _{i-1})-s_{i+1}\int _{0}^{t}r_{i+1} {\text{d}}\tau +\chi _{i-1}+\frac{2}{\chi _{i}}\tanh ^{2}(\frac{\chi _{i}}{\varpi _{i}})\eta _{i,k}(y), \end{aligned}$$

(47)

where $\eta _{i,k}(y)=b_{k}y^{2}{\bar{\varphi }}_{i,2}^{2}(y),$ which is estimated by FLSs

$$\begin{aligned} \Psi _{i,k}=\Phi _{i,k}^{T}S_{i,k}+\vartheta _{i,k}, \end{aligned}$$

(48)

where $\Phi _{i,k}$ are the weights of the FLSs $\Psi _{i,k}$, $S(X)_{i,k}$ are basis function vectors, and $\vartheta _{i,k}$ is a bounded functions that satisfies $|\vartheta _{i,k}|\le \varepsilon _{i,k}$, where $\varepsilon _{i,k}$ is a positive constant.

Then, we have

$$\begin{aligned} {\dot{V}}_{i}= & {} {\dot{V}}_{i-1}+\chi _{i}({\hat{\zeta }}_{i+1}-\mu _{i,k}{\hat{\zeta }}_{1}-{\dot{\alpha }}_{i-1}+s_{i}({\hat{\zeta }}_{i}-\alpha _{i-1}))\nonumber \\= & {} {\dot{V}}_{i-1}+\chi _{i}({\hat{\zeta }}_{i+1}+\Psi _{i,k}-\frac{\chi _{i}}{2}+s_{i+1}\int _{0}^{t}r_{i+1} {\text{d}}\tau -\chi _{i-1}-\frac{2}{\chi _{i}}\tanh ^{2}(\frac{\chi _{i}}{\varpi _{i}})\eta _{i,k}(y))\nonumber \\\le & {} {\dot{V}}_{i-1}+\chi _{i}\alpha _{i}+\chi _{i}\chi _{i+1}+\frac{\chi _{i}^{2}\theta }{2a_{i}^{2}}+\frac{a_{i}^{2}+\varepsilon _{i,k}^{2}}{2}-\chi _{i-1}\chi _{i}-2\tanh ^{2}(\frac{\chi _{i}}{\varpi _{i}})\eta _{i,k}(y). \end{aligned}$$

(49)

Substituting $\alpha _{i}$ into (49) gives

$$\begin{aligned} {\dot{V}}_{i}\le & {} \frac{{\tilde{\beta }}\chi _{1}^{2}}{\beta }\Big(c_{1}+\frac{{\hat{\theta }}}{2a_{1}^{2}}\Big)+\frac{1}{2}e^{T}e+\varphi _{11}^{2}(|\varsigma |)+\chi _{i-1}\chi _{i}\nonumber \\&+\sum _{j=1}^{i-1}\Big\{\frac{\chi _{j}^{2}{\tilde{\theta }}}{2a_{j}^{2}}-c_{j}\chi _{j}^{2}+\frac{a_{j}^{2}+\varepsilon _{j,k}^{2}}{2}-2\tanh ^{2}(\frac{\chi _{j}}{\varpi _{j}})\eta _{j,k}(y)\Big\}\nonumber \\&+\chi _{i}\alpha _{i}+\chi _{i}\chi _{i+1}+\frac{\chi _{i}^{2}\theta }{2a_{i}^{2}}+\frac{a_{i}^{2}+\varepsilon _{i,k}^{2}}{2}-\chi _{i-1}\chi _{i}-2\tanh ^{2}\Big(\frac{\chi _{i}}{\varpi _{i}}\Big)\eta _{i,k}(y)\nonumber \\\le & {} \frac{{\tilde{\beta }}\chi _{1}^{2}}{\beta }\Big(c_{1}+\frac{{\hat{\theta }}}{2a_{1}^{2}}\Big)+\frac{1}{2}e^{T}e+\varphi _{11}^{2}(|\varsigma |)+\chi _{i}\chi _{i+1}\nonumber \\&+\sum _{j=1}^{i}\Big\{\frac{\chi _{j}^{2}{\tilde{\theta }}}{2a_{j}^{2}}-c_{j}\chi _{j}^{2}+\frac{a_{j}^{2}+\varepsilon _{j,k}^{2}}{2}-2\tanh ^{2}(\frac{\chi _{j}}{\varpi _{j}})\eta _{j,k}(y)\Big\}. \end{aligned}$$

(50)

Step n: Calculating the derivative of $\chi _{n}$ gets

$$\begin{aligned} {\dot{\chi }}_{n}= & \, {\dot{r}}_{n}+s_{n}r_{n}\nonumber \\= & \, \dot{{\hat{\zeta }}}_{n}-{\dot{\alpha }}_{n-1}+s_{n}({\hat{\zeta }}_{n}-\alpha _{n-1})\nonumber \\= & \, u-\mu _{n,k}{\hat{\zeta }}_{1}-{\dot{\alpha }}_{n-1}+s_{n}({\hat{\zeta }}_{n}-\alpha _{n-1}). \end{aligned}$$

(51)

Select the Lyapunov function as

$$\begin{aligned} V_{n,k}=V_{k}^{*}+{\bar{V}}+V_{n-1}+\frac{1}{2}\chi _{n}^{2}+\frac{1}{2\jmath }{\tilde{\theta }}^{2}+\frac{1}{2\beta }{\tilde{\beta }}^{2}, \end{aligned}$$

(52)

where ${\bar{V}}=\int _{0}^{V_{\varsigma }}\rho (s) {\text{d}}s$ is a new function which is used to deal with state $\varsigma (t)$ and $\rho (s)> 0$ is a smooth decreasing function satisfying $\rho (0)=0$.

Unknown function $\Psi _{n,k}$ in this step is defined as

$$\begin{aligned} \Psi _{n,k}= & {} \frac{\chi _{n}}{2}-\mu _{n,k}{\hat{\zeta }}_{1}-{\dot{\alpha }}_{n-1}+s_{n}({\hat{\zeta }}_{n}-\alpha _{n-1})+\chi _{n-1}+\frac{2}{\chi _{n}}\tanh ^{2}\Big(\frac{\chi _{n}}{\varpi _{n}}\Big)\eta _{n,k}(y), \end{aligned}$$

(53)

where $\eta _{n,k}(y)=b_{k}y^{2}({\bar{\varphi }}_{n2}^{2}(y)+1)+\rho (\frac{4n_{0}\gamma (|y|)}{a_{0}})n_{0}\gamma (|y|)$. Bsing FLSs, one has

$$\begin{aligned} \Psi _{n,k}=\Phi _{n,k}^{T}S_{n,k}+\vartheta _{n,k}, \end{aligned}$$

(54)

where $\Phi _{n,k}$ is the weight of the FLSs $\Psi _{n,k}$ , $S(X)_{n,k}$ is a basis function vector, and $\vartheta _{n,k}$ is a bounded function that satisfies $|\vartheta _{n,k}|\le \varepsilon _{n,k}$, where $\varepsilon _{n,k}$ is a positive constant.

The derivative of ${V}_{n,k}$ is calculated as

$$\begin{aligned} {\dot{V}}_{n,k}&={\dot{V}}_{k}^{*}+\dot{{\bar{V}}}+{\dot{V}}_{n-1}+\chi _{n}(u-\mu _{n,k}{\hat{\zeta }}_{1}-{\dot{\alpha }}_{n-1}+s_{n}({\hat{\zeta }}_{n}-\alpha _{n-1}))-\frac{1}{\jmath }{\tilde{\theta }}\dot{{\hat{\theta }}}-\frac{1}{\beta }{\tilde{\beta }}\dot{{\hat{\beta }}}\nonumber \\&={\dot{V}}_{k}^{*}+\dot{{\bar{V}}}+{\dot{V}}_{n-1}+\chi _{n}(u+\phi _{n,k}-\frac{\chi _{n}}{2}-\chi _{n-1}-\frac{2}{\chi _{n}}\tanh ^{2}(\frac{\chi _{n}}{\varpi _{n}})\eta _{n,k}(y))-\frac{1}{\jmath }{\tilde{\theta }}\dot{{\hat{\theta }}}-\frac{1}{\beta }{\tilde{\beta }}\dot{{\hat{\beta }}}\nonumber \\&\le {\dot{V}}_{k}^{*}+\dot{{\bar{V}}}+{\dot{V}}_{n-1}+\chi _{n}u+\frac{\chi _{n}^{2}\theta }{2a_{n}^{2}}+\frac{a_{n}^{2}+\varepsilon _{n,k}^{2}}{2}-\chi _{n-1}\chi _{n}-2\tanh ^{2}\Big(\frac{\chi _{n}}{\varpi _{n}}\Big)\eta _{n,k}(y) -\frac{1}{\jmath }{\tilde{\theta }}\dot{{\hat{\theta }}}-\frac{1}{\beta }{\tilde{\beta }}\dot{{\hat{\beta }}}. \end{aligned}$$

(55)

Substituting (18) (22) (24) (25) into (55) leads to

$$\begin{aligned} {\dot{V}}_{n,k}\le & {} -e^{T}e+b_{k}y^{2}\Big(\sum _{i=1}^{n}{\bar{\varphi }}_{i,2}^{2}(y)+1\Big)+8\Vert P_{k}\Vert ^{2}\sum _{i=1}^{n}\varphi _{i,1}^{2}(|\varsigma |)+d_{0,k}\nonumber \\&+\rho (V_{\varsigma })[-a_{0}V_{\varsigma }(\varsigma )+n_{0}\gamma (|y|)]+\frac{1}{2}e^{T}e+\varphi _{11}^{2}(|\varsigma |)+\sum _{i=1}^{n}\Big\{-c_{i}\chi _{i}^{2}\nonumber \\&+\frac{a_{i}^{2}+\varepsilon _{i,k}^{2}}{2}-2\tanh ^{2}\Big(\frac{\chi _{i}}{\varpi _{i}}\Big)\eta _{i,k}(y)\Big\}+\frac{\hbar }{\jmath }{\tilde{\theta }}{\hat{\theta }}+\frac{\imath }{\beta }{\tilde{\beta }}{\hat{\beta }}. \end{aligned}$$

(56)

Note that ${\bar{V}}=\int _{0}^{V_{\varsigma }}\rho (s) {\text{d}}s\le V_{\varsigma }(\varsigma )\rho (V_{\varsigma }(\varsigma )).$ The following inequality holds

$$\begin{aligned}&\rho (V_{\varsigma })[-a_{0}V_{\varsigma }(\varsigma )+n_{0}\gamma (|y|)]\nonumber \\&\quad =-a_{0}\rho (V_{\varsigma })V_{\varsigma }(\varsigma )+\rho (V_{\varsigma })n_{0}\gamma (|y|)\nonumber \\&\quad =-\frac{1}{2}a_{0}{\bar{V}}-\frac{1}{4}a_{0}\rho (V_{\varsigma })V_{\varsigma }(\varsigma )-\frac{1}{4}a_{0}\rho (V_{\varsigma })V_{\varsigma }(\varsigma )+\rho (V_{\varsigma })n_{0}\gamma (|y|). \end{aligned}$$

(57)

Case 1 $n_{0}\gamma (|y|)< \frac{1}{4}a_{0}V_{\varsigma }(\varsigma )$. We have

$$\begin{aligned}&\rho (V_{\varsigma })[-a_{0}V_{\varsigma }(\varsigma )+n_{0}\gamma (|y|)]\nonumber \\&\quad \le -\frac{1}{2}a_{0}{\bar{V}}-\frac{1}{4}a_{0}\rho (V_{\varsigma })V_{\varsigma }(\varsigma ). \end{aligned}$$

(58)

Case 2 $n_{0}\gamma (|y|)\ge \frac{1}{4}a_{0}V_{\varsigma }(\varsigma )$. Then $V_{\varsigma }(\varsigma )\le \frac{4n_{0}\gamma (|y|)}{a_{0}}$, one has

$$\begin{aligned}&\rho (V_{\varsigma })[-a_{0}V_{\varsigma }(\varsigma )+n_{0}\gamma (|y|)]\nonumber \\&\quad \le -\frac{1}{2}a_{0}{\bar{V}}-\frac{1}{4}a_{0}\rho (V_{\varsigma })V_{\varsigma }(\varsigma )+\rho \Big(\frac{4n_{0}\gamma (|y|)}{a_{0}}\Big)n_{0}\gamma (|y|). \end{aligned}$$

(59)

By combining (58) with (59), (56) can be transformed as

$$\begin{aligned} {\dot{V}}_{n,k}\le & {} -e^{T}e+b_{k}y^{2}\Big(\sum _{i=1}^{n}{\bar{\varphi }}_{i,2}^{2}(y)+1\Big)+8\Vert P_{k}\Vert ^{2}\sum _{i=1}^{n}\varphi _{i,1}^{2}(|\varsigma |)+d_{0,k}-\frac{1}{2}a_{0}{\bar{V}}\nonumber \\&-\frac{1}{4}a_{0}\rho (V_{\varsigma })V_{\varsigma }(\varsigma )+\rho \Big(\frac{4n_{0}\gamma (|y|)}{a_{0}}\Big)n_{0}\gamma (|y|)+\frac{1}{2}e^{T}e+\varphi _{11}^{2}(|\varsigma |)+\sum _{i=1}^{n}\{-c_{i}\chi _{i}^{2}\nonumber \\&+\frac{a_{i}^{2}+\varepsilon _{i,k}^{2}}{2}-2\tanh ^{2}\Big(\frac{\chi _{i}}{\varpi _{i}}\Big)\eta _{i,k}(y)\}+\frac{\hbar }{\jmath }{\tilde{\theta }}{\hat{\theta }}+\frac{\imath }{\beta }{\tilde{\beta }}{\hat{\beta }}. \end{aligned}$$

(60)

Choose the appropriate function $\rho$ such that

$$\begin{aligned} 8\Vert P_{k}\Vert ^{2}\sum _{i=1}^{n}\varphi _{i,1}^{2}(|\varsigma |)+\varphi _{11}^{2}(|\varsigma |)\le \frac{1}{4}a_{0}\rho (V_{\varsigma })V_{\varsigma }(\varsigma ). \end{aligned}$$

(61)

Notice that the following inequalities hold

$$\begin{aligned}{\tilde{\theta }}{\hat{\theta }}&={\tilde{\theta }}(\theta -{\tilde{\theta }})\le -\frac{1}{2}{\tilde{\theta }}^{2}+\frac{1}{2}\theta ^{2},\nonumber \\{\tilde{\beta }}{\hat{\beta }}&={\tilde{\beta }}(\beta -{\tilde{\beta }})\le -\frac{1}{2}{\tilde{\beta }}^{2}+\frac{1}{2}\beta ^{2}. \end{aligned}$$

(62)

Then we have

$$\begin{aligned} {\dot{V}}_{n,k}\le & {} -p_{1}V_{n,k}+p_{2}+\eta _{k}(y)+\sum _{i=1}^{n}\Big\{-2\tanh ^{2}\Big(\frac{\chi _{i}}{\varpi _{i}}\Big)\eta _{i,k}(y)\Big\}\nonumber \\= & {} -p_{1}V_{n,k}+p_{2}+\sum _{i=1}^{n}\Big\{\Big(1-2\tanh ^{2}\Big(\frac{\chi _{i}}{\varpi _{i}}\Big)\Big)\eta _{i,k}(y)\Big\}. \end{aligned}$$

(63)

where $p_{1}=\min \{\frac{1}{2\lambda _{\max }(P_{k})}, 2c_{i}, \hbar , \imath , \frac{1}{2}a_{0}\}$, $p_{2}=\max \{d_{0,k}+\frac{a_{i}^{2}+\varepsilon _{i,k}^{2}}{2}+\frac{\hbar }{2\jmath }\theta ^{2}+\frac{\imath }{2}\beta \}$, $\eta _{k}(y)=\eta _{1,k}(y)+\eta _{2,k}(y)+\cdots +\eta _{n,k}(y)=\sum _{i=1}^{n}b_{k}y^{2}(\sum _{i=1}^{n}{\bar{\varphi }}_{i2}^{2}(y)+1)+\rho (\frac{4n_{0}\gamma (|y|)}{a_{0}})n_{0}\gamma (|y|).$

Remark 7

The controller designed in this paper has a PI form that features a simple structure and a more explicit physical meaning. To achieve the above objectives, the generalized errors are introduced, and the nonlinear functions $\Psi _{i,k}$ are intelligently constructed in each step. These functions can be approximated via FLSs because of their continuity.

Remark 8

The polynomial $\frac{1}{2}\chi _{1}l^{2}h^{2}{w^{*}}^{2}+\frac{1}{4}l^{2}\chi _{1}w_{1k}^{2}+\breve{\beta }w_{1k}\varphi _{12}(y)$ is introduced in $\Psi _{1,k}$ to counteract the nonlinear functions $\frac{1}{2}\chi ^{2}_{1}l^{2}h^{2}{w^{*}}^{2}$, $\frac{1}{4}l^{2}\chi ^{2}_{1}w_{1k}^{2}$ and $\chi _{1}\breve{\beta }w_{1k}\varphi _{12}(y)$ produced in (32) and (33).

Remark 9

The function $\frac{\chi _{i}}{2}$ is introduced in $\Psi _{i,k}$ to counteract the function $\frac{\chi ^{2}_{i}}{2}$ produced $\chi _{i}\vartheta _{i,k}\le \frac{\chi ^{2}_{i}}{2}+\frac{\varepsilon ^{2}_{i,k}}{2}$; in order to construct the virtual control laws with a PI structure and deal with the function $\eta _{k}(y)$, the polynomial $-s_{i+1}\int _{0}^{t}r_{i+1} {\text{d}}\tau +\frac{2}{\chi _{i}}\tanh ^{2}(\frac{\chi _{i}}{\varpi _{i}})\eta _{i,k}(y)$ is introduced.

Remark 10

To estimate the nonlinear term $\eta _{k}(y)$, the function $\tanh ^{2}(\frac{\chi _{i}}{\varpi _{i}})$ is introduced because of $\lim \limits _{\chi _{i}\rightarrow 0}\frac{\tanh ^{2}(\frac{\chi _{i}}{\varpi _{i}})}{\chi _{i}}=0$, thus, it can be reconstructed using FLSs. As a result, the difficulty caused by the existence of the nonlinear function $\eta _{k}(y)$ is solved.

3.3 Stability Analysis

Theorem 1

Consider an uncertain switched nonlinear system (1) with Assumptions 1–3 and an average dwell time $\tau _{a}> \frac{ln \mu }{p_{1}} (\mu =\max \{\frac{\lambda _{\max }(P_{k})}{\lambda _{\min }(P_{l})}\}, k,l\in {\mathcal {P}}; p_{1}=\min \{\frac{1}{2\lambda _{\max }(P_{k})}, 2c_{i}, \hbar , \imath , \frac{1}{2}a_{0}\})$, the PI controller (22) and the adaptive laws (24)–(25) can guarantee that all the signals in the closed-loop system and tracking error are bounded.

Proof

We will discuss the stability of the system in three cases.

Case 1 If $\chi _{i}\not \in {\mathcal {E}}_{\chi _{i}},$ $i=1,2,\ldots ,n$, by applying Lemma 2, (63) is rewritten as

$$\begin{aligned} {\dot{V}}_{n,k}\le & {} -p_{1}V_{n,k}+p_{2}+\sum _{i=1}^{n}\Big\{\Big(1-2\tanh ^{2}\Big(\frac{\chi _{i}}{\varpi _{i}}\Big)\Big)\eta _{i,k}(y)\Big\}\nonumber \\\le & {} -p_{1}V_{n,k}+p_{2}. \end{aligned}$$

(64)

Integrating both sides of (64) on $[t_{j}, t_{j+1})$ yields

$$\begin{aligned} V_{n,k}(t)\le & {} e^{-p_{1}(t-t_{j})}V_{n,k}(t_{j})+p_{2}\int _{t_{j}}^{t}e^{-p_{1}(t-s)} {\text{d}}s, \end{aligned}$$

(65)

where $t_{j}$ denotes switching time, $j=0,1,\ldots ,N_{\sigma }(t,0)-1$. We know that ${\mathcal {V}}_{n,k}\le \mu {\mathcal {V}}_{n,l}$ in [53], where $k,l\in {\mathcal {P}}$, and $\mu =\max \{\frac{\lambda _{\max }(P_{k})}{\lambda _{\min }(P_{l})}\}\ge 1.$

Let $t_{0}=0$. For any $t> 0$, iterating the (65) leads to

$$\begin{aligned} V_{n,k}(t)\le & {} e^{-p_{1}(t-t_{N_{\sigma }(t,0)})}V_{n,k}(t_{N_{\sigma }(t,0)})+p_{2}\int _{t_{N_{\sigma }(t,0)}}^{t}e^{-p_{1}(t-s)} {\text{d}}s\nonumber \\\le & {} \mu e^{-p_{1}(t-t_{N_{\sigma }(t,0)})}V_{n,\sigma }(t_{N_{\sigma }(t,0)}^{-})+p_{2}\int _{t_{N_{\sigma }(t,0)}}^{t}e^{-p_{1}(t-s)} {\text{d}}s\nonumber \\\le & {} \mu e^{-p_{1}(t-t_{N_{\sigma }(t,0)})}[e^{-p_{1}(t_{N_{\sigma }(t,0)}-t_{N_{\sigma }(t,0)-1})}V(t_{N_{\sigma }(t,0)-1})+p_{2}\int _{t_{N_{\sigma }(t,0)-1}}^{t_{N_{\sigma }(t,0)}}e^{-p_{1}(t_{N_{\sigma }(t,0)}-s)}{\text{d}}s]\nonumber \\&+p_{2}\int _{t_{N_{\sigma }(t,0)}}^{t}e^{-p_{1}(t-s)} {\text{d}}s\nonumber \\\le & {} \cdots \nonumber \\\le & {} \mu ^{N_{\sigma }(t,0)}e^{-p_{1} t}V_{n,\sigma (0)}(0)+p_{2}\int _{0}^{t}\mu ^{N_{\sigma }(t,s)}e^{-p_{1} (t-s)}{\text{d}}s. \end{aligned}$$

(66)

Choose $\tau _{a}> \frac{\ln \mu }{p_{1}}$. According to the definition of the average dwell time [53, 54] and for arbitrary $\gamma \in (0,p_{1}-\frac{\ln \mu }{\tau _{a}})$, we have

$$\begin{aligned} N_{\sigma }(t,0)\le N_{0}+\frac{(p_{1}-\gamma )t}{\ln \mu }. \end{aligned}$$

(67)

Taking (67) into (66) yields

$$\begin{aligned} V_{n,\sigma }(t)\le & {} \mu ^{N_{0}+\frac{(p_{1}-\gamma )t}{\ln \mu }}e^{-p_{1} t}{\mathcal {V}}_{\sigma (0)}(0)+p_{2}\int _{0}^{t}\mu ^{N_{0}+\frac{(p_{1}-\gamma )(t-s)}{\ln \mu }}e^{-p_{1}(t-s)}{\text{d}}s\nonumber \\= & {} \mu ^{N_{0}}e^{(p_{1}-\gamma )t}e^{-p_{1} t}V_{\sigma (0)}(0)+\mu ^{N_{0}}p_{2}\int _{0}^{t}e^{(p_{1}-\gamma )(t-s)}e^{-p_{1}(t-s)}{\text{d}}s\nonumber \\= & {} \mu ^{N_{0}}e^{-\gamma t}V_{\sigma (0)}(0)+\mu ^{N_{0}}\frac{p_{2}}{\gamma }(1-e^{-\gamma t}). \end{aligned}$$

(68)

Thus, we can obtain $V_{n,\sigma }(t)\le \mu ^{N_{0}}\frac{p_{2}}{\gamma }$ when $t\rightarrow \infty$. Therefore, $e_{i}, \chi _{i}$ and ${\tilde{\theta }}$, $i=1,2,\ldots ,n$ are bounded; then, $\alpha _{1}$, $\alpha _{2},\ldots ,\alpha _{n-1}$, u, ${\hat{\theta }}$, ${\hat{\beta }}$ are bounded. Then we can further obtain $r_{i}$, ${\tilde{\zeta }}_{i}$, ${\hat{\zeta }}_{i}$, $\zeta _{i}$, y, $\varsigma$, and $x_{i}$ are bounded.

According to the above analysis, the following inequality holds

$$\begin{aligned} \frac{1}{2}\chi _{1}^{2}\le \mu ^{N_{0}}\frac{p_{2}}{\gamma }, \end{aligned}$$

(69)

so

$$\begin{aligned} |\chi _{1}|\le \sqrt{2\mu ^{N_{0}}\frac{p_{2}}{\gamma }}. \end{aligned}$$

(70)

Note that

$$\begin{aligned} \chi _{1}=r_{1}+s_{1}\int _{0}^{t}r_{1}{\text{d}}\tau . \end{aligned}$$

(71)

Let $p=\int _{0}^{t}r_{1}{\text{d}}\tau$. We have

$$\begin{aligned} \chi _{1}={\dot{p}}+s_{1}p. \end{aligned}$$

(72)

Furthermore, we obtain

$$\begin{aligned} -\sqrt{2\mu ^{N_{0}}\frac{p_{2}}{\gamma }}\le {\dot{p}}+s_{1}p\le \sqrt{2\mu ^{N_{0}}\frac{p_{2}}{\gamma }}. \end{aligned}$$

(73)

Multiplying both sides by $\hbox {exp}(s_{1}t)$ produces

$$\begin{aligned} -\hbox {exp}(s_{1}t)\sqrt{2\mu ^{N_{0}}\frac{p_{2}}{\gamma }}\le \frac{d(p\hbox {exp}(s_{1}t))}{{\text{d}}t}\le \hbox {exp}(s_{1}t)\sqrt{2\mu ^{N_{0}}\frac{p_{2}}{\gamma }}. \end{aligned}$$

(74)

Integrating (74) leads to

$$\begin{aligned}&-\frac{\sqrt{2\mu ^{N_{0}}\frac{p_{2}}{\gamma }}}{s_{1}}+\bigg [p(0)+\frac{\sqrt{2\mu ^{N_{0}}\frac{p_{2}}{\gamma }}}{s_{1}}\bigg ]\hbox {exp}(-s_{1}t) \le p\nonumber \\&\le \frac{\sqrt{2\mu ^{N_{0}}\frac{p_{2}}{\gamma }}}{s_{1}}+\bigg [p(0)-\frac{\sqrt{2\mu ^{N_{0}}\frac{p_{2}}{\gamma }}}{s_{1}}\bigg ]\hbox {exp}(-s_{1}t). \end{aligned}$$

(75)

Thus we have

$$\begin{aligned} |p|\le \frac{\sqrt{2\mu ^{N_{0}}\frac{p_{2}}{\gamma }}}{s_{1}}. \end{aligned}$$

(76)

Combining (72) with (76) gives

$$\begin{aligned} \lim _{t\rightarrow \infty }|y-y_{d}|=|r_{1}|\le 2\sqrt{2\mu ^{N_{0}}\frac{p_{2}}{\gamma }}. \end{aligned}$$

(77)

Case 2 If $\chi _{i}\in {\mathcal {E}}_{\chi _{i}}$, $i=1,2,\ldots ,n$, thus $|\chi _{i}|\le \iota \varpi _{i}$ is bounded. Furthermore, from the choice of the adaptive laws ${\hat{\theta }}$ in (23), we can infer that ${\hat{\theta }}$ is bounded for any bounded $\chi _{i}$, which means that ${\tilde{\theta }}$ is also bounded. Similar to Case 1, $\alpha _{1}$, $\alpha _{2},\ldots ,\alpha _{n-1}$, u, $r_{i}$, $\varsigma$, ${\hat{\zeta }}$ and y are bounded, and given that ${\bar{\varphi }}_{i,2}(y)$ and $\varphi _{i,1}(|\varsigma |)$ are smooth functions, then ${\bar{\varphi }}_{i,2}(y)$ and $\varphi _{i,1}(|\varsigma |)$ are bounded, and ${\tilde{\zeta }}_{i}$, $\zeta _{i}$ and $x_{i}$ are bounded when $\tau _{a}$ satisfies $\tau _{a}> \frac{\ln \mu }{{p_{1}}}$. There exist some positive constants $M_{i}$, such that $\max _{k\in {\mathcal {P}}}\{\eta _{i,k}\}\le M_{i}$, and we can further obtain $(1-2\tanh ^{2}(\frac{\chi _{i}}{\varpi _{i}}))\eta _{i,k}\le 3M_i$. Then (63) can be written as

$$\begin{aligned} {\dot{V}}_{n,k}\le {\bar{p}}_{2}-p_{1}V_{n,k}, \end{aligned}$$

(78)

where ${\bar{p}}_{2}=p_{2}+3\sum _{i=1}^{n}M_{i}$.

Similar to Case 1, we can get

$$\begin{aligned} \lim _{t\rightarrow \infty }|y-y_{d}|=|r_{1}|\le 2\iota \varpi _{1}. \end{aligned}$$

(79)

Case 3. If $\chi _{j}\not \in {\mathcal {E}}_{\chi _{j}}$ and $\chi _{i}\in E_{\chi _{i}}$, $i\ne j.$ (63) can be rewritten as

$$\begin{aligned} \dot{{\mathcal {V}}}_{n,k}\le & {} -p_{1}V_{n,k}+p_{2}+\sum _{i=1}^{n}\Big\{\Big(1-2\tanh ^{2}\Big(\frac{\chi _{i}}{\varpi _{i}}\Big)\Big)\eta _{i,k}(y)\Big\}.\nonumber \\= & {} -p_{1}V_{n,k}+p_{2}+\Sigma _{\chi _j\not \in E_{\chi _{j}}}\Big\{\Big(1-2\tanh ^{2}\Big(\frac{\chi _{j}}{\varpi _{j}}\Big)\Big)\eta _{j,k}(y)\Big\}\nonumber \\&+ \Sigma _{\chi _i\in E_{\chi _i}}\Big\{\Big(1-2\tanh ^{2}\Big(\frac{\chi _{i}}{\varpi _{i}}\Big)\Big)\eta _{i,k}(y)\Big\}. \end{aligned}$$

(80)

Combining Case 1 with Case 2 yields

$$\begin{aligned} \lim _{t\rightarrow \infty }|y-y_{d}|\le \max \bigg \{2\sqrt{2\mu ^{N_{0}}\frac{p_{2}}{\gamma }}, 2\iota \varpi _{1} \bigg \}. \end{aligned}$$

(81)

Based on the discussed above, Theorem 1 is proved.

The specific implementation steps are summarized as follows:

• 1. Choose the appropriate parameters $\mu _{i,k}$ such that $A_{k}$ is a Hurwitz matrix, $i=1,2,\ldots ,n.$

• 2. Calculate the corresponding $P_{k}$ through (13).

• 3. Select the positive constants $\hbar$, $\jmath$, $c_{1}$, $\imath$ and $a_{i}$ to determine the adaptive law ${\hat{\theta }}$, ${\hat{\beta }}$.

• 4. Choose the parameters $c_{i}> 0$, $s_{i}>0$ to determine the virtual control functions $\alpha _{i}$, $i=1,2,\ldots ,n-1.$

• 5. Select the parameters $c_{n}> 0$, $s_{n}>0$ to determine the controller u.

• 6. Choose the average dwell time $\tau _{a}$ by calculating $\frac{ln \mu }{p_{1}}$.

Remark 9

According to (81), to achieve a good control performance, we can add the value of $\gamma$ and reduce the value of $p_{2}$ by adjusting the correlative parameters. However, this adjustment may also influence other performance aspects such as the resulting large controlled quantity. Thus, a specific control performance and control action are achieved via regulation parameters.

4 Simulation Results

In this section, two examples are given to demonstrate the effectiveness of the developed method.

Example 1

Consider the following switched nonlinear systems with unmodeled dynamics:

$$\begin{aligned} {\dot{\varsigma }}= & \, q_{\sigma (t)}(\varsigma ,y,d(t)),\nonumber \\ {\dot{x}}_1= & \, h_{1}x_2+f_{1,\sigma (t)}(x_{1})+\Delta _{1,\sigma (t)}(\varsigma ,y,d(t)),\nonumber \\ {\dot{x}}_2= & \, h_{2}x_3+f_{2,\sigma (t)}(x_{1},x_{2})+\Delta _{2,\sigma (t)}(\varsigma ,y,d(t)),\nonumber \\ {\dot{x}}_n= & \, h_{3}u+f_{3,\sigma (t)}(x_{1},x_{2},x_{3})+\Delta _{3,\sigma (t)}(\varsigma ,y,d(t)),\nonumber \\ y= & \, D(x_1), \end{aligned}$$

(82)

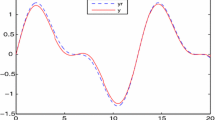
where $q_{1}=-\varsigma +0.125y^{2}\cos ^{2}(y)$, $q_{2}=-2\varsigma +0.05y^{2}\sin ^{2}(y)$, $f_{1,1}=0.1\sin (x_{1})$, $f_{1,2}=0.1\cos (x_{1})$, $f_{2,1}=0.1\sin (x_{1}x_{2})$, $f_{2,2}=0.1\sin (x_{1})\cos (x_{2})$, $f_{3,1}=0.1\cos (x_{1}^{2}x_{2}x_{3})$, $f_{3,2}=0.1\sin (x_{1}x_{2}) \cos (x_{3})$, $\Delta _{1,1}=0.1\sin (y\varsigma )+0.1e^{-t^{2}}$, $\Delta _{1,2}=0.1\cos (y\varsigma )-0.1e^{-t^{2}}$, $\Delta _{2,1}=0.1\sin (y\varsigma )+0.2\sin (t^{2})$, $\Delta _{2,2}=0.1\sin (y^{2}\varsigma )+0.2\cos (t^{4})$, $\Delta _{3,1}=0.1\sin (y\varsigma )+e^{-t^{4}}$, $\Delta _{3,2}=0.1\cos (y\varsigma )+0.5e^{-t^{2}}$. We choose the tracking signal as $y_{d}=0.5\cos (0.5t)+\sin (0.5t)$. Choose $\mu _{1,1}=\mu _{1,2}=3$, $\mu _{2,1}=\mu _{2,2}=5$, $\mu _{3,1}=\mu _{3,2}=2$, $\tau _{a}=29.03> \ln 13.8392/0.0905$. choose the initial conditions $x_{1}(0)=0.2$, $x_{2}(0)=0.3$, $x_{3}(0)=-0.2$, ${\hat{\zeta }}_{1}(0)={\hat{\zeta }}_{2}(0)={\hat{\zeta }}_{3}(0)=0$, ${\hat{\theta }}(0)=0$, ${\hat{\beta }}(0)=0.03$. Select the parameters as: $l=0.2$, $v=0.01$, $\jmath _{1}=2.5$, $\hbar =0.1$, $\imath =0.001$, $a_{1}=2$, $a_{2}=1$, $a_{3}=3$, $s_{1}=s_{2}=s_{3}=2$, $c_{1}=2$, $c_{2}=7$, $c_{3}=100$, $h_{1}=1$, $h_{2}=3$, $h_{3}=70$. The simulation results are shown in Figs. 2, 3, 4, 5, 6, 7, 8, and 9. Figure 2 gives the trajectories of y and $y_{d}$ whereas Fig. 3 shows the curve of tracking error. From Figs. 2 and 3, we can distinctly observe that the system has a good tracking performance. Figure 4 presents the curves of $x_{1}$, $x_{2}$, $x_{3}$ and $\varsigma$. Curves of ${\hat{\zeta }}_{1}$, ${\hat{\zeta }}_{2}$, and ${\hat{\zeta }}_{3}$ are shown in Fig. 5. Figures 6 and 7 depict curves of the adaptive parameters ${\hat{\theta }}$ and ${\hat{\beta }}$, respectively. Figure 8 shows curve of the control input u. Figure 9 depicts the switching signal. To prove the superiority of the proposed scheme, we compare the simulation results with [55]. For convenience, the scheme proposed in this paper is denoted as scheme 1, whereas the scheme proposed in [55] is denoted as scheme 2. To ensure a fair comparison, we choose the same $q_{k}$, $f_{i,k}$,$\Delta _{i,k}$, and $h_{i}$. The simulation results for scheme 2 are shown in Figs. 10, 11, and 12. Figure 10 shows curves of the y and $y_{d}$. Curve of tracking error is presented in Fig. 10, and 12 depicts the trajectories of u. Figures 13 and 14 show the comparison of tracking performance and control quantity between scheme 1 and scheme 2. It can be observed that scheme 1 has better tracking performance than scheme 2 provided that the two control quantities are close to each other.

In order to verify the robustness of the proposed scheme, we choose the nonlinear functions as $f_{1,1}=0.1\sin (x_{1})$, $f_{1,2}=0.1\cos (x_{1})$, $f_{2,1}=0.1\sin (x_{1}x_{2})$, $f_{2,2}=0.1\sin (x_{1})\cos (x_{2})$, $f_{3,1}=0.1\cos (x_{1}^{2}x_{2}x_{3})$, $f_{3,2}=0.1\sin (x_{1}x_{2})\cos (x_{3})$ when $t< 75s$; while $t\ge 75s,$ the nonlinear functions are selected as $f_{1,1}=0.3\sin (x_{1})$, $f_{1,2}=0.3\cos (x_{1})$, $f_{2,1}=0.3\sin (x_{1}x_{2})$, $f_{2,2}=0.3\sin (x_{1})\cos (x_{2})$, $f_{3,1}=0.3\cos (x_{1}^{2}x_{2}x_{3})$, $f_{3,2}=0.3\sin (x_{1}x_{2})\cos (x_{3})$. The tracking performance under parameter perturbation is shown in Fig. 15, which demonstrates that the proposed scheme has a significant robustness. Finally, we investigate the noise rejection performance of the system. A noise with an SNR of 60 dB is added to the output channel (82). Curves of system tracking error with sensor noise is depicted in Fig. 16. Curve of the input u is shown in Fig. 17. It can be clearly observed that the tracking error has a satisfactory performance when the systems are subject to sensor noise.

Fig. 2

Curves of y and $y_{d}$ for Example 1

Fig. 3

Curve of tracking error $y-y_{d}$ for Example 1

Fig. 4

Curves of $x_{1}$, $x_{2}$, $x_{3}$ and $\varsigma$ for Example 1

Fig. 5

Curves of ${\hat{\zeta }}_{1},{\hat{\zeta }}_{2}$ and ${\hat{\zeta }}_{3}$ for Example 1

Fig. 6

Curve of ${\hat{\theta }}$ for Example 1

Fig. 7

Curve of ${\hat{\beta }}$ for Example 1

Fig. 8

Curve of control input u for Example 1

Fig. 9

Curve of the switching signal for Example 1

Fig. 10

Curves of y and $y_{d}$ for scheme 2 in Example 1

Fig. 11

Curve of tracking error $y{-}y_{d}$ for scheme 2 in Example 1

Fig. 12

Curve of control input u for scheme 2 in Example 1

Fig. 13

Comparison of tracking performance between scheme 1 and scheme 2

Fig. 14

Comparison of controlled quantity between scheme 1 and scheme 2

Fig. 15

Curve of the tracking error under the parameter perturbation

Fig. 16

Curve of tracking error with noise

Fig. 17

Curve of controller u with noise

Example 2

(Electromechanical system). An electromechanical system [56] can be modeled as follows

$$\begin{aligned}&P\ddot{z}+M{\dot{z}}+Q\sin (z)=I\nonumber \\&L{\dot{I}}=U_{\epsilon }-RI-K_{B}{\dot{z}}, \end{aligned}$$

(83)

where $P=\frac{N}{K_{\tau }}+\frac{m_{0}l^{2}}{3K_{\tau }}+\frac{m_{1}l^{2}}{K_{\tau }}+\frac{2m_{1}R_{0}^{2}}{5K_{\tau }}$, $Q=\frac{m_{0}lG}{2K_{\tau }}+\frac{m_{1}lG}{K_{\tau }}$, $M=\frac{D_{0}}{K_{\tau }}$, z is angular motor position, I represents motor armature current, $L=1.429\times 10^{-2} H$ denotes armature inductance, $U_{\epsilon }$ means the input control voltage, $R=1\times 10^{-2} \Omega$ is called armature resistance, $K_{B}=2\times 10^{-3} N m/A$ is back-emf coefficient, $K_{\tau }=0.9 N m/A$ is a coefficient which means the electromechanical conversion of armature current to torque, $N=16.25\times 10^{-2} kg m^{2}$ represents the rotor inertia, $m_{0}=5.06\times 10^{-2} kg$ and $m_{1}=4.34\times 10^{-2} kg$ denote link mass and load mass, respectively. $l=5\times 10^{-2} m$ is the link length, $R_{0}=2.3\times 10^{-2} m$ is called radius of the load, $G=9.8 m/s^{2}$ represents the gravity coefficient, and $D_{0}=1.625\times 10^{-3} N m s/rad$ represents the coefficient of viscous friction at the joint. Let $x_{1}=z, x_{2}={\dot{z}}, x_{3}=\frac{I}{P}, u=U_{\epsilon }$. Considering the disturbances, unmodeled dynamics and dead-zone output, the system (83) can be expressed as

$$\begin{aligned} {\dot{\varsigma }}= & \, q_{\sigma (t)}(\varsigma ,y,d(t)),\nonumber \\ {\dot{x}}_1= & \, h_{1}x_2+f_{1,\sigma (t)}(x_{1})+\Delta _{1,\sigma (t)}(\varsigma ,y,d(t)),\nonumber \\ {\dot{x}}_2= & \, h_{2}x_3+f_{2,\sigma (t)}(x_{1},x_{2})+\Delta _{2,\sigma (t)}(\varsigma ,y,d(t)),\nonumber \\ {\dot{x}}_n= & \, h_{3}u+f_{3,\sigma (t)}(x_{1},x_{2},x_{3})+\Delta _{3,\sigma (t)}(\varsigma ,y,d(t)),\nonumber \\ y= & \, D(x_1), \end{aligned}$$

(84)

where $q_{1}=-\varsigma +0.05y^{2}\sin ^{2}(y)$, $q_{2}=-0.1\varsigma +0.1y^{2}\cos ^{2}(y)$, $f_{1,1}=f_{1,2}=0$, $f_{2,1}=-\frac{Q}{P}\sin (x_{1})-\frac{M}{P}x_{2}$, $f_{2,2}=-\frac{Q}{P}\sin (x_{1})-\frac{M}{P}x_{2}+0.2\sin (x_{1})\cos (x_{2})$, $f_{3,1}=-\frac{K_{B}}{PL}x_{2}-\frac{R}{L}x_{3}$, $f_{3,2}=-\frac{K_{B}}{PL}x_{2}-\frac{R}{L}x_{3}+0.1\sin (x_{1}x_{2})\cos (x_{3})$, $\Delta _{1,1}=0.1\sin (y\varsigma )+0.1e^{-t^{2}}$, $\Delta _{1,2}=0.1\cos (y\varsigma )-0.1e^{-t^{2}}$, $\Delta _{2,1}=0.1\sin (y\varsigma ^{2})+0.2\sin (t^{2})$, $\Delta _{2,2}=0.1\sin (y^{2}\varsigma )+0.2\cos (t^{4})$, $\Delta _{3,1}=\Delta _{3,2}=0$, $h_{1}=h_{2}=1$, $h_{3}=\frac{1}{PL}$.

In this example, $y_{d}=0.5\cos (0.5t)+\sin (0.5t)$. Select the initial conditions $x_{1}(0)=0.2$, $x_{2}(0)=0.3$, $x_{3}(0)=-0.2$, ${\hat{\zeta }}_{1}(0)={\hat{\zeta }}_{2}(0)={\hat{\zeta }}_{3}(0)=0$, ${\hat{\theta }}(0)=0$, ${\hat{\beta }}(0)=0.03$. We choose $\mu _{1,1}=\mu _{1,2}=3$, $\mu _{2,1}=\mu _{2,2}=5$, $\mu _{3,1}=\mu _{3,2}=2$, $\tau _{a}=29.03> \ln 13.8392/0.0905$. $l=0.2$, $v=0.01$, $\jmath _{1}=2.5$, $\hbar =0.1$, $\imath =0.001$, $a_{1}=2$, $a_{2}=1$, $a_{3}=3$, $s_{1}=s_{2}=s_{3}=2$, $c_{1}=4$, $c_{2}=9$, $c_{3}=120$. The simulation results are given in Figs. 18, 19, 20, 21, 22, 23, 24, and 25. The trajectories of y and $y_{d}$ are depicted in Figs. 18, and 19 shows curve of the tracking error, we can see that the tracking error tends to be in a small neighborhood of the origin. Figure 20 shows curves of $x_{1}$, $x_{2}$, $x_{3}$ and $\varsigma$. Figure 21 shows curves of ${\hat{\zeta }}_{1}$, ${\hat{\zeta }}_{2}$, and ${\hat{\zeta }}_{3}$. Figure 22, 23 and 24 depict adaptive parameters ${\hat{\theta }}$, ${\hat{\beta }}$ and control input u, respectively. Figure 25 shows the switching signal.

Fig. 18

Curves of y and $y_{d}$ for Example 2

Fig. 19

Curve of tracking error $y-y_{d}$ for Example 2

Fig. 20

Curves of $x_{1}$, $x_{2}$, $x_{3}$ and $\varsigma$ for Example 2

Fig. 21

Curves of ${\hat{\zeta }}_{1},{\hat{\zeta }}_{2}$ and ${\hat{\zeta }}_{3}$ for Example 2

Fig. 22

Curve of ${\hat{\theta }}$ for Example 2

Fig. 23

Curve of ${\hat{\beta }}$ for Example 2

Fig. 24

Curve of control input u for Example 2

Fig. 25

Curve of the switching signal for Example 2

5 Conclusions

In this paper, the problem of adaptive fuzzy PI output feedback tracking control for a class of uncertain switched nonlinear systems with unmodeled dynamics, unknown control coefficients and dead-zone output has been addressed. The proposed controller has a PI structure, which constitutes a more intuitive structure and has a stronger physical sense. The boundedness of all signals and tracking error of the closed-loop system has been analyzed using the Lyapunov stability theory. The validity of the scheme has been demonstrated through two examples.