Numerical Solution of Fuzzy Differential Equations by Variational Iteration Method

Abstract

In this paper, variational iteration method is presented to solve the linear and nonlinear fuzzy differential equations. This technique provides a sequence of functions which converges to the exact solution of the problem. Sufficient condition for convergence of the proposed method is given and also a maximum absolute truncation error is estimated. This method provides remarkable accuracy in comparison with the analytical solution. Several numerical examples are given to illustrate the efficiency and performance of the presented method.

1 Introduction

Many physical problems are governed by fuzzy differential equations, and finding the solution of these equations has been the subject of many investigators in recent years [1–12]. In [13], Ji-Huan He presented a very lucid as well as an elementary discussion of the variational iteration method (VIM); the method was further developed by the originator himself [14–16]. The main property of the method is its flexibility and ability to solve nonlinear equations accurately and conveniently, the solution procedure is simple, and results are acceptable and have been applied to a wide class of nonlinear problems [17–25]. This scheme is used for solving linear system of first-order fuzzy differential equations with fuzzy constant coefficients and nth-order fuzzy differential equations in [12, 17], respectively. The aim of this paper is to extend the VIM for solving the linear and nonlinear fuzzy differential equations, whenever these equations possess unique fuzzy solutions. The VIM provides a new approach to solve the fuzzy differential equations without discretization. Numerical examples are presented to illustrate the efficiency of the VIM. The rest of paper is organized as follows. In Sect. 2, we briefly present the basic definitions. In Sect. 3, VIM for solving fuzzy differential equations is introduced. In Sect. 4, the sufficient condition is presented to guarantee the convergence of the method, and an estimation of the maximum absolute error is presented. The proposed method is illustrated by solving three examples in Sect. 5.

2 Preliminaries

The basic concepts of fuzzy numbers are given in [11]. In this section, we review some of them.

Definition 2.1

[11] A fuzzy number U is a pair of functions $({\underline{U}}(r),\,{\overline{U}}(r)),$ for every $0\le r \le 1,$ which satisfies the following requirements:

• (a) ${\underline{U}}(r)$ is a bounded, left continuous, and nondecreasing function over [0, 1].

• (b) ${\overline{U}}(r)$ is a bounded, left continuous, and nonincreasing function over [0, 1].

• (c) ${\underline{U}}(r) \le {\overline{U}}(r),\,0\le r \le 1.$

A crisp number $\alpha$ is simply represented by ${\underline{U}}(r) = {\overline{U}}(r) = \alpha ,\,0\le r \le 1.$ The fuzzy number space can be embedded to the Banach space $B={\overline{C}}[0,\,1]\times {\overline{C}}[0,\,1],$ where the metric is usually defined as

$$\begin{aligned} \Vert (U,\,V)\Vert =\max \left\{ \sup _{0\le r \le 1}|U(r)|,\,\sup _{0\le r \le 1}|V(r)|\right\} , \end{aligned}$$

(1)

for arbitrary $(U,\,V)\in {\overline{C}}[0,\,1]\times {\overline{C}}[0,\,1].$

A first-order fuzzy differential equation is defined by

$$\begin{aligned} x^{\prime }(t)=f(t,\,x), \end{aligned}$$

where x is a fuzzy function of t and $f(t,\,x)$ is a fuzzy function of the crisp variable t and the fuzzy variable $x^{\prime }$ is the fuzzy derivative of x. If an initial value $x(t_{0})=x_{0}$ is given, we obtain a fuzzy Cauchy problem of first order:

$$\begin{aligned} \left\{ \begin{array}{l} x^{\prime }(t)=f(t,\,x),\\ x(t_{0})=x_{0}. \end{array} \right. \end{aligned}$$

(2)

Sufficient conditions for the existence of a unique solution to Eq. (2) are that f is continuous and that a Lipschitz condition

$$\begin{aligned} \Vert f(t,\,x)-f(t,\,y)\Vert \le L \Vert x-y\Vert ,\quad L>0, \end{aligned}$$

(3)

is fulfilled. By Theorem 5.2 in [8] we may replace Eq. (2) by the equivalent system

$$\begin{aligned} \left\{ \begin{array}{ll} {\underline{x}}^{\prime }(t)={\underline{f}}(t,\,x)=F(t,\,{\underline{x}},\,{\overline{x}}),&{} {\underline{x}}(t_{0})={\underline{x}}_0, \\ {\overline{x}}^{\prime }(t)={\overline{f}}(t,\,x)=G(t,\,{\underline{x}},\,{\overline{x}}),&{} {\overline{x}}(t_{0})={\overline{x}}_{0}, \end{array} \right. \end{aligned}$$

(4)

which possesses a unique solution $({\underline{x}},\,{\overline{x}})\in B$ and it is a fuzzy function, i.e., for each t,  the pair $({\underline{x}}(t,\,r),\,{\overline{x}}(t,\,r))$ is a fuzzy number. The parametric form of Eq. (4) is given by

$$\begin{aligned} \left\{ \begin{array}{ll} {\underline{x}}^{\prime }(t,\,r)=F(t,\,{\underline{x}}(t,\,r),\,{\overline{x}}(t,\,r)),&{} {\underline{x}}(t_{0},\,r)={\underline{x}}_0(r),\\ {\overline{x}}^{\prime }(t,\,r)=G(t,\,{\underline{x}}(t,\,r),{\overline{x}}(t,\,r)),&{} {\overline{x}}(t_{0},\,r)={\overline{x}_{0}}(r), \end{array} \right. \end{aligned}$$

(5)

for $0 \le r \le 1.$ A solution of Eq. (5) must solve Eq. (4) as well by using the sup norm, an equality between two fuzzy numbers in B  yields a pointwise equality.

3 Variational Iteration Method (VIM)

In order to solve the system given in Eq. (5), by VIM, we can construct following correction functionals:

$$\begin{aligned} {\underline{x}}_{n+1}(t,\,r)={\underline{x}}_{n}(t,\,r)+\displaystyle \int _{0}^{t}\lambda _{1}(s)\left[ {\underline{x}}_{n}^{\prime }(s,\,r)-F(s,\,{\tilde{\underline{x}}}(s,\,r),\,{\tilde{\overline{x}}}(s,\,r))\right] \mathrm{d}s, \end{aligned}$$

$$\begin{aligned} {\overline{x}}_{n+1}(t,\,r)={\overline{x}}_{n}(t,\,r)+\displaystyle \int _{0}^{t}\lambda _{2}(s)\left[ {\overline{x}}_{n}^{\prime }(s,\,r)-G(s,\,{\tilde{\underline{x}}}(s,\,r),\,{\tilde{\overline{x}}}(s,\,r))\right] \mathrm{d}s, \end{aligned}$$

where $\lambda _{1}(s)$ and $\lambda _{2}(s)$ are general Lagrange multipliers and they can be identified via variational theory. Here, ${\tilde{\underline{x}}}_{n}$ and ${\tilde{\overline{x}}}_{n}$ denote restricted variations, i.e., $\delta {\tilde{\underline{x}}}_{n}=\delta {\tilde{\overline{x}}}_{n}=0.$

Making the above correct functionals stationary, note that

$$\begin{aligned} \delta {\underline{x}}_{n}(0,\,r)=\delta {\overline{x}}_{n}(0,\,r)=0, \end{aligned}$$

$$\begin{aligned} \delta {\underline{x}}_{n+1}(t,\,r)=\delta {\underline{x}}_{n}(t,\,r)+\lambda _{1}(s)\delta {\underline{x}}_{n}(s,\,r)|_{0}^{t}-\displaystyle \int _{0}^{t}\lambda _{1}^{\prime }(s)\delta {\underline{x}}_{n}(s,\,r)\mathrm{d}s=0, \end{aligned}$$

$$\begin{aligned} \delta {\overline{x}}_{n+1}(t,\,r)=\delta {\overline{x}}_{n}(t,\,r)+\lambda _{2}(s)\delta {\overline{x}}_{n}(s,\,r)|_{0}^{t}-\displaystyle \int _{0}^{t}\lambda _{2}^{\prime }(s)\delta {\overline{x}}_{n}(s,\,r)\mathrm{d}s=0, \end{aligned}$$

and the following stationary conditions can be obtained as,

$$\begin{aligned} \lambda _{1}^{\prime }(s)=\lambda _{2}^{\prime }(s)=0, \end{aligned}$$

$$\begin{aligned} 1+\lambda _{1}(s)|_{s=t}=0,\quad 1+\lambda _{2}(s)|_{s=t}=0. \end{aligned}$$

The Lagrange multipliers can be identified as follows:

$$\begin{aligned} \lambda _{1}(s)=\lambda _{2}(s)={-}1, \end{aligned}$$

and it implies the following iteration formula,

$$\begin{aligned} \left\{ \begin{array}{l} {\underline{x}}_{n+1}(t,\,r)={\underline{x}}_{n}(t,\,r)-\displaystyle \int _{0}^{t}[{\underline{x}}_{n}^{\prime }(s,\,r)-F(s,\,{\underline{x}}_{n}(s,\,r),\,{\overline{x}}_{n}(s,\,r))]\mathrm{d}s, \\ {\overline{x}}_{n+1}(t,\,r)={\overline{x}}_{n}(t,\,r)-\displaystyle \int _{0}^{t}[{\overline{x}}_{n}^{\prime }(s,\,r)-G(s,\,{\underline{x}}_{n}(s,\,r),\,{\overline{x}}_{n}(s,\,r))]\mathrm{d}s, \end{array} \right. \end{aligned}$$

(6)

where ${\underline{x}}_{0}(t,\,r)={\underline{x}}(0,\,r)$ and ${\overline{x}}_{0}(t,\,r)={\overline{x}}(0,\,r).$

Now, we define the operator $A=[A_{1},\,A_{2}],$ as [24],

$$\begin{aligned} \left\{ \begin{array}{l} A_{1}[x]={-}\displaystyle \int _{0}^{t}[{\underline{x}}^{\prime }-F(s,\,{\underline{x}},\,{\overline{x}})]\mathrm{d}s, \\ A_{2}[x]={-}\displaystyle \int _{0}^{t}[{\overline{x}}^{\prime }-G(s,\,{\underline{x}},\,{\overline{x}})]\mathrm{d}s, \end{array} \right. \end{aligned}$$

(7)

and define the components $V_{k}=({\underline{V}}_{k},\,{\overline{V}}_{k}),\,k=0,\,1,\,2,\ldots ,$ as

$$\begin{aligned} \left\{ \begin{array}{l} {\underline{V}}_{0}={\underline{x}}_{0},\, {\overline{V}}_{0}={\overline{x}}_{0},\\ {\underline{V}}_{1}=A_{1}[V_{0}],\, {\overline{V}}_{1}=A_{2}[V_{0}],\\ {\underline{V}}_{2}=A_{1}[V_{0}+V_{1}],\\ {\overline{V}}_{2}=A_{2}[V_{0}+V_{1}],\\ \vdots \\ {\underline{V}}_{k+1}=A_{1}[V_{0}+V_{1}+\cdots +V_{k}],\\ {\overline{V}}_{k+1}=A_{2}[V_{0}+V_{1}+\cdots +V_{k}]. \end{array} \right. \end{aligned}$$

(8)

It implies that,

$$\begin{aligned} {\underline{x}}(t,\,r)=\lim _{k\rightarrow \infty }{\underline{x}}_{k}(t,\,r)=\displaystyle \sum _{k=0}^{\infty }{\underline{V}}_{k}(t,\,r), \end{aligned}$$

$$\begin{aligned} {\overline{x}}(t,\,r)=\lim _{k\rightarrow \infty }{\overline{x}}_{k}(t,\,r)=\displaystyle \sum _{k=0}^{\infty }{\overline{V}}_{k}(t,\,r). \end{aligned}$$

Therefore, as a result, the solution of problem (5) can be obtained from (7) and (8), in the series form,

$$\begin{aligned} \left\{ \begin{array}{l} {\underline{x}}(t,\,r)=\displaystyle \sum \nolimits _{k=0}^{\infty }{\underline{V}}_{k}(t,\,r),\\ {\overline{x}}(t,\,r)=\displaystyle \sum \nolimits _{k=0}^{\infty }{\overline{V}}_{k}(t,\,r). \end{array} \right. \end{aligned}$$

(9)

Here, we approximate the solutions (9) by the nth-order truncated series $\displaystyle \sum \nolimits _{k=0}^{n}{\underline{V}}_{k}(t,\,r)$ and $\displaystyle \sum \nolimits _{k=0}^{n}{\overline{V}}_{k}(t,\,r).$

It is easy to see that the above procedure can be easily extended to the nth-order fuzzy differential equation,

$$\begin{aligned} \left\{ \begin{array}{l} x^{(n)}(t)=f(t,\,x,\,x^{\prime },\ldots ,x^{(n-1)}),\\ x^{(i)}(t_{0})=c_{i},\,i=0,\,1,\ldots ,n-1, \end{array} \right. \end{aligned}$$

(10)

where $c_{i},\, 0\le i\le n-1,$ are given fuzzy numbers. Using VIM to solve Eq. (10), we have,

$$\begin{aligned} \lambda _{1}(s)=\lambda _{2}(s)=(-1)^{n}\frac{{(s-t)}^{n-1}}{(n-1)!}, \end{aligned}$$

and the following iteration formula will be derived as,

$$\begin{aligned} \left\{ \begin{array}{l} {\underline{x}}_{k+1}(t,\,r)={\underline{x}}_{k}(t,\,r)+\displaystyle \int _{0}^{t}(-1)^{n}\frac{{(s-t)}^{n-1}}{(n-1)!}[{\underline{x}}_{k}^{(n)}(s,\,r)\\ \qquad \qquad \qquad \qquad -F(s,\,{\underline{x}}_{k}^{(i)}(s,\,r),\,{\overline{x}}_{k}^{(i)}(s,\,r))|_{i=0,\ldots ,n-1}]\mathrm{d}s, \\ {\overline{x}}_{k+1}(t,\,r)={\overline{x}}_{k}(t,\,r)+\displaystyle \int _{0}^{t}(-1)^{n}\frac{{(s-t)}^{n-1}}{(n-1)!}[{\overline{x}}_{k}^{(n)}(s,\,r)\\ \qquad \qquad \qquad \qquad -G(s,\,{\underline{x}}_{k}^{(i)}(s,\,r),\,{\overline{x}}_{k}^{(i)}(s,\,r))|_{i=0,\ldots ,n-1}]\mathrm{d}s, \end{array} \right. \end{aligned}$$

where

$$\begin{aligned} {\underline{x}}_{0}(t,\,r)=\displaystyle \sum _{i=0}^{n-1}\frac{{\underline{c}}_{i}}{i!}t^{i}, \end{aligned}$$

and

$$\begin{aligned} {\overline{x}}_{0}(t,\,r)=\displaystyle \sum _{i=0}^{n-1}\frac{{\overline{c}}_{i}}{i!}t^{i}. \end{aligned}$$

4 Convergence Analysis

In this section, we study the convergence of the VIM when applied to problem (6) [24]. The sufficient conditions for convergence of the method and the error estimate are presented. The main results are proposed in the following theorems.

Theorem 4.1

Let A, defined in (7), be an operator from a Banach space B to B. The series solutions $\displaystyle \sum \nolimits _{k=0}^{\infty }{\underline{V}}_{k}(t,\,r),\,\displaystyle \sum \nolimits _{k=0}^{\infty }{\overline{V}}_{k}(t,\,r)$ defined in (9), converges if there exists $0<\gamma <1$ such that $\Vert V_{k+1}\Vert \le \gamma \Vert V_{k}\Vert$ for $k\in \mathbb {N}\cup \{0\}.$

The proof is straightforward.

Theorem 4.2

If the series solution $x(t,\,r)=\displaystyle \sum \nolimits _{k=0}^{\infty }V_{k}(t,\,r),$ defined in (9), converges then it is an exact solution of the nonlinear problem (5).

Proof

Suppose that the series solution (9) converges. Set $S(t,\,r)=\displaystyle \sum \nolimits _{k=0}^{\infty }V_{k}(t,\,r),$ then we have

$$\begin{aligned} \lim _{j\rightarrow \infty }V_{j}=0, \quad \displaystyle \sum _{j=0}^{n}\left[ V_{j+1}-V_{j}\right] =V_{n+1}-V_{0}, \end{aligned}$$

and so,

$$\begin{aligned} \displaystyle \sum _{j=0}^{\infty }\left[ V_{j+1}-V_{j}\right] =\lim _{j\rightarrow \infty }V_{j}-V_{0}={-}V_{0}. \end{aligned}$$

(11)

By assuming that the infinite summation (11) and derivation can be replaced, we apply the derivative operator to both sides of Eq. (11) and we obtain

$$\begin{aligned} \displaystyle \sum _{j=0}^{\infty }\left[ V_{j+1}-V_{j}\right] ^{\prime }={-}V_{0}^{\prime }=0. \end{aligned}$$

(12)

On the other hand, from definition (8), we have,

$$\begin{aligned} \left[ V_{j+1}-V_{j}\right] ^{\prime }=\left[ A\left[ V_{0}+V_{1}+\cdots +V_{j}\right] -A\left[ V_{0}+V_{1}+\cdots +V_{j-1}\right] \right] ^{\prime }, \end{aligned}$$

when $j\ge 1$ and so, using definition (7), we get,

$$\begin{aligned} \left[ {\underline{V}}_{j+1}-{\underline{V}}_{j}\right] ^{\prime }= & {} {-}\frac{\mathrm{d}}{\mathrm{d}t}\displaystyle \int _{0}^{t}\left[ \left[ {\underline{V}}_{0}+{\underline{V}}_{1}+\cdots +{\underline{V}}_{j}\right] ^{\prime }-\left[ {\underline{V}}_{0}+{\underline{V}}_{1}+\cdots +{\underline{V}}_{j-1}\right] ^{\prime },\right. \end{aligned}$$

$$\begin{aligned}&\left. \quad {-}F\left( z,\,\displaystyle \sum _{i=0}^{j}{\underline{V}}_{i},\,\displaystyle \sum _{i=0}^{j}{\overline{V}}_{i}\right) +F\left( z,\,\displaystyle \sum _{i=0}^{j-1}{\underline{V}}_{i},\,\displaystyle \sum _{i=0}^{j-1}{\overline{V}}_{i}\right) \right] \mathrm{d}z, \end{aligned}$$

$$\begin{aligned} \left[ {\overline{V}}_{j+1}-{\overline{V}}_{j}\right] ^{\prime }= & {} {-}\frac{\mathrm{d}}{\mathrm{d}t}\displaystyle \int _{0}^{t}\left[ \left[ {\overline{V}}_{0}+{\overline{V}}_{1}+\cdots +{\overline{V}}_{j}\right] ^{\prime }-\left[ {\overline{V}}_{0}+{\overline{V}}_{1}+\cdots +{\overline{V}}_{j-1}\right] ^{\prime }\right. \end{aligned}$$

$$\begin{aligned}&\left. \quad {-}G\left( z,\,\displaystyle \sum _{i=0}^{j}{\underline{V}}_{i},\,\displaystyle \sum _{i=0}^{j}{\overline{V}}_{i}\right) +G\left( z,\,\displaystyle \sum _{i=0}^{j-1}{\underline{V}}_{i},\,\displaystyle \sum _{i=0}^{j-1}{\overline{V}}_{i}\right) \right] \mathrm{d}z, \end{aligned}$$

for $j\ge 1.$ It implies that,

$$\begin{aligned} {-}\left[ {\underline{V}}_{j+1}-{\underline{V}}_{j}\right] ^{\prime }=\left[ {\underline{V}}_{j}\right] ^{\prime }-F\left( t,\,\displaystyle \sum _{i=0}^{j}{\underline{V}}_{i},\,\displaystyle \sum _{i=0}^{j}{\overline{V}}_{i}\right) +F\left( t,\,\displaystyle \sum _{i=0}^{j-1}{\underline{V}}_{i},\,\displaystyle \sum _{i=0}^{j-1}{\overline{V}}_{i}\right) , \end{aligned}$$

$$\begin{aligned} {-}\left[ {\overline{V}}_{j+1}-{\overline{V}}_{j}\right] ^{\prime }=\left[ {\overline{V}}_{j}\right] ^{\prime }-G\left( t,\,\displaystyle \sum _{i=0}^{j}{\underline{V}}_{i},\,\displaystyle \sum _{i=0}^{j}{\overline{V}}_{i}\right) +G\left( t,\,\displaystyle \sum _{i=0}^{j-1}{\underline{V}}_{i},\,\displaystyle \sum _{i=0}^{j-1}{\overline{V}}_{i}\right) , \end{aligned}$$

for $j\ge 1.$

Consequently, we have,

$$\begin{aligned}&(-1)\displaystyle \sum _{j=0}^{n}\left[ {\underline{V}}_{j+1}-{\underline{V}}_{j}\right] ^{\prime }=\left[ {\underline{V}}_{0}^{\prime }-F\left( t,\,{\underline{V}}_{0},\,{\overline{V}}_{0}\right) \right] \end{aligned}$$

$$\begin{aligned}&\quad +\left[ {\underline{V}}_{1}^{\prime }-F\left( t,\,{\underline{V}}_{0}+{\underline{V}}_{1},\,{\overline{V}}_{0}+{\overline{V}}_{1}\right) +F\left( t,\,{\underline{V}}_{0},\,{\overline{V}}_{0}\right) \right] +\cdots + \end{aligned}$$

$$\begin{aligned}&\left[ {\underline{V}}_{n}^{\prime }-F\left( t,\,\displaystyle \sum _{i=0}^{n}{\underline{V}}_{i},\,\displaystyle \sum _{i=0}^{n}{\overline{V}}_{i}\right) +F\left( t,\,\displaystyle \sum _{i=0}^{n-1}{\underline{V}}_{i},\,\displaystyle \sum _{i=0}^{n-1}{\overline{V}}_{i}\right) \right] , \end{aligned}$$

and

$$\begin{aligned}&(-1)\displaystyle \sum _{j=0}^{n}\left[ {\overline{V}}_{j+1}-{\overline{V}}_{j}\right] ^{\prime }=\left[ {\overline{V}}_{0}^{\prime }-G\left( t,\,{\underline{V}}_{0},\,{\overline{V}}_{0}\right) \right] \end{aligned}$$

$$\begin{aligned}&\quad +\left[ {\overline{V}}_{1}^{\prime }-G\left( t,\,{\underline{V}}_{0}+{\underline{V}}_{1},\,{\overline{V}}_{0}+{\overline{V}}_{1}\right) +G\left( t,\,{\underline{V}}_{0},\,{\overline{V}}_{0}\right) \right] +\cdots + \end{aligned}$$

$$\begin{aligned}&\left[ {\overline{V}}_{n}^{\prime }-G\left( t,\,\displaystyle \sum _{i=0}^{n}{\underline{V}}_{i},\,\displaystyle \sum _{i=0}^{n}{\overline{V}}_{i}\right) +G\left( t,\, \displaystyle \sum _{i=0}^{n-1}{\underline{V}}_{i},\,\displaystyle \sum _{i=0}^{n-1}{\overline{V}}_{i}\right) \right] . \end{aligned}$$

Thus,

$$\begin{aligned} \left\{ \begin{array}{l} (-1)\displaystyle \sum \nolimits _{j=0}^{\infty }[{\underline{V}}_{j+1}-{\underline{V}}_{j}]^{\prime }=\left[ \displaystyle \sum \nolimits _{j=0}^{\infty }{\underline{V}}_{j}\right] ^{\prime } -F\left( t,\,\displaystyle \sum \nolimits _{j=0}^{\infty }{\underline{V}}_{j},\,\displaystyle \sum \nolimits _{j=0}^{\infty }{\overline{V}}_{j}\right) ,\\ (-1)\displaystyle \sum \nolimits _{j=0}^{\infty }[{\overline{V}}_{j+1}-{\overline{V}}_{j}]^{\prime }=\left[ \displaystyle \sum \nolimits _{j=0}^{\infty }{\overline{V}}_{j}\right] ^{\prime } -G\left( t,\,\displaystyle \sum \nolimits _{j=0}^{\infty }{\underline{V}}_{j},\,\displaystyle \sum \nolimits _{j=0}^{\infty }{\overline{V}}_{j}\right) .\\ \end{array} \right. \end{aligned}$$

(13)

From (12) and (13), we can observe that $S(t,\,r)=\displaystyle \sum \nolimits _{j=0}^{\infty }V_{j}(t,\,r)$ is an exact solution of problem (5). $\square$

Theorem 4.3

Assume that the series solution $\displaystyle \sum \nolimits _{k=0}^{\infty }V_{k}(t,\,r),$ defined in (9), is convergent to the solution $x(t,\,r).$ If the truncated series $\displaystyle \sum \nolimits _{k=0}^{m}V_{k}(t,\,r),$ is used as an approximation to the solution $x(t,\,r)$ of problem (5), then the maximum error, $E_{m}(t,\,r),$ is estimated as,

$$\begin{aligned} E_{m}(t,\,r)\le \frac{\gamma ^{m+1}}{1-\gamma }\Vert V_{0}\Vert . \end{aligned}$$

Proof

From Theorem 4.1, we have

$$\begin{aligned} \left\| S_{n}-S_{m}\right\| \le \frac{\gamma ^{m+1}}{1-\gamma }\left\| V_{0}\right\| , \end{aligned}$$

for $n\ge m.$ Now, as $n\rightarrow \infty$ we have $S_{n}\rightarrow x(t,\,r).$ So,

$$\begin{aligned} \left\| x(t,\,r)-\displaystyle \sum _{k=0}^{m}V_{k}(t,\,r)\right\| \le \frac{\gamma ^{m+1}}{1-\gamma }\left\| V_{0}\right\| . \end{aligned}$$

$\square$

In summary, Theorems 4.1 and 4.2 state that the variational iteration solution of nonlinear problem (5), obtained using the iteration formula (6) or (8), converges to exact solution under the condition that, there exists $0<\gamma <1$ such that $\Vert V_{k+1}\Vert \le \gamma \Vert V_{k}\Vert ,$ for every $k\in \mathbb {N}\cup \{0\}.$ In other words, if we define, for every $i\in \mathbb {N}\cup \{0\},$ the parameters,

$$\begin{aligned} \beta _{i} = \left\{ \begin{array}{ll} \frac{\Vert V_{i+1}\Vert }{\Vert V_{i}\Vert } &{} \mathrm{if}\,\Vert V_{i}\Vert \ne 0,\\ 0 &{} \mathrm{if}\,\Vert V_{i}\Vert = 0, \end{array} \right. \end{aligned}$$

then the series solution $\displaystyle \sum \nolimits _{k=0}^{\infty }V_{k}(t,\,r)$ of problem (5) converges to exact solution, $x(t,\,r),$ when $0\le \beta _{i}<1,$ for $i\in \mathbb {N}\cup \{0\}.$ Moreover, as stated in Theorem 4.3, the maximum absolute truncation error is estimated to be

$$\begin{aligned} \left\| x(t,\,r)-\displaystyle \sum _{k=0}^{m}V_{k}(t,\,r)\right\| \le \frac{\beta ^{m+1}}{1-\beta }\left\| V_{0}(t,\,r)\right\| , \end{aligned}$$

where $\beta =\max \{\beta _{i},\, i=0,\ldots ,m\}.$ The convergence discussion, which is presented in this section, can be easily extended to nth-order fuzzy differential equation (10).

5 Numerical Examples

In this section, some interesting problems are solved by proposed method. It should be noted that by VIM a continuous and smooth approximation of exact solution can be obtained, whereas based on finite difference methods, just a discrete approximate solution can be achieved. Furthermore, it can be seen that the results obtained by proposed method have high accuracy.

Example 5.1

Consider the fuzzy initial value problem [6],

$$\begin{aligned} \left\{ \begin{array}{l} x^{\prime }(t)=x(t),\quad t\ge 0,\\ x(0)=(0.75+0.25r,\,1.125-0.125r), \end{array} \right. \end{aligned}$$

for $r\in (0,\,1].$ The exact solution is given by

$$\begin{aligned} \left\{ \begin{array}{l} {\underline{x}}(t,\,r)={\underline{x}}(0,\,r)e^{t},\\ {\overline{x}}(t,\,r)={\overline{x}}(0,\,r)e^{t}. \end{array} \right. \end{aligned}$$

According to Eq. (5), we have,

$$\begin{aligned} \left\{ \begin{array}{l} {\underline{x}}^{\prime }(t,\,r)={\underline{x}}(t,\,r),\, {\underline{x}}(0,\,r)=0.75+0.25r,\\ {\overline{x}}^{\prime }(t,\,r)={\overline{x}}(t,\,r),\, {\overline{x}}(0,\,r)=1.125-0.125r. \end{array} \right. \end{aligned}$$

Applying VIM, defined in (6), we get,

$$\begin{aligned} \left\{ \begin{array}{l} {\underline{x}}_{n+1}(t,\,r)={\underline{x}}_{n}(t,\,r)-\displaystyle \int _{0}^{t}[{\underline{x}}_{n}^{\prime }(s,\,r)-{\underline{x}}_{n}(s,\,r)]\mathrm{d}s,\\ {\overline{x}}_{n+1}(t,\,r)={\overline{x}}_{n}(t,\,r)-\displaystyle \int _{0}^{t}[{\overline{x}}_{n}^{\prime }(s,\,r)-{\overline{x}}_{n}(s,\,r)]\mathrm{d}s, \end{array} \right. \end{aligned}$$

where ${\underline{x}}_{0}(t,\,r)=0.75+0.25r$ and ${\overline{x}}_{0}(t,\,r)=1.125-0.125r.$

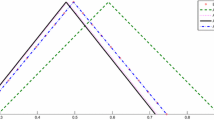
Approximate solution $({\underline{x}}_{40}(t,\,r),\,{\overline{x}}_{40}(t,\,r)),$ at $t=1,$ and the obtained absolute errors, $|{\underline{x}}(t,\,r)-{\underline{x}}_{40}(t,\,r)|$ and $|{\overline{x}}(t,\,r)-{\overline{x}}_{40}(t,\,r)|,$ for $(t,\,r)\in [0,\,1]\times [0,\,1].$ are given in Figs. 1, 2, and 3, respectively.

Fig. 1

Approximate solutions ${\underline{x}}_{40}(1,\,r)$ and ${\overline{x}}_{40}(1,\,r)$ of VIM in Example 5.1

Fig. 2

Absolute error $|{\underline{x}}(t,\,r)-{\underline{x}}_{40}(t,\,r)|,$ which is obtained about $4\times 10^{-41},$ for Example 5.1

Fig. 3

Absolute error $|{\overline{x}}(t,\,r)-{\overline{x}}_{40}(t,\,r)|,$ which is obtained about $4\times 10^{-41},$ for Example 5.1

Example 5.2

Consider the fuzzy initial value problem [6],

$$\left\{ \begin{array}{l} x^{\prime }(t)=C x(t),\,0\le t\le 1,\\ x(0)=(8+0.5r,\,9-0.5r), \end{array} \right.$$

where $C=(1+r,\,3-r)$ and the exact solution is

$$\begin{aligned} \left\{ \begin{array}{l} {\underline{x}}(t,\,r)=(8+0.5r)e^{(1+r)t},\\ {\overline{x}}(t,\,r)=(9-0.5r)e^{(3-r)t}, \end{array} \right. \end{aligned}$$

for $0\le r\le 1.$

Using the VIM, we obtain,

$$\begin{aligned} \left\{ \begin{array}{l} {\underline{x}}_{n+1}(t,\,r)={\underline{x}}_{n}(t,\,r)-\displaystyle \int _{0}^{t}[{\underline{x}}_{n}^{\prime }(s,\,r)-(1+r){\underline{x}}_{n}(s,\,r)]\mathrm{d}s,\\ {\overline{x}}_{n+1}(t,\,r)={\overline{x}}_{n}(t,\,r)-\displaystyle \int _{0}^{t}[{\overline{x}}_{n}^{\prime }(s,\,r)-(3-r){\overline{x}}_{n}(s,\,r)]\mathrm{d}s, \end{array} \right. \end{aligned}$$

where ${\underline{x}}_{0}(t,\,r)=8+0.5r$ and ${\overline{x}}_{0}(t,\,r)=9-0.5r.$

Approximate solution $({\underline{x}}_{40}(t,\,r),\,{\overline{x}}_{40}(t,\,r)),$ at $t=1$ and the obtained absolute errors $|{\underline{x}}(t,\,r)-{\underline{x}}_{40}(t,\,r)|$ and $|{\overline{x}}(t,\,r)-{\overline{x}}_{40}(t,\,r)|,$ for $(t,\,r)\in [0,\,1]\times [0,\,1],$ are plotted in Figs. 4, 5, and 6, respectively.

Fig. 4

Approximate solutions ${\underline{x}}_{40}(1,\,r)$ and ${\overline{x}}_{40}(1,\,r)$ of VIM in Example 5.2

Fig. 5

Absolute error $|{\underline{x}}(t,\,r)-{\underline{x}}_{40}(t,\,r)|,$ which is obtained about $6\times 10^{-37},$ for Example 5.2

Fig. 6

Absolute error $|{\overline{x}}(t,\,r)-{\overline{x}}_{40}(t,\,r)|,$ which is obtained about $1.1\times 10^{-29},$ for Example 5.2

Example 5.3

Consider the following fuzzy differential equation[7],

$$\begin{aligned} \left\{ \begin{array}{l} x^{\prime \prime \prime }(t)=2x^{\prime \prime }(t)+3x^{\prime }(t),\\ x(0)=(3+r,\,5-r),\\ x^{\prime }(0)=(-1-r,\,{-}3+r),\\ x^{\prime \prime }(0)=(8+r,\,10-r), \end{array} \right. \end{aligned}$$

where $0\le r,\,t \le 1.$ The exact solution is

$$\begin{aligned} x(t,\,r)=\left( \frac{-1}{3}+\frac{7}{12}e^{3t}+\left( \frac{11}{4}+r\right) e^{-t},\,\frac{-1}{3}+\frac{7}{12}e^{3t}+\left( \frac{19}{4}-r\right) e^{-t}\right) ,\quad 0\le r \le 1. \end{aligned}$$

Using the VIM, we obtain,

$$\begin{aligned} \left\{ \begin{array}{l} {\underline{x}}_{n+1}(t,\,r)={\underline{x}}_{n}(t,\,r)-\frac{1}{2}\displaystyle \int _{0}^{t}(s-t)^{2}[{\underline{x}}_{n}^{\prime \prime \prime }-2{\underline{x}}_{n}^{\prime \prime }-3{\underline{x}}_{n}^{\prime }](s,\,r)\mathrm{d}s,\\ {\overline{x}}_{n+1}(t,\,r)={\overline{x}}_{n}(t,\,r)-\frac{1}{2}\displaystyle \int _{0}^{t}(s-t)^{2}[{\overline{x}}_{n}^{\prime \prime \prime }-2{\overline{x}}_{n}^{\prime \prime }-3{\overline{x}}_{n}^{\prime }](s,\,r)\mathrm{d}s, \end{array} \right. \end{aligned}$$

where ${\underline{x}}_{0}(t,\,r)=3+r-(1+r)t+(8+r)\frac{t^{2}}{2}$ and ${\overline{x}}_{0}(t,\,r)=5-r+(r-3)t+(10-r)\frac{t^{2}}{2}.$ The results are shown in Figs. 7, 8, and 9, respectively.

Fig. 7

Approximate solutions ${\underline{x}}_{20}(1,\,r)$ and ${\overline{x}}_{20}(1,\,r)$ of VIM in Example 5.3

Fig. 8

Absolute error $|{\underline{x}}(t,\,r)-{\underline{x}}_{20}(t,\,r)|,$ which is obtained about $2\times 10^{-15},$ for Example 5.3

Fig. 9

Absolute error $|{\overline{x}}(t,\,r)-{\overline{x}}_{20}(t,\,r)|,$ which is obtained about $2\times 10^{-15},$ for Example 5.3

Example 5.4

Consider the nonlinear fuzzy initial value problem [3],

$$\begin{aligned} \left\{ \begin{array}{l} x^{\prime }(t)=0.5x(t)(1-x(t)),\, 0\le t\le 1,\\ x(0)=(0.4+0.2r,\,0.9-0.3r), \end{array} \right. \end{aligned}$$

with the exact solution,

$$\begin{aligned} x(t,\,r)=\left( \frac{{\underline{x}}_{0}}{{\underline{x}}_{0}-({\underline{x}}_{0}-1)e^{-0.5t}},\, \frac{{\overline{x}}_{0}}{{\overline{x}}_{0}-({\overline{x}}_{0}-1)e^{-0.5t}}\right) , \end{aligned}$$

for $0\le r\le 1.$

According to VIM, we have,

$$\begin{aligned} \left\{ \begin{array}{l} {\underline{x}}_{n+1}(t,\,r)={\underline{x}}_{n}(t,\,r)-\displaystyle \int _{0}^{t}[{\underline{x}}_{n}^{\prime }(s,\,r)+0.5{\underline{x}}_{n}(s,\,r)({\underline{x}}_{n}(s,\,r)-1)]\mathrm{d}s,\\ {\overline{x}}_{n+1}(t,\,r)={\overline{x}}_{n}(t,\,r)-\displaystyle \int _{0}^{t}[{\overline{x}}_{n}^{\prime }(s,\,r)+0.5{\overline{x}}_{n}(s,\,r)({\overline{x}}_{n}(s,\,r)-1)]\mathrm{d}s, \end{array} \right. \end{aligned}$$

where ${\underline{x}}_{0}(t,\,r)=0.2+0.2r$ and ${\overline{x}}_{0}(t,\,r)=0.9-0.3r.$

Table 1 shows the comparison between the exact solution and approximate solution $({\underline{x}}_{6},\,{\overline{x}}_{6}),$ at $t=1.$ Also, Fig. 10 shows the approximate solution by VIM, at $t=1.$

Table 1 Exact and approximate solutions of VIM, with $N=6,$ in Example 5.4

Fig. 10

Approximate solutions, ${\underline{x}}_{6}(1,\,r)$ and ${\overline{x}}_{6}(1,\,r)$ of VIM in Example 5.4

6 Conclusion

In this paper, an efficient iterative method has been presented to solve fuzzy differential equations. The theorems of convergence and error estimation have been discussed. Furthermore, several numerical examples of the proposed method have been presented, and the comparisons with the exact solutions confirm that the method is capable of generating accurate solutions. The proposed method can be easily implemented for a system of fuzzy differential equations. To solve boundary value, fuzzy problems can be studied using VIM in future work.