Solving fuzzy fractional differential equations by a generalized differential transform method

Abstract

In this paper, a computational method for solving a class of fuzzy fractional differential equations is presented. The proposed method is based on a generalized differential transform method in the sense of the Caputo fractional derivative. The advantage of the differential transform method is that the derivatives are calculated in an iterative way instead of evaluating symbolically. Furthermore, a convergence theorem is derived with a different perspective. Some numerical examples are also given to illustrate the accuracy and efficiency of the method.

1 Introduction

The interest in the study of differential equations of fractional order lies in the fact that fractional derivatives provide an excellent tool for the description of memory and hereditary properties of various materials and processes such as control [4], signal processing [17], viscoelastic [11], electrolyte-electrolyte polarization [9] and etc. More precisely, when one intends to analyze a real world phenomenon, it is also necessary to deal with uncertain factors. In this case, the theory of fuzzy sets is one of the best non-statistical or non-probabilistic approach, which leads us to investigate fuzzy fractional models.

So far, a few papers have been published about the topic of fuzzy fractional differential equations for instance, authors of [1] have presented a method based on tau method with Jacobi polynomials for the solution of fuzzy linear fractional differential equations of order $0\le \alpha \le 1$. The existence and uniqueness of solutions of fuzzy fractional differential equations (FFDEs) under Caputo’s H-differentiability have been studied in [16] by Salahshore et al. Also, Salahshour have solved fuzzy fractional differential equations by using fuzzy Laplace transforms in the sense of the Riemann-Liouville H-derivative. Recently Mazandarani and Vahidian have used the modified fractional Euler method to solve fuzzy fractional initial value problems in [12]. Also, a variational iteration method have been used for approximating the solutions of fractional differential equations with a fuzzy initial condition by Khodadadi and Çelik in [10].

In this study we intend to apply the generalized differential method for solving the fuzzy fractional differential equations (FFDE). The differential transform method was first introduced by Zhou [18]. Then it was applied by many researchers for the ordinary and partial differential equations, the integro-differential equations and several special equations. Also, Arikoglu and Ozkol extended it to ordinary differential equations of fractional order [3]. Later, a new technique has been presented and called generalized differential transform method by Odibat [13].

The present paper is organized as follows: in Sect. 2, some preliminary concepts of fuzzy calculus are introduced and are reviewed. In Sect. 3, as well as introducing the fractional integral and derivative, the generalized Taylors series and give its convergent theorems are stated. In Sect. 4, definitions of the fuzzy fractional integral and derivative are given. In the rest of the paper, first the generalized differential transform method is described, then the fuzzy fractional differential equations are proposed. Finally, some different numerical examples are presented to confirm the efficiency and simplicity of the method.

2 Basic concepts

In this section we give some necessary definitions and theorems of fuzzy theory which are used in the paper.

We denote the set of all real numbers by $\mathbb {R}$ and the set of all fuzzy numbers on $\mathbb {R}$ is indicated by $\mathbb {R}_{\mathscr {F}}$. A fuzzy number is a mapping $u:\mathbb {R}\rightarrow [0,1]$ with the following properties [6]:

• (i) u is upper semi-continuous,

• (ii) u is fuzzy convex, i.e., $\forall x,y\in \mathbb {R}$, $\lambda \in [0,1]$, $u(\lambda x+(1-\lambda )y)\ge \min \{u(x),u(y)\}$,

• (iii) u is normal, i.e., $\exists ~ x_0 \in \mathbb {R}$ for which $u(x_0)=1$,

• (iv) $supp~u=\{x\in \mathbb {R}|u(x)>0\}$ is the support of the u, and its closure cl(supp u) is compact.

The r-cut set of a fuzzy number $u(x)\in \mathbb {R}_\mathscr {F}$ denoted by $[u(x)]^r$, is defined as

$$\begin{aligned}{}[u(x)]^r=\left\{ \begin{array}{ll} \{x\in \mathbb {R}| u(x)\ge r\}&{}\quad 0<r\le 1\\ cl(supp~u(x)) &{}\quad r=0. \end{array}\right. \end{aligned}$$

An equivalent parametric definition for fuzzy numbers is as follows:

Definition 1

[2] A fuzzy number u in parametric forms is a pair $(\underline{u}(r),\overline{u}(r))$ of functions $\underline{u}(r),\overline{u}(r)$, $0\le r\le 1$, which satisfy the following requirements:

• (i) $\underline{u}(r)$ is a bounded non-decreasing left continuous function in (0, 1], and right continuous at 0,

• (ii) $\overline{u}(r)$ is a bounded non-increasing left continuous function in (0, 1], and right continuous at 0,

• (iii) $\underline{u}(r)\le \overline{u}(r)$, $0\le r\le 1$.

It is well known that the r-cut set of fuzzy numbers is a closed and bounded interval $[\underline{u}(x;r),\overline{u}(x;r)]$, where $\underline{u}(x;r)$ denotes the left-hand endpoint of $[u(x)]^r$ and $\overline{u}(x;r)$ the right-hand endpoint $[u(x)]^r$.

A triangular fuzzy number denoted by $u=(a,b,c)$ such that $a\le b\le c$, $a,b,c\in \mathbb {R}$ where $\underline{u}(r)=a+r(b-a)$ , $\overline{u}(r)=c-r(c-b)$ are the endpoint of the r-cut set, for all $0\le r \le 1$.

Addition and subtractions and scalar multiplication are defined as [6]:

• $[u+v]^r=[\underline{u}(r)+\underline{v}(r),\overline{u}(r)+\overline{v}(r)]$

• $[u-v]^r=[\underline{u}(r)-\overline{v}(r),\overline{u}(r)-\underline{v}(r)]$

• $[ku]^r=\left\{ \begin{array}{l} \,[k\underline{u}(r),k\overline{u}(r)]\quad k\ge 0 \\ \,[k\overline{u}(r),k\underline{u}(r)] \quad k<0. \end{array} \right.$

Definition 2

[6] Let $u,v\in \mathbb {R}_\mathscr {F}$. If there exists $w\in \mathbb {R}_\mathscr {F}$ such that $u=v+w$, then w is called the Hukuhara difference (H-difference) of u, v, and it is denoted by $u\ominus v$. Note that $u\ominus v \ne u+(-1)v$.

The hausdorff distance between fuzzy numbers given by $D:\mathbb {R}_\mathscr {F} \times \mathbb {R}_\mathscr {F}\rightarrow \mathbb {R}^+ \cup \{0\}$,

$$\begin{aligned} D(u,v)=\sup _{r\in [0,1]}\max \{|\underline{u}(r)-\underline{v}(r)|,|\overline{u}(r)-\overline{v}(r)|\}, \end{aligned}$$

where r-cut sets of u and v are $[u]^r=(\underline{u}(r),\overline{u}(r))$ and $[v]^r=(\underline{v}(r),\overline{v}(r))$ respectively.

It is easy to see that D is a metric in $\mathbb {R}_\mathscr {F}$ and $(D,\mathbb {R}_\mathscr {F})$ is a complete metric space [5].

Note that the r-cut of fuzzy-valued functions $f:A\subseteq \mathbb {R}\rightarrow \mathbb {R}_\mathscr {F}$, can be expressed by $[f(x)]^r=[\underline{f}(x;r),\overline{f}(x;r)]$, $x\in A\subseteq \mathbb {R}$ and $0\le r \le 1$.

Theorem 1

[15] Let f be a fuzzy function on $[a,\infty )$ represented by r-cut set $(\underline{f}(x;r),\overline{f}(x;r))$. For any fixed $r\in [0, 1]$, assume $\underline{f}(x;r)$ and $\overline{f}(x;r)$ are Riemann-integrable on [a, b] for every $b\ge a$, and assume there are two positive functions $\underline{M}(r)$ and $\overline{M}(r)$ such that $\int _{a}^{b}|\underline{f}(x;r)|dx\le \underline{M}(r)$ and $\int _{a}^{b}|\overline{f}(x;r)|dx\le \overline{M}(r)$ for every $b\ge a$. Then f(x) is fuzzy improper Riemann-integrable on $[a,\infty )$ and the fuzzy improper Riemann-integral is a fuzzy number. Furthermore, we have

$$\begin{aligned} \int _{a}^{\infty }f(x;r)dx=\left[ \int _{a}^{\infty }\underline{f}(x;r)dx,\int _{a}^{\infty }\overline{f}(x;r)dx\right] . \end{aligned}$$

We denote $C^{\mathbb {F}}[a,b]$ as the space of all continuous fuzzy-valued functions on [a, b]. Also, we denote the space of all Lebesque integrable fuzzy valued functions on the bounded interval $[a,b]\subset \mathbb {R}$ by $L^{\mathbb {F}}[a,b]$.

Definition 3

[5] Let $f:(a,b)\rightarrow \mathbb {R}_\mathscr {F}$ be a fuzzy function and $x_0\in (a,b)$, we say that f is strongly generalized differential at $x_0$, if there exists an element $f'(x_0)\in \mathbb {R}_\mathscr {F}$, such that

• (i) for all $h>0$ sufficiently small, $\exists f(x_0 +h)\ominus f(x_0),f(x_0)\ominus f(x_0-h)$ and the limits (in the metric D)

  $$\begin{aligned} \lim _{h\rightarrow 0}\frac{f (x_0+h)\ominus f (x_0)}{h}=\lim _{h\rightarrow 0}\frac{f(x_0)\ominus f(x_0-h)}{h}=f'(x_0), \end{aligned}$$

  or

• (ii) for all $h>0$ sufficiently small, $\exists f(x_0)\ominus f(x_0+h)$, $f(x_0-h)\ominus f(x_0)$ and the limits

  $$\begin{aligned} \lim _{h\rightarrow 0}\frac{f(x_0)\ominus f(x_0+h)}{(-h)}=\lim _{h\rightarrow 0} \frac{f(x_0-h)\ominus f(x_0)}{(-h)}=f'(x_0), \end{aligned}$$

  or

• (iii) for all $h>0$ sufficiently small, $\exists f(x_0+h)\ominus f(x_0)$, $f(x_0-h)\ominus f(x_0)$ and the limits

  $$\begin{aligned} \lim _{h\rightarrow 0}\frac{f(x_0+h)\ominus f(x_0)}{h}=\lim _{h\rightarrow 0}\frac{f(x_0-h)\ominus f(x_0)}{(-h)}= f'(x_0), \end{aligned}$$

  or

• (iv) for all $h>0$ sufficiently small, $\exists f(x_0)\ominus f (x_0+h)$, $f(x_0)\ominus f (x_0-h)$ and the limits

  $$\begin{aligned} \lim _{h\rightarrow 0}\frac{f(x_0)\ominus f(x_0+h)}{(-h)}=\lim _{h\rightarrow 0}\frac{f(x_0)\ominus f (x_0-h)}{h}=f'(x_0). \end{aligned}$$

3 Generalized Taylor’s and convergence

As we know, the fractional derivatives have several different kinds of definitions, among which the Riemann-Liouville fractional derivative and the Caputo fractional derivative are two of the most important ones in applications. In the both definitions from the Riemann-Liouville fractional integration and the derivatives of integer order are used. The difference between the two definitions is in the order of evaluation. The Riemann-Liouville fractional integration of order $\alpha$ is defined as

$$\begin{aligned} J^\alpha _{x_0} f(x)=\dfrac{1}{\Gamma (\alpha )} \int _{x_0}^x (x-t)^{\alpha -1} f(t)dt, \quad \alpha >0,~~~~ x>0 \end{aligned}$$

(1)

which has the following properties [13]:

$$\begin{aligned} (J^{\alpha }_{x_0}J^{\beta }_{x_0}f)(x)=(J^{\beta }_{x_0}J^{\alpha }_{x_0}f)(x)=(J^{\alpha +\beta }_{x_0}f)(x)\quad \quad \alpha , \beta >0 \end{aligned}$$

(2)

$$\begin{aligned} J^{\alpha }_{x_0}x^{\gamma }=\frac{\Gamma (\gamma +1)}{\Gamma (\gamma +\alpha +1)}x^{\gamma +\alpha }, \quad \quad \gamma >-1. \end{aligned}$$

(3)

The next two equations define the Riemann-Liouville and Caputo fractional derivative of order $\alpha$, in the case crisp, respectively,

$$\begin{aligned} \begin{array}{l} {^{\mathscr {RL}}}D^\alpha _{x_0}f(x)=\dfrac{d^m}{dx^m}[J^{m-\alpha }_{x_0}f(x)],\\ {^{\mathscr {C}}}D^\alpha _{x_0}f(x)=J^{m-\alpha }_{x_0}[\dfrac{d^m}{dx^m} f(x)], \end{array} \end{aligned}$$

(4)

where $m-1<\alpha \le m$ and $m\in \mathbb {N}$. The Riemann-Liouville fractional derivative first computes a fractional integral followed by an ordinary derivative to achieve the desired order of fractional derivative. The Caputo fractional derivative is computed in the reverse order. The Caputo concept satisfies in the following lemma.

Lemma 1

[13] If $m-1<\alpha < m$, $m\in \mathbb {N}$, then $^\mathscr {C}D^\alpha _{x_0} J^\alpha _{x_0} f(x)=f(x)$, and

$$\begin{aligned} (J^{\alpha }_{x_0}{^\mathscr {C}}D^{\alpha }_{x_0}f)(x)=J^m_{x_0}D^mf(x)=f(x)-\sum _{k=0}^{m-1} f^{(k)}(0)\frac{x^k}{k!},~~~x>0. \end{aligned}$$

(5)

For the Caputo derivative, we have [7]:

$$\begin{aligned} ^{\mathscr {C}}D^\alpha _{x_0} k=0 \quad \quad k~ \text {is a constant}, \end{aligned}$$

$$\begin{aligned} ^{\mathscr {C}}D^\alpha _{x_0} x^\beta = \left\{ \begin{array}{ll} 0,&{}\quad \text {for}~\beta \in \mathbb {N}_0 ~ \text {and}~ \beta <\lceil \alpha \rceil ;\\ \frac{\Gamma (\beta +1)}{\Gamma (\beta -\alpha +1)}x^{\beta -\alpha }, &{}\quad \text {for} ~\beta \in \mathbb {R} ~\text {and}~ \beta \ge \lfloor \alpha \rfloor \end{array}\right. \end{aligned}$$

(6)

where $\lceil \alpha \rceil$ is the ceiling function giving the smallest integer greater than or equal to $\alpha$, and $\lfloor \alpha \rfloor$ is the floor function giving the biggest integer smaller than or equal to $\alpha$.

Theorem 2

[13] Suppose that $(^{\mathscr {C}}D^{\alpha }_a)^n f(x),(^{\mathscr {C}}D^{\alpha }_a)^{n+1}f(x)\in (a,b]$, for $0<\alpha \le 1$, then we have

$$\begin{aligned} (J^{n\alpha }_a(^{\mathscr {C}}D^\alpha _a)^n f)(x)-(J^{(n+1)\alpha }_a(^{\mathscr {C}}D^\alpha _a)^{n+1}f)(x)=\dfrac{(x-\alpha )^{n\alpha }}{\Gamma (n\alpha +1)}((^{\mathscr {C}}D^\alpha _a)^n f)(a^+), \end{aligned}$$

(7)

where $(^{\mathscr {C}}D^\alpha _a)^n=~^{\mathscr {C}}D^\alpha _a.~^{\mathscr {C}}D^\alpha _a...^{\mathscr {C}}D^\alpha _a.$    (n-times)

Theorem 3

Assume that $0<\alpha <1$ and f has continuous Caputo fractional derivative of order $(n+1)\alpha$ in some open interval I containing a, and define $E_n(x)$ for any x in I by the equation

$$\begin{aligned} f(x)=\sum _{i=0}^{n} \frac{(^{\mathscr {C}}D^\alpha _a)^i f(a^+)}{\Gamma (i\alpha +1)}(x-a)^{i\alpha }+E_n(x), \end{aligned}$$

(8)

where $0<\alpha <1$. Then $E_n(x)$ is also given by the integral

$$\begin{aligned} E_n(x)=J^{(1+n)\alpha }(^{\mathscr {C}}D^\alpha _a)^{(n+1)}f(x)). \end{aligned}$$

(9)

Proof

The proof is by induction on n. For $n=1$ we have

$$\begin{aligned} E_n(x)&=f(x)-f(a^+)- \frac{(^{\mathscr {C}}D^\alpha _a)f(a^+)}{\Gamma (\alpha +1)}(x-a)^\alpha \nonumber \\&=f(x)-f(a^+)-J^\alpha _a(^{\mathscr {C}}D^\alpha _a f(a^+)), \end{aligned}$$

(10)

according to Theorem 2 $J^\alpha _a(^{\mathscr {C}}D^\alpha _a f(a^+))=(J^\alpha _a(^{\mathscr {C}}D^\alpha _a f))(x)-(J^{2\alpha }_a(^{\mathscr {C}}D^{2\alpha }_a f))(x)$,

$$\begin{aligned} E_n(x)&=f(x)-f(a^+)-(J^\alpha _a(^{\mathscr {C}}D^\alpha _a)f)(x)+(J^{2\alpha }_a(^{\mathscr {C}}D^{2\alpha }_a f)(x) \nonumber \\ {}&=(J^{2\alpha }_a(^{\mathscr {C}}D^{2\alpha }_a f)(x), \end{aligned}$$

(11)

since $(J^\alpha _a(^{\mathscr {C}}D^\alpha _a)f)(x)=f(x)-f(a^+)$. Now we assume (9) is true for n and prove it for $n+1$. From (8) we have

$$\begin{aligned} E_{n+1}(x)=E_n(x)-\frac{(^{\mathscr {C}}D^\alpha _a)^{n+1}f(a^+)}{\Gamma ((n+1)\alpha +1)}(x-a)^{(n+1)\alpha }, \end{aligned}$$

(12)

since $\dfrac{(^{\mathscr {C}}D^\alpha _a)^{n+1}f(a^+)}{\Gamma ((n+1)\alpha +1)}(n-a)^{(n+1)\alpha }=J^{(n+1)\alpha }_a(^{\mathscr {C}}D^\alpha _a)^{(n+1)}f(x) -J^{(n+2)\alpha }_a(^{\mathscr {C}}D^\alpha _a)^{(n+2)}f(x),$

$$\begin{aligned} E_{n+1}(x)&=J^{(n+1)\alpha }_a(^{\mathscr {C}}D^\alpha _a)^{(n+1)}f(x) -J^{(n+1)\alpha }_a(^{\mathscr {C}}D^\alpha _a)^{(n+1)}f(x) + J^{(n+2)\alpha }_a(^{\mathscr {C}}D^\alpha _a)^{(n+2)} f(x) \nonumber \\&=J^{(n+2)\alpha }_a(^{\mathscr {C}}D^\alpha _a)^{(n+2)}f(x), \end{aligned}$$

(13)

and the proof is complete. $\square$

Remark 1

The change of variable $t=x+(a-x)u$ transforms the integral in (9) to the form

$$\begin{aligned} E_n(x)=\dfrac{(x-a)^{(n+1)\alpha }}{\Gamma ((n+1)\alpha )+1}\int _{0}^{1}u^{(n+1)\alpha }(^{\mathscr {C}}D^\alpha _a)^{n+1}f(x-xu)du, \end{aligned}$$

(14)

for all $x\in [0,\lambda ]$.

Theorem 4

Assume that $0<\alpha <1$ and f and all its fractional derivatives of multiple of $\alpha$ are nonnegative on a compact interval $[a,a+\lambda ]$, $\lambda >0$. Then, if $a\le x \le a+\lambda$ the Taylor’s series

$$\begin{aligned} \sum _{i=0}^\infty \dfrac{(^{\mathscr {C}}D^\alpha _a)^i f(a^+)}{\Gamma ((n+1)\alpha +1)}(x-a)^{i\alpha }, \end{aligned}$$

(15)

converges to f.

Proof

Without loss of generality we can assume that $a=0$. This result is trivial for $x=0$ so we assume $0<x<\lambda$. We use Taylor’s formula with reminder and write

$$\begin{aligned} f(x)=\sum _{k=0}^n \dfrac{(^{\mathscr {C}}D^\alpha _0)^if(0^+)}{\Gamma (i\alpha +1)} x^{i\alpha }+E_n(x). \end{aligned}$$

(16)

We will prove that the error term satisfies the inequalities

$$\begin{aligned} 0\le E_n(x)\le \left( \dfrac{x}{\lambda }\right) ^{(n+1)\alpha }f(\lambda ). \end{aligned}$$

(17)

This implies that $E_n(x)\rightarrow 0$ as $n\rightarrow \infty$ since $(x/\lambda )^{n+1}\rightarrow 0$ if $0<x<\lambda$. To prove (17) we use (14) with $a=0$ and find

$$\begin{aligned} E_n(x)=J^{(n+1)\alpha }_0(^{\mathscr {C}}D^\alpha _0)^{n+1}f(x)= \dfrac{x^{(n+1)\alpha }}{\Gamma ((n+1)\alpha +1)}\int _0^1 u^{(n+1)\alpha } ({}^{\mathscr {C}}D^\alpha _0)^{n+1}f(x-xu)du, \end{aligned}$$

(18)

for all $x\in [0,\lambda ]$. If $x\ne 0$, let

$$\begin{aligned} F_n(x)=\dfrac{E_n(x)}{x^{(n+1)\alpha }}=\dfrac{1}{\Gamma ((n+1)\alpha +1)}\int _0^1 u^{(n+1)\alpha }(^{\mathscr {C}}D^\alpha _0)^{n+1}f(x-xu)du. \end{aligned}$$

(19)

The function $({}^{\mathscr {C}}D^\alpha _0)^{n+1}f$ is monotonic increasing on $[0,\lambda ]$ since its fractional derivative (i.e. ${}^{\mathscr {C}}(D^\alpha _0)^{n+1}f$) is nonnegative. Therefore we have

$$\begin{aligned} (^{\mathscr {C}}D^{\alpha }_0)^{n+1}f(x-xu)=(^{\mathscr {C}}D^{\alpha }_0)^{n+1}f(x(1-u))\le (^{\mathscr {C}}D^{\alpha }_0)^{n+1}f(\lambda (1-u)), ~~~0\le u\le 1, \end{aligned}$$

(20)

and this implies $F_n(x)\le F_n(\lambda )$ if $0<x\le \lambda$. In other words, $E_n(x)/x^{(n+1)\alpha }\le E_n(x)/{\lambda }^{(n+1)\alpha }$, or

$$\begin{aligned} E_n(x)\le \left( \frac{x}{\lambda }\right) ^{(n+1)\alpha } E_n(\lambda ). \end{aligned}$$

(21)

putting $x=\lambda$ in (16), we see that $E_n(\lambda )\le f(\lambda )$ since each term in the sum is nonnegative. Using this in (21), we obtain (17) which, in turn, completes the proof. $\square$

According to Theorem 4, a few functions satisfy the conditions of the theorem. Now based on the generalized Taylor in [13] we state the conditions which the generalized Taylor series generated by f converges to f.

Theorem 5

[13] Suppose that $^\mathscr {C}D^{k\alpha }_0f(x)\in C(0,a]$ for $k=0,1,...,n+1$, where $0<\alpha \le 1$. Then we have

$$\begin{aligned} f(x)=\sum _{i=0}^{n}\dfrac{x^{i\alpha }}{\Gamma (i\alpha +1)}~ (^{\mathscr {C}}D^{i\alpha }_0 f)(0^+)+\dfrac{(^{\mathscr {C}}D^{(n+1)\alpha }_0f)(\xi )}{\Gamma ((n+1)\alpha +1)}(x)^{(n+1)\alpha }, \end{aligned}$$

(22)

with $0\le \xi \le x, \forall x\in (0,a]$.

Hence a necessary and sufficient condition for generalized Taylor’s series to converge to f(x) is that for each $x\in (0,a]$

$$\begin{aligned} \lim _{n\rightarrow \infty } \dfrac{(^{\mathscr {C}}D^{(n+1)\alpha }_0f)(\xi )}{\Gamma ((n+1)\alpha +1)}x^{(n+1)\alpha }=0. \end{aligned}$$

(23)

Theorem 6

Assume that $^\mathscr {C}D^{k\alpha }_0 f(x)\in C(0,a]$ and there is a neighborhood $B(0^+)=(0,\gamma )$ and a constant M such that $|^\mathscr {C}D^{n\alpha }f(x)|\le M^n$ for every x in $B(0^+)\cap (0,a]$ and any $n=1,2,...$. Then for each x in $B(0^+)\cap (0,a]$, we have

$$\begin{aligned} f(x)=\sum _{i=0}^{\infty }\dfrac{(^{\mathscr {C}}D^{i\alpha }_0f)(0^+)}{\Gamma (i\alpha +1)}~ (x)^{i\alpha }. \end{aligned}$$

(24)

Proof

We have

$$\begin{aligned} |\dfrac{(^{\mathscr {C}}D^{\alpha n}_0f)(\xi )}{\Gamma (n \alpha +1)}(x)^{n\alpha }|\le \dfrac{M^n |x^{n\alpha }|}{|\Gamma (n \alpha +1)|}, \end{aligned}$$

(25)

since $\sum _{n=0}^{\infty }\dfrac{x^{n\alpha }}{\Gamma (n\alpha +1)}=E_{\alpha ,1}(x^\alpha )$ is absolutely convergence where $E_{\alpha ,\beta }(t)=\sum _{k=0}^{\infty }\frac{t^{k}}{\Gamma (k\alpha +\beta )}$, $\alpha ,\beta >0, \alpha ,\beta \in \mathbb {R}$ is mittag function. Hence, $\lim _{n\rightarrow \infty }\dfrac{x^{n\alpha }}{\Gamma (n\alpha +1)}=0$, thus the proof complete. $\square$

4 Fuzzy fractional derivatives

Definition 4

[15] Let $f(x)\in C^{\mathbb {F}}[a,b]\cap L^{\mathbb {F}}[a,b]$. The fuzzy Riemann-Liouville integral of fuzzy-valued function f is defined as the following

$$\begin{aligned} J^\alpha _{x_0} f(x)=\frac{1}{\Gamma (\alpha )} \int _{x_0}^x (x-t)^{\alpha -1} f(t)dt, \quad 0<\alpha \le 1,~~~~ x>0. \end{aligned}$$

(26)

Let us consider the r-cut representation of fuzzy-valued function f as $f(x;r)=[\underline{f}(x;r),\overline{f}(x;r)]$, for $0 \le r\le 1$, then we can indicate the fuzzy Riemann-Liouville integral of fuzzy-valued function f based on the lower and upper functions as follows

Theorem 7

[15] Let $f\in C^{\mathbb {F}}[a,b]\cap L^{\mathbb {F}}[a,b]$ is a fuzzy-valued function. The fuzzy Riemann-Liouville integral of a fuzzy-valued function f can be expressed as follows:

$$\begin{aligned} J^\alpha _{x_0}f(x;r)=[J^\alpha _{x_0}\underline{f}(x;r),J^\alpha _{x_0}\overline{f}(x;r)],\quad \quad r\in [0,1], \end{aligned}$$

(27)

where

$$\begin{aligned} J^\alpha _{x_0}\underline{f}(x;r)=\dfrac{1}{\Gamma (\alpha )}\int _{x_0}^x (x-t)^{\alpha -1} \underline{f}(t)dt, \end{aligned}$$

(28)

$$\begin{aligned} J^\alpha _{x_0}\overline{f}(x;r)=\dfrac{1}{\Gamma (\alpha )}\int _{x_0}^x (x-t)^{\alpha -1} \overline{f}(t)dt. \end{aligned}$$

(29)

If in the definition of Riemann-Liouville fractional derivative and that of Caputo, we use the fuzzy generalized derivatives instead of the ordinary derivatives and the fuzzy Riemann-Liouville integration instead of the Riemann-Liouville integration, we obtain the fuzzy fractional derivative definitions. Hence, we will consider the fuzzy Caputo’s fractional derivative as the following:

Definition 5

[15] Let $f\in C^{\mathbb {F}} \cap L^{\mathbb {F}}$ be a fuzzy-valued function and $0 <\alpha \le 1$ . Then f is said to be Caputo’s H-differentiable at x when

$$\begin{aligned} ({^\mathscr {C}}D^{\alpha }_{x_0}f)(x)=\dfrac{1}{\Gamma (1-\alpha )}\int _{x_0}^{x}(x-t)^{-\alpha }f'(t)dt. \end{aligned}$$

(30)

Note that later we indicate $^{\mathscr {C}}D^\alpha _0 f(t)$ by $^{\mathscr {C}}D^\alpha f(t)$.

We have the following result for fuzzy Caputo’s fractional derivatives:

Theorem 8

[15] Let $f\in C^{\mathbb {F}}[a,b]\cap L^{\mathbb {F}}[a,b]$,   $x_0\in (a,b)$ and $0<\alpha \le 1$. Then

• (i) if f is (i)-differentiable fuzzy-valued function, then

  $$\begin{aligned} (_i^{\mathscr {C}}D^{\alpha }_{x_0}f)(x;r)=[(^{\mathscr {C}}D^{\alpha }_{x_0})\underline{f}(x;r),~(^{\mathscr {C}}D^{\alpha }_{x_0})\overline{f}(x;r)],\quad 0\le r \le 1, \end{aligned}$$

  (31)

• (ii) if f is (ii)-differentiable fuzzy-valued function, then

  $$\begin{aligned} (_{ii}^{\mathscr {C}}D^{\alpha }_{x_0}f)(x;r)=[(^{\mathscr {C}}D^{\alpha }_{x_0})\overline{f}(x;r),~(^{\mathscr {C}}D^{\alpha }_{x_0})\underline{f}(x;r)],\quad 0\le r \le 1. \end{aligned}$$

  (32)

Remark 2

Note that if f is (iii) or (iv) differentiable in Definition 3 then $({^\mathscr {C}}D^\alpha f)(x)\in \mathbb {R}$.

Remark 3

We say f is $^{\mathscr {C}}[(i)-\alpha ]$-differentiable while f is (i)-differentiable in equation (30), and f is $^{\mathscr {C}}[(ii)-\alpha ]$-differentiable while f is (ii)-differentiable in Eq. (30).

For $1<\alpha \le 2$ we have the following theorem:

Theorem 9

[12] Let $f(x)\in C^{\mathbb {F}}[0,b]\cap L^{\mathbb {F}}[0,b]$ be a fuzzy function and $[f(x)]^{r}=[\underline{f}(x;r),\overline{f}(x;r)]$, for $r\in [0,1]$, and $x\in (0,b)$. Then

• (i) if $_i^\mathscr {C}D^{\alpha }_{x_0}f$ be the (i)-Caputo type fuzzy fractional differentiable, then for $1<\alpha \le 2$

  $$\begin{aligned}{}[_{i,i}^{\mathscr {C}}D^{\alpha }_{x_0}f(x)]^r=[^{\mathscr {C}}D^{\alpha }_{x_0}\underline{f}(x;r),~^{\mathscr {C}}D^{\alpha }_{x_0}\overline{f}(x;r)], \end{aligned}$$

  (33)

• (ii) if ${_{i}^\mathscr {C}}D^{\alpha }_{x_0}f$ be the (ii)-Caputo type fuzzy fractional differentiable, then for $1<\alpha \le 2$

  $$\begin{aligned}{}[_{i,ii}^{\mathscr {C}}D^{\alpha }_{x_0}f(x)]^r=[^{\mathscr {C}}D^{\alpha }_{x_0}\overline{f}(x;r),~^{\mathscr {C}}D^{\alpha }_{x_0}\underline{f}(x;r)], \end{aligned}$$

  (34)

• (iii) if ${_{ii}^\mathscr {C}}D^{\alpha }_{x_0}f$ be the (i)-Caputo type fuzzy fractional differentiable, then for $1<\alpha \le 2$

  $$\begin{aligned}{}[_{ii,i}^{\mathscr {C}}D^{\alpha }_{x_0}f(x)]^r=[^{\mathscr {C}}D^{\alpha }_{x_0}\overline{f}(x;r),~^{\mathscr {C}}D^{\alpha }_{x_0}\underline{f}(x;r)], \end{aligned}$$

  (35)

• (iv) if ${_{ii}^\mathscr {C}}D^{\alpha }_{x_0}f$ be the (ii)-Caputo type fuzzy fractional differentiable, then for $1<\alpha \le 2$

  $$\begin{aligned}{}[_{ii,ii}^{\mathscr {C}}D^{\alpha }_{x_0}f(x)]^r=[ ^{\mathscr {C}}D^{\alpha }_{x_0}\underline{f}(x;r),~^{\mathscr {C}}D^{\alpha }_{x_0}\overline{f}(x;r)]. \end{aligned}$$

  (36)

Lemma 2

Suppose that $n-1<\alpha <n$, $\beta =\alpha -(n-1), (0<\beta <1)$, $n\in \mathbb {N}$, $\alpha ,\beta \in \mathbb {R}$ and the fuzzy valued function f(t) is such that $^{\mathscr {C}}D^\alpha f(t)$ exists. Then

$$\begin{aligned} ^{\mathscr {C}}D^{\alpha }= ~^{\mathscr {C}}D^{\beta }D^{n-1}f(t). \end{aligned}$$

Proof

$$\begin{aligned} ^{\mathscr {C}}D^\alpha _{x_0} f(t)=J^{\alpha -n}_{x_0}D^{n}f(t)=J^{\beta -1}_{x_0}D^1(D^{n-1}f(t))= ~^{\mathscr {C}}D^\beta _{x_0} D^{n-1}f(t). \end{aligned}$$

(37)

$\square$

Remark 4

Notice that $\alpha -(n-1)$ is a real number between 0 and 1. Hence, studying the behavior of the Caputo derivative of order $\beta \in (0,1)$ is sufficient for finding the Caputo derivatives of arbitrary order.

5 Generalized differential transform method

In this section, we apply the fractional generalized differential transform method to obtain the approximate analytical solutions of fuzzy fractional differential equations. The differential transform method evaluates the approximate solution by the Taylor series. But, the derivative is not computed directly; instead, the related derivatives are calculated by an iteration procedure. The generalized differential transform is also based on generalized Taylor’s formula and the Caputo fractional derivative.

Theorem 10

[12] Let $f(x)\in C^{\mathbb {F}}[0,b]\cap \L ^{\mathbb {F}}[0,b]$ and suppose that $({^\mathscr {C}}D^{\alpha })^kf\in C^{\mathbb {F}}[0,b]$ for $k=0,1,2,3,...,n+1$ where $0<\alpha \le 1$, $0\le x_0 \le x$ and $x\in (0,b]$. Then we have

$$\begin{aligned}{}[f(x)]^{r}=[\underline{f}^r(x),\overline{f}^r(x)], \end{aligned}$$

$$\begin{aligned} \underline{f}^{r}(x)=\sum _{i=0}^{n} \frac{x^{i\alpha }}{\Gamma (i\alpha +1)}(^{\mathscr {C}}D^\alpha )^i\underline{f}^r(0)+\frac{({^\mathscr {C}}D^{\alpha })^{n+1}\underline{f}^r(x_0)}{\Gamma (n\alpha +\alpha +1)}x^{(n+1)\alpha }, \end{aligned}$$

(38)

$$\begin{aligned} \overline{f}^{r}(x)=\sum _{i=0}^{n} \frac{x^{i\alpha }}{\Gamma (i\alpha +1)}({^{\mathscr {C}}}D^{\alpha })^i\overline{f}^r(0)+\frac{({^{\mathscr {C}}}D^{\alpha })^{n+1}\overline{f}^r(x_0)}{\Gamma (n\alpha +\alpha +1)}x^{(n+1)\alpha }, \end{aligned}$$

(39)

where ${^\mathscr {C}}D^\alpha \underline{f}^{r}(0)= {^\mathscr {C}}D^\alpha \underline{f}^{r}(x)|_{x=0}$, ${^\mathscr {C}}D^\alpha \overline{f}^{r}(0)= {^\mathscr {C}}D^\alpha \overline{f}^{r}(x)|_{x=0}$.

Now, we describe the generalized differential transform method. As know this method is based on generalized Taylor’s formula and the generalized differential transform of the kth derivative of real-value function f(x) in one variable define as follows:

$$\begin{aligned} F_{\alpha }(k)=\frac{1}{\Gamma (\alpha k+1)}[(^{\mathscr {C}}D^{\alpha }_{x_0})^k f(x)]\mid _{x=x_0}, \end{aligned}$$

(40)

where $0<\alpha \le 1$, $(^{\mathscr {C}}D^{\alpha }_{x_0})^k=~^{\mathscr {C}}D^{\alpha }_{x_0}~^{\mathscr {C}}D^{\alpha }_{x_0}\ldots ~^{\mathscr {C}}D^{\alpha }_{x_0}$, k-times, and the differential inverse transform of $F_{\alpha }(k)$ is defined as the following:

$$\begin{aligned} f(x)=\sum _{k=0}^{\infty } F_{\alpha }(k) (x-x_0)^{\alpha k}. \end{aligned}$$

(41)

substituting (40) into (41), we get

$$\begin{aligned} \sum _{k=0}^{\infty } F_{\alpha }(k)(x-x_0)^{\alpha k}=\sum _{k=0}^{\infty }\frac{(x-x_0)^{\alpha k}}{\Gamma (\alpha k+1)}((D^{\alpha }_{x_0})^kf)(x_0)=f(x). \end{aligned}$$

(42)

So, (41) is the inverse transform of the generalized differential transform (40). In the case of $\alpha =1$, the generalized differential transform (40) reduces to the classical differential transform. From (40) and (41), some basic properties of the generalized differential transform are introduced in below[13]:

• 1. If $f(x)=g(x)\pm h(x)$, then $F_{\alpha }(k)=G_{\alpha }(k)\pm H_{\alpha }(k)$.

• 2. If $f(x)=ag(x)$, then $F_\alpha (k)=a G_\alpha (k)$.

• 3. If $f(x)=g(x)h(x)$, then $F_\alpha (k)=\sum _{l=0}^{k} G_{\alpha }(l)H_{\alpha }(k-l)$.

• 4. If $f(x)=D^{\alpha }_{x_0} g(x)$, then $F_\alpha (k)=\frac{\Gamma (\alpha (k+1)+1)}{\Gamma (\alpha k+1)}G_{\alpha }(k+1)$.

• 5. If $f(x)=(x-x_0)^{n\alpha }$, then $F_\alpha (k)=\delta (k-n)$, where

  $$\begin{aligned} \delta (k)= \left\{ \begin{array}{ll} 1 &{}\quad \text {if}~ k=0\\ 0&{}\quad \text {if}~k\ne 0. \end{array}\right. \end{aligned}$$

In general, we know that the fractional calculus does not commute the derivative operation or even it doesn’t have the exponential property, i.e. $^{\mathscr {C}}D^{\alpha }(^{\mathscr {C}}D^{\beta }f(x))\ne ~$

$^{\mathscr {C}}D^{\beta }(^{\mathscr {C}}D^{\alpha }f(x))= ~^{\mathscr {C}}D^{\alpha +\beta }f(x)$ and $^{\mathscr {C}}D^{\alpha }(^{\mathscr {C}}D^{\beta }f(x))=~ ^{\mathscr {C}}D^{\beta }(^{\mathscr {C}}D^{\alpha }f(x)) \ne ~^{\mathscr {C}}D^{\alpha +\beta }f(x)$.

Example If $\alpha =\frac{1}{4}$ and $\beta =\frac{1}{2}$ and $f(x)=x^{\frac{1}{2}}$, we obtain

$^{\mathscr {C}}D^{\alpha }(^{\mathscr {C}}D^{\beta }f(x))=0$    and    $^{\mathscr {C}}D^{\beta }(^{\mathscr {C}}D^{\alpha }f(x))=~^{\mathscr {C}}D^{\beta +\alpha }f(x)=\frac{\Gamma (\frac{3}{2})}{\Gamma (\frac{3}{4})}x^{\frac{-1}{4}}$,

or generally for $0<\alpha ,\beta <1$,

$^{\mathscr {C}}D^{\alpha }~^{\mathscr {C}}D^{\beta }t^{\alpha }=0$    and     $^{\mathscr {C}}D^{\beta }~ ^{\mathscr {C}}D^{\alpha }t^\alpha =~^{\mathscr {C}}D^{\alpha +\beta }t^{\alpha }=\dfrac{\Gamma (\alpha +1)}{\Gamma (-\beta +1)}t^{-\beta }.$

In the following theorem, we find precise conditions under which the exponential property holds for arbitrary fractional operators. This result is very useful on the presented approach for solving differential equations and also fuzzy differential equations of fractional order.

Theorem 11

[13] Suppose that $f(x)=x^{\lambda } g(x)$, where $\lambda >-1$ and g(x) has the generalized power series expansion $g(x)=\sum _{n=0}^{\infty }a_n.(x-a)^{n \alpha }$ with radius of convergence $R>0$, $0<\alpha \le 1$. Then

$$\begin{aligned} ^{\mathscr {C}}D^{\gamma }_a~^{\mathscr {C}}D^{\beta }_af(x)=~^{\mathscr {C}}D^{\gamma +\beta }_a f(x), \end{aligned}$$

(43)

for all $t\in (0,R)$ if:

• (a) $\beta <\lambda +1$ and $\alpha$ arbitrary

  or

• (b) $\beta \ge \lambda +1$, $\gamma$ arbitrary, and $a_k=0$ for $k=0,1,\ldots , m-1$, where $m-1<\beta \le m.$

Theorem 12

[13] If $f(x)=~^{\mathscr {C}}D^{\beta }g(x)$, $m-1<\beta \le m$ and the function g(x) satisfies the condition in Theorem 11, then

$$\begin{aligned} F_{\alpha }(k)=\frac{\Gamma (\alpha k+\beta +1)}{\Gamma (\alpha k+1)}G_a(k+\beta /\alpha ). \end{aligned}$$

(44)

6 Fuzzy fractional differential equations

Consider the following fuzzy fractional differential initial value problem (FFIVP)

$$\begin{aligned} \left\{ \begin{array}{l} ^{\mathscr {C}}D^\alpha y(x)=f(x,y)\\ y(x_0)=y_0\in \mathbb {R}_\mathscr {F},~~~ x\in [x_0,b],~~~ \alpha \in [0,1] \end{array} \right. \end{aligned}$$

(45)

Using Theorem 8, the FFIVP and the union of the following two systems of fractional differential equations can be considered equivalent

$$\begin{aligned} \left\{ \begin{array}{l} ^{\mathscr {C}}D^\alpha \underline{y}(x;r)=\underline{f}(x,\underline{y}(x;r),\overline{y}(x;r)),\\ ^{\mathscr {C}}D^\alpha \overline{y}(x;r)=\overline{f}(x,\underline{y}(x;r),\overline{y}(x;r)),\\ \underline{y}(x_0)=\underline{y}_0(r) \quad \overline{y}(x_0)=\overline{y}_0(r), \end{array} \right. \end{aligned}$$

(46)

$$\begin{aligned} \left\{ \begin{array}{l} ^{\mathscr {C}}D^\alpha \underline{y}(x;r)=\overline{f}(x,\underline{y}(x;r),\overline{y}(x;r)),\\ ^{\mathscr {C}}D^\alpha \overline{y}(x;r)=\underline{f}(x,\underline{y}(x;r),\overline{y}(x;r)),\\ \underline{y}(x_0)=\underline{y}_0(r) \quad \overline{y}(x_0)=\overline{y}_0(r). \end{array} \right. \end{aligned}$$

(47)

Remark 5

Note that in above, we only consider $\alpha$th order of the fuzzy Caputo derivative for $0<\alpha \le 1$, however for $1<\alpha \le 2$ we can obtain a union of four systems which is equivalent with the given FFIVP.

Using Theorem 12 and applying the generalized differential transform method for real valued functions $\underline{f}(x)$ and $\overline{f}(x)$, we solve the systems (47) and (46). In this regard, we will approximate two functions $\underline{y}(x)$ and $\overline{y}(x)$ by two finite series as

$$\begin{aligned} \underline{y}(x)=\sum _{k=0}^{n} \underline{Y}_{\alpha }(k)(x-x_0)^{\alpha k}, ~~~~\text {and~~} ~~~~~\overline{y}(x)=\sum _{k=0}^{n} \overline{Y}_{\alpha }(k)(x-x_0)^{\alpha k}. \end{aligned}$$

(48)

7 Numerical examples

Example 1

Consider the linear fuzzy fractional differential equation from

$$\begin{aligned} \left\{ \begin{array}{l} ^{\mathscr {C}}D^\alpha y(x)=-y(x),\\ y(0)=(0.5,1,1.5). \end{array} \right. \end{aligned}$$

(49)

This equation under $^{\mathscr {C}}[(ii)-\alpha ]$ differentiation equivalent with

$$\begin{aligned} \left\{ \begin{array}{l} ^{\mathscr {C}}D^\alpha \underline{y}(x;r)=-\underline{y}(x;r),\\ ^{\mathscr {C}}D^\alpha \overline{y}(x;r)=-\overline{y}(x;r),\\ \underline{y}(0)=0.5+0.5 r, \\ \overline{y}(0)=1.5-0.5 r, \end{array} \right. \end{aligned}$$

(50)

and its exact solution is

$$\begin{aligned} \left\{ \begin{array}{l} Y1=(0.5+0.5r)E_{\alpha ,1}((-t)^\alpha ),\\ Y2=(1.5-0.5r)E_{\alpha ,1}((-t)^\alpha ). \end{array}\right. \end{aligned}$$

(51)

Applying the generalized differential transform to both sides of system (50), it transforms to

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\Gamma (\alpha (k+1)+1)}{\Gamma (\alpha k+1)}\underline{Y}_{\alpha }(k+1)=-\underline{Y}_{\alpha }(k),\\ \frac{\Gamma (\alpha (k+1)+1)}{\Gamma (\alpha k+1)}\overline{Y}_{\alpha }(k+1)=-\overline{Y}_{\alpha }(k),\\ \underline{Y}_{\alpha }(0)=0.5+0.5 r,\\ \overline{Y}_{\alpha }(0)=1.5-0.5 r. \end{array} \right. \end{aligned}$$

(52)

that is

$$\begin{aligned} \left\{ \begin{array}{l} \underline{Y}_{\alpha }(k+1)=-\frac{\Gamma (\alpha (k)+1)}{\Gamma (\alpha (k+1)+1}\underline{Y}_{\alpha }(k),\\ \overline{Y}_{\alpha }(k+1)=-\frac{\Gamma (\alpha (k)+1)}{\Gamma (\alpha (k+1)+1}\overline{Y}_{\alpha }(k),\\ \underline{Y}_{\alpha }(0)=0.5+0.5 r,\\ \overline{Y}_{\alpha }(0)=1.5-0.5 r. \end{array} \right. \end{aligned}$$

(53)

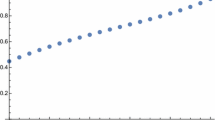
The recurrence relation (53) yields the approximations up to $O(x^{8\alpha })$ for $\underline{y}$ and $\overline{y}$ which are the solutions of the Eq. (49), as (Tables 1, 2 and Fig. 1):

$$\begin{aligned} \underline{y}(x)&=(0.5\,{+}\,0.5 r)\left( 1\!-\!\dfrac{\Gamma (\alpha \,{+}\,1)}{\Gamma (2\alpha \,{+}\,1)}x^{\alpha }\,{+}\,\dfrac{\Gamma (2\alpha \,{+}\,1)}{\Gamma (3 \alpha \,{+}\,1)}x^{2\alpha }\,{-}\,\dfrac{\Gamma (3\alpha \,{+}\,1)}{\Gamma (4\alpha \,{+}\,1)}x^{3\alpha }\,{+}\,\dfrac{\Gamma (4\alpha \,{+}\,1)}{\Gamma (5\alpha \,{+}\,1)}x^{4\alpha }\right. \\&\quad \left. -\dfrac{\Gamma (5\alpha \,{+}\,1)}{\Gamma (6\alpha \,{+}\,1)}x^{5\alpha }\,{+}\,\dfrac{\Gamma (6\alpha \,{+}\,1)}{\Gamma (7\alpha \,{+}\,1)}x^{6\alpha }\,{-}\,\dfrac{\Gamma (7\alpha \,{+}\,1)}{\Gamma (8\alpha \,{+}\,1)}x^{7\alpha }\,{+}\,\dfrac{\Gamma (8\alpha \,{+}\,1)}{\Gamma (9\alpha \,{+}\,1)}x^{8\alpha }\right) , \end{aligned}$$

$$\begin{aligned} \overline{y}(x)&=(1.5\!-\!0.5 r)\left( 1\,{-}\,\dfrac{\Gamma (\alpha \,{+}\,1)}{\Gamma (2\alpha \,{+}\,1)}x^{\alpha }\,{+}\,\dfrac{\Gamma (2\alpha \,{+}\,1)}{\Gamma (3 \alpha \,{+}\,1)}x^{2\alpha }\,{-}\,\dfrac{\Gamma (3\alpha \,{+}\,1)}{\Gamma (4\alpha \,{+}\,1)}x^{3\alpha }\,{+}\,\dfrac{\Gamma (4\alpha \,{+}\,1)}{\Gamma (5\alpha \,{+}\,1)}x^{4\alpha }\right. \\&\quad -\left. \dfrac{\Gamma (5\alpha \,{+}\,1)}{\Gamma (6\alpha \,{+}\,1)}x^{5\alpha }\,{+}\,\dfrac{\Gamma (6\alpha \,{+}\,1)}{\Gamma (7\alpha \,{+}\,1)}x^{6\alpha }\,{-}\,\dfrac{\Gamma (7\alpha \,{+}\,1)}{\Gamma (8\alpha \,{+}\,1)}x^{7\alpha }\,{+}\,\dfrac{\Gamma (8\alpha \,{+}\,1)}{\Gamma (9\alpha \,{+}\,1)}x^{8\alpha }\right) . \end{aligned}$$

Table 1 Numerical results for $\underline{y}$ in Example 1 with $n=8$ and $\alpha =3/4$

Table 2 Numerical results for $\overline{y}$ in Example 1 with $n=8$ and $\alpha =3/4$

Example 2

Consider the nonlinear fuzzy fractional logistic differential equation

$$\begin{aligned} \left\{ \begin{array}{l} ^{\mathscr {C}}D^{\beta }y=0.5y(1-y),\\ y(0) = (0.4 + 0.2 r,0.9 -0.3 r),\quad 0 \le r \le 1. \end{array}\right. \end{aligned}$$

(54)

Equation (54) under $^{\mathscr {C}}[(ii)-\beta ]$ derivative is equivalent with

$$\begin{aligned} \left\{ \begin{array}{l} ^{\mathscr {C}}D^{\beta }\underline{y}(t;r)=0.5\underline{y}(t;r)(1-\underline{y}(t;r)),\\ ^{\mathscr {C}}D^{\beta }\overline{y}(t;r)=0.5\overline{y}(t;r)(1-\overline{y}(t;r)),\\ \underline{y}(0)=0.4 + 0.2 r, \\ \overline{y}(0)=0.9 -0.3 r. \end{array}\right. \end{aligned}$$

(55)

The system (55) is transformed by using property (3) of the differential transform as follows

$$\begin{aligned} \begin{array}{l} \underline{Y}_{\beta }(k+1)=\dfrac{0.5\Gamma (\beta (k)+1)}{\Gamma (\beta (k+1)+1)}\left[ \sum _{l=0}^{k}\underline{Y}_{\beta }(l)(\delta (k-l)-\underline{Y}_{\beta }(k-l))\right] ,\\ \overline{Y}_{\beta }(k+1)=\dfrac{0.5\Gamma (\beta (k)+1)}{\Gamma (\beta (k+1)+1)}\left[ \sum _{l=0}^{k}\overline{Y}_{\beta }(l)(\delta (k-l)-\overline{Y}_{\beta }(k-l))\right] . \end{array} \end{aligned}$$

(56)

Tables 3 and 4 show the numerical results for approximation solutions of $\underline{y}$ and $\overline{y}$ for some $r \in [0,1]$ (Figs. 2, 3).

Fig. 1

Exact solution for $\alpha =1$ and approximated solutions for $\alpha =1/4,~ 2/4,~ 3/4,~ 1$ at $x=0.7$ with $^\mathscr {C}[(ii)-\alpha ]$ derivative and $n=8$ in Example 1

Remark 6

Figure 3 reveals that by increasing n we may expect to have an approximate solution close to the exact solution. In other words, the proposed method is convergent. However, in the most of the practical cases, the exact solution is not available, hence the computation of the absolute error is impossible.

Example 3

Consider the following linear fuzzy fractional differential equation

$$\begin{aligned} \left\{ \begin{array}{l} ^{\mathscr {C}}D^{\gamma }y(t)=3t^2y(t),\\ y(0)=(0.96+0.04 r,1.01-0.01 r). \end{array} \right. \end{aligned}$$

(57)

Equation (57), in the case $^{\mathscr {C}}[(ii)-\gamma ]$ derivative is equivalent by

$$\begin{aligned} \left\{ \begin{array}{l} ^{\mathscr {C}}D^{\gamma }\underline{y}(t;r)=3t^2\overline{y}(t;r),\\ ^{\mathscr {C}}D^{\gamma }\overline{y}(t;r)=3t^2\underline{y}(t;r),\\ \underline{y}(0)=0.96+0.04 r,\\ \overline{y}(0)=1.01-0.01 r. \end{array} \right. \end{aligned}$$

(58)

Table 3 Numerical results for $\underline{y}$ in Example 2 with $n=8$ and $\beta =1/2$

Table 4 Numerical results for $\underline{y}$ in Example 2 with $n=8$ and $\beta =1/2$

which is transformed as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \underline{Y}_{\gamma }(k+1)= \frac{3\Gamma (\gamma k+1)}{\Gamma (\gamma (k+1)+1)}\sum _{l=0}^{k}\delta (l-2)\overline{Y}_{\gamma }(k-l),\\ \overline{Y}_{\gamma }(k+1)= \frac{3\Gamma (\gamma k+1)}{\Gamma (\gamma (k+1)+1)}\sum _{l=0}^{k}\delta (l-2)\underline{Y}_{\gamma }(k-l),\\ \underline{Y}_{\gamma }=0.96+0.04 r,\\ \overline{Y}_{\gamma }=1.01-0.01 r. \end{array} \right. \end{aligned}$$

(59)

Tables 5 and 6 show the numerical results for $n=20$ and $\gamma =2/3$ (Fig. 4).

Fig. 2

Exact solution for $\beta =1$ and approximated solutions for $\beta =1/2,~ 1/4,~ 1$ at $t=1$ with $n=8$ for Example 2 in the sense of $^\mathscr {C}[(ii)-\beta ]$ differentiability

Fig. 3

Exact and approximated solutions at $t=1$ with $n=4$ and $n=8$ in Example 2 in the sense of $^\mathscr {C}[(ii)-1]$ differentiability

Example 4

In this example, let us consider the fuzzy Basset equation as follows

$$\begin{aligned} \left\{ \begin{array}{l} y'(t)+a(^{\mathscr {C}}D_{0}^{\frac{1}{2}}y(t))+y(t)=(0.95,1,1.05) (a>0, t>0)\\ y(0)=(-0.1,0,0.1) \end{array} \right. \end{aligned}$$

(60)

which is equivalent with the following systems

$$\begin{aligned} \left\{ \begin{array}{l} \underline{y}'(t)+a~(^{\mathscr {C}}D_{0}^{\frac{1}{2}}\underline{y}(t))+\underline{y}(t)=0.95+0.05r\\ \overline{y}'(t)+a`(^{\mathscr {C}}D_{0}^{\frac{1}{2}}\overline{y}(t))+\overline{y}(t)=1.05-0.05r\\ \underline{y}(0)=-0.1+0.1r\\ \overline{y}(0)=0.1-0.1r \end{array} \right. \end{aligned}$$

(61)

$$\begin{aligned} \left\{ \begin{array}{l} \overline{y}'(t)+a~^{\mathscr {C}}D_{0}^{\frac{1}{2}}\overline{y}(t)+\underline{y}(t)=1.05-0.05r\\ \underline{y}'(t)+a~^{\mathscr {C}}D_{0}^{\frac{1}{2}}\underline{y}(t)+\overline{y}(t)=0.95+0.05r\\ \underline{y}(0)=-0.1+0.1r\\ \overline{y}(0)=0.1-0.1r \end{array} \right. \end{aligned}$$

(62)

Using the proposed differential transform method for the system (62), we have

$$\begin{aligned} \left\{ \begin{array}{l} \underline{Y}_{\frac{1}{2}}(k+2)=-a\dfrac{\Gamma (\frac{k}{2}+\frac{3}{2})}{\Gamma (\frac{k}{2}+2)}\underline{Y}_{\frac{1}{2}}(k+1)-\dfrac{\Gamma (\frac{k}{2}+1)}{\Gamma (\frac{k}{2}+2)}\overline{Y}_{\frac{1}{2}}(k)+(0.95+0.05r)\delta (k),\\ \overline{Y}_{\frac{1}{2}}(k+2)=-a\dfrac{\Gamma (\frac{k}{2}+\frac{3}{2})}{\Gamma (\frac{k}{2}+2)}\overline{Y}_{\frac{1}{2}}(k+1)-\dfrac{\Gamma (\frac{k}{2}+1)}{\Gamma (\frac{k}{2}+2)}\underline{Y}_{\frac{1}{2}}(k)+(1.05-0.05r)\delta (k), \end{array}\right. \end{aligned}$$

(63)

Table 5 Numerical results for $\underline{y}$ of Example 3 when $n=20$ and $\gamma =2/3$

Table 6 Numerical results for $\overline{y}$ of Example 3 when $n=20$ and $\gamma ={2/3}$

Fig. 4

Exact solution for $\gamma =1$ and approximated solutions for $\gamma =1/3,~ 2/3,~ 1$ at $t=0.04$ with $n=20$ for Example 3 in the sense of $^\mathscr {C}[(ii)-\gamma ]$ differentiability

Fig. 5

Approximated solution for Example 4 at $t=0.5$ with $n=20$ and $a=3$ in the sense of $^\mathscr {C}[(ii)-\alpha ]$ differentiability

Figure 5 shows the numerical results.