Introduction

Hurricanes are among the most destructive climatic events. They are points of concern for society, especially in this era of climate change (Webster 2008; Schreck et al. 2014; Seneviratne et al. 2012). Physically, hurricanes are composed of storms, with dozens of convective system cores that "surround" the center of these systems (Yan and Zhang 2022).

In recent years, significant progress has been made in the numerical modeling of these systems, both theoretically and computationally. During this period, parametric and non-parametric models have been developed to predict and understand hurricanes. Schloemer (1954) and later Holland (1980) were the first to develop parametric representations for the pressure and wind field in hurricanes, identifying coherent and easily understandable representations of these systems. On the other hand, Willoughby and Rahn (2004) discovered that the intensification of these systems, mainly through the decay of pressure and wind speed, can lead to a better understanding of the dynamics, enabling the comprehension of the evolution of hurricanes along their trajectory.

According to Vickery et al. (2009), parametric models can be useful in forecasting storm systems, where winds, surface pressure, and sea temperature are used as predictors for diagnosing these systems. With the increasing need for more accurate and complex models, it is important to identify additional asymmetric properties (Vickery and Wadhera 2008; Arthur 2021; Yan and Zhang 2022).

Lin and Chavas (2012), using a parametric model to identify maximum wind, found that the most sensitive parameters for this estimate are surface wind speeds, which aligns with Chan (2005) mention that maximum surface wind can be estimated more simply by summing the azimuthal winds, which is directly linked to the system's translational velocity.

Another important factor in hurricane prediction, especially in identifying the intensity of this system, was mentioned by Emanuel (1986), where the tangential wind above the Planetary Boundary Layer (PBL) plays a crucial role in the balance of thermal wind. In this way, the air parcel above the PBL flows upward and out of the upper troposphere, generating conservation of absolute angular momentum and increased variability of moist entropy.

More recently, Mendes et al. (2023) enhanced the model proposed by Holland (1980) through new parameterizations. The authors included absolute angular momentum as an initial spin-up, where centrifugal force becomes significant as the wind accelerates in a hurricane.

In a previous investigation, Chavas and Lin (2016) developed a simple physical model to structure the radial azimuthal wind within a hurricane at lower levels. They observed that the wind variation was inherently linked to external parameters of the hurricane, such as the maximum wind speed and the maximum wind radius. Prior to these studies, Smith (2006), and Tang and Emanuel (2012) had already identified that the most turbulent region of a hurricane could be associated with inversely correlated changes with the radius of maximum winds, as corroborated by Vickery et al, (2009).

The pressure and wind in hurricanes have already been parametrically represented, allowing for an efficient description of these atmospheric systems (Bryan and Rotunno 2009; Vickery et al 2009). The analysis of interactions among various parameters, such as the decay of pressure in the eye of the system, maximum wind speed, and the maximum wind radius, contributes to a thorough understanding of hurricanes (Willoughby and Rahn 2004). Vickery et al. (2009) emphasized that parametric models assist in creating synthetic storm systems, enabling the modeling of strong winds. Furthermore, Olfateh et al. (2017) observed that the winds in this system can transform the pattern from a perfectly symmetric vortex motion to an asymmetric, radial, and/or azimuthal motion relative to the system's "eye."

It is important to emphasize that the presence of asymmetric convection, resulting from friction in the Lower Atmospheric Boundary Layer and Coriolis gradients, is crucial, as these factors influence the formation or reinforcement of wind and pressure asymmetry in dynamic systems such as hurricanes (Holland 1980; Olfateh et al. 2017). However, parameters are lacking in existing models to adequately describe the asymmetric properties of these systems, including maximum wind (Vickery and Wadhera 2008; Olfateh et al. 2017). Therefore, improving the accuracy of a parametric model can optimize studies on these systems. An example is seen in Xie et al. (2011), who studied the effects of wind asymmetry in four hurricanes, finding wind asymmetry in 30% of the analyzed data, which contributed to an increase of up to 16% in the height of ocean waves associated with intense storms.

Numerous empirical formulations found in the literature are based on the calculation of the maximum radius (Rmax) under asymmetric conditions (Takagi and Esteban 2016). Among these processes, the one presented by Xie et al. (2011) stands out, where wind radii are implemented in four quadrants, referred to as R34, R50, R64, and Rmax, with the first three applied to determine Rmax. On the other hand, the wind structures of tropical cyclones, hurricanes, and typhoons are based on two components in the Northern Hemisphere (NH): i) the counterclockwise wind motion in the southern sector at the surface, and ii) the storm's translational velocity (Elsner et al. 1999).

In previous studies, several models have adopted analytical parametric formulations to represent radial wind profiles in hurricanes, as evidenced by Holland et al. (2010). These systems are classified as "parametric" when the variation of radial wind is conditioned only by a few parameters, such as maximum wind speed, radius of maximum wind, and central pressure, as pointed out by Holland (1980) and reaffirmed by Holland et al. (2010). The simplicity, low computational cost, and good spatial resolution make the use of parametric winds appealing for estimating the return periods of winds in tropical cyclones, hurricanes, and typhoons, as well as for modeling the risk associated with these events, as observed by Vickery and Wadhera (2008), Holland et al. (2010), and Bhardwaj et al. (2019).

Mendes et al. (2023) present a parametric model to describe the asymmetry of winds in hurricanes, aiming to predict the dynamic conditions of these systems and affected regions. The model was applied to Hurricane Ike in September 2008. The authors observed that as the hurricane evolves, the tangential velocity also evolves, resulting in a change in static, baroclinic, and inertial stability. The model included a radial exponential reduction for the maximum velocity, allowing to identify that the maximum winds were consistently to the right of the hurricane's trajectory. Furthermore, the near-surface suction experienced an inflow into the system induced by the drag between the air and the surface.

In this manner, in addition to employing the previously mentioned proposed model, information regarding the Planetary Boundary Layer (PBL) height, latent heat flux (LHF), and sensible heat flux (SHF) at the surface were incorporated.

Therefore, in addition to using the proposed model mentioned above, information about the Planetary Boundary Layer (PBL) height, Latent Heat Flux (LHF), and Sensible Heat Flux (SHF) at the surface was incorporated.

Why Hurricane Katrina?

Katrina was a Category 5 hurricane that caused significant damage and loss of life, being one of the deadliest ever recorded in the United States (Mansury et al. 2021). According to the NHC (2005), Katrina was responsible for the deaths of 1833 people and generated $108 billion in damages. The hurricane's formation began on August 23, 2005, when a tropical depression formed southeast of the Bahamas. The following day, the depression evolved into Tropical Storm Katrina, which moved westward and hit Florida on August 25th, already classified as a Category 1 hurricane with winds exceeding 80 mph (NHC 2005).

Throughout its trajectory, Hurricane Katrina moved westward across the southern Florida towards the warmer waters of the Gulf of Mexico. Once in the Gulf, the hurricane rapidly intensified, reaching Category 4 with winds exceeding 175 mph on August 28th (NHC 2005). The city of New Orleans was the most affected when Katrina made landfall. Vigdor (2008) identified that a significant portion of the city and its surroundings were inundated, and its residents were evacuated. Nearly 2 years after the storm, almost half of the evacuees had not yet returned to the city.

We believe that a comprehensive study of Katrina's dynamics, utilizing a parametric model, can contribute to a better understanding and predictability of intense systems such as Katrina. The non-parametric model proposed here will be employed with novel parameterizations. In contrast to parametric models, which require an assumption about data distribution, non-parametric models are better suited for dealing with complex and heterogeneous data, such as the information collected during a natural disaster.

Furthermore, the new parameterizations proposed by the authors will enable a more accurate and detailed analysis of the impact of Hurricane Katrina. These parameterizations encompass data regarding wind speed, atmospheric pressure, and sea surface temperature—critical factors for the development and intensity of a hurricane. By utilizing these novel parameterizations, it will be feasible to conduct more precise and comprehensive assessments of the effects of Hurricane Katrina, encompassing wind intensity, among other aspects.

Data and model

Data

The initial conditions are a premise for the proper functioning of any dynamic model. In the case of the used model, the ERA5 reanalysis data was employed as input conditions (Hersbach et al. 2020). The variables that served as initial conditions include: (i) Sea Level Pressure (SLP, kPa), zonal winds (u, m/s), and meridional winds (v, m/s) (all levels), Air Temperature (Tair, ºC)—(all levels), Relative Humidity (UR, %)—(all levels), and Sea Surface Temperature (SST, ºC).

For spatial discretization, the values and derivatives of the mentioned variables were represented at discrete points on a regular grid, with latitude (Lat, º) and longitude (Lon, º). It is important to highlight that the spectral method was chosen to be employed due to its advantages in calculating the differential terms of dynamic conditions, with a spacing of 0.5° in latitude and longitude, and a temporal integration of 6 h.

Model

We will take a simpler approach to all the processes used in this article regarding the parameterization of this model.

The equations addressed in this context explore the fundamental structure of hurricanes, where the pressure at the surface decreases exponentially towards the center of the hurricane, stabilizing in the "eye" of the storm. Paradoxically, the winds grow exponentially in the opposite direction, towards the wall of the "eye." As mentioned by Schloemer (1954), in this model, the rotation of a solid body within the eye wall is assumed. Thus, the tangential winds decrease radially in a rectangular hyperbolic approximation.

In this article, we will employ the model suggested by Holland (1980) and modified by Mendes et al. (2023), where the radial wind profile shows significant variations in hurricane winds. Holland (1980) made modifications to the equation initially proposed by Schloemer (1954) to represent a spectrum of rectangular hyperbolas with pressure variation. Therefore, the equations of the model use the basic structure of hurricanes, where the pressure at the surface tends to decrease exponentially towards the center of the system and stabilize in the vicinity of the "eye," as mentioned earlier.

For a more precise analysis, the flows from the top of the cloud, latent heat (LE), and sensible heat (SH) have been included.

Spin-up

Some systems such as tornadoes originate due to the tilting of horizontal wind (Kalourazi et al. 2020). However, hurricanes, tropical cyclones, and typhoons are associated with convergence, which means that rotation always occurs towards the center of low pressure (Kalourazi et al. 2020). During convergence, angular momentum, which is linked to Earth's rotation, becomes concentrated and consequently connected to hurricane winds. Thus, the formula to calculate absolute angular momentum is expressed by Eq. (1).

$${A}_{m}=\frac{{f}_{c}\cdot {R}^{2}}{2}+{V}_{tan}\cdot R$$
(1)

In this context, Vtan (m/s) represents the tangential velocity at a radius R (km) from the center of the hurricane, as described by Mendes et al. (2023), while fc (s−1) is the Coriolis parameter. Equation (1) represents the absolute angular momentum, implying that the measurement encompasses the hurricane's relative angular momentum as well as the angular momentum associated with Earth's rotation. If hurricanes experienced no surface friction, this angular momentum would be conserved as air converged. Thus, the tangential wind velocity (Vtan) at a smaller radius (Rf) could be established even if the air at an initial radius (Ri) exhibited no rotation (Vtan = 0). Consequently, we incorporate the following formulation into the modeling, as shown in Eq. (2):

$${V}_{tan}=\frac{f}{2}\cdot \left(\frac{{R}_{i}^{2}-{R}_{f}^{2}}{{R}_{f}}\right)$$
(2)

Based on Malkus and Riehl (1960) and Wood and White (2011), it is established that frictional drag should not be disregarded in a hurricane. Consequently, the tangential winds are smaller than those calculated by Eq. (2).

As the wind acceleration in a hurricane increases, the centrifugal force becomes increasingly relevant. Therefore, it is essential to incorporate the pressure gradient formulation into the model, as specified by Eq. (3).

$$\frac{\Delta P}{\Delta R}=\rho \cdot \left(f\cdot {V}_{tan}+\frac{{V}_{tan}^{2}}{R}\right)$$
(3)

where \(\frac{\Delta p}{\Delta R}\) is the radial pressure gradient and ρ is the air density. The last term (\(\frac{{V}_{tan}^{2}}{R})\) represents the centrifugal force.

The concept that the gradient wind is applicable at all radii from the center of the storm associated with a hurricane, as well as at all latitudes except for areas near the bottom of the PBL and the top of the clouds (anvils), is an important point established by Yoshizumi (1968) and Wang et al. (2017). However, it is possible to adopt a simplification, suggesting that the Coriolis force can be neglected near the center of the most intense hurricanes, where the winds are fast. Nevertheless, this assumption introduces the idea that the tangential winds of the hurricane can be approximated by the cyclostrophic wind, as expressed in Eq. (4).

$${V}_{tan}={V}_{c}$$
(4)

where \({V}_{ c}\) represents the cyclostrrophic wind, implying:

$${V}_{tan}=\sqrt{\left(\frac{R}{\rho }\cdot \frac{\Delta P}{\Delta R}\right)}$$
(5)

In a hurricane, it is crucial to consider the sea surface drag, as this condition drives the spiral winds towards the eye wall. The gradient wind equation in the PBL is a fundamental tool to describe this flow.

An extremely important process is related to the updrafts in the storm's eye wall, which swiftly move and transport air upward. This causes the cyclonic air in the PBL to be carried to the top of the troposphere through convection. This process is very rapid, and it implies that its inertia prevents it from immediately transitioning to an anticyclonic flow. In other words, initially, the outflow moves in the opposite direction around the top of the system.

In this model, we treat the warmer core of the system as follows:

In the center of a hurricane, where the release of latent heat (LH) occurs through organized convection and adiabatic heating due to subsidence in the system's eye, the surrounding air appears cooler. This phenomenon is extensively documented, demonstrating that moist air rises adiabatically in storms around the core, while dry air descends in the system's eye after losing vapor due to precipitation.

In a hurricane, the center of the system is warm, surrounded by cold air, establishing a thermal gradient known as the radial temperature gradient. This gradient induces a reversal in the pressure gradient as altitude increases, due to the thermal wind effect (Hart 2003). To determine this pressure gradient, we adopt the sea-level pressure at the hurricane's eye as Pb, considering the surrounding pressure tends toward infinity (Pb∞). At the top of the hurricane, we define the central pressure as Pt, and similarly to Pb, the pressures around it also tend towards infinity (Pt∞).

Thus, the pressure gradient (ΔP) at the top can be expressed as the difference between the pressure at the top of the troposphere approaching infinity (Pt∞) and the pressure at the top of the eye (hurricane) (Pte). Therefore, we have the following relationship, highlighting the references:

$$\Delta {P}_{t}\approx a\cdot \Delta {P}_{b}-b\cdot \Delta T$$
(6)

where a = 0.15, being one-dimensional, b = 0.7 kPa/K (7 hPa/K), and ∆T = Te—T∞, with ∆T representing the average temperature difference across the troposphere. Such a thermal gradient (∆T) is always negative.

It is important to mention the characteristics of tangential wind, which cyclonically rotates around the eye of the system near the surface, and its anticyclonic spirals near the top of the hurricane, that is, far from the center of the system. In this context, it is observed that the tangential velocity decreases with altitude and eventually changes direction. To describe this behavior, we resort to the Ideal Gas Law, which allows us to perceive how the tangential component of the wind (Vtan) varies with altitude (h). Thus, we can express this relationship through Eq. (7):

$$\frac{\Delta T}{\Delta R}=\frac{T}{g}\cdot \left(\frac{\Delta {V}_{tan}}{\Delta h}\right)\cdot \left(\frac{2{V}_{tan}}{R}+{f}_{c}\right)$$
(7)

In this study, we employed the reverse differentiation of pressure according to Eq. (6), emphasizing that we utilized the hypsometric equation to establish a relationship between the pressure in the upper region of the hurricane's eye. This approach was also applied to the surroundings of the eye, resulting in the derivation of Eq. (8). In this context, it is important to mention that Eq. (8) is related to the references of R, the radius, g, the acceleration due to gravity (9.8 m/s2), and the mean temperature \(\overline{T }\).

$$\Delta {P}_{t}={P}_{b\infty }\cdot exp\left(\frac{-g\cdot {h}_{max}}{\left(R\cdot \overline{{T }_{\infty }}\right)}\right)-{P}_{be}\cdot exp\left(\frac{-g\cdot {h}_{max}}{(R\cdot \overline{{T }_{e})}}\right)$$
(8)

We use a first-order approximation for these exponentials, therefore, \(a=exp\left(\frac{-g\cdot {h}_{max}}{(R\cdot \overline{{T }_{e})}}\right)\).

Where we approximate a to be 0.15 and \(b=-\left(\frac{g\cdot {h}_{max}\cdot {P}_{b\infty }}{\left(R\cdot \overline{{T }_{e}}\cdot \overline{{T }_{\infty }}\right)}\right).\)

Approximately 0.7 kPa/K (7 hPa/K), where g is the acceleration due to gravity (9.81 m/s2), and R is the universal gas constant for dry air (R = 287.04 m2s–2 K–1).

One of the measures of intensity of a system like a hurricane is the pressure difference, as given by Eq. (9):

$${\Delta P}_{max}={P}_{\infty }-{P}_{e}$$
(9)

where the pressure distribution on the surface is approximated by:

$$\frac{\Delta P}{\Delta {P}_{max}}\left\{{\left(\frac{R}{{5R}_{0}}\right)}^{4} \quad for \,R\le {R}_{0}\right.$$
(10a)
$$\frac{\Delta P}{\Delta {P}_{max}}\left\{1-\frac{4}{5}\cdot \frac{{R}_{0}}{R}\right. \to for \,R> {R}_{0}$$
(10b)

The R is the radial distance from the center of the eye, R0 is the critical radius where the maximum tangential winds are identified. It is important to mention that R0 is twice the eye's radius.

Another important factor is related to the maximum wind radius (Vmax), which refers to the distance from the center of the system to the location within its structure where Vmax occurs.

The maximum radius (Rmax) plays an extremely important role in the system's conditions, as highlighted by Holand (1980).

According to the authors, Rmax is determined by the latitude, the difference between the central surface pressure and the ambient pressure, as well as the translational velocity of the hurricane, as also mentioned by Kalourazi et al. (2020).

$${R}_{max}=28.25\cdot tang[0.0873\cdot \left(\varnothing -28\right)+12.22\cdot \mathrm{exp}\left(\frac{{\Delta P}_{max}}{33.86}\right)+0.2\cdot {V}_{max}+37.2$$
(11)

where ∅ is the latitude of the hurricane's center, \({\Delta P}_{max}\) is the maximum pressure gradient (Eq. (9)), and Vmax is the maximum wind obtained through \({V}_{max}=K\sqrt{\Delta {P}_{max}}\), where K is a proportionality constant equal to 13.4 (Atkinson and Holliday 1977).

Due to the consideration of winds as cyclostrophic, where the drag against the sea surface and the Coriolis force were neglected, the previous approximation for the pressure distribution (Eq. 11) was used to obtain a distribution of tangential velocity near the surface.

$$\frac{{V}_{tan}}{{V}_{max}}\left\{{\left(\frac{R}{{R}_{0}}\right)}^{2} for \,R\le {R}_{0}\right.$$
(12a)
$$\frac{{V}_{tan}}{{V}_{max}}\left\{\sqrt{\frac{{R}_{0}}{R}} \quad for \,R>{R}_{0}\right.$$
(12b)

where the maximum speed occurs is at the critical radius (R0).

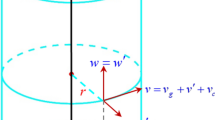
It is important to mention that the total wind speed relative to the surface is the vector sum of translational velocity and rotational velocity.

Radial velocity

In a hurricane, an interesting phenomenon takes place wherein the air near the surface becomes "trapped" beneath the PBL, while the surrounding air converges horizontally towards the eyewall (Merril 1984). This specific situation necessitates the preservation of horizontal continuity in cylindrical coordinates.

$${V}_{rad}\cdot R=Constant$$
(13)

According to Weatherford and Gray (1988), it is important to highlight that Vrad represents the radial component of velocity, being negative when referring to an inflow. In this context, it can be observed that the velocity originates far from the hurricane, as R decreases towards R0. Consequently, the magnitude of the inflow tends to increase.

The relationship between the radial velocity (Vrad) and the maximum velocity (Vmax) is defined according to the following equations, taking into consideration the previously established assumptions in Eq. (14).

$$\frac{{V}_{rad}}{{V}_{max}}=-\frac{R}{{R}_{0}}\cdot \left[\frac{1}{5}\cdot {\left(\frac{R}{{R}_{0}}\right)}^{3}+\frac{1}{2}\cdot \frac{{\omega }_{S}}{{V}_{max}}\cdot \frac{{R}_{0}}{{h}_{i}}\right] \quad for \,R\le {R}_{0}$$
(14a)
$$\frac{{V}_{rad}}{{V}_{max}}=-\frac{{R}_{0}}{R}\cdot \left[\frac{1}{5}+\frac{1}{2}\cdot \frac{{\omega }_{S}}{{V}_{max}}\cdot \frac{{R}_{0}}{{h}_{i}}\right] \quad for \,R> {R}_{0}$$
(14b)

The term ωS stands out for representing the average subsidence velocity in the eye of the hurricane. This magnitude, whose value is negative, is responsible for characterizing the horizontal area of the eye, acting as an indicator of the total kinematic mass flow. Furthermore, we have hi, which describes the depth of the boundary layer and is fixed at a constant value of 1000 m. Lastly, we cannot fail to mention Vmax, which refers to the maximum tangential velocity, revealing the maximum magnitude of this natural phenomenon.

Vertical velocity

When the radius of a hurricane (with greater intensity) is smaller than R0, the air rapidly converges and accumulates, then rises out of the PBL as a convection process along the eyewall. The vertical velocity towards the top of the PBL can be expressed by the mass continuity equation, as indicated by Eq. (15):

$$\frac{\omega }{{V}_{max}}=\frac{{h}_{i}}{{R}_{0}}\cdot {\left(\frac{R}{{R}_{0}}\right)}^{3}+\frac{{\omega }_{s}}{{V}_{max}} \quad for \,R \le {R}_{0}$$
(15)

The value of \(\frac{\omega }{{V}_{max}}=0\) for R > R.

To simplify, the upward motion that occurs in regions where there is precipitation is disregarded when R > R0. Furthermore, ωs is negative for subsidence. However, subsidence only operates within the eye, although the mentioned relationship applies to all locations within R0, aiming for simplification.

Thermal Processes

The relationships between temperature difference, pressure difference, and altitude within the hurricane are of utmost importance for an understanding of thermal processes. These processes are crucial for comprehending the internal structure of the storm and how it evolves and intensifies. To achieve this, we utilize Eq. (16).

$$\Delta T\left(R\right)=c\cdot [\Delta {P}_{max}-\Delta P\left(R\right)]$$
(16)

where, \(c=1.64\frac{K}{kPa}\)

At the top, there is a pressure difference (\(\Delta P=P\left(R\right)-{P}_{e})\) and a temperature difference (\(\Delta T\left(R\right)={T}_{e}-T(R))\) (Rotunno and Emanuel 1987), thus, we have:

$$\frac{\Delta T}{\Delta {T}_{max}}=1-\frac{1}{5}{\left(\frac{R}{{R}_{0}}\right)}^{4} \quad for \,R\le {R}_{0}$$
(17a)
$$\frac{\Delta T}{\Delta {T}_{max}}=\frac{4}{5}\cdot \frac{{R}_{0}}{R} \quad for \,R>{R}_{0}$$
(17b)

where, \(\Delta {T}_{max}={T}_{e}-{T}_{\infty }=c\cdot \Delta {P}_{max}\) e \(c=1.64\frac{K}{kPa}.\)

The necessary dynamic conditions for the formation of a hurricane are related to three main factors: low vertical wind shear, increased Coriolis force, and initiation of convection, usually through tropical atmospheric waves and tropospheric depressions (Tapiador et al. 2007). Hurricanes are extremely efficient in dissipating energy in the form of heat and are capable of self-sustainment. However, for this to occur, an excess of energy is required (Bister and Emanuel 1998). Essentially, hurricanes are highly efficient heat dissipation systems, acting as nearly perfect machines, removing energy in the form of enthalpy in the lower troposphere and dissipating it through radiative cooling in the upper levels of the troposphere (Emanuel 2003).

Planetary boundary layer

The method used to solve the horizontal momentum equations in the Boundary Layer of a hurricane is based on the prescribed pressure distribution and air density as a constant (Meng et al. 1995). Thus, the equation governing the wind in an intense system like a hurricane is derived from the Coriolis force (f), wind velocity (v), time (t), constant air density (ρ), and pressure (p). To solve the equation, the velocity (v) is expressed as the sum of the wind gradient in a free atmosphere (vf) and the frictional component close to the ground (v0).

$$V={v}_{f}+{v}_{0}$$
(18)

In this way, it is possible to employ the Richardson Bulk (RB) method proposed by Zhang et al. (2014), which involves the relationship between buoyancy force and the force associated with wind shear. Thus, it is feasible to obtain a quantification of atmospheric turbulence in hurricanes and assess the conditions under which these systems form.

$${R}_{B}=\frac{(\frac{g}{{\theta }_{{v}_{s}}})\cdot ({\theta }_{{v}_{z}}-{\theta }_{{v}_{s}})\cdot z}{{V}^{2}}$$
(19)

In which, g is the gravitational acceleration measured in \(m/{s}^{2}\); \({\theta }_{{v}_{s}}\) is the virtual potential temperature at the surface (K), \({\theta }_{{v}_{z}}\) is the virtual temperature at level z (K), and V is the total wind, as per Eq. (18).

For the calculations of potential temperatures (θ) used in Eq. (19), we employed the formulations proposed by Bolton (1980).

An important piece of information to highlight is that the Richardson Bulk (RB) assumes that the height of the Boundary Layer is the height at which the RB value reaches a critical value, representing the transition between laminar flow and turbulent flow (Wallace and Hobbs 2006).

This critical value has been defined as 0.25, a value found in previous studies (Stull 1988; Oliveira Júnior et al. 2010).

It's worth noting that RB is calculated based on the acceleration due to gravity (g) measured in m/s2, the potential virtual temperature at the surface (\({\theta }_{{v}_{s}}\)) in Kelvin (K), the virtual temperature at a level z (\({\theta }_{{v}_{z}}\)) in K, and the total wind velocity (V).

Sensible heat flux

To calculate the sensible heat flux, we utilize the Barsugli and Battisti (1998) premise. Thus, we have:

$${F}_{sen}={C}_{atms}\cdot ({T}_{atms}-{T}_{surf\_sea})$$
(20)

where, Catms = 22,5 W/Km2, the thermal damping effect is defined as the temperature difference between the air temperature at the surface (Tatms) and the sea surface temperature (Tsurf_sea). These conditions (Tatms; Tsurf_sea) constitute the model's spin-up and were extracted from ERA5 reanalyses.

Ma and Fei (2022) point out that the sensible heat flux is much less effective in the intensification of hurricanes when compared to the latent heat flux during the intensification phase of this system. The authors also mention that the energy input threshold required to generate a highly intense system like a hurricane is lower in the form of latent heat than in the form of sensible heat. Despite these conditions, as mentioned by Ma and Fei (2022), we find it necessary to emphasize these conditions in the proposed study here.

Latent heat flow

Regarding the latent heat flux (LHF), we adopt the definition proposed by Wallace and Hobbs (2006), which establishes a direct relationship between the latent heat flux at the surface layer and the evaporation rate. Thus, we can express it as follows:

$${F}_{lat}=\rho \cdot {L}_{v}\cdot {C}_{E}\cdot U\cdot ({q}_{surf}-{q}_{air})$$
(21)

In which, ρ is equal to 1.201 kg/m3 (air density), Lv is equal to 540 cal/g (latent heat of vaporization), CE is the coefficient of turbulent flux, U is the wind speed, obtained from ERA5, qsurf is the specific humidity at the surface, and qair is the specific humidity at a level closer to the surface, which we standardize as being 1000 mb.

Results

With the purpose of organizing the article, we analyzed the variables in topics, where each topic displays the evolution of Hurricane Katrina between the 27th and 30th of August, 2005.

Maximum wind speed

The maximum wind of a hurricane is determined by a variety of factors, including the depth of the atmosphere, air temperature, and humidity. The most common analytical method for identifying the maximum wind involves calculating the planetary boundary layer (PBL). The PBL is influenced by the conservation of momentum, drag forces, and vertical turbulent diffusion. These factors have a direct influence on the maximum wind.

In addition to these factors, the displacement speed of the system also has a linear effect on the maximum wind. To model this effect, we employ an exponential radial reduction coefficient, as suggested by Schwerdt et al. (1979). These conditions can be observed in Fig. 1, where the maximum speed is consistently to the east of the system's trajectory.

Fig. 1
figure 1

Tangential Wind (m/s) for the days 27 (a), 28 (b), 29 (c), and 30 (d) of August 2005 at 0000 UTC

Full size image

Figure 1 shows that Hurricane Katrina's maximum velocity was to the east of the system's trajectory. This is consistent with the linear effect of the system's displacement velocity on the maximum wind. The exponential radial reduction coefficient used to model this effect is also in accordance with the simulation results.

It is important to remember that the maximum velocity (Vmax) is the vector sum of translational velocity and rotational velocity. In the eastern quadrant of the system's movement, the rotational velocity is added to the translational velocity, resulting in the highest Vmax values. To the west of the system, the rotational velocity is subtracted from the translational velocity, resulting in a less intense Vmax (Zhay and Jiang, 2014).

Hurricane Katrina was in the Gulf of Mexico on August 27, 2005. It was classified as a Category 1 hurricane at 0000 UTC, according to NHC (2005). In Fig. 1a, the model positioned Katrina to the west of Florida, with maximum winds of up to 26 m/s. The peak wind maximum occurred east of the system's center and northeast of the translational direction. This positioning follows the typical pattern of northern hemisphere systems, as mentioned by Holland (1980).

During its trajectory, on August 28, Katrina began to move slowly northwestward over the Gulf of Mexico. There was a significant expansion of its convective cloud coverage, mainly at dawn, as reported by NHC (2005).

Figure 1b displays an increase in the maximum wind intensity on August 27th, along with an expansion in the coverage diameter of this maximum wind, resulting in a higher intensity of Hurricane Katrina. This was in line with the transformation of the system into a Category 5 hurricane by the end of the day, reaching a minimum pressure of 902 hPa at 1800 UTC, as recorded by the NHC (2005). In Fig. 1c, at 0000 UTC on August 29th, the model identified a well-defined and circular system, with its maximum intensity located to the northeast of the hurricane's eye, and a gentler reduction of the core. By August 28th, at 0000 UTC, Hurricane Katrina had already reached Category 3. The following day, on August 29th, Katrina weakened and became a tropical depression. The model exhibited a significant reduction in the maximum wind speed, which did not exceed 16 m/s (Fig. 1d), with the peak located to the south and along the coast of Louisiana, United States. It's important to note that the model employs an exponential radial reduction coefficient, following the proposal by Schwerdt et al. (1979). This coefficient influences the speed and allows for the linearization of the maximum speed over time, demonstrating the actual evolution of this variable during the intensification and weakening of the system.

Radial velocity

Understanding the dynamics of a hurricane, we recognize that the air in the PBL remains confined below the top, as there is a horizontal convergence of air towards the edge of the hurricane's "eye," as described by Ghosh and Chakravarty (2018). As the wind speed intensifies towards the "eye" of the system, a coupling occurs between the sea surface height and the radial and tangential velocities. When calculating the height of the PBL, we take into account these concepts suggested by Ghosh and Chakravarty (2018). Furthermore, Shapiro (1983) provides another significant contribution to understanding the intensification of radial velocity in hurricanes, such as the vertical and relative velocities that move radially, resulting in the asymmetric conservation of surface drag.

This expansion observed on August 28th further intensified on the 29th, both in speed and in the diameter of the maximum radial wind coverage, as shown in Fig. 2c. It is crucial to note that on this day, the system decreased in intensity and was reclassified as a category 3 according to the National Hurricane Center (NHC 2005).

Fig. 2
figure 2

Radial velocity (m/s 1) for the days 27 (a), 28 (b), 29 (c), and 30 (d) of August 2005 at 0000 UTC

Full size image

Additionally, in the implementation of the parameterization to determine the PBL, we take into account the assumptions suggested by Ghosh and Chakravarty (2018). They emphasize the horizontal convergence of air towards the hurricane's "eye" and the interaction between radial and tangential velocities at the sea surface height.

Another important aspect raised by Shapiro (1983), which we also take into consideration, was the asymmetric conservation of surface drag. In this case, both the maximum velocity and the relative velocity move radially, as depicted in Fig. 2.

On September 30th, when Hurricane Katrina weakened and transformed into a tropical storm upon making landfall, the model indicated a reduction in radial velocity (Fig. 2d), which was more pronounced only in the coastal region of the states of Louisiana, Mississippi, and Florida.

Friction velocity

Frictional stress in the lower troposphere, up to the 900 hPa level, leads to a decrease in the tangential wind speed, resulting in the formation of the so-called friction layer, as elucidated by Kepert et al. (2016). Imbalances of forces within this layer trigger the movement of air parcels, generating a frictional component.

During the evolution of Hurricane Katrina, an increase in frictional velocity was observed, as indicated in Fig. 3a, d. This phenomenon was triggered by the escalation of surface winds.

Fig. 3
figure 3

Friction velocity (m/s – 1) for the days 27 (a), 28 (b), 29 (c), and 30 (d) of August 2005 at 0000 UTC

Full size image

On August 27th at 0000 UTC (Fig. 3a), a more intense frictional velocity is shown on the eastern flank of Katrina's direction of movement, intensifying on August 28th (Fig. 3b), reaching its peak on August 29th at 0000 UTC (Fig. 3c), and expanding the region of influence of the radial wind. Even when Katrina was downgraded to a tropical storm on August 30th, a relatively intense influence of frictional velocity could still be identified on this day (Fig. 3d).

Latent heat flux

The transfer of latent energy (LE) at the interface between the ocean and the atmosphere exerts a significant influence on the formation and evolution of hurricanes (Nadimpalli et al. 2020). During the intensification phase of these systems, LE fluxes tend to increase. However, the various dynamic processes involved in this phase are not yet fully understood (Emanuel 2003; Bell and Montgomery 2008).

When water vapor in the troposphere condenses on the inner wall of the system's "eye," large amounts of Latent Heat Flux (LHF) are released, causing thermal expansion of the atmospheric column, and consequently reducing surface pressure. Analyzing LHF conditions during the intensification of Hurricane Katrina (Fig. 4), a progression can be observed as the storm intensifies.

Fig. 4
figure 4

Latent heat flux from the surface (J.m–2) for the days 27 (a), 28 (b), 29 (c), and 30 (d) of August 2005 at 0000 UTC

Full size image

On August 27 at 0000 UTC (Fig. 4a), when Katrina was west of the state of Florida and over the ocean, the system already exhibited higher LHF intensity northeast/east of the system's track, as illustrated in Fig. 4a. However, on the following day (Fig. 4b), when the system reached Category 5, the entire area around the "eye" intensified.

Consequently, on August 29th at 0000 UTC (Fig. 4c), the latent heat flux (LHF) continued to intensify, where two regions are identified around the system, a more intense one near the "eye" of Katrina and a less intense one in the periphery of Katrina. Finally dissipating almost completely on August 30th, when the system had already made landfall, as illustrated in Fig. 4d. Thus, it becomes evident that the model was effective in mapping the expansion of LHF during the system's development, suggesting an adequate representation of the feedback between the ocean and the atmosphere.

Sensible heat flux

As evidenced by Emanuel (1986), heat exchange on a surface is influenced by the wind, allowing us to consider a hurricane as an approximation of a Carnot machine. It is essential to emphasize that heat fluxes originating from the oceanic surface play a vital role in hurricane intensification. This observation is supported by the studies of Craig and Gray (1996), Nadimpalli et al. (2020).

In Fig. 5, we identify the expansion of sensible heat flux during the evolution of Hurricane Katrina, particularly between August 27th, 28th, and 29th (as detailed in Fig. 5a–c). It is important to note that the transfer of Sensible Heat Flux (SHF) from the surface functions as a thermal instability between the ocean and the atmosphere. This dynamic results in an increased transfer of SHF from the surface to the atmosphere, mainly on the northeast/east flank of the system, as evidenced in Fig. 5.

Fig. 5
figure 5

Sensible heat flux at the surface (J m–2) for August 27 (a), August 28 (b), August 29 (c), and August 30 (d), 2005, at 0000 UTC time

Full size image

On August 28th at 0000 UTC (Fig. 5b), Hurricane Katrina had already reached category 3 and continued to intensify. The maximum incidence of SHF was observed in the eastern and northeastern areas of the system's trajectory, as mentioned earlier. This distribution resulted in a more intense thermal instability, generating feedback between the warm ocean and the atmosphere. On August 29th (Fig. 5c), Katrina escalated to category 5. At this point, the intensification of SHF became more pronounced, covering the entire region affected by the system.

It is important to mention that on this day (August 29th), the system exhibited a typical condition of a very intense system, where the highest SHF values are located in regions where the maximum wind was most intense (Fig. 1c), corroborating Vickery and Wadhera (2008) and Ma et al. (2015).

Planetary boundary layer height

Several crucial physical processes for the formation and development of a hurricane cannot be directly resolved and therefore require parameterization (Louis 1979). This includes processes occurring on smaller scales, such as the microphysics involved in cloud and precipitation formation, heat, humidity, and momentum exchange at the ocean–atmosphere interface, as well as the origin, structure, and maintenance of the planetary boundary layer (PBL).

In the context of a system with high intensity, the PBLH has traditionally been numerically addressed in most models. In the original version of the model, which we use here, the PBLH is considered unchanged for parameterization purposes. However, with the introduction of a new parameter, it is now possible to represent the evolution of the PBL height more accurately.

By employing the proposed model in the study of Hurricane Katrina, we identified an increase in PBLH, mainly on the periphery of Katrina during the intensification phase (Fig. 6a–c) and the deintensification phase (Fig. 6d) of the hurricane. It was observed that this increase in PBLH on the "eye" wall of the system is inherently linked to the transfer of heat, humidity, and momentum between the ocean surface and the atmosphere, as proposed by Eliassen (1971) and Kepert et al., (2016).

Fig. 6
figure 6

Boundary layer height (J m–2) for August 27 (a), August 28 (b), August 29 (c), and August 30 (d), 2005, at 0000 UTC

Full size image

The scientific literature, although not specifically discussing PBLH for phenomena like hurricanes, only defines a limit or standard height. During the evolution of Katrina, it was evident that the region near the "eye" reached a maximum height of 1800 m, mainly on August 28th and 29th (Fig. 6b, c). It was observed that the PBL height gradually decreases as one moves away from this region, reaching a minimum of 800 m (Fig. 6a–d).

Furthermore, an additional interpretation for the higher PBLH near the "eye" wall was proposed by Shapiro (1983). He suggested that the maximum azimuthal winds are located at the top of the PBL, causing excessive upward inflow.

Ekman transport

Shen and Gong (2009) emphasized the potential influence of Ekman transport on coastal flooding events, with a pronounced impact during slow-moving weather phenomena such as hurricanes, where winds align with the coastline orientation. In a more recent study, Mendes et al. (2023) demonstrated through numerical simulation that hurricanes near the coast induce resonance of ocean waves, notably in the eastern and northeastern directions of the system's trajectory in the Northern Hemisphere. The researchers also underscored the significance of the Ekman spiral, a description of the variation in direction and speed of transport based on ocean depth. It is noted that the spiral is more intense in regions with higher surface friction. Thus, under cyclonic motion conditions to the east of the system in the Northern Hemisphere, the Ekman spiral exhibits greater intensity in this region.

An intensification of Ekman transport was observed during Hurricane Katrina, as shown in Fig. 7. Specifically, between August 27th and 28th (Fig. 7a, b), when the system underwent rapid intensification, reaching category 5 on August 28th, as reported by the NHC (2005). On August 29th (Fig. 7c), there was an expansion of the Ekman transport activity area.

Fig. 7
figure 7

Ekman Transport (m2/s) for August 27 (a), August 28 (b), August 29 (c), and August 30 (d), 2005, at 0000 UTC

Full size image

On August 30th (Fig. 7d), with Katrina already over the mainland, an increase in Ekman transport was observed near the coast in the states of Louisiana and Mississippi. Such conditions favor the formation of a steady state, in which Ekman transport generates intense ocean waves (Vincent et al. 2013) and promotes interactions among the upper ocean layers (Bueti et al. 2014; Dieng et al. 2021).

Discussion

Hurricane Katrina, recognized as one of the deadliest and most destructive episodes in the history of natural disasters, resulted in a colossal scale of material destruction and loss of lives. Therefore, enhancing the diagnosis and prediction of these extreme climatic events is essential, relying on sophisticated numerical models.

A significant step in this direction was proposed by several authors, including Holland (1980); Meng et al. (1995); Montgomery and Smith (2020); and others—introducing a model with innovative parameterizations that can establish accurate estimates for various physical conditions associated with these intense climatic systems. A highly positive aspect is the model's ability to define intensity, as well as to identify, for example, the maximum winds closest to the hurricane's eyewall. Furthermore, the model proposed here presents satisfactory results in the evolution of radial velocity over time, especially during intensification.

Another noteworthy aspect is that the model is capable of detecting the region of intense frictional velocity near the "eye" of the system. Even during moments of system intensification and de-intensification, the model proves effective in identifying the dynamic conditions of Katrina, although it encounters difficulties with the increase in the system's central pressure.

Regarding latent heat flux, the model clearly identifies its increase near the "eye" of the system. As the system develops, there is a greater release of latent heat on the eyewall due to the condensation of water vapor in the troposphere. Simultaneously, the model detects an increase in sensible heat flux as Hurricane Katrina evolves. This indicates that the heat exchange instability mechanism at the surface evolves in response to the increase in cyclonic wind at the surface during this phase of evolution (Morey et al. 2006).

It is possible to conclude that the method proposed here accurately identifies the height of the boundary layer, showing an increase in this height in the NE and E directions of the system's displacement. This increase in height is associated with a greater transfer of heat, moisture, and momentum between the surface and the atmosphere (Shapiro 1983; Kepert et al. 2016).

In conclusion, the innovative parameterizations implemented in this article can consistently predict the physical and dynamic conditions of an intense climatic system, such as Hurricane Katrina.