1 Introduction

Tropical cyclones are intense, cyclostrophically rotating low vortices weather systems that form over the tropical oceans. The wind speed ranges from \(17\,\hbox {m/s}\) (\(60\,\hbox {Km/h}, 32\,\hbox {Kn}\)) to greater than \(33\,\hbox {m/s}\) (\(120\,\hbox {Km/h}, 64\,\hbox {Kn}\)). Tropical cyclones are classified according to their place of occurrence and intensity. They are named differently in different places of the world. They are called hurricanes over the Atlantic Ocean, the East Pacific Ocean and the Caribbean Sea. Over the Western North Pacific Ocean they are called typhoons and in India known as cyclones. The cyclones forming over North Indian Ocean are mainly monitored by India Meteorological Department. According to intensity cyclones are classified into the following 7 categories, viz. (1) depression (speed ranges 17–27 Kn or 31–50 Km/h), (2) deep depression (speed ranges 28–33 Kn or 51–62 Km/h), (3) cyclonic storm (speed ranges 34–47 Kn or 51–62 Km/h), (4) severe cyclonic storm (speed ranges 48–63 Kn or 89–117 Km/h), (5) very severe cyclonic storm (speed ranges 64–89 Kn or 118–165 Km/h), (6) extremely severe cyclonic storm (speed ranges 90–119 Kn or 116–220 Km/h), (7) super cyclonic storm (speed \(\ge \, 120\,\hbox {Kn}\) or \(221\,\hbox {Km/h}\)).

Fig. 1
figure 1

a, b Discussed in Sect. 5

Full size image
Fig. 2
figure 2

The variation of radial velocity (u) versus radial distance of separation (r) of the field point from the cyclone axis

Full size image

The Rankine vortex model proposed by Giaiotti and Stel (2006) describes about the vorticity of tropical cyclones. Vorticity, i.e., microscopic rotational parameter of a turbulence, is an important structural characteristics of a cyclone. Recently propounded works like Convective forcing in the inter tropical convergence zone of The Eastern Pacific (2003), The mechanics of the gross moist stability, etc., by Raymond et al. (2009) also describes some important critical parameters regarding the formation of tropical cyclones. We can briefly sum up the main factors for cyclone formation as follows:

  1. (1)

    Warm ocean waters of at least \( 26\,^{\circ}\hbox {C}\).

  2. (2)

    At least \( 5^{\circ}\) latitude from the equator.

  3. (3)

    Low vertical wind shear.

  4. (4)

    Moisture in the mid-troposphere.

  5. (5)

    Unstable conditions.

  6. (6)

    Pre-existing disturbances.

Literature survey suggests that a lot of researches have been done on the above-mentioned six parameters to discuss about the critical phenomenon of tropical cyclones. Whitney and Hobgood (1997) figured out a function between sea surface temperatures and maximum intensities of tropical cyclones. Relationships between sea surface temperature and intensification rate of tropical cyclones have also been derived by Crinivec et al. (2015). Arora and Dash (2016), Kotal et al. (2009) etc., also developed relationship between sea surface temperature and maximum intensity of tropical cyclones. Emanuel (2005) described the increasing destructiveness of tropical cyclones for the past 30 years.

Fig. 3
figure 3

The variation of f(z) versus z (the vertical height of the field point from the sea level)

Full size image
Fig. 4
figure 4

The variation of tangential velocity (v) versus r

Full size image

De Maria and Kaplan (1994a, b) also developed empirical relationship between Atlantic tropical cyclones sustained velocity and corresponding sea surface temperature (nonlinear relationship). Recently Wang et al. (2016) did a detailed intercomparison of extra tropical cyclone activity on 9 reanalysis data sets. Cyclones generally occur in the equatorial and tropical regions. In the polar regions tropical cyclones are not available. Cyclone genesis is also strengthened at places of location \(5^0\) latitude due to the rotation of the earth about its axis. Vertical shear is defined as the difference in wind speed and direction at two different heights in the atmosphere. Carrying moisture from sea level in low vertical shear environment the warm air rises to great heights without change of velocity and direction. At upper troposphere they condense and release latent heat. Latent heat is released in the form of potential energy.

Fig. 5
figure 5

The variation of vertical velocity (w) versus z

Full size image
Fig. 6
figure 6

The variation of CSP versus r

Full size image
Table 1 u versus r data for tropical cyclone boundary layer obtained from ‘lectures on tropical cyclone ’ by Smith (2006)
Full size table

The presence of moisture in the mid-troposphere fuels up the storm intensity of tropical cyclones. A relationship between water vapor path and precipitation over tropical oceans has been derived by Bretherton et al. (2004).

Unstable conditions and pre-existing disturbances also fuel up the intensity of tropical cyclones. Unstable air is dry warm air that rises vigorously to great height, i.e., they satisfy the condition, low vertical shear. A sumptuous analytic concept about tropical cyclone observation, formation, dynamics, etc., can be obtained from lectures on tropical cyclone by Smith (2006). Also the tropical cyclone inner core dynamics is vividly described in Emanuel (2011) and Holton (1972).

The prediction and forecasting of cyclone is a challenging research area nowadays. The work of Lala et al. (2014) shows how a tropical cyclone dies out faster in an undulating tilted landform compared to flat landforms. The works on cyclone dynamics by Williams and Taft (2013), Sobel et al. (2009) and Mandal (1986) also bear special significance. Kilroy et al. (2014) studied the cause behind intensification of tropical cyclones at lower latitudes. They concluded that the dynamics of the frictional boundary layer is the most important factor behind rapid intensification of tropical cyclones. Williams and Taft (2013) studied the shock-like structures in the tropical cyclone boundary layer. They studied the dynamics of some hurricanes and concluded that the velocity advection term in the radial momentum equation is mainly responsible for the shock-like structure. Regarding analytic work on tropical cyclone dynamics the paper of Ghosh and Chakravarty (2017) also deserves to mention. De Maria and Kaplan (1994a, b, 1999) developed statistically hurricane intensity prediction schemes over the Atlantic and East North Pacific Ocean. Sessions et al. (2007) developed a theory for the spin-up of tropical depressions. Kieu (2004a, b) developed an analytic model of tropical depressions. The dissipation energy of the cyclone has been a major concern in the work of Wang and Xu (2010). The maximum potential intensity (MPI) parameter has been highlighted in the work of Wang and Wu (2004). They used numerical simulation for calculating energy production, frictional dissipation energy and maximum intensity of a tropical cyclone. Emanuel (2007) showed how environmental factors affect tropical cyclone power dissipation. The intensity and devastation effect of a tropical cyclone depends on its geometry and also on the orientation of its axis.

In this work we have chosen an analytic expression of the cyclone radial velocity (i.e., the velocity along the radius vector of the cyclone) studying the dynamics of tropical cyclone following Smith (2006). Then the expression of the transverse velocity (i.e., the velocity perpendicular to the radius vector of the cyclone) is solved from the guiding nonlinear equation on cyclone dynamics using ‘Wentzel–Kramers–Brillouin (WKB) approximation’ (Griffiths 2005) at the sea level and near the wall cloud of the cyclone. We have also introduced a new parameter called the cyclone stability parameter (CSP) depending on radial and transverse (cross-radial) velocity. The Navier–Stokes equation in cylindrical coordinate system has been solved analytically with some necessary assumptions. From the solution we get a satisfactory explanation of cyclone dynamics and stability analysis. Still today there is no well-defined parameter from which we can make our forecast for a cyclone when the system is in the depression stage. In our work we try to address this problem. The parameter (CSP) which we have defined on a physical basis can help us to take decision for forecasting cyclone at the stage of depression. So the importance of this work in the field of theoretical dynamic meteorology and cyclone forecasting is immense.

2 Formulation of the problem

2.1 The proposed model

In steady state the equation of momentum conservation in cylindrical polar coordinate system for a fluid mass in transverse direction is given by:

$$\begin{aligned} u\frac{\partial {v}}{\partial {r}}+\frac{uv}{r}+w\frac{\partial {v}}{\partial {z}}+fu=\frac{\partial }{\partial {r}}\left[ k_{r}\left( \frac{\partial {v}}{\partial {r}}+\frac{v}{r}\right) \right] +\frac{1}{\rho }\left[ \frac{\partial }{\partial {z}}\left( {\rho k_{z}\frac{\partial {v}}{\partial {z}}}\right) \right] . \end{aligned}$$
(1)

where u, v and w are radial, transverse and vertical velocity of the fluid mass, respectively.

The equation of continuity is given by:

$$\begin{aligned} \frac{\partial }{\partial {r}}\left( \rho ur\right) +\frac{\partial }{\partial {z}}\left( \rho wr\right) =0. \end{aligned}$$
(2)

The equation of state is given by:

$$\begin{aligned} p=\rho RT \end{aligned}$$
(3)

The equation of hydrostatic balance is given by:

$$\begin{aligned} \frac{\partial p}{\partial z}=-g\rho \end{aligned}$$
(4)

The stream function \( \psi \) is defined by:

$$\begin{aligned} \frac{\partial {\psi }}{\partial {z}}= & {} \rho ur \end{aligned}$$
(5)
$$\begin{aligned} \frac{\partial {\psi }}{\partial {r}}= & {} -\rho wr. \end{aligned}$$
(6)

3 The solution of the problem

3.1 Some tactic assumptions and proposed form of radial velocity (u)

In the proposed model, the number of unknowns is 6 and the no. of equations is 4 so complete solution of the unknowns without some tactic assumptions is not possible. That is why we have taken the following assumptions:

(a) A cyclone is assumed to be axially symmetric system like a right circular cylinder.

(b) To connect the cyclone structure with its dynamics we define a parameter, ‘Cyclone area rate’ (N), which is proportional to the cyclone velocity flux coming in/out through its curve-bounded closed surface.

Thus,

$$\begin{aligned} \oint _{s}u.\hbox {d}S=KN \end{aligned}$$
(7)

For a closed surface S the total cyclone velocity flux is \(\oint _{s}u.\hbox {d}S\).

K has the dimension of length.

(c) We define another parameter (\(\lambda \)) as the cyclone area rate per unit volume. \(\lambda \) can be obtained from cyclone size. The parameter named outermost closed isobar (OCI) is used to calculate cyclone size. We need surface observations to calculate OCI. Radius of 34 knot winds (R34) is used to calculate cyclone size. R34 can be calculated from reconnaissance flight data. Tropical cyclone gale wind radii forecasting has been done by Sampson and Knaff (2015). Estimation of size of Atlantic tropical cyclones from the expression of outer radius has also been done by Dean et al. (2009). Volume of the cyclone is obtained from height of the cyclone which needs satellite data. The size or area of the wind field could be important because it may be related to wind damage or potential storm surge. Cyclone area is used to calculate factors like integrated kinetic energy (IKE). IKE is an important parameter in calculation of wind fields for a cyclone. The strength of a tropical cyclone in terms of its IKE finds its expression in the work of Powell and Reinhold (2007). The analogous cyclone structure is shown in Fig. 1b. The inner cylinder (A) of radius \(r_{1}\) here represented as the eye, while the outer cylinder (B) of radius \( r_{2}\) as the wall cloud.

We now apply the assumptions a, b and c up to the wall cloud periphery and consider a field point P(r) within the cyclone where we shall calculate the profile of air flow. If the point P(r) lies between A and B, i.e., \(r_{1}\le r\le r_{2}\), then from (5) we obtain,

$$\begin{aligned} u=\frac{\lambda K}{2r}\left( r^{2}-r_{1}^{2}\right) \end{aligned}$$
(8)

where \(\oint u.\hbox {d}s\) is the total velocity flux at P(r). Theoretically the maximum value of u is reached at \(r=r_{2}\)

Now,

$$\begin{aligned} u_{\mathrm{max}}=\frac{\lambda K}{2r_{2}}\left( r_{2}^{2}-r_{1}^{2}\right) \end{aligned}$$
(9)

as u is also a function of z so we choose a function of z as f(z), \(f(z)=C e^{\pm (z-\frac{7H}{10})}\), where C is a scaling constant.

We defined this from the concept of z versus cyclone velocity plot from the work of rapid intensification of tropical cyclones at low latitudes by Kilroy et al. (2014). \( f(z)=C e^{(z-\frac{7H}{10})}\), where \(z\le H\);

\(f(z)=C e^{-(z-\frac{7H}{10})}\), where \( z>H\);

\(H =\) Upper troposphere limit of the cyclone which is taken \(20\,\hbox {Km}\) above sea level.

Thus the complete solution for u becomes,

$$\begin{aligned} u=\alpha \left( r^{2}-r_{1}^{2}\right) \hbox {e}^{\pm \left( z-\frac{7H}{10}\right) } \end{aligned}$$
(10)

We can calculate the value of the constant \(\alpha =C\frac{\lambda K}{2}\) as 0.0002092 SI unit using Table 1. Now if the location of field point P(r) is beyond wall cloud, the expression of u is given by:

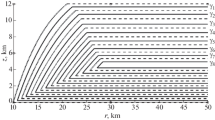
$$\begin{aligned} u= \alpha \left( r_{2}^{2}-r_{1}^{2}\right) \hbox {e}^{\pm \left( z-\frac{7H}{10}\right) } \end{aligned}$$
(11)

As per this assumption the plot of u versus r and f(z) versus z for different ranges is shown in Figs. 2 and 3, respectively.

3.2 Solution of transverse velocity (v)

It is very difficult to solve Eq. (1) for v, and thus to avoid complication on putting the value of u from Eq. (10) in (1), we assume that cyclone is mostly active in the vicinity of the sea level, i.e., \(z=0\) and also assume \(\frac{\partial v}{\partial z}=0\). If we try to solve Eq. (1) for v in the vicinity of \(r=r_{1}\) where the cyclone impact is the most destructive or the cyclone dynamics is the most active with the above assumption, Eq. (1) becomes,

$$\begin{aligned} \frac{\hbox {d}^{2}v}{\hbox {d}r^{2}}+P\frac{\hbox {d}v}{\hbox {d}r}+Qv=R \end{aligned}$$
(12)

where \(P=\frac{1}{k_{r}}[\frac{1}{r}(Ar_{1}^{2}+1)-Ar]\), \(Q=-\frac{1}{k_{r}}[\frac{1}{r^{2}}+A(1-\frac{r_{1}^{2}}{r_{2}^{2}})]\), \(R=fA(r-\frac{r_{1}^{2}}{r})\), \(A=-\frac{C\lambda k}{2}e^{-\frac{7H}{10}}\) and ‘f’ is the Coriolis parameter.

Using the technique of elimination of first-order derivative in Eq. (10) and the subsequent WKB approximation in the solution of v, the ultimate solution becomes

$$\begin{aligned} v= & {} \frac{1}{[f(r)]^{\frac{1}{4}}}\left\{ \left( \frac{r}{r_{1}}\right) ^{-\frac{Ar_{1}^{2}+1}{2k_{r}}}\right\} \hbox {exp}\left\{ \frac{A}{4k_{r}^{2}}(r^{2}-r_{1}^{2})\right\} \left( C_{1} \hbox {exp}\left[ -B^{\frac{1}{4}}\left\{ r-\frac{\sqrt{B}}{10}r^{5}+\frac{G}{2\sqrt{B} r}-\frac{H}{4\sqrt{B}}r^{2}\right\} \right] \right. \nonumber \\&\quad \left. +C_{2} \hbox {exp}\left[ \root 4 \of {B}\left\{ r-\frac{\sqrt{B}}{10}r^{5}+\frac{G}{2\sqrt{B} r}-\frac{H}{4\sqrt{B}}r^{2}\right\} \right] \right) \end{aligned}$$
(13)

where \(C_{1}, C_{2}\) constants. \(f(r)=Br^{4}+\frac{G}{r^{2}}-Hr-\sqrt{B}\), \(B=\frac{A^{2}}{4k_{r}^{2}},\) \(G=\frac{3Ar_{1}^{2}}{2k_{r}}-\frac{1}{2k_{r}} +\frac{1}{4k_{r}^{2}}+\frac{Ar_{1}^{2}}{4k_{r}^{2}}, H=\frac{A}{2k_{r}}(Ar_{1}^{2}+1)\).

In the vicinity of \(r= r_{1}\)

\(\hbox {exp}\left\{ \frac{A}{4k_{r}^{2}}(r^{2}-r_{1}^{2})(\frac{r}{r_{1}})^{\frac{Ar_{1}^{2}+1}{2k_{r}}}\right\} = 1\)

As r is nearly equal to \(r_{1}\), we make a tactic assumption by considering the value of \(C_{1}\) and \(C_{2}\) as

\(C_{1}=3000 \hbox {exp}[B^{1/4}\lbrace r_{1}-\frac{\sqrt{B}}{10}r_{1}^{5}+\frac{G}{2\sqrt{B}r_{1}}-\frac{H}{4\sqrt{B}}r_{1}^{2}]\)

\(C_{2}=3000 \hbox {exp}[-B^{1/4}\lbrace r_{1}-\frac{\sqrt{B}}{10}r_{1}^{5}+\frac{G}{2\sqrt{B}r_{1}}-\frac{H}{4\sqrt{B}}r_{1}^{2}]\)

We are now in a position to define a parameter called the cyclone stability parameter (CSP) \(=\) \(\frac{v}{u}\). Subsequently in Sect. 5 we will discuss how this parameter helps to determine the stability of the system.

Considering the expressions of u and v from (10) and (13) in the vicinity of \(r_{1}\) and \(z=0\) we see that CSP of a cyclone is a function of r only.

4 Solution of the vertical velocity (w)

From (3), (5), (6) and (10) after some manipulations we get the solution for w

when, \(r_{1} \le r < r_{2}\) ; \(z\le \frac{7H}{10}\)

$$\begin{aligned} w=\frac{E \hbox {exp}\left( -\frac{7H}{10}\right) }{1+D}\left\{ \hbox {exp}\left( z\right) -\hbox {exp}\left( -Dz\right) \right\} \end{aligned}$$
(14)

where \( E=-C\lambda K\) is a constant; \(D = \frac{g}{RT}\) is a constant.

When, \(r_{1}\le r<r_{2}\) ; \(z> \frac{7H}{10}\) then

$$\begin{aligned} w=\frac{E \hbox {exp}\left( \frac{7H}{10}\right) }{D-1}\left\{ \hbox {exp}\left( -z\right) -\hbox {exp}\left\{ -Dz+z_{1}\left( D-1\right) \right\} \right\} \end{aligned}$$
(15)

where \( z_{1}\) is a constant height above \(\frac{7H}{10}\).

When \(r>R\) and \(z<\frac{7H}{10}\),

$$\begin{aligned} w=F \hbox {exp}(-Dz) \end{aligned}$$
(16)

where F is scaling constant.

When \(r>R\) and \(z>\frac{7H}{10}\) then,

$$\begin{aligned} w=G \hbox {exp}\left\{ -D(z-z_{1})\right\} \end{aligned}$$
(17)

5 Results and discussion

In this study we have assumed an analytic form of the radial velocity of a cyclone (Eq. 8) and hence calculated a suitable form of the transverse velocity on the sea surface and in the region close to the cyclone eye wall given by Eq. (13). From these the sea surface vortex rotation/swing can be measured. We have also defined a new critical parameter for cyclone stabilization called cyclone stability parameter (CSP) from which we can conclude for which specific value of the radial separation from cyclone axis will the vortices of cyclone be stabilized. Due to azimuthal symmetry the azimuthal angle dependency is not obtained in the three-component velocities. The expression of radial velocity as obtained both within eye wall and beyond eye wall is according to the general structure of the penultimate stages of the life cycle, viz. tropical storm and hurricane stage of tropical cyclones. The numerical value of the proportionality constants is estimated from Table 1 which has been obtained utilizing the velocity model of cyclone dynamics as has been suggested from ‘lectures on tropical cyclones’ by Smith (2006). The expressions of the cross-radial velocity (at sea level in the vicinity of the eye wall) and the vertical velocity (for all possible cases of the radial location of the field point) are obtained by solving the Navier–Stokes equation (with WKB approximation) in analytical way. Figure 1a gives the description of the inner core general structure of a tropical cyclone. This structure has been conceived from ‘lectures on tropical cyclone’ by Smith (2006). Figure 2b gives the rotating cylinder analogue of Fig. 1a. The most innermost portion is called the eye of a cyclone where the cyclone dynamics is calm. After eye comes the wall cloud and spiral bands portion where the cyclone is most destructive. The intensity of the cyclone hence decreases from the cirrus overcast and cirrus outflow region. In Figs. 2 and 3 the variation of the radial velocity w.r.t. radial distance of separation from the cyclone axis (r) and the vertical distance of separation from the sea level (z) are plotted. It is quiet clear that the radial velocity achieves maximum value around the wall cloud radius and at a height of 14 Km above sea level. In Figs. 4 and 5 the cross-radial or tangential velocity is plotted w.r.t. r and the vertical velocity is plotted w.r.t. z respectively. The cross-vertical velocity becomes maximum for \(z= 14\,\hbox {Km}\) above sea level, and when the cross-radial velocity is plotted w.r.t. r, it decreases with increase in r. Lastly in Fig. 6 the CSP is plotted w.r.t. r. There is also a break in the graph for r around 14 Km. This is due to the transition of the cyclone from eye to eye wall. Also Fig. 6 shows the CSP value becomes maximum in the eye of the cyclone and decreases with the increase in radial distance of separation from cyclone axis. So accordingly we can say that the cyclone stability is more for low values of the radial distance of separation from cyclone axis than for high values.

6 Conclusions

In this work we have done a broad analysis of tropical cyclone dynamics in the form of solving the guiding equation of motion. With the help of some basic assumptions like the WKB approximation, the complex Navier–Stokes equation is solved semi-analytically for a fluid parcel and the three-component velocities of a certain point of a tropical cyclone have been addressed. These results also abide by the actual dynamics of a cyclone as has been suggested by Smith (2006). We have also estimated a critical parameter named as CSP which gives handsome physical explanation regarding the genesis of a tropical cyclone from a disturbance in the weather. In future one can address the problem of cyclone genesis with real data and forecast well in advance that which depression will become a cyclone.