1 Introduction

In the last four decades, numerical models of Numerical Weather Prediction (NWP) and climate have evolved significantly, mainly in the design of new parameterizations and development of numerical codes, as well as computational advances with the advent of high-performance computing (HPC)—(Bauer et al. 2015; Váňa et al. 2017). The NWP and climate models are described by differential equations representing variability in time and space (Kalnay 2003; Warner 2010). These models can identify and track hurricanes and, therefore, evaluate the disasters caused in the economic and environmental sphere (Osuri et al. 2013; Luitel et al. 2018).

Tropical cyclones are usually associated with hurricanes with high-energy, highly destructible weather systems that cause massive material damage in coastal areas that exceed one billion dollars a year, as well as loss of human life (Knutson et al. 2019; Martinez 2020).

In recent years, several studies have pointed out that the damage caused by tropical cyclones (such as storms, ocean waves, and floods) depends heavily on the extent of maximum winds, in addition to the interference of climate change (Powell and Reinhold 2007; Zhao and Held 2010a, b; Knutson et al. 2019, 2020).

Thus, the numerical representation of maximum winds is fundamental for a more realistic definition of both systems preceding this event and the intensity of tropical cyclones. In the 1980s, Holland (1980) proposed a parametric radial profile of hurricane winds, being the basis for a broad study regarding the intensity of tropical cyclones. Chavas and Lin (2016) developed a simple physical model for the radial structure of the azimuthal wind at low levels within a hurricane, identifying that wind variability was directly linked to its external parameters, for example, the maximum wind speed and maximum wind radius. Previously, Smith (1980) and Tang and Emanuel (2012) identified that the most turbulent aspect of a hurricane might be associated with changes as opposed to the radius of maximum winds (Vigh et al. 2012).

A parametric representation of the pressure and wind fields in tropical cyclones, hurricanes, and typhoons facilitated the robust representation of these atmospheric systems (Schloemer 1954; Bryan and Rotunno 2009; Vickery 2005). In addition, the behavior and relationships between the various parameters, for example, pressure decay, maximum speed, and maximum wind speed radius, contribute to a better understanding of tropical cyclones (Willoughby and Rahn 2004). Vickery et al. (2009) mentioned that parametric models assist in constructing synthetic storm systems to allow the modeling of intense winds. Moreover, Olfateh et al. (2017) identified that winds from tropical cyclones, hurricanes, and typhoons could change from a perfectly asymmetric vortex movement to an asymmetric, radial, and/or azimuthal with the system’s eye.

It is important to highlight that the presence of asymmetric convection due to the friction of the lower planetary boundary layer (PBL), the southern gradients of Coriolis acceleration aid the generation or intensification of wind and pressure asymmetry in the system (Holland 1980; Olfateh et al. 2017). However, these models lack parameters for describing asymmetric properties for tropical cyclones, such as maximum wind (Vickery and Wadhera 2008; Olfateh et al. 2017). Therefore, a parametric model with greater precision can improve studies on tropical cyclones. For example, Xie et al. (2011) investigated the effects of wind asymmetry in four hurricanes and identified that 30% of the measured data presented wind asymmetry, contributing to an increase of up to 16% in the height of ocean waves associated with severe storms.

Several empirical formulations existing in the literature use the calculation of the maximum radius (Rmax) under asymmetric conditions (Knaff et al. 2007; Takagi et al. 2012). Among these methods, the one proposed by Xie et al. (2006) introduced significant wind rays in four quadrants, defined as R34, R50, R64, and Rmax, in which the first three were used to estimate Rmax. On the other hand, tropical cyclones, hurricanes, and typhoons have a wind structure based on two components in the northern hemisphere (NH): (i) the anti-clockwise rotation of the wind in the southern sector on the surface and (ii) the speed of translation of the storm (Elsner et al., 1999). This method has already been used in the literature by Lin and Chavas (2012) and Chavas et al. (2016), as they mathematically merged existing theoretical solutions for the radial wind structure at the top of PBL in the hurricane's internal ascending region. The authors used the solution Emanuel and Ratunno (2011) proposed, where the convective transfer of moisture and heat was persistent. The Emanuel solution (2004) was used for external convection to which the convection was absent.

Many studies in tropical cyclone modeling use aerodynamic formulas to identify angular momentum and enthalpy flows at the sea surface. These results show that the intensification of a hurricane is very sensitive, especially the values of the coefficients defined in these formulas (Emanuel 1995). The use of these formulations allows the model to make mass estimates of these flows as a function of wind speed.

The model proposed by Hu et al. (2012) consists of a parametric wind model for a hurricane based on asymmetric vortex models (Holland 1980). The authors included the impact of Coriolis deflection on the hurricane shape parameter. In addition, they the speed of translation of hurricanes prior to the application vortex Holland model (1980) to avoid excessive wind asymmetry.

The present study proposes:

  1. 1.

    Applications of parametric formulations to evaluate the spatial and punctual monitoring of tropical cyclones, hurricanes and typhoons;

  2. 2.

    Propose a new parameterization, in order to improve the ideal at Holland (1980).

2 Area of study and data

2.1 Tropical cyclone Ike

Hurricane Ike originated from a tropical wave on September 1st of 2008, about 775 miles west of the Cape Verde archipelago. The depression quickly intensified into a tropical storm, which became a hurricane on September 3rd of 2008, with its peak intensity on September 4th of 2008. Winds were estimated to reach 123 kt (category 4) when it was located 550 miles northeast (NE) from the Leeward Islands. However, Ike weakened and regained its Category 4 hurricane status shortly before hitting the Turks and Caicos Islands on September 7th of 2008 (NHC 2008).

Hurricane Ike turned into the West direction (W), hitting Cuba's NE coast early on September 8th of 2008, with maximum winds at 117 kt, category 4. On the same day, Ike moved toward the Mexican coast, with winds of 69 kt (category 1), which intensified over the Gulf of Mexico, where it moved northwest (NW). Then it gradually intensified when crossing the Gulf of Mexico toward the coast of Texas, USA. Finally, Ike hit the US coast on the morning of September 13th, being category 2, with winds of up to 95 kt. After entering the continent, Hurricane Ike weakened, becoming an extratropical cyclone (NHC 2008).

Hurricane Ike left a trail of deaths and destruction, killing 74 people in Haiti and two in the Dominican Republic. The Turks and Caicos Islands and the Southeastern (SE) of the Bahamas suffered widespread damage, where seven deaths were recorded in Cuba. In addition, Ike devastated the Bolivar Peninsula—Texas/USA, with huge waves and intense winds responsible for flooding and property damage to homes and buildings. Twenty-one people died in the United States, mainly in Texas, Louisiana, and Arkansas. In the Florida Keys, approximately 15,000 people were evacuated as Hurricane Ike approached the coast. The damage caused by Hurricane Ike was estimated at over US$60 million in the Turks and Caicos Islands, between US$50 million and US$200 million in the Bahamas, and between US$3 billion and US$4 billion in Cuba (NHC 2008).

2.2 Data

As a premise of the entire dynamic model, it is necessary to introduce initial conditions for its proper functioning. In this case, reanalysis data ERA5 was used as an entry condition (Hersbach et al. 2020). The variables used as initial conditions were: (i) Sea-Level Pressure (SLP, kPa), zonal (u, m.s−1) and meridional (v, m.s−1) winds (all levels), Air temperature (Tair, ºC)—(all levels), Relative Humidity (RH, %)—(all levers) and Sea Surface Temperature (SST, ºC). In spatial discretization, the values and derivatives of the variables used in the model were represented in discrete points on a regular grid, with Latitude (Lat, º) and Longitude (Lon, º). It is noteworthy that the spectral method was used once that it has advantages of calculating the differential terms of dynamic conditions, with a spacing of 0.5° latitude and longitude and an integration of 6 h in time.

3 Model idealization—contextualization

Previously, several models used analytical parametric formulations that represent radial wind profiles in tropical cyclones (Holland et al. 2010). The schemes are "parametric" when the variation of the radial wind depends only on some parameters, such as maximum wind, maximum wind radius, and central pressure (Holland et al. 1984; Holland et al. 2010). The simplicity, computational cost, and spatial resolution favor the use of parametric winds to assess wind return periods in tropical cyclones, hurricanes, and typhoons and still manage to model the risk of these events (Vickery and Twisdale 1995; Holland et al. 2010; Bhardwaj et al. 2020). The equations mentioned here explore the basic structure of hurricanes, in which surface pressure decreases exponentially toward the center of the hurricane and stabilizes in the hurricane’s eye. However, winds increase exponentially in reverse toward the eye wall. Schloemer (1954) mentioned that the radial wind evolved the formulation of Rankine's combined vortex, in which the rotation of a solid body is assumed within the eye wall, and thus, tangential winds decrease on a radial scale to a rectangular hyperbolic approach. Therefore, this article will use the scheme proposed by Holland (1980), in which the radial wind profile presents significant variations in the winds of tropical cyclones. Holland (1980) modified the equation proposed by Scholoemer (1954) to represent a spectrum of rectangular hyperbole with pressure variation.

Although widely used, the formulation proposed by Holland (1980) is known for presenting some limitations, one of which is the non-representation of the walls of the Hurricane eye in a double way. Another limitation is the inability to accurately represent the winds of the eye wall and the external core simultaneously, on the other hand, it can identify the external wind profile with some precision but fails to capture the rapid decrease of wind outside the eye wall, which in several cases occurs the underestimation of the maximum wind (Vmax). However, the greatest limitation scan of Holland's model (1980) is 2D projection, which implies symmetrical vortices. Unfortunately, winds in tropical cyclones are rarely symmetrical, especially when the system enters the Earth's surface. Xie et al. (2006) improved Holland model (1980) by considering asymmetry. Then, Mattocks and Forbes (2008) developed an asymmetric wind model based on Xie et al. (2006), in which they employ a storm wave model. In this model, the authors replaced Rm with a directionally variable (Rm(h)), where h is the azimuthal angle around the storm's center, improving the wind field estimation in tropical cyclones.

3.1 Initial spin up

Systems associated with supercells, such as tornadoes, are formed by the horizontal wind inclination, while tropical cyclones are associated with convergence, i.e., rotation is always towards the low center (Kalourazi et al. 2020). During convergence, the angular momentum associated with the Earth's rotational motion is concentrated at the angular momentum and, therefore, associated with the hurricane's winds. Thus, the calculation of the absolute angular momentum is given by Eq. (1):

$$ AM = V_{\tan } \cdot R + \frac{1}{2}f_{c} \cdot R^{2} $$
(1)

where, \({V}_{tan}\) (m.s−1) is the tangential velocity in an R (km) radius of the hurricane center (Harasti 2003) and \({f}_{c}\) (s−1) is the Coriolis parameter. Thus, Eq. (1) shows the absolute angular momentum, meaning that this amount includes the relative angular momentum of the hurricane, followed by the angular momentum associated with the Earth's rotational motion.

This angular moment would be conserved if tropical cyclones did not experience surface friction as long as the air converged. Thus, the tangential wind velocity (\({V}_{tan}\)) in a smaller radius (\({R}_{final})\) could be created even if the air in some initial radius (\({R}_{init})\) did not have rotation \(({V}_{{tan}_{init}}=0)\). Therefore, the formulation was added to the model, in Eq. (2):

$$ V_{\tan } = \frac{{f_{c} }}{2} \cdot \left( {\frac{{R_{{{\text{init}}}}^{2} - R_{{{\text{final}}}}^{2} }}{{R_{{{\text{final}}}} }}} \right) $$
(2)

In tropical cyclones, it is known that frictional drag cannot be overlooked (Malkus and Riehl 1960; Wood and White 2011). Thus, tangential winds are smaller than those calculated in Eq. (2).

As wind acceleration in a hurricane intensifies, centrifugal force gains importance. Therefore, it is important to include in the model of the pressure gradient formulation, given by Eq. (3):

$$ \frac{\Delta p}{{\Delta R}} \cdot \frac{1}{\rho } = f_{c} \cdot V_{\tan } + \frac{{V_{\tan }^{2} }}{R} $$
(3)

where, \(\frac{\Delta p}{\Delta R}\) is the radial pressure gradient and ρ is the air density. The last term (\(\frac{{V}_{tan}^{2}}{R})\) represents centrifugal force.

Moreover, the gradient wind applies to all radius of the center storms, associated with the hurricane, and all latitudes. Except in the proximity of the bottom, within the PBL and in the top clouds (Yoshizumi 1968a, b; Wang et al. 2017).

For a rough approach, it is important to overlook the strength of Coriolis in the vicinity of the center of the most intense hurricanes, where winds are fast, however, the idea that the cyclotrophic wind can approach the tangential winds of the hurricane was introduced, Eq. (4):

$$ V_{{{\text{ciclo}}}} = V_{\tan } $$
(4)

This implies:

$$ V_{\tan } = \left( {\frac{R}{\rho } \cdot \frac{\Delta P}{{\Delta R}}} \right)^{\frac{1}{2}} $$
(5)

In a hurricane, the shallow drag of the sea causes the winds to spiral toward the eye wall. The gradient wind equation in PBL describes this flow well. If there was no such drag-related influx, the storms on the eyewall would not get hot and humid air, which would result in the hurricane dissipates. An important process is related to the upward storm currents in the eye wall, which move, and the air rises rapidly. In this way, the output is related to the air that moves cyclically from the PBL and is driven to the top of the hurricane by air currents in the eye wall quickly that its inertia, preventing it from changing instantly to an anticyclonic flow, that is, the output flow is initially moving in the wrong direction and around the top of the system.

The center of a hurricane is hotter than the surrounding air, and this occurs due to the release of latent heat (LH) by organized convection and adiabatic heating due to subsidence in the system's eye. In this way, the air rises adiabatically moist in the storm cluster, but after losing water due to precipitation, the air descends more adiabatically dry in the system’s eye.

It is known that a hurricane has a warm core and is surrounded by cold air. This thermal gradient, called the radial temperature gradient, causes a reversal of the pressure gradient with the increase of the altitude due to the thermal wind (Hart 2003).

Thus, to determine this pressure gradient, the pressure at sea level in the hurricane’s eye was defined as Pb, and in the surroundings, as Pb∞ tends to infinity (∞). At the top of the hurricane, it was set the central pressure with Pt, and around as already mentioned for Pb, the pressures tend to infinite Pt∞.

Thus, the pressure gradient (ΔP) at the top is: \(\Delta {P}_{t}={P}_{t\infty }-{P}_{te}\), i.e., the difference between the pressure at the top tending to infinity, minus the pressure at the top of the eye, so the proportionality between the pressure on the surface or base (suffix b): \(\Delta {P}_{b}={P}_{b\infty }-{P}_{be}\), so:

$$ \Delta P_{t} \approx a \cdot \Delta P_{b} - b \cdot \Delta T $$
(6)

In which, \(a=0.15\), being one-dimensional, \(b=0.7\, kPa/K (7\, hPa/K)\), and \(\Delta T={T}_{e}-{T}_{\infty }\) being the average temperature difference along the troposphere and thermal gradient (∆T) is always negative.

In this way, the tangential winds were considered, where these winds are spirals cyclically around the system’s eye, in the vicinity of the surface, but are spiraled anticyclonically near the top of the hurricane, that is, away from the system’s eye. Then, the tangential velocity decreases with altitude and eventually changes the signal. Thus, the Ideal Gases Law was used, in order to show how the tangential component of the wind (\(V_{tan}\)) varies with the altitude (h), Eq. (7):

$$ \left( {\frac{{2 \cdot V_{\tan } }}{R} + f_{c} } \right) \cdot \frac{{\Delta V_{\tan } }}{\Delta h} = \frac{g}{{\overline{T}}} \cdot \frac{\Delta T}{{\Delta R}} $$
(7)

where R is the radius, g the acceleration of gravity (9.8 m/s2), and \( \overline{T}\) the average temperature.

The reverse pressure derivation in relation to Eq. (6) was applied, obtaining the hypsometric equation to relate the pressure in the top of the hurricane's eye. Therefore, it was also applied to the surroundings of the eye, obtaining Eq. (8):

$$ \Delta P_{t} = P_{b\infty } \cdot {\text{EXP}}\left[ {\frac{{ - g \cdot h_{\max } }}{{\left( {R \cdot \overline{{T_{\infty } }} } \right)}}} \right] - P_{be} \cdot {\text{EXP}}\left[ {\frac{{ - g \cdot h_{\max } }}{{(R \cdot \overline{{T_{e} )}} }}} \right] $$
(8)

in which, \(P_{b} = (P_{b\infty } - \Delta P_{b}\)), where exponential terms are multiplied by\({P}_{b\infty }\). And finally, a first-order approach was used to these exponentials, generating Eq. (6). Where, \(a=EXP[\frac{-g\bullet {h}_{max}}{(R\bullet \overline{{T }_{e})}}]\), where this value is approximated to 0.15, and \(b=-[\frac{g\bullet {h}_{max}\bullet {P}_{b\infty }}{\left(R\bullet \overline{{T }_{e}}\bullet \overline{{T }_{\infty }}\right)}]\), having approximate value of \(0.7 \,kPa/K (7 hPa/K)\). Gravity acceleration (g), R the universal gas constant for dry air (R = 287.04 m2 s−2 K−1).

Although systems can be quite complex, the idealization of a model becomes necessary for a better understanding of the system. For example, one of the intensity measures of tropical cyclones is the pressure difference, according to Eq. (9):

$$ \Delta P_{\max } = P_{\infty } - P_{e} $$
(9)

Surface pressure distribution can be approximated by:

$$ \frac{\Delta P}{{\Delta P_{\max } }}\left\{ {\frac{1}{5} \cdot \left( {\frac{R}{{R_{0} }}} \right)^{4} } \right. \to {\text{for}} \,R \le R_{0} \quad {\text{and}}\quad \frac{\Delta P}{{\Delta P_{\max } }}\left\{ {1 - \frac{4}{5} \cdot \frac{{R_{0} }}{R}} \right. \to {\text{for }}R > R_{0} $$
(10)

In which \(\Delta P = P\left( R \right) - P_{e}\), R is the radial distance from the center of the eye, \(R_{0} \) is the critical radius where maximum tangential winds are identified. In this model, \({R}_{0}\) has twice the radius of the eye.

To form a hurricane, winds must be at least 33 m.s−1 in the vicinity of the surface. It is important to mention that as the pressure at sea level in the hurricane’s eye decreases, the maximum tangential winds (\({V}_{max}\)) around the eye increase.

The maximum wind radius (\({V}_{max}\)) refers to the distance from the center of the system to the location within its structure where vmax occurs. The maximum radius (\({R}_{max}\)) plays a significant role in the characteristics of the system. Graham and Nunn (1959) suggested to Eq. (11), where \({R}_{max}\) is a function of latitude, a difference of central surface pressure and ambient pressure, as well as the speed of translation of the hurricane (Kalourazi et al. 2020).

$$ R_{\max } \,= \,28.25 \cdot {\text{tang}}[0.0873 \cdot \left( {\emptyset - 28} \right) + 12.22 \cdot \exp \left( {\frac{{\Delta P_{\max } }}{33.86}} \right) + 0.2 \cdot V_{\max } + 37.2 $$
(11)

In which, ∅ is the latitude of the center of the hurricane, \({\Delta P}_{max}\) is the maximum pressure gradient (Eq. 9), and \({V}_{max}\) the maximum wind obtained through \({V}_{max}=K{\left({\Delta P}_{max}\right)}^\frac{1}{2}\), being K = 13.4 is a proportionality constant (Atkinson and Holliday 1977).

As the winds were considered cyclotrophic (drag against the sea surface and the Coriolis force were neglected), then the previous approach to pressure distribution (Eq. 11) was used to give a tangential velocity distribution near the surface.

$$ \frac{{V_{\tan } }}{{V_{\max } }}\left\{ {\left( {\frac{R}{{R_{0} }}} \right)^{2} } \right. \to {\text{for}} \,R \le R_{0} \,{\text{and}}\, \frac{{V_{\tan } }}{{V_{\max } }}\left\{ {\left( {\frac{{R_{0} }}{R}} \right)^{\frac{1}{2}} } \right. \to {\text{for}} \,R > R_{0} $$
(12)

where \({R}_{0}\) is the maximum speed occurs in the critical radius.

It is important to mention that the total wind speed relative to the surface is the vector sum of the translation speed and the speed of rotation.

3.2 Radial velocity

In a hurricane, the air near the surface is "trapped" below the top of the PBL, with the air converging horizontally toward the eye wall (Merril 1984), so horizontal continuity in cylindrical coordinates requires:

$$ V_{{{\text{rad}}}} \cdot R = {\text{Constant}} $$
(13)

where \({V}_{rad}\) is the component of radial velocity, and negative for the influx. Therefore, it starts away from the hurricane, as R slows down toward R0, and the magnitude of the influx should increase (Weatherford and Gray 1988).

Equation (14) considers the previous assumptions, and the relationship between the \({V}_{rad}\) and the speed \(V_{\max }\) according to the following equations:

$$ \frac{{V_{{{\text{rad}}}} }}{{V_{\max } }} = \left\{ { - \frac{R}{{R_{0} }} \cdot \left[ {\frac{1}{5} \cdot \left( {\frac{R}{{R_{0} }}} \right)^{3} + \frac{1}{2} \cdot \frac{{\omega_{S} }}{{V_{\max } }} \cdot \frac{{R_{0} }}{{h_{i} }}} \right] \to } \right.for \, R \le R_{0} $$
(14a)
$$ \frac{{V_{{{\text{rad}}}} }}{{V_{\max } }} = \left\{ { - \frac{{R_{0} }}{R} \cdot \left[ {\frac{1}{5} + \frac{1}{2} \cdot \frac{{\omega_{S} }}{{V_{\max } }} \cdot \frac{{R_{0} }}{{h_{i} }}} \right] \to } \right.{\text{for}} \,R > R_{0} $$
(14b)

where, \({\omega }_{S}\) is negative and represents the average subsidence velocity in the hurricane’s eye, i.e., the horizontal area of the eye, gives the total kinematic mass flow. The \({h}_{i}\) is the depth of the boundary layer, being constant in 1000 m. While \({V}_{max}\) is the maximum tangential speed.

3.3 Vertical speed

When the rays are smaller than R0, the air converges quickly and accumulates, then ascends out of the PBL as convection inside the eye wall. Thus, the vertical velocity to the top of the PBL is represented by the equation of mass continuity (Gray 1968), according to Eq. (15):

$$ \frac{\omega }{{V_{\max } }} = \left\{ {\frac{{h_{i} }}{{R_{0} }} \cdot \left( {\frac{R}{{R_{0} }}} \right)^{3} + \frac{{\omega_{s} }}{{V_{\max } }} \to {\text{for}} \,R < R_{0} } \right. $$
(15)

\(\frac{\omega }{{V_{max} }} = 0\) for R > R0.

For simplification, the upward movement in the regions where there is precipitation is neglected, that is, when R > R0. In addition, \({\omega }_{s}\) is negative for subsidence. However, subsidence acts only within the eye, but the above ratio applies to all places within the R0 to simplify.

3.4 Thermal conditions

Assuming that the difference between the eye and the surroundings at the top of the hurricane is equal to and opposite to the bottom, generating Eq. (16):

$$ \Delta T\left( R \right) = c \cdot \left[ {\Delta P_{\max } - \Delta P\left( R \right)} \right] $$
(16)

where, \(c = 1.64\frac{K}{kPa}\). The pressure difference at the bottom is \(\Delta P = P\left( R \right) - P_{e}\), where the temperature difference calculated over the entire depth of the hurricane is (Rotunno and Emanuel 1987): \(\Delta T\left( R \right) = T_{e} - T\left( R \right)\), according to Eq. (17):

$$ \frac{\Delta T}{{\Delta T_{\max } }} = \left\{ {1 - \frac{1}{5}\left( {\frac{R}{{R_{0} }}} \right)^{4} \to {\text{for}} \,R \le R_{0} } \right. $$
(17a)
$$ \frac{\Delta T}{{\Delta T_{\max } }} = \left\{ {\frac{4}{5} \cdot \frac{{R_{0} }}{R} \to {\text{for}} \,R > R_{0} } \right. $$
(17b)

where, \(\Delta T_{\max } = T_{e} - T_{\infty } = c \cdot \Delta P_{\max }\), e \(c = 1.64\frac{K}{kPa}.\)

Entropy is another variable related to the activities of a hurricane because these systems are atmospheric structures that dissipate energy efficiently through irreversible processes. Bister and Emanuel (1998) mentioned that entropy in a hurricane grows by exchanging enthalpy of the sea surface in latent vaporization heat (lv) and by turbulent dissipation of kinetic energy in PBL.

The dynamic conditions required for the formation of a hurricane are related to low vertical wind shear, increased Coriolis force, and a convection trigger, through tropical atmospheric waves, tropospheric depressions (Tapiador et al. 2007). Therefore, the hurricane is a very efficient heat machine, which maintains itself, where it dissipates energy as efficiently as possible, but in order to occur, there has to be excess energy supply (Bister and Emanuel 1998). In other words, hurricanes are efficient heat systems, or almost perfect machines in energy dissipation, removing enthalpy energy in the low troposphere and dissipating it through radiative restrained at the upper levels of the troposphere (Emanuel 2003). Thus, the entropy condition (S) was introduced to the model to verify this thermal efficiency, according to Eq. (18):

$$ S = c_{p} \cdot \ln \left( {\frac{T}{{T_{0} }}} \right) + \frac{{l_{v} \cdot r}}{T} - R \cdot \ln \left( {\frac{P}{{P_{0} }}} \right) $$
(18)

where, \({c}_{p}=1004\, J{kg}^{-1}{K}^{-1}\) is the specific heat of the air at a constant pressure, T is the absolute temperature, \({l}_{v}=2500\, J/{g}_{\mathrm{water vapor}}\) is the latent heat of vaporization, r is the mixing ratio, \(R=287 \,{\mathrm{Jkg}}^{-1}{\mathrm{K}}^{-1}\) is the ideal gas constant, P is the pressure, T0 = 273.15 K, and P0 = 1000 hPa, are arbitrary reference values.

4 Results and discussion

4.1 Punctual analysis

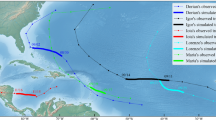
Figure 1 shows the hurricane's Ike trajectory in September of 2008 based on the data available by the National Hurricane Center (NHC)—(NHC 2008) and estimated by the model idealized in this work. It is important to mention that a geostrophic adjustment has been made in the field of Mean Sea Level Pressure (MSLP) to adjust the minimum pressure identified for a relationship close to the real, that is, the decay rate of this pressure is directly correlated with the relative cyclonic vorticity gain of the system, followed by the wind intensity, whether geostrophic or vertical. Furthermore, to make the criterion independent of latitude, the pressure decay rate was geostrophically adjusted for a given reference latitude, according to Eq. (19):

$$ \frac{{{\text{dP}}}}{{{\text{dt}}}} = \left( {\frac{{{\text{dP}}}}{{{\text{dt}}}}} \right) \cdot \left( {\frac{{{\text{sen}}\varphi_{{{\text{ref}}}} }}{{{\text{sen}}\varphi }}} \right) $$
(19)

where \(\frac{dP}{{dt}}\) represents the decay rate of the system, \(\varphi\) is the latitude of the center of the system, and \(\varphi_{ref}\) is the reference latitude, defined as 25°N.

Fig. 1
figure 1

Observed trajectory (red line) and predicted by the idealized model (black line) of Hurricane Ike, between 3 and 12 September 2008

Full size image

When analyzing Fig. 1, it was possible to identify similarity between the observed trajectory (red line) and that predicted by the idealized model (black line), except for dissimilarity between the trajectories close to the latitude of 23 °N and longitude of 78° W, where the idealized model tends to anticipate and rewind the trajectory with the trajectory of observation (red line). In the later trajectories, there was quite a similarity based on the root-mean-square error (RMSE) between positions and trajectories was of the order of 0.502°, which equates to approximately 98 miles or 157.7 km.

Regarding dynamic conditions such as azimuthal tangential velocity (Fig. 2), again the idealized model could simulate the relationship between normalized tangential velocity and the radial distance also normalized for two distinct moments of the hurricane (0600 UTC on September 4th, 2008—when the system is at its maximum intensity; and when the system reaches the coast, 1200 UTC on September 12th, 2008).

Fig. 2
figure 2

Normalized radial wind velocity (m.s−1) and normalized radial distance (km) for two different days. 0600 UTC—September 4th (observed—Blue line; Model—Orange dashed line) and 1200 UTC—September 12th (observed—Lilac line; Model—Yellow dashed line)

Full size image

The first peak of the azimuthal tangential velocity occurred between 60 and 110 km from the center of the system, where the model (dashed orange line) anticipated this maximum to observation (blue line continues). After the maximum azimuthal tangential wind, there is a decrease in intensity when it moves away from the eye wall of the hurricane, but the model has an oscillation when compared to the observation (Wood and White 2011).

Then, at 1200 UTC on September 12th, there was convergence in the maximum azimuthal tangential velocity of the model (dashed yellow line), and the observation (continuous lilac line) highlighted that the hurricane was already in the process of dissipating intensity (NHC 2008).

Then, at 1200 UTC on September 12th, there was convergence in the maximum azimuthal tangential velocity of the model (dashed yellow line), and the observation (continuous lilac line) highlighted that the hurricane was already in the process of dissipating intensity (NHC 2008). Therefore, the azimuthal tangential wind predicted by the idealized model appears as an important factor, which characterized similar oscillation as identified by the observation, that is, oscillation when moving away from the eye wall to the idealized model and linear decrease observed when it moves away from its maximum. The RMSE between the observation and the model idealized for 0600 UTC on September 4th, 2008 was 0.98 m/s and 0.99 m/s for 1200 UTC on September 12th, 2008. Thus, as we move away from the hurricane center, the vortex at the edge of the eye loses its effect, while speeds begin to follow a standard logarithmic profile, identified in Fig. 2 at both times.

In a hurricane, the air has mass and acquires tangential velocity when it enters the circulation at a certain distance from the system's center, where mass has angular momentum.

The angular moment of this air mass in the cyclonic circulation is preserved because only the external torque changes the angular momentum, and much of this torque is represented by the torques of friction with the sea surface itself (Vigh and Schubert 2009; Knutson et al. 2019). As the air mass approaches the cyclonic center over time, the ascending air column acts as a "vacuum cleaner" resulting from the pressure gradient force and thus gains tangential velocity so that the angular momentum is conserved (Holland and Merrill 1984; Knutson et al. 2019).

4.2 Spatial analysis

4.2.1 Tangential speed

The wind speed in a hurricane suffers asymmetry due to the system's advancing speed. A simple overlap of hurricane advancing speed and maximum wind drives the higher speeds of the hurricane's right side in the HN (Holland and Merrill 1984). In Fig. 3, between September 8th and 13th, the tangential winds were quite intense to the right of the hurricane's advance, to which this effect can be included in an asymmetric model. Another significant factor was the asymmetry in the drag force at the lower limit, due to the asymmetry of the wind speed due to the speed of advance of the hurricane, which introduces asymmetric convection and an asymmetric wind distribution in the PBL (Holland and Merrill 1984).

Fig. 3
figure 3

Tangential Wind (m/s) around hurricane Ike, 0000 UTC 08 September 2008 to 0000 UTC 13 September 2008. The m and n are zoom for around hurricane in 0600 and 1200 UTC 12 September 2008

Full size image

4.2.2 Maximum speed

In the idealized model, the height of the PBL delimited was 100 m. This procedure, along with other dynamic forces, resulted in higher wind speed, as mentioned earlier on the hurricane's right side in the HN. Shapiro (1983) identified this configuration by numerical means, followed by Kepert (2001) by analytical method. Kepert (2001) used a solution where PBL was disturbed in the conservation equation of momentum and, thus, considered the drag forces and the vertical turbulent diffusion of the momentum. Another factor identified in the study was d linked to the linear effect of the hurricane's advancing velocity. The idealized model included using an exponential radial reduction coefficient, as previously suggested by Schwerdt et al. (1979).

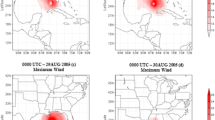
This condition previously mentioned was explained in Fig. 4, where the maximum velocity was identified to the right of the hurricane's trajectory. This maximum wind (Vmax) is the vector sum of the translation speed and rotation speed. Therefore, in this quadrant, the right of the translation allocation movement, it was identified that the Vmax was present, and hurricanes are faster in this quadrant.

Fig. 4
figure 4

Maximum Wind (m/s) around hurricane Ike, 0000 UTC 08 September 2008 to 0000 UTC 13 September 2008. The m and n are zoom for around hurricane in 0600 and 1200 UTC 12 September 2008

Full size image

In the left part of the hurricane, the translation allocated velocity is subtracted from tangential velocity so that the total or maximum velocity in this quadrant (left) is not as intense as in the right quadrant. On September 12th and 13th at 0000 UTC, we identify is this condition, with greater intensity in the right quadrant of Hurricane Ike (Fig. 4e, f).

4.2.3 Radial speed

When idealizing a hurricane, it is known that PBL air is confined below the top of this layer, as the air converges horizontally towards the eye wall (Ghosh and Chakravarty 2018). As the wind speed increases in the direction of the eye wall, the height of the sea surface tends to "couple" radial and tangential velocities. Figure 5 shows a higher radial velocity located in the right quadrant of the system's direction of displacement. This configuration can occur due to a drag-induced influx between air and the sea surface. This influx eventually converges the ascent through the PBL and radial pumping process. As a result, vertical velocity and relative vorticity move radially out, reinforcing that this configuration was identified in Fig. 5, following the asymmetric conservation of surface drag, according to Shapiro (1983).

Fig. 5
figure 5

Radial wind (m.s−1) around hurricane Ike, 0000 UTC 08 September 2008 to 0000 UTC 13 September 2008. The m and n are zoom for around hurricane in 0600 and 1200 UTC 12 September 2008

Full size image

4.2.4 Ekman transport

Ekman's spiral describes how the current direction and velocity vary with depth. The Ekman's liquid transport accumulated at all depths is perpendicular to the surface wind direction. As with the radial velocity in NH, the liquid transport of seawater is to the right of the maximum wind (Vincent et al. 2013). Then, as the hurricane approaches the continent, winds along its front and right edge become almost parallel to the coast (Fig. 6), and consequently, there is a liquid Ekman's transport directly to the coast.

Fig. 6
figure 6

Ekman transport (m2/s) around hurricane Ike, 0000 UTC 08 September 2008 to 0000 UTC 13 September 2008. The m and n are zoom for around hurricane in 0600 and 1200 UTC 12 September 2008

Full size image

If the hurricane "hovered" along the coast long enough to allow the development of a steady-state condition, thus, Ekman's transport toward the coast would be balanced by the slope of the swell (Vincent et al. 2013). This process shown by the idealized model (Fig. 6) corroborates with the results obtained by Jullien et al. (2012). In addition, the authors suggest that the winds of a hurricane intensify the wind strain wave in the center of a hurricane's basin and thus contribute to a background Ekman pumping (Bueti et al. 2014).

Furthermore, it is worth noting that the influence of Ekman's transport was not deepened in the study. However, it was necessary, especially in oceanic conditions, due to the displacement of the thermocline after the passage of a storm resembles Ekman's solution, as suggested by Gill (1982) in an inertial oscillation.

As a hurricane has a high range, the most relevant Ekman transport is in the quadrant to the right of the hurricane shift. In this way, the amount of water accumulates higher between the hurricane and the continental coast and south of the system (Fig. 6), this creates waves, and these waves always travel with the coast to their right, so that there is a higher amplitude.

4.2.5 Entropy

The maximum increase in moist entropy and the tropopause temperature determines the wind speed on the eye wall. The energy production of LE and sensitive (H) flows because more heat generated by viscous dissipation applies and balances friction dissipation (Bister and Emanuel 1998).

High SST values increase the balance of moist air entropy (S*) and energy production under the eye wall (Emanuel 1995). However, the imbalance of wet entropy on the eye wall was also influenced by the air thermodynamic characteristics when it approaches the eye wall. Therefore, the flow of air entering the eye wall region with higher wet entropy will have a minor imbalance in the ocean–atmosphere system and less energy production under the eye wall.

Figure 7 displays entropy for the period September 8–13th, 2008. There is a "pocket" of entropy around the hurricane’s eye (with variations between 400 and 402 J.kg−1.K−1). This process showed the thermal efficiency of the hurricane because it converts thermal energy into mechanical energy (Emanuel 1995).

Fig. 7
figure 7

Entropy (J kg−1 K−1) around hurricane Ike, 0000 UTC 08 September 2008 to 0000 UTC 13 September 2008. The m and n are zoom for around hurricane in 0600 and 1200 UTC 12 September 2008

Full size image

Thus, by assuming the eye wall is in the Maximum Wind Radius (MWR). Outside the MWR, the air temperature is radially constant, as the flow of H to air over the ocean, which in turn balances gradual adiabatic cooling as a function of decreased pressure. Therefore, it is worth noting that relative humidity (RH) remained with its environmental values outside the MWR once that it was identified that the air moisture flows over the ocean were balanced by the turbulent flows at the top of PBL.

5 Conclusions

Hurricane Ike's passage resulted in 80 fatalities and a loss of more than US$ 4 billion (NHC 2008) across the Caribbean and the southeastern United States. Therefore, like every hurricane, predictability is paramount for preventing loss of life and property damage. To this end, the idealized model based on parametric formulations fed from initial conditions (ERA5 reanalysis) showed similarity in the trajectory between the geographic coordinates of the minimum pressure during the life of the hurricane with the lowest error (RMSE = 0.502°–157 km).

The relationship between observation and prediction by the azimuthal tangential velocity model is satisfactory mainly in the eye wall, with lower errors obtained. However, it is noteworthy that the idealized model identified a decrease in wind intensity after reaching the maximum azimuthal tangential wind.

Spatially, the highest tangential velocities occur on the hurricane's right side, directly related to the drag force's asymmetry due to the hurricane's advance, which the idealized model well represented.

The maximum winds occurred to the right of the hurricane's trajectory due the cyclonic movement of the hurricane and a radial exponent reduction, as shown by the idealized model. In addition, this simple model presented satisfactory results for a Category 4 Hurricane, which can be very useful in weather forecasting centers around the world in identifying and assessing hurricanes.

The comparison between the modeled and the observation was not performed, mainly in Figs. 3, 4, 5, 6, 7, as there are no spatial observations that can compare the results of the model and the real one. We remind you that our purpose with these new parameterizations is to add new formulations that can be used in future studies to improve the predictability of tropical cyclones, hurricanes and typhoons.