A $C^{1}-C^{0}$ conforming virtual element discretization for the transmission eigenvalue problem

Abstract

In this study, we present and analyze a virtual element discretization for a nonselfadjoint fourth-order eigenvalue problem derived from the transmission eigenvalue problem. Using suitable projection operators, the sesquilinear forms are discretized by only using the proposed degrees of freedom associated with the virtual spaces. Under standard assumptions on the polygonal meshes, we show that the resulting scheme provides a correct approximation of the spectrum and prove an optimal-order error estimate for the eigenfunctions and a double order for the eigenvalues. Finally, we present some numerical experiments illustrating the behavior of the virtual scheme on different families of meshes.

1 Introduction

This paper deals with the numerical approximation by the virtual element method (VEM) [5] of the transmission eigenvalue problem. This problem has important applications in inverse scattering. For instance, it can be used to obtain estimates for the material properties of the scattering object and have a theoretical importance for the analysis of reconstruction in inverse scattering theory. For these reasons, this problem has attracted much interest in the last years.

From the mathematical point of view, the transmission eigenvalue problem is nonstandard and difficult to treat. As a consequence, different variational formulations have been proposed and analyzed to solve the eigenvalue problem. More precisely, the problem can be formulated as a fourth-order quadratic eigenvalue problem, as a mixed eigenvalue problem, among others. Several conforming and nonconforming finite element methods, mixed formulations have been proposed during the last years. We cite as a minimal sample of them [14,15,16, 20, 23, 26, 32, 41, 44, 47].

Among the existing techniques, in [15] it has been introduced and analyzed a variational formulation in $H^2(\varOmega )\times H^1(\varOmega )$. The resulting variational problem is obtained by considering an additional second-order elliptic problem to write a double-size linear eigenvalue problem. By using Argyris and Lagrange finite element spaces, a conforming discretization is proposed. A complete analysis of the method including error estimates is proved using the theory for compact nonselfadjoint operators. Following a similar approach, in [46] it has been written a weak formulation in $H^2(\varOmega )\times L^2(\varOmega )$ for the transmission eigenvalue problem which is based on a linearization technique by considering an additional unknown in $L^2$. The authors have proposed a conforming $C^1-C^1$ finite element discretization in 2D and 3D, and error estimates have been obtained. We recall that fourth-order problems require the use of globally $C^1$ polynomial spaces. The construction of $C^1$-conforming finite elements is difficult in general, since they usually involve a large number of degrees of freedom [21]; thus, they are often viewed as prohibitively expensive due to their high polynomial degree.

The VEM is a recent technology introduced in [5] as a generalization of finite element method which among its advantages permits to easily implement highly regular conforming discrete spaces. This makes the method very feasible to solve fourth-order problems [2, 3, 7, 9, 13, 35]. The method has been also used to solve eigenvalue problems, among which we mention the following recent works [8, 11, 18, 19, 24, 25, 29,30,31, 33,34,35, 37].

Regarding the approximation by VEM of the transmission eigenvalue problem, in [36] it has been presented a $C^1-C^0$-conforming virtual element method to solve the spectral problem on general polygonal meshes. This scheme is based on the formulation presented in [15]. Optimal-order error estimates for the eigenfunctions and a double order for the eigenvalues are derived. More recently, in [38] it has been introduced and analyzed a conforming $C^1-C^1$ VEM on polytopal meshes by considering the variational formulation introduced in [46]. Optimal-order error estimates for the eigenfunctions and a double order for the eigenvalues are derived. The aim of this work is to consider the same continuous formulation as in [38, 46] and use a different discretization for the additional unknown introduced to transform the problem into an equivalent double-size linear eigenvalue. We remark that by considering this new discretization, we obtain a smaller generalized eigenvalue problem.

In the present paper, we consider a $C^1-C^0$-conforming virtual element method to solve the transmission eigenvalue problem. The variational formulation leads to a fourth-order quadratic eigenvalue problem, which is transformed into an equivalent double-size linear eigenvalue problem that fits within the functional framework for nonselfadjoint compact bounded operators. At the continuous level, we follow [39] to obtain an appropriate spectral characterization. Next, we propose a $C^1-C^0$-conforming virtual element approximation that applies to general polygonal meshes. More precisely, the scheme is based on the discrete space introduced in [2] for the Cahn-Hilliard equations and in [1] for the linear reaction-diffusion equation. We construct proper $\mathrm {L}^2$-projection operators that are used to approximate the sesquilinear form presented in the system. At the discrete level, we use once again [39] to prove that the spectrum is correctly approximated and to obtain error estimates.

Outline This paper is structured as follows: we introduce in Sect. 2 the interior transmission eigenvalue problem, first in terms of a system of second-order equations and then in an equivalent form as a linear nonselfadjoint fourth-order eigenvalue problem. In Sect. 3, we present the discrete spaces together with their properties. In Sect. 4, we construct the discrete sesquilinear forms by using the projection operators. Moreover, we introduce the virtual element discrete formulation. In Sect. 5, we present the error analysis of the virtual scheme. In Sect. 6, we report three numerical tests that allow us to assess the convergence properties of the virtual element scheme.

2 Model problem

The transmission eigenvalue problem can be stated as follows (see, for instance, [22, 42]). Find $k\in {\mathbb {C}}$ and $\psi ,\phi \in \mathrm {L}^2(\varOmega )$ with $\psi -\phi \in \mathrm {H}^2(\varOmega )$ such that

$$\begin{aligned} \varDelta \psi + k^2 n \psi =0&\quad \text{ in } \varOmega , \end{aligned}$$

(2.1a)

$$\begin{aligned} \varDelta \phi + k^2 \phi =0&\quad \text{ in } \varOmega , \end{aligned}$$

(2.1b)

$$\begin{aligned} \psi -\phi =0&\quad \text{ on } \varGamma , \end{aligned}$$

(2.1c)

$$\begin{aligned} \partial _\nu \psi - \partial _\nu \phi =0&\quad \text{ on } \varGamma . \end{aligned}$$

(2.1d)

System (2.1a)–(2.1d) corresponds to the scattering problem for an isotropic inhomogeneous medium for the Helmholtz equation, where $\varOmega \subseteq {\mathbb {R}}^2$ is a bounded simply connected Lipschitz domain with boundary $\varGamma :=\partial \varOmega$. Here, $\nu$ denotes the outward unit normal vector to $\varGamma$, $\partial _\nu$ denotes the normal derivative, and n is the index of refraction. We assume that $n({\varvec{x}})=:n\in \mathrm {W}^{2,\infty }(\varOmega )$ satisfying either one of the following assumptions for all ${\varvec{x}}\in \varOmega$:

$$\begin{aligned} \begin{aligned} 1<n_{*}\le n({\varvec{x}}) \le n^{*}<\infty ,\\ 0<n_{*}\le n({\varvec{x}}) \le n^{*}<1. \end{aligned} \end{aligned}$$

(2.2)

The transmission eigenvalue problem is often solved by reformulating it as a fourth-order eigenvalue problem. More precisely, by introducing a new unknown $u:=(\psi -\phi )\in \mathrm {H}_0^2(\varOmega )$, model problem (2.1a)–(2.1d) can be rewritten as follows:

$$\begin{aligned} \begin{aligned} (\varDelta + k^2 n )\frac{1}{n-1}(\varDelta + k^2)u=0\quad \text{ in } \varOmega . \end{aligned} \end{aligned}$$

(2.3)

In this section we introduce a continuous variational formulation associated with fourth-order transmission eigenvalue problem (cf. (2.3)) and its spectral characterization. With this aim, we multiply identity (2.3) by $w\in \mathrm {H}_0^2(\varOmega )$ and we arrive at the following quadratic eigenvalue problem: find $k\in {\mathbb {C}}$ and $u\in \mathrm {H}_0^2(\varOmega )$, $u\ne 0$ such that

$$\begin{aligned}&\int _\varOmega \frac{1}{n-1}\varDelta u \varDelta {\overline{w}} + k^2\int _\varOmega \varDelta u\Big ( \frac{n}{n-1} {\overline{w}}\Big )\nonumber \\&+ k^2 \int _\varOmega \frac{1}{n-1}u \varDelta {\overline{w}} + k^4\int _\varOmega \frac{n}{n-1}u{\overline{w}}=0 \quad \forall w\in \mathrm {H}_0^2(\varOmega ). \end{aligned}$$

(2.4)

One of the main difficulties of variational formulation (2.4) is the nonlinearity with respect to the parameter $k^2$. For the theoretical analysis it is convenient to transform the above variational problem into a double-size linear eigenvalue problem. There are different options to do that. In this work we will follow the approach used in [38, 45, 46]. More precisely, we consider an auxiliary variable denoted by z and defined as:

$$\begin{aligned} z&:= k^2 u\quad \text{ in } \varOmega . \end{aligned}$$

(2.5)

Now, we denote by ${\mathbf {H}}$ the product space ${\mathbf {H}}:=\mathrm {H}_0^2(\varOmega )\times \mathrm {L}^2(\varOmega )$, endowed with the following product norm

$$\begin{aligned} ||(w,v) ||_{{\mathbf {H}}}:= \big (||D^2 w||_{0,\varOmega }^2 + || v ||_{0,\varOmega }^2\big )^{1/2}, \end{aligned}$$

where $D^2 w$ denotes the Hessian matrix of w. Moreover, it is clear that the above norm is equivalent with the usual norm in $\mathrm {H}_0^2(\varOmega )\times \mathrm {L}^2(\varOmega )$.

Using (2.5) we arrive at the following weak formulation of the transmission eigenvalue problem:

Problem 1

Find $(\lambda ,(u,z))\in {\mathbb {C}}\times {\mathbf {H}}$ with $(u,z)\ne {\varvec{0}}$ such that

$$\begin{aligned}&\int _\varOmega \frac{1}{n-1}\varDelta u\varDelta {\overline{w}}+\int _\varOmega z{\overline{v}}\\&=\lambda \left( \int _\varOmega \varDelta u \Big (\frac{n}{n-1}{\overline{w}}\Big ) +\int _\varOmega \frac{1}{n-1}u \varDelta {\overline{w}} +\int _\varOmega \frac{n}{n-1} z {\overline{w}} -\int _\varOmega u{\overline{v}}\right) , \end{aligned}$$

for all $(w,v)\in {\mathbf {H}}$ and with $\lambda :=-k^2$.

In order to write the problem in a compact form, we introduce the following forms:

$$\begin{aligned}&{\mathcal {A}}:{\mathbf {H}}\times {\mathbf {H}}\rightarrow {\mathbb {C}},\quad {\mathcal {A}}((u,z),(w,v)):=\int _\varOmega \frac{1}{n-1}\varDelta u\varDelta {\overline{w}}+\int _\varOmega z{\overline{v}}, \end{aligned}$$

(2.6)

$$\begin{aligned}&{\mathcal {B}}:{\mathbf {H}}\times {\mathbf {H}}\rightarrow {\mathbb {C}},\quad {\mathcal {B}}((u,z),(w,v)):= \int _\varOmega \varDelta u \Big (\frac{n}{n-1}{\overline{w}}\Big ) +\int _\varOmega \frac{1}{n-1}u \varDelta {\overline{w}}\nonumber \\&+\int _\varOmega \frac{n}{n-1} z {\overline{w}} -\int _\varOmega u{\overline{v}}. \end{aligned}$$

(2.7)

Thus, the nonselfadjoint eigenvalue problem can be written as follows:

Problem 2

Find $(\lambda ,(u,z))\in {\mathbb {C}}\times {\mathbf {H}}$ with $(u,z)\ne {\varvec{0}}$ such that

$$\begin{aligned} {\mathcal {A}}((u,z),(w,v))=\lambda {\mathcal {B}}((u,z),(w,v))\qquad \forall (w,v)\in {\mathbf {H}}. \end{aligned}$$

The following lemma establishes some properties for the forms ${\mathcal {A}}(\cdot ,\cdot )$ and ${\mathcal {B}}(\cdot ,\cdot )$, which will play an important role in the analysis of the solution operator.

Lemma 1

There exist positive constants $\alpha _0$ and C that depend on the index of refraction n such that

$$\begin{aligned}&{\mathcal {A}}((w,v),(w,v))\ge \alpha _0 ||(w,v) ||_{{\mathbf {H}}}^2, \end{aligned}$$

(2.8)

$$\begin{aligned}&|{\mathcal {A}}((u,z),(w,v))|\le C ||(u,z) ||_{{\mathbf {H}}} ||(w,v) ||_{{\mathbf {H}}}, \end{aligned}$$

(2.9)

$$\begin{aligned}&|{\mathcal {B}}((u,z),(w,v))|\le C ||(u,z) ||_{{\mathbf {H}}} ||(w,v) ||_{{\mathbf {H}}}, \end{aligned}$$

(2.10)

for all $(u,z),(w,v)\in {\mathbf {H}}$.

According to Lemma 1, we are in a position to introduce the solution operator.

$$\begin{aligned} \begin{array}{cll} {\varvec{T}}: {\mathbf {H}}&{} \longrightarrow &{}\quad {\mathbf {H}}\\ \qquad (f,g)&{}\longmapsto &{}{\varvec{T}}(f,g)=({\widehat{u}},{\widehat{z}}) \end{array} \end{aligned}$$

defined as the unique solution of the following source problem (see Lemma 1):

$$\begin{aligned}&{\mathcal {A}}(({\widehat{u}},{\widehat{z}}),(w,v))={\mathcal {B}}((f,g),(w,v))\qquad \forall (w,v)\in {\mathbf {H}}. \end{aligned}$$

(2.11)

Thus, we have that the linear operator ${\varvec{T}}$ is well defined and bounded. Moreover, we have that $(\lambda ,(u,z))$ solves Problem 1 if and only if $(\mu ,(u,z))$ is an eigenpair of ${\varvec{T}}$, i.e., ${\varvec{T}}(u,z)=\mu (u,z)$, with $\mu :=1/\lambda$.

We observe that no spurious eigenvalues are introduced into the problem. In fact, if $\mu \ne 0$, then (0, z) is not an eigenfunction of the problem.

The following is an additional regularity result associated with the solution of source problem (2.11). The proof follows from the classical regularity result for the biharmonic problem (see for instance [10, 27, 40]).

Lemma 2

There exist $s\in (0,1]$ and a positive constant C depending on the index of refraction n such that for all $(f,g)\in {\mathbf {H}}$, the unique solution $({\widehat{u}},{\widehat{z}})$ of problem (2.11) satisfies $({\widehat{u}},{\widehat{z}})\in \mathrm {H}^{2+s}(\varOmega )\times \mathrm {H}_0^2(\varOmega )$ and

$$\begin{aligned} ||{\widehat{u}}||_{2+s,\varOmega } + ||{\widehat{z}}||_{2,\varOmega }\le C ||(f,g)||_{{\mathbf {H}}}. \end{aligned}$$

Proof

On the one hand, by testing problem (2.11) with $(w,0)\in {\mathbf {H}}$, we obtain a biharmonic problem with its right-hand side in $H^{-1}(\varOmega )$. Thus, the estimate for ${\widehat{u}}$ follows. On the other hand, by testing problem (2.11) with $(0,v)\in {\mathbf {H}}$, we obtain that ${\widehat{z}}=f\in \mathrm {H}_0^{2}(\varOmega )$ and we conclude the proof. $\square$

Now, as a consequence of Lemma 2 and the compact inclusion $\mathrm {H}^{2+s}(\varOmega )\times \mathrm {H}_0^2(\varOmega )\hookrightarrow {\mathbf {H}}$, we obtain that operator ${\varvec{T}}$ is compact. In addition, we have the following spectral characterization result.

Lemma 3

The spectrum of ${\varvec{T}}$ satisfies $\mathop {\mathrm {sp}}\nolimits ({\varvec{T}}) = \{0\}\cup \{\mu _k \}_{k\in {\mathbb {N}}}$, where $\{\mu _k \}_{k\in {\mathbb {N}}}$ is a sequence of complex eigenvalues which converges to 0 and their corresponding eigenspaces lie in $\mathrm {H}^{2+s}(\varOmega )\times \mathrm {H}^{2+s}(\varOmega )$ and

$$\begin{aligned} ||u||_{2+s,\varOmega } + ||z||_{2+s,\varOmega }\le C ||(u,z)||_{{\mathbf {H}}}. \end{aligned}$$

In addition, $\mu =0$ is not an eigenvalue of ${\varvec{T}}$.

3 Virtual element discretization

In this section, we will introduce the virtual element spaces (local and global) to be used in the discretization of Problem 2.

We begin with the mesh construction and the assumptions considered to introduce the discrete virtual element spaces (see e.g., [1, 5]). Let $\left\{ {\mathcal {T}}_h\right\} _{h>0}$ be a sequence of decompositions of $\varOmega$ into general polygonal elements $E$. We will denote by $h_E$ the diameter of the element $E$ and by h the maximum of the diameters of all the elements of the mesh, i.e., $h:=\max _{E\in {\mathcal {T}}_h}h_E$. In addition, we denote by $N_E$ and $N_{\mathop {\mathrm {\,v}}\nolimits }^{E}$ the number of polygons in ${\mathcal {T}}_{h}$ and the number of vertices of $E$, respectively. Moreover, we denote by e a generic edge of ${\mathcal {T}}_{h}$ and for all $e\in \partial E$, we define a unit normal vector $\nu _E^e$ that points outside of $E$.

As in [5], we need to assume regularity of the polygonal meshes in the following sense: there exists a positive real number $\gamma$ such that, for every h and every $E\in {\mathcal {T}}_h$,

A$_1$::

$E\in {\mathcal {T}}_h$ is star-shaped with respect to every point of a ball of radius $\gamma h_E$;

A$_2$::

the ratio between the shortest edge and the diameter $h_E$ of $E$ is larger than $\gamma$.

Now, for all $m\in {\mathbb {N}}$, we will denote by ${\mathbb {P}}_m({\mathcal {O}})$ the space of polynomials of degree up to m defined on the subset ${\mathcal {O}}\subseteq {\mathbb {R}}^2$.

We introduce on each element $E\in {\mathcal {T}}_h$ the following finite-dimensional spaces:

$$\begin{aligned} {\widetilde{W}}_h(E):=\left\{ w_h\in \mathrm {H}^2(E) : \varDelta ^2w_h\in {\mathbb {P}}_{2}(E), w_h|_{\partial E}\in C^0(\partial E), w_h|_e\in {\mathbb {P}}_3(e)\,\,\forall e\in \partial E,\right. \\ \left. \nabla w_h|_{\partial E}\in [C^0(\partial E)]^2, \partial _{\nu _{E}^e} w_h|_e\in {\mathbb {P}}_1(e)\,\,\forall e\in \partial E\right\} , \end{aligned}$$

and

$$\begin{aligned} {\widetilde{V}}_h(E):=\{v_h\in \mathrm {H}^1(E):\varDelta v_h \in {\mathbb {P}}_1(E), v_h|_{\partial E}\in C^0(\partial E), v_h|_{e}\in {\mathbb {P}}_1(e) \ \forall e \in \partial E\}. \end{aligned}$$

Moreover, in ${\widetilde{W}}_h(E)$ and ${\widetilde{V}}_h(E)$ we define the following sets of linear operators. For all $w_{h}\in {\widetilde{W}}_h(E)$ and $v_h\in {\widetilde{V}}_h(E)$ we consider

$\mathbf{D }_\mathbf{W1 }$::

evaluation of $w_{h}$ at the $N_{\mathop {\mathrm {\,v}}\nolimits }^{E}$ vertices of $E$;

$\mathbf{D }_\mathbf{W2 }$::

evaluation of $\nabla w_h$ at the $N_{\mathop {\mathrm {\,v}}\nolimits }^{E}$ vertices of $E$;

$\mathbf{D }_\mathbf{V }$::

evaluation of $v_{h}$ at the $N_{\mathop {\mathrm {\,v}}\nolimits }^{E}$ vertices of $E$.

Projection operators and local virtual spaces In order to introduce the local virtual space, we define the projector $\varPi _{E}^{\varDelta }:{\widetilde{W}}_h(E)\longrightarrow {\mathbb {P}}_2(E)$ as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \int _{E} D^2\varPi _{E}^{\varDelta }w_h:D^2q=\int _{E} D^2w_h:D^2q&{}\quad \forall q\in {\mathbb {P}}_2(E),\\ \displaystyle (( \varPi _{E}^{\varDelta }w_h, q ))_{E}=(( w_h, q ))_{E}&{}\quad \forall q \in {\mathbb {P}}_1(E), \end{array}\right. \end{aligned}$$

(3.1)

where $((\varphi _h,\phi _h ))_{E}$ is defined as follows:

$$\begin{aligned} ((\varphi _h,\phi _h))_{E}:= \sum _{i=1}^{N_{\mathop {\mathrm {\,v}}\nolimits }^{E}} \varphi _h(\mathop {\mathrm {\,v}}\nolimits _i)\phi _h(\mathop {\mathrm {\,v}}\nolimits _i) \qquad \forall \varphi _h,\phi _h \in C^{0}(\partial E), \end{aligned}$$

with $\mathop {\mathrm {\,v}}\nolimits _i$, $1\le i \le N_{\mathop {\mathrm {\,v}}\nolimits }^{E}$, being the vertices of $E$.

Remark 1

The second equation in (3.1) is to select an element from the nontrivial kernel of the operator $\varPi _{E}^{\varDelta }$. We mention that it could be substituted by any other appropriate compatible average on $\partial E$, for instance,

$$\begin{aligned} (\varPi _{E}^{\varDelta }w_h,q)_{\partial E}=(w_h,q)_{\partial E}\quad \forall q \in {\mathbb {P}}_1(E), \end{aligned}$$

where $(\cdot ,\cdot )_{\partial E}$ is the standard $\mathrm {L}^2$ inner product over the boundary of $E$.

We refer to [2] to prove that operator $\varPi _{E}^{\varDelta }$ is computable from the output values of the sets $\mathbf{D }_\mathbf{W1 }$ and $\mathbf{D }_\mathbf{W2 }$.

In a similar way, we define the projector $\varPi _{E}^{\nabla }:\ {\widetilde{V}}_h(E)\longrightarrow {\mathbb {P}}_1(E)$ for each $\psi \in {\widetilde{V}}_h(E)$ as the solution of

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \int _{E} \nabla \varPi _E^{\nabla }v_h\cdot \nabla q=\int _{E} \nabla v_h\cdot \nabla q&{}\quad \forall q\in {\mathbb {P}}_1(E),\\ (\varPi _E^{\nabla }v_h,q)_{\partial E}=(v_h,q)_{\partial E}&{}\quad \forall q \in {\mathbb {P}}_0(E). \end{array}\right. \end{aligned}$$

We observe that operator $\varPi ^{\nabla }_E$ can be computed using only the output values of the set $\mathbf{D }_\mathbf{V }$ (see [1]).

We introduce on each element $E\in {\mathcal {T}}_h$ the following local virtual space $W_h(E)$ (see, for instance, [2]).

$$\begin{aligned} W_h(E):=\left\{ w_h\in {\widetilde{W}}_h(E) : \int _{E}(\varPi _{E}^{\varDelta } w_h)q =\int _{E}w_hq\qquad \forall q\in {\mathbb {P}}_{2}(E)\right\} . \end{aligned}$$

Now, since $W_h(E)\subseteq {\widetilde{W}}_h(E)$ the projector $\varPi _{E}^{\varDelta }$ is well defined and computable in $W_h(E)$. Moreover, the sets of linear operators $\mathbf{D }_\mathbf{W1 }$ and $\mathbf{D }_\mathbf{W2 }$ constitute a set of degrees of freedom for $W_h(E)$; we refer to [2, Lemma 2.3] for further details.

Now, we introduce the following local virtual space (see [1]):

$$\begin{aligned} V_h(E):=\left\{ v_h \in {\widetilde{V}}_h(E): \int _E(\varPi _E^{\nabla }v_h)q=\int _Ev_h q \qquad \forall q\in {\mathbb {P}}_1(E) \right\} . \end{aligned}$$

It is clear that $V_h(E)\subseteq {\widetilde{V}}_h(E)$. Thus, the linear operator $\varPi _E^{\nabla }$ is well defined on $V_h(E)$. Moreover, the set of operators $\mathbf{D }_\mathbf{V }$ constitutes a set of degrees of freedom for the space $V_h(E)$ (see [1]).

We also have that ${\mathbb {P}}_2(E)\times {\mathbb {P}}_1(E)\subseteq W_h(E)\times V_h(E)$. This will guarantee the good approximation properties for the spaces.

Now, for all $m\in {\mathbb {N}}\cup \{0 \}$ and $E\in {\mathcal {T}}_h$, we define the following projector:

$$\begin{aligned} \varPi _{E}^{m}:\mathrm {L}^2(E)\rightarrow {\mathbb {P}}_m(E); \qquad \quad \ \int _E(r-\varPi _{E}^{m}r)q=0\qquad \qquad \forall q \in {\mathbb {P}}_m(E). \end{aligned}$$

(3.2)

It easy to check that for all $w_h\in W_h(E)$ the scalar functions $\varPi _{E}^{2}w_h$ and $\varPi _{E}^{0}\varDelta w_h$ are computable from the degrees of freedom $\mathbf{D }_\mathbf{W1 }$ and $\mathbf{D }_\mathbf{W2 }$ (see [2]). Moreover, for all $v_h\in V_h(E)$ the scalar function $\varPi _{E}^{1}v_h$ is computable from the degrees of freedom $\mathbf{D }_\mathbf{V }$ (see [1]).

Global virtual spaces

Now, we introduce the global virtual spaces to be used in the discretization of Problem 2.

For every decomposition ${\mathcal {T}}_h$ of $\varOmega$ into simple polygons $E$, the first global virtual element space is defined as

$$\begin{aligned} W_h:=\left\{ w_h\in \mathrm {H}_0^2(\varOmega ): w_h|_{E}\in W_h({E})\right\} . \end{aligned}$$

A set of degrees of freedom for $W_h$ is given by all pointwise values of $w_h$ on all vertices of ${\mathcal {T}}_h$ together with all pointwise values of $\nabla w_h$ on all vertices of ${\mathcal {T}}_h$, excluding the vertices on the boundary (where the values vanish).

Next, we introduce the following global virtual space.

$$\begin{aligned} V_h:= \{v_h\in \mathrm {H}_0^1(\varOmega ): v_h|_{E}\in V_h(E)\}. \end{aligned}$$

In this case, a set of degrees of freedom for $V_h$ is given by all pointwise values $v_h$ on all vertices of ${\mathcal {T}}_h$ excluding the vertices on the boundary (where the values vanish).

Finally, for every decomposition ${\mathcal {T}}_h$ of $\varOmega$ into simple polygons $E$, we introduce the global virtual space denoted by ${\mathbf {H}}_h$ as follows:

$$\begin{aligned} {\mathbf {H}}_h:=W_h\times V_h. \end{aligned}$$

Remark 2

We observe that the virtual element space $V_h$ is a conforming space in $\mathrm {H}^1(\varOmega )$. This space will be used for the approximation of the auxiliary variable $z\in \mathrm {L}^2(\varOmega )$. This choice permits us to incorporate a Dirichlet boundary condition for z and also facilitates the analysis of the proposed virtual method. Other virtual element discretizations based on piecewise discontinuous polynomials will be studied in a future work.

4 Discrete spectral problem

In this section, we will introduce a virtual element scheme to approximate the spectrum of the transmission eigenvalue problem stated in Problem 2 and using the virtual spaces introduced in Sect. 3

In what follows, for simplicity, we assume that the index of refraction n is piecewise constant with respect to the decomposition ${\mathcal {T}}_h$, i.e., n is constant on each polygon $E\in {\mathcal {T}}_h$.

Next, we decompose continuous sesquilinear forms (2.6)–(2.7) in an element by element contribution as follows:

$$\begin{aligned} \begin{aligned} {\mathcal {A}}((u,z),(w,v)):=\,&{\mathcal {A}}^{1}(u,w)+{\mathcal {A}}^{2}(z,v),\\ =\,&\sum _{E\in \varOmega _h}[{\mathcal {A}}^{1}_{E}(u,w)+{\mathcal {A}}^{2}_{E}(z,v)], \end{aligned} \end{aligned}$$

with

$$\begin{aligned} {\mathcal {A}}^{1}_{E}(u,w):=\int _E\frac{1}{n-1}\varDelta u\varDelta {\overline{w}}, \quad \text {and}\quad {\mathcal {A}}^{2}_{E}(z,v):=\int _Ez{\overline{v}}. \end{aligned}$$

Moreover, we introduce

$$\begin{aligned} {\mathcal {B}}_E((u,z),(w,v)):= \int _E\varDelta u \Big (\frac{n}{n-1}{\overline{w}}\Big ) +\int _E\frac{1}{n-1}u \varDelta {\overline{w}} +\int _E\frac{n}{n-1} z {\overline{w}} -\int _Eu{\overline{v}}. \end{aligned}$$

Now, in order to propose the discrete scheme, we need to introduce some definitions. First, we consider ${\mathcal {S}}_E^{\varDelta }(\cdot ,\cdot )$ and ${\mathcal {S}}_E^{0}(\cdot ,\cdot )$ any Hermitian positive definite forms satisfying:

$$\begin{aligned}&\alpha _{*}{\mathcal {A}}^1_{E}(w_h,w_h)\le {\mathcal {S}}_E^{\varDelta }(w_h,w_h)\le \alpha ^{*}{\mathcal {A}}^1_{E}(w_h,w_h) \quad \forall w_h\in W_h(E)\quad \varPi _{E}^{\varDelta }w_h=0, \end{aligned}$$

(4.1)

$$\begin{aligned}&{\beta }_{*}{\mathcal {A}}^2_{E}(v_h,v_h)\le {\mathcal {S}}_E^{0}(v_h,v_h)\le {\beta }^{*}{\mathcal {A}}^2_{E}(v_h,v_h) \quad \forall v_h\in V_h(E), \end{aligned}$$

(4.2)

where $\alpha _{*},\beta _{*}$ and $\alpha ^{*},\beta ^{*}$ are positive constants depending only on the constant $\gamma$ from mesh assumptions A$_{1}$–A$_{2}$.

Next, we define the discrete versions of the sesquilinear forms presented in (2.6)–(2.7) as follows:

$$\begin{aligned}&{\mathcal {A}}^{1h}:W_h\times W_h\rightarrow {\mathbb {C}}; \qquad {\mathcal {A}}^{1h}(u_h,w_h) :=\sum _{E\in {\mathcal {T}}_h}{\mathcal {A}}^{1h}_{E}(u_h,w_h) ,&\\&{\mathcal {A}}^{2h}:V_h\times V_h\rightarrow {\mathbb {C}}; \qquad {\mathcal {A}}^{2h}(z_h,v_h) :=\sum _{E\in {\mathcal {T}}_h}{\mathcal {A}}^{2h}_{E}(z_h,v_h) ,&\\&{\mathcal {B}}^h:{\mathbf {H}}_h\times {\mathbf {H}}_h\rightarrow {\mathbb {C}};\ \quad {\mathcal {B}}^h((u_h,z_h),(w_h,v_h)) :=\sum _{E\in {\mathcal {T}}_h}{\mathcal {B}}^{h}_{E}((u_h,z_h),(w_h,v_h)),&\end{aligned}$$

where

$$\begin{aligned} {\mathcal {A}}^{1h}_{E}:W_h(E) \times W_h(E) \rightarrow {\mathbb {C}},\quad {\mathcal {A}}^{2h}_{E}:V_h(E) \times V_h(E) \rightarrow {\mathbb {C}},\quad {\mathcal {B}}^h_{E}:{\mathbf {H}}_h^{E} \times {\mathbf {H}}_h^{E} \rightarrow {\mathbb {C}}, \end{aligned}$$

are local sesquilinear forms given by

$$\begin{aligned}&{\mathcal {A}}^{1h}_{E}(u_h,w_h) :={\mathcal {A}}^1_{E}(\varPi _{E}^{\varDelta } u_h,\varPi _{E}^{\varDelta } w_h) + {\mathcal {S}}_E^{\varDelta }(u_h-\varPi _{E}^{\varDelta }u_h,w_h-\varPi _{E}^{\varDelta }w_h), \end{aligned}$$

(4.3)

$$\begin{aligned}&{\mathcal {A}}^{2h}_{E}(z_h,v_h):={\mathcal {A}}^2_{E}(\varPi _{E}^{1}z_h, \varPi _{E}^{1}v_h) +{\mathcal {S}}_E^{0}(z_h-\varPi _{E}^{1}z_h,v_h-\varPi _{E}^{1}v_h), \end{aligned}$$

(4.4)

$$\begin{aligned}&{\mathcal {B}}^h_{E}((u_h,z_h),(w_h,v_h)) :=\int _E\frac{n}{n-1}\varPi _{E}^{0}\varDelta u_h \varPi _{E}^{2}{\overline{w}}_h +\int _E\frac{1}{n-1}\varPi _{E}^{2}u_h\varPi _{E}^{0}\varDelta {\overline{w}}_h\nonumber \\&+\int _E\frac{n}{n-1} \varPi _{E}^{1}z_h\varPi _{E}^{2}{\overline{w}}_h -\int _E\varPi _{E}^{2}u_h\varPi _{E}^{1}{\overline{v}}_h, \end{aligned}$$

(4.5)

with ${\mathbf {H}}_h^{E}:=W_h(E) \times V_h(E)$.

The following lemma establishes properties of consistency and stability for the local sesquilinear forms ${\mathcal {A}}^{1h}_{E}(\cdot ,\cdot )$ and ${\mathcal {A}}^{2h}_{E}(\cdot ,\cdot )$. The proof follows standard arguments in the VEM literature (see [1]).

Proposition 1

The local forms ${\mathcal {A}}^{1h}_{E}(\cdot ,\cdot )$ and ${\mathcal {A}}^{2h}_{E}(\cdot ,\cdot )$ satisfy the following properties:

• Consistency for all $h > 0$ and for all $E\in {\mathcal {T}}_h$ we have that

  $$\begin{aligned}&{\mathcal {A}}^{1h}_{E}(q,w_h)={\mathcal {A}}^1_{E}(q,w_h)\qquad \forall q\in {\mathbb {P}}_{2}(E) \quad \forall w_h\in W_h(E); \end{aligned}$$

  (4.6)
  $$\begin{aligned}&{\mathcal {A}}^{2h}_{E}(q,v_h)={\mathcal {A}}^2_{E}(q,v_h)\qquad \forall q\in {\mathbb {P}}_{1}(E) \quad \forall v_h\in V_h(E). \end{aligned}$$

  (4.7)

• Stability and boundedness There exist positive constants $\alpha _1,\alpha _2, \beta _1,\beta _2$ depending on the index of refraction n and the constant $\gamma$ from mesh assumptions A$_{1}$–A$_{2}$ such that:

  $$\begin{aligned} \alpha _1 {\mathcal {A}}^1_{E}(w_h,w_h)&\le {\mathcal {A}}^{1h}_{E}(w_h,w_h)\le \alpha _2 {\mathcal {A}}^1_{E}(w_h,w_h)&\quad \forall w_h\in W_h(E); \end{aligned}$$

  (4.8)
  $$\begin{aligned} \beta _1 {\mathcal {A}}^2_{E}(v_h,v_h)&\le {\mathcal {A}}^{2h}_{E}(v_h,v_h)\le \beta _2 {\mathcal {A}}^2_{E}(v_h,v_h)&\quad \forall v_h\in V_h(E) . \end{aligned}$$

  (4.9)

Now, for all $(u_h,z_h),(w_h,v_h)\in {\mathbf {H}}_h$, we introduce the discrete sesquilinear form

$$\begin{aligned} {\mathcal {A}}^h:{\mathbf {H}}_h\times {\mathbf {H}}_h\rightarrow {\mathbb {C}};\qquad {\mathcal {A}}^h((u_h,z_h),(w_h,v_h)):={\mathcal {A}}^{1h}(u_h,w_h)+{\mathcal {A}}^{2h}(z_h,v_h). \end{aligned}$$

(4.10)

As a consequence of Proposition 1, we have the following result, which is the discrete version of Lemma 1.

Lemma 4

There exist positive constants C and $\alpha$ that depend on the index of refraction n and the constants in (4.8)–(4.9) such that for all $(u_h,z_h), (w_h,v_h) \in {\mathbf {H}}_h$ we have

$$\begin{aligned}&{\mathcal {A}}^h((w_h,v_h),(w_h,v_h))\ge \alpha ||(w_h,v_h) ||_{{\mathbf {H}}}^2, \end{aligned}$$

(4.11)

$$\begin{aligned}&|{\mathcal {A}}^h((u_h,z_h),(w_h,v_h))|\le C ||(u_h,z_h) ||_{{\mathbf {H}}} ||(w_h,v_h) ||_{{\mathbf {H}}}, \end{aligned}$$

(4.12)

$$\begin{aligned}&|{\mathcal {B}}^h((u_h,z_h),(w_h,v_h))|\le C ||(u_h,z_h) ||_{{\mathbf {H}}} ||(w_h,v_h) ||_{{\mathbf {H}}}. \end{aligned}$$

(4.13)

Proof

It is straightforward to prove estimates (4.11)–(4.13) from Proposition 1 and definition (4.5). $\square$

For the sesquilinear form ${\mathcal {B}}^h (\cdot ,\cdot )$, we do not require any lower bound. Thus, we do not need to stabilize this form.

Now, we are in a position to write the virtual element discretization of Problem 2.

Problem 3

Find $(\lambda _h,(u_h,z_h))\in {\mathbb {C}}\times {\mathbf {H}}_h$ with $(u_h,z_h)\ne {\varvec{0}}$ such that

$$\begin{aligned} {\mathcal {A}}^h((u_h,z_h),(w_h,v_h))=\lambda _h {\mathcal {B}}^h((u_h,z_h),(w_h,v_h)) \qquad \forall (w_h,v_h)\in {\mathbf {H}}_h. \end{aligned}$$

(4.14)

In order to characterize the spectrum of Problem 3, we introduce the discrete version of the solution operator ${\varvec{T}}$.

$$\begin{aligned} \begin{array}{cll} {\varvec{T}}_h: {\mathbf {H}}&{} \longrightarrow &{}\quad {\mathbf {H}}_h\subseteq {\mathbf {H}}\\ \qquad (f,g)&{}\longmapsto &{}{\varvec{T}}_h(f,g)=({\widehat{u}}_h,{\widehat{z}}_h), \end{array} \end{aligned}$$

defined as the unique solution of the following source problem (see Lemma 4):

$$\begin{aligned}&{\mathcal {A}}^h(({\widehat{u}}_h,{\widehat{z}}_h),(w_h,v_h))={\mathcal {B}}^h((f,g),(w_h,v_h))\qquad \forall (w_h,v_h)\in {\mathbf {H}}_h. \end{aligned}$$

(4.15)

We have that operator ${\varvec{T}}_h$ is well defined and uniformly bounded. Once more, as in the continuous case, we have that $(\lambda _h,(u_h,z_h))$ solves Problem 3 if and only if $(\mu _h,(u_h,z_h))$ is an eigenpair of ${\varvec{T}}_h$, i.e., ${\varvec{T}}_h(u_h,z_h)=\mu _h (u_h,z_h)$, with $\mu _h:=1/\lambda _h$.

5 Convergence and error estimates

In what follows, we focus on proving the convergence and error analysis of the proposed virtual element scheme for the transmission eigenvalue problem. First, we recall some well-known results on star-shaped polygons [12].

Proposition 2

There exists a positive constant C, such that for all $w\in \mathrm {H}^{\delta }(E)$ there exists $w_{\pi }\in {\mathbb {P}}_k(E)$, $k\in {\mathbb {N}}$ such that

$$\begin{aligned} \vert w-w_{\pi }\vert _{\ell ,E}\le C h_E^{\delta -\ell }|w|_{\delta ,E}\quad 0\le \delta \le k+1, \ell =0,\ldots ,[\delta ], \end{aligned}$$

with $[\delta ]$ denoting largest integer equal to or smaller than $\delta \in {{\mathbb {R}}}_{+}$.

Now, we consider interpolation operators in the virtual element spaces $W_h$ and $V_h$. First, for the $C^1$ interpolation operator, we have the following result and the proof can be found in [2, Proposition 3.1].

Proposition 3

Assume A$_{1}$–A$_{2}$ are satisfied, let $w\in \mathrm {H}^{\varepsilon }(\varOmega )$ with $\varepsilon \in [2,3]$. Then, there exist $w_I\in W_h$ and $C>0$, independent of h, such that

$$\begin{aligned} \Vert w-w_{I}\Vert _{\ell ,\varOmega }\le Ch^{\varepsilon -\ell }\Vert w\Vert _{\varepsilon ,\varOmega },\qquad \ell =0,1,2. \end{aligned}$$

For the $C^0$ interpolation operator, we have the following result whose proof can be obtained by repeating the arguments in [17, Theorem 11] (see also [34, Proposition 4.2]).

Proposition 4

Assume A$_{1}$–A$_{2}$ are satisfied, let $v\in \mathrm {H}^{2}(\varOmega )$. Then, there exist $v_I\in V_h$ and $C>0$, independent of h, such that

$$\begin{aligned} \Vert v-v_{I}\Vert _{0,\varOmega }+h\vert v-v_{I}\vert _{1,\varOmega }\le Ch^{2}\Vert v\Vert _{2,\varOmega }. \end{aligned}$$

The following lemma shows that ${\varvec{T}}_h$ converges in norm to ${\varvec{T}}$ as h goes to zero.

Lemma 5

There exist $s\in (0,1]$ and a positive constant $C>0$ that depends on the index of refraction n, both independent of the meshsize h such that: For all $(f,g)\in {\mathbf {H}}$, if $({\widehat{u}},{\widehat{z}})={\varvec{T}}(f,g)$ and $({\widehat{u}}_h,{\widehat{z}}_h)={\varvec{T}}_h(f,g)$, then

$$\begin{aligned} ||\left( {\varvec{T}}-{\varvec{T}}_h\right) (f,g)||_{{\mathbf {H}}}&\le Ch^{s}|| (f,g)||_{{\mathbf {H}}}. \end{aligned}$$

Proof

Let $(f,g)\in {\mathbf {H}}$. As a consequence of Lemma 2, there exists $s\in (0,1]$ such that $({\widehat{u}},{\widehat{z}})\in \mathrm {H}^{2+s}(\varOmega )\times \mathrm {H}^{2}(\varOmega )$. Let $({\widehat{u}}_I,{\widehat{z}}_I)\in {\mathbf {H}}_h$ be such that Propositions 3 and 4 hold true. By using the triangle inequality, we have

$$\begin{aligned} ||\left( {\varvec{T}}-{\varvec{T}}_h\right) (f,g)||_{{\mathbf {H}}}&= ||({\widehat{u}},{\widehat{z}})-({\widehat{u}}_h,{\widehat{z}}_h) ||_{{\mathbf {H}}}\nonumber \\&\le ||({\widehat{u}},{\widehat{z}})-({\widehat{u}}_I,{\widehat{z}}_I) ||_{{\mathbf {H}}} + ||({\widehat{u}}_I,{\widehat{z}}_I) -({\widehat{u}}_h,{\widehat{z}}_h)||_{{\mathbf {H}}}. \end{aligned}$$

(5.1)

We define $(w_h,v_h):=({\widehat{u}}_h-{\widehat{u}}_I,{\widehat{z}}_h-{\widehat{z}}_I)\in {\mathbf {H}}_h$. Then, for all ${\widehat{u}}_{\pi }\in {\mathbb {P}}_2(E)$ and ${\widehat{z}}_{\pi }\in {\mathbb {P}}_1(E)$, from (4.11) (ellipticity of the sesquilinear form ${\mathcal {A}}^h(\cdot ,\cdot )$), we have

$$\begin{aligned} \alpha ||(w_h,v_h) ||_{{\mathbf {H}}}^2\le&{\mathcal {A}}^h((w_h,v_h),(w_h,v_h)) \end{aligned}$$

(5.2)

$$\begin{aligned} =&{\mathcal {A}}^h(({\widehat{u}}_h,{\widehat{z}}_h),(w_h,v_h))- {\mathcal {A}}_h(({\widehat{u}}_I,{\widehat{z}}_I),(w_h,v_h))\nonumber \\ =&{\mathcal {B}}^h((f,g),(w_h,v_h)) - \sum \limits _{E\in {\mathcal {T}}_h}\Big \{{\mathcal {A}}^{1h}_{E}({\widehat{u}}_I,w_h) + {\mathcal {A}}^{2h}_{E}({\widehat{z}}_I,v_h) \Big \}\nonumber \\ =&{\mathcal {B}}^h((f,g),(w_h,v_h)) - \sum \limits _{E\in {\mathcal {T}}_h}\Big \{ \{{\mathcal {A}}^{1h}_{E}({\widehat{u}}_I-{\widehat{u}}_{\pi },w_h) +{\mathcal {A}}^1_{E}({\widehat{u}}_{\pi }-{\widehat{u}},w_h)\} \nonumber \\&+\{{\mathcal {A}}^{2h}_{E}({\widehat{z}}_I-{\widehat{z}}_{\pi },v_h) + {\mathcal {A}}^2_{E}({\widehat{z}}_{\pi }-{\widehat{z}},v_h) \} + \{{\mathcal {A}}^1_{E}({\widehat{u}},w_h) +{\mathcal {A}}^2_{E}({\widehat{z}},v_h) \} \Big \}\nonumber \\ =&\sum _{E\in {\mathcal {T}}_h}\underbrace{ \{{\mathcal {B}}^h_{E}((f,g),(w_h,v_h)) - {\mathcal {B}}_{E}((f,g),(w_h,v_h)) \}}_{R_E^{1}} \nonumber \\&- \sum _{E\in {\mathcal {T}}_h}\underbrace{ \{{\mathcal {A}}^{1h}_{E}({\widehat{u}}_I-{\widehat{u}}_{\pi },w_h) +{\mathcal {A}}^1_{E}({\widehat{u}}_{\pi }-{\widehat{u}},w_h) \}}_{R_E^{2}}\nonumber \\&- \sum _{E\in {\mathcal {T}}_h}\underbrace{ \{{\mathcal {A}}^{2h}_{E}({\widehat{z}}_I-{\widehat{z}}_{\pi },v_h) + {\mathcal {A}}^2_{E}({\widehat{z}}_{\pi }-{\widehat{z}},v_h)\}}_{R_E^{3}}, \end{aligned}$$

(5.3)

where we have used the definition of the solution operators ${\varvec{T}}$ and ${\varvec{T}}_h$ and consistency properties (4.6) and (4.7). In what follows, we will bound the terms $R_E^{1},R_E^{2}$ and $R_E^{3}$.

We start with the term $R_E^{1}$: we use the definitions of ${\mathcal {B}}_{E}(\cdot ,\cdot )$ and ${\mathcal {B}}^h_{E}(\cdot ,\cdot )$ (cf. (2.7) and (4.5), respectively) to obtain

$$\begin{aligned} R_E^{1}&= \underbrace{\int _{E}\Big \{ \frac{n}{n-1}\varPi _{E}^{0}\varDelta f \varPi _{E}^{2}{\overline{w}}_h -\frac{n}{n-1} \varDelta f {\overline{w}}_h \Big \}}_{R_E^{11}}\nonumber \\&\quad +\underbrace{ \int _{E}\Big \{ \frac{1}{n-1} \varPi _{E}^{2}f \varPi _{E}^{0}\varDelta {\overline{w}}_h -\frac{1}{n-1} f \varDelta {\overline{w}}_h \Big \}}_{R_E^{12}}\nonumber \\&\quad +\underbrace{\int _{E} \Big \{\frac{n}{n-1}\varPi _{E}^{1}g\varPi _{E}^{2}{\overline{w}}_h - \frac{n}{n-1}g{\overline{w}}_h\Big \}}_{R_E^{13}} +\underbrace{\int _{E} \Big \{\varPi _{E}^{2}f\varPi _{E}^{1}{\overline{v}}_h - f{\overline{v}}_h \Big \}}_{R_E^{14}} \nonumber \\&=: R_E^{11}+ R_E^{12}+ R_E^{13}+ R_E^{14} . \end{aligned}$$

(5.4)

Thus, we have to bound each term on the right-hand side above. First, the terms $R_E^{11}$ and $R_E^{12}$ can be bounded repeating the same arguments in [38, Lemma 4.2]. We obtain

$$\begin{aligned} R_E^{11}\le Ch_{E}\left\| \frac{n}{n-1}\right\| _{\mathrm {L}^{\infty }(E)}| f|_{2,E} \Big \{ |w_h|_{2,E} + | w_h |_{1,E}\Big \}, \end{aligned}$$

(5.5)

and

$$\begin{aligned} R_E^{12}\le Ch_{E}\left\| \frac{n}{n-1}\right\| _{\mathrm {L}^{\infty }(E)}\Big \{ |f|_{2,E} + |f|_{1,E}\Big \}| w_h|_{2,E}. \end{aligned}$$

(5.6)

Now, to bound the term $R_E^{13}$, we use the fact that n is piecewise constant, the definition of $\varPi _{E}^{1}$ and $\varPi _{E}^{2}$, the Cauchy–Schwarz inequality and $n/(n-1)\in \mathrm {L}^{\infty }(\varOmega )$ to have

$$\begin{aligned} R_E^{13}&=\int _{E} \Big \{\frac{n}{n-1} \varPi _{E}^{1}g\varPi _{E}^{2}{\overline{w}}_h -\frac{n}{n-1}g{\overline{w}}_h \Big \} \end{aligned}$$

(5.7)

$$\begin{aligned}&=\int _{E} \frac{n}{n-1}\varPi _{E}^{1}g(\varPi _{E}^{2}{\overline{w}}_h -\varPi _{E}^{1}{\overline{w}}_h) +\int _{E}\frac{n}{n-1}(\varPi _{E}^{1}g-g)(\varPi _{E}^{1}{\overline{w}}_h -{\overline{w}}_h)\nonumber \\&\le Ch_{E}^2\left\| \frac{n}{n-1}\right\| _{\mathrm {L}^{\infty }(E)}||g||_{0,E}|{\overline{w}}_h|_{2,E}. \end{aligned}$$

(5.8)

For the term $R_E^{14}$, we use the definition of $\varPi _{E}^{2}$ and the Cauchy–Schwarz inequality to obtain

$$\begin{aligned} R_E^{14}&=\int _{E} \Big \{\varPi _{E}^{2}f\varPi _{E}^{1}{\overline{v}}_h - f{\overline{v}}_h \Big \} \end{aligned}$$

(5.9)

$$\begin{aligned}&=\int _{E} (\varPi _{E}^{2}f -\varPi _{E}^{1}f)\varPi _{E}^{1}{\overline{v}}_h +\int _{E}(\varPi _{E}^{1}f-f)(\varPi _{E}^{1}{\overline{v}}_h -{\overline{v}}_h)\nonumber \\&\le Ch_{E}^2|f|_{2,E}||{\overline{v}}_h||_{0,E} . \end{aligned}$$

(5.10)

Now, taking sum over $E$ in terms (5.5),(5.6),(5.8) and (5.10) and applying Cauchy–Schwarz inequality for sequences we obtain

$$\begin{aligned} \sum \limits _{E\in {\mathcal {T}}_h} R^{1,E}&\le Ch \max \left\{ \left\| \frac{n}{n-1}\right\| _{\mathrm {L}^{\infty }(E)}, \left\| \frac{1}{n-1}\right\| _{\mathrm {L}^{\infty }(E)} \right\} ||(f,g)||_{{\mathbf {H}}}||(w_h,v_h)||_{{\mathbf {H}}}. \end{aligned}$$

(5.11)

Next, we bound the term $\sum \limits _{E\in {\mathcal {T}}_h}R_E^{2}$. By using the Cauchy–Schwarz inequality and the stability and boundedness properties of ${\mathcal {A}}^1_{E}(\cdot ,\cdot )$ (cf. (4.8)), we obtain

$$\begin{aligned} \sum \limits _{E\in {\mathcal {T}}_h}R_E^{2}=&\sum \limits _{E\in {\mathcal {T}}_h} \Big \{ {\mathcal {A}}^{1h}_{E}({\widehat{u}}_I-{\widehat{u}}_{\pi },w_h) +{\mathcal {A}}_1^{E}({\widehat{u}}_{\pi }-{\widehat{u}},w_h)\Big \}\\ \le&\sum \limits _{E\in {\mathcal {T}}_h} \Big \{|{\widehat{u}}_I-{\widehat{u}}_{\pi }|_{2,E}|w_h|_{2,E} + |{\widehat{u}}_{\pi }-{\widehat{u}}|_{2,E}|w_h|_{2,E}\Big \}\\ \le&\sum \limits _{E\in {\mathcal {T}}_h} \Big \{|{\widehat{u}}_I-{\widehat{u}}|_{2,E} +2|{\widehat{u}}-{\widehat{u}}_{\pi }|_{2,E} \Big \}|w_h|_{2,E}. \end{aligned}$$

Next, from Propositions 2, 3 and Lemma 2, we have

$$\begin{aligned} \sum \limits _{E\in {\mathcal {T}}_h}R_E^{2}\le Ch^{s}|| (f,g)||_{{\mathbf {H}}} ||(w_h,v_h) ||_{{\mathbf {H}}}. \end{aligned}$$

(5.12)

To bound the last term: $\sum \limits _{E\in {\mathcal {T}}_h}R_E^{3}$, we use the Cauchy–Schwarz inequality and we add and subtract the term ${\widehat{z}}$, to obtain

$$\begin{aligned} \sum \limits _{E\in {\mathcal {T}}_h}R_E^{3}=&\sum _{E\in {\mathcal {T}}_h} \Big \{{\mathcal {A}}^{2h}_{E}({\widehat{z}}_I-{\widehat{z}}_{\pi },v_h) + {\mathcal {A}}^2_{E}({\widehat{z}}_{\pi }-{\widehat{z}},v_h)\Big \}\\ \le&\sum _{E\in {\mathcal {T}}_h} \Big \{ ||{\widehat{z}}_I-{\widehat{z}} ||_{0,E} + 2||{\widehat{z}}-{\widehat{z}}_{\pi }||_{0,E} \Big \}||v_h||_{0,E}. \end{aligned}$$

Hence, applying Proposition 2 and Proposition 4 (with $\ell =0$), and Lemma 2 in the above inequality we deduce

$$\begin{aligned} \sum \limits _{E\in {\mathcal {T}}_h}R_E^{3}\le Ch^2||(f,g)||_{{\mathbf {H}}} ||(w_h,v_h) ||_{{\mathbf {H}}}. \end{aligned}$$

(5.13)

Now, by combining (5.3) with (5.11), (5.12) and (5.13), we obtain

$$\begin{aligned} ||({\widehat{u}}_I,{\widehat{z}}_I) -({\widehat{u}}_h,{\widehat{z}}_h)||_{{\mathbf {H}}} \le \frac{C}{\alpha }h^{s}|| (f,g)||_{{\mathbf {H}}} . \end{aligned}$$

(5.14)

Finally, we complete the proof from (5.1), (5.14), Propositions 3, 4 and Lemma 2. $\square$

Since Problem 1 is nonselfadjoint, we need to analyze the adjoint solution operators (continuous and discrete). Thus, first we introduce the adjoint solution operator ${\varvec{T}}^{*}$:

$$\begin{aligned} \begin{array}{cll} {\varvec{T}}^{*}: {\mathbf {H}}&{} \longrightarrow &{}\quad {\mathbf {H}}\\ \qquad (f,g)&{}\longmapsto &{}{\varvec{T}}^{*}(f,g)=({\widehat{u}}^{*},{\widehat{z}}^{*}) \end{array} \end{aligned}$$

defined as the unique solution (see Lemma 1) of the following source problem:

$$\begin{aligned}&{\mathcal {A}}((w,v),({\widehat{u}}^{*},{\widehat{z}}^{*})) ={\mathcal {B}}((w,v),(f,g))\qquad \forall (w,v)\in {\mathbf {H}}. \end{aligned}$$

(5.15)

It is simple to prove that if $\mu$ is an eigenvalue of ${\varvec{T}}$ with multiplicity m, ${\bar{\mu }}$ is an eigenvalue of ${\varvec{T}}^{*}$ with the same multiplicity m. In addition, a result analogous to Lemma 2 can be proven in this case.

Lemma 6

There exist $s\in (0,1]$ and a positive constant C depending on the index of refraction n such that for all $(f,g)\in {\mathbf {H}}$, the unique solution $({\widehat{u}}^{*},{\widehat{z}}^{*})$ of (5.15) satisfies $({\widehat{u}}^{*},{\widehat{z}}^{*})\in \mathrm {H}^{2+s}(\varOmega )\times \mathrm {H}_0^2(\varOmega )$ and

$$\begin{aligned} ||{\widehat{u}}^{*}||_{2+s,\varOmega } + ||{\widehat{z}}^{*}||_{2,\varOmega }\le C ||(f,g)||_{{\mathbf {H}}}. \end{aligned}$$

Now, let ${\varvec{T}}_h^*:{\mathbf {H}}\rightarrow {\mathbf {H}}_h\subseteq {\mathbf {H}}$ be the adjoint operator of ${\varvec{T}}_h$. This operator is defined by ${\varvec{T}}^*_h(f,g):=({\widehat{u}}_h^*,{\widehat{z}}_h^*)$, where $({\widehat{u}}_h^*,{\widehat{z}}_h^*)$ is the unique solution of the following source problem:

$$\begin{aligned} {\mathcal {A}}^h((w_h,v_h),({\widehat{u}}_h^*,{\widehat{z}}_h^*))&={\mathcal {B}}^h((w_h,v_h),(f,g))\quad \forall (w_h,v_h)\in {\mathbf {H}}_h. \end{aligned}$$

(5.16)

The next result establishes the convergence in norm of the operator ${\varvec{T}}_h^*$ to ${\varvec{T}}^*$ as h goes to zero. The proof follows repeating the same arguments as those used to prove Lemma 5.

Lemma 7

There exists a positive constant C that depends on the index of refraction n and $s\in (0,1]$, both independent of the meshsize h, such that: For all $(f,g)\in {\mathbf {H}}$, if $({\widehat{u}}^*,{\widehat{z}}^*)={\varvec{T}}^*(f,g)$ and $({\widehat{u}}_h^*,{\widehat{z}}_h^*)={\varvec{T}}_h^*(f,g)$, then

$$\begin{aligned} ||\left( {\varvec{T}}^*-{\varvec{T}}_h^*\right) (f,g)||_{{\mathbf {H}}}&\le Ch^{s}||(f,g)||_{{\mathbf {H}}}. \end{aligned}$$

Now we are ready to prove the convergence and obtain error estimates of the eigenvalue problem. First, we recall that in [39], the author gives the convergence conditions under which the eigenvalues of ${\varvec{T}}_h$ converge to those of ${\varvec{T}}$, where ${\varvec{T}}$ is a nonselfadjoint compact operator (see also [4]).

We first recall the definition of the spectral projectors. Let $\mu$ be a nonzero eigenvalue of ${\varvec{T}}$ with algebraic multiplicity m. Denote by ${\mathcal {C}}$ a circle in the complex plane centered at $\mu$ such that no other eigenvalue lies inside ${\mathcal {C}}$. Define the spectral projection ${\mathcal {E}}$ as

$$\begin{aligned} {\mathcal {E}}:=(2\pi i)^{-1}\int _{{\mathcal {C}}} (z-{\varvec{T}})^{-1}dz. \end{aligned}$$

In a similar way, we define the spectral projector ${\mathcal {E}}^{*}$ as follows:

$$\begin{aligned} {\mathcal {E}}^*:=(2\pi i)^{-1}\int _{{\mathcal {C}}} (z-{\varvec{T}}^*)^{-1}dz. \end{aligned}$$

We have that ${\mathcal {E}}$ and ${\mathcal {E}}^{*}$ are projections onto the space of generalized eigenvectors $R({\mathcal {E}})$ and $R({\mathcal {E}}^*)$, respectively. It is easy to check that $R({\mathcal {E}}),R({\mathcal {E}}^*)\in \mathrm {H}^{2+s}(\varOmega )\times \mathrm {H}^{2+s}(\varOmega )$ (see Lemma 3).

As a consequence of the convergence in norm of ${\varvec{T}}_h$ to ${\varvec{T}}$ (cf. Lemma 5), there exist m eigenvalues (which lie in ${\mathcal {C}}$) $\mu _h^{(1)},\ldots ,\mu _h^{(m)}$ of ${\varvec{T}}_h$ (repeated according to their respective multiplicities) which will converge to $\mu$ as h goes to zero.

Analogously, we introduce the following spectral projector ${\mathcal {E}}_h:=(2\pi i)^{-1}\int _{{\mathcal {C}}} (z-{\varvec{T}}_h)^{-1}dz$, which is a projector onto the invariant subspace $R({\mathcal {E}}_h)$ of ${\varvec{T}}_h$ spanned by the generalized eigenvectors of ${\varvec{T}}_h$ corresponding to $\mu _h^{(1)},\ldots ,\mu _h^{(m)}$.

We recall the definition of the gap ${\widehat{\delta }}$ between two closed subspaces ${\mathcal {X}}$ and ${\mathcal {Y}}$ of a Hilbert space ${\mathbf {H}}$:

$$\begin{aligned} {\widehat{\delta }}({\mathcal {X}},{\mathcal {Y}}) :=\max \left\{ \delta ({\mathcal {X}},{\mathcal {Y}}),\delta ({\mathcal {Y}},{\mathcal {X}})\right\} , \quad \text {where}\quad \delta ({\mathcal {X}},{\mathcal {Y}}) :=\sup _{x\in {\mathcal {X}}:\ \left\| x\right\| _{{\mathbf {H}}}=1} \left( \inf _{y\in {\mathcal {Y}}}\left\| x-y\right\| _{{\mathbf {H}}}\right) . \end{aligned}$$

The following error estimates for the approximation of eigenvalues and eigenfunctions hold true.

Theorem 1

There exists a strictly positive constant C that depends on the index of refraction such that

$$\begin{aligned} {\widehat{\delta }}(R({\mathcal {E}}),R({\mathcal {E}}_h))&\le C h^{{s}}, \end{aligned}$$

(5.17)

$$\begin{aligned} \left| \mu -{\hat{\mu }}_h\right|&\le C h^{2{s}}, \end{aligned}$$

(5.18)

where ${\hat{\mu }}_h:=\frac{1}{m}\sum \limits _{i=1}^{m}\mu _h^{(i)}$ and $s\in (0,1]$ as in Lemma 3.

Proof

The proof follows repeating the same arguments used in [38, Theorem 4.1]. $\square$

6 Numerical results

We report in this section a series of numerical tests to approximate the transmission eigenvalues k described in system (2.1a)–(2.1d), using the virtual element method proposed and analyzed in this paper. Thus, we have implemented in a MATLAB code the proposed VEM on arbitrary polygonal meshes (see [6]). Moreover, the spectral problem is solved by using the built-in function eigs in MATLAB.

In order to compare our results with the ones reported in the literature of the transmission eigenvalue problem, we have chosen three configurations for the computational domain $\varOmega$:

$$\begin{aligned}&\text{ Square } \text{ domain: } \qquad \varOmega _\mathbf{S }:=(0,1)^2, \end{aligned}$$

(6.1)

$$\begin{aligned}&\text{ L-shaped } \text{ domain: } \quad \varOmega _\mathbf{L }:=(-1/2,1/2)^2\backslash ([0,1/2]\times [-1/2,0]), \end{aligned}$$

(6.2)

$$\begin{aligned}&\text{ Circular } \text{ domain: } \ \quad \varOmega _\mathbf{C }:=\{(x,y)\in {\mathbb {R}}^2: x^2+y^2<1/4\}. \end{aligned}$$

(6.3)

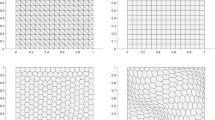
Additionally, we have tested the method by using different families of polygonal meshes (see Fig. 1):

• $Omega_h^{s}$: Quadrilateral meshes;

• $\varOmega _{h}^{{tz}}$: Trapezoidal meshes;

• $\varOmega _{h}^{{t}}$: Triangular meshes;

• $\varOmega _{h}^{{hex}}$: Hexagonal meshes made of convex hexagons;

• $\varOmega _{h}^{{v}}$: Voronoi meshes which have been partitioned with $N_P$ number of polygons.

Fig. 1

Sample meshes: $\varOmega _h^{s}$ (top left), $\varOmega _h^{tz}$ (top middle), $\varOmega _h^{hex}$ (top right), $\varOmega _h^t$ (bottom left) and $\varOmega _h^{v}$ (bottom right)

On the other hand, to complete the choice of the VEM scheme, we had to fix the forms ${\mathcal {S}}_E^{\varDelta }(\cdot ,\cdot )$ and ${\mathcal {S}}_E^{0}(\cdot ,\cdot )$ satisfying (4.1) and (4.2), respectively. In particular, we have considered the forms

$$\begin{aligned} {\mathcal {S}}_E^{\varDelta }(u_h,w_h)&:=h^{-2}_E\sum \limits _{i=1}^{N_{\mathop {\mathrm {\,v}}\nolimits }^{E}}[u_h(\mathop {\mathrm {\,v}}\nolimits _i)w_h(\mathop {\mathrm {\,v}}\nolimits _i) +h_{\mathop {\mathrm {\,v}}\nolimits _i}^2\nabla u_h(\mathop {\mathrm {\,v}}\nolimits _i)\cdot \nabla w_h(\mathop {\mathrm {\,v}}\nolimits _i)]&\quad \forall u_h,w_h\in W_h(E),\\ {\mathcal {S}}_E^{0}(z_h,v_h)&:=h^2_{E}\sum \limits _{i=1}^{N_{\mathop {\mathrm {\,v}}\nolimits }^{E}}z_h(\mathop {\mathrm {\,v}}\nolimits _i)v_h(\mathop {\mathrm {\,v}}\nolimits _i)&\quad \forall z_h,v_h\in V_h(E), \end{aligned}$$

where $\mathop {\mathrm {\,v}}\nolimits _1,\ldots ,\mathop {\mathrm {\,v}}\nolimits _{N_{\mathop {\mathrm {\,v}}\nolimits }^{E}}$ are the vertices of $E$, $h_{\mathop {\mathrm {\,v}}\nolimits _i}$ corresponds to the maximum diameter of the elements with $\mathop {\mathrm {\,v}}\nolimits _i$ as a vertex. With the above choice, we have that (4.1) and (4.2) are satisfied (see [1, 2] for further details).

6.1 Test 1: square domain $\varOmega _\mathbf{S }$

In this numerical test, we have computed the three lowest transmission eigenvalues $k_{ih}$, $i=1,2,3$, with three different index of refraction n on the unit square $\varOmega _\mathbf{S }$.

We report in Table 1 the three lowest in magnitude transmission eigenvalues computed with the virtual scheme introduced in this work. The table includes orders of convergence as well as accurate values extrapolated by means of a least-squares fitting. We consider three different values for the index of refraction and three different families of meshes. We compare the results with the ones reported in references [20, 23, 28, 36, 38].

Table 1 Test 1: Lowest transmission eigenvalues $k_{ih}$, $i=1,2,3$, computed on different families of meshes, on the square domain $\varOmega _\mathbf{S}$ and with different index of refraction

It can be seen from Table 1 that the eigenvalue approximation order of the proposed method is quadratic and that the results obtained by the different methods agree perfectly well. We illustrate in Fig. 2 the eigenfunctions corresponding to the four lowest transmission eigenvalues obtained with meshes $\varOmega _{h}^{hex}$ and $n=16$.

Fig. 2

Test 1. Eigenfunctions: $u_{1h}$ (top left), $u_{2h}$ (top right), $u_{3h}$ (bottom left) and $u_{4h}$ (bottom right) obtained with meshes $\varOmega _{h}^{hex}$ and $n=16$

6.2 Test 2: L-shaped domain $\varOmega _\mathbf{L }$

In order to compare our results with those presented in the literature of the transmission eigenvalue (for instance [15, 36, 38]), in this numerical test we have computed the three lowest transmission eigenvalues $k_{ih}$, $i=1,2,3$, with the index of refraction $n=16$ on the L-shaped domain $\varOmega _\mathbf{L }$ and with meshes $\varOmega _{h}^{t}$ and $\varOmega _{h}^{s}$.

We report in Table 2 the three lowest in magnitude transmission eigenvalues, for $n=16$, and computed with VEM (4.14) on the meshes $\varOmega _{h}^{{t}}$ (triangular meshes), and $\varOmega _{h}^{s}$ (square meshes) (cf. Fig. 1). The table includes orders of convergence as well as accurate values extrapolated by means of a least-squares fitting. Once again, the last rows show the values obtained by extrapolating those computed with different methods presented in [15, 36, 38].

Table 2 Test 2: Lowest transmission eigenvalues $k_{ih}$, $i=1,2,3$, computed on meshes $\varOmega _{h}^{{t}}$ and $\varOmega _{h}^{{s}}$ with an index of refraction $n=16$ on the L-shaped domain $\varOmega _\mathbf{L}$

Fig. 3

Test 2. Eigenfunctions: $u_{1h}$ (top left), $u_{2h}$ (top right), $u_{3h}$ (bottom left) and $u_{4h}$ (bottom right) obtained with meshes $\varOmega _{h}^{t}$ and $n=16$

Table 3 Test 3: Lowest transmission eigenvalues $k_{ih}$, $i=1,2,3$, computed on different families of meshes, on the circular domain $\varOmega _\mathbf{C}$ and with different index of refraction

It can be seen from Table 2 that the results obtained by our method agree perfectly well with those reported in [15, 36, 38]. Moreover, we observe that for the first transmission eigenvalue the associated eigenfunction presents a singularity. Thus, the order of convergence is affected by this singularity and we obtain an order close to 1.54, which corresponds to the Sobolev regularity for the biharmonic equation in both cases. In addition, the method converges with larger orders for the rest of the transmission eigenvalues ($k_{2h}$ and $k_{3h}$).

Figure 3 shows the eigenfunctions corresponding to the four lowest transmission eigenvalues with index of refraction $n=16$ on an L-shaped domain with meshes $\varOmega _{h}^{{t}}$.

6.3 Test 3: Circular domain $\varOmega _\mathbf{C }$

Finally, we have computed the three lowest transmission eigenvalues $k_{ih}$, $i=1,2,3$, with three different index of refraction n on the circular domain $\varOmega _\mathbf{C }$. The domain $\varOmega _C$ is partitioned using a sequence of polygonal meshes (centroidal Voronoi tessellation) created with PolyMesher [43].

We report in Table 3 the three lowest in magnitude transmission eigenvalues computed with the virtual scheme introduced in this work. The table includes orders of convergence as well as accurate values extrapolated by means of a least-squares fitting. We consider three different values for the index of refraction and three different families of meshes. Once again, a quadratic order of convergence can be clearly appreciated from Table 3. Moreover, Fig. 3 shows the eigenfunctions corresponding to the four lowest transmission eigenvalues on a circular domain with index of refraction $n=16$.