A Virtual Element Method for the Steklov Eigenvalue Problem Allowing Small Edges

Abstract

The aim of this paper is to analyze the influence of small edges in the computation of the spectrum of the Steklov eigenvalue problem by a lowest order virtual element method. Under weaker assumptions on the polygonal meshes, which can permit arbitrarily small edges with respect to the element diameter, we show that the scheme provides a correct approximation of the spectrum and prove optimal error estimates for the eigenfunctions and a double order for the eigenvalues. Finally, we report some numerical tests supporting the theoretical results.

1 Introduction

In this paper we are interested in the approximation by virtual elements of the eigenvalues and eigenfunctions of the Steklov problem which is characterized by the presence of the eigenvalue on the boundary condition. This problem has attracted much attention in recent years due to the important applications in many physical subjects. For instance, it appears in the study of the dynamic of liquids in moving containers, the so called sloshing problem [6, 20, 24]. Also, this problem have interesting applications in inverse scattering [35, 47], among other works.

There are several studies on the finite element approximations of the Steklov eigenvalue problem, for example, see [3, 4, 15, 27, 33, 46, 48]. Traditionally, finite element methods rely on triangular (simplicial) and quadrilateral meshes. However, in complex simulations one often encounters general polygonal or polyhedral meshes. In recent years there has been a significant growth in the mathematical and engineering literature in developing numerical methods that can make use of general polytopal meshes; among the large number of papers on this subject, we cite as a minimal sample [7, 9, 21, 26, 44, 45].

The VEM has been introduced in [7] and has been applied successfully in a large range of problems arising from engineering and physics phenomenons; see for instance [1, 2, 8, 10, 12, 14, 19, 22, 36, 43]. Regarding VEM for eigenvalue problems, we mention the following recent works [23, 25, 28, 29, 38,39,40,41,42]. In particular, an a priori and a posteriori VEM discretization for the Steklov eigenvalue problem has been presented in [40, 41]. However, the theoretical results and error estimates for the eigenvalues and eigenfunctions were obtained under the standard mesh assumptions introduced in [7], which do not allow to consider meshes containing elements with small edges compared to the element diameter.

In [11, 13, 18] has been recently analyzed the possibility to consider in VEM discretizations polygonal meshes with arbitrarily small edges with respect to the element diameter. This new framework for VEM opens the possibility to solve interesting coupled problems, such as fluid-structure interactions, in a different way. In fact, the small edges approach takes relevance in this context and becomes a natural path to deal with such problems, for instance, by gluing different meshes in each domain in fluid-structure interactions or in coupling of fluid flow with porous media flow. We also mention that numerical methods that permit arbitrarily small edges in the polygonal meshes can be useful in adaptive schemes by considering refined meshes as a tool to handle solutions with corner singularities. In particular, the present work aims to apply this new framework for the numerical solution of an eigenvalue problem. More precisely, we will follow the VEM approach presented in [11], for the Poisson equation, to write a virtual scheme for the Steklov eigenvalue problem.

The aim of this paper is to propose a virtual element method of lowest order to solve the Steklov eigenproblem, allowing small edges in the polygons of the mesh. We will consider the continuous variational formulation presented in [40]; however, we will write a different discrete virtual scheme, which is based on a different stabilization bilinear form (see [49]). We will use the so-called Babuška-Osborn abstract spectral approximation theory (see [5]), to show that under weaker assumptions on the polygonal meshes, the resulting virtual element scheme provides a correct approximation of the spectrum and prove optimal order error estimates for the eigenfunctions and a double order for the eigenvalues. In particular, our theoretical estimates fully support meshes with arbitrarily small edges with respect to the element diameter. In addition, we remark that spurious modes were not found for different values of the h-scalling used in the definition of the stabilization form (see in particular Sect. 5.1 below). This numerical evidence strongly support the possibility to extend the present analysis to more challenging eigenvalue problems in continuum mechanics such as the elastoacustic problem [16, 37], among others.

The paper is organized as follows: In Sect. 2, we present the model problem and preliminary results related to the solution operator and eigenfunctions. More precisely, we will establish the spectral characterization of the solution operator, which allows to study the numerical method. Section 3 is dedicated to present the virtual element method. Here we will introduce the assumptions on the mesh. We will present approximation results that will be the key point of our analysis, which will depend on the particular choice of the stabilization form. Section 4, contains the error estimates for the eigenfunctions and a double order for the eigenvalues. Finally, in Sect. 5 we present some numerical results on different families of polygonal meshes with small edges, in order to confirm the theoretical rates of convergence proved in the paper and to confirm that it is not polluted with spurious modes.

Throughout the article we will use standard notations for Sobolev spaces, norms and seminorms. Moreover, we will denote by C a generic constant independent of the mesh parameter h, which may take different values in different occurrences.

2 The Spectral Problem

Let $\Omega \subset \mathbb {R}^2$ be a bounded domain with polygonal boundary $\partial \Omega$. Let $\Gamma _0$ and $\Gamma _1$ be disjoint open subsets of $\partial \Omega$ such that $\partial \Omega =\bar{\Gamma }_0\cup \bar{\Gamma }_1$ and $\left| \Gamma _0\right| \ne 0$. We denote by n the outward unit normal vector to $\partial \Omega$.

In what follows, we recall the variational formulation of the Steklov eigenvalue problem proposed in [40]. Also, we summarize some results from this reference.

The Steklov eigenvalue problem reads as follows: Find $(\lambda ,u)\in \mathbb {R}\times H^1(\Omega )$, $u\ne 0$, such that

$$\begin{aligned} \left\{ \begin{array}{l} \Delta u=0\quad \text {in }\Omega , \\ [0.1cm] \partial _n u =\left\{ \begin{array}{ll} \lambda u &{} \text {on }\Gamma _0, \\ 0 &{} \text {on }\Gamma _1, \end{array}\right. \end{array}\right. \end{aligned}$$

where $\partial _n u$ denotes the normal derivative of u. By testing the first equation above with $v\in H^1(\Omega )$ and integrating by parts, we arrive at the following equivalent variational formulation:

Problem 1

Find $(\lambda ,u)\in \mathbb {R}\times H^1(\Omega )$, $u\ne 0$, such that

$$\begin{aligned} \int _{\Omega }\nabla u\cdot \nabla v =\lambda \int _{\Gamma _0}uv\qquad \forall v\in H^1(\Omega ). \end{aligned}$$

Observe that the left-hand side is not $H^1(\Omega )$-elliptic. A remedy for this is to use a shift argument to rewrite Problem 1 in the following form:

Problem 2

Find $(\widehat{\lambda },u)\in \mathbb {R}\times H^1(\Omega )$, $u\ne 0$, such that

$$\begin{aligned} \widehat{\varvec{a}}(u,v) =\widehat{\lambda }b(u,v) \qquad \forall v\in H^1(\Omega ), \end{aligned}$$

where $\widehat{\lambda }=\lambda +1$ and the bilinear form $\widehat{\varvec{a}}:H^1(\Omega )\times H^1(\Omega )\rightarrow \mathbb {R}$ is defined by

$$\begin{aligned} \widehat{\varvec{a}}(u,v)&:=a(u,v)+b(u,v) \qquad u,v\in H^1(\Omega ), \end{aligned}$$

with $a,b:H^1(\Omega )\times H^1(\Omega )\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} a(u,v) :=\int _{\Omega }\nabla u\cdot \nabla v, \qquad b(u,v) :=\int _{\Gamma _0}uv \qquad u,v\in H^1(\Omega ). \end{aligned}$$

All the previous bilinear forms are bounded and symmetric. In addition, the next result, proved in [40, Lemma 2.1], establishes that $\widehat{a}(\cdot ,\cdot )$ is $H^1(\Omega )$-elliptic.

Lemma 2.1

There exists a constant $\alpha >0$, depending on $\Omega$, such that

$$\begin{aligned} \widehat{\varvec{a}}(v,v) \ge \alpha \left\| v\right\| _{1,\Omega }^2 \qquad \forall v\in H^1(\Omega ). \end{aligned}$$

Next, we define the solution operator associated with Problem 2:

$$\begin{aligned} T:\ H^1(\Omega )&\longrightarrow H^1(\Omega ), \\ f&\longmapsto Tf:=w, \end{aligned}$$

where $w\in H^1(\Omega )$ is the unique solution (as a consequence of Lemma 2.1 and the Lax-Milgram Theorem) of the following source problem:

$$\begin{aligned} \widehat{\varvec{a}}(w,v)=b(f,v) \qquad \forall v\in H^1(\Omega ). \end{aligned}$$

(2.1)

Thus, the linear operator T is well defined and bounded. Also, T is self-adjoint with respect to the inner product $\widehat{\varvec{a}}(\cdot ,\cdot )$ in $H^1(\Omega )$ (see [40, Section 2]).

Notice that $(\widehat{\lambda },u)\in \mathbb {R}\times H^1(\Omega )$ solves Problem 2 (and hence $(\lambda ,u)\in \mathbb {R}\times H^1(\Omega )$ solves Problem 1) if and only if $Tu=\mu u$ with $\mu \ne 0$ and $u\ne 0$, in which case $\mu :=1/\widehat{\lambda }$.

The following additional regularity result for the solution of problem (2.1) and consequently, for the eigenfunctions of T, has been proved in [40, Lemma 2.2].

Lemma 2.2

• i) for all $f\in H^1(\Omega )$, there exist $r\in (1/2,1]$ and $C>0$ such that the solution w of problem (2.1) satisfies $w\in H^{1+r}(\Omega )$ and

  $$\begin{aligned} \left\| w\right\| _{1+r,\Omega } \le C\left\| f\right\| _{1,\Omega }; \end{aligned}$$

• ii) if u is an eigenfunction of Problem 1 with eigenvalue $\lambda$, there exist $r>1/2$ and $C>0$ (depending on $\lambda$) such that $u\in H^{1+r}(\Omega )$ and

  $$\begin{aligned} \left\| u\right\| _{1+r,\Omega } \le C\left\| u\right\| _{1,\Omega }. \end{aligned}$$

Remark 2.1

The constant $r>1/2$ is the Sobolev exponent for the Laplace problem with Neumann boundary conditions. If $\Omega$ is convex, then $r\ge 1$, whereas, otherwise, $r:=\pi /\omega$ with $\omega$ being the largest reentrant angle of $\Omega$ (see [31]).

Hence, as a consequence of the compact inclusion $H^{1+r}(\Omega )\hookrightarrow H^1(\Omega )$, T is a compact operator. We have the following spectral characterization for the operator T.

Theorem 2.1

The spectrum of T decomposes as follows: $\mathop {\mathrm {sp}}\nolimits (T)=\left\{ 0,1\right\} \cup \left\{ \mu _k\right\} _{k\in \mathbb {N}}$, where:

i):

$\mu =1$ is an eigenvalue of T and its associated eigenspace is the space of constant functions in $\Omega$;

ii):

$\mu =0$ is an infinite-multiplicity eigenvalue of T with associated eigenspace is $H^1_{\Gamma _0}(\Omega ):=\left\{ q\in H^1(\Omega ):\ q=0\ \text{ on } \Gamma _0\right\}$;

iii):

$\left\{ \mu _k\right\} _{k\in \mathbb {N}}\subset (0,1)$ is a sequence of finite-multiplicity eigenvalues of T which converge to 0 and their corresponding eigenspaces lie in $H^{1+r}(\Omega )$.

3 VEM Discretization

We will study in this section, the virtual element numerical approximation of the eigenproblem presented in Problem 2, by considering weaker mesh assumptions than the mesh assumptions considered in [40]. We will follow some recent results from [11, 18] for the Poisson problem. With this aim, first we recall the mesh construction.

Let $\left\{ \mathcal {T}_h\right\} _h$ be a sequence of decompositions of $\Omega$ into polygons $K$. Let $h_K$ denote the diameter of the element $K$ and h the maximum of the diameters of all the elements of the mesh, i.e., $h:=\max _{K\in \mathcal {T}_h}h_K$. For $\mathcal {T}_h$ we will consider the following assumption:

• A1. There exists $\gamma >0$ such that, for all meshes $\mathcal {T}_h$, each polygon $K\in \mathcal {T}_h$ is star-shaped with respect to a ball of radius greater than or equal to $\gamma h_{K}$.

The next results will be obtained only under assumption A1. In particular, we can consider meshes with edges arbitrarily small with respect to the element diameter $h_{K}$.

We consider now a simple polygon $K$, we define

$$\begin{aligned} \mathbb {B}_1(\partial K) :=\left\{ v\in C^0(\partial K):v|_e\in \mathbb {P}_1(e) \text { for all edges }e\subset \partial K\right\} . \end{aligned}$$

We then consider the finite-dimensional space defined as follows:

$$\begin{aligned} V^{K}:=\left\{ v\in H^1(K): \ v|_{\partial K}\in \mathbb {B}_1(\partial K) \text { and }\Delta v|_{K}=0\right\} . \end{aligned}$$

As in [11], we choose the following degrees of freedom: For all $v_h\in V^{K}$, these are defined as follows:

• values of $v_h$ at the $N_K$ vertices of $K$.

Next, for every decomposition $\mathcal {T}_h$ of $\Omega$ into simple polygons $K$, we define the global virtual space

$$\begin{aligned} V_h:=\left\{ v\in H^1(\Omega ):\ v|_{K}\in V^{K}\right\} . \end{aligned}$$

In order to construct the discrete scheme, we need some preliminary definitions. First, we split the bilinear form $\widehat{\varvec{a}}(\cdot ,\cdot )$ as follows:

$$\begin{aligned} \widehat{\varvec{a}}(w,v)=\sum _{K\in \mathcal {T}_h}a^{K}(w,v)+b(w,v) \qquad w,v\in H^1(\Omega ), \end{aligned}$$

where

$$\begin{aligned} a^{K}(w,v) :=\int _{K}\nabla w\cdot \nabla v \qquad w,v\in H^1(\Omega ). \end{aligned}$$

Next, for any $K\in \mathcal {T}_h$ and for any sufficiently regular function v, we define first

$$\begin{aligned} \overline{v}:=\vert \partial K\vert ^{-1}\int _{\partial K}v. \end{aligned}$$

(3.1)

Now, we define the projector $\Pi ^{K}:V^{K}\longrightarrow \mathbb {P}_1(K)\subseteq V^{K}$ for each $v\in V^{K}$ as the solution of

$$\begin{aligned} a^{K}\big (\Pi ^{K}v,q\big )&=a^{K}(v,q) \qquad \forall q\in \mathbb {P}_1(K), \\ \overline{\Pi ^{K}v}&=\overline{v}. \end{aligned}$$

Now, we introduce the following symmetric and semi-positive definite bilinear form on $V^{K}\times V^{K}$ (see [49]). For all elements $K\in \mathcal {T}_h$:

$$\begin{aligned} S^{K}(w_h,v_h):=h_{K}\int _{\partial {K}}\partial _{s}w_h\partial _s v_h\qquad \forall w_h,v_h\in V^{K}, \end{aligned}$$

(3.3)

where $\partial _s$ denotes a derivative along the edge.

Then, set

$$\begin{aligned} a_h(w_h,v_h) :=\sum _{K\in \mathcal {T}_h}a_h^{K}(w_h,v_h) \qquad w_h,v_h\in V_h, \end{aligned}$$

where $a_h^{K}(\cdot ,\cdot )$ is the bilinear form defined on $V^{K}\times V^{K}$ by

$$\begin{aligned} a_h^{K}(w,v) :=a^{K}\big (\Pi ^{K}w,\Pi ^{K}v\big ) +S^{K}\big (w-\Pi ^{K}w,v-\Pi ^{K}v\big ) \qquad w,v\in V^{K}. \end{aligned}$$

(3.4)

Remark 3.1

It is immediate to verify that $\mathbb {P}_1(K)\subseteq V^{K}$. Thus, from (3.4) we have that

$$\begin{aligned} a_h^{K}(w,p)=a^{K}(w,p)\qquad \forall p\in \mathbb {P}_1(K),\,\,\forall w\in V^{K}. \end{aligned}$$

(3.5)

Now, we introduce the following discrete semi-norm:

$$\begin{aligned} {\left| \left| \left| v \right| \right| \right| }_{K}^2:=a^{K}\big (\Pi ^{K}v,\Pi ^{K}v)+S^{K}(v-\overline{v},v-\overline{v})\qquad \forall v\in V^{K}+\mathcal {V}^{K}, \end{aligned}$$

(3.6)

where $\mathcal {V}^{K}\subseteq H^1(K)$ is a subspace of sufficiently regular functions for $S^{K}(\cdot ,\cdot )$ to make sense.

Now, for any sufficiently regular functions, we introduce the following global semi-norms

$$\begin{aligned} {\left| \left| \left| v \right| \right| \right| }^2:=\sum _{K\in \mathcal {T}_h}{\left| \left| \left| v \right| \right| \right| }_{K}^2,\qquad \left| v\right| _{1,h}^2 :=\sum _{K\in \mathcal {T}_h}\left\| \nabla v\right\| _{0,K}^2. \end{aligned}$$

It has been proved in [11, Lemma 3.1 and Proposition 4.4] that for our choice of the stabilization form (3.3), there exist positive constants $C_1,C_2,C_{3}$, independent of h, such that

$$\begin{aligned} C_1{\left| \left| \left| v \right| \right| \right| }_{K}^2\le a_h^{K}(v,v)\le C_2{\left| \left| \left| v \right| \right| \right| }_{K}^2\quad \forall v\in V^{K}, \end{aligned}$$

(3.7)

$$\begin{aligned} a_h^{K}(v,v)\le C_3({\left| \left| \left| v \right| \right| \right| }^2+\vert v\vert _{1,K}^2)\quad \forall v\in V^{K}. \end{aligned}$$

(3.8)

In addition, it holds

$$\begin{aligned} a^{K}(v,v)\le C_4{\left| \left| \left| v \right| \right| \right| }_{K}^2\quad \forall v\in V^{K},\nonumber \\ {\left| \left| \left| p \right| \right| \right| }_{K}^2\le C_5 a^{K}(p,p)\quad \forall p\in \mathbb {P}_1(K), \end{aligned}$$

(3.9)

where $C_4,C_5$ are independent of h.

Now we are in a position to write the virtual element discretization of Problem 1.

Problem 3

Find $(\lambda _h,u_h)\in \mathbb {R}\times V_h$, $u_h\ne 0$, such that

$$\begin{aligned} a_h(u_h,v_h) =\lambda _h b(u_h,v_h) \qquad \forall v_h\in V_h. \end{aligned}$$

We use again a shift argument to rewrite this discrete eigenvalue problem in the following convenient equivalent form.

Problem 4

Find $(\widehat{\lambda }_h,u_h)\in \mathbb {R}\times V_h$, $u_h\ne 0$, such that

$$\begin{aligned} \widehat{\varvec{a}}_h(u_h,v_h) =\widehat{\lambda }_hb(u_h,v_h) \qquad \forall v_h\in V_h, \end{aligned}$$

where $\widehat{\lambda }_h=\lambda _h+1$ and the bilinear form $\widehat{\varvec{a}}_h:V_h\times V_h\rightarrow \mathbb {R}$ is defined by

$$\begin{aligned} \widehat{\varvec{a}}_h(u_h,v_h) :=a_h(u_h,v_h)+b(u_h,v_h) \qquad u_h,v_h\in V_h. \end{aligned}$$

Clearly $\widehat{\varvec{a}}_h(\cdot ,\cdot )$ is symmetric and continuous. In the following result we prove that $\widehat{\varvec{a}}_h(\cdot ,\cdot )$ is elliptic in $V_h$.

Lemma 3.1

There exists a constant $\beta >0$, independent of h, such that

$$\begin{aligned} \widehat{\varvec{a}}_{h}(v_h,v_h) \ge \beta \left\| v_h\right\| _{1,\Omega }^2 \qquad \forall v_h\in V_h. \end{aligned}$$

Proof

From the definition of the bilinear form $\widehat{\varvec{a}}_h(\cdot ,\cdot )$, we have that

$$\begin{aligned} \widehat{\varvec{a}}_{h}(v_h,v_h)= & {} a_h(v_h,v_h)+b(v_h,v_h)\\= & {} \sum _{K\in \mathcal {T}_h}a_h^{K}\big (v_h,v_h\big )+b(v_h,v_h) \ge \sum _{K\in \mathcal {T}_h}C_1{\left| \left| \left| v_h \right| \right| \right| }_{K}^2+\Vert v_h\Vert _{0,\Gamma _0}^{2}\\\ge & {} C\sum _{K\in \mathcal {T}_h}a^{K}\big (v_h,v_h\big )+\Vert v_h\Vert _{0,\Gamma _0}^{2}\\\ge & {} C\vert v_h\vert _{1,\Omega }^2+\Vert v_h\Vert _{0,\Gamma _0}^{2} \ge \beta \left\| v_h\right\| _{1,\Omega }^2 \qquad \forall v_h\in V_h, \end{aligned}$$

where we have used (3.7), (3.9) and the generalized Poincaré inequality. This concludes the proof.$\square$

With this coercivity result at hand, we are in a position to introduce the discrete solution operator

$$\begin{aligned} T_h:\ H^1(\Omega )&\longrightarrow H^1(\Omega ), \\ f&\longmapsto T_hf:=w_h, \end{aligned}$$

where $u_h\in V_h$ is the solution of the following discrete source problem

$$\begin{aligned} \widehat{\varvec{a}}_h(w_h,v_h)=b(f,v_h) \qquad \forall v_h\in V_h. \end{aligned}$$

Notice that Lemma 3.1 implies that the linear operator $T_h$ is well defined and bounded uniformly with respect to h. Moreover, as in the continuous case, $(\widehat{\lambda }_h,u_h)\in \mathbb {R}\times V_h$ solves Problem 4 (and hence $(\lambda _h,u_h)\in \mathbb {R}\times V_h$ solves Problem 3) if and only if $T_hu_h=\mu _h u_h$ with $\mu _h\ne 0$ and $u_h\ne 0$, in which case $\mu _h:= 1/\widehat{\lambda }_h$. Also, $T_h|_{V_h}:\ V_h\longrightarrow V_h$ is self-adjoint with respect to $\widehat{\varvec{a}}_{h}(\cdot ,\cdot )$.

As a consequence, we have the following spectral characterization for $T_h$.

Theorem 3.1

The spectrum of $T_h|_{V_h}$ consists of $M_h:=\mathop {\mathrm {\,dim}}\nolimits (V_h)$ eigenvalues, repeated according to their respective multiplicities. It decomposes as follows: $\mathop {\mathrm {sp}}\nolimits (T_h|_{V_h}) =\left\{ 0,1\right\} \cup \left\{ \mu _{h}^{(k)}\right\} _{k=1}^{N_h}$, where:

i):

the eigenspace associated with $\mu _h=1$ is the space of constant functions in $\Omega$;

ii):

the eigenspace associated with $\mu _h=0$ is $Z_h:=V_h\cap H^1_{\Gamma _0}(\Omega )=\left\{ q_h\in V_h:\ q_h=0\ \text{ on } \Gamma _0\right\}$;

iii):

$\mu _{h}^{(k)}\subset (0,1)$, $k=1,\dots ,N_h:=M_h-\mathop {\mathrm {\,dim}}\nolimits (Z_h)-1$, are non-defective eigenvalues repeated according to their respective multiplicities.

4 Convergence and Error Estimates

In order to prove that the solutions of the discrete problem converge to those of the continuous problem, we will follow the standard procedure for spectral theory for compact operators [5], which consists in showing that $T_h$ converges in norm to T as h tends to zero.

With this end, we begin by proving the following result.

Lemma 4.1

There exists $C>0$, independent of h, such that, for all $f\in H^1(\Omega )$, if $w=Tf$ and $w_h=T_hf$, then

$$\begin{aligned} \left\| w-w_h\right\| _{1,\Omega } \le C\left( \left\| w-w_I\right\| _{1,\Omega }+ \left| w_{\pi }-w\right| _{1,h} +{\left| \left| \left| w-w_{I} \right| \right| \right| }+{\left| \left| \left| w-w_{\pi } \right| \right| \right| }\right) , \end{aligned}$$

(4.1)

for all $w_I\in V_h$ and for all $w_{\pi }\in L^2(\Omega )$ such that $w_{\pi }|_{K}\in \mathbb {P}_1(K)$ $\forall K\in \mathcal {T}_h$. In addition

$$\begin{aligned} {\left| \left| \left| w_{h}-w_{I} \right| \right| \right| } \le C\left( \left\| w-w_I\right\| _{1,\Omega } + \left| w_{\pi }-w\right| _{1,h}+{\left| \left| \left| w-w_{I} \right| \right| \right| }+{\left| \left| \left| w-w_{\pi } \right| \right| \right| }\right) . \end{aligned}$$

(4.2)

Proof

Let $w=Tf$ and $w_h=T_hf$. From the triangle inequality we have

$$\begin{aligned} \Vert w-w_{h}\Vert _{1,\Omega }\le \Vert w-w_{I}\Vert _{1,\Omega }+\Vert w_{I}-w_{h}\Vert _{1,\Omega }. \end{aligned}$$

Our task is to estimate the norms of the right hand side above. To do this, we follow the arguments on the proof of Lemma 3.1.

Now, for $w_I\in V_h$, we set $v_h:=w_h-w_I$ and thanks to Lemma 3.1, the definitions of $a_h^{K}(\cdot ,\cdot )$ (cf. (3.4)) and those of T and $T_h$, we have

$$\begin{aligned} \left( {\left| \left| \left| v_{h} \right| \right| \right| }+\left\| v_h\right\| _{0,\Gamma _{0}}\right) ^{2}&\le 2\left( {\left| \left| \left| v_{h} \right| \right| \right| }^{2}+\left\| v_h\right\| ^2_{0,\Gamma _{0}}\right) \\&\le C\widehat{\varvec{a}}_h(v_h,v_h)=C(\widehat{\varvec{a}}_h(w_h,v_h)-\widehat{\varvec{a}}_h(w_I,v_h)) \\&=C\left( b(f,v_h)-\sum _{K\in \mathcal {T}_h}a_h^K(w_I,v_h)-b(w_I,v_h)\right) \\&=C\Big (b(f,v_h)-b(w_I,v_h)\\&\left. -\sum _{K\in \mathcal {T}_h} \left( a_h^K(w_I-w_{\pi },v_h)+a^K(w_{\pi }-w,v_h)+a^K(w,v_h)\right) \right) \\&=C\left( b(w-w_I,v_h) -\sum _{K\in \mathcal {T}_h} \left( a_h^K(w_I-w_{\pi },v_h)+a^K(w_{\pi }-w,v_h)\right) \right) . \end{aligned}$$

Therefore, from the trace theorem, (3.7) and the boundedness of $a_h^K(\cdot ,\cdot )$ (3.8) and $a^K(\cdot ,\cdot )$, we get

$$\begin{aligned} \left( {\left| \left| \left| v_{h} \right| \right| \right| }+\left\| v_h\right\| _{0,\Gamma _0}\right) ^{2}&\le C\Big (\left\| w-w_I\right\| _{0,\Gamma _0} \left\| v_h\right\| _{0,\Gamma _0}\\&\quad \left. +\sum _{K\in \mathcal {T}_h} \left( C({\left| \left| \left| w_I-w_{\pi } \right| \right| \right| }_{K}+\left| w_I-w_{\pi }\right| _{1,K}) {\left| \left| \left| v_h \right| \right| \right| }_{K} +\left| w_{\pi }-w\right| _{1,K} \left| v_h\right| _{1,K}\right) \right) \\&\le C\left( \left\| w-w_I\right\| _{0,\Gamma _0} \left\| v_h\right\| _{0,\Gamma _0} +\sum _{K\in \mathcal {T}_h} \left\{ C\left( {\left| \left| \left| w_I-w_{\pi } \right| \right| \right| }_{K}+\left| w_{\pi }-w\right| _{1,K}\right) {\left| \left| \left| v_h \right| \right| \right| }_{K}\right\} \right) \\&\le C \left( \left\| w-w_I\right\| _{0,\Gamma _0}+{\left| \left| \left| w_I-w_{\pi } \right| \right| \right| }+ \left| w_{\pi }-w\right| _{1,h}\right) \left( \Vert v_{h}\Vert _{0,\Gamma _0}+{\left| \left| \left| v_{h} \right| \right| \right| }\right) . \end{aligned}$$

Therefore, we have

$$\begin{aligned} {\left| \left| \left| v_{h} \right| \right| \right| }+\left\| v_h\right\| _{0,\Gamma _{0}} \le \widetilde{C} \left( \left\| w-w_I\right\| _{1,\Omega } +{\left| \left| \left| w-w_{\pi } \right| \right| \right| }+{\left| \left| \left| w-w_{I} \right| \right| \right| }+ \left| w_{\pi }-w\right| _{1,h}\right) . \end{aligned}$$

Finally, (4.1) follows from the triangle inequality and the generalized Poincaré inequality. Moreover, (4.2) follows from the above estimate.$\square$

Let us introduce the following approximation result for polynomials in star-shaped domains (see for instance [17]), which is derived by results of interpolation between Sobolev spaces (see for instance [30, Theorem I.1.4]), leading to an analogous result for integer values of s. Moreover, we remark that the result for integer values is stated in [7, Proposition 4.2] and follows from the well establish Scott-Dupont theory (see [17]).

Lemma 4.2

If assumption A1 is satisfied, then there exists a positive constant C, depending only on k and $\gamma$, such that for every s with $0\le s\le k$ and for every $v\in H^{1+s}(K)$, there exists $v_{\pi }\in \mathbb {P}_k(K)$ such that

$$\begin{aligned} \left\| v-v_{\pi }\right\| _{0,K} +h_{K}\left| v-v_{\pi }\right| _{1,K} \le Ch_{K}^{1+s}\left\| v\right\| _{1+s,K}. \end{aligned}$$

Now, we have the following approximation result in the virtual space $V_h$, which follows from [11, Theorem 3.4].

Lemma 4.3

Under the assumption A1, then, for each s with $1/2<s\le 1$, there exist $\widehat{t}>1/2$ and a positive constant C, independent of h, such that for every $v\in H^{1+s}(\Omega )$, there exists $v_I\in V_h$ that satisfies

$$\begin{aligned} \left| v-v_I\right| _{1+t,K}&\le Ch_{K}^{s-t}\left| v\right| _{1+s,K}, \qquad 0\le t<\min \{\widehat{t},s\}, \end{aligned}$$

(4.3)

$$\begin{aligned} \left\| v-v_I\right\| _{0,K}&\le Ch_{K}\left| v\right| _{1+s,K}. \end{aligned}$$

(4.4)

Proof

Estimate (4.3) has been obtained in [11, Theorem 3.4]. To obtain (4.4), with $1/2<s\le 1$, first we use the Poincaré and the Cauchy-Schwarz inequalities, to obtain (see [13, Remark 4.1]),

$$\begin{aligned} \left\| v-v_I\right\| _{0,K}&\le C\left( \int _{\partial K}|v-v_{I}|ds+h_{K}|v-v_{I}|_{1,K}\right) \\&\le C\left( h_{K}^{1/2}\Vert v-v_{I}\Vert _{0,\partial K}+h_{K}|v-v_{I}|_{1,K}\right) \\&\le C\left( h_{K}^{1/2}h_{K}^{1/2}|v|_{1/2,\partial K}+h_{K}|v-v_{I}|_{1,K}\right) \\&\le C\left( h_{K}|v|_{1,K}+h_{K}|v-v_{I}|_{1,K}\right) \\&\le Ch_{K}|v|_{1+s,K}, \end{aligned}$$

where we have use an standard approximation estimate in one dimension, since $v_I|_{\partial K}$ corresponds to the standard piecewise linear Lagrange interpolant of v and then $|v|_{1/2,\partial K}\le |v|_{1,K}$ (see [34] for instance). This concludes the proof.$\square$

Now we are in position to establish the convergence in norm of $T_h$ to T as $h\rightarrow 0$.

Lemma 4.4

There exist $r\in (1/2,1]$ (cf. Lemma 2.2(i)) and $C>0$, independent of h, such that

$$\begin{aligned} \left\| \left( T-T_h\right) f\right\| _{1,\Omega } \le Ch^{r}\left\| f\right\| _{1,\Omega } \qquad \forall f\in H^1(\Omega ). \end{aligned}$$

Proof

The result follows from Lemma 4.1. In particular, we have to bound the term on the right and side of (4.1). For the first and second terms, using Lemmas 4.3 and 4.2, respectively, we obtain

$$\begin{aligned} ||w-w_{I}||_{1,\Omega }+|w-w_{\pi }|_{1,h}\le C\sum _{K\in \mathcal {T}_{h}}h_{K}^{r}|w|_{1+r,K}\le Ch^{r}|w|_{1+r,\Omega }. \end{aligned}$$

(4.5)

Now, we bound the term ${\left| \left| \left| w-w_{I} \right| \right| \right| }$. To do this task, we invoke the definition of ${\left| \left| \left| \cdot \right| \right| \right| }$ given in (3.6), (3.1) and, operating as in the proof of [11, Theorem 4.5] we have

$$\begin{aligned} \sum _{K\in \mathcal {T}_{h}}{\left| \left| \left| w-w_I \right| \right| \right| }_{K}^{2}&=\sum _{K\in \mathcal {T}_{h}}\left\{ a^K\left( \Pi ^{K}(w-w_I), \Pi ^{K}(w-w_I) \right) \right. \nonumber \\&\left. +S^K\left( (w-w_I)-\overline{(w-w_{I})},(w-w_I)-\overline{(w-w_{I})}\right) \right\} \nonumber \\&\le C\sum _{K\in \mathcal {T}_{h}}\left( |\Pi ^{K}(w-w_I)|^2_{1,K}+S^K(w-w_I,w-w_I) \right) \nonumber \\&=C\sum _{K\in \mathcal {T}_{h}}\left( |w-w_I|^2_{1,K}+h_K|w-w_I|_{1,\partial K}^2\right) . \end{aligned}$$

(4.6)

Let $\sigma$ be such that $1/2<\sigma <r$. Using a scaled trace inequality, we get

$$\begin{aligned} h_K|w-w_I|_{1,\partial K}^2\le C \left( |w-w_{I}|_{1,K}^{2} +h^{2\sigma }|w-w_{I}|_{1+\sigma ,K}^{2}\right) \le Ch_{K}^{2r}|w|_{1+r,K}^{2}. \end{aligned}$$

Using the above estimate in (4.6) and Proposition 4.3, we obtain

$$\begin{aligned} {\left| \left| \left| w-w_{I} \right| \right| \right| }=\left( \sum _{K\in \mathcal {T}_{h}} {\left| \left| \left| w-w_I \right| \right| \right| }_{K}^{2}\right) ^{1/2}&\le C\left( \sum _{K\in \mathcal {T}_{h}}h_{K}^{2r}|w|_{1+r,K}^{2}\right) ^{1/2} \le Ch^{r}|w|_{1+r,\Omega }. \end{aligned}$$

(4.7)

Similarly, we obtain

$$\begin{aligned} {\left| \left| \left| w-w_\pi \right| \right| \right| }\le Ch^{r}|w|_{1+r,\Omega }. \end{aligned}$$

thus, the lemma follows from (4.5)–(4.7) and Lemma 2.2(i).$\square$

We conclude the analysis of our paper deriving error estimates for our method. In particular, we are going to present error estimates for eigenfunctions and eigenvalues. With this aim, and with Lemma 4.4 at hand we will prove that isolated parts of $\mathop {\mathrm {sp}}\nolimits (T)$ are approximated by isolated parts of $\mathop {\mathrm {sp}}\nolimits (T_h)$ (see [32]).

Let $\mu \in (0,1)$ be an isolated eigenvalue of T with multiplicity m and let $\mathcal {E}$ be its associated eigenspace. Then, there exist m eigenvalues $\mu ^{(1)}_h,\dots ,\mu ^{(m)}_h$ of $T_h$ (repeated according to their respective multiplicities) which converge to $\mu$. From now and on, let $\mathcal {E}_h$ be the discrete subspace associated to $\mathcal {E}$, corresponding to the direct sum of their corresponding associated eigenspaces.

We recall the definition of the gap $\widehat{\delta }$ between two closed subspaces $\mathcal {X}$ and $\mathcal {Y}$ of $H^1(\Omega )$:

$$\begin{aligned} \widehat{\delta }(\mathcal {X},\mathcal {Y}) :=\max \left\{ \delta (\mathcal {X},\mathcal {Y}),\delta (\mathcal {Y},\mathcal {X})\right\} , \quad \text {where}\quad \delta (\mathcal {X},\mathcal {Y}) :=\sup _{x\in \mathcal {X}:\ \left\| x\right\| _{1,\Omega }=1} \left( \inf _{y\in \mathcal {Y}}\left\| x-y\right\| _{1,\Omega }\right) . \end{aligned}$$

The following error estimates for the approximation of eigenvalues and eigenfunctions hold true.

Theorem 4.1

There exists a strictly positive constant C such that

$$\begin{aligned} \widehat{\delta }(\mathcal {E},\mathcal {E}_h)&\le C\gamma _h,\\ \left| \mu -\mu _h^{(i)}\right|&\le C\gamma _h,\qquad i=1,\dots ,m, \end{aligned}$$

where

$$\begin{aligned} \gamma _h :=\sup _{f\in \mathcal {E}:\ \left\| f\right\| _{1,\Omega }=1} \left\| (T-T_h)f\right\| _{1,\Omega }. \end{aligned}$$

Proof

As a consequence of Lemma 4.4, $T_h$ converges in norm to T as h goes to zero. Then, the proof follows as a direct consequence of Theorems 7.1 and 7.3 from [5].$\square$

The theorem above yields error estimates depending on $\gamma _h$. The next step is to show an optimal order estimate for this term.

Theorem 4.2

There exist $r\in (1/2,1]$ and a positive constant C such that

$$\begin{aligned} \left\| (T-T_h)f\right\| _{1,\Omega } \le Ch^{r} \left\| f\right\| _{1,\Omega } \qquad \forall f\in \mathcal {E}, \end{aligned}$$

and, consequently,

$$\begin{aligned} \gamma _h\le Ch^{r}. \end{aligned}$$

Proof

See [40, Theorem 4.2].$\square$

The error estimate for the eigenvalue $\mu \in (0,1)$ of T leads to an analogous estimate for the approximation of the eigenvalue $\lambda =\frac{1}{\mu }-1$ of Problem 1 by means of the discrete eigenvalues $\lambda _h^{(i)}:=\frac{1}{\mu _h^{(i)}}-1$, $1\le i\le m$, of Problem 3.

We are able to improve the convergence order of Theorem 4.1 for the eigenvalues. The following result shows in fact that the convergence order is quadratic.

Theorem 4.3

There exist $r\in (1/2,1]$ and a positive constant C such that

$$\begin{aligned} \left| \lambda -\lambda _h^{(i)}\right| \le Ch^{2r}. \end{aligned}$$

Proof

Let $u_h$ be such that $(\lambda _h^{(i)},u_h)$ is a solution of Problem 3 with $\left\| u_h\right\| _{1,\Omega }=1$. According to Theorems 4.1 and 4.2, there exists a solution $(\lambda ,u)$ of Problem 1 such that

$$\begin{aligned} \left\| u-u_h\right\| _{1,\Omega }\le Ch^{r}. \end{aligned}$$

(4.8)

From the symmetry of the bilinear forms and the facts that $a(u,v)=\lambda b(u,v)$ for all $v\in H^1(\Omega )$ (cf. Problem 1) and $a_h(u_h,v_h)=\lambda _h^{(i)}b(u_h,v_h)$ for all $v_h\in V_h$ (cf. Problem 3), we have

$$\begin{aligned} a(u-u_h,u-u_h)-\lambda b(u-u_h,u-u_h)&=a(u_h,u_h)-\lambda b(u_h,u_h) \\&=\left[ a(u_h,u_h)-a_h(u_h,u_h)\right] -\left( \lambda -\lambda _h^{(i)}\right) b(u_h,u_h), \end{aligned}$$

from which we obtain the following identity:

$$\begin{aligned} \left( \lambda _h^{(i)}-\lambda \right) b(u_h,u_h) =a(u-u_h,u-u_h)-\lambda b(u-u_h,u-u_h) +\left[ a_h(u_h,u_h)-a(u_h,u_h)\right] . \end{aligned}$$

(4.9)

The next step is to bound each term on the right hand side above. The first and the second ones are easily bounded from the continuity of $a(\cdot ,\cdot )$ and $b(\cdot ,\cdot )$, the trace theorem and (4.8) as follows

$$\begin{aligned} \left| a(u-u_h,u-u_h)\right| +\lambda \left| b(u-u_h,u-u_h)\right| \le Ch^{2r}. \end{aligned}$$

(4.10)

For the last term on the right hand side of (4.9), we consider $u_\pi \in \mathbb {P}_1(K)$ and $u_I\in V_h$ such that Lemmas 4.2 and 4.3 hold true, respectively. Now, we add and subtract $u_\pi$ in the local bilinear forms $a_{h}^{K}(\cdot ,\cdot )$ and $a^{K}(\cdot ,\cdot )$, using property (3.5) and invoking (4.2), we obtain

$$\begin{aligned} \left| a_h(u_h,u_h)-a(u_h,u_h)\right|&=\left| \sum _{K\in \mathcal {T}_{h}} a_{h}^{K}(u_h-u_\pi ,u_h-u_\pi )-a^{K}(u_h-u_\pi ,u_h-u_\pi )\right| \\&\le \sum _{K\in \mathcal {T}_{h}} {\left| \left| \left| u_h-u_\pi \right| \right| \right| }_{K}^2+\sum _{K\in \mathcal {T}_{h}}|u_h-u_\pi |_{1,K}^2\\&={\left| \left| \left| u_h-u_\pi \right| \right| \right| }^2+|u_h-u_\pi |_{1,h}^2\\&\le C\left( {\left| \left| \left| u-u_h \right| \right| \right| }^2+{\left| \left| \left| u-u_\pi \right| \right| \right| }^2+|u-u_h|^2_{1,h}+|u-u_\pi |^2_{1,h} \right) \\&\le C\left( {\left| \left| \left| u-u_I \right| \right| \right| }^2+{\left| \left| \left| u_{h}-u_I \right| \right| \right| }^2 +{\left| \left| \left| u-u_\pi \right| \right| \right| }^2+|u-u_h|^2_{1,h}+|u-u_\pi |^2_{1,h} \right) \\&\le C\left( {\left| \left| \left| u-u_I \right| \right| \right| }^2+{\left| \left| \left| u-u_\pi \right| \right| \right| }^2 +\Vert u-u_{I}\Vert _{1,\Omega }^{2}+|u-u_{\pi }|_{1,h}^{2}+|u_h-u|^2_{1,\Omega } \right) . \end{aligned}$$

Next, the terms on the right hand side above can be bounded repeating the argument used in the proof of Lemma 4.4 and using the additional regularity result presented in Lemma 2.2(ii). We get

$$\begin{aligned} \left| a_h(u_h,u_h)-a(u_h,u_h)\right| \le Ch^{2r}. \end{aligned}$$

(4.11)

On the other hand, by virtue of Lemma 3.1 and the fact that $\lambda _h^{(i)}\rightarrow \lambda$ as h goes to zero, we know that there exists $C>0$ such that

$$\begin{aligned} b(u_h,u_h) =\frac{\widehat{\varvec{a}}_h(u_h,u_h)}{\lambda _h^{(i)}+1} \ge \frac{\beta \left\| u_h\right\| _{1,\Omega }^2}{\lambda _h^{(i)}+1} \ge \frac{\beta }{C}>0. \end{aligned}$$

Finally, the proof follows from (4.9), by using the above estimate together with (4.10) and (4.11).$\square$

5 Numerical Experiments

In the present section we will report some numerical tests in order to asses the performance of the proposed lowest order VEM with meshes allowing small edges. All the reported numerical results have been obtained with a MATLAB code. In order to observe the performance and accuracy of the proposed method, we will consider different computational domains, where the eigenfunctions, on one hand, can be smooth enough and, on the other, can be singular due to the non-convex domains.

For all the tests, we will report the computed eigenvalues for different polygonal meshes and the order of convergence. Our results will be compared with some references and exact solutions in the cases where it is available. In the cases where it is not possible to have a close form of the solution, we will present extrapolated values for the eigenvalues (see (5.3)).

5.1 Square Domain: The Sloshing Problem.

We begin with a convex domain. In this case we consider $\Omega :=(0,1)^2$ as computational domain. We fix $\Gamma _0$ on the top of the boundary (representing a free surface) and $\Gamma _1$ will be the rest of the boundary. In Fig. 1, we present the physical configuration of the problem.

Fig. 1

Sloshing in a square domain

For this problem there are analytical solutions of the form

$$\begin{aligned} \lambda _n=n\pi \tanh (n\pi ), \quad u_n(x,y)=\cos (n\pi x)\sinh (n\pi x), \quad n\in \mathbb {N}. \end{aligned}$$

(5.1)

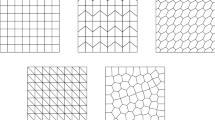
In Fig. 2, we present plots of the polygonal meshes that we will consider for our tests. We note that the family of polygonal meshes $\mathcal {T}_h^1$ have been obtained by gluing two different polygonal meshes at $y=0.6$. It can be seen that very small edges compared with the element diameter appears on the interface of the resulting mesh. The second family of polygonal meshes $\mathcal {T}_h^2$ have been obtained from a triangular mesh with an additional point on each edge as a new degree of freedom which has been moved to a distance $h_e^{2}$ from one vertex and $(h_{e}-h_{e}^{2})$ from the other. We observe that this family satisfy $\mathbf {A1}$ but fail to satisfy the usual assumption that distance between any two of its vertices is greater than or equal to $Ch_{K}$ for each polygon, since the length of the smallest edge is $h_e^2$, while the diameter of the element is bounded above by a multiple of $h_e$. The refinement level for the meshes will be denoted by N, which corresponds to the number of subdivisions in the abscissae.

Fig. 2

Sample meshes with small edges. From left to right: $\mathcal {T}_h^1$ and $\mathcal {T}_h^2$ for $N=4$

In Table 1, we report the first six eigenvalues computed with meshes $\mathcal {T}_h^1$ and $\mathcal {T}_h^2$. The row “Order” reports the convergence order of the eigenvalues, computed with respect to the exact ones obtained with (5.1), which are presented in the row “Exact”.

Table 1 Test 1. The lowest computed eigenvalues $\lambda _{h}^{(i)}$, $1\le i\le 6$ for different meshes

The order of convergence is clearly $\mathcal {O}(h^{2})$, which is expectable according to Theorem 4.3 and due the smoothness of the eigenfunctions for this configuration of the problem. Moreover, the nature of the meshes and the fact that we are allowing small edges for the polygons, does not affect the order of convergence and no spurious eigenvalues were found.

In the next test, we will study the effects of the stabilization (3.3) in the computation of the spectrum. We will consider the same physical configuration as in the previous test. Since the stabilization depends on the size of the element K (see (3.3)), we will compute the first six eigenvalues for different values $h_K^{\alpha }$ using the family of meshes $\mathcal {T}_h^2$.

Table 2 Test 1. The lowest computed eigenvalues $\lambda _{h}^{(i)}$, $1\le i\le 6$ for different $h_{K}^{\alpha }$, $\alpha =\{1/2, 3/4, 1, 5/4, 3/2\}$ with meshes $\mathcal {T}_{h}^{2}$

We observe from the results of Table 2 that the method converges to the exact eigenvalues with an optimal quadratic order and no spurious eigenvalues were found for any chosen stability parameter $h_K^{\alpha }$. We remark that these results are also valid for other families of polygonal meshes allowing small edges.

In the following test, we are going to compare the approach presented in this work which is characterized by the stabilization term (3.3) with a VEM discretization by considering the following standard stabilization term (for each polygon $K$):

$$\begin{aligned} S_{*}^{K}(u,v):=\sum _{r=1}^{N_{K}}u(P_r)v(P_r), \qquad u,v\in V^{K}, \end{aligned}$$

(5.2)

where $P_1,\dots ,P_{N_{K}}$ are the vertices of $K$. The analysis of a VEM scheme by considering the above stabilizer has been presented in [40].

More precisely, the aim of this test is to analyze the influence of the stabilizing bilinear forms on the computed spectrum, to know whether the quality of the computations can be affected. With this aim, for any $\sigma _{K}>0$, we consider the following scaled stabilizing bilinear forms $\sigma _{K}S^{K}(\cdot ,\cdot )$ (cf. (3.3)) and $\sigma _{K}S_{*}^{K}(\cdot ,\cdot )$ (cf. (5.2)).

In Table 3 we report the three lowest eigenvalues computed for different stability terms with varying values of $\sigma _{K}$ on a fixed mesh $\mathcal {T}_{h}^{2}$ with refinement level $N = 8$. The table also includes in the last column the three lowest exact eigenvalues. The computed eigenvalues into boxes correspond to approximations of these physical eigenvalues, whereas the rest correspond to spurious spectrum.

Table 3 Test 1. Computed lowest eigenvalues for $\sigma _K=4^{-k}$ with $-3\le k\le 3$ on a fixed mesh $\mathcal {T}_{h}^{2}$ with refinement level $N = 8$

It can be seen from the Table 3 that the VEM method with the stability term $S_{*}^{K}(\cdot ,\cdot )$ (cf. (5.2)) leads to spurious eigenvalues for some values of the parameter $\sigma _K$ with meshes allowing small edges. Spurious eigenvalues have been also reported in [40, Section 5.2] for this method on more restricted meshes. On the other hand, to compute the three lowest eigenvalues, the VEM method with the stability term $S^{K}(\cdot ,\cdot )$ (cf. (3.3)) do not introduce spurious eigenvalues for all values of the parameter $\sigma _K$. Moreover, the same behavior has been obtained for family of meshes $\mathcal {T}_{h}^{1}$. This represents an important advantage of the proposed scheme.

5.2 Rotated T Domain

In the following test we will consider a non-convex domain which we call rotated T, and it is defined by $\Omega _T:=(-0.5, 0.5)\times (-0.5, 0)\cup (-0.25,0.25)\times (0,1)$ with boundary condition $\Gamma _0=\partial \Omega _T$. This non-convex domain presents two reentrant angles of the same size $\omega =\frac{3\pi }{2}$ (cf. Figure 3), and as a consequence, the eigenfunctions of this problem may present singularities. More precisely, the Sobolev exponent for the eigenfunctions is 2/3 (cf. Remark 2.1), so that the eigenfunctions will belong to $H^{1+r}(\Omega )$ for all $r<2/3$, but in general not to $H^{1+\frac{2}{3}}(\Omega )$. Therefore, according to Theorem 4.3, the convergence rate for the eigenvalues should be $\vert \lambda -\lambda _h\vert \approx h^{4/3}$.

In Fig. 3, we present the meshes that we will consider for this numerical test. We note that the families of polygonal meshes $\mathcal {T}_h^3$, $\mathcal {T}_h^4$ and $\mathcal {T}_h^5$ have been obtained by gluing two different polygonal meshes at $x=0$. It can be seen that very small edges compared with the element diameter appears on the interface of the resulting meshes.

Fig. 3

Sample meshes with small edges. From left to right: $\mathcal {T}_h^3$, $\mathcal {T}_h^4$ and $\mathcal {T}_h^5$, for $N=8$

Table 4 Test 2. Computed lowest eigenvalues $\lambda _{h}^{(i)}$, $1\le i\le 4$, on different polygonal meshes

Fig. 4

From top left to bottom right, plots of the first four eigenfunctions for the rotated T domain, computed with $\mathcal {T}_h^5$

Fig. 5

Sample meshes: inicial mesh $\mathcal {T}_{h}^{6}$ with $N=16$ (top left), $\mathcal {T}_{h}^{6,1}$ (top right), $\mathcal {T}_{h}^{6,2}$ (bottom left) and $\mathcal {T}_{h}^{6,3}$ (bottom right)

In Table 4, we report the computed eigenvalues and the corresponding convergence rates, the last row, that we called ’Extrap.’, corresponds to extrapolated values obtained with a least square fitting of the form

$$\begin{aligned} \lambda _{h}^{(i)}\approx \lambda _{i}+C_ih^{\alpha _i}, \end{aligned}$$

(5.3)

where $\alpha _i$ is the approximated rate of convergence of each $\lambda _i$, with $i\in \mathbb {N}$.

We observe from Table 4 that for the first Steklov eigenvalue the method converges with order close to 4/3 which corresponds to the Sobolev regularity for the Steklov problem on $\Omega _T$ (non-convex domain). We also note that the method converges larger orders for the rest of the Steklov eigenvalues.

In Fig. 4 we present plots for the first four eigenfunctions for the Steklov problem in the rotated T domain, computed with $\mathcal {T}_h^5$ and $N=30$.

5.3 L-shaped Domain

In this numerical example, we test the properties of the proposed method on an L-shaped domain: $\Omega _L:=(0,1)\times (0,1)\backslash [0.5,1)\times [0.5,1)$ with $\Gamma _{0}=\partial \Omega _L$. For this test, we will adopt a refinement with hanging nodes, which implies to consider once again polygons with small edges. More precisely, this test is focused to validate the use of refined meshes as a tool to handle solutions with corner singularities. With this purpose, we have considered two families of meshes, namely: $\mathcal {T}_h^6$ (see upper left picture in Fig. 5) and $\mathcal {T}_h^{6,\ell }$. The initial uniform mesh $\mathcal {T}_h^{6}$ has $N=32$ elements on each edge and the last one has $N = 128$ elements on each edge.

On the other hand, the mesh $\mathcal {T}_h^{6,\ell }$ is obtained by refining a patch around the re-entrant corner of $\Omega _L$, starting from an initial uniform quadrilateral mesh $\mathcal {T}_h^{6,0}$, which corresponds to the first mesh of $\mathcal {T}_h^6$. The procedure consists in splitting each element which belongs to the following region:

$$\begin{aligned} R_{\ell }:=\left\{ (x,y)\in \mathbb {R}^2: |x-1/2|\le \frac{6}{N}2^{1-\ell } \quad \text{ and } \quad |y-1/2|\le \frac{6}{N}2^{1-\ell }\right\} \cap \overline{\Omega }_L \qquad \ell =1,2,\ldots ,\widehat{\ell }, \end{aligned}$$

into three quadrilaterals by connecting the barycenter of the element with the midpoint of each edge, where $\widehat{\ell }$ is the number of meshes to refine, with the convention that $\mathcal {T}_h^{6,0}:=\mathcal {T}_h^{6}$ (the initial mesh with $N=32$). Note that although this process is initiated with a quadrilateral mesh, the successively created meshes will contain other kind of convex polygons as can be appreciated in Fig. 5.

Table 5 reports the lowest Steklov eigenvalue computed on an L-shaped domain with the method analyzed in this paper with different polygonal meshes. The table also includes the corresponding “Errors” which have been obtained against a reference value “ref.” which corresponds to extrapolated values obtained with a least square fitting on finer uniform meshes.

Finally, it can be seen from Table 5 that the reported errors are similar in the last row of each mesh; however, the dofs in the case of corner-refined meshes are much less than the case of uniform meshes. Therefore, we conclude that the possibility of using small edges in the polygons of the mesh, allow us easier refinements near edges and/or corners of the domain to handle solutions with corner singularities.

Table 5 Test 3. Numerical example with an L-shaped domain. Number of degrees of freedom, computed lowest eigenvalue and errors, by using uniform square meshes and polygonal meshes with hanging nodes