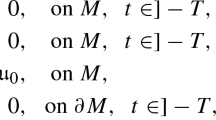Existence of a Conjugate Point in the Incompressible Euler Flow on a Three-Dimensional Ellipsoid

Abstract

The existence of a conjugate point on the volume-preserving diffeomorphism group of a compact Riemannian manifold M is related to the Lagrangian stability of a solution of the incompressible Euler equation on M. The Misiołek curvature is a reasonable criterion for the existence of a conjugate point on the volume-preserving diffeomorphism group corresponding to a stationary solution of the incompressible Euler equation. In this article, we introduce a class of stationary solutions on an arbitrary Riemannian manifold whose behavior is nice with respect to the Misiołek curvature and give a positivity result of the Misiołek curvature for solutions belonging to this class. Moreover, we also show the existence of a conjugate point in the three-dimensional ellipsoid case as its corollary.

1 Introduction

Let (M, g) be a compact n-dimensional Riemannian manifold without boundary. Consider the incompressible Euler equation on M:

$$\begin{aligned} \frac{\partial u}{\partial t}+\nabla _{u}u= & {} -{\text {grad}}p, \nonumber \\ {\text {div}}u= & {} 0,\\ u|_{t=0}= & {} u_{0}. \nonumber \end{aligned}$$

(1.1)

Let u be a stationary solution of this equation and v a divergence-free vector field on M. Then, the Misiołek curvature ${{\mathfrak {m}}}{{\mathfrak {c}}}_{u,v}$ is defined by

$$\begin{aligned} {{\mathfrak {m}}}{{\mathfrak {c}}}_{u,v}:= - \int _{M} g([u,v],[u,v]) \mu - \int _{M} g(u,[[u,v],v]) \mu , \end{aligned}$$

(1.2)

where $\mu$ is the volume form on M (see [20, Lem. B.6]). The importance of this functional is that ${{\mathfrak {m}}}{\mathfrak c}_{u,v}>0$ implies that the solution u contains a conjugate point when viewed as a geodesic in the group ${{\mathcal {D}}}^{s}_{\mu }(M)$ of volume-preserving Sobolev $H^{s}$ diffeomorphisms of M starting at the identity [21, Fact. 1.1] (see also Fact 2.2).

The question of whether geodesics in ${{\mathcal {D}}}^{s}_{\mu }(M)$ contain conjugate points goes back to Arnold [1, 2]. Examples have been found by multiple authors, e.g., [3,4,5, 12, 13, 17,18,19] among others, using several different techniques.

Conjugate points are related to the Lagrangian stability of the corresponding flow [4, 5, 7, 12, 16, 22]. They can also be used to obtain detailed local information about the data-to-solution map of the Cauchy problem (1.1) in Lagrangian coordinates [10, 14].

Despite the aforementioned efforts, we still lack a good understanding of the nature and structure of the set of conjugate points. This motivates our search for new examples.

The criterion (1.2) was first used in [13] by Misiołek and recently attracted attention again [7, 20,21,22]. A variant of this criterion was used in [5] to construct examples of conjugate points along non-stationary geodesics.

In particular, the second and third authors considered two-dimensional ellipsoids, and showed the positivity of the Misiołek curvature corresponding to almost every zonal flow Z on them in [21], motivated by the existence of stable multiple zonal jet flow on Jupiter, whose mechanism is not yet well understood.

The first aim of this article was to generalize the result of [21] to the three-dimensional ellipsoid case. However, the result of [21] concerns zonal flows, which are only defined on two-dimensional spheres or ellipsoids. Thus, to generalize the result of [21], we give a new definition of a zonal flow on an arbitrary Riemannian manifold (cf. Remark 1.3 below).

Unexpectedly, this definition behaves nicely with respect to the Misiołek curvature and we obtain the following criterion for the positivity of the Misiołek curvature. See Definition 3.4 for the meaning of non-geodesic, positive and $S^1$-zonal flows.

Theorem 1.1

Let Z be a non-geodesic positive $S^{1}$-zonal flow on a compact Riemannian manifold M with $\dim M\ge 3$. Then, there exists a divergence-free vector field Y on M satisfying

$$\begin{aligned} {{\mathfrak {m}}}{{\mathfrak {c}}}_{Z,Y}>0. \end{aligned}$$

As a corollary of Theorem 1.1, we obtain an analog of the result in [21] in the case of three-dimensional ellipsoids. More precisely, let

$$\begin{aligned} M_{a}^{3}:=\{ (x,y,z,w)\in {{\mathbb {R}}}^{4}\mid x^{2}+y^{2}=a^{2}(1-z^{2}-w^{2}) \} \end{aligned}$$

for $a>0$, and let

$$\begin{aligned} N:= & {} \{ (x, y, 0, 0) \in {\mathbb {R}}^4 \,: \, x^2 + y^2 = a^2 \},\nonumber \\ S:= & {} \{ (0, 0, z, w) \in {\mathbb {R}}^4 \,: \, z^2 + w^2 = 1 \}. \end{aligned}$$

(1.3)

Then, we have

Corollary 1.2

There exists a family $Z = Z(f, p, q)$ of non-geodesic positive $S^1$-zonal flows on $M_{a}^{3}$ supported on $M^{3}_{a}\backslash (N\cup S)$. This family is parametrized by $p, q \in {\mathbb {Q}}$ with $p^2 a^2 \ne q^2$ and a single variable function f (see Sect. 5 for the detailed construction of these flows). All such flows develop conjugate points, by M-criterion (Fact 2.2) and Theorem 1.1.

Remark 1.3

Let M be an arbitrary Riemannian manifold with $\dim M=3$. In [11], the first author, G. Misiołek, and S. C. Preston considered the space of axisymmetric vector fields u on M, which means that u satisfies $[u,X]=0$ for some fixed Killing vector field X on M [11, Sect. 3]. If $Z=fX$ is a zonal flow in the sense of Definition 3.4, we have in particular that

$$\begin{aligned}{}[Z,X]=[fX,X]=f[X,X]-X(f)X=0. \end{aligned}$$

This implies that any zonal flow can be regarded as an axisymmetric vector field on M. By Theorem 1.1, any non-geodesic positive $S^{1}$-zonal flow Z on M has a conjugate point on ${{\mathcal {D}}}^{s}_{\mu }(M)$ by the M-criterion (Fact 2.2) if M is compact.

Remark 1.4

Any zonal flow on the two-dimensional sphere or an ellipsoid in the sense of [21] is a non-geodesic $S^{1}$-zonal flow in the sense of this article. Thus, Theorem 1.1 can be regarded as a generalization of [21, Thm. 1.2].

Remark 1.5

A different criterion for the existence of conjugate points was derived by S. Preston in [17, Thm. 3.1 and (3.32)]. It differs from the M-criterion in that it is specific to the 3D case, and relies on finding nontrivial solutions to an ODE localized to some point $p \in M$. That criterion can also be used to prove the existence of the conjugate points provided here. Nevertheless, our examples had never been found before, to the best of our knowledge.

This paper is organized as follows. We begin by reviewing material relevant to the geometric approach to the Euler equations of hydrodynamics in Sect. 2. In Sect. 3, we propose a definition of a zonal flow on an arbitrary Riemannian manifold and investigate its properties. In Sect. 4, we calculate the Misiołek curvature of a zonal flow, obtain a sufficient condition for the positivity of the Misiołek curvature, and prove Theorem 1.1. Section 5 contains our construction of a family of zonal flows admitting conjugate points and the proof of Corollary 1.2. In Appendix A, we prove some useful lemmas regarding compactly supported divergence-free vector fields on Euclidean space.

2 Diffeomorphism Groups and Misiołek Curvature

In this section, we recall the theory of diffeomorphism groups in the context of inviscid fluid flows for completeness. Our main references are [8, 12].

Let (M, g) be a compact n-dimensional Riemannian manifold without boundary and ${{\mathcal {D}}}^{s}(M)$ the group of Sobolev $H^{s}$ diffeomorphisms of M and ${{\mathcal {D}}}_{\mu }^{s}(M)$ the subgroup of ${{\mathcal {D}}}^{s}(M)$ consisting volume preserving elements, where $\mu$ is the volume form on M defined by g. If $s>1+\frac{n}{2}$, the group ${{\mathcal {D}}}^{s}(M)$ can be given a structure of an infinite-dimensional weak Riemannian manifold (see [8]) and ${{\mathcal {D}}}^{s}_{\mu }(M)$ becomes a weak Riemannian submanifold (The term “weak” means that the topology induced from the metric is weaker than the original topology of ${{\mathcal {D}}}^{s}(M)$ or ${{\mathcal {D}}}^{s}_{\mu }(M)$).

This weak Riemannian metric is given as follows: The tangent space $T_{\eta }{{\mathcal {D}}}^{s}(M)$ of ${{\mathcal {D}}}^{s}(M)$ at a point $\eta \in {{\mathcal {D}}}^{s}(M)$ consists of all $H^{s}$ vector fields on M which cover $\eta$, namely, all $H^{s}$ sections of the pullback bundle $\eta ^{*}TM$. Thus for $x\in M$ and $V, W\in T_{\eta }{{\mathcal {D}}}^{s}(M)$, we have $V(x), W(x) \in T_{\eta (x)}M$. Then the $L^2$ metric on $T_{\eta }{{\mathcal {D}}}^{s}(M)$ is defined by

$$\begin{aligned} \langle V, W\rangle := \int _{M} g(V(x),W(x))\mu (\eta (x)) \end{aligned}$$

(2.1)

and we let $|V|:=\sqrt{\langle V, V\rangle }$. This metric descends to a right-invariant metric on the subgroup ${\mathcal D}^{s}_{\mu }(M)$. In fact, it induces a direct sum decomposition

$$\begin{aligned} T_{\eta }{{\mathcal {D}}}^{s}(M)= T_{\eta }{{\mathcal {D}}}^{s}_{\mu }(M) \oplus \{ (\textrm{grad} f) \circ \eta \mid f\in H^{s+1}(M)\}, \end{aligned}$$

(2.2)

with associated projections

$$\begin{aligned}{} & {} P_{\eta }: T_{\eta }{{\mathcal {D}}}^{s}(M) \rightarrow T_{\eta }{\mathcal D}^{s}_{\mu }(M), \\{} & {} Q_{\eta }: T_{\eta }{{\mathcal {D}}}^{s}(M) \rightarrow \{ (\textrm{grad} f) \circ \eta \mid f\in H^{s+1}(M)\}, \end{aligned}$$

which follows from the fact that the gradient is the adjoint of the negative divergence.

The metric (2.1) also induces the right invariant Levi-Civita connections ${\bar{\nabla }}$ and ${\widetilde{\nabla }}$ on ${{\mathcal {D}}}^{s}(M)$ and ${{\mathcal {D}}}^{s}_{\mu }(M)$, respectively. They can be defined as follows. Let V, W be vector fields on ${{\mathcal {D}}}^{s}(M)$. We write $V_{\eta }\in T_{\eta }{\mathcal D}^{s}(M)$ for the value of V at $\eta \in {{\mathcal {D}}}^{s}(M)$. Then we have $V_{\eta }\circ \eta ^{-1}, W_{\eta }\circ \eta ^{-1}\in T_{e}{{\mathcal {D}}}^{s}(M)$, where $e\in {{\mathcal {D}}}^{s}(M)$ is the identity element of ${{\mathcal {D}}}^{s}(M)$. Namely, $V_{\eta }\circ \eta ^{-1}$ and $W_{\eta }\circ \eta ^{-1}$ are vector fields on M. Moreover, we have $W_{\eta }\circ \eta ^{-1}$ is a vector field of class $C^{1}$ on M by Sobolev embedding theorem and the assumption $s>1+\frac{n}{2}$. Thus we can consider $\nabla _{V_{\eta }\circ \eta ^{-1}}W_{\eta }\circ \eta ^{-1}$, where $\nabla$ is the Levi-Civita connection on M. Take a path $\varphi$ on ${\mathcal D}^{s}(M)$ satisfying $\varphi (0)=\eta$ and $V_{\eta }=\partial _t\varphi (0)\in T_{\eta }{\mathcal D}_{\mu }^{s}(M)$, then we define

$$\begin{aligned} ({{\bar{\nabla }}}_{V}W)_{\eta }:= & {} \frac{d}{dt}\left( W_{\varphi (t)}\circ \varphi ^{-1}(t) \right) |_{t=0}\circ \eta +(\nabla _{V_{\eta }\circ \eta ^{-1}} W_{\eta }\circ \eta ^{-1})\circ \eta . \end{aligned}$$

(2.3)

Moreover, if V and W are vector fields on ${\mathcal D}^{s}_{\mu }(M)$, we define

$$\begin{aligned} ({\widetilde{\nabla }}_{V}W)_{\eta }:= & {} P_\eta ({\bar{\nabla }}_{V}W)_{\eta } . \end{aligned}$$

(2.4)

These definitions are independent of the particular choice of $\varphi (t)$. We note that $({{\bar{\nabla }}}_{V}W)_{\eta }=({{\bar{\nabla }}}_{V}W)_{e}\circ \eta$ if V and W are right invariant vector fields on ${{\mathcal {D}}}^{s}(M)$ (i.e., ${\bar{\nabla }}$ is right invariant). This is because if W is right invariant, or equivalently, if W satisfies $W_{\eta }=W_{e}\circ \eta$ for any $\eta \in {\mathcal D}^{s}_{\mu }(M)$, the first term of (2.3) vanishes.

A geodesic joining the identity element $e\in {\mathcal D}^{s}_{\mu }(M)$ and $p\in {{\mathcal {D}}}^{s}_{\mu }(M)$ can be obtained from a variational principle as a stationary point of the energy function:

$$\begin{aligned} E(\eta )^{t_{0}}_{0}:=\frac{1}{2} \int _{0}^{t_{0}} \left| {\dot{\eta }}(t) \right| ^{2}\textrm{d}t, \end{aligned}$$

(2.5)

where $\eta$ is a curve on ${{\mathcal {D}}}^{s}_{\mu }(M)$ satisfying $\eta (0)=e$ and $\eta (t_{0})=p$ and we set ${\dot{\eta }}(t):=\partial _{t}\eta (t)\in T_{\eta (t)}{\mathcal D}^{s}_{\mu }(M)$. Let $\xi (r,t):(-\varepsilon ,\varepsilon )\times [0,t_{0}]\rightarrow {\mathcal D}^{s}_{\mu }(M)$ be a variation of a geodesic $\eta (t)$ with fixed endpoints, namely, it satisfies $\xi (r,0) = \eta (0)$, $\xi (r,t_{0}) = \eta (t_{0})$ and $\xi (0,t)=\eta (t)$ for $t\in [0,t_{0}]$. We sometimes write $\xi _{r}(t)$ for $\xi (r,t)$. Let $X(t):=\partial _{r}\xi (r,t)|_{r=0}\in T_{\eta (t)}{\mathcal D}^{s}_{\mu }(M)$ be the associated vector field on ${\mathcal D}^{s}_{\mu }(M)$. Then the first and the second variations of the above integral are given by

$$\begin{aligned} 0= E'(\eta )_{0}^{t_{0}}(X) =&\langle X(t_{0}),{\dot{\eta }}(t_{0}) \rangle - \langle X(0),{\dot{\eta }}(0) \rangle \nonumber \\&- \int _{0}^{t_{0}} \langle X(t), {\widetilde{\nabla }} _{{\dot{\eta }}(t)}{\dot{\eta }}(t) \rangle dt, \nonumber \\ E''(\eta )^{t_0}_{0}(X,X) =&\int _{0}^{t_{0}} \{ \langle {\widetilde{\nabla }}_{{\dot{\eta }}} X, {\widetilde{\nabla }}_{{\dot{\eta }}} X \rangle - \langle {\widetilde{R}}_{\eta } (X, {\dot{\eta }} ){\dot{\eta }}, X \rangle \}dt. \end{aligned}$$

(2.6)

The reason why the geometry of ${{\mathcal {D}}}_{\mu }^{s}(M)$ is important is that geodesics in ${{\mathcal {D}}}^{s}_{\mu }(M)$ correspond to inviscid fluid flows on M, which was first remarked by Arnol’d [1]. This correspondence is accomplished in the following way. If $\eta (t)$ is a geodesic on ${\mathcal D}^{s}_{\mu }(M)$ (i.e., ${\widetilde{\nabla }}_{{\dot{\eta }}}\eta =0$) joining e and $\eta (t_{0})$, a time-dependent vector field on M defined by $u(t):={\dot{\eta }}(t)\circ \eta ^{-1}(t)$ is a solution to the Euler equations on M:

$$\begin{aligned}&\partial _tu + \nabla _{u} u = - {\text {grad}}p \qquad t \in [0,t_{0}], \nonumber \\&{\text {div}} u=0, \nonumber \\&u|_{t=0} = {\dot{\eta }}(0), \end{aligned}$$

(2.7)

with a scalar function (pressure) p(t) determined by u(t). Here, ${\text {grad}}p$ (resp. ${\text {div}}u$) is the gradient (resp. divergent) of p (resp. u) with respect to the Riemannian metric g of M. In this context, the existence of conjugate points along a geodesic $\eta$ can be related to the Lagrangian stability of a fluid flow $u={\dot{\eta }}\circ \eta ^{-1}$.

In this context, Misiołek essentially established a criterion for the existence of a conjugate point on a geodesic corresponding to a stationary solution of (2.7) in [13], which we call M-criterion.

Definition 2.1

([13, 21, (2.14)], [20, Lem. B.6]) Let u be a stationary solution of (2.7) and v a divergence-free vector field on M. Then, the Misiołek curvature ${{\mathfrak {m}}}{{\mathfrak {c}}}_{u,v}$ is defined by

$$\begin{aligned} {{\mathfrak {m}}}{{\mathfrak {c}}}_{u,v}:= & {} \langle \nabla _{u}[u,v]+ \nabla _{[u,v]}v,v\rangle \\= & {} -|[u,v]|^{2} - \langle u, [[u,v],v] \rangle . \end{aligned}$$

Fact 2.2

([13, Lems. 2 and 3], [21, Fact. 1.1]) Let M be a compact n-dimensional Riemannian manifold without boundary and $s>2+\frac{n}{2}$. Suppose that $u\in T_{e}{\mathcal D}^{s}_{\mu }(M)$ is a stationary solution of (2.7) on M and take a geodesic $\eta (t)$ on ${{\mathcal {D}}}^{s}_{\mu }(M)$ satisfying $u={\dot{\eta }}\circ \eta ^{-1}$. Then, if $v\in T_{e}{\mathcal D}^{s}_{\mu }(M)$ satisfies ${{\mathfrak {m}}}{{\mathfrak {c}}}_{u,v}>0$, then, there exists a point conjugate to $e\in {\mathcal D}^{s}_{\mu }(M)$ along $\eta (t)$ on $0\le t\le t^{*}$ for some $t^{*}>0$.

3 A Generalization of Zonal Flow

In this section, we propose a definition of a zonal flow on an arbitrary closed Riemannian manifold and investigate its properties.

3.1 Killing Vector Fields

In this section, we recall several properties of Killing vector fields, and provide some of their proofs for convenience. See [6, Sect. 3] for further details.

A vector field X on a Riemannian manifold (M, g) is Killing if and only if

$$\begin{aligned} g(\nabla _{V}X,W) = - g(\nabla _{W}X,V) \end{aligned}$$

(3.1)

for any vector fields V, W on M, where $\nabla$ is the Levi-Civita connection on M.

Lemma 3.1

Let X be a Killing vector field on a Riemannian manifold M. Then, we have the following identities.

$$\begin{aligned} 2\nabla _{X}X=-{\text {grad}}(\Vert X\Vert ^{2}) \qquad \text {and}\qquad X(\Vert X\Vert ^{2})=0. \end{aligned}$$

(3.2)

In particular, $\nabla _{X}X=0$ if and only if $\Vert X\Vert$ is a constant function.

Proof

For the first identity, it is sufficient to prove

$$\begin{aligned} 2g(\nabla _{X}X,W)=-g({\text {grad}}(\Vert X\Vert ^{2}),W) \end{aligned}$$

(3.3)

for any vector field W on M by the nondegeneracy of the Riemannian metric g. However, we have

$$\begin{aligned} g({\text {grad}}(\Vert X\Vert ^{2}),W) = W(\Vert X\Vert ^{2}) = 2g(\nabla _{W}X,X). \end{aligned}$$

(3.4)

The second identity follows from (3.1) with $V = W = X$. $\square$

Lemma 3.2

Let M be a Riemannian manifold, X a Killing vector field on M, and f a function on $U:=\{x\in M \mid X(x)\ne 0\}$. Then, fX is a Killing vector field on U if and only if f is constant.

Proof

We only show the “only if” part because the “if” part is obvious. Suppose that fX is Killing. Then, we have

$$\begin{aligned} 0 = {\text {div}}(fX) = X(f)+f{\text {div}}(X) = X(f) \end{aligned}$$

(3.5)

because any Killing vector field is divergence-free. Moreover, substituting fX (resp. X) for X (resp. W) in (3.1), we have

$$\begin{aligned} V(f)\Vert X\Vert ^{2} + f g(\nabla _{V}X,X) = -X(f)g(X,V) - fg(\nabla _{X}X,V) \end{aligned}$$

(3.6)

for any vector field V on U. By (3.1) and (3.5), this is equivalent to

$$\begin{aligned} V(f)\Vert X\Vert ^{2} = 0 \end{aligned}$$

(3.7)

because X is Killing. Because $U=\{x\in M \mid X(x)\ne 0\}$, this implies $V(f)=0$ on U. Since V is arbitrary, f is constant. This completes the proof. $\square$

We recall the following fact, whose proof can be found in [15, Lem. 3].

Lemma 3.3

Let M be a Riemannian manifold and $X_1, X_2$ be two Killing vector fields defined on a connected open subset $U\subset M$. If there exists a point $p \in U$ such that $X_1(p) = X_2(p)$ and $\nabla X_1(p) = \nabla X_2(p)$, then $X_1 = X_2$ on U.

3.2 A Definition of Zonal Flow

In this section, we propose a definition of a zonal flow on an arbitrary Riemannian manifold M equipped with its Riemannian volume form $\mu$. Recall that $T_e{\mathcal {D}}^s(M)$ and $T_e{\mathcal {D}}^s_{\mu }(M)$ denote the sets of all vector fields and divergence-free vector fields, respectively, of class $H^s$ on M. Denote by

$$\begin{aligned} \begin{aligned} P:=P_{e}: T_{e}{{\mathcal {D}}}^{s}(M)&\rightarrow T_{e}{{\mathcal {D}}}^{s}_{\mu }(M) \\ V&\mapsto P(V):= V - {\text {grad}}f \end{aligned} \end{aligned}$$

the $L^{2}$ orthogonal projection at the identity e, where $f:=\Delta ^{-1}{\text {div}}(V)$. Thus, for $V\in T_{e}{{\mathcal {D}}}^{s}(M)$, $P(V)=0$ if and only if $V=-{\text {grad}} f$ for some function f on M.

Definition 3.4

A vector field Z on M is called a zonal flow if it satisfies the following three conditions.

• (1) There exist a function f and a Killing vector field X on M such that $Z=fX$,

• (2) ${\text {div}}(Z)=0$,

• (3) $P(\nabla _{Z}Z)=0$.

In addition to this definition, we say that a zonal flow Z is:

A geodesic zonal flow if $\nabla _Z Z = 0$ everywhere.

A positive zonal flow if there exists a point in M where the vectors $\textrm{grad}(\Vert X\Vert ^2)$ and $\textrm{grad}(f^2)$ are both nonzero and point in the same direction, i.e., one is a positive multiple of the other (see also Definition 3.9).

An $S^1$-zonal flow if X is induced by an $S^1$-action on M.

We make several important remarks regarding Definition 3.4.

First, note that if $Z = fX$ with X Killing, then condition (2) is equivalent to $Xf = 0$, since

$$\begin{aligned} \textrm{div}(Z) = \textrm{div}(fX) = Xf + f\textrm{div}(X) = Xf \end{aligned}$$

(3.8)

and every Killing vector field is divergence free.

Condition (3) implies that any zonal flow is a steady solution of the incompressible Euler equations, whereas the much stronger geodesic condition means that the flow of Z is a geodesic on the group of all diffeomorphisms of M, not just volume-preserving, under the $L^2$ metric. Although these flows can also develop conjugate points, the M-criterion can fail to detect them. One such example is a rotation on a sphere (cf. [21, Rem. 3]).

As will be shown in Lemma 3.6 below, the gradients of $f^2$ and $\Vert X\Vert ^2$ are always linearly dependent for any zonal flow. Thus, the positivity condition in the above definition is really an alignment condition: if $f^2$ and $\Vert X\Vert ^2$ increase in the same direction, then this combined growth can lead to conjugate points.

Moreover, as will be shown in Lemma 3.7, the representation of a zonal flow Z as a product of a function f and a Killing vector field X is essentially unique up to a nonzero constant multiple. Therefore, the notion of an $S^{1}$-zonal flow is well-defined because the property of being a vector field induced by an $S^{1}$-action is invariant by nonzero constant multiple.

Remark 3.5

The condition (3) of Definition 3.4 is unnecessary in the case of the two-dimensional sphere or an ellipsoid considered in [21]. Namely, if a vector field $Z=fX$ with a function f and a Killing vector field X on

$$\begin{aligned} M_{a}^{2}:= \{ (x,y,z)\in {{\mathbb {R}}}^{3} \mid x^{2}+y^{2} = a^{2}(1-z^{2}) \} \qquad ( a>0) \end{aligned}$$

satisfies ${\text {div}}(Z)=0$ (the condition (2) of Definition 3.4), then Z also satisfies the condition (3) of Definition 3.4. However, in the general case, the condition (2) of Definition 3.4 does not imply the condition (3) of Definition 3.4. An example is $Z=f(\mu )\partial _{\xi }$ on $M_{a}^{3}$ for a non-constant function $f=f(\mu )$ depending only on the variable $\mu$ in the notation of Sect. 5. This is because the gradients of $f(\mu )^{2}$ and $\Vert \partial _{\xi }\Vert ^{2}$ are not linearly dependent by (5.6) and (5.11) if $f(\mu )$ is not constant, which contradicts to Lemma 3.6.

Given a Killing vector field X and a function f with $Xf = 0$, it is natural to ask what further restrictions on f and X are imposed by condition (3) above, in order that $Z = fX$ be a zonal flow. We address this question below.

Lemma 3.6

Let $Z = fX$ for some function f and some Killing vector field X on M, such that $Xf = 0$. Then

$$\begin{aligned} \nabla _{Z}Z = f^{2}\nabla _{X}X = -\frac{f^{2}}{2}{\text {grad}}(\Vert X\Vert ^{2}). \end{aligned}$$

(3.9)

Furthermore, if Z is a zonal flow, then ${\textrm{grad}(f^2)}$ and ${\textrm{grad}(\Vert X \Vert ^2)}$ are everywhere linearly dependent. If the first cohomology group $H^1(M)$ vanishes, then the converse holds.

Proof

A direct computation using Lemma 3.1 shows that

$$\begin{aligned} \begin{aligned} \nabla _ZZ = \nabla _{fX}fX = f\Big ( (Xf)X + f\nabla _XX\Big ) = -\frac{f^2}{2} \text {grad}( \Vert X\Vert ^2) . \end{aligned} \end{aligned}$$

(3.10)

Now if Z is a zonal flow, then by definition we can write

$$\begin{aligned} \begin{aligned} -\frac{f^2}{2} \text {grad}( \Vert X\Vert ^2) = \text {grad}(p) \end{aligned} \end{aligned}$$

(3.11)

for some function p. Changing this equation to 1-forms and taking an exterior derivative gives

$$\begin{aligned} d(f^2) \wedge d(\Vert X\Vert ^2) = 0 \end{aligned}$$

(3.12)

which is equivalent to the gradients of $f^2$ and $\Vert X\Vert ^2$ being linearly dependent. Conversely, if we assume $H^1(M) = 0$, then linear dependence of $\textrm{grad}(f^2)$ and $\textrm{grad}(\Vert X\Vert ^2)$ implies that the 1-form $-(f^2/2) \textrm{d}\! \left( \Vert X \Vert ^2\right)$ is closed, therefore exact, and Z is a zonal flow. $\square$

The following lemma shows that the representation of a zonal flow Z as a product of a function f and a Killing vector field X is essentially unique, up to a nonzero constant.

Lemma 3.7

Let Z be a nonzero zonal flow on a connected Riemannian manifold M. If $Z=f_{1}X_{1}=f_{2}X_{2}$ with functions $f_{1},f_{2}$ and Killing vector fields $X_{1},X_{2}$ on M, then we have $f_{1}=Cf_{2}$ and $CX_{1}=X_{2}$ for some $C\in {\mathbb R}\backslash \{0\}$.

Proof

By Lemma 3.3, it is sufficient to prove that there exists a nonempty open subset $U\subset M$ on which we have $X_{1}=CX_{2}$. By the nonzero assumption of Z,

$$\begin{aligned} U:=\{x\in M\mid f_{1}(x)\ne 0\} \end{aligned}$$

is nonempty. Setting $h:=\frac{f_{2}}{f_{1}}$, we have

$$\begin{aligned} X_{1}=hX_{2} \end{aligned}$$

(3.13)

on U. Because $X_{1}$ and $X_{2}$ are Killing, we can apply Lemma 3.2. This completes the proof because the nonzero assumption of Z implies $h\not \equiv 0$. $\square$

The following lemma expresses the positivity condition for a zonal flow in terms of a proportionality function F, which will also play a key role in the Misiołek curvature.

Lemma 3.8

Let $Z=fX$ be a zonal flow on M and $U_{0}:=\{x\in M\mid {\text {grad}}(\Vert X\Vert ^{2})\ne 0\}$. Then, there exists a function F on $U_{0}$, unique up to a positive constant multiple, such that

$$\begin{aligned} {\text {grad}}(f^{2})= & {} F{\text {grad}}(\Vert X\Vert ^{2}). \end{aligned}$$

(3.14)

Moreover, we have

$$\begin{aligned} X(F)=0. \end{aligned}$$

(3.15)

Proof

The existence of F follows from Lemma 3.6, since $\textrm{grad}(f^2)$ and $\textrm{grad}(\Vert X\Vert ^2)$ are linearly dependent and the latter is nonzero on $U_0$.

The uniqueness follows from the fact that f and X are unique up to a constant multiple, by Lemma 3.7.

To see that $X(F) = 0$, switching (3.14) to 1-forms and taking an exterior derivative on both sides gives

$$\begin{aligned} d(f^2) = F\, d(\Vert X\Vert ^2) ~\Rightarrow ~ 0 = dF \wedge d(\Vert X\Vert ^2). \end{aligned}$$

(3.16)

Evaluating this 2-form on the pair $(X,\, \textrm{grad}(\Vert X\Vert ^2))$ gives

$$\begin{aligned} dF \wedge d(\Vert X\Vert ^2)(X, \textrm{grad}(\Vert X\Vert ^2)) = dF(X) \Vert \textrm{grad}(\Vert X\Vert ^2)\Vert ^2 \end{aligned}$$

(3.17)

since the term containing $d(\Vert X\Vert ^2)(X)$ vanishes by (3.2). It follows that $dF(X)=X(F) = 0$ within $U_0=\{x\in M\mid {\text {grad}}(\Vert X\Vert ^{2})\ne 0\}$. $\square$

It turns out that the signature of F will be important in Sect. 4.2. Therefore we make the following definition.

Definition 3.9

Let Z be a zonal flow on M. Then, we define ${\text {sgn}}(Z):M\rightarrow \{-1,0,1\}$ by

$$\begin{aligned} {\text {sgn}}(Z):= {\left\{ \begin{array}{ll} {\text {sgn}}(F) &{} \text {on }U_{0}:=\{ x\in M\mid {\text {grad}}(\Vert X\Vert ^{2})\ne 0 \}\\ 0&{} \text {on }M\backslash U_{0}, \end{array}\right. } \end{aligned}$$

(3.18)

where F is the function defined in Lemma 3.8 and ${\text {sgn}}:{\mathbb R}\rightarrow \{-1,0,1\}$. In terms of this definition, Z is a positive zonal flow (see Definition 3.4) if the set

$$\begin{aligned} U^{+}:=\{x\in M\mid {\text {sgn}}(Z)>0\} \end{aligned}$$

is nonempty.

It can be shown by a calculation that $\textrm{sgn}(Z)$ depends only on Z and not on the particular representation of Z through f and X. In fact, the following formula holds.

$$\begin{aligned} {\text {sgn}}(Z)= - {\text {sgn}}( g({\text {grad}}(\Vert Z\Vert ^{2}) + 2\nabla _{Z}Z, 2\nabla _{Z}Z) ). \end{aligned}$$

We omit its proof since it will not be used in the paper.

3.3 $S^{1}$-Zonal Flows

In this section, we specialize our discussion to zonal flows $Z = fX$ where X is induced by an $S^1$-action on M, which we call $S^1$-zonal flows (Definition 3.4).

They will be used in Sect. 4.2 to produce a sufficient condition for the positivity of the Misiołek curvature.

Lemma 3.10

Let Z be a positive $S^{1}$-zonal flow on M. Then, $U^{+}:=\{x\in M \mid {\text {sgn}}(Z)>0\}$ is an $S^{1}$-invariant open subset of M.

Proof

Let $Z=fX$ with a function f and a Killing vector field on M. Take the function F on $U_{0}:=\{x\in M \mid {\text {grad}}(\Vert X\Vert ^{2})\ne 0\}$ defined in Lemma 3.8. Then, we have

$$\begin{aligned} X(F)=0 \end{aligned}$$

by Lemma 3.8. Thus, F is constant on any $S^{1}$-orbit because X is induced by the $S^{1}$-action. This completes the proof because it is obvious that $U^{+}$ is open. $\square$

We recall the principal orbit type theorem for compact Lie groups.

Fact 3.11

([23, (1.1.4) and Lem. 1.1.5]) Let a compact Lie group G act on a connected compact manifold M. Then, there exist a homogeneous G-space G/H and a dense open G-invariant subset $M_{pr}$ of M such that for any $x\in M_{pr}$, there exists a G-equivariant open embedding

$$\begin{aligned} \phi _{x}: G/H\times {{\mathbb {R}}}^{\dim M-\dim G/H} \rightarrow M \end{aligned}$$

(3.19)

satisfying

$$\begin{aligned} \phi _{x}(G/H\times \{0\})=G\cdot x. \end{aligned}$$

(3.20)

Here, G acts on $G/H\times {{\mathbb {R}}}^{\dim M-\dim G/H}$ via the first factor.

In other words, this fact means that M looks like the product of the orbit $G\cdot x$ and ${{\mathbb {R}}}^{\dim M-\dim G/H}$ in a small neighborhood of $G\cdot x$ for each $x\in M_{pr}$.

Corollary 3.12

Let $S^{1}$ act nontrivially on a connected compact manifold M. Then, there exist a one-dimensional homogeneous $S^{1}$-space N and a dense open $S^{1}$-invariant subset $M_{pr}$ of M such that for any $x\in M_{pr}$, there exists an $S^{1}$-equivariant open embedding

$$\begin{aligned} \phi _{x}: N\times {{\mathbb {R}}}^{\dim M-1} \rightarrow M \end{aligned}$$

(3.21)

satisfying

$$\begin{aligned} \phi _{x}(N\times \{0\})=S^{1}\cdot x. \end{aligned}$$

(3.22)

Proof

All assertion follows from Fact 3.11 except for the one-dimensionality of N. By the nontriviality of the action, there exists a point $x_{0}\in M$ such that the $S^{1}$-orbit of $x_{0}$ is one-dimensional. By the continuity of the action, there exists an open neighborhood W of $x_{0}$ such that for any $x\in W$, the $S^{1}$-orbit of x is one-dimensional. This implies N is one-dimensional because $M_{pr}\cap W$ is nonempty by the density of $M_{pr}$. $\square$

The aim of this section is to prove the following lemma, which is used in Sect. 4.2 in order to establish a sufficient condition for the positivity of the Miciołek curvature.

Lemma 3.13

Let Z be a positive $S^{1}$-zonal flow on a Riemannian manifold M. Then, there exist a one-dimensional homogeneous $S^{1}$-space N and an $S^{1}$-equivariant open embedding

$$\begin{aligned} \phi :N \times {{\mathbb {R}}}^{\dim M-1} \rightarrow M \end{aligned}$$

(3.23)

satisfying

$$\begin{aligned} \phi (N\times {{\mathbb {R}}}^{\dim M-1})\subset U^{+}:=\{x\in M\mid {\text {sgn}}(Z)>0\}. \end{aligned}$$

(3.24)

Proof

The assertion of this lemma is local, we can assume M is connected. Moreover, the positivity of Z implies that the $S^{1}$-action is nontrivial. Thus, by Corollary 3.12, there exist a homogeneous $S^{1}$-space N and a dense open subset $M_{pr}$ of M such that for any $x\in M_{pr}$, there exists an $S^{1}$-equivariant open embedding

$$\begin{aligned} \phi _{x}:N \times {{\mathbb {R}}}^{\dim M-1}\rightarrow & {} M \end{aligned}$$

(3.25)

satisfying

$$\begin{aligned} \phi _{x}(N\times \{0\})=S^{1}\cdot x. \end{aligned}$$

(3.26)

On the other hand, $U^{+}=\{x\in M \mid {\text {sgn}}(Z)>0\}$ is nonempty because Z is positive (see Definition 3.9). Because $M_{pr}$ is dense by Corollary 3.12 and $U^{+}$ is open by Lemma 3.10, $U^{+}\cap M_{pr}$ is nonempty. Take $x_{0}\in U^{+}\cap M_{pr}$ and consider the map of (3.25) for $x_{0}$

$$\begin{aligned} \phi _{x_{0}}:N \times {{\mathbb {R}}}^{\dim M-1} \rightarrow M, \end{aligned}$$

(3.27)

which satisfies

$$\begin{aligned} \phi _{x_{0}}(N\times \{0\})=S^{1}\cdot x_{0}. \end{aligned}$$

(3.28)

We note that $U^{+}$ is $S^{1}$-invariant by Lemma 3.10. Thus, $x_{0}\in U^{+}$ implies

$$\begin{aligned} \phi _{x_{0}}(N \times \{0\}) = S^{1}\cdot x_{0}\subset U^{+}. \end{aligned}$$

(3.29)

Therefore, there exists a sufficiently small open subset $W\subset {{\mathbb {R}}}^{\dim M-1}$, we have

$$\begin{aligned} \phi _{x_{0}}(N\times W) \subset U^{+} \end{aligned}$$

(3.30)

because $U^{+}$ is an $S^{1}$-invariant open subset and $\phi _{x_{0}}$ is $S^{1}$-equivariant. Taking some diffeomorphism $\psi :{{\mathbb {R}}}^{\dim M-1} \simeq W$ and $\phi :=\phi _{x_{0}}\circ ({\text {id}}_{N}\times \psi )$, we have the lemma. $\square$

4 Misiołek Curvature of Zonal Flow

In this section, we calculate the Misiołek curvature for a zonal flow on an arbitrary compact Riemannian manifold M. Moreover, we establish a sufficient condition for the positivity of the Misiołek curvature.

4.1 A Formula of Misiołek Curvature of Zonal Flow

The $L^2$ metric will be denoted by

$$\begin{aligned} \langle V,W\rangle:= & {} \int _{M}g(V,W)\mu , \end{aligned}$$

(4.1)

$$\begin{aligned} |V|^{2}:= & {} \langle V,V\rangle \end{aligned}$$

(4.2)

for any vector fields V and W on M. Recall that the Misiołek curvature ${{\mathfrak {m}}}{{\mathfrak {c}}}$ is defined as

$$\begin{aligned} {{\mathfrak {m}}}{{\mathfrak {c}}}_{Z,Y}:= -|[Z,Y]|^{2} - \langle Z, [[Z,Y],Y] \rangle \end{aligned}$$

(4.3)

for a stationary solution Z of the Euler equations (1.1) and a divergence-free vector field Y.

Lemma 4.1

Let $Z = fX$ be a zonal flow on M. Then, we have

$$\begin{aligned} \begin{aligned} {{\mathfrak {m}}}{{\mathfrak {c}}}_{Z,Y}&= -|f[X,Y]|^{2} + \langle 2Y(f^{2})X, [X,Y] \rangle \\&-\langle f^{2}X, [[X,Y],Y] \rangle - \frac{1}{2} \int _{M} Y^{2}(f^{2}) \Vert X\Vert ^{2} \mu . \end{aligned} \end{aligned}$$

Proof

We have

$$\begin{aligned}{}[Z,Y]= & {} [fX,Y] \\= & {} f[X,Y] - Y(f) X, \\ ~[[Z,Y],Y]= & {} [f[X,Y] - Y(f) X, Y] \\= & {} f[[X,Y],Y] - 2Y(f)[X,Y] + Y^{2}(f)X. \end{aligned}$$

Therefore, we have

$$\begin{aligned} |[Z,Y]|^{2}= & {} |f[X,Y]|^{2} - 2 \langle f[X,Y], Y(f)X \rangle + |Y(f)X|^{2} \end{aligned}$$

and

$$\begin{aligned} \langle Z, [[Z,Y],Y] \rangle= & {} \langle fX, f[[X,Y],Y] \rangle - \langle fX, 2Y(f)[X,Y] \rangle + \langle fX, Y^{2}(f)X \rangle . \end{aligned}$$

By (4.3), we have

$$\begin{aligned} {{\mathfrak {m}}}{{\mathfrak {c}}}_{Z,Y}= & {} - |f[X,Y]|^{2} + 2 \langle fY(f)[X,Y], X \rangle - \langle Y(f)^{2}X, X \rangle \\{} & {} - \langle f^{2}X, [[X,Y],Y] \rangle + 2 \langle fY(f)[X,Y], X \rangle - \langle fY^{2}(f)X, X \rangle . \end{aligned}$$

We note that

$$\begin{aligned} 2fY(f)= & {} Y(f^{2}), \end{aligned}$$

(4.4)

$$\begin{aligned} Y(f)^{2}+fY^{2}(f)= & {} \frac{1}{2} Y^{2}(f^{2}). \end{aligned}$$

(4.5)

Then,

$$\begin{aligned} {{\mathfrak {m}}}{{\mathfrak {c}}}_{Z,Y}= & {} - |f[X,Y]|^{2} + 2 \langle Y(f^{2})[X,Y], X \rangle \\{} & {} \quad - \langle f^{2}X, [[X,Y],Y] \rangle - \frac{1}{2} \langle Y^{2}(f^{2})X, X \rangle . \end{aligned}$$

We note

$$\begin{aligned} \langle Y^{2}(f^{2})X, X \rangle= & {} \int _{M} g(Y^{2}(f^{2})X,X)\mu \end{aligned}$$

(4.6)

$$\begin{aligned}= & {} \int _{M} Y^{2}(f^{2}) \Vert X\Vert ^{2}\mu . \end{aligned}$$

(4.7)

This completes the proof of Lemma 4.1. $\square$

Before stating the next lemma, we recall that if $Z=fX$ is a zonal flow, then, there exists a function F unique up to positive constant multiple on $U_{0}:=\{x\in M\mid {\text {grad}}(\Vert X\Vert ^{2})\ne 0\}$ satisfying

$$\begin{aligned} {\text {grad}}(f^{2})=F{\text {grad}}(\Vert X\Vert ^{2}) \end{aligned}$$

(4.8)

on $U_{0}$ by Lemma 3.8.

Lemma 4.2

Let $Z=fX$ be a zonal flow on M and F a function on $U_{0}:=\{x\in M\mid {\text {grad}}(\Vert X\Vert ^{2})\ne 0\}$ satisfying (4.8). Then, for any divergence-free vector field Y on M with $[X,Y]=0$, we have

$$\begin{aligned} {{\mathfrak {m}}}{{\mathfrak {c}}}_{Z,Y} = \frac{1}{2} \int _{U_{0}}FY(\Vert X\Vert ^{2})^{2}\mu . \end{aligned}$$

Proof

By Lemma 4.1 and the assumption $[X,Y]=0$, we have

$$\begin{aligned} {{\mathfrak {m}}}{{\mathfrak {c}}}_{Z,Y} = -\frac{1}{2} \int _{M}Y^{2}(f^{2})\Vert X\Vert ^{2}\mu . \end{aligned}$$

(4.9)

Applying the Stokes theorem, we have

$$\begin{aligned} {{\mathfrak {m}}}{{\mathfrak {c}}}_{Z,Y}= & {} \frac{1}{2} \int _{M}Y(f^{2})Y(\Vert X\Vert ^{2})\mu \end{aligned}$$

(4.10)

$$\begin{aligned}= & {} \frac{1}{2} \int _{M} g({\text {grad}}(f^{2}),Y)Y(\Vert X\Vert ^{2})\mu \end{aligned}$$

(4.11)

$$\begin{aligned}= & {} \frac{1}{2} \int _{U_{0}} g({\text {grad}}(f^{2}),Y)Y(\Vert X\Vert ^{2})\mu \end{aligned}$$

(4.12)

because

$$\begin{aligned} Y(\Vert X\Vert ^{2}) = g({\text {grad}}(\Vert X\Vert ^{2}),Y) =0 \end{aligned}$$

on $M\backslash U_{0}=\{x\in M\mid {\text {grad}}(\Vert X\Vert ^{2})=0\}$. Then, (4.8) implies

$$\begin{aligned} {{\mathfrak {m}}}{{\mathfrak {c}}}_{Z,Y}= & {} \frac{1}{2} \int _{U_{0}} Fg({\text {grad}}(\Vert X\Vert ^{2}),Y)Y(\Vert X\Vert ^{2})\mu \end{aligned}$$

(4.13)

$$\begin{aligned}= & {} \frac{1}{2} \int _{U_{0}} FY(\Vert X\Vert ^{2})^{2}\mu . \end{aligned}$$

(4.14)

This completes the proof. $\square$

Recall that ${\text {sgn}}(Z)$ is the signature of F for a zonal flow Z (Definition 3.9).

Corollary 4.3

Let $Z = fX$ be a zonal flow on M and Y a divergence-free vector field. Suppose that Y satisfies the following.

• (a) $[X,Y]=0$.

• (b) ${\text {supp}}(Y)\subset U^{+}:=\{x\in M\mid {\text {sgn}}(Z)>0\}$.

• (c) $Y(\Vert X\Vert ^{2})\ne 0$ on $U^{+}$.

Then, we have

$$\begin{aligned} {{\mathfrak {m}}}{{\mathfrak {c}}}_{Z,Y} >0. \end{aligned}$$

Proof

Let F be the function for Z satisfying (4.8) on $U_{0}:=\{x\in M\mid {\text {grad}}(\Vert X\Vert ^{2})\ne 0\}$. Then, by the assumption on Y, Lemma 4.2 implies

$$\begin{aligned} {{\mathfrak {m}}}{{\mathfrak {c}}}_{Z,Y}= & {} \frac{1}{2} \int _{U_{0}}FY(\Vert X\Vert ^{2})^{2}\mu \\= & {} \frac{1}{2} \int _{U^{+}}FY(\Vert X\Vert ^{2})^{2}\mu . \end{aligned}$$

Then, because F is positive on $U^{+}$ by definition and $Y(\Vert X\Vert ^{2})\ne 0$ by the assumption, we have the corollary. $\square$

4.2 A Sufficient Condition for ${{\mathfrak {m}}}{{\mathfrak {c}}}>0$

In this section, we give a sufficient condition for ${\mathfrak m}{{\mathfrak {c}}}_{Z,Y}>0$. Namely, we prove Theorem 1.1.

Proof of Theorem 1.1

By Corollary 4.3, it is sufficient to show that there exists a divergence-free vector field Y on M, which satisfies the following conditions:

• (a) $[X,Y]=0$,

• (b) ${\text {supp}}(Y)\subset U^{+}:=\{x\in M\mid {\text {sgn}}(Z)>0\}$,

• (c) $Y(\Vert X\Vert ^{2})\ne 0$ on $U^{+}$.

On the other hand, by Lemma 3.13, there exist a one-dimensional homogeneous $S^{1}$-space N and an $S^{1}$-equivariant open embedding

$$\begin{aligned} \phi :N \times {{\mathbb {R}}}^{\dim M-1} \rightarrow M \end{aligned}$$

(4.15)

satisfying

$$\begin{aligned} \phi (N\times {{\mathbb {R}}}^{\dim M-1})\subset U^{+}:=\{x\in M\mid {\text {sgn}}(Z)>0\}. \end{aligned}$$

(4.16)

By this embedding, we regard

$$\begin{aligned} N\times {{\mathbb {R}}}^{\dim M-1} \subset U^{+}. \end{aligned}$$

(4.17)

Thus, the existence of Y follows from Lemma 4.4 below by substituting $h=\Vert X\Vert ^{2}$, $\omega =\mu$, and $k=\dim M-1$. We note that Lemma 4.4 is applicable because $X(\Vert X\Vert ^{2})=0$ by Lemma 3.1, $\Vert X\Vert ^{2}$ is not constant by the non-geodesic assumption of Z, $k=\dim M-1\ge 2$ by the assumption of Theorem 1.1, and $\mu$ is $S^{1}$-invariant by the assumption that X is Killing and induced by the $S^{1}$-action. $\square$

Lemma 4.4

Let N be a one-dimensional homogeneous $S^{1}$-space, $\omega$ be an $S^{1}$-invariant volume form on $N\times {{\mathbb {R}}}^{k}$, X a vector field on $N\times {{\mathbb {R}}}^{k}$ induced by the $S^{1}$-action, and h a non-constant function on $N\times {\mathbb R}^{k}$ satisfying $X(h)=0$. Then, if $k\ge 2$, there exists a compactly supported divergence-free vector field Y on $N\times {{\mathbb {R}}}^{k}$ satisfying $[X,Y]=0$ such that $Y(h)\ne 0$.

Proof

Although this is probably obvious, we prove this lemma in Appendix A for completeness. $\square$

5 Zonal Flows on 3D Ellipsoids

In this section, we construct a class of zonal flows on three-dimensional ellipsoids that will be shown to develop conjugate points.

5.1 Construction of the Family of Flows Z(f, p, q)

In this section, we calculate some formulae on three-dimensional ellipsoid in coordinates to describe the particular class of flows we will be interested in. Recall that our ellipsoid is defined for $a > 0$ by

$$\begin{aligned} M_{a}^{3}:=\{(x,y,z,w)\in {{\mathbb {R}}}^{4}\mid x^{2}+y^{2}=a^{2}(1-z^{2}-w^{2})\}. \end{aligned}$$

(5.1)

Under the coordinate system

(5.2)

we have

$$\begin{aligned} \partial _{\xi }\mapsto & {} (-a\sin (\xi )\sin (\chi ),a\cos (\xi )\sin (\chi ),0,0), \\ \partial _{\mu }\mapsto & {} (0,0,-\sin (\mu )\cos (\chi ),\cos (\mu )\cos (\chi )), \\ \partial _{\chi }\mapsto & {} (a\cos (\xi )\cos (\chi ),a\sin (\xi )\cos (\chi ),-\cos (\mu )\sin (\chi ),-\sin (\mu )\sin (\chi )). \end{aligned}$$

Let g be the Riemannian metric on $S^{3}$ induced by ${\mathbb R}^{4}$. Then, we have

$$\begin{aligned} g=(g_{ij})=(g(\partial _{i},\partial _{j}))= \begin{pmatrix} a^{2}\sin ^{2}(\chi )&{}0&{}0\\ 0&{}\cos ^{2}(\chi )&{}0\\ 0&{}0&{}a^{2}\cos ^{2}(\chi )+\sin ^{2}(\chi ) \end{pmatrix}, \nonumber \\ \end{aligned}$$

(5.3)

where we make a correspondence

$$\begin{aligned} 1 \mapsto \xi ,\qquad 2\mapsto \mu ,\qquad 3\mapsto \chi . \end{aligned}$$

(5.4)

Then, the inverse matrix of g is

$$\begin{aligned} g^{-1}=(g^{ij})= \begin{pmatrix} 1/a^{2}\sin ^{2}(\chi )&{}0&{}0\\ 0&{}1/\cos ^{2}(\chi )&{}0\\ 0&{}0&{}1/(a^{2}\cos ^{2}(\chi )+\sin ^{2}(\chi )) \end{pmatrix}\nonumber \\ \end{aligned}$$

(5.5)

and the gradient of f is given by

$$\begin{aligned} {\text {grad}}f= & {} \frac{\partial _{1}f}{a^{2}\sin ^{2}(\chi )} \partial _{1} + \frac{\partial _{2}f}{\cos ^{2}(\chi )} \partial _{2} + \frac{\partial _{3}f}{a^{2}\cos ^{2}(\chi )+\sin ^{2}(\chi )} \partial _{3} \end{aligned}$$

(5.6)

for any function f on $M^{3}_{a}$. It is clear from the metric coefficients that for any $p, q \in {\mathbb {R}}$, the vector field

$$\begin{aligned} X_{p, q} = p\partial _{\xi } + q\partial _{\mu } \end{aligned}$$

(5.7)

is Killing. For any such vector field, we have

$$\begin{aligned} \begin{aligned} \Vert X_{p, q} \Vert ^2&= a^{2}p^{2}\sin ^{2}(\chi ) + q^{2}\cos ^{2}(\chi )\\&= a^{2}p^{2} - (a^{2}p^{2}-q^{2})\cos ^{2}(\chi ). \end{aligned} \end{aligned}$$

(5.8)

In particular, if $a^2p^2 \ne q^2$, then $\Vert X_{p, q} \Vert ^2$ is not constant. Now let $f = f(\chi )$ be a scalar function of $\chi$ with the property that for some $\varepsilon >0$,

$$\begin{aligned} f(\chi )\equiv 0,\quad \text { on } \chi \in [0,\varepsilon ) \cup \left( \frac{\pi }{2}-\varepsilon ,\frac{\pi }{2}\right] \end{aligned}$$

(5.9)

and let $Z(f, p, q) = f(\chi )X_{p, q}$. Then, we have ${\text {supp}}(Z(f,p,q))\subset M_{a}^{3}\backslash (N\cup S)$ by (5.9) (see (1.3) for the definitions of N and S). We assume also that f is non-trivial (i.e., not a constant function).

Theorem 5.1

The vector fields Z(f, p, q) constructed above are all non-geodesic positive zonal flows on $M^3_a$.

Proof

Let $Z = f(\chi )X_{p, q}$ be one such vector field. By construction $X_{p, q} f = 0$, so Z is divergence-free. By Lemma 3.6, we have

$$\begin{aligned} \nabla _Z Z = -\frac{f^2}{2}\textrm{grad}(\Vert X_{p, q}\Vert ^2). \end{aligned}$$

(5.10)

A straightforward computation shows

$$\begin{aligned} {\text {grad}}(\Vert X_{p, q}\Vert ^{2})= & {} \frac{2(a^{2}p^{2}-q^{2})\sin (\chi )\cos (\chi )}{a^{2}\cos ^{2}(\chi )+\sin ^{2}(\chi )}\partial _{\chi }. \end{aligned}$$

(5.11)

The formulae (5.6), (5.10), and (5.11) imply that we have $\nabla _{Z}Z={\text {grad}}h$ for some function $h=h(\chi )$ by integrating the coefficient of $\partial _{\chi }$. Thus, Z is a zonal flow. Moreover, (5.11) implies that $\textrm{grad}(\Vert X_{p, q}\Vert ^2)$ never vanishes on $0< \chi < \pi /2$ by our assumption $a^2p^2 \ne q^2$. Since f is not identically zero, (5.10) shows that $\nabla _Z Z$ does not vanish identically, which means Z is non-geodesic.

To see that Z is positive (Definition 3.4), note that

$$\begin{aligned} {\text {grad}}(f^{2}) = \frac{\partial _{\chi }(f^{2})}{a^{2}\cos ^{2}(\chi )+\sin ^{2}(\chi )}\partial _{\chi } \end{aligned}$$

by (5.6). However, the existence of a maximal value of $f^{2}$ implies that $\partial _{\chi }(f^{2})$ takes both positive and negative values on $\chi \in (0,\frac{\pi }{2})$. Because $a^{2}\cos ^{2}(\chi )+\sin ^{2}(\chi )$ is always positive and the signature of ${\text {grad}}(\Vert X_{p,q}\Vert ^{2})$ is constant on $0<\chi <\pi /2$ by (5.11), this completes the proof. $\square$

We conclude this section with the proof of Corollary 1.2. In view of Theorem 5.1, it suffices to show that in the special case where $p, q \in {\mathbb {Q}}$, still under the assumption $p^2a^2 \ne q^2$, the vector fields Z(f, p, q) are $S^1$-zonal flows, in addition to being non-geodesic and positive. Note that because to be $S^{1}$-zonal flow is invariant by nonzero constant multiple, we can assume that $p,q\in {{\mathbb {Z}}}$ (with $p^2a^2 \ne q^2$). We also note that for each fixed $0< \chi _0 < \pi /2$, the vector fields $\partial _{\xi }$ and $\partial _{\mu }$ are tangent to the torus $\chi = \chi _0$ sitting inside $M^3_a$, which is just like the Clifford torus in $S^3$. For integer p and q, the map

$$\begin{aligned} \Phi _t(\xi , \mu , \chi ) = (\xi + tp, \mu + tq, \chi ) \end{aligned}$$

(5.12)

generates an action of $S^1 = {\mathbb {R}}/2\pi {\mathbb {Z}}$ whose induced vector field is $X_{p, q}$. This concludes the proof of Corollary 1.2.

A Proof of Lemma 4.4

In this section, we prove Lemma 4.4. For this end, we prepare some elementary lemmas in the following three sections.

1.1 A.1 Compactly Supported Divergence Free Vector Fields on ${{\mathbb {R}}}^{k}$

In this section, we prove an elementary lemma, which states that there exist many compactly supported divergence-free vector fields on ${{\mathbb {R}}}^{k}$ with respect to any volume form on ${\mathbb R}^{k}$.

Let M be an orientable manifold with a volume form $\mu$, namely, $\mu$ is a nowhere vanishing $(\dim M)$-form on M. Note that we do not assume M is a Riemannian manifold. Recall that the divergence of a vector field Y on M is defined by

$$\begin{aligned} {\text {div}}(Y)\mu = L_{Y}(\mu ) = d\circ i_{Y}(\mu ), \end{aligned}$$

(A.1)

where $L_{Y}$ is the Lie derivative, $i_{Y}$ is the interior derivative, and d is the exterior derivative. We also write ${\text {div}}_{\mu }(Y):= {\text {div}}(Y)$ when we want to emphasis that we calculate the divergence with respect to $\mu$. Let

$$\begin{aligned} {{\mathfrak {X}}}_{\mu }(M):=\{X\in {{\mathfrak {X}}}(M)\mid {\text {div}}_{\mu }(X)=0\} \end{aligned}$$

(A.2)

be the space of divergence-free vector fields on M.

Lemma A.1

Let M be a manifold with a volume form $\mu$ and H a nowhere vanishing function on M. Define another volume form on M by $\mu _{H}:=H\mu$. Then, we have

$$\begin{aligned} {\text {div}}_{\mu _{H}}(Y)H = {\text {div}}_{\mu }(HY). \end{aligned}$$

(A.3)

In particular, $Y\in {{\mathfrak {X}}}_{\mu _{H}}(M)$ if and only if $HY\in {{\mathfrak {X}}}_{\mu }(M)$.

Proof

We have

$$\begin{aligned} {\text {div}}_{\mu _{H}}(Y)H\mu= & {} {\text {div}}_{\mu _{H}}(Y)\mu _{H} \\= & {} d\circ i_{Y}(\mu _{H}) \\= & {} d\circ i_{Y}(H\mu ) \\= & {} d\circ i_{HY}(\mu ) \\= & {} {\text {div}}_{\mu }(HY)\mu , \end{aligned}$$

which shows (A.3). The latter assertion follows from (A.3) and the assumption that H is nowhere vanishing. $\square$

Let ${\text {ev}}_{p}:{{\mathfrak {X}}}(M)\rightarrow T_{p}M$ be the evaluation map, where $T_{p}M$ is the tangent space of M at $p\in M$. Namely,

$$\begin{aligned} {\text {ev}}_{p}:{{\mathfrak {X}}}(M)\rightarrow & {} T_{p}M, \end{aligned}$$

(A.4)

$$\begin{aligned} Y\mapsto & {} {\text {ev}}_{p}(Y):=Y_{p}. \end{aligned}$$

(A.5)

We write ${{\mathfrak {X}}}_{\mu ,c}(M)$ for the space of compactly supported divergence-free vector fields on M.

Lemma A.2

Let $k\ge 2$ and $\mu _{0}$ the usual volume form on ${\mathbb {R}}^{k}$. Then, for any $p\in {{\mathbb {R}}}^{k}$, the restriction of the evaluation map ${\text {ev}}_{p}:{\mathfrak X}_{\mu _{0},c}({{\mathbb {R}}}^{k}) \rightarrow T_{p}{{\mathbb {R}}}^{k}$ is surjective.

Proof

We only prove in the case $k=2$ and $p=(0,0)\in {{\mathbb {R}}}^{2}$. Let $\rho :{{\mathbb {R}}}\rightarrow {{\mathbb {R}}}$ be a compactly supported smooth function satisfying $\rho \equiv 1$ on $[-1,1]$. Define functions $R_{1},R_{2}$ by

$$\begin{aligned} R_{1}:= & {} \sqrt{(x-1)^{2}+y^{2}}, \\ R_{2}:= & {} \sqrt{x^{2}+(y-1)^{2}}, \end{aligned}$$

for $(x,y)\in {{\mathbb {R}}}^{2}$. Moreover, we define vector fields

$$\begin{aligned} Y_{1}:= & {} \rho (R_{1}) \left( y\partial _{x} - (x-1)\partial _{y} \right) , \\ Y_{2}:= & {} \rho (R_{2}) \left( (y-1)\partial _{x} - x\partial _{y} \right) . \end{aligned}$$

Recall that for a vector field $u=a\partial _{x}+b\partial _{y}$, we have

$$\begin{aligned} {\text {div}}_{\mu _{0}}(u) = \partial _{x}a + \partial _{y}b. \end{aligned}$$

(A.6)

Thus, it is obvious that $Y_{1},Y_{2}\in {\mathfrak X}_{\mu _{0},c}({{\mathbb {R}}}^{k})$ and

$$\begin{aligned} {\text {ev}}_{(0,0)}(Y_{1})=\partial _{y}, \quad {\text {ev}}_{(0,0)}(Y_{1})=-\partial _{x}. \end{aligned}$$

(A.7)

This completes the proof. $\square$

Corollary A.3

Let $k\ge 2$ and $\mu$ a volume form on ${{\mathbb {R}}}^{k}$. Then, for any $p\in {{\mathbb {R}}}^{k}$, the restriction of the evaluation map ${\text {ev}}_{p}:{{\mathfrak {X}}}_{\mu ,c}({{\mathbb {R}}}^{k}) \rightarrow T_{p}{{\mathbb {R}}}^{k}$ is surjective.

Proof

By the assumption, there exists a nowhere vanishing function on ${{\mathbb {R}}}^{k}$ such that

$$\begin{aligned} \mu =H\mu _{0}, \end{aligned}$$

(A.8)

where $\mu _{0}$ is the usual volume form on ${{\mathbb {R}}}^{k}$. Then, $Y\in {{\mathfrak {X}}}_{\mu ,c}(M)$ if and only if $HY\in {\mathfrak X}_{\mu _{0},c}(M)$ for any $Y\in {{\mathfrak {X}}}(M)$ by Lemma A.1. By definition, we have

$$\begin{aligned} {\text {ev}}_{p}(HY) = H(p) {\text {ev}}_{p}(Y). \end{aligned}$$

(A.9)

Moreover, $H(p)\ne 0$ because H is nowhere vanishing. Thus, we have

$$\begin{aligned} {\text {ev}}_{p} \left( {{\mathfrak {X}}}_{\mu ,c}({{\mathbb {R}}}^{k}) \right) = {\text {ev}}_{p} \left( {\mathfrak X}_{\mu _{0},c}({{\mathbb {R}}}^{k}) \right) . \end{aligned}$$

Therefore, the corollary follows from Lemma A.2. $\square$

1.2 A.2 Lie Group Theory

In this section, we recall some elementary theories of Lie groups. For example, see [9] for more details.

Let G be a Lie group, G/H a homogeneous G-space, and G act on $G/H\times {{\mathbb {R}}}^{k}$ via the first factor. We write ${{\mathfrak {X}}}(G/H\times {{\mathbb {R}}}^{k})^{G}$ for the space of G-invariant vector fields on $G/H\times {{\mathbb {R}}}^{k}$. For any $gH\in G/H$, let $\iota _{gH}$ be a closed embedding

$$\begin{aligned} \iota _{gH}:{{\mathbb {R}}}^{k}\rightarrow & {} G/H\times {{\mathbb {R}}}^{k}, \\ x\mapsto & {} \iota _{gH}(x):=(gH,x). \end{aligned}$$

Then, there exists an injection

$$\begin{aligned} \begin{aligned} {{\mathfrak {X}}}({{\mathbb {R}}}^{k})\hookrightarrow&{} {{\mathfrak {X}}}(G/H\times {{\mathbb {R}}}^{k})^{G}, \\ Y\mapsto&{} \left( (gH,x) \mapsto {\widetilde{Y}}_{(gH,x)}:= \iota _{gH*}(Y_{x}) \right) ,\end{aligned} \end{aligned}$$

(A.10)

where $\iota _{gH*}$ is the pushforward by $\iota _{gH}$. Moreover, if G is connected, we have

$$\begin{aligned} {{\mathfrak {X}}}(G/H\times {{\mathbb {R}}}^{k})^{G} = {\mathfrak X}(G/H\times {{\mathbb {R}}}^{k})^{{\mathfrak {g}}}, \end{aligned}$$

(A.11)

where ${{\mathfrak {g}}}$ is the Lie algebra of G and we set

$$\begin{aligned} {{\mathfrak {X}}}(G/H\times {{\mathbb {R}}}^{k})^{{\mathfrak {g}}}:= \{ Z\in {{\mathfrak {X}}}(G/H\times {{\mathbb {R}}}^{k})\mid [X,Z]=0\text { for any } X\in {{\mathfrak {g}}} \}. \end{aligned}$$

(A.12)

Here, we identify $X\in {{\mathfrak {g}}}$ with the corresponding vector field on $G/H\times {{\mathbb {R}}}^{k}$.

Next, we suppose that there exists a G-invariant n-form $\omega _{0}$ on G/H, where $n:=\dim G/H$. Let

$$\begin{aligned} p:G/H\times {{\mathbb {R}}}^{k}\rightarrow G/H, \quad q:G/H\times {\mathbb R}^{k}\rightarrow {{\mathbb {R}}}^{k} \end{aligned}$$

(A.13)

be the projections for each factor. Then, we have an isomorphism

$$\begin{aligned} {{\mathcal {E}}}^{k}({{\mathbb {R}}}^{k})\simeq & {} {\mathcal E}^{n+k}(G/H\times {{\mathbb {R}}}^{k})^{G} ,\\ \mu\mapsto & {} p^{*}(\omega _{0})\wedge q^{*}(\mu ), \nonumber \end{aligned}$$

(A.14)

where ${{\mathcal {E}}}^{k}({{\mathbb {R}}}^{k})$ is the space of k-forms on ${{\mathbb {R}}}^{k}$ and $p^{*}$ is the pull back by p.

The following lemma states that the injection (A.10) preserves the divergent if a given volume form on $G/H\times {{\mathbb {R}}}^{k}$ is G-invariant.

Lemma A.4

Let G be a Lie group, G/H a homogeneous G-space. Suppose that there exists a G-invariant n-form $\omega _{0}$ on G/H with $n:=\dim G/H$. Then, for any G-invariant $(n+k)$-form $\omega$ on $G/H\times {{\mathbb {R}}}^{k}$, there exists a k-form $\mu$ on ${{\mathbb {R}}}^{k}$ such that we have

$$\begin{aligned} {\text {div}}_{\mu }(Y) = {\text {div}}_{\omega }({\widetilde{Y}}) \end{aligned}$$

for any $Y\in {{\mathfrak {X}}}({{\mathbb {R}}}^{k})$, where ${\widetilde{Y}}$ is defined in (A.10). In particular, the injection (A.10) induces

$$\begin{aligned} \begin{aligned} {{\mathfrak {X}}}_{\mu }({{\mathbb {R}}}^{k})\hookrightarrow&{} {\mathfrak X}_{\omega }(G/H\times {{\mathbb {R}}}^{k})^{G}, \\ Y\mapsto&{} {\widetilde{Y}}. \end{aligned} \end{aligned}$$

(A.15)

Proof

Let $\omega$ be a G-invariant $(n+k)$-form on $G/H \times {\mathbb R}^{k}$, namely, $\omega \in {{\mathcal {E}}}^{n+k}(G/H\times {\mathbb R}^{k})^{G}$. Then, by the isomorphism (A.14), there exists a k-form $\mu$ on ${{\mathbb {R}}}^{k}$ such that we have

$$\begin{aligned} \omega =p^{*}(\omega _{0})\wedge q^{*}(\mu ). \end{aligned}$$

(A.16)

Moreover, for any $Y\in {{\mathfrak {X}}}_{\mu }({{\mathbb {R}}}^{k})$, we have

$$\begin{aligned} {\text {div}}_{\omega }({\widetilde{Y}})\omega= & {} d\circ i_{{\widetilde{Y}}} \left( p^{*}(\omega _{0})\wedge q^{*}(\mu ) \right) \end{aligned}$$

by (A.1). By the graded Leibniz rule of the interior derivative, we have

$$\begin{aligned} i_{{\widetilde{Y}}} \left( p^{*}(\omega _{0})\wedge q^{*}(\mu ) \right)= & {} \left( i_{{\widetilde{Y}}} p^{*}(\omega _{0}) \right) \wedge q^{*}(\mu ) + (-1)^{n} p^{*}(\omega _{0}) \wedge \left( i_{{\widetilde{Y}}} q^{*}(\mu )\right) . \end{aligned}$$

By the definition of the pull back, this is equal to

$$\begin{aligned}= & {} p^{*}\left( i_{p_{*}{\widetilde{Y}}} (\omega _{0}) \right) \wedge q^{*}(\mu ) + (-1)^{n} p^{*}(\omega _{0}) \wedge q^{*} \left( i_{q_{*}{\widetilde{Y}}} (\mu ) \right) . \end{aligned}$$

(A.17)

However, by the definition of ${\widetilde{Y}}$, we have

$$\begin{aligned} p_{*}({\widetilde{Y}})=0, \quad q_{*}({\widetilde{Y}})=Y. \end{aligned}$$

Thus, (A.17) is equal to

$$\begin{aligned}= & {} (-1)^{n} p^{*}(\omega _{0}) \wedge q^{*} \left( i_{Y} (\mu ) \right) . \end{aligned}$$

Thus, we have

$$\begin{aligned} {\text {div}}_{\omega }({\widetilde{Y}})\omega= & {} d \left( (-1)^{n} p^{*}(\omega _{0}) \wedge q^{*} \left( i_{Y} (\mu ) \right) \right) . \end{aligned}$$

By the graded Leibniz rule of the exterior derivative, this is equal to

$$\begin{aligned}= & {} (-1)^{n} \left( d p^{*}(\omega _{0}) \right) \wedge q^{*} \left( i_{Y} (\mu ) \right) + (-1)^{2n} p^{*}(\omega _{0}) \wedge \left( d q^{*} \left( i_{Y} (\mu ) \right) \right) \\= & {} p^{*}(\omega _{0}) \wedge \left( d q^{*} \left( i_{Y} (\mu ) \right) \right) . \end{aligned}$$

Because d and the pull back is commutative, we have

$$\begin{aligned} {\text {div}}_{\omega }({\widetilde{Y}})\omega= & {} p^{*}(\omega _{0}) \wedge \left( q^{*}\left( d \circ i_{Y} (\mu ) \right) \right) \\= & {} p^{*}(\omega _{0}) \wedge \left( q^{*}\left( {\text {div}}_{\mu }(Y) \mu \right) \right) \\= & {} {\text {div}}_{\mu }(Y) \left( p^{*}(\omega _{0}) \wedge q^{*}\left( \mu \right) \right) \\= & {} {\text {div}}_{\mu }(Y) \omega . \end{aligned}$$

This completes the proof. $\square$

1.3 A.3 $S^{1}$ Case

In this section, we apply the results of Sect. A.2 to the case $G=S^{1}$.

Let N be a one-dimensional $S^{1}$-space. Then, it is obvious that there exists an $S^{1}$-invariant 1-form $\omega _{0}$ on N. Therefore we have the following.

Lemma A.5

Let N be a one-dimensional $S^{1}$-homogeneous space. Then, for any $S^{1}$-invariant $(k+1)$-from $\omega$ on $N\times {\mathbb R}^{k}$, there exists a k-form $\mu$ on ${{\mathbb {R}}}^{k}$ such that we have an injection

$$\begin{aligned} \begin{aligned} {{\mathfrak {X}}}_{\mu ,c}({{\mathbb {R}}}^{k})\hookrightarrow&{} {\mathfrak X}_{\omega ,c}(N\times {{\mathbb {R}}}^{k})^{S^{1}}, \\ Y\mapsto&{} {\widetilde{Y}}. \end{aligned} \end{aligned}$$

Proof

Note that N is compact because $S^{1}$ is compact. Moreover, the injection (A.15) preserves the compact support property because N is compact. Thus, this is an immediate corollary of Lemma A.4. $\square$

Corollary A.6

Let N be a one-dimensional $S^{1}$-homogeneous space, and X a vector field on $N\times {{\mathbb {R}}}^{k}$ induced by the $S^{1}$-action. Then, for any $S^{1}$-invariant $(k+1)$-from $\omega$ on $N\times {{\mathbb {R}}}^{k}$, there exists a k-form $\mu$ on ${{\mathbb {R}}}^{k}$ such that we have an injection

$$\begin{aligned} \begin{aligned} {{\mathfrak {X}}}_{\mu ,c}({{\mathbb {R}}}^{k})\hookrightarrow&{} {\mathfrak X}_{\omega ,c}(N\times {{\mathbb {R}}}^{k})^{X}, \\ Y\mapsto&{} {\widetilde{Y}}, \end{aligned} \end{aligned}$$

where we set

$$\begin{aligned} {{\mathfrak {X}}}_{\omega ,c}(N\times {{\mathbb {R}}}^{k})^{X}:= \{ Z\in {{\mathfrak {X}}}_{\omega ,c}(N\times {{\mathbb {R}}}^{k})\mid [X,Z]=0 \}. \end{aligned}$$

(A.18)

Proof

Because $S^{1}$ is connected, we have

$$\begin{aligned} {{\mathfrak {X}}}_{\omega ,c}(N\times {{\mathbb {R}}}^{k})^{S^{1}} = {{\mathfrak {X}}}_{\omega ,c}(N\times {{\mathbb {R}}}^{k})^{{\mathfrak {g}}} \end{aligned}$$

(A.19)

by (A.11), where ${{\mathfrak {g}}}$ is the Lie algebra of $S^{1}$. Moreover, we have ${{\mathfrak {g}}}={\mathbb R}X$ because $S^{1}$ is one-dimensional. Thus, by the definitions (A.12) and (A.18), we have

$$\begin{aligned} {{\mathfrak {X}}}_{\omega ,c}(N\times {{\mathbb {R}}}^{k})^{{\mathfrak {g}}} = {{\mathfrak {X}}}_{\omega ,c}(N\times {{\mathbb {R}}}^{k})^{X}. \end{aligned}$$

(A.20)

The equations (A.19) and (A.20) complete the proof by Lemma A.5. $\square$

Recall that the evaluation map ${\text {ev}}_{p}$ defined in (A.4).

Corollary A.7

Let N be a one-dimensional $S^{1}$-homogeneous space, $\omega$ an $S^{1}$-invariant $(k+1)$-form on $N\times {{\mathbb {R}}}^{k}$, X a vector field on $N\times {{\mathbb {R}}}^{k}$ induced by the $S^{1}$-action. Then, we have

$$\begin{aligned} T_{p}(N\times {{\mathbb {R}}}^{k}) = {{\mathbb {R}}}X + {\text {ev}}_{p} \left( {{\mathfrak {X}}}_{\omega ,c}(N\times {{\mathbb {R}}}^{k})^{X} \right) \end{aligned}$$

for any $p\in N\times {{\mathbb {R}}}^{k}$.

Proof

Set $G:=S^{1}$ and write $N\simeq G/H$ and $p=(gH,x)\in G/H\times {{\mathbb {R}}}^{k}$. Then, for any $Y\in {{\mathfrak {X}}}({\mathbb R}^{k})$, we have

$$\begin{aligned} {\text {ev}}_{p}({\widetilde{Y}})= & {} {\widetilde{Y}}_{(gH,x)} \nonumber \\= & {} \iota _{gH*}(Y_{x}) \nonumber \\= & {} \iota _{gH*}{\text {ev}}_{x}(Y) \end{aligned}$$

(A.21)

by definition of ${\widetilde{Y}}$ (see (A.10)). Therefore, the injection of Corollary A.6 and (A.21) imply

$$\begin{aligned} \begin{aligned} {\text{ ev }}_{p} \left( {{\mathfrak {X}}}_{\omega ,c}(N\times {{\mathbb {R}}}^{k})^{X} \right) \supset&{} \iota _{gH*} \left( {\text{ ev }}_{x}({{\mathfrak {X}}}_{\mu ,c}({{\mathbb {R}}}^{k})) \right) \\=&{} \iota _{gH*}(T_{x}{{\mathbb {R}}}^{k}) \end{aligned} \end{aligned}$$

by Corollary A.3. Because

$$\begin{aligned} T_{p}(N\times {{\mathbb {R}}}^{k})= & {} {{\mathbb {R}}}X + \iota _{gH*} \left( T_{x}{{\mathbb {R}}}^{k} \right) , \end{aligned}$$

we have the corollary. $\square$

1.4 A.4 Proof of Lemma 4.4

We rewrite Lemma 4.4 using the notation introduced in this section.

Lemma A.8

Let N be a one-dimensional homogeneous $S^{1}$-space, $\omega$ be an $S^{1}$-invariant volume form on $N\times {{\mathbb {R}}}^{k}$, X a vector field on $N\times {{\mathbb {R}}}^{k}$ induced by the $S^{1}$-action, and h a non-constant function on $N\times {\mathbb R}^{k}$ satisfying $X(h)=0$. Then, if $k\ge 2$, there exists $Y\in {{\mathfrak {X}}}_{\omega ,c}(N\times {{\mathbb {R}}}^{k})^{X}$ such that $Y(h)\ne 0$.

Proof

Suppose that for any $Y\in {{\mathfrak {X}}}_{\omega ,c}(N\times {\mathbb R}^{k})^{X}$, we have $Y(h)= 0$. Then, because $X(h)=0$ by the assumption, Corollary A.7 implies that h is killed by all the derivatives. This contradicts the non-constant assumption of h. Thus, we have the lemma. $\square$