1 Introduction

In the past few decades, different control techniques have addressed high order nonlinear systems, which could be categorized in four strategies: nonlinear controller [1, 2], single linear controller [3], multiple-model controllers [4], and Reduced Multiple-Model (RMM) controllers [5]. Heating, Ventilating, and Air Conditioning (HVAC), Type 1 Diabetes Mellitus (T1DM), and PH neutralization systems are best example of high order nonlinear systems [3, 4, 6]. Order and nonlinearity complexities in considered systems could result in modelling, control design and analysis and control implementation challenges requiring proper treatment. Among all strategies cited in the previous literatures, RMM control design could adequately resolve the mentioned problems in both aspects of order and nonlinearity [5].

Two tools should be employed to benefit from RMM control design in such complex systems: Order Reduction (OR) and Multiple-Model (MM) [5]. Therefore, the variety of OR and MM methods should be considered in this regard [7,8,9,10,11], all of which bring about different results in the closed-loop sense. A new control approach that combines MM and OR can cope well with order and nonlinearity characteristics [5]. Undeniable achievements of this combination are reducing computational loads, saving time, simplifying control design, and simplifying control implementation.

Although RMM control design has received a considerable attention during the past decade, the closed-loop stability has remained a closed book to some extent. One of the most efficient methods in MM approach is based on gap metric and stability margin [7, 12], which is only able to fulfill the local stability for each linear model, while there is no guarantee for stabilization of the nonlinear system constructed by weighted reduce multiple models [13, 14]. Indeed, each local controller can just stabilize the local model, while the combination of all local controllers does not necessarily stabilize the nonlinear system. In the closed-loop stability analysis context, the stability condition is obtained according to quadratic Lyapunov approach, which depends on existence of a common positive definite matrix for all reduce multiple models [15]. Although this approach is facilitated via Linear Matrix Inequalities (LMI) [16, 17], which could be efficiently solved by convex programming techniques, finding the common positive definite matrix may become difficult when the set of reduced multiple models is large [18]. This occurs due to conservatism of Lyapunov function. Piecewise quadratic Lyapunov function has been replaced by the previous one to deal with the numerous numbers of models [19]. However, it is proven that this method is not acceptable for saturated systems [20]. A none quadratic Lyapunov function is another solution which result in time derivate problem [21]. In this paper, we mainly focus on closed-loop stability analysis of RMM control algorithm based on quadratic Lyapunov approach to solve complexity problems for high order nonlinear systems.

The contribution of this paper is to design RMM controller based on LMI for such complex systems, while the closed-loop stability is guaranteed. To do so, we first determine the reduced multiple models and then each reduced model is formulated as an LMI to analyze stability. In this way a set of LMI families, which has as equal number as the reduced multiple models, are constructed by all reduced multiple models. This can be solved analytically. The solution includes control coefficients for the closed-loop stability driven via Lyapunov approach.

To illustrate the effectiveness of the proposed approach T1DM is examined. T1DM is one of the commonest diseases which could seriously lead to probable dangers in body parts. Diabetic patients are not capable of producing insulin, so artificial pancreas is responsible for producing Blood Glucose (BG) level in their bodies. Many scholars have introduced mathematical modeling of T1DM [22], one of which is Hovorka [1]. The variety of approaches are proposed to regulate BG, including H∞, MPC, adaptive, PID to name but a few. Although these efforts are valuable, further research should be conducted to account for the complexity in Hovorka model. RMM-based control design is one of the promising methods by which an artificial pancreas could be made to protect the patient from hypoglycemia where the BG level drops too low. According to this fact we design an LMI-based RMM controller for T1DM, while the closed-loop stability is also considered.

The contribution of the present work is adjusting the controller parameter in a simple way to control a high order nonlinear system so that the close loop stability is attained. Although many researchers have addressed how to design the controller for such systems, complexity is not considered carefully. Therefore, to simplify the controller design for such complex system still is a desired and challenging problem.

This paper is organized as follows. Section 2 presents prerequisites used in the current work. The proposed method and the closed-loop stability analysis are discussed in Sect. 3. In order to design the LMI-based RMM controller, an algorithm is proposed that reduces complexities in high order nonlinear systems while satisfies the closed-loop stability as well. Implementation of the proposed control algorithm on T1DM is illustrated in Sect. 4. Finally, conclusions are drawn in Sect. 5.

2 Prerequisites

Strong nonlinearity and high order are two main characteristics which could lead to complexity in controller design and implementation. MM and OR are two mathematical tools to simplify the procedure by reducing the nonlinearity and order complexities, respectively.

Let the high order nonlinear dynamic system is described by

$$ \begin{gathered} \dot{x} = f\left( {x,u} \right) \hfill \\ y = g\left( x \right), \hfill \\ \end{gathered} $$
(1)

where \(x\in {\mathbb{R}}^{n}\), \(u\in {\mathbb{R}}\), and \(y\in {\mathbb{R}}\) are state, control input, and output vectors, respectively. \(f:{\mathbb{R}}^{n}\to {\mathbb{R}}^{n}\) and \(g:{\mathbb{R}}^{n}\to {\mathbb{R}}\) are known nonlinear differentiable vector-valued functions and \(f\) is Lipschitz function.

Definition 1

\(\theta \) is scheduling variable which could be a set of measurable vectors:\(x\), \(u\), and/or \(y\).

Definition 2

\(\psi\) is named the global operating space coming from the variable space of \(\theta \) gridded into \(N\) points.

Definition 3

\(\psi_{i}\) represents the operating space obtained from decomposition of \(\psi\) into \(N_{s}\) subspaces \(\left( {\psi { = }\mathop {\text{U}}\limits_{i = 1}^{{N_{s} }} \psi_{i} } \right)\).

Remark 1

\({N}_{s}\ll N\), where \({N}_{s}\) is the number of operating points and \(N\) is the number of global operating points.

Definition 4

\(\left({x}_{e},{u}_{e},{y}_{e}\right)\) is called an equilibrium point if \(f\left({x}_{e},{u}_{e}\right)=0\), \({y}_{e}=g\left({x}_{e}\right)\).

Definition 5

\(\left\{\left({x}_{e},{u}_{e},{y}_{e}\right)|f\left({x}_{e},{u}_{e}\right)=0, {y}_{e}=g\left({x}_{e}\right)\right\}\) is named equilibrium manifold constructed from the set of \(\left({x}_{e},{u}_{e},{y}_{e}\right)\).

\(N\) local linear models, called High Order Local Linear Models (HOLLMs), are obtained via linearizing the high order nonlinear system described in (1) around operating points \(\left( {x_{ei} ,u_{ei} ,y_{ei} } \right)\), \(i = 1, \ldots ,N\)

$$ \begin{gathered} \delta \dot{x}_{i} = A_{i} \delta x_{i} + B_{i} \delta u_{i} \hfill \\ \delta y_{i} = C_{i} \delta x_{i} , \hfill \\ \end{gathered} $$
(2)

where \({A}_{i}={\left.\partial f/\partial x\right|}_{\left({x}_{ei},{u}_{ei}\right)}\), \({B}_{i}={\left.\partial f/\partial u\right|}_{\left({x}_{ei},{u}_{ei}\right)}\), \({C}_{i}={\left.\partial g/\partial x\right|}_{\left({x}_{ei},{u}_{ei}\right)}\), \(\delta {x}_{i}=x-{x}_{ei}\), \(\delta {u}_{i}=u-{u}_{ei}\), and \(\delta {y}_{i}=y-{y}_{ei}\).

Remark 2

Dichotomy algorithm is implemented to grid \({\uppsi }\) into \(N\) operating subspaces [23].

MM as a wise approach to deal with strong nonlinearity in high order nonlinear systems consists of two steps: decomposition and combination. In decomposition step, \(N\) HOLLMs are obtained according to Remark 2. Then \({N}_{s}\) High Order Nominal Linear Models (HONLMs) are selected so that the redundancy problem does not happen [24]. Various ways to find the number and location of HONLMs have been introduced so far, one of which is the selection of the nominal model based on the gap metric and stability margin. Gap metric is a criterion to compute gap between two linear models (\({G}_{1}\left(s\right)={\mathcal{M}}_{1}^{-1}\left(s\right){\mathcal{N}}_{1}\left(s\right)\) and \({G}_{2}\left(s\right)={\mathcal{M}}_{2}^{-1}\left(s\right){\mathcal{N}}_{2}\left(s\right)\)) in closed-loop sense [25],

$$ \begin{aligned}\delta \left( {G_{1} ,G_{2} } \right) =&\, \max \Bigg( \mathop {\inf }\limits_{{Q \in {\text{H}}_{\infty } }} \left\| {\left[ {\begin{array}{*{20}c} {{\mathcal{M}}_{1} } \\ {\mathcal{N}}_{1} \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} {{\mathcal{M}}_{2} } \\ {{\mathcal{N}}_{2} } \\ \end{array} } \right]Q} \right\|_{\infty } ,\\ &\mathop {\inf }\limits_{{Q \in {\text{H}}_{\infty } }} \left\| {\left[ {\begin{array}{*{20}c} {{\mathcal{M}}_{2} } \\ {{\mathcal{N}}_{2} } \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} {{\mathcal{M}}_{1} } \\ {{\mathcal{N}}_{1} } \\ \end{array} } \right]Q} \right\|_{\infty } \Bigg).\end{aligned} $$
(3)

If \(\delta \left({G}_{1},{G}_{2}\right)\) is close to the minimum value (\(\delta \left({G}_{1},{G}_{2}\right)\approx 0\)), linear models behave similarly. This is while they differ in the close-loop sense if the gap metric is close to the maximum value (\(\delta \left({G}_{1},{G}_{2}\right)\approx 1\)).

Stability margin is a criterion for HONLMs selection. This is compared with gap metric to complete model selection efficiently. The maximum stability margin of a linear model \(G\) is computed as

$$ \begin{aligned} b_{{{\text{opt}}}} \left( G \right) =&\, \left\{ {\mathop {\inf }\limits_{{L\;{\text{stablizing}}}} \left\| {\left[ {\begin{array}{*{20}c} I \\ L \\ \end{array} } \right]\left( {I + GL} \right)^{{ - 1}} \left[ {\begin{array}{*{20}c} I & G \\ \end{array} } \right]} \right\|_{\infty } } \right\}^{{ - 1}}\\ =&\, \sqrt {1 - \left\| {\left[ {\begin{array}{*{20}c} {\mathcal{N}} & {\mathcal{M}} \\ \end{array} } \right]} \right\|_{{\text{H}}}^{2} } < 1,\end{aligned} $$
(4)

where \(L\) is a controller that stabilizes \(G\). \({\Vert .\Vert }_{\mathrm{H}}\) is Hankel norm. There is also a relation between the gap metric and maximum stability margin cited in Theorem 1.

Theorem 1

In [26] Suppose that controller \(L\) stabilizes \(G\). Let \(\Sigma : = \{ G_{\Delta } : \delta \left( {G,G_{\Delta } } \right) < \Upsilon\) with \(G_{\Delta } = \left( {{\mathcal{M}}\left( s \right) + \Delta_{{\mathcal{M}}} } \right)^{ - 1} \left( {{\mathcal{N}}\left( s \right) + \Delta_{{\mathcal{N}}} } \right)\), where \(\left[ {\begin{array}{*{20}c} {\Delta_{{\mathcal{M}}} } \\ {\Delta_{{\mathcal{N}}} } \\ \end{array} } \right]_{\infty } < \varepsilon \in {\mathbb{R}}\), then \(L\) is a robust controller for all \(G_{\Delta } \in {\Sigma }\) if and only if \(\Upsilon \le b_{{{\text{opt}}}} \left( G \right)\).

Remark 3

The number of HONLMs (\({N}_{s}\)) is computable via Theorem 1.

Remark 4

The local stability is guaranteed according to Theorem 1.

Remark 5

\({N}_{s}\) operating point(s) and \(N\) global operating points construct HONLM(s) and HOLLMs, respectively.

In combination, the second step in MM approach, HONLMs are combined via weighting functions (\({\omega }_{i}\in {\mathbb{R}}\) to describe the nonlinear system as

$$ \begin{array}{*{20}l} {\dot{x} = \mathop \sum \limits_{i = 1}^{{N_{s} }} \omega_{i} \left( {A_{i} x_{i} + B_{i} u_{i} - A_{i} x_{ei} - B_{i} u_{ei} } \right)/\mathop \sum \limits_{i = 1}^{{N_{s} }} \omega_{i} \left( k \right)} \hfill \\ {y = \mathop \sum \limits_{i = 1}^{{N_{s} }} \omega_{i} \left( {C_{i} x_{i} + g\left( {x_{ei} } \right) - C_{i} x_{ei} - D_{i} u_{ei} } \right)/\mathop \sum \limits_{i = 1}^{{N_{s} }} \omega_{i} \left( k \right)} \hfill \\ \end{array} . $$
(5)

The simpler model could be obtained provided that OR approach is performed along with MM, i.e., each HONLMs described in (2) could be reduced via common reduction methods to construct Reduced Order Nominal Linear Models (RONLMs) [11, 27]

$$ \begin{array}{*{20}l} {\mathop {\delta \hat{x}_{i} }\limits^{ \cdot } = \hat{A}_{i} \delta \hat{x}_{i} + \hat{B}_{i} \delta u_{i} } \hfill \\ {\delta y_{i} = \hat{C}_{i} \delta \hat{x}_{i} } \hfill \\ \end{array} ,\;i = 1, \ldots ,N_{s} , $$
(6)

where \({\widehat{x}}_{i}\in {\mathbb{R}}^{{n}_{{\mathrm{r}}_{i}}}\) (\({n}_{{r}_{i}}<n\)) represent reduced states and \({\widehat{A}}_{i}\in {\mathbb{R}}^{{n}_{{\mathrm{r}}_{i}}\times {n}_{{\mathrm{r}}_{i}}}\), \({\widehat{B}}_{i}\in {\mathbb{R}}^{{n}_{{\mathrm{r}}_{i}}}\), \({\widehat{C}}_{i}\in {\mathbb{R}}^{1\times {n}_{{\mathrm{r}}_{i}}}\).

The following technical lemmas are essential in our future discussions.

Lemma 1

Let \(M\) and \(N\) be real constant matrices of appropriate dimensions and \(P\) be a positive matrix. Then for any \(\varepsilon >0\) we have.

$$ M^{T} PN + N^{T} PM \le \varepsilon M^{T} PM + \varepsilon^{ - 1} N^{T} PN. $$
(7)

Proof

The following condition satisfies the conclusion of Lemma 1.

$$\left(\sqrt{\varepsilon }{M}^{T}-\frac{1}{\sqrt{\varepsilon }}{N}^{T}\right)P\left(\sqrt{\varepsilon }M-\frac{1}{\sqrt{\varepsilon }}N\right)\ge 0$$
(8)

Lemma 2

(Schur complements) [28]. Consider constant matrices \({\Omega }_{1}\), \({\Omega }_{2}\), and \({\Omega }_{3}\), where \({\Omega }_{1}={\Omega }_{1}^{T}\) and \({\Omega }_{2}={\Omega }_{2}^{T}\), then.

$$ {\Omega }_{2} > 0,\;{\Omega }_{1} - {\Omega }_{3}^{T} {\Omega }_{2}^{ - 1} {\Omega }_{3} < 0, $$
(9)

if only if

$$ \left[ {\begin{array}{*{20}c} {{\Omega }_{1} } & {{\Omega }_{3}^{T} } \\ {{\Omega }_{3} } & { - {\Omega }_{1} } \\ \end{array} } \right] < 0. $$

Proof

See [28].

3 Proposed method

In order to cope with both strong nonlinearity and high order characteristics in high order nonlinear systems, combination of MM and OR would be a wise choice. In this view, RMM control is simply designed for such systems. To do this, at first RONLMs are obtained and then the local controllers are designed, each of them is able to stabilize its own RONLM according to Theorem 1, whereby the local stability is guaranteed as mentioned in Remark 4 [12], while nonlinear system will not be necessarily stable. Indeed, the local stability does not guarantee the global one.

3.1 Closed-loop stability analysis via LMI

Whenever a high order nonlinear system is described by RONLMs, it means that the model selection and simplification has been successfully done. This is the time to design the RMM controller. In this regard, each RONLMs described in (6) are discretized as

$$ \begin{array}{*{20}l} {x_{i} \left( {k + 1} \right) = \hat{A}_{di} x_{i} \left( k \right) + \hat{B}_{di} u_{i} \left( k \right)} \hfill \\ {y_{i} \left( k \right) = \hat{C}_{di} x_{i} \left( k \right)} \hfill \\ \end{array} ,\;i = 1, \ldots , N_{s}, $$
(10)

where \({\widehat{A}}_{di}\in {\mathbb{R}}^{{n}_{{\mathrm{r}}_{i}}\times {n}_{{\mathrm{r}}_{i}}}\), \({\widehat{B}}_{di}\in {\mathbb{R}}^{{n}_{{\mathrm{r}}_{i}}\times 1}\), \({\widehat{C}}_{di}\in {\mathbb{R}}^{1\times {n}_{{\mathrm{r}}_{i}}}\). Then, the nonlinear system can be described using weighting functions as follows

$$ x\left( {k + 1} \right) = \frac{{\mathop \sum \nolimits_{i = 1}^{{N_{s} }} \omega_{i} \left( k \right)\left( {\hat{A}_{di} x_{i} \left( k \right) + \hat{B}_{di} u_{i} \left( k \right) + \tilde{f}_{i} \left( {x\left( k \right)} \right)} \right)}}{{\mathop \sum \nolimits_{i = 1}^{{N_{s} }} \omega_{i} \left( k \right)}}, $$
(11)

where

$$ \tilde{f}_{i} \left( {x\left( k \right)} \right) = f\left( {x\left( k \right),u\left( k \right)} \right) - \hat{A}_{di} x_{i} \left( k \right) + \hat{B}_{di} u_{i} \left( k \right), $$

and \(\widetilde{{f}_{i}}\left(x\left(k\right)\right)\in {\mathbb{R}}^{{n}_{{\mathrm{r}}_{i}}}\) is a Lipschitz nonlinear function.

In order to guarantee the global stability for the nonlinear system, the closed-loop system can be obtained by substituting the control law, which is described as \(u_{i} = L_{i} x_{i} \left( k \right),\;i = 1, \ldots N_{s} ,\) in (11) as

$$ x\left( {k + 1} \right) = \frac{{\mathop \sum \nolimits_{i = 1}^{{N_{s} }} \omega_{i} \left( k \right)\left( {\left( {\hat{A}_{di} + \hat{B}_{di} L_{i} } \right)x_{i} \left( k \right) + \tilde{f}_{i} \left( {x\left( k \right)} \right)} \right)}}{{\mathop \sum \nolimits_{i = 1}^{{N_{s} }} \omega_{i} \left( k \right)}}. $$
(12)

Let first \(Z_{i} = \left( {\hat{A}_{di} + \hat{B}_{di} L_{i} } \right)x_{i} \left( k \right) + \tilde{f}_{i} \left( {x\left( k \right)} \right)\), where \(Z_{i} \in {\mathbb{R}}^{{n_{{{\text{r}}_{i} }} }}\) and then rewrite (12) as,

$$ x\left( {k + 1} \right) = \frac{{\mathop \sum \nolimits_{i = 1}^{{N_{s} }} \omega_{i} \left( k \right)Z_{i} }}{{\mathop \sum \nolimits_{i = 1}^{{N_{s} }} \omega_{i} \left( k \right)}}. $$
(13)

Theorem 2

In [29] Consider a discrete system by \(x\left(k+1\right)=f\left(x\left(k\right)\right)\), where \(x(k)\in {\mathbb{R}}^{n}\), \(f\left(x\left(k\right)\right):{\mathbb{R}}^{n}\to {\mathbb{R}}^{n}\) with \(f\left(0\right)=0\) for all \(k\). Suppose that there is a scalar function \(V(x\left(k\right))\) continuous in \(x(k)\) so that 1) \(V\left(0\right)=0\), 2) \(V(x\left(k\right))>0\) for \(x(k)\ne 0\), and 3) \(V(x\left(k\right))\to \infty \) if \(\Vert x(k)\Vert \to \infty \). Then the equilibrium state \({x}_{e}=0\) is asymptotically stable with \(V(x\left(k\right))\) as the Lyapunov function, which could be considered as quadratic form \(V(x\left(k\right))={x}^{T}\left(k\right)Px(k)\), where \(P\in {\mathbb{R}}^{n\times n}\) is a positive definite matrix, if \(\Delta V(x\left(k\right))<0\) for \(x(k)\ne 0\).

$$\begin{aligned}\Delta V\left( {x\left( k \right)} \right) &= V\left( {x\left( {k + 1} \right)} \right) - V\left( {x\left( k \right)} \right) = x^{T} \left( {k + 1} \right)Px\left( {k + 1} \right) - x^{T} \left( k \right)Px\left( k \right) \\ &= \left( {\frac{{\mathop \sum \nolimits_{i = 1}^{{N_{s} }} \omega_{i} \left( k \right)Z_{i}^{T} }}{{\mathop \sum \nolimits_{i = 1}^{{N_{s} }} \omega_{i} \left( k \right)}}} \right)P\left( {\frac{{\mathop \sum \nolimits_{i = 1}^{{N_{s} }} \omega_{i} \left( k \right)Z_{i} }}{{\mathop \sum \nolimits_{i = 1}^{{N_{s} }} \omega_{i} \left( k \right)}}} \right) - x^{T} \left( k \right)Px\left( k \right) = \frac{{\mathop \sum \nolimits_{i, j = 1}^{{N_{s} }} \omega_{i} \left( k \right)\omega_{j} \left( k \right)\left( {Z_{i}^{T} PZ_{j} - x^{T} \left( k \right)Px\left( k \right)} \right)}}{{\mathop \sum \nolimits_{i, j = 1}^{{N_{s} }} \omega_{i} \left( k \right)\omega_{j} \left( k \right)}} \\ &= \frac{{\mathop \sum \nolimits_{i = 1}^{{N_{s} }} \omega_{i} \left( k \right)^{2} \left( {Z_{i}^{T} PZ_{i} - x^{T} \left( k \right)Px\left( k \right)} \right) + \mathop \sum \nolimits_{i < j}^{{N_{s} }} \omega_{i} \left( k \right)\omega_{j} \left( k \right)\left( {Z_{i}^{T} PZ_{j} + Z_{j}^{T} PZ_{i} - 2x^{T} \left( k \right)Px\left( k \right)} \right)}}{{\mathop \sum \nolimits_{i, j = 1}^{{N_{s} }} \omega_{i} \left( k \right)\omega_{j} \left( k \right)}} \end{aligned}$$
(14)

Lemma 3

In [29] If \(P\) is a positive definite matrix such that \({Z}_{i}^{T}P{Z}_{i}-{x}^{T}\left(k\right)Px\left(k\right)<0\) and \({Z}_{j}^{T}P{Z}_{j}-{x}^{T}\left(k\right)Px\left(k\right)<0\), then \({Z}_{i}^{T}P{Z}_{j}+{Z}_{j}^{T}P{Z}_{i}-2{x}^{T}\left(k\right)Px\left(k\right)<0\).

Proof

Based on [29] \({Z}_{i}^{T}P{Z}_{j}+{Z}_{j}^{T}P{Z}_{i}-2{x}^{T}\left(k\right)Px\left(k\right)<0\) could be rewritten as follows.

$$ \begin{aligned} & Z_{i}^{T} PZ_{j} + Z_{j}^{T} PZ_{i} - 2x^{T} \left( k \right)Px\left( k \right)\\ &\quad = - \left( {Z_{i} - Z_{j} } \right)^{T} P\left( {Z_{i} - Z_{j} } \right) + Z_{i}^{T} PZ_{i} + Z_{j}^{T} PZ_{j} \\ &\quad\quad - 2x^{T} \left( k \right)Px\left( k \right) = - \left( {Z_{i} - Z_{j} } \right)^{T} P\left( {Z_{i} - Z_{j} } \right)+ Z_{i}^{T} PZ_{i}\\ & \quad \quad - x^{T} \left( k \right)Px\left( k \right) + Z_{j}^{T} PZ_{j} - x^{T} \left( k \right)Px\left( k \right) < 0 \end{aligned}$$
(15)

Since \(P\) is positive definite matrix, \(-{\left({Z}_{i}-{Z}_{j}\right)}^{T}\break P\left({Z}_{i}-{Z}_{j}\right)\le 0\), then conclusions of Lemma 3, i.e., \({Z}_{i}^{T}P{Z}_{i}-{x}^{T}\left(k\right)Px\left(k\right)<0\) and \({Z}_{j}^{T}P{Z}_{j}-{x}^{T}\left(k\right)Px\left(k\right)<0\), hold.

Theorem 3

In [29] If a common positive definite matrix \(P\) exists such that \({Z}_{i}^{T}P{Z}_{i}-P<0\), \(i=1,\dots ,{N}_{s}\) is satisfied for all subsystems, then system described in (11) will be globally asymptotically stable.

Remark 6

If conditions of Theorem 3 hold, then the Lyapunov function will be decaying for all \({x}_{i}(k)\), i.e., \(\Delta V\left({x}_{i}\left(k\right)\right)=V\left({x}_{i}\left(k+1\right)\right)-V\left({x}_{i}\left(k\right)\right)<0\). Consequently, the closed-loop systems including the nonlinear system and designed controllers will be globally asymptotically stable.

Theorem 4

Consider the discrete-time systems in (11). The closed-loop system with \(V(x\left(k\right))\) is asymptotically stable if there exist \(1+{N}_{s}\) positive definite matrixes \(X\) and \({Y}_{i}\), \(i=1,\dots , {N}_{s}\) and \(2{N}_{s}+1\) positive constants \(\mu \), \({\varepsilon }_{i}\), \(i=1,\dots , {N}_{s}\), and \({W}_{i}\), \(i=1,\dots , {N}_{s}\) so that the set of following LMIs holds. Moreover, a desired control law is given by \(u=\sum_{i=1}^{{N}_{s}}{\omega }_{i}{L}_{i}{x}_{i}(k)/\sum_{i=1}^{{N}_{s}}{\omega }_{i}(k)\), where \({L}_{i}={Y}_{i}{X}^{-1}\).

$$ \psi_{i} = \left[ {\begin{array}{*{20}c} { - X} & {X\hat{A}_{di}^{T} + Y_{i}^{T} \hat{B}_{di}^{T} } & X \\ {\hat{A}_{di} X + \hat{B}_{di} Y_{i} } & { - \frac{X}{{\left( {1 + \varepsilon_{i} } \right)}}} & 0 \\ X & 0 & { - \frac{1}{{\left( {1 + \varepsilon_{i}^{ - 1} } \right)\mu W_{i} }}} \\ \end{array} } \right] < 0,\;i = 1, \ldots , N_{s} $$
(16)

Proof

In order to obtain (16), the conclusion of Lemma 3 is rewritten for each RONLM as

$$\begin{aligned} &\Delta V\left( {x_{i} \left( k \right)} \right) = V\left( {x_{i} \left( {k + 1} \right)} \right) - V\left( {x_{i} \left( k \right)} \right) < 0, \\ & \left( \left( {\hat{A}_{di} + \hat{B}_{di} L_{i} } \right)x_{i} \left( k \right) + \tilde{f}_{i} \left( {x\left( k \right)} \right) \right)^{T}\\ & P\left( \left( {\hat{A}_{di} + \hat{B}_{di} L_{i} } \right)x_{i} \left( k \right) + \tilde{f}_{i} \left( {x\left( k \right)} \right) \right) - x_{i}^{T} \left( k \right)Px_{i} \left( k \right) < 0 \\ & x_{i}^{T} \left( k \right)\left( {\hat{A}_{di} + \hat{B}_{di} L_{i} } \right)^{T} P\left( {\hat{A}_{di} + \hat{B}_{di} L_{i} } \right)x_{i} \left( k \right)\\ &\qquad + x_{i}^{T} \left( k \right)\left( {\hat{A}_{di} + \hat{B}_{di} L_{i} } \right)^{T}\\ & P\tilde{f}_{i} \left( {x\left( k \right)} \right) + \tilde{f}_{i}^{T} \left( {x\left( k \right)} \right)P\left( {\hat{A}_{di} + \hat{B}_{di} L_{i} } \right)x_{i} \left( k \right) + \tilde{f}_{i}^{T} \left( {x\left( k \right)} \right)\\ & P\tilde{f}_{i} \left( {x\left( k \right)} \right) - x_{i}^{T} \left( k \right)Px_{i} \left( k \right) < 0. \end{aligned}$$
(17)

By applying Lemma 1 it can be reformulated as follows.

$$\begin{aligned} & x_{i}^{T} \left( k \right)\left( {\hat{A}_{di} + \hat{B}_{di} L_{i} } \right)^{T}\\ & P\left( {\hat{A}_{di}+ \hat{B}_{di} L_{i} } \right)x_{i} \left( k \right) + \varepsilon_{i} x_{i}^{T} \left( k \right)\left( {\hat{A}_{di} + \hat{B}_{di} L_{i} } \right)^{T}\\ & P\left( {\hat{A}_{di} + \hat{B}_{di} L_{i} } \right)x_{i} \left( k \right) + \varepsilon_{i}^{ - 1} \tilde{f}_{i}^{T} \left( {x\left( k \right)} \right)P\tilde{f}_{i} \left( {x\left( k \right)} \right)\\ & \qquad + \tilde{f}_{i}^{T} \left( {x\left( k \right)} \right)P\tilde{f}_{i} \left( {x\left( k \right)} \right) - x_{i}^{T} \left( k \right)Px_{i} \left( k \right) < 0 \\ & x_{i}^{T} \left( k \right)\left( {\left( {1 + \varepsilon_{i} } \right)\left( {\hat{A}_{di} + \hat{B}_{di} L_{i} } \right)^{T} P\left( {\hat{A}_{di} + \hat{B}_{di} L_{i} } \right) - P} \right)x_{i} \left( k \right) \\ & \qquad+ \left( {1 + \varepsilon_{i}^{ - 1} } \right)\tilde{f}_{i}^{T} \left( {x\left( k \right)} \right)P\tilde{f}_{i} \left( {x\left( k \right)} \right) < 0 \end{aligned}$$
(18)

By considering \(P<{\lambda }_{\mathrm{max}}I<\mu I\), where \({\lambda }_{\mathrm{max}}\) is the maximum eigenvalue of \(P\) and \(\mu \) is its upper bound, (18) is simplified as

$${x}_{i}^{T}\left(k\right)\left({\left(1+{\varepsilon }_{i}\right)\left({\widehat{A}}_{di}+{\widehat{B}}_{di}{L}_{i}\right)}^{T}P\left({\widehat{A}}_{di}+{\widehat{B}}_{di}{L}_{i}\right)-P\right){x}_{i}\left(k\right)+(1+{\varepsilon }_{i}^{-1})\mu {\widetilde{f}}_{i}^{T}\left(x\left(k\right)\right){\widetilde{f}}_{i}\left(x\left(k\right)\right)<0.$$
(19)

Since \({\widetilde{f}}_{i}\left(.\right)\) is bounded as the usual Lipschitz conditions

$$ \tilde{f}_{i}^{T} \left( {x\left( k \right)} \right)\tilde{f}_{i} \left( {x\left( k \right)} \right) \le W_{i} x_{i}^{T} \left( k \right)x_{i} \left( k \right),\;i = 1, \ldots , N_{s} , $$
(20)

then

$$\begin{aligned} & x_{i}^{T} \left( k \right)\left( {\left( {1 + \varepsilon_{i} } \right)\left( {\hat{A}_{di} + \hat{B}_{di} L_{i} } \right)^{T} P\left( {\hat{A}_{di} + \hat{B}_{di} L_{i} } \right) - P} \right)x_{i} \left( k \right)\\ &\qquad + \left( {1 + \varepsilon_{i}^{ - 1} } \right)\mu W_{i} x_{i}^{T} \left( k \right)x_{i} \left( k \right) < 0. \end{aligned} $$
(21)

This will be true if

$$ \left( {1 + \varepsilon_{i} } \right)\left( {\hat{A}_{di} + \hat{B}_{di} L_{i} } \right)^{T} P\left( {\hat{A}_{di} + \hat{B}_{di} L_{i} } \right) - P + \left( {1 + \varepsilon_{i}^{ - 1} } \right)\mu W_{i} < 0. $$
(22)

Now, pre- and post-multiplying (22) by \(X = P^{ - 1}\) gives

$$ \left( {1 + \varepsilon_{i} } \right)X\left( {\hat{A}_{di} + \hat{B}_{di} L_{i} } \right)^{T} P\left( {\hat{A}_{di} + \hat{B}_{di} L_{i} } \right)X - X + \left( {1 + \varepsilon_{i}^{ - 1} } \right)\mu W_{i} X^{2} < 0. $$
(23)

Substituting \(Y_{i} = L_{i} X\) into above equation leads to

$$ \left( {1 + \varepsilon_{i} } \right)\left( {X\hat{A}_{di}^{T} + Y_{i}^{T} \hat{B}_{di}^{T} } \right)P\left( {\hat{A}_{di} X + \hat{B}_{di} Y_{i} } \right) - X + \left( {1 + \varepsilon_{i}^{ - 1} } \right)\mu W_{i} X^{2} < 0. $$
(24)

Note that, according to Lemma 2 (Schur complements) (24) becomes

$$ \psi_{i} = \left[ {\begin{array}{*{20}c} { - X} & {X\hat{A}_{di}^{T} + Y_{i}^{T} \hat{B}_{di}^{T} } & X \\ {\hat{A}_{di} X + \hat{B}_{di} Y_{i} } & { - \frac{X}{{\left( {1 + \varepsilon_{i} } \right)}}} & 0 \\ X & 0 & { - \frac{1}{{\left( {1 + \varepsilon_{i}^{ - 1} } \right)\mu W_{i} }}} \\ \end{array} } \right] < 0,\;i = 1, \ldots , N_{s} . $$
(25)

The proof of this theorem is complete.

To get more insight, the LMI-based RMM control scheme is presented in the following subsection.

3.2 LMI-based RMM control design algorithm

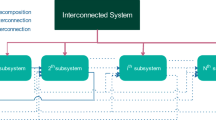
The RMM control design procedure is presented in an algorithm to handle both order and nonlinearity complexities in high order nonlinear systems. Figure 1 depicts the proposed strategy in this paper. As it is shown, the high order nonlinear system’s model is first decomposed into \(N\) HOLLMs (\(G_{i}^{{{\text{HL}}}}\), \(i = 1, \ldots ,N\)) to build High Order Model Bank (HOMB). Then, MM is applied to select HONLM: \(G_{i}^{{{\text{HN}}}}\), \(i = 1, \ldots ,N_{s}\) in each sub-region. Then, OR approach is employed to construct RONLMs: \(G_{i}^{{{\text{RN}}}}\), \(i = 1, \ldots ,N_{s}\). Local controllers are then designed for each RONLM in each sub-region based on LMI problem to guarantee the closed-loop stability. Finally, the global controller is constructed via combination of weighted local controllers. For more detailed insight, the following algorithm describes how RMM controller is designed.

Fig. 1
figure 1

Schematic diagram of the LMI-based RMM control design

Full size image

4 Algorithm. LMI-based RMM control design

  1. A.1.

    Gridding global operation space: Grid the scheduling variable (\(\theta\)) in global operation space (\({\uppsi }\)) to find \(N\) operating points using the dichotomy algorithm [23].

  2. A.2.

    Linearization and finding HOLLMs: Linearize the nonlinear system’s model around \(N\) operating points and obtain HOLLMs (\(G_{i}^{{{\text{HL}}}}\), \(i = 1, \ldots ,N\)). In this way HOMB is constructed.

  3. A.3.

    Computing gap metric: Compute the gap between all pairs of \(N\) HOLLMs based on (3) (\(\mathrm{gap}=\left[{\delta }_{i,j}\right]={\left[\delta \left({G}_{i}^{\mathrm{RL}},{G}_{j}^{\mathrm{RL}}\right)\right]}_{N\times N}\)).

  4. A.4.

    Calculating maximum stability margin: Calculate the maximum stability margin for \(N\) HOLLMs according to (4) (\({B}_{\mathrm{opt}}={\left[{b}_{\mathrm{opt}}\left({G}_{i}^{\mathrm{RL}}\right)\right]}_{N\times 1}\)).

  5. A.5.

    Set \(i=1\).

  6. A.6.

    Set \(j=i+1\).

  7. A.7.

    Selecting HONLMs: Select HONLMs (\({G}^{\mathrm{HN}}\)) among the \(i\)th to \(j\mathrm{th}\) HOLLMs according to the following criterion.

$${G}^{\mathrm{HN}}\triangleq \left\{{G}_{k}^{\mathrm{HL}}|\underset{i\le k\le j}{\mathrm{min}}\underset{i\le m\le j}{\mathrm{max}}\delta \left({G}_{m}^{\mathrm{HL}},{G}_{k}^{\mathrm{HL}}\right)\right\}$$
(26)
  1. A.8.

    Finding biggest gap: Find the biggest gap between \({G}^{\mathrm{HN}}\) and other HOLLM from \({\delta }^{*}=\underset{i\le m\le j}{\mathrm{max}}\delta \left({G}^{\mathrm{HN}},{G}_{m}^{\mathrm{HN}}\right)\).

  2. A.9.

    Checking local stability: check local stability based on Theorem 1. If \({\delta }^{*}\le {b}_{\mathrm{opt}}\left({G}^{\mathrm{HN}}\right)\) then set \(j=j+1\) and back to A7 (include another linearized model into the current sub-region). Otherwise (\({b}_{\mathrm{opt}}\left({G}^{\mathrm{HN}}\right)<{\delta }^{*}\)), go to A10.

  3. A.10.

    Classifying sub-region: Set \(j=j-1\). The \(j-i+1\) HOLLMs are classified in one sub-region. Find the HONLM \({G}^{\mathrm{HN}}\) from (26). Set \(i=j\) and back to A6. Repeat the above steps until all \(N\) local models are classified into different sub-regions.

  4. A.11.

    Order reduction and finding RONLMs: Reduce HONLMs and obtain RONLMs (\({G}_{i}^{\mathrm{RN}}\), \(i=1,\dots ,{N}_{s}\)) based on (6).

  5. A.12.

    Designing local controllers: Design local controllers (\({L}_{i}\), \(i=1,\dots ,{N}_{s}\)) based on LMI for each RONLM according to (16).

  6. A.13.

    Constructing global controller: Combine the local controllers to construct the global one via proper weighing functions (\({\omega }_{i}\), \(i=1,\dots , {N}_{s}\)).

5 Simulations

In this section, a T1DM system is studied to demonstrate the effectiveness of the proposed method, in which an LMI-based RMM controller is designed to stabilize the closed-loop system. Given that T1DM has both strong nonlinearity and high order features, it could be a wise choice to be examined as an example of complex nonlinear system. Hovorka model, which is widely used, is expressed by the following equation [22],

$$\left\{\begin{array}{l}{\dot{Q}}_{1}(t)=-{F}_{01}^{C}(t)-{x}_{1}(t){Q}_{1}(t)+{k}_{12}{Q}_{2}(t)\\ \quad\quad\quad\quad-{F}_{R}(t)+{U}_{G}(t)+{\mathrm{EGP}}_{0}(1-{x}_{3}(t))\\ {\dot{Q}}_{2}(t)={x}_{1}(t){Q}_{1}(t)-\left({k}_{12}+{x}_{2}(t)\right){Q}_{2}(t)\\ {\dot{S}}_{1}(t)=u(t)-\frac{{S}_{1}(t)}{{t}_{\mathrm{maxI}}}\\ {\dot{S}}_{2}(t)=\frac{{S}_{1}(t)}{{t}_{\mathrm{maxI}}}-\frac{{S}_{2}(t)}{{t}_{\mathrm{maxI}}} ,\\ \dot{I}(t)=\frac{{S}_{2}(t)}{{V}_{\mathrm{I}}{t}_{\mathrm{maxI}}}-{k}_{e}I(t)\\ {\dot{x}}_{1}(t)=-{k}_{a1}{x}_{1}(t)+{k}_{a1}{S}_{\mathrm{IT}}I(t)\\ {\dot{x}}_{2}(t)=-{k}_{a2}{x}_{2}(t)+{k}_{a2}{S}_{\mathrm{ID}}I(t)\\ {\dot{x}}_{3}\left(t\right)=-{k}_{a3}{x}_{3}(t)+{k}_{a3}{S}_{\mathrm{IE}}I(t)\end{array}\right.$$
(27)

where \(u\) and \({U}_{G}\) are external insulin infusion rate in \(\mathrm{mU}/\mathrm{min}\) and input disturbance in gram, respectively. Here, \({F}_{01}^{C}(t)\) and \({F}_{R}(t)\) are modeled as

$$ F_{01}^{C} \left( t \right) = \left\{ {\begin{array}{*{20}l} {\frac{{f_{01} }}{4.5}y} \hfill & {{\text{if}}} \hfill & {y < 4.5\frac{{{\text{mmol}}}}{{\text{L}}}} \hfill \\ {f_{01} } \hfill & {{\text{if}}} \hfill & {y \ge 4.5\frac{{{\text{mmol}}}}{{\text{L}}}} \hfill \\ \end{array} } \right.,\;F_{R} \left( t \right) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {{\text{if}}} \hfill & {y < 9\frac{{{\text{mmol}}}}{{\text{L}}}} \hfill \\ {0.003\left( {y - 9} \right)V_{G} } \hfill & {{\text{if}}} \hfill & {y \ge 9\frac{{{\text{mmol}}}}{{\text{L}}}} \hfill \\ \end{array} } \right., $$

where \(y={Q}_{1}/{V}_{G}\) is BG level measured as the system output. The saturation nature of \({F}_{01}^{C}\left(t\right)\) and \({F}_{R}(t)\) is the main source of the nonlinearity [1], which has given rise to strong nonlinearity for this research. As considered insulin-glucose system is modeled by eight states, the other requirement is provided. States are mass of glucose in accessible compartment (\({Q}_{1}\)), mass of glucose in non-accessible compartment (\({Q}_{2}\)), insulin absorption in compartment 1 (\({S}_{1}\)), insulin absorption in compartment 2 (\({S}_{2}\)), plasma insulin concentration (\(I\)), effect of insulin on glucose distribution/transport (\({x}_{1}\)), effect of insulin on glucose disposal (\({x}_{2}\)), and effect of insulin on endogenous glucose production (\({x}_{3}\)). The model parameters are described in Table 1.

Table 1 T1DM parameters
Full size table

The main goal, on the one hand, is to regulate BG in the safe level (\(70-180 \mathrm{mg}/\mathrm{dL}\)), while input disturbance could have impact on output. On the other hand, insulin infusion rate should be acceptable for diabetic patient’s body. So, in the closed-loop control system i.e., artificial pancreas, BG should be within the permissible rang even in the presence of disturbance via acceptable amount of insulin. In the system, input disturbance is the meal intake often eaten three different carbohydrates meal types over a day. Therefore, the system could be faced various types of carbohydrate such as \(\left[\begin{array}{ccc}50& 60& 55\end{array}\right]\mathrm{ g}\) meal disturbances at times \(\left[\begin{array}{ccc}7& 14& 20\end{array}\right]\mathrm{ h}\) [30].

\(\theta \) is the BG which is able to characterize nonlinear behavior. \({\uppsi }\), global operating space, is divided into two vital terms during a day: Hypoglycemia and Hyperglycemia. If BG level is less than \(70\mathrm{ mg}/\mathrm{dL}\), diabetic patient may become unconscious called Hypoglycemia. In contrast, dangerously high BG level (\(y > 180{\text{ mg}}/{\text{dL}}\)), which is called Hypoglycemia, could lead to a diabetic coma. So, in order to consider both Hypoglycemia and Hyperglycemia conditions, \(100 \le {\uppsi } \le 400 {\text{mg}}/{\text{dL}}\) is assumed and BG should be regulated on \(y_{d} = 100 {\text{mg}}/{\text{dL}}\). Since the input could able to inject acceptable rate of insulin, it is not reasonable to define \({{\uppsi < 100 }}\;{\text{mg/dL}}\).

Remark 7

External insulin injection is the only input to keep BG level in secure level.

According to operating points, \(N=6\) local linear models will be obtained by the dichotomy algorithm, all of which are not vital to maintain BG level in the allowed rang before and after 2 h of meals. The gap metric values between all pairs of the local linear models are calculated based on (3) \({\delta }_{\mathrm{max}}=0.4244\) and depicted in Fig. 2. In addition, the maximum stability margin (\({b}_{opt}=0.1849\)) is less than \({\delta }_{\mathrm{max}}\). Therefore, a single nominal linear model (\({N}_{s}=1\)) would not be enough to control T1DM properly. The proposed algorithm is implemented to get more insight to studied system.

Fig. 2
figure 2

Distance between HOLLMs of the T1DM system

Full size image

The results of implementing the algorithm are summarized in Table 2. As it is clearly shown, two RONLM are able to explain the nonlinearity of T1DM. \(P=2.1758\) in Lyapunov function is obtained via LMI problem in (16). Now the question is how to define multiple trajectories in T1DM so that MM could be reasonable. Constant desired and Glucose-Dependent Desired (GDD) trajectories (for more detail on desired trajectory see [31]) are very common to complete control design procedure. The GDD trajectory is considered to avoid hypoglycemia. In GDD trajectory, which could bring about less insulin injection, the dummy desired trajectory (\({y}_{dd}\)) is defined to be tracked by designed controller in the first step, and then BG is controlled in the secure range. The errors between BG and both \({y}_{d}\) and \({y}_{dd}\) are measurable. As soon as the error between BG and dummy desired trajectory (\(\begin{array}{c}{e}_{dd}(t)=y(t)-{y}_{dd}\end{array}\)) becomes more than the other one (\({e}_{d}(t)=y(t)-{y}_{d}\)), switching should be imposed.

Table 2 Results of proposed method on T1DM
Full size table

Remark 8

Constant desired and GDD trajectories are both used in the closed-loop control system of T1DM.

Remark 9

In GDD, error signal between BG and current trajectory is a decision maker to switch both the desired trajectory and the controller.

According to Remark 9, trajectories are defined for each proposed strategy as follow.

$$ y_{1d} \left( t \right) = 100 {\text{mg}}/{\text{dL}}\;{\text{and}}\;y_{2d} \left( t \right) = \left\{ {\begin{array}{*{20}l} {100{\text{ mg}}/{\text{dL}},} \hfill & {e_{dd} \left( t \right) > e_{d} \left( t \right)} \hfill \\ {300 {\text{mg}}/{\text{dL}},} \hfill & {e_{dd} \left( t \right) \le e_{d} \left( t \right)} \hfill \\ \end{array} } \right. $$
(28)

The initial values are considered \({Q}_{1}\left(0\right)=4.5 \mathrm{mmol}\), \({Q}_{2}\left(0\right)=2.5 \mathrm{mmol}\), \({S}_{1}\left(0\right)=0 \mathrm{mU}\), \({S}_{2}\left(0\right)=0 \mathrm{mU}\), \(I\left(0\right)=13 \mathrm{mU}/\mathrm{L}\), \({x}_{1}\left(0\right)=0 {\mathrm{min}}^{-1}\), \({x}_{2}\left(0\right)=0 {\mathrm{min}}^{-1}\), and \({x}_{3}\left(0\right)=0 {\mathrm{min}}^{-1}\). \({Q}_{1}\left(0\right)\) leads to Hyperglycemia (\(y\left(0\right)=500 \mathrm{mg}/\mathrm{dL}\)). So, at the outset of the closed-loop process, \(y\left(0\right)=500 \mathrm{mg}/\mathrm{dL}\), so \({e}_{dd}\left(0\right)<{e}_{d}(0)\). Therefore, \({y}_{dd}\) would be the reference until \({e}_{d}(t)<{e}_{dd}(t)\) when \({y}_{d}\) will be replaced by \({y}_{dd}\).

The proposed algorithm is implemented and the closed-loop response under LMI-based RMM controller is depicted in Fig. 3, where \(u\) and \({u}_{G}\) denote insulin infusion rate and meal disturbances during a day, respectively. \(y\) and \(u\) denote the BG per \(\mathrm{mg}/\mathrm{dL}\) and insulin infusion rate per \(\mathrm{U}/\mathrm{h}\), respectively. As it can be seen from the figure, during a day and night two controllers need to track the desired BG so that the hypoglycemia will not happen. To this goal, two levels of insulin are injected to diabetic patients to keep them safe from the probable danger. In the considered system, being at the safe level is the main goal. The controller must ensure that the patient’s BG levels are maintained to reduce the risk of hypoglycemia and hyperglycemia. As it is clear from the proposed method, not only the normal level is met, but also stability is achieved even during mealtime consumption.

Fig. 3
figure 3

Closed-loop response of the T1DM under the proposed approach

Full size image

6 Conclusion

In this paper, a closed-loop stability analysis of an RMM control algorithm is presented, which is based on LMI. High order nonlinear systems which are countered complexities in both order and nonlinearity are examined in this regard. The LMI-based RMM controller is designed for such systems so that the closed-loop stability will be guaranteed. In the proposed algorithm, firstly the model of system is simplified based on MM and OR methods and then controller is designed according to LMI approach. Two tools, gap metric and stability margin, benefit us in model selection procedure. This could provide local stability. In RMM control design algorithm, local controllers are adjusted to fulfill the closed-loop stability by solving an LMI problem. In order to examine the suggested method, type 1 diabetes mellitus is considered. One undeniable success is that the analysis of such complex system, control design and implementation will be easily performed.