Aeroelastic reliability and sensitivity analysis of a plate interacting with stochastic axial airflow

Abstract

The aeroelastic reliability and sensitivity of a simply supported isotropic plate interacting with upper axial airflow are investigated. Based on the assumed mode method and the linear potential flow theory, the equation of motion of the plate interacting with axial airflow is established using the Hamilton’s principle. The limit state function representing the aeroelastic failure mode is obtained from aerodynamic stability analysis of the plate. The mean value first order second moment method is adopted to analyze the aeroelastic reliability and sensitivity of the plate. The effects of the stochastic properties of the flow velocity, flow density, and the plate geometry dimensions on the aeroelastic reliability are analyzed. From the results, it can be seen that the aeroelastic reliability decreases with increasing velocity and mass density of the airflow. The flow mass density has more significant effects on the reliability sensitivity than the flow velocity. The reliability decreases with increasing length and width, and increases with increasing thickness of the plate. The standard deviation of the thickness of the plate has more significant effects on the aeroelastic reliability than the length and width. This study provides a new perspective on understanding the instability behaviors of the plate in airflow.

1 Introduction

The outer surface of the travelling aircraft, vehicles or high speed trains can be modeled as isotropic plates interacting with outside axial airflow. The influence of the axial airflow on the flat plates shows up as changing the mass, damping and stiffness coefficients of the plates. While the flow velocity increasing, the plate may exhibit instability of the divergence or flutter types [1]. Since 1950s, the stability of the plate interacting with axial flow has been investigated by many scholars [2,3,4,5,6]. Their investigations showed that with the flow velocity increasing, the plate with fixed boundary conditions exhibits instability of the divergence type and with the flow velocity increasing further, the plate may exhibit flutter type of instability. The critical divergence flow velocity is determined by the density and velocity of the airflow, the boundary conditions, the material properties and the geometry dimension of the plate.

For the dynamics of the plate interacting with axial flow, Tang and Dowell [7], and Tang and Païdoussis [8] researched the limit circle oscillations of a two-dimensional plate with cantilevered boundary conditions in subsonic airflow. From their studies, it can be seen that with the flow velocity increasing, the plate exhibits the flutter type of instability. The limit circle oscillation can be seen in their investigations.

In recent studies, Korbahti and Uzal [9] studied the stability of an anisotropic plate in subsonic airflow.They found that the flutter velocity increases when the fibers are placed along the flow direction. Tan et al. [10] investigated the stability of a two-dimensional panel with spring support in incompressible axial flow.Their investigation found that the addition of highly localised stiffening was a very effective means to postpone the instability of an otherwise homogeneous flexible panel. Kerboua et al. [11] and Yao and Li [12] studied the chaotic motion of a composite laminated plate in subsonic airflow. The effects of the flow velocity and amplitude of the external excitation on the chaotic motion of the plate were studied. Tubaldi and Amabili [13] studied the variation of the natural frequencies of the periodically supported plate interacting with flowing flow using the Rayleigh–Ritz method.

From the prevent investigations, it is known that the axial flowing fluid produces gyroscopic and centrifugal forces on the plate, which makes the plate lose stability of the divergence and flutter types [14, 15]. The divergence and flutter types of instabilities are necessary conditions for unstable nonlinear vibrations such as the chaotic motion and limit circle oscillation of the plate [16]. So we can define the divergence or flutter instability as a kind of “failure state” in reliability theory. In such case, the traditional stability analysis becomes the reliability analysis.

Reliability is defined as the probability of a structure or device will perform its intended function during a specified period of time under given conditions [17]. In fact, the uncertainties widely exist in fluid–structure systems such as the error during the manufacturing process of the structure and the randomness of the flowing fluid, which makes it uncertain of the structural stability. In order to guarantee the safety of the outer surface of the flying machines, the reliability of the plate interacting with outside airflow is worth of investigation. To our best knowledge, very few literatures have taken into account the uncertainties of the plate and the flowing airflow. This motivated us to carry out the present study.

In this paper,the uncertainties of a fluid–structure system are taken into account and the aeroelastic reliability and sensitivity of a plate interacting with potential axial airflow are investigated. The equation of motion of the plate interacting with axial airflow is established based on the Kirchhoff plate theory and linear potential flow theory. The limit state function is obtained from analyzing the stability of the plate and expanded by the Taylor series to the second approximation. The mean value first order second moment method (MVFOSM) is adopted to analyze the aeroelastic reliability and sensitivity of the plate. The effects of the statistic parameters of the stochastic parameters on the aeroelastic reliability of the system are discussed and some significant conclusions are drawn.

2 Structural modeling

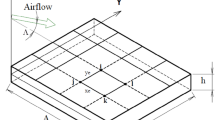
A plate interacting with axial airflow is shown in Fig. 1 The length, width and thickness of the plate are a, b and h. The $x{\hbox {Oy}}$ plane of the Cartesian coordinate locates at the middle surface of the plate. The displacements of the plate along x, y and z directions are u, v and w. According to the Kirchhoff plate theory, the membrane strain and bending curvature vectors are expressed as

$$\begin{aligned}&{\varvec{\upvarepsilon }}_0 =\left[ {\frac{\partial u}{\partial x},}\quad {\frac{\partial v}{\partial y},}\quad {\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}} \right] ^{\mathrm{T}}, \end{aligned}$$

(1)

$$\begin{aligned}&{\varvec{\upkappa }}=\left[ {-\frac{\partial ^{2}w}{\partial x^{2}},}\quad {-\frac{\partial ^{2}w}{\partial y^{2}},} \quad {-2} \frac{\partial ^{2}w}{\partial x\partial y}\right] ^{\mathrm{T}}, \end{aligned}$$

(2)

where ${\varvec{\upvarepsilon }}_{0}$ is the membrane strain vector and ${\varvec{\upkappa }}$ is the bending curvature vector.

Fig. 1

Configuration of a plate in axial airflow

The strain–displacement relations can be expressed as

$$\begin{aligned} {\varvec{\upvarepsilon }}=\left[ {\varepsilon _x,}\quad {\varepsilon _y,}\quad {\gamma _{xy}} \right] ^{\mathrm{T}}={\varvec{\upvarepsilon }}_0 +z{{\varvec{\upkappa }}}, \end{aligned}$$

(3)

where ${\varvec{\upvarepsilon }}$ is the strain vector and $\upvarepsilon _{x}$, $\upvarepsilon _{y}$ and ${\gamma }_{xy}$ are normal and shear strains.

The constitutive equation of the plate can written as

$$\begin{aligned} \sigma _x= & {} \frac{E}{1-\nu ^{2}}(\varepsilon _x +\nu \varepsilon _y ), \quad \sigma _y =\frac{E}{1-\nu ^{2}}(\varepsilon _y +\nu \varepsilon _x ),\nonumber \\ \tau _{xy}= & {} \frac{E}{2(1+\nu )}\gamma _{xy} , \end{aligned}$$

(4)

where $\sigma _{x,}\sigma _{y},\uptau _{xy}$,are the stress components, E is the elastic modulus and $\nu$ is Poisson’s ratio. The potential energy of the plate is expressed as

$$\begin{aligned} U=\frac{1}{2}\int _0^a {\int _0^b {\int _{-\frac{h}{2}}^{\frac{h}{2}} {(\sigma _x \varepsilon _x +\sigma _y \varepsilon _y +\tau _{xy} \gamma _{xy} ){\textit{dzdydx}}}}} , \end{aligned}$$

(5)

where U is the strain energy of the plate.

The kinetic energy can be written as

$$\begin{aligned} T=\frac{1}{2}\int _0^a {\int _0^b {\rho h(\dot{u}+\dot{v}+\dot{w}){\textit{dydx}}} } , \end{aligned}$$

(6)

where T is the kinetic energy, $\rho$ is the mass density of the plate and “$\cdot$” denotes derivation with respect to time.

The virtual work done by the perturbation aerodynamic pressure is expressed as

$$\begin{aligned} \delta W=\int _0^a \int _0^b \Delta p \delta {\textit{wdydx}}, \end{aligned}$$

(7)

where $\delta W$ is the virtual work and $\Delta p$ is the perturbation aerodynamic pressure.

The simply boundary conditions of the plate can be expressed as

$$\begin{aligned}&w=\frac{\partial ^{2}w}{\partial x^{2}}=0\,\,(x=0,x=a),\nonumber \\&w=\frac{\partial ^{2}w}{\partial y^{2}}=0\,\,(y=0,y=b). \end{aligned}$$

(8)

In the study, the displacements of the plate at x, y and z directions are expanded through the assumed mode method, which is a technique to discretize the vibration of a continua into a set ordinary different equations. Its limitation is the higher modes of the vibration are truncated. However, it has good convergence properties with the mode expansion number increasing. According to the displacement boundary conditions given in Eq. (8), the displacements are written as

$$\begin{aligned} u(x,y,t)= & {} \sum _{i=1}^M{\sum _{j=1}^N\cos \left( \frac{i\pi {\textit{x}}}{a}\right) \sin \left( \frac{j\pi {\textit{x}}}{b}\right) }p_{\textit{ij}}(t)\nonumber \\= & {} \mathbf{U}(x,y)^{\mathrm{T}}{} \mathbf{p}(t),\nonumber \\ v(x,y,t)= & {} \sum _{i=1}^M{\sum _{j=1}^N\sin \left( \frac{i\pi {\textit{x}}}{a}\right) \cos \left( \frac{j\pi x}{b}\right) }s_{\textit{ij}}(t)\nonumber \\= & {} \mathbf{V}(x,y)^{\mathrm{T}}{} \mathbf{s}(t),\nonumber \\ w(x,y,t)= & {} \sum _{i=1}^M \sum _{j=1}^N \sin \left( \frac{i\pi {\textit{x}}}{a}\right) \sin \left( \frac{j\pi {\textit{x}}}{b}\right) q_{\textit{ij}}(t)\nonumber \\= & {} \mathbf{W}(x,y)^{\mathrm{T}}{} \mathbf{q}(t), \end{aligned}$$

(9)

where M and N are mode expansion numbers, $\mathbf{U}(x, y), \mathbf{V}(x, y)$ and $\mathbf{W}(x, y)$ are mode shape functions satisfying the displacement boundary conditions, and $\mathbf{p}(t)$, $\mathbf{s}(t)$ and $\mathbf{q}(t)$ are generalized coordinates.

3 Aerodynamic force

The perturbation aerodynamic pressure is established through the linear potential flow theory. In this study, the axial airflow along the plate is incompressible, inviscid, and irrotational. So the flow field can be described by the following Laplace equation [1]

$$\begin{aligned} \frac{\partial ^{2}\phi }{\partial x^{2}}+\frac{\partial ^{2}\phi }{\partial y^{2}}+\frac{\partial ^{2}\phi }{\partial z^{2}}=0, \end{aligned}$$

(10)

where $\phi$ is the perturbation velocity potential function. The perturbation aerodynamic pressure can be expressed by the following linear Bernoulli equation

$$\begin{aligned} \Delta p=\left. {\rho _\infty \left( \frac{\partial \phi }{\partial t}+U_\infty \frac{\partial \phi }{\partial x}\right) } \right| _{z=\frac{h}{2}} , \end{aligned}$$

(11)

where $\rho _{\infty }$ is the mass density of the airflow. The motion of the plate and the axial airflow can be coupled by the following boundary condition

$$\begin{aligned} \left. {\frac{\partial \phi }{\partial z}} \right| _{z=\frac{h}{2}} =\left\{ {\begin{array}{ll}{l} \frac{\partial w}{\partial t}+U_\infty \frac{\partial w}{\partial x},&{}\quad \hbox {on the plate}, \\ 0, &{}\quad \hbox {off the plate}. \\ \end{array}}\right. \end{aligned}$$

(12)

The perturbation velocity potential function is associated with x, y, z and time t, In the present study, the perturbation velocity potential function is worked out by using a undetermined function method. The solution of Eq. (10) is described by the following expression

$$\begin{aligned} \phi (x,y,z,t)=\sum _{i=1}^M {\sum _{j=1}^N {\sin \left( \frac{i\pi x}{a}\right) \sin \left( \frac{j\pi x}{b}\right) \psi _{\textit{ij}} (z)} } f_{\textit{ij}} (t), \end{aligned}$$

(13)

where $\psi _{\textit{ij}}(z)$ and $f_{\textit{ij}}(t)$ are undetermined functions of variables z and t. Substituting Eq. (13) into Eq. (10) and eliminating $f_{\textit{ij}}(t)$, one can obtain the following linear differential equation about $\psi _{\textit{ij}}(z)$.

$$\begin{aligned} \frac{d^{2}\psi _{\textit{ij}} (z)}{dz^{2}}-\left( \frac{i^{2}\pi ^{2}}{a^{2}}+\frac{j^{2}\pi ^{2}}{b^{2}}\right) \psi _{\textit{ij}}(z)=0. \end{aligned}$$

(14)

Considering the finiteness of the velocity potential function when z $\rightarrow +\infty$ and $\phi =0$ at $z = 0$, the solution of Eq. (14) is chosen as

$$\begin{aligned} \psi _{\textit{ij}} (z)=\exp \left( -\sqrt{\frac{i^{2}\pi ^{2}}{a^{2}}+\frac{j^{2}\pi ^{2}}{b^{2}}}z\right) . \end{aligned}$$

(15)

Substituting Eq. (15) into Eq.(11), the perturbation aerodynamic pressure can be presented by

$$\begin{aligned} \Delta p= & {} \rho _\infty \sum _{i=1}^M \sum _{j=1}^N \left\{ \frac{\psi _{\textit{ij}} (h/2)}{{\psi }'_{\textit{ij}} (h/2)}\left[ W_{\textit{ij}} \ddot{q}_{\textit{ij}} (t)+2U_\infty \frac{\partial W_{\textit{ij}} }{\partial x}\dot{q}_{\textit{ij}} (t)\right. \right. \nonumber \\&\left. \left. +\,U_\infty ^2 \frac{\partial ^{2}W_{\textit{ij}} }{\partial x^{2}}q_{\textit{ij}} (t)\right] \right\} , \end{aligned}$$

(16)

where $W_{\textit{ij}}$ is the $i\times j$th element of mode shape function $\mathbf{W}(x,y)$. Introducing the following substitutions

$$\begin{aligned} \tilde{W}_{\textit{ij}} (x,y)=\frac{-ab}{\pi \sqrt{i^{2}b^{2}+j^{2}a^{2}}}W_{\textit{ij}} (x,y), \end{aligned}$$

(17)

The perturbation aerodynamic force can be express as

$$\begin{aligned} \Delta p= & {} \rho _\infty \left[ {\tilde{{\mathbf{W}}}}^{\mathrm{T}}(x,y){\ddot{\mathbf{q}}}(t)+2U_\infty \frac{\partial { \tilde{\mathbf{W}}}^{\mathrm{T}}(x,y)}{\partial x}{\dot{\mathbf{q}}}(t)\right. \nonumber \\&\left. +\,U_\infty ^2 \frac{\partial ^{2}{\tilde{\mathbf{W}}}^{\mathrm{T}}(x,y)}{\partial x^{2}}{} \mathbf{q}(t)\right] . \end{aligned}$$

(18)

Equation (18) is the perturbation aerodynamic pressure of the plate in axial airflow. It can be seen in Eq. (18) that the pressure is consist of the inertia, gyroscopic and centrifugal forces to the plate. It should be noted that the perturbation aerodynamic pressure in Eq. (18) is available only for simply supported plate interacting with ideal flow.

4 Equation of motion and stability analysis

The equation of motion can be established through the Hamilton’s principle

$$\begin{aligned} \int _{t_1 }^{t_2 } {(\delta T-\delta U)} dt+\int _{t_1 }^{t_2 } {\delta Wdt} =0, \end{aligned}$$

(19)

where $\delta$ denotes the first variation and $t_{1}$ and $t_{2}$ are integration time limits.

Substituting Eq. (9) into Eqs. (5–7), the potential energy U, kinetic energy T and the virtual work $\delta \hbox {W}$ can be expressed as

$$\begin{aligned}&U=\mathbf{p}^{\mathrm{T}}{} \mathbf{K}_1 \mathbf{p}+\mathbf{s}^{\mathrm{T}}{} \mathbf{K}_2 \mathbf{s}+\mathbf{q}^{\mathrm{T}}{} \mathbf{K}_3 \mathbf{q}+\mathbf{p}^{\mathrm{T}}\mathbf{K}_4 \mathbf{s}, \end{aligned}$$

(20)

$$\begin{aligned}&T=\frac{1}{2}({\dot{\mathbf{p}}}^{\mathrm{T}}{} \mathbf{M}_1 {\dot{\mathbf{p}}}+{ \dot{\mathbf{s}}}^{\mathrm{T}}{} \mathbf{M}_2 {\dot{\mathbf{s}}}+{\dot{\mathbf{q}}}^{\mathrm{T}}{} \mathbf{M}_3 { \dot{\mathbf{q}}}), \end{aligned}$$

(21)

$$\begin{aligned}&\delta W=({ \ddot{\mathbf{q}}}^{\mathrm{T}}{} \mathbf{M}_f +{ \dot{\mathbf{q}}}^{\mathrm{T}}{} \mathbf{C}_f +\mathbf{q}^{\mathrm{T}}{} \mathbf{K}_f )\mathrm {\delta }{} \mathbf{q}, \end{aligned}$$

(22)

where the matrixes $\mathbf{K}_{1}, \mathbf{K}_{2}, \mathbf{K}_{3}$, $\mathbf{K}_{4}$, $\mathbf{M}_{1}$, $\mathbf{M}_{2}$, $\mathbf{M}_{3}$, $\mathbf{M}_{f}$, $\mathbf{C}_{f}$ and $\mathbf{K}_{f}$ are listed in the “Appendix”. Substituting Eqs. (20–22) into Eq. (19) and performing the variation operation in terms of the generalized coordinates $\mathbf{p}, \mathbf{s}$, and $\mathbf{q}$, one can obtain the following equation of motion of the fluid–structure system

$$\begin{aligned}&{} \mathbf{M}_1^\mathrm{T}{\ddot{\mathbf{p}}}+\left( \mathbf{K}_1 +\mathbf{K}_1^\mathrm{T}\right) \mathbf{p}+\mathbf{K}_4 \mathbf{s}=\mathbf{0},\nonumber \\&{} \mathbf{M}_2^\mathrm{T} {\ddot{\mathbf{s}}}+\left( \mathbf{K}_2 +\mathbf{K}_2^\mathrm{T}\right) \mathbf{s}+\mathbf{K}_4^\mathrm{T} \mathbf{p}=\mathbf{0},\nonumber \\&(\mathbf{M}_3^\mathrm{T} -\mathbf{M}_f^\mathrm{T} ){\ddot{\mathbf{q}}}-\mathbf{C}_f^\mathrm{T} {\dot{\mathbf{q}}}+\left( \mathbf{K}_3 +\mathbf{K}_3^\mathrm{T} -\mathbf{K}_f^\mathrm{T}\right) \mathbf{q}=\mathbf{0}. \end{aligned}$$

(23)

Introducing $\mathbf{M}, \mathbf{C}, \mathbf{K}$ and ${\varvec{\xi }}$ as follows

$$\begin{aligned} \mathbf{M}= & {} \left[ {{\begin{array}{cccc} {\mathbf{M}_1^\mathrm{T} }&{}\quad \mathbf{0}&{}\quad \mathbf{0} \\ \mathbf{0}&{}\quad {\mathbf{M}_2^\mathrm{T} }&{}\quad \mathbf{0} \\ \mathbf{0}&{}\quad \mathbf{0}&{}\quad {\mathbf{M}_3^\mathrm{T} -\mathbf{M}_f^\mathrm{T} } \\ \end{array} }} \right] , \quad \mathbf{C}=\left[ {{\begin{array}{cccc} \mathbf{0}&{}\quad \mathbf{0}&{}\quad \mathbf{0} \\ \mathbf{0}&{}\quad \mathbf{0}&{}\quad \mathbf{0} \\ \mathbf{0}&{}\quad \mathbf{0}&{}\quad {-\mathbf{C}_f^\mathrm{T} } \end{array} }} \right] ,\nonumber \\ \mathbf{K}= & {} \left[ {{\begin{array}{cccc} {\mathbf{K}_1 +\mathbf{K}_1^\mathrm{T} }&{}\quad {\mathbf{K}_4 }&{}\quad \mathbf{0} \\ {\mathbf{K}_4^\mathrm{T} }&{}\quad {\mathbf{K}_2 +\mathbf{K}_2^\mathrm{T} }&{}\quad \mathbf{0} \\ \mathbf{0}&{}\quad \mathbf{0}&{}\quad {\mathbf{K}_3 +\mathbf{K}_3^\mathrm{T} -\mathbf{K}_f^\mathrm{T} } \\ \end{array} }} \right] ,\nonumber \\ {{\varvec{\xi }} }= & {} \left[ {\begin{array}{cccc} {\mathbf{p}^{\mathrm{T}}}&{\mathbf{s}^{\mathrm{T}}}&{\mathbf{q}^{\mathrm{T}}} \end{array}}\right] ^{\mathrm{T}}, \end{aligned}$$

(24)

Equation (23) is then transformed into

$$\begin{aligned} {\mathbf{M}\ddot{{\varvec{\xi }} }}+{\mathbf{C}\ddot{{\varvec{\xi }}}}+{\mathbf{K} {{\varvec{\xi }}}}=\mathbf{0}. \end{aligned}$$

(25)

Equation (25) is the equation of motion of the plate under axial airflow. It relates the transverse deflection with the velocity and mass density of the flowing fluid. From the definition of the matrices in Eq. (24), it can be seen that the airflow affects the mass, damping and stiffness matrices. By analyzing the stability of this equation, the critical divergence flow velocity of the plate can be obtained.

It is well known that when the plate is in divergence type instability, the non-zero points of equilibrium exist in the equilibrium equation of Eq. (25). By substituting ${\ddot{{\varvec{\xi }} }}=\mathbf{0}$ and ${\dot{{\varvec{\xi }}}}=0$ into Eq. (25), one can obtain the linear algebra equation for the points of equilibrium

$$\begin{aligned} {\mathbf{K}{\varvec{\xi }} }=\mathbf{0}. \end{aligned}$$

(26)

The sufficient and necessary condition for $\mathbf{\xi }\ne \mathbf{0}$ is $\hbox {det}(\mathbf{K}) = 0$. So the critical instability flow velocity can be defined as

$$\begin{aligned} U_d =\min \{\left. {U_\infty } \right| \det (\mathbf{K})=0\}. \end{aligned}$$

(27)

In this study, the displacements of the plate are expanded to the first four modes, i.e. $M=2$ and $N=2$. From Eq. (27), one can obtain the critical divergence flow velocity

$$\begin{aligned} U_d =\pi ^{\frac{1}{2}}\sqrt{\frac{Eh^{3}(a^{2}+b^{2})^{\frac{5}{2}}}{12\rho _f a^{3}b^{5}(1-\nu ^{2})}}. \end{aligned}$$

(28)

By expanding b to be infinite, we can obtain the divergence flow velocity of a two-dimensional plate.

$$\begin{aligned} U_d^*= & {} \mathop {\lim }\limits _{b\rightarrow +\infty } \pi ^{\frac{1}{2}}\sqrt{\frac{Eh^{3}(a^{2}+b^{2})^{\frac{5}{2}}}{12\rho _f a^{3}b^{5}(1-\nu ^{2})}}\nonumber \\= & {} \pi ^{\frac{1}{2}}\sqrt{\frac{Eh^{3}}{12\rho _f a^{3}(1-\nu ^{2})}}, \end{aligned}$$

(29)

where $U_d^*$ denotes the divergence flow velocity of a two-dimensional plate with simply supported boundary conditions. The result shown in Eq. (29) is in agreement with the critical divergence flow velocity given in Ref. [3], which proves the validity of the present study.

5 Reliability and sensitivity analysis of the plate

The reliability of a stochastic structural system is defined as

$$\begin{aligned} {{\varvec{R}}}=\hbox {P}[\hbox {g}(\mathbf{X})>0]=\int \limits _{\mathbf{g}(\mathbf{X})>0} {\hbox {f}(\mathbf{X})d\mathbf{X}} , \end{aligned}$$

(30)

where $\mathbf{X }= [X_{1}, X_{2},{\ldots },X_{n}]^\mathrm{T}$ is the stochastic parameter vector of the system, $X_{1}$, $X_{2},{\ldots }, X_{n}$ are independent random variables, R is the reliability of the system defined as the probability of $\hbox {g}(\mathbf{X}) > 0, \hbox {f}(\mathbf{X})$ is the probability density function, and $\hbox {g}(\mathbf{X})$ is the state function representing different states of the system

$$\begin{aligned} \left\{ {\begin{array}{lll} \hbox {g}(\mathbf{X})<0&{}\quad \hbox { failure state,} \\ \hbox {g}(\mathbf{X})=0&{}\quad \hbox { threshold state,} \\ \hbox {g}(\mathbf{X})>0&{}\quad \hbox { safe state.} \\ \end{array}}\right. \end{aligned}$$

(31)

In this study, the system parameters follow the normal distribution, i.e. $X_k \sim N(\mu _k ,\sigma _k^2 )(k = 1, 2, {\ldots },n)$. The mean value vector and covariance matrix are expressed as

$$\begin{aligned}&E(\mathbf{X})={\bar{\mathbf{X}}}=({\begin{array}{cccc} {\mu _1 }&{\mu _2 }&\ldots&{\mu _n } \end{array} })^{\mathrm{T}},\nonumber \\&\hbox {cov}(\mathbf{X})=\hbox {diag(}{\begin{array}{cccc} {\sigma _1^2 }&{} {\sigma _2^2 }&{} \ldots &{} {\sigma _n^2 } \\ \end{array} }\hbox {)}. \end{aligned}$$

(32)

In this study, the reliability and sensitivity of the plate interacting with axial airflow are presented using the mean value first order second moment method (MVFOSM) [18,19,20], which is based on and more accurate than the traditional first-order reliability method (FORM) [21,22,23] for nonlinear state functions.

Expanding g(X) to the second-order approximation Taylor series yields

$$\begin{aligned} \hbox {g}(\mathbf{X})= & {} \hbox {g}({\overline{\mathbf{X}}})+[\nabla \hbox {g}({ \overline{\mathbf{X}}})]^{\mathrm{T}}[\mathbf{X}-{\overline{\mathbf{X}}}]\nonumber \\&\quad +\,\frac{1}{2}[\mathbf{X}-{\overline{\mathbf{X}}}]^{\mathrm{T}}[\nabla ^{2}\hbox {g}({\overline{\mathbf{X}}})][\mathbf{X}-{\overline{\mathbf{X}}}] \end{aligned}$$

(33)

where $\nabla \hbox {g}({\overline{\mathbf{X}}})$ and $\nabla ^{2}\hbox {g}({ \overline{\mathbf{X}}})$ are the gradient and Hessian matrix of g(X) at ${\overline{\mathbf{X}}}$. From Eq. (33), it is possible to obtain the mathematical expectation and variance of g(X) as

$$\begin{aligned} \mu _\mathrm{g}= & {} \hbox {E}[\hbox {g}(\mathbf{X})]=\hbox {g}(\mathbf{\overline{{X}}})+\frac{1}{2}\sum _{k=1}^n {\sigma _k^2 } \frac{\partial ^{2}\hbox {g}(\mathbf{\overline{{X}}})}{\partial \mu _k^2 },\nonumber \\ \sigma _{\mathrm{g}}^2= & {} \hbox {E}[\hbox {g}(\mathbf{X})^{2}]-\mu _{g}^2\nonumber \\= & {} \sum _{k=1}^n {\left[ \frac{\partial \hbox {g}({\overline{\mathbf{X}}})}{\partial X_k }\right] ^{2}\sigma _k^2 } -\frac{1}{4}\left( \sum _{k=1}^n {\sigma _k^2 } \frac{\partial ^{2}\hbox {g}({\overline{\mathbf{X}}})}{\partial \mu _k^2 }\right) ^{2}\nonumber \\&+ \frac{1}{4}\sum _{r=1}^n \sum _{s=1}^n \sum _{z=1}^n \sum _{l=1}^n \frac{\partial ^{2}\hbox {g}({ \overline{\mathbf{X}}})}{\partial \mu _r \partial \mu _s } \frac{\partial ^{2}\hbox {g}({\overline{\mathbf{X}}})}{\partial \mu _z \partial \mu _l}\nonumber \\&\hbox {E}[(X_r -\mu _r )(X_s -\mu _s )(X_z -\mu _z )(X_l -\mu _l )], \end{aligned}$$

(34)

where $\mu _\mathrm{g}$ and $\sigma _{\mathrm{g}}^2$ are the mean value and variation of g(X) with second-order approximation.

The reliability index is defined as

$$\begin{aligned} \beta =\frac{\mu _\mathrm{g}}{\sigma _\mathrm{g}}. \end{aligned}$$

(35)

Generally, the state function g(X) is a complicated function of the parameter vector X. For most cases, the exact distribution of g(X) is impossible to work out. According to the central limit theorem, g(X) approximately follows the normal distribution. Thus the reliability of the system can be written as

$$\begin{aligned} R=\hbox {P}[\hbox {g}(\mathbf{X})>0]=\text {P}\left[ \frac{\text {g}(\mathbf{X})-\mu _{\mathrm{g}} }{\sigma _{\mathrm{g}} }>-\beta \right] =\Phi (\beta ), \end{aligned}$$

(36)

where ${\Phi }$ denotes the distribution function of the standard normal distribution.

The sensitivity of the reliability with respect to the mean value and the variance of the stochastic parameter variables can be expressed as

$$\begin{aligned}&\frac{\partial R}{\partial \mu _k }=\frac{1}{\sqrt{2\pi }} e^-\frac{\beta ^2}{2} \left( \frac{1}{\sigma _{\mathrm{g}}} \frac{\partial \mu _\mathrm{g}}{\partial \mu _k}-\frac{\mu _\mathrm{g}}{\sigma _{\mathrm{g}}^2} \frac{\partial \sigma _{\mathrm{g}}}{\partial \mu _k}\right) ,\nonumber \\&\frac{\partial R}{\partial \sigma _k }=\frac{1}{\sqrt{2\pi }}e^{-\frac{\beta ^{2}}{2}}\left( \frac{1}{\sigma _{\mathrm{g}}}\frac{\partial \mu _{\mathrm{g}}}{\partial \sigma _k}-\frac{\mu _{\mathrm{g}} }{\sigma _{\mathrm{g}}^2}\frac{\partial \sigma _{\mathrm{g}} }{\partial \sigma _k }\right) . \end{aligned}$$

(37)

Equations (36) and (37) are the reliability and sensitivity formulations of the stochastic system with second-order approximation. From these analytical expressions, the effects of the statistical characters of different stochastic parameters on the reliability of the system can be analyzed.

In this paper, the stochastic parameter vector is chosen as $\mathbf{X}=[{\begin{array}{cccccc} a&{}b&{}h&{}{\rho _\infty }&{} {U_\infty } \\ \end{array} }]^{\mathrm{{T}}}$. The plate is stable while $U_{d }> U_{\infty }$. Thus the state function is defined as

$$\begin{aligned} g(\mathbf{X})=\pi ^{\frac{3}{2}}\sqrt{\frac{Eh^{3}(a^{2}+b^{2})^{\frac{5}{2}}}{12\rho _f a^{3}b^{5}(1-\mu ^{2})}}-U_\infty . \end{aligned}$$

(38)

Substituting Eq. (38) to the procedure from Eqs. (33) to (37), the reliability and sensitivity of the plate can be analyzed.

Fig. 2

Variations of the first four natural frequencies with respect to the flow velocity ($a = 0.8$ m, $b = 1.5$ m, $h = 0.002$ m, $\rho _f = 1.29\,\text {kg}/\text {m}, E = 200\,\text {Gpa})$

6 Numerical simulations and discussions

A plate interacting with axial airflow on the upper surface as shown in Fig. 1 is taken into consideration. The material parameters of the plate are $E = 200$ GPa, $\nu = 0.3$ and $\rho = 7850$ kg/m$^{3}$. The geometry dimension of the plate, the flow velocity and the flow mass density are stochastic variables following the normal distributions. The mean values of these parameters are $\mu _{a} = 0.8\,\text {m}, \mu _{b} = 1.5\,\text {m}, \mu _{h} = 0.002\,\hbox {m}$, $\mu _{\rho } = 1.29$ kg/m$^{3}$ and $\mu _{f} = 114$ m/s, where $\mu _{a}$, $\mu _{b}$, $\mu _{h}$, $\mu _{\rho }$ and $\mu _{f}$ are mean values of a, b, h, $\rho _{\infty }$ and $U_{\infty }$. The standard deviations of these parameters are expressed as $\sigma _{a}=C_{a}\times \mu _{a}$, $\sigma _{b}=C_{b}\times \mu _{b}$, $\sigma _{h}=C_{h}\times \mu _{h}$, $\sigma _{\rho }=C_{\rho }\times \mu _{\rho }$, and $\sigma _{f}=C_{f}\times \mu _{f}$, where $\sigma _{a}$, $\sigma _{b}$, $\sigma _{h}$, $\sigma _{\rho }$ and $\sigma _{f}$ are standard deviations of a, b, h, $\rho _{\infty }$ and $U_{\infty }$, and $C_{a}$, $C_{b}$, $C_{h}$, $C_{\rho }$ and $C_{f}$ are the deviation coefficients.

Fig. 3

Displacement–time responses of the plate when $\hbox {U}_\infty = 110$ m/s and $\hbox {U}_\infty = 120$ m/s

Fig. 4

The reliability and sensitivity of the system with respect to flow velocity

Fig. 5

The reliability and sensitivity of the system with respect to the mass density of the airflow

Figure 2 shows the dynamic properties of the plate with increasing flow velocity. It can be seen in Fig. 2 that with the flow velocity increasing, the first four natural frequencies of the plate decrease. When the flow velocity increases to 113.4 m/s, the fundamental natural frequency of the plate decreases to 0, which imply that the fundamental vibration of the plate disappears and the plate is in a unstable divergence state. The critical divergence flow velocity is also can be calculated by using Eq. (28). The critical divergence flow velocity obtained from Eq. (28) and from Fig. 2 are in good agreement, which proves the correctness of Eq. (28). From Fig. 2, the dynamic properties of the plate before and after the divergence instability are clearly understood.

Figure 3 shows the displacement–time response of the plate for stable state when $\hbox {U}_{\infty }= 110$ m/s and for unstable state when $\hbox {U}_\infty = 120$ m/s. In the simulation, the external excitation is a transient impulse of 1N lasting for 0.001 second. The actuating point is located at $(\hbox {a}/3, \hbox {b}/3)$ on the plate. It can be seen in Fig. 3 that when the plate is in stable state, the amplitude of the forced vibration is $1\times 10^{-4}$m and the point of equilibrium of the vibration is $w = 0$. When the plate is in divergence state, the vibration amplitude is 1$\times 10^{-3}\hbox {m}$ and $w = 0$ is no longer the equilibrium point of the vibration. Figure 3 gives a direct expression for the stable and unstable states of the plate.

Figure 4 shows the effects of the mean value of the flow velocity on the reliability of the plate. In the simulation, the deviation coefficients are chosen as $C_{a }=C_{b}=C_{h}=C_{\rho }=C_{f}= 0.005$ and $\mu _{f}$ is set as stochastic variable. From Fig. 4a, it can be seen that with $\mu _{f}$ increasing from 112 m/s, the reliability of the system decreases from 1. When $\mu _{f} > 116.5$ m/s, the reliability decreases to 0, which indicates that the plate is in divergence type of instability. Fig. 3b represents the sensitivity of the reliability with respect to $\mu _{f}$. From Fig. 4b, it can be seen that the sensitivity is negative when $112\,\text {m}/\text {s}<\mu _{f} < 116.5$ m/s and the minimum of the sensitivity is obtained when $\mu _{f}$ = 114.2 m/s. It also can be concluded from Fig. 4 that the critical divergence flow velocity is between 112 and 116.5 m/s.

Figure 5 shows the variations of the reliability and sensitivity of the system with respect to the mean value of the flow mass density. In the simulation, the mean value of the flow mass continuously changes from 1.25 to 1.35 kg/m$^{3}$. From Fig. 5, it can be seen that the reliability decreases with increasing $\mu _{\rho }$. It also can be seen in Figs. 4 and 5 that the reliability is more sensitive to $\mu _{\rho }$ than $\mu _{f}$.

In order to analyze the effects of the geometry dimension of the plate on the reliability, the mean values of the length, width and thickness of the plate are separately set as variables. Figure 6 shows the reliability and sensitivity with respect to the mean values of the geometry dimension. From Fig. 6, it can be seen that the reliability decreases with $\mu _{a}$ and $\mu _{b}$ increasing, and increases with $\mu _{h}$ increasing, which indicates that the plate with shorter length, more narrow width and higher thickness is more stable in axial airflow. It also can be seen in Fig. 6 that the sensitivity of the reliability with respect to $\mu _{a}$ and $\mu _{b}$ are in the same order of magnitude, and the maximum of the sensitivity with respect to $\mu _{h}$ is about $4.5\times 10^{4}$, which indicates that the stability of the plate is quite sensitive to the thickness of the plate.

Fig. 6

The reliability and sensitivity of the system with respect to the geometric dimensions of the plate

Figure 7 shows the derivatives of the reliability with respect to $\sigma _{a}$, $\sigma _{b}$, and $\sigma _{h}$ for different deviation coefficients. From Fig. 1 configuration of a plate in axial airflow. From Fig. 7, it can be seen that the reliability of the system is more sensitive to $\sigma _{h}$ than $\sigma _{a}$ and $\sigma _{b}$. This reminds us the deviation of the thickness of the plate should be strictly restricted while designing the outer surfaces of the traveling machines.

Fig. 7

Sensitivity of the system reliability with respect to deviation standards of the geometric dimensions for different deviation coefficients

7 Conclusions

In this paper, the reliability and sensitivity of an isotropic plate interacting with axial airflow is conducted. The limit state function is obtained by analyzing the stability of the plate and expanded by the Taylor series to the second order approximation. The reliability and sensitivity of the plate are obtained using the mean value first order second moment method (MVFOSM). From the analysis and numerical simulation, the following conclusions can be drawn

• 1. With the velocity and the mass density of the axial airflow increasing, the reliability of the plate decreases. The mean value of the flow mass density has greater impact on the reliability sensitivity of the plate than the flow velocity.

• 2. With the mean values of the length and width of the plate increasing, the reliability decreases. The reliability of the system increases with increasing plate thickness. The reliability sensitivity is more sensitive to the thickness than the length and width of the plate.

• 3. The reliability sensitivity of the plate is more dependent on the standard deviation of the thickness than the length and width of the plate, which reminds us while designing the aeroelasitic system like the outer surface of a flying machine, the thickness deviation of the plate should be strictly limited.

This study can be helpful for the stability and reliability analysis of the plate interacting with axial airflow.

Appendix

$$\begin{aligned} \mathbf{K}_1= & {} \int _0^b {\int _0^a {\frac{Eh}{2(1-\nu ^{2})}\frac{\partial \mathbf{U}}{\partial x}\frac{\partial \mathbf{U}^{\mathrm{T}}}{\partial x}+\frac{Eh}{4(1+\nu )}\frac{\partial \mathbf{U}}{\partial y}\frac{\partial \mathbf{U}^{\mathrm{T}}}{\partial y}dxdy} }\end{aligned}$$

(A-1)

$$\begin{aligned} \mathbf{K}_2= & {} \int _0^b {\int _0^a {\frac{Eh}{2(1-\nu ^{2})}\frac{\partial \mathbf{V}}{\partial y}\frac{\partial \mathbf{V}^{\hbox {T}}}{\partial y}+\frac{Eh}{4(1+\nu )}\frac{\partial \mathbf{V}}{\partial x}\frac{\partial \mathbf{V}^{\mathrm{T}}}{\partial x}dxdy} }\end{aligned}$$

(A-2)

$$\begin{aligned} \mathbf{K}_3= & {} \int _0^b \int _0^a \frac{Eh^{3}}{12(1-\nu ^{2})}\left[ \nu \frac{\partial ^{2}{} \mathbf{W}}{\partial x^{2}}\frac{\partial ^{2}\mathbf{W}^{\mathrm{T}}}{\partial y^{2}}+\frac{1}{2}\left( \frac{\partial ^{2}\mathbf{W}}{\partial x^{2}}\frac{\partial ^{2}{} \mathbf{W}^{\mathrm{T}}}{\partial x^{2}}\right. \right. \nonumber \\&\left. +\frac{\partial ^{2}{} \mathbf{W}}{\partial y^{2}}\frac{\partial ^{2}{} \mathbf{W}^\mathrm{T}}{\partial y^{2}}\right) +\left( 1-\nu \right) \frac{\partial ^{2}{} \mathbf{W}}{\partial x\partial y}\left. \frac{\partial ^{2}{} \mathbf{W}^{\mathrm{T}}}{\partial x\partial y}\right] dxdy\end{aligned}$$

(A-3)

$$\begin{aligned} \mathbf{K}_4= & {} \int _0^b {\int _0^a {\frac{\nu Eh}{(1-\nu ^{2})}\frac{\partial \mathbf{U}}{\partial x}\frac{\partial \mathbf{V}^{\mathrm{T}}}{\partial y}+\frac{Eh}{2(1+\nu )}\frac{\partial \mathbf{V}}{\partial x}\frac{\partial \mathbf{U}^{\mathrm{T}}}{\partial y}dxdy} }\end{aligned}$$

(A-4)

$$\begin{aligned} \mathbf{M}_1= & {} \int _0^b {\int _0^a {\rho h\mathbf{UU}^{\mathrm{T}}dxdy} } , \quad \mathbf{M}_2 =\int _0^b {\int _0^a {\rho h\mathbf{VV}^{\mathrm{T}}dxdy} } , \nonumber \\ \mathbf{M}_3= & {} \int _0^b {\int _0^a {\rho h\mathbf{WW}^{\mathrm{T}}dxdy}}\end{aligned}$$

(A-5)

$$\begin{aligned} \mathbf{M}_f= & {} \int _0^b {\int _0^a {\rho _\infty {\tilde{\mathbf{W}}{} \mathbf{W}}^{\mathrm{T}}dxdy} } ,\end{aligned}$$

(A-6)

$$\begin{aligned} \mathbf{C}_f= & {} \int _0^b {\int _0^a {2\rho _\infty U_\infty \frac{\partial {\tilde{\mathbf{W}}}}{\partial x}{} \mathbf{W}^{\mathrm{T}}dxdy} } ,\end{aligned}$$

(A-7)

$$\begin{aligned} \mathbf{K}_f= & {} \int _0^b {\int _0^a {\rho _\infty U_\infty ^2 \frac{\partial ^{2}{\tilde{\mathbf{W}}}}{\partial x^{2}}\mathbf{W}^{\mathrm{T}}dxdy} } \end{aligned}$$

(A-8)