1 Introduction

Aeroelasticity is an essential topic for scientists and engineers working especially in aerospace and aeronautics engineering applications. Studying the loss of stability of thin walled structures interacting with an airflow improves the reliability of design in many engineering applications. The prediction of stability bounds of fluid–structure systems is crucial for the safety requirements. Flutter is a self-excited oscillation of elastic structure when exposed to airflow. In the practical sense, flutter means an oscillation which grows and finally either breaks the structure or remains bounded at some amplitude whose value is dependent upon the departure from linear laws [1]. Flutter is dangerous and must be taken into account to avoid disasters. There have been many incidents reported in the literature like the German V-2 rocket of World War II, the X-15 and the Saturn launch vehicle of the Apollo program which were failures and are due to flutter of their panels [2]. Considerable efforts have been devoted to comprehend flutter behaviors of plates and shells under supersonic airflow. According to Singha and Ganapathi [3], it was Jordan in 1956 who was the first to identify such problem in his work on the physical nature on panel flutter. To avoid aeroelastic instability, the technique of active flutter suppression has drawn much attention. Extensive research and development efforts have been dedicated to the challenge of active flutter suppression (AFS). Among the studies in this field, those were published by Huang, Hu [4,5,6].

The flutter analysis of plates and shells with different boundary conditions using different aerodynamic theories has been studied extensively by experimental, analytical and numerical approaches. In 1967, Olson [7] applied finite elements to panel flutter where the panel is reduced to a wide beam. To include the aerodynamic forces, he extended the analysis of Leckie and Lindberg [8]. Later, in 1970 Olson [9] employed two rectangular and one triangular plate bending elements to simulate supersonic flutter problems. Sander, Bon [10] followed a finite element method for the analysis of supersonic panel flutter, and it consists in representing the nonstationary aerodynamic forces also by finite elements. The resulting advantage is an increased flexibility and generality in the structural configurations that can be treated. Rossettos and Tong [11] proposed a hybrid stress finite element method to study the flutter of cantilever anisotropic plates. Srinivasan and Babu [12] published a finite element flutter analysis of cantilevered plates. Linear plate theory has been used for computing the strain energy and kinetic energy of the plate, and piston theory [13] has been used to describe the aerodynamic pressure distribution. A review of the finite element method applied to the problem of supersonic aeroelastic stability of plates and shells is presented by Bismarck-Nasr [14]. For the study of supersonic flutter behavior of laminated composite skew flat plates, Singha and Ganapathi [3] used a shear deformable finite element approach.

For predicting the supersonic flutter of circular cylindrical shells, Sabri and Lakis [15] proposed a combination of Sander’s thin shell theory and the classic finite element method, in which the nodal displacements are found from the exact solution of shell governing equations rather than approximated by polynomial functions. The authors concluded that reliable results could be obtained at less computational cost compared to commercial FEM software and analytical methods. Following the same procedure, Sabri and Lakis [16] published a hybrid finite element method applied to supersonic flutter of an empty or partially liquid-filled truncated conical shell. Using the combination of Sanders’ shell theory and the standard finite element method, the problems that have been studied by the same team are: effects of sloshing on flutter prediction of partially liquid-filled circular cylindrical shell [17]. Hydroelastic vibration of partially liquid-filled circular cylindrical shells under combined internal pressure and axial compression [18]. Flutter prediction of functionally graded cylindrical shells [19]. This hybrid method was tested and validated also for the flutter analysis of spherical shells [20, 21].

For thin elastic isotropic rectangular plates, a method for the dynamic analysis was proposed by Charbonneau and Lakis [22]. The method is a hybrid of finite element and classical thin plate theory. The displacement functions are derived from Sanders' thin-shell equations and are expanded in power series. Based on this approach Kerboua, Lakis [23] explored the effect of various geometrical parameters and boundary conditions on the dynamic response of rectangular plates. Kerboua, Lakis [24] investigated the natural frequencies of rectangular plates completely submerged in water or floating on its free surface. The hybrid approach has been adopted by Kerboua, Lakis [25] for modeling of plates subjected to flowing fluid under various boundary conditions. In 2021, we presented a finite element model for vibration analysis of square plates coupled with a supersonic airflow [26]. The study of the aeroelastic behavior about rectangular flat plates under regular boundary conditions has received considerable attention in the literature. However, to the best of authors’ knowledge, the investigation of the flutter behavior in case of irregular boundary conditions has not been yet accomplished. Irregular boundary conditions occur after the accidental failure of one or more supports. In these catastrophic cases, it is important to predict the evolution of the stability bounds of such configurations.

This study presents a finite element approach for flutter analysis of rectangular flat plates in supersonic airflow with an arbitrary flow direction. The main objective of this work is to extend a hybrid of classical finite element method and Sanders’ shell theory to study the aeroelastic instabilities in a Cartesian coordinate system. The supersonic airflow is predicted using the first-order piston theory. The other main contribution of this work is the investigation of aeroelastic bounds in the case of irregular boundary conditions. The formulation developed herein is validated with other published research works. A parametric study has been carried out to highlight the effect of aspect ratios, flow direction and various boundary conditions on the aeroelastic behavior of rectangular flat plates.

2 Mathematical modeling

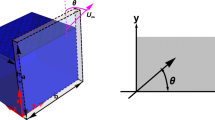
The geometry of a rectangular plate subjected to supersonic airflow is shown in Fig. 1. The length, width and thickness of the plate are A, B and h. The finite element considered in this study is a rectangular element with four nodes and six degrees of freedom at each node. The panel is subjected to a parallel supersonic airflow making an angle Λ with the x-axis.

Fig. 1
figure 1

A rectangular plate under supersonic airflow

Full size image

2.1 Structure modeling

The plate is assumed to be thin, homogeneous and isotropic. For modeling the plate, we used the hybrid combination of the finite element method and Sanders’ shell theory proposed by Kerboua, Lakis [23]. The in-plane membrane displacement components are presented in terms of bidimensional polynomials and the bending displacement component by a function that represents a general form of the exact solution of the equations of motion [22]. Hence, the displacement field may be defined as follows:

$$ U(x,y,t) = C_{1} + C_{2} \frac{x}{A} + C_{3} \frac{y}{B} + C_{4} \frac{xy}{{AB}} $$
(1)
$$ V(x,y,t) = C_{5} + C_{6} \frac{x}{A} + C_{7} \frac{y}{B} + C_{8} \frac{xy}{{AB}} $$
(2)
$$ \begin{aligned} W(x,y,t) & = C_{9} + C_{{10}} \frac{x}{A} + C_{{11}} \frac{y}{B} + C_{{12}} \frac{{x^{2} }}{{2A^{2} }} + C_{{13}} \frac{{xy}}{{AB}} \\ & + C_{{14}} \frac{{y^{2} }}{{2B^{2} }} + C_{{15}} \frac{{x^{3} }}{{6A^{3} }} + C_{{16}} \frac{{x^{2} y}}{{2A^{2} B}} + C_{{17}} \frac{{xy^{2} }}{{2AB^{2} }} \\ & + C_{{18}} \frac{{y^{3} }}{{6B^{3} }} + C_{{19}} \frac{{x^{3} y}}{{6A^{3} B}} + C_{{20}} \frac{{x^{2} y^{2} }}{{4A^{2} B^{2} }} + C_{{21}} \frac{{xy^{3} }}{{6AB^{3} }} \\ & + C_{{22}} \frac{{x^{3} y^{2} }}{{12A^{3} B^{2} }} + C_{{23}} \frac{{x^{2} y^{3} }}{{12A^{2} B^{3} }} + C_{{24}} \frac{{x^{3} y^{3} }}{{36A^{3} B^{3} }} \\ \end{aligned} $$
(3)

\(U\) and \(V\) represent the in-plane displacement components of the middle surface in \(X\) and \(Y\) directions. \(W\) is the transversal displacement of the middle surface. A and B are the plate dimensions, and \(C_{i}\) are unknown constants.

Using a matrix form, Eqs. 1, 2 and 3 can be written as follows:

$$ \left. {\left\{ \begin{gathered} U \hfill \\ V \hfill \\ W \hfill \\ \end{gathered} \right.} \right\} = \left[ R \right]\left\{ {\left. C \right\}} \right. $$
(4)

where \(\left[ R \right]\) is a 3 × 24 matrix and \(\left\{ C \right\}\) is the unknown constant vector of order 24.

The used element has four nodes and 6 degrees of freedom at each node. The nodal displacement vector is given as:

$$ \left\{ {\left. \delta \right\}} \right. = \left\{ {\left. {\left\{ {\left. {\delta_{i} } \right\}} \right.^{T} ,\left\{ {\left. {\delta_{j} } \right\}} \right.^{T} ,\left\{ {\left. {\delta_{k} } \right\}} \right.^{T} ,\left\{ {\left. {\delta_{l} } \right\}} \right.^{T} } \right\}} \right.^{T} $$
(5)
$$ \left\{ {\left. {\delta_{i} } \right\}} \right. = \left\{ {\left. {U_{i} ,V_{i} ,W_{i} ,\frac{{\partial W_{i} }}{\partial x},\frac{{\partial W_{i} }}{\partial y},\frac{{\partial^{2} W_{i} }}{\partial x\partial y}} \right\}^{T} } \right. $$
(6)

By introducing Eqs. (1, 2, 3, 4 and 5), the nodal displacement vector is written:

$$ \left\{ {\left. \delta \right\}} \right. = \left[ A \right]\left\{ {\left. C \right\}} \right. $$
(7)
$$ \left\{ {\left. C \right\}} \right. = \left[ A \right]^{ - 1} \left\{ {\left. \delta \right\}} \right. $$
(8)

Substituting Eq. (8) in Eq. (4), the expression of the displacement field becomes:

$$ \left\{ {\left. \begin{gathered} U \hfill \\ V \hfill \\ W \hfill \\ \end{gathered} \right\}} \right. = \left[ R \right]\left[ A \right]^{ - 1} \left\{ {\left. \delta \right\}} \right. = \left[ {\begin{array}{*{20}c} {\left[ {N^{(1)} } \right]} \\ {\left[ {N^{(2)} } \right]} \\ {\left[ {N^{(3)} } \right]} \\ \end{array} } \right]\left\{ \delta \right\} = \left[ N \right]\left\{ {\left. \delta \right\}} \right. $$
(9)

\([N]\) is a 3 × 24 order matrix representing the displacement shape function of the finite element.

The strain–displacement relations for rectangular plates are written [25]:

$$ \left\{ {\left. \begin{gathered} \varepsilon_{x} \hfill \\ \varepsilon_{y} \hfill \\ 2\varepsilon_{xy} \hfill \\ \kappa_{x} \hfill \\ \kappa_{y} \hfill \\ \kappa_{xy} \hfill \\ \end{gathered} \right\} = } \right.\left[ {\begin{array}{*{20}c} {\frac{\partial U}{{\partial x}}} & {\frac{\partial V}{{\partial y}}} & {\frac{\partial V}{{\partial x}} + \frac{\partial U}{{\partial y}}} & { - \frac{{\partial^{2} W}}{{\partial x^{2} }}} & {\; - \frac{{\partial^{2} W}}{{\partial y^{2} }}} & { - 2\frac{{\partial^{2} W}}{\partial x\partial y}} \\ \end{array} } \right]^{T} $$
(10)

Substituting the displacement components Eq. (9) in Eq. (10), we obtain:

$$ \left\{ {\left. \varepsilon \right\}} \right. = \left[ Q \right]\left[ A \right]^{ - 1} \left\{ {\left. \delta \right\}} \right. = \left[ B \right]\left\{ {\left. \delta \right\}} \right. $$
(11)

where [Q] is a 6 × 24 order matrix.

The forces and moments per unit length are written:

$$ \left\{ t \right\} = \left\{ {\begin{array}{*{20}c} {N_{x} } \\ {N_{y} } \\ {N_{xy} } \\ {M_{x} } \\ {M_{y} } \\ {M_{xy} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\int_{ - h/2}^{h/2} {\sigma_{x} \;dz} } \\ {\int_{ - h/2}^{h/2} {\sigma_{y} \;dz} } \\ {\int_{ - h/2}^{h/2} {\sigma_{xy} \;dz} } \\ {\int_{ - h/2}^{h/2} {\sigma_{x} \,z\;dz} } \\ {\int_{ - h/2}^{h/2} {\sigma_{y} \,z\;dz} } \\ {\int_{ - h/2}^{h/2} {\sigma_{xy} \,z\;\,dz} } \\ \end{array} } \right\} $$
(12)

For isotropic plate, we have:

$$ \left\{ {\begin{array}{*{20}c} {N_{x} } \\ {N_{y} } \\ {N_{xy} } \\ {M_{x} } \\ {M_{y} } \\ {M_{xy} } \\ \end{array} } \right\} = \left[ \begin{gathered} {\kern 1pt} {\kern 1pt} \,D\;\;\;\upsilon \,D\;\quad \quad 0\;\quad \quad \quad 0\;\quad \quad {\kern 1pt} 0\quad {\kern 1pt} \quad \;0 \hfill \\ \upsilon \,D\;\;\,\,\,D\;\quad \quad 0\;\quad \quad \quad 0\;\quad \quad {\kern 1pt} 0\quad \quad \;\;0 \hfill \\ \;0\;\quad \,0\;\quad \frac{D(1 - \upsilon )}{2}\;\quad \;0\quad \quad \,\;0\quad \quad \;\;0 \hfill \\ \;0\;\quad \;\,0\;\quad \quad 0\;\quad \quad \quad K\;\quad \quad \upsilon \,K\quad \;\;0 \hfill \\ \;0\;\quad \,\;0\;\quad \quad 0\;\quad \quad \quad \upsilon \,K\;\quad \,\,K\quad \;\;\;\,\;0 \hfill \\ \;0\;\quad \;\;0\;\quad \quad 0\;\quad \quad \quad 0\;\quad \quad \,\,0\quad \;\frac{K(1 - \upsilon )}{2} \hfill \\ \end{gathered} \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\varepsilon_{xy} } \\ {k_{x} } \\ {k_{y} } \\ {k_{xy} } \\ \end{array} } \right\} $$
(13)

where \(K = \frac{{Eh^{3} }}{{12(1 - \upsilon^{2} )}}\) and \(D = \frac{Eh}{{1 - \upsilon^{2} }}\).

By the substitution of Eq. (11) in Eq. (13), we can obtain:

$$ \left\{ {\left. t \right\}} \right. = \left[ P \right]\left[ B \right]\left\{ {\left. \delta \right\}} \right. $$
(14)

Using Hamilton’s principle [27], the elementary mass and stiffness matrices \(\left( {\left[ m \right]^{e} \;{\text{and}}\;\left[ k \right]^{e} } \right)\) can be expressed by:

$$ \left[ m \right]^{{{\kern 1pt} e}} = \rho_{m} h\int\limits_{{A^{e} }} {\left[ N \right]}^{T} \left[ N \right]{\text{d}}A $$
(15)
$$ \left[ k \right]^{{{\kern 1pt} e}} = \int\limits_{{A^{e} }} {\left[ B \right]}^{T} \left[ P \right]\left[ B \right]{\text{d}}A $$
(16)

where \(\rho_{m}\) is the material density. By using Eq. (9), Eq. (11) and by substituting them in Eq. (15) and Eq. (16), we obtain:

$$ \left[ m \right]^{{{\kern 1pt} e}} = \rho_{m} h\left[ {\left[ A \right]^{ - 1} } \right]^{T} (\int\limits_{0}^{{y_{e} }} {\int\limits_{0}^{{x_{e} }} {\left[ R \right]^{T} } } \left[ R \right]{\text{d}}x{\text{d}}y)\left[ A \right]^{ - 1} $$
(17)
$$ \left[ k \right]^{{{\kern 1pt} e}} = \left[ {\left[ A \right]^{ - 1} } \right]^{T} \left( {\int\limits_{0}^{{y_{e} }} {\int\limits_{0}^{{x_{e} }} {\left[ Q \right]^{T} } } \left[ P \right]\left[ Q \right]{\text{d}}x{\text{d}}y} \right)\left[ A \right]^{ - 1} $$
(18)

2.2 Aerodynamic modeling

The aerodynamic pressure of the airflow applied to the external surface of the plate is modeled by piston theory, which is introduced by Ashley and Zartarian [13]. Generally, first-order piston theory aerodynamics is used for linear panel flutter analysis at high supersoic Mach numbers [28]; its expression is giving as follows:

$$\begin{aligned}& p_{a} = \frac{{ - \rho \;U_{\infty }^{2} }}{{\sqrt {(M_{\infty }^{2} - 1)} }}\\ & \left( {\left( {\frac{\partial W}{{\partial x}}\cos \Lambda + \frac{\partial W}{{\partial y}}\sin \Lambda } \right) + \frac{1}{{U_{\infty } }}\frac{{M_{\infty }^{2} - 2}}{{M_{\infty }^{2} - 1}}\frac{\partial W}{{\partial t}}} \right)\end{aligned} $$
(19)

where \(\rho\),\(U_{\infty }\) and \(M_{\infty }\) denote the air density, the free stream velocity and the Mach number.

Based on Eq. (9), we can write the deflection \(W\) as function of nodal displacements as follows:

$$ W = \left[ {N_{1}^{(3)} N_{2}^{(3)} N_{3}^{(3)} \ldots N_{24}^{(3)} } \right]\left\{ \delta \right\} = \left[ {N^{(3)} } \right]\left\{ \delta \right\} $$
(20)

Therefore, the aerodynamic pressure is written:

$$\begin{aligned} & p_{a} = - \lambda_{a} \left( {\left[ {\frac{{\partial N^{(3)} }}{\partial x}} \right]\cos \Lambda + \left[ {\frac{{\partial N^{(3)} }}{\partial y}} \right]\sin \Lambda } \right)\;\left\{ \delta \right\}\,\\ & - g_{a} \left[ {N^{(3)} } \right]\,\left\{ {\dot{\delta }} \right\}\end{aligned} $$
(21)

\(\lambda_{a}\) is the aerodynamic stiffness parameter and \(g_{a}\) is the aerodynamic damping parameter and they are defined as follows:

$$ \lambda_{a} = \frac{2q}{{\sqrt {\left( {M_{\infty }^{2} - 1} \right)} }} $$
(22)
$$ g_{a} = \frac{{2q\left( {U_{\infty }^{2} - 2} \right)}}{{U_{\infty } \left( {U_{\infty }^{2} - 1} \right)}} $$
(23)

where \(q = \frac{{\rho U_{\infty }^{2} }}{2}\).

By applying the principle of virtual work, we have:

$$ \int\limits_{{A^{e} }} {P_{a} \;W\;{\text{d}}A\; = \int\limits_{{A^{e} }} {\left\{ {\begin{array}{*{20}c} 0 & 0 & {P_{a} } \\ \end{array} } \right\}} \,\left\{ {\begin{array}{*{20}c} U \\ V \\ W \\ \end{array} } \right\}\,{\text{d}}A = \int\limits_{{A^{e} }} {\left\{ {P_{a} } \right\}^{T} \,} \left\{ {\begin{array}{*{20}c} U \\ V \\ W \\ \end{array} } \right\}\,{\text{d}}A} $$
(24)

The equivalent nodal forces due to the aerodynamic pressure are presented by:

$$ \left\{ {F^{P} } \right\}^{e} \, = \int\limits_{{A^{e} }} {\left[ N \right]^{T} \,\left\{ {P_{a} } \right\}\,} dA\;\, $$
(25)

\(\left\{ {F^{P} } \right\}^{e}\) is the equivalent nodal forces vector.

$$ \begin{aligned} &\left\{ {F^{P} } \right\}^{e} = - \lambda_{a} \left( {\int\limits_{{A^{e} }} {\left[ N \right]^{T} \left[ {\begin{array}{*{20}c} {\left[ 0 \right]} \\ {\left[ 0 \right]} \\ {\left[ {\frac{{\partial N^{(3)} }}{\partial x}} \right]} \\ \end{array} } \right]} \,{\text{d}}A\,\;\cos \Lambda \; + \int\limits_{{A^{e} }} {\left[ N \right]^{T} \left[ {\begin{array}{*{20}c} {\left[ 0 \right]} \\ {\left[ 0 \right]} \\ {\left[ {\frac{{\partial N^{(3)} }}{\partial y}} \right]} \\ \end{array} } \right]} \,{\text{d}}A\,\;\sin \Lambda } \right)\,\left\{ \delta \right\} \\ & - g_{a} \,\left( {\int\limits_{{A^{e} }} {\left[ N \right]^{T} } \left[ {\begin{array}{*{20}c} {\left[ 0 \right]} \\ {\left[ 0 \right]} \\ {\left[ {N^{(3)} } \right]} \\ \end{array} } \right]\;dA} \right)\;\left\{ {\dot{\delta }} \right\} \\ \end{aligned} $$
(26)

Based on Eq. (24), the elementary aerodynamic stiffness matrix \(\left[ {k_{a} } \right]^{e}\) and damping matrix \(\left[ {c_{a} } \right]^{e}\) are obtained as follows:

$$ \left[ {k_{a} } \right]^{e} = - \lambda_{a} \left( {\int\limits_{{A^{e} }} {\left[ N \right]^{T} \left[ {\begin{array}{*{20}c} {\left[ 0 \right]} \\ {\left[ 0 \right]} \\ {\left[ {\frac{{\partial N^{(3)} }}{\partial x}} \right]} \\ \end{array} } \right]} \,{\text{d}}A\,\;\cos \Lambda \; + \int\limits_{{A^{e} }} {\left[ N \right]^{T} \left[ {\begin{array}{*{20}c} {\left[ 0 \right]} \\ {\left[ 0 \right]} \\ {\left[ {\frac{{\partial N^{(3)} }}{\partial y}} \right]} \\ \end{array} } \right]} \,{\text{d}}A\,\;\sin \Lambda } \right) $$
(27)
$$ \left[ {c_{a} } \right]^{e} = - g_{a} \,\left( {\int\limits_{{A^{e} }} {\left[ N \right]^{T} } \left[ {\begin{array}{*{20}c} {\left[ 0 \right]} \\ {\left[ 0 \right]} \\ {\left[ {N^{(3)} } \right]} \\ \end{array} } \right]\;{\text{d}}A} \right) $$
(28)

The elementary equations of motion are:

$$ \left[ m \right]^{e} \left\{ {\left. {\ddot{\delta }} \right\}} \right.^{e} - \left[ {c_{a} } \right]^{e} \left\{ {\left. {\dot{\delta }} \right\}} \right.^{e} + \left( {\left[ k \right]^{e} - \left[ {k_{a} } \right]^{e} } \right)\left\{ \delta \right\}^{e} = \left\{ {\left. 0 \right\}} \right. $$
(29)

2.3 Flutter analysis

From equation Eq. (29) and using the assembly technique with the application of the necessary boundary conditions, we intuitively obtain the formulation of the governing equations of motion in a global system:

$$ \left[ m \right]^{e} \left\{ {\left. {\ddot{\delta }} \right\}} \right. - \left[ {c_{a} } \right]\left\{ {\left. {\dot{\delta }} \right\}} \right. + \left( {\left[ k \right] - \left[ {k_{a} } \right]} \right)\left\{ \delta \right\} = \left\{ {\left. 0 \right\}} \right. $$
(30)

where \(\left\{ \delta \right\}\), \(\left[ m \right]\), \(\left[ k \right]\), \(\left[ {c_{a} } \right]\) and \(\left[ {k_{a} } \right]\) denote global displacement vector, the global mass matrix, the global stiffness matrix, the global aerodynamic damping matrix and the global aerodynamic stiffness matrix, respectively.

Then, Eq. (30) is reformulated as follows:

$$ \left[ \begin{gathered} \left[ 0 \right]\quad \quad \left[ m \right] \hfill \\ \left[ m \right]\quad - \left[ {c_{a} } \right] \hfill \\ \end{gathered} \right]\left\{ {\left. \begin{gathered} {\ddot{\delta }} \hfill \\ {\dot{\delta }} \hfill \\ \end{gathered} \right\}} \right. + \left[ \begin{gathered} - \left[ m \right]\quad \quad \quad \;\left[ 0 \right] \hfill \\ \;\,\;\left[ 0 \right]{\kern 1pt} \quad \quad \left[ k \right] - \left[ {k_{a} } \right] \hfill \\ \end{gathered} \right]\left\{ {\left. \begin{gathered} {\dot{\delta }} \hfill \\ \delta \hfill \\ \end{gathered} \right\}} \right. = \left\{ {\left. 0 \right\}} \right. $$
(31)

The general solution of Eq. (31) can be expressed as:

$$ \left\{ {\left. \delta \right\}} \right. = \left\{ {\left. {\delta_{0} } \right\}} \right.e^{\Omega \,t} $$
(32)

where \(\Omega\) and \(\left\{ {\delta_{0} } \right\}\) are the eigenvalue and the eigenvector of the equation.

The substitution of the general solution into Eq. (31) leads to an eigenvalue problem. Complex eigenvalues can be obtained as:

$$ \Omega = \Omega_{r} + i\Omega_{i} $$
(33)

where \(\Omega_{r}\) and \(\Omega_{i}\) denote the real part of the eigenvalue and the imaginary part of the eigenvalue. The imaginary part referred to the natural frequencies of the panel and the real one to its damping. For convenience, we define the non-dimensional dynamic pressure parameter \(\lambda^{*}\), the non-dimensional frequency \(\Omega_{i}^{*}\) and the non-dimensional damping \(\Omega_{r}^{*}\) as follows:

$$ \lambda^{*} = \frac{{2\,q\,A^{3} }}{{K\,\sqrt {M^{2} - 1} }} $$
(34)
$$ \Omega_{i}^{*} = \Omega_{i} \,A^{2} \sqrt {\frac{{\rho_{m} \,h}}{K}} $$
(35)
$$ \Omega_{r}^{*} = \Omega_{r} \,A^{2} \sqrt {\frac{{\rho_{m} \,h}}{K}} $$
(36)

It is important to prevent structural failure due to divergence or flutter [29]. Theoretically, divergence occurs when the linear response of the system grows exponentially with time [30]. This type of instability is observed when natural frequency decreases and tends to 0 [31]. The occurrence of flutter is usually estimated by the first coalescence of two consecutive natural frequencies of the panel, and the corresponding aerodynamic pressure is called the critical flutter aerodynamic pressure [32, 33].

3 Results and discussions

In this section, we present the results of numerical investigations obtained using a developed in-house code. The considered plates are made of an aluminum alloy considered isotropic with the modulus of elasticity \(E = 70\;{\text{GPa}}\), the Poisson’s ratio \(\nu = 0.3\) and the mass density \(\rho_{m} = 2700\;{\text{kg/m}}^{{3}}\).

As illustrated in Fig. 2, SSSS, CCCC, PSSSS and FCFF panels are investigated. S, C and PS denote fully simply supported, clamped and point-supported boundary conditions, respectively.

Fig. 2
figure 2

Considered boundary conditions

Full size image

3.1 Validation and comparison

At first, the present formulation is validated by considering flutter analysis of a fully simply supported isotropic square plate as studied by Song and Li [34]. It is well known that the accuracy of the finite element method depends on the used number of elements. Therefore, a set of calculations were done to find the minimum number of elements required for plate discretizing. As shown in Fig. 3, for a fully simply supported square plate in supersonic airflow, grid independence has been investigated by analyzing cases with different mesh sizes until consistent results are achieved. It is observed that satisfactory results are obtained for 6 × 6 elements. For closer meshes, there are no observed variations of the critical frequency and the natural frequencies of the plate in vacuo.

Fig. 3
figure 3

Frequency versus number of elements for a fully simply supported square plate (-a- first-mode frequency in vacuo, -b- second-mode frequency in vacuo & -c- critical frequency)

Full size image

The flutter is an aeroelastic instability induced by the interactions of aerodynamic, inertial and elastic forces. It occurs when two modes coincide at the same critical dynamic pressure [31]. The variation of frequencies for increasing values of dynamic pressure parameter is shown in Fig. 4. It is observed that the first and second modes of the plate coalesce into one mode for. \(\lambda^{*} = 511.37\), and these obtained results show a classical flutter instability phenomenon. Also, in Fig. 4, it can be observed that the present results are well accordant with those published by Song and Li [34] in their study on the flutter analysis of a fully simply supported flat plate coupled with supersonic airflow. To obtain satisfactory results, we used only 36 elements, whereas Song and Li [34] used 225 elements for the same case. The proposed method reveals better convergence behavior compared to Song and Li [34].

Fig. 4
figure 4

Obtained frequencies for a fully simply supported coupled plate compared to those presented by Song and Li [34] (\(A = B = 0.1\;{\text{m}}\), \(h = 0.001\;{\text{m}}\), \(E = 210\,{\text{GPa}}\), \(\upsilon = 0.33\) and \(\rho = 7930\;{{{\text{kg}}} \mathord{\left/ {\vphantom {{{\text{kg}}} {{\text{m}}^{{3}} }}} \right. \kern-\nulldelimiterspace} {{\text{m}}^{{3}} }}\))

Full size image

Figure 5 presents the evolution of the first- and second-mode shapes for an increase in dynamic pressure (0, 500 and 511.37). It is interesting to note that the first- and second-mode shapes corresponding to the critical dynamic pressure are similar.

Fig. 5
figure 5

Influence of dynamic pressure on mode shapes

Full size image

3.2 Effect of regular boundary conditions on flutter bounds

In this assessment, we consider two types of boundary conditions SSSS and CCCC. As illustrated in Fig. 6a, for a fully simply supported square plate, the frequency of the first mode increases, while the frequency of the second mode decreases as the dynamic pressure parameter \(\lambda\) increases. For higher values of \(\lambda\), these frequencies merge into a single-mode. Mode 3 and mode 4 coalesce for a greater value of dynamic pressure.

Fig. 6
figure 6

Flutter bounds for different boundary conditions: a & b SSSS; c & d CCCC; e and f comparison of the first two eigenvalues

Full size image

A positive damping explicitly signifies a state of instability [35]. In Fig. 6b, by increasing the dynamic pressure, the damping branch corresponding to one of the modes 1 or 2 vanishes and then changes the sign to positive. The same behavior is observed for the damping of the third and fourth modes. Figure 6c-d shows the flutter bounds for a fully clamped panel. A similar behavior to that observed in the previous case is depicted.

The effect of the boundary conditions on the flutter onset is illustrated in Fig. 6e–f. This last depicts a comparison of the evolution of the first two eigenvalues for SSSS and FFFF panels. It is observed that for the fully simply supported case, the flutter onset occurs for \(\lambda = 511.45\) while the critical dynamic pressure for a fully clamped plate is \(\lambda = 850.58\). This is because the clamped plates are stiffer than fully simply supported ones.

As summarized in Table 1, the obtained results using the proposed approach are compared to various numerical and analytical results found in previously published studies [10,11,12, 36,37,38,39,40,41,42]. For different boundary conditions (SSSS, CCCC, FCFF, PSSSS), it was observed that natural frequencies and dynamic pressure parameters are found with reasonable accuracy.

Table 1 Numerical comparison of flutter bounds for different boundary conditions
Full size table

3.3 Effect of arbitrary airflow direction on flutter bounds

A key factor in predicting dynamic instability boundaries is the airflow orientation. The influence of this crucial parameter is investigated for rectangular panels of various aspect ratios.

3.3.1 Square plate

According to the results given in Fig. 7, there is a significant effect of the flow angle on the critical dynamic pressure parameter for a fully simply supported square plate. The results evaluated by the proposed approach are found to be in good agreement with the available results published by Sander, Bon [10]. A symmetric variation of the critical dynamic pressure is observed, and the maximum value corresponds to \(\Lambda = 45^\circ\).

Fig.7
figure 7

Influence of flow angle on critical dynamic pressure of fully simply supported square plate \(\left( {\frac{A}{h} = 100} \right)\)

Full size image

The values of dynamic pressure are the same for \(\Lambda = 30^\circ\) and \(\Lambda = 60^\circ\) and also for \(\Lambda = 0^\circ\) and \(\Lambda = 90^\circ\). It is clear that the most critical case is when the airflow is perpendicular to one of the edges of the plate.

3.3.2 Rectangular plate

The last numerical results presented relate to the effect of flow angle on the aeroelastic stability bounds of SSSS plates. Figure 8a shows the variation of natural frequencies of a rectangular plate with an aspect ratio of 0.5. For flow angle \(\Lambda\) = 30°, 45°, 60° and 90°, the plate loses its stability through flutter due to the coupling of the first and second modes. However, for = 0°,

Fig. 8
figure 8

The variation of natural frequencies of a rectangular plate with aspect ratio 0.5 for different flow direction: a \(\Lambda = 30^\circ ,\;45^\circ ,\;60^\circ ,\;90^\circ\); b \(\Lambda = 0^\circ\)

Full size image

The first coupling corresponding to the critical dynamic pressure occurred between modes 3 and 2, as shown in Fig. 8b. In Figs. 9 and 10, for panels of aspect ratios of 1.25 and 2, it is observed that the increase in flow angle results in a shift of the critical dynamic pressure to higher values. It is important to note that for aspect ratios greater than 1 (1.25 and 2), for the flow angle \(\Lambda\) = 90° the critical mode is produced by the coupling of the second and third modes.

Fig. 9
figure 9

The variation of natural frequencies of a rectangular plate with aspect ratio 1.25 for different flow direction: a \(\Lambda = 0^\circ ,\;30^\circ ,\;45^\circ ,\;60^\circ\); b \(\Lambda = 90^\circ\)

Full size image
Fig. 10
figure 10

The variation of natural frequencies of a rectangular plate with aspect ratio 2.0 for different flow direction: a \(\Lambda = 0^\circ ,\;30^\circ ,\;45^\circ ,\;60^\circ\); b \(\Lambda = 90^\circ\)

Full size image

In Fig. 11, the critical dynamic pressure parameter is plotted against the flow angle for different aspect ratios. It is clear that critical dynamic pressure is sensitive to the variation of flow angle and aspect ratio. For aspect ratios A/B = 0.5, the dynamic pressure decreases as the flow angle increases. For aspect ratios greater than 1 (i.e., A/B = 1.25 and 2), the most dangerous case is observed when the flow angle is equal to 0°, i.e., the flow is aligned along the longer side.

Fig. 11
figure 11

Influence of flow angle on critical dynamic pressure for different aspect ratios

Full size image

3.4 Effect of irregular boundary conditions

The main goal of these numerical simulations is to investigate a variety of potentially catastrophic scenarios and assess their impact on aeroelastic characteristics. For that, we investigated the configurations depicted in Fig. 12.

Fig. 12
figure 12

Schematic diagrams of panels with different boundary conditions

Full size image

Boundary conditions play a major role in the dynamic stability of the structure. When examining the results in Fig. 13, for Λ = 0°, it is shown that the lack of one support to the edges along the flow direction or in the direction perpendicular to the airflow causes major modifications in the behavior of the structure. Plates in case 1 and case 2 exhibit a flutter type instability at \(\lambda_{cr} = 275.71\) and \(\lambda_{cr} = 256.11\), respectively. However, for cases 3 and 4, a divergence type instability occurs at a much lower dimensionless dynamic pressure \(\lambda_{cr} \approx 172\). By examining these results, it is clear that removing one support to the edges along or perpendicular to the flow direction has different effects on dynamic stability. The lack of one support at the edge perpendicular to the airflow significantly reduces the stability limits, making the divergence the dominant mode of instability.

Fig. 13
figure 13

Non-dimensional frequency variation as a function of the non-dimensional aerodynamic pressure

Full size image

The predicted critical dynamic pressures are presented in Table 2 for different flow directions. Results show that for case 1, the instability is governed by the flutter phenomenon. It is also observed that the lowest critical dynamic pressures are due to divergence type instabilities. The most critical configurations is that of cases 3 and 4 for \(\Lambda = 0^{^\circ }\). One can note that the removal of the support located on the edge perpendicular to the airflow exposes the structure to instability by divergence.

Table 2 Influence of flow orientation for a square plate
Full size table

As seen in Table 3, for \(1 < \frac{A}{B} \le 1.75\) the explored configurations experienced flutter instability. However, for \(0.5 \le \frac{A}{B} \le 1\), cases 1 and 2 still governed by flutter instability, while cases 3 and 4 lose their stability by divergence.

Table 3 Critical non-dimensional dynamic pressure for different aspect ratios
Full size table

The aforementioned parametric analysis results can be used as a data set for a future optimization study on the multi-objective optimal design of aeroelastic flutter of flat plates. Suitable optimization methods should be used to identify the ideal values for aspect ratio, flow direction, thickness and support arrangement to achieve an optimized design. The critical aerodynamic pressure can be raised considerably, and the optimization procedure could significantly improve the structure's stability.

4 Conclusion

This paper is devoted to a finite element approach for predicting flutter properties of a rectangular plate in supersonic airflow with different flow directions and boundary conditions. We used a hybrid method combining a finite element analysis and Sanders’ shell theory to model the solid sub-domain. The aerodynamic pressure loading is approximated by the first-order piston theory. Convergence and comparison studies confirm the validity and reliability of the proposed model.

It was observed that flutter bounds are very sensitive to the flow angularity variations. For square plates, the maximum critical dynamic pressure occurs for flow angle \(\Lambda = 45^\circ\) and minimum for \(\Lambda = 0^\circ\) and \(\Lambda = 90^\circ\). The lowest dynamic pressure is observed for rectangular plates when the flow is along the longer side. It was shown that the lack of one support to the edges causes significant modifications in the stability bounds. In this case, plates with irregular boundary conditions undergo a flutter or divergence type instability depending on aspect ratio and airflow orientation.

This research provides a good database, especially for flutter characteristics of plates under irregular boundary conditions that could interest other researchers. The quality of the obtained results leads us to believe in the proposed approach's capacity to predict other interesting problems such as supersonic panel flutter under a thermal environment and modeling shallow shells.