Optimal treatment control and bifurcation analysis of a tuberculosis model with effect of multiple re-infections

Abstract

We derive and analyze a tuberculosis (TB) model including exogenous re-infection and endogenous reactivation, and the re-infection among the treated individuals. The disease-free equilibrium and the existence criterion of endemic equilibrium are investigated. The basic reproduction number $R_0$ is derived and it is found that the disease-free equilibrium is stable when $R_0 <1$, unstable for $R_0 >1$, and the system undergoes a transcritical bifurcation at the disease-free equilibrium when $R_0 =1$. Furthermore, for $R_0 <1$, there are two endemic equilibria, one of which is stable and other one is unstable, indicating the occurrence of backward bifurcation. The local stability analysis of the disease-free and the endemic equilibrium is shown. Also, we studied the sensitivity analysis of the system in refer to some crucial model parameters and the sensitivity indices of $R_0$ to parameters for the TB model are obtained. Using Pontryagin’s maximum principle, we have discussed about the optimal control of the disease. Various simulation works are given throughout the paper to support our analytical results.

1 Introduction

Mathematical models are used to guide public health policy decisions and explore questions in different infectious disease control. Therefore, among the areas of mathematical biology rather in epidemiology the building and analysis of mathematical models, describing the spread and control of infectious diseases, have a great practical influence. The spread of infectious diseases in human population depends upon various factors such as the number of susceptible and infective; types of transmission (carriers, bacteria, vector etc.); environmental and ecological conditions etc. Anderson and May [1], Diekmann and Heesterbeek [2], Ruan and Wang [3], Takeuchi et al. [4] have studied mathematical models for investigating the transmission dynamics of infectious diseases and the asymptotic behaviors of these epidemic models. Several infectious diseases are transmitted by direct contact between susceptible and infective individuals, but there are some other diseases such as tuberculosis (TB), typhoid etc. which are transmitted to the human population indirectly by the flow of bacteria from infectious individuals into the air. In this paper, we are going to deal with the outbreak of TB disease that maintains a relation with bacteria, called Mycobacterium tuberculosis (MTB). It is also transmitted by both the direct and indirect contacts with the infectious individuals (see [5–8]).

The multiple re-infections play an important role in TB dynamics to progress the disease at the next stage. For example, the rate of exogenous re-infection and endogenous reactivation are two crucial terms in TB model that produce a new infection. The tuberculosis disease has a latent or incubation period during which the individuals are infected but not infectious. The long period of latency in MTB infection gives additional ambiguity to the beginning of active disease into understanding the disease progression. Moreover, due to the endogenous reactivation the disease shifts from latent class to the infectious class and the latent individuals who have been previously infected may acquire a new infection, called exogenous re-infection, from another infectious individual due to low immunity of persons. Therefore, the tuberculosis disease may also result in some patients from exogenous re-infection in a second stage of MTB. Exogenous re-infection how effects in MTB disease have been reported by Chaves et al. [9], Small et al. [10] and Nardell et al. [11]. But, the rate of exogenous re-infection is regarded as ‘super-infection’ by Martcheva and Thieme [12].

The basic reproduction number is one of the most important parameter in epidemic model and it lays down whether a disease can be attacked in the naive population. Generally, each infectious individual will give rise to more than one new case when the basic reproduction number is above one but when it is below one, the disease totally extinct from the population. In fact, in most of the epidemic models, the bifurcation at $R_0=1$ is forward (supercritical), that is there is no endemic equilibrium for $R_0<1$. However, in recent years, some authors (see [13–17]) have found another type of bifurcation at $R_0 =1$, in many epidemic models, called backward bifurcation and this type of bifurcation confirms the existence of multiple endemic equilibria of the given system when $R_0 <1$. Arino et al. [18] investigated global results for an epidemic model with vaccination that exhibits backward bifurcation leading to bistability can occur.

There is a great excitement in the developments of new tools, play an important role to stop TB. In fact, it becomes complex matter for every country to control the tuberculosis disease. But, as the modern medical science is progressively more developed, so it is possible the TB can be prevented by extra treatment to the infectious individuals. The mathematical techniques of optimal control are ideal tool to explore strategies for the reduction of TB from the community where it has been found to be endemic. Optimal control provides a method to assign a trade-off between the costs of the treatment including the risk of side effects of the treatment and the reduction of the infectious individuals. In this paper, our motivation is to minimize the infectious individuals as well as the cost of treatment that relate to various clinical tests, medicine, hospitalization etc. using optimal control theory (see [19, 20]). To asses the use of interventions such as vaccination, treatment and isolation, optimal control theory have been applied in different epidemiological models (see [21–25]) elucidated optimal control analysis of a malaria disease transmission model including treatment and vaccination with waning immunity. They derived conditions under which it is optimal to eradicate the disease and examined the impact of combined vaccination and treatment strategies on the disease transmission. Joshi et al. [26] illustrated the concept of optimal control in two different disease models. In the first example, they showed how optimal control theory can be applied to find an optimal vaccination strategy that will minimize the size of the infectious population as well as the cost of vaccination. In the second example, they considered a model describing the interaction between the virus and the immune cell population in an individual under drug treatment and described how optimal control theory can be used to determine a drug treatment strategy that minimizes the side effects of the drug together with the viral population at any point in time. Looking into backward bifurcation, Blayneh et al. [27] studied a deterministic model for the transmission dynamics of West Nile virus in the mosquito–bird–human zoonotic cycle using mosquito reduction strategies and human protection strategies as control measures. The numerical simulations of their optimal control problem suggest that mosquito reduction strategies should be emphasized ahead of human protection measures in order to reduce the disease burden.

The outline of the remainder of this paper is as follows. In Sect. 2, a mathematical model is constructed for describing the TB infection and multiple re-infections, and then some basic results are investigated. Section 3 is devoted to study the existence of equilibria, stability analysis of both disease-free and endemic equilibrium and of bifurcations. Furthermore, some numerical simulations are given in this section showing that our model system exhibits a backward (subcritical) bifurcation. Optimal control problem is formulated in Sect. 4 to derive possible treatment strategies using Pontryagin’s maximum principle. Some numerical simulations on optimal control theory are given in Sect. 5. Various concluding remarks of our research effort are then given in Sect. 6.

2 Model formulation

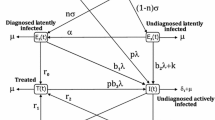
Based on epidemiological status, we divide the total host population N into four classes as susceptible (S), exposed (infected but not yet infectious) (E), infectious (I) and treated (T). We present a basic tuberculosis model is of the form SEITE including both slow and fast progressions of the disease. Some assumptions are made in the formulation of this model. First, we assume that A is the total recruitment at any time t. Secondly, we consider $\beta$ as the contact or infection rate of the disease and the force of infection is assumed to be the mass action incidence of the form $\beta SI$. Thirdly, if $p\in (0, 1)$ be a proportion of exogenous re-infection, then $p\beta EI$ models the exogenous re-infection rate and the disease acquire a new infection due to long latency period $k^{-1}$,where k is the endogenous reactivation rate. In our model, we also assume another parameter q which is the portion of primary progression of the disease and this parameter lays down the portion of infectious individuals $(q\beta SI)$ that moves directly from susceptible class into the infectious class and it is possible due to the low immunity of some susceptible individuals. It is true that the susceptible individuals are probably at greater risk of progressing directly to active TB. The initial treatment may reduce the infection but it may not be able to eliminate the infection completely. Therefore, we model this incidence by including a factor $\sigma (0\le \sigma \le 1)$, taken as the re-infection rate among the treatment individuals. Here $\sigma =0$ indicates that the treatment is perfectly effective and $\sigma =1$ means that the treatment has no effect. The individuals, who acquire a new infection, stay in the infectious class during a period of time $r^{-1}$, where r is the treatment rate. Moreover, we assume that the natural death rate is $\mu (>$0) and the infectious individuals are died by the attack of disease at a rate $d(\ge$0).

Based on the above assumptions, the dynamical system may be modeled by the following system of ordinary differential equations:

$$\begin{aligned}&\frac{\textit{dS}}{\textit{dt}}= A-\beta \textit{SI}-q\beta \textit{SI}-\mu S, \nonumber \\&\frac{\textit{dE}}{\textit{dt}}= \beta \textit{SI}+\sigma \beta \textit{TI}-p\beta \textit{EI}-(k+\mu )E, \nonumber \\&\frac{\textit{dI}}{\textit{dt}}= p\beta \textit{EI}+q\beta \textit{SI}+\textit{kE}-(d+r+\mu )I, \nonumber \\&\frac{\textit{dT}}{\textit{dt}}= \textit{rI}-\sigma \beta \textit{TI}-\mu T, \end{aligned}$$

(1)

As $N=S+E+I+T$, we have from the system (1)

$$\begin{aligned} \frac{\textit{dN}}{\textit{dt}}= A-\mu N-dI. \end{aligned}$$

(2)

The Jacobian matrix $\Sigma$ of the system (1) at (S, E, I, T) is

$$\begin{aligned} \Sigma =\left( {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} -\mu -\beta I-q\beta I &{} 0 &{} -\beta S-q\beta S &{} 0 \\ \beta I &{} -p\beta I-(k+\mu ) &{} \beta S-p\beta E+\sigma \beta T &{} \sigma \beta I \\ q\beta I &{} p\beta I+k &{} p\beta E+q\beta S-(d+r+\mu ) &{} 0 \\ 0 &{} 0 &{} r- \sigma \beta T &{} -\sigma \beta I-\mu \\ \end{array}} \right) . \end{aligned}$$

Lemma 1

The non-negative orthant $\mathfrak {R}_+^4$ is positively invariant for the system (1).

Proof

The system (1) can be written as

$$\begin{aligned} \left\{ {\begin{array}{l} \frac{\textit{dS}}{\textit{dt}}= A-\beta SI-q\beta SI-\mu S, \\ \frac{\textit{dY}}{\textit{dt}}=PY,\\ \end{array}} \right. \end{aligned}$$

(3)

where

$$\begin{aligned} Y=\left( {\begin{array}{l} E\\ I\\ T\\ \end{array}} \right) , P=\left( {\begin{array}{ccc} -p\beta I-k-\mu &{} \beta S &{} \sigma \beta I \\ p\beta I+k &{} q\beta S-d-r-\mu &{} 0 \\ 0 &{} r &{} -\sigma \beta I-\mu \\ \end{array}} \right) . \end{aligned}$$

Following Emvudu et al. [28], we state that $\mathfrak {R}_+^3$ is positive invariant for the system

$$\begin{aligned} \frac{dY}{dt}=PY. \end{aligned}$$

(4)

Also, the system (1) without infection becomes

$$\begin{aligned} \frac{dS}{dt}= A-\mu S. \end{aligned}$$

(5)

The constant $S_0 =A/\mu$ is unique such that:

$$\begin{aligned} A-\mu S>0 \quad \hbox {for}\,\,0\le S<S_0 \end{aligned}$$

and

$$\begin{aligned} A-\mu S<0\quad \hbox {for}\,\,S>S_0 . \end{aligned}$$

Hence the orthant $\mathfrak {R}_+^4$ is positively invariant for the system (1). $\square$

Lemma 2

Let $\Omega =\{(S,E,I, T)\in \mathfrak {R}^{4}{:}S, E, I, T\ge 0, 0<S+E+I+T\le A/\mu +\varepsilon , \varepsilon \in \mathfrak {R}\}$. The trajectories of the system are bounded and the compact set $\Omega$ is a positive invariant and absorbing set that attracts all solutions of the system (1).

Proof

Adding all the equations of the system (1), we obtain

$$\begin{aligned} \frac{dN}{dt}=A-\mu N-dI\le A-\mu N. \end{aligned}$$

This implies

$$\begin{aligned} 0\le N(t)\le A/\mu +N(0)e^{-\mu t}, \end{aligned}$$

where N(0) is the total population at time $t=0$.

$$\begin{aligned} \therefore 0\le \mathop {\lim }\limits _{t\rightarrow \infty } N(t)\le A/\mu . \end{aligned}$$

Hence all the trajectories are bounded and also for $\varepsilon >0$, the set $\Omega$ is an attractive set.

Furthermore, consider a function F defined by

$$\begin{aligned}&F{:}\,\mathfrak {R}_+^4 \rightarrow \mathfrak {R}\\&\quad F(S,E,I,T)=S+E+I+T. \end{aligned}$$

Then F is a differentiable function and its gradient is given by

$$\begin{aligned} \nabla F(x)=(1, 1, 1, 1),\quad \forall x\in \mathfrak {R}_+^4 . \end{aligned}$$

Let the field X be defined by

$$\begin{aligned}&X:\mathfrak {R}_+^4 \rightarrow \mathfrak {R}^{4}\\&(x_1 , x_2 , x_3 , x_4 )=(S, E, I, T)\\&\qquad \mapsto (X_1 , X_2 , X_3 , X_4) i.e. X(x_i)\\&\qquad =X_i , i=1, 2, 3, 4 \end{aligned}$$

with

$$\begin{aligned} X_1= & {} A-\beta SI-q\beta SI-\mu S, \\ X_2= & {} \beta SI+\sigma \beta TI-p\beta EI-(k+\mu )E, \\ X_3= & {} p\beta EI+q\beta SI+kE-(d+r+\mu )I, \\ X_4= & {} rI-\sigma \beta TI-\mu T. \end{aligned}$$

Now,

$$\begin{aligned} \left. {\left\langle {X(x), \nabla F(x)} \right. } \right\rangle \!=\!\dot{S}+\!\dot{E}+\!\dot{I}+\!\dot{T},\quad \forall x\in F^{-1}(A/\mu +\varepsilon ). \end{aligned}$$

Thus,

$$\begin{aligned} \left\langle X(x), \nabla F(x) \right\rangle =\dot{N}=A-\mu N-dI. \end{aligned}$$

Since $\forall x\in F^{-1}(A/\mu +\varepsilon ),\, N=A/\mu +\varepsilon$,

therefore,

$$\begin{aligned} \langle {\left. {X(x), \nabla F(x)} \right\rangle =-\varepsilon \mu -dI\le 0,\quad \forall x\in F^{-1}(A/\mu +\varepsilon ).} \end{aligned}$$

Hence $\Omega$ is a positive invariant set [28]. $\square$

3 Equilibria, bifurcation and stability criteria

Obviously, $P_0 =(A/\mu ,0,0,0)$ is the disease-free equilibrium of the system (1) and it is always exists. If $P^{*}=(S^{*}, E^{*}, I^{*}, T^{*})$ be the endemic equilibrium of the system (1), then we have $S^{*}=A/\{\mu +(1+q)\beta I^{*}\},\, E^{*}=\{(d+r+\mu )(\mu +\beta I+q\beta I^{*})-Aq\beta \}I^{*} \, /(k+p\beta I^{*})(\mu +\beta I^{*}+q\beta I^{*}),T^{*}=rI^{*}/(\mu +\sigma \beta I^{*})$ and $I^{*}$ is a positive root of the equation

$$\begin{aligned} x_1 I^{3}+x_2 I^{2}+x_3 I+x_4 =0, \end{aligned}$$

(6)

where

$$\begin{aligned} x_1= & {} p(1+q)(d+\mu )\sigma \beta ^{3}, \\ x_2= & {} \beta ^{3}\{(1+q)(d+r+\mu )(p\!+\!\sigma )\mu +k(1+q)(d\!+\!\mu )\sigma \\&+\,p(d+\mu )\mu \sigma \!-\!Ap(1\!+\!q)\sigma \beta \} , \\ x_3= & {} k\beta \{(1+q)r\mu -A(1+q)\sigma \beta \\&+\,(1+q+\sigma )\mu ^{2}\}+d\mu \beta \{k(1+q+\sigma ) \\&+\,(1+p+q+\sigma )\mu \} \\&+\,\mu \beta \{(1\!+\!p\!+\!q\!+\!\sigma )(r\!+\!\mu )\mu \!-\!A(p+pq+q\sigma )\beta \}, \\ x_4= & {} (d+r+\mu )(k+\mu )\mu ^{2}(1-R_0 ), \\ \end{aligned}$$

and $R_0$ is the basic reproduction number given by

$$\begin{aligned} R_0 =\left( {\frac{A(k+kq+q\mu )}{\mu (k+\mu )}} \right) \left( {\frac{\beta }{d+r+\mu }} \right) . \end{aligned}$$

(7)

This basic reproduction number provides the average number of secondary cases produced by an average infectious individual during his or her effective infectious period in a totally susceptible population. Clearly, the basic reproduction number is an increasing function of the disease transmission rate $\beta$ as well as the primary progression rate q. The Fig. 1 represents the variation of the basic reproduction number with the endogenous reactivation rate, that is, the rate of progression to active TB. Biologically it means that the numbers of exposed individuals become infectious while the latent period decreases.

Fig. 1

Basic reproduction number increases with the endogenous reactivation

The standard form of the Eq. (6) is

$$\begin{aligned} z^{3}+3Hz+G=0, \end{aligned}$$

(8)

where

$$\begin{aligned}&z=I+\frac{x_2}{3x_1 },\quad H=\frac{3x_1 x_3 -x_2^2 }{9x_1^2 },\\&\quad G=\frac{27x_1^2 x_4 -9x_1 x_2 x_3 +2x_2^3 }{27x_1^3 }. \end{aligned}$$

All the Sturm’s functions are

$$\begin{aligned}&h(z)=z^{3}+3Hz+G, \quad h_{1}(z)=Z^{2}+H,\\&h_2 (z)=-2Hz-G \,\hbox { and }\, h_3 (z)=-(G^{2}+4H^{3}) \end{aligned}$$

Using Sturm’s theorem one can verify that all the roots of the cubic Eq. (8) are real and distinct if $G^{2}+4H^{3}<0$. Therefore, all the positive roots of (8) yield the positive root of (6) if $x_2 \le 0$.

Now $G^{2}+4H^{3}<0$ implies $H<0$. Therefore, $h(\infty )>0$ and $h_i (\infty )>0 \quad (i=1, 2, 3)$. Also, $h(0)=G, h_1 (0)<0, h_2 (0)=-G$ and $h_3 (0)>0$. Thus, the cubic equation (6) has exactly one positive root if $G<0$ and exactly two positive root if$G>0$. Now, $x_4 <0$ i.e. $R_0 >1$ and $x_2 \le 0$ imply $G<0$ but $R_0 <1,x_2 \le 0$ and $x_3 >0$ imply $G>0$. Hence, from the above discussion we can state the following theorem:

Theorem 1

• (i) If $R_0 >1$, then the system (1) has at least one endemic equilibrium point.

• (ii) If $G^{2}+4H^{3}<0,\, R_0 <1,x_2 \le 0$ and $x_3 >0$, then the system (1) has exactly two endemic equilibria, on the other hand if $G^{2}+4H^{3}<0,\, R_0 >1$ and $x_2 \le 0$, then the system has exactly one endemic equilibrium.

• (iii) If $R_0 <1,x_2 >0$ and $x_3 >0$, then the system (1) has no endemic equilibrium.

From the above theorem, it is observed that our model system admits multiple endemic equilibria when the basic reproduction number is below one and in this scenario our system reveals a new subcritical bifurcation, called ‘backward bifurcation’ that is there is a branch of endemic equilibria bifurcating backwards from the disease free equilibrium at $R_0 =1$ (see [29]). Therefore, in our model system, it is not enough to eradicate the disease when the basic reproduction number is below one.

3.1 Simulation and sensitivity analysis

Simulations and sensitivity analysis are important in epidemiology to determine how the disease can be quickly reduced from the population studying the relative importance of different factors responsible for its transmission and prevalence. Generally speaking, initial disease transmission is directly related to the basic reproduction number and the prevalence of disease is directly related to the endemic equilibrium point, specifically to the magnitude of I. We calculate the sensitivity keys of the basic reproduction number $R_0$ and the endemic equilibrium point to the parameters in the model. For this purpose, we choose a set of parameter values as: $A=9, \mu =0.07,\beta =0.5, p=0.13, q=0.02, k=0.002,d=0.17,r=5.6$ and $\sigma =0.34$. For these parameter values, we have $R_0 =0.52593<1$ and there exist two endemic equilibria (30.0896, 79.7543, 0.4492, 17.1872) and $(9.9355, 86.6901, 1.6389, 26.3267)$. Thus, we find that the system has multiple endemic equilibria when $R_0 <1$ and it indicates the existence of backward bifurcation (see Fig. 2). The eigenvalues for the first endemic equilibrium are $-0.926357, -0.103986,-0.0577127,0.186297$ and for the second are $-1.28873,-0.192856,-0.0285937\pm 0.164238i$. Therefore, the system has both unstable and stable endemic equilibria when the basic reproduction is below one. In Fig. 2, we pointed out two critical points $0.4492=I_1$ (say) and $1.6389=I_2$ (say), where $I_1$ and $I_2$ lie on unstable branch and stable branch respectively. The Fig. 3 be a sign of backward bifurcation depending on the exogenous re-infection and endogenous reactivation but not on the re-infection parameter $\sigma$. Therefore, if the treated individuals are completely effective that is if $\sigma =0$, then the system may exhibits a backward bifurcation at $R_0 =1$ and this bifurcation confirms that the system has multiple endemic equilibria when the basic reproduction number is below one, numerically presented in Fig. 3.

Fig. 2

Variation of infective population with reproduction number

Fig. 3

Variation of infectious population versus reproduction number in absence of re-infection among the treated individuals with the other parameters value are $A=9,\mu =0.07, \beta =0.5, p=0.13, q=0.02,k=0.002, d=0.17,r=5.6$

3.2 Sensitivity analysis of basic reproduction number

Since we have the explicit expression for $R_0$, we can derive an analytical expression for its sensitivity to each parameter using the normalized forward sensitivity index as described by Chitnis et al. [30]. Table 1 shows the sensitivity indices of $R_0$ with respect to each of the nine parameters used in the model. The sensitivity indices of $R_0$ with respect to the parameters A and $\beta$ are equals to 1.0. So, the most sensitive parameters to the reproductive number are the recruitment and contact rate. The least sensitive parameter is the natural death rate for $R_0$. The negative sign of the sensitivity indices for $R_0$ implies that increase in the relevant parameter leads to the decrease in the corresponding reproductive number.

Table 1 Sensitivity indices of $R_0$ to parameters for the TB model

Theorem 2

The disease-free equilibrium $P_0 =(A/\mu , 0, 0, 0)$ is locally asymptotically stable when $R_0 <1$ and unstable when $R_0 >1$.

Proof

The characteristic equation at the disease-free equilibrium is

$$\begin{aligned} (\lambda +\mu )^{2}(\lambda ^{2}+a_1 \lambda +a_2 )=0, \end{aligned}$$

(9)

where

$$\begin{aligned} a_1= & {} d+k+r+2\mu -Aq\beta /\mu , \\ a_2= & {} (k+\mu )(d+r+\mu )-A(k+kq+q\mu )\beta /\mu . \end{aligned}$$

Clearly, $a_2 >0$ implies $a_1 >0$. Therefore, all the eigenvalues of (9) will be negative or will have negative real parts if $a_2 >0$ i.e. if $R_0 <1$.

Thus the disease-free equilibrium $P_0$ is locally asymptotically stable when $R_0<1$ and unstable when $R_0>1$. $\square$

Note 1

From the above Theorem 2, we can conclude that the stability of the disease-free equilibrium changes from stable to unstable when the basic reproduction number $R_0$ increases through 1, but when its value is equal to one, the system achieves a bifurcation at the disease-free equilibrium called transcritical bifurcation, which is proved in the next theorem.

Theorem 3

The system (1) undergoes transcritical bifurcation at the equilibrium point $P_0$ when the bifurcation parameter $R_0 =1$.

Proof

When $R_0 =1$, Jacobian matrix $(\Sigma )_{P_0 }$ has a geometrically simple zero eigenvalue with right eigenvector $\phi =col\left( {-\frac{A(1+q)\beta }{\mu ^{2}}, \frac{A\beta }{\mu (k+\mu )}, 1, \frac{r}{\mu }} \right)$ and left eigenvector $\psi =\left( {0, 1, \frac{k+\mu }{k}, 0} \right)$.

Now

$$\begin{aligned} f(X, \beta )= & {} \left( {\begin{array}{c} A-\mu S-\beta SI-q\beta SI \\ \beta SI-p\beta EI-(k+\mu )E+\sigma \beta TI \\ p\beta EI+q\beta SI+kE-(d+r+\mu )I \\ rI-\sigma \beta TI-\mu T \\ \end{array}} \right) \\= & {} \left( {\begin{array}{l} f_1 \\ f_2 \\ f_3 \\ f_4 \\ \end{array}} \right) \hbox { and } X=col(S, E, I, T).\\ \therefore D_\beta f= & {} \left( {\begin{array}{c} -(1+q)SI \\ SI-pEI+\sigma TI \\ pEI+qSI \\ -\sigma TI \\ \end{array}} \right) . \end{aligned}$$

From the above results, we obtain

$$\begin{aligned} \left( {\psi (D_X D_\beta f)\phi } \right) _{P_0 } =\frac{A}{\mu }\left( {1+\frac{k+\mu }{k}q} \right) \ne 0 \end{aligned}$$

and

$$\begin{aligned}&\psi \left( {(D_{XX} f)(\phi , \phi )} \right) =\left( {\psi \sum _{i=1}^4 {(e_i \phi ^{t}D_X (D_X f_i )^{t}\phi )} } \right) _{P_0 } \\&\quad =-\frac{2A\beta ^{2}}{k}\left\{ {\frac{(1+q)(k+kq+q\mu )}{\mu ^{2}}-\frac{p}{k+\mu }} \right\} \\&\qquad +\frac{2r\sigma \beta }{\mu } \ne 0. \end{aligned}$$

Hence the system (1) undergoes transcritical bifurcation at the disease-free equilibrium $P_0$ (see [31]). $\square$

3.3 Stability of endemic equilibrium and bifurcation analysis

The characteristic equation at the endemic equilibrium $P^{*}=(S^{*}, E^{*}, I^{*}, T^{*})$ becomes

$$\begin{aligned} \lambda ^{4}+b_1 \lambda ^{3}+b_2 \lambda ^{2}+b_3 \lambda +b_4 =0, \end{aligned}$$

(10)

where

$$\begin{aligned} b_1= & {} k+\mu +p\beta I^{*}+\frac{kE^{*}}{I^{*}}+\frac{A}{S^{*}}+\frac{rI^{*}}{T^{*}}, \\ b_2= & {} [q(1+q)\beta ^{2}S^{*2}I^{*2}T^{*}+S^{*}I^{*}\{rI^{*}(\mu +p\beta I^{*})\\&+\,kr(E^{*}+I^{*})-p\beta \mu E^{*}T^{*}\} \\&+\,A\{rI^{*2}+(\mu +p\beta I^{*})I^{*}T^{*}\\&+\,k(E^{*}+I^{*})T^{*}\}]/S^{*}I^{*}T^{*},\\ b_3= & {} [(1+q)\beta ^{2}S^{*2}I^{*}\{qrI^{*} \\&+\,(k+kq+q\mu +p\beta I^{*}+pq\beta I^{*})T^{*}\}\\&+\,A\{rI^{*}(\mu +p\beta I^{*}) \\&+\,kr(E^{*}+I^{*})-p\mu \beta E^{*}T^{*}\}-\mu \beta S^{*}\{prE^{*}I^{*}\\&+\,\sigma (k+p\beta I^{*})T^{*2}\}]/S^{*}T^{*}, \\ b_4= & {} \beta [(1+q)r\beta S^{*2}I^{*2}(k+kq+q\mu +p\beta I^{*}\\&+\,pq\beta I^{*})-A\mu \{prE^{*}I^{*} \\&+\,\sigma (k+p\beta I^{*})T^{*2}\}]/S^{*}T^{*}. \end{aligned}$$

By Routh–Hurwitz criteria, the endemic equilibrium is locally asymptotically stable if all $b_i (i=1, 2, 3, 4)$ are positive and $b_1 b_2 b_3 >b_3^2 +b_1^2 b_4$. $\square$

Now we consider $A=18,\mu =0.06,\beta =0.4,p=0.12, q=0.05,k=0.006,d=0.17,r=2.8$ and $\sigma =0.09$ for our model system (1). For these parameter values, the system has a unique endemic equilibrium point (1.01288, 62.5176, 42.1693, 74.8206) and the basic reproductive number $R_0 =5.58056$. The eigenvalues at the endemic equilibrium point $(1.01288, 62.5176, 42.1693, 74.8206)$ are $-17.8031,\, -0.238539$ and $-1.70331\pm 0.478295i$. Therefore, the endemic equilibrium point (1.01288, 62.5176, 42.1693, 74.8206) is locally asymptotically stable. From Fig. 7, it is observed that every trajectory of the state variables converges around their endemic level while the initial values of susceptible, exposed, infectious and treated individual are taken as 80, 20, 10 and 5 respectively. The numbers of infectious individuals versus re-infection parameters and the disease transmission coefficient are respectively plotted in Figs. 9 and 10. The each bifurcation curves in Figs. 8 and 9 represents supercritical bifurcation indicating the bifurcation is forward. From Figs. 8 and 9, we may further conclude that the number of infectious individuals is an increasing function of the re-infection parameters and the disease transmission rate. Again, we discuss the sensitivity analysis of the system (1) varying the force of infection $\beta$. From Figs. 10 and 11, it is seen that the number of exposed and infectious individuals are directly proportional with the disease transmission rate $\beta$. Specifically, if the time unit is taken as months, then the Figure 11 indicates that the number of infectious individuals may extinct from the population after 4 months when the force of infection is below 0.01. But, in this scenario, we can’t conclude that the total population is free from infection as the exposed individuals (i.e. infected but, not infectious) persist in the population (see Fig. 10).

4 Application of optimal control problem

In the previous section we describe the dynamical behavior of the system. Throughout the discussions we have not considered any treatment to the infectious individuals. But in this section we analyze the phenomena if we give some treatment to the infectious individuals. Now, we introduce a control function $u(t) \,(0\le u(t)\le 1)$, to our model system (1), represents the fraction of infectious individuals that will be put under treatment to reduce the number of infectious individuals. In this situation optimal control theory becomes a powerful mathematical tool that can be applied to the optimal control problem.

Our main aim is to minimize the infectious individuals as well as to reduce the costs require to control the disease. For this purposes Pontryagin’s maximum principle will be applied (see [32, 33]). Now we form the objective functional of our optimal control problem is as follows:

$$\begin{aligned} J(u)=\mathop {\min }\limits _u \int _0^{t_f } {[BI(t)+Cu^{2}(t)]dt} , \end{aligned}$$

(11)

subject to

$$\begin{aligned} \left\{ {\begin{array}{lll} \frac{dS}{dt}= A-\mu S-\beta \textit{SI}-q\beta \textit{SI}, \\ \frac{dE}{dt}= \beta \textit{SI}-p\beta \textit{EI}-(\mu +k)E+\sigma \beta \textit{TI}, \\ \frac{dI}{dt}= p\beta EI+q\beta \textit{SI}+\textit{kE}-(d+r+\mu +u)I, \\ \frac{dT}{dt}= (r+u)I-\mu T-\sigma \beta \textit{TI}, \\ \end{array}} \right. \end{aligned}$$

(12)

with initial conditions

$$\begin{aligned}&S(0) = S_0 \ge 0,\quad E(0)=E_0 \ge 0,\quad I(0)=I_0 \ge 0, \nonumber \\&\quad T(0) = T_0 \ge 0. \end{aligned}$$

(13)

Our objective functional is a continuously differentiable function of state variables and control. Pontryagin’s maximum principle gives the necessary conditions to determine a feasible value of the control for which the objective functional would be optimized. If this feasible control exists, then it is said to be the optimal control (see [34]). The weight factors B and C balance out the relative importance of the two terms in the objective functional. The square of the control parameter is taken to remove the harmness causes due to the side effect and overdose of the control (see [33, 35]).

The control induced basic reproduction number for the control system (12) is

$$\begin{aligned} R_0^c =\left( {\frac{A(k+kq+q\mu )}{\mu (k+\mu )}} \right) \left( {\frac{\beta }{d+r+\mu +u}} \right) . \end{aligned}$$

To find the optimal solution of the optimal control problem (11), we first find the Lagrangian of our optimal control problem as follows:

$$\begin{aligned} L( I, u)=BI(t)+Cu^{2}(t). \end{aligned}$$

(14)

Also, to find the minimum value of the Lagrangian, we define the Hamiltonian H for the optimal control problem as

$$\begin{aligned}&H(x(t), u, \lambda _1 , \lambda _2 , \lambda _3 , \lambda _4 , t)=L(I, u,) \nonumber \\&\quad +\,\lambda _1 (t)\{ A-\mu S-\beta SI-q\beta SI\} \nonumber \\&\quad +\,\lambda _2 (t)\{ \beta SI-p\beta EI-(\mu +k)E+\sigma \beta TI\} \nonumber \\&\quad +\,\lambda _3 (t)\{p\beta EI+q\beta SI+kE-(d+r+\mu +u)I\} \nonumber \\&\quad +\, \lambda _4 (t)\{(r+u)I-\mu T-\sigma \beta TI\}, \end{aligned}$$

(15)

where $x(t)=(S(t), E(t), I(t), T(t))$ and $\lambda _i$ for $i=1, 2, 3, 4$ are known as the adjoint variables or the costate variables.

To prove the existence of an optimal control, we use the results of [20, 36–38], stated and proved in the following theorem:

Theorem 4

There exists an optimal control $u^{*}(t)$ for $t\in [0, t_f ]$ such that $J(u^{*})=\mathop {\min }\limits _{u\in U^{c}} J(u)$, subject to the control system (12).

Proof

As the control variable and all the state variables are nonnegative, so the control variable u(t) is convex. Moreover, the control space $U^{c}=\{u(t): u$ is measurable and $0\le u(t)\le 1$ for $t\in [0, t_f ]\}$ is convex and closed. The optimal system is bounded which determines the compactness needed for the existence of the optimal control. In addition, the Lagrangian is convex on the controls. Therefore, these conditions determine the existence of the optimal control $u^{*}(t)$ which minimizes the objective functional (11) for $t\in [0, t_f ]$ with the help of the system of differential equations (12). Also, we can easily see that, there exist a constant $\eta >1$, positive numbers $\xi _1$ and $\xi _2$ such that

$$\begin{aligned} J(u(t))\ge \xi _2 +\xi _1 \left( |u|^{2}\right) ^{\eta /2}, \end{aligned}$$

which completes the existence of an optimal controls. $\square$

To find the optimal solution, we use the Pontryagin’s maximum principle [34, 39] to the Hamiltonian H and obtain the following theorem.

Theorem 5

If $S^{*}(t), E^{*}(t), I^{*}(t), T^{*}(t)$ are the solutions of the control system (12) together with the control variable $u^{*}(t)$ for the optimal control problem (11), then there exist adjoint variables $\lambda _1 (t), \lambda _2 (t), \lambda _3 (t)$ and $\lambda _4 (t)$ that satisfy the following conditions

$$\begin{aligned} {\lambda }'_1 (t)= & {} \beta (\lambda _1 (t)-\lambda _2 (t))I^{*}(t)+q\beta (\lambda _1 (t)-\lambda _3 (t))I^{*}(t) \nonumber \\&+\,\,\mu \lambda _1 (t), \nonumber \\ {\lambda }'_2 (t)= & {} (\lambda _2 (t)-\lambda _3 (t))(k+p\beta I^{*}(t))+\mu \lambda _2 (t), \nonumber \\ {\lambda }'_3 (t)= & {} \beta (\lambda _1 (t)-\lambda _2 (t))S^{*}(t)+q\beta (\lambda _1 (t)-\lambda _3 (t))S^{*}(t) \nonumber \\&+\,\,p\beta (\lambda _2 (t)-\lambda _3 (t))E^{*}(t) \nonumber \\&+\,\,\sigma \beta (\lambda _4 (t)-\lambda _2 (t))T^{*}(t)\nonumber \\&+\,\,(r+u^{*}(t))(\lambda _3 (t)-\lambda _4 (t)) \nonumber \\&+\,\,(d+\mu )\lambda _3 (t)-B, \nonumber \\ {\lambda }'_4 (t)= & {} \sigma \beta (\lambda _4 (t)-\lambda _2 (t))I^{*}(t)+\mu \lambda _4 (t), \end{aligned}$$

(16)

with transversality conditions (or boundary conditions)

$$\begin{aligned} \lambda _1 (t_f )=\lambda _2 (t_f )=\lambda _3 (t_f )=\lambda _4 (t_f )=0. \end{aligned}$$

(17)

Also, the optimal control variable is given by

$$\begin{aligned} u^{*}(t)=\max \left\{ {\min \left( {\frac{(\lambda _3 (t)-\lambda _4 (t))I^{*}(t)}{2C}, 1} \right) , 0} \right\} . \end{aligned}$$

(18)

Proof

Suppose $S(t)=S^{*}(t),\, E(t)=E^{*}(t),\, I(t)=I^{*}(t)$ and $T(t)=T^{*}(t)$.

Differentiating (15) with respect to S, E, I, T, we obtain

$$\begin{aligned}&\frac{d\lambda _1 (t)}{dt}=-\frac{\partial H}{\partial S}=\beta (\lambda _1 (t)-\lambda _2 (t))I^{*}(t)+ q\beta (\lambda _1 (t) \\&\quad -\,\,\lambda _3 (t))I^{*}(t)+\mu \lambda _1 (t), \\&\frac{d\lambda _2 (t)}{dt}=-\frac{\partial H}{\partial E}=(\lambda _2 (t)-\lambda _3 (t))(k+p\beta I^{*}(t))\\&\quad +\,\,\mu \, \lambda _2 (t), \\&\frac{d\lambda _3 (t)}{dt}=-\frac{\partial H}{\partial I}=\beta (\lambda _1 (t)-\lambda _2 (t))S^{*}(t)+q\beta (\lambda _1 (t)\\&\quad -\,\,\lambda _3 (t))S^{*}(t)+p\beta (\lambda _2 (t)-\lambda _3 (t))E^{*}(t)+\sigma \beta (\lambda _4 (t)\\&\quad -\,\,\lambda _2 (t))T^{*}(t)+(r+u^{*}(t))(\lambda _3 (t)-\lambda _4 (t))\\&\quad +\,\,(d+\mu )\lambda _3 (t)-B, \\&\frac{d\lambda _4 (t)}{dt}=-\frac{\partial H}{\partial T}=\sigma \beta (\lambda _4 (t)-\lambda _2 (t))I^{*}(t)+\mu \lambda _4 (t). \end{aligned}$$

By the optimality conditions, we get

$$\begin{aligned} 0=\frac{\partial H}{\partial u}=2Cu(t)-\lambda _3 (t)I^{*}(t)+\lambda _4 (t)I^{*}(t). \end{aligned}$$

Using the property of the control space [40], we have

$$\begin{aligned} u^{*}(t)=\left\{ {\begin{array}{l@{\quad }l} 0, &{}\quad \textit{if} \,\,\, \frac{(\lambda _3 (t)-\lambda _4 (t))I^{*}(t)}{2C}\le 0 \\ \frac{(\lambda _3 (t)-\lambda _4 (t))I^{*}(t)}{2C}, &{} \quad \textit{if} \,\,\, 0<\frac{(\lambda _3 (t)-\lambda _4 (t))I^{*}(t)}{2C}<1 \\ 1, &{}\quad \textit{if}\,\,\, \frac{(\lambda _3 (t)-\lambda _4 (t))I^{*}(t)}{2C}\ge 1. \\ \end{array}} \right. \end{aligned}$$

This result can be rewritten as

$$\begin{aligned} u^{*}(t)=\max \left\{ {\min \left( {\frac{(\lambda _3 (t)-\lambda _4 (t))I^{*}(t)}{2C}, 1} \right) , 0} \right\} . \end{aligned}$$

$\square$

5 Numerical simulations and discussions

In this section, we shall give some numerical simulations on optimal treatment strategy of our TB model. The optimal treatment strategy is obtained by solving the optimality system (11) consisting of the state equations (12) and the adjoint equations (16) together with the treatment control relation (18). An iterative method is used for solving the optimality system. Using a forward fourth order Runge–Kutta procedure we start to solve the state equations with an estimate for the control over the simulated time. Parameters are chosen as $A=18,\mu =0.06, \beta =0.4,p=0.12,q=0.05,k=0.006,d=0.17, \sigma =0.09,r=2.8$. Because of the transversality conditions (17), the adjoint equations are solved by a backward fourth order Runge–Kutta method using the current solution of the state equations (see [34]). We assume the weight factors as

$B=1$ and $C=5$ associated with the infectious individuals and the treatment control respectively, and the initial state values are chosen as $S_0 =80, E_0 =20, I_0 =10,T_0 =5$. The results are presented in Figs. 12, 13, 14 and 15 with control (dash-dot curve) and without control (solid curve). In Fig. 12, it is observed that the number of susceptible individuals decreases slowly in presence of treatment control where as the number of latent individuals’ gradually increases at first and after long time they have been decreasing because of the latent TB become infectious and the treatment is applied to the infectious individual which is depicted in Fig. 13. But it was inferred from Fig. 14 that the number of infectious individuals drops very rapidly during the treatment period and in this period it is observed from the Fig. 15 that the numbers of treated individuals have been increased. Figure 16 represents the control $u^{*}(t)$ and the optimal paths of control variable are plotted for different values of the weight factor C. It is found that the treatment control takes maximum value one in starting time period when the weight factor $C=5, 10, 20$ and to the end of the duration of application of control it goes down and then the control admits the value zero at the end of the time interval. It has also been noticed that when the value of the weight factor associated with the treatment control is increased, the amount of treatment control decreases. So, the percentage of treatment control is inversely proportional to the weight factor C. For this reason, the treatment cost $Cu^{2}$ increases while the weight factor C decreases and if it increases, the treatment cost for the patient decreases. Therefore, it is evident that to recover the TB disease in very tiny time the more power treatment and consciousness is required. Solving the four adjoint equations by backward Runge–Kutta fourth order procedure, the variation of four adjoint variables $\lambda _1 , \lambda _2 , \lambda _3$ and $\lambda _4$ with time are plotted in Fig. 17. As the time derivatives of the adjoint variables are negative of the corresponding partial derivatives of the Hamiltonian H with respect to the state variables, the Fig. 17 confirms that the adjoint variables are directly related to the change of the value of the Hamiltonian. When we study the figure for the adjoint variables, it is found that $\lambda _1 , \lambda _2 , \lambda _3$ and $\lambda _4$ slowly decrease as time increases and all the adjoint variables assume zero at the final time during our time period. This phenomenon ensures that to get the minimum value of the objective functional (11) and the rate of change of Hamiltonian H will be increasing with the changes of the state variables S, E, I and T.

6 Conclusions

In this paper, we have analyzed a tuberculosis epidemic model considering the effects of exogenous re-infection, endogenous reactivation and the re-infection rate among the treated individuals. The basic reproduction number $(R_0 )$ is obtained and found that it is an increasing function of the disease transmission rate and also of the recruitment rate. It is also found that the disease-free equilibrium is stable when $R_0 <1$, unstable when $R_0 >1$, and for $R_0 =1$, the system undergoes a transcritical bifurcation at the disease-free equilibrium. Furthermore, two endemic equilibria of our system has been investigated for $R_0 <1$ and out of these two endemic equilibria one is unstable and other is stable indicating a new type of subcritical bifurcation, called backward bifurcation which is shown in Fig. 2. Therefore, the basic reproduction number $R_0$ may not be a sufficient threshold parameter in our model system to eradicate the disease from the population when its value is below one. We have observed that for a very small change of the level of exogenous re-infection (p), there is a drastic change in the backward bifurcation. Among the treated individuals if there is no re-infection term (i.e. $\sigma =0$), our model system will also be revealed backward bifurcation which is demonstrated in Fig. 3.

We have also plotted some bifurcation curves between the fraction of infectious individuals vs. the level of exogenous re-infection, the rate of re-infection among the treated individuals, endogenous reactivation and rate of primary progression which are depicted in Fig. 4. The two branches of the bifurcation curves in Fig. 4 are seen and out of these two branches one is unstable branch and other is stable branch. In Fig. 4a, b, the movement of these two curves change from unstable to stable when the level of exogenous re-infection $p=0.1285$ and the infection rate of treatment individuals $\sigma =0.35$ respectively. Therefore, these two bifurcations are known as subcritical bifurcation and also identify as backward bifurcation. In Fig. 4c, d, it has been noticed that the backward bifurcation starts respectively at $k=0.005337$ and $q=0.06307$ which are the two critical points. This bifurcation also indicates that our system can be sustained at multiple endemic equilibria one of which is unstable and other is stable. Therefore, we can conclude that the latently infected individuals are likely to be at greater risk of progressing to active TB than the susceptible individuals. The figure 5 represents the variation of the disease transmission rate $\beta$ with the exogenous re-infection rate and these two parameters are related inversely to each other, and this figure indicates that when transmission rate i.e. contact rate not increases, the exposed individuals become infectious due to the higher level of exogenous re-infection. Also, it is seen from the Fig. 6 that the level of exogenous re-infection deceases when the primary disease progression rate increases.

Fig. 4

Variation of infectious population with exogenous re-infection parameter, re-infection parameter in treated individuals, the endogenous reactivation parameter and primary progression rate respectively are presented in Figure (a–d). The each bifurcation curve has two branch one is unstable and other is stable. Therefore, this type of bifurcation will also be a subcritical bifurcation indicating backward bifurcation

Fig. 5

We plot the transmission coefficient as a function of the exogenous re-infection parameter. This figure shows that the probability of the disease transmission is a decreasing function of the exogenous re-infection

Fig. 6

We plot the change of exogenous re-infection parameter with the primary progression rate of disease. This figure shows that when the value of the primary progression decreases, the level of exogenous re-infection increases

The local stability of endemic equilibrium is elucidated analytically and its simulation is shown in Fig. 7. In this figure we have seen that every trajectory of the state variables asymptotically converges around their endemic level. Using these set of parameter values we have drawn three bifurcation (supercritical) curves taking the fraction of infectious individuals as a function of re-infection parameters and the contact rate which are individually presented in Figs. 8 and 9. It is found in Figs. 8(i), (ii) that the disease may persist in the population when the model system does not contain any re-infection parameter that is when the super-infection (exogenous re-infection) and the rate of re-infection among the treated individuals are not applied in our model system. For example, we obtain from Fig. 8(ii) a critical value of the infectious individual as $I^{*}=4.616$ when the rate of re-infection among the treated individuals is zero. Furthermore, the Fig. 9 represents the variation of infectious individuals with the contact rate. A sharp increase in the number of infectious individuals have been observed and the forward bifurcation starts at the critical value $\beta =0.07168$. The sensitivity analysis of the system (1) is also investigated giving time series evolution in Figs. 10 and 11 depicting the dynamical behavior of the exposed and infectious individuals against time for different values of contact rate $\beta$. Blower and Dowlatabadi [41] studied the sensitivity and uncertainty analysis of an HIV model. For discussing sensitivity analysis they used two important methods namely, Latin hypercube sampling (LHS), which is an extremely efficient sampling design and partial rank correlation coefficients (PRCC), which indicates the degree of monotonicity between the specific input variable and the particular outcome variable.

Fig. 7

The figure shows that all the trajectories of the state variables are asymptotically stable

Fig. 8

Variation of infectious population with exogenous re-infection and re-infection parameter among the treated individuals

Fig. 9

Variation of infectious population with disease transmission coefficient. The bifurcation curve indicates forward bifurcation.

Fig. 10

Sensitivity of exposed individuals for different values of contact rate

Fig. 11

Sensitivity of infectious individuals for different values of contact rate

From the aforesaid conclusion any one can be persuaded that the MTB is a fatal disease in our society and to control this disease, we have presented optimal control system using one treatment control variable into the infectious individuals. In this situation our aim is to get maximum disease control by using minimum cost. It is clearly observed that the basic reproductive number will be greater than the control induced reproductive number and it means that the disease will fully persist in the population while the control induced reproductive ratio is above one. Applying optimal control theory to our control system, the control variable and the adjoint system are investigated. The Figs. 12, 13, 15 and 15 are plotted for both with and without treatment control. We have seen that the number of susceptible individuals decrease slowly and the number of exposed individual gradually increases during our treatment period. Moreover, the numbers of infectious individuals have been decreased very rapidly in presence of treatment control where as the number of treated individuals’ increase throughout the treatment period. In Fig. 14, it is found that the treatment cost is inversely proportional to the weight factor associated with the control function. Lastly, we can conclude that the treatment control is too much necessary for this type of fatal disease and it is also evident that the TB can be controlled by applying extra treatment strategies.

Fig. 12

This figure represents the susceptible individuals for both with and without controls

Fig. 13

This figure represents the exposed individuals for both with and without controls

Fig. 14

This figure represents the infectious individuals for both with and without controls

Fig. 15

This figure represents the treated individuals for both with and without controls

Fig. 16

The treatment control variable is plotted as a function of time

Fig. 17

The figure is drawn for the adjoint variables $\lambda _1 , \lambda _2 , \lambda _3 , \lambda _4$