Keywords

1 Introduction

Tuberculosis (TB) is a communicable disease that affects the lungs. Some studies have suggested that up to a third of the world human population has contracted the disease [1]. Tuberculosis is caused by family of bacteria called Mycobacterium Tuberculosis. This airborne infectious disease is a public health challenge worldwide: in USA [2] and European nation [3, 4], and developing countries. In other words, tuberculosis remains a major epidemic that contributes to the morbidity and mortality [5, 6] of both human and animal populations [7]. Usually, when the disease is contracted by individuals, it is not immediately obvious. For instance, when a person is infected, he/she may remain infected for years, or even latently-infected for life [8]. It is attested to be highly prevalent in middle-income countries, among other regions [6]. The prevalence of TB, globally, in 2018 was about 1 million cases more than that of HIV/AIDS, and there were up to 1.5 million more deaths [6].

Mostly, TB can be transmitted whether through direct or indirect contact with an infected person [4, 9]. The symptoms of tuberculosis include bad cough that produces blood and/or sputum (phlegm from deep inside the lungs), which can persist for up to three weeks, chest pain, fever, and sweating at night, among others [10]. TB may take from two to three months to become symptomatic, due to long incubation period. The long latent period of MTb bacteria prolongs the start of the active phase of the disease, which further makes it difficult to understand how the disease develops. Another point related to the spread of this disease is the level of exogenous re-infection (see [5, 11]). Already infected Individuals (even in the dormant stage), with low levels of immunity may become newly infected through contact with an infectious individual [12]. Therefore, anyone in the latent phase of TB can move to the active phase due to exogenous re-infection rate [12].

Bandera et al. [13] discussed exogenous re-infection in locations with low prevalence of TB; the authors established that re-infection occurs at a lower rate in developed countries than in high-risk areas. Uys et al. [14] studied a deterministic model of TB with the probability of re-infection component and suggested that the rate of re-infection is a multiple of the rate of first time infection. Other studies have investigated the influences of re-infection or multiple infections (see [11, 15]) as well as on the effects of exogenous re-infection on the transmission dynamics of TB see [17,18,19,20,21]. Feng et al. [16] proposed a deterministic model for TB with exogenous re-infection and submitted that an infectious individual can infect another one with each contact per unit of time.

The present paper is motivated by the study of [12], in which the authors proposed a TB model with SEIT components, and it is later being reduced to SEI model. The present study built on the work of [12], by finding the equilibria and the stability of the equilibria, as well as using simulation for the bifurcation part. We investigate the significant impacts of transmission rate \(\beta \) and exogenous re-infection p on the bifurcational changes in dynamics in this epidemiological system.

This article is presented as follows: a mathematical model of TB is considered in Sect. 2. In Sect. 3 we focus on the existence of steady state and stability of disease free (DFE). In Sect. 4 stability of endemic equilibrium point (EEP) and bifurcation analysis are carried out. The numerical simulation and bifurcation analysis results are reported in Sect. 5. Finally, the discussion and conclusion of the study are given in Sect. 6.

2 Model Formulation

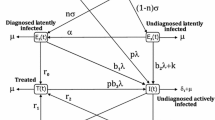
We examined the transmission dynamics of TB by employing a nonlinear ODE system of SEIT type system, which is developed by Kar and Mondal [12]. Our aim is to better understand the interplay between exogenous re-infection and transmission rate. In determining the outbreaks of TB. The whole population N(t)is classified into four (4) compartments, S, E, I and T, which respectively denote susceptible, exposed, infected and treated individuals. Kar and Mondal [12] assumed that individuals that have been treated can be re-infected if their immunity is low. This leads to S-E-I-T-E type system to the model transmission dynamics of TB. The SEITE process of TB spreading is shown in Fig. 1.

Fig. 1
figure 1

The schematic diagram of SEITE TB model by [12]

Full size image

In this epidemiological system, the susceptible compartment is increased by recruiting individuals, either by immigration or birth, into the population at the constant rate \(\varLambda \). The term \(\mu \) is taken to be natural death rate. The exposed compartment becomes infectious and progresses to active infected state at a constant rate \(\kappa \). Infected individuals also develop active tuberculosis because of exogenous re-infection (can acquire new infection from another infectious individual) at a rate p. Infected individuals are recovered at the rate r. The treated individuals return to the exposed compartment due to low immunity at the rate \(\sigma \).

2.1 The Model

The nonlinear model that is considered in this study consists of a system of ordinary differential equations (ODE):

$$\begin{aligned} \begin{array}{l} {\frac{dS}{dt} =\varLambda -\mu S- \beta S I } \\ \\ {\frac{dE}{dt} =\beta S I - p\beta EI -\left( \kappa +\mu \right) E}+ \sigma \beta T I \\ \\ {\frac{dI}{dt} = p\beta EI+ \kappa E -\left( \mu + r \right) I} \\ \\ {\frac{dT}{dt} =rI -\mu T - \sigma \beta T I } \end{array} \end{aligned}$$
(1)

with

$$N = S+E+I+T.$$

3 Mathematical Model Analysis

In this section, we seek to qualitatively study dynamical properties of the TB model (1) by means of invariant and positivity solutions.

3.1 Invariant Region

Theorem 1

Let

$$\varPhi =\{(S,E,I,T)\in R_{+}^{4}:N\le \frac{\varLambda }{\mu }\}$$

The region \(\varPhi \) is positively-invariant and attract all positive solutions of the model.

Proof

As \( N = S+E+I+T\), adding all the equations of the system (1), we have

$$\begin{aligned} \frac{dN}{dt}=\varLambda -\mu N \end{aligned}$$
(2)

By standard comparison theorem in [22] we see that

$$\begin{aligned} \frac{dN}{dt}\le \varLambda -\mu N \end{aligned}$$
(3)

which yield (by method of integration factor).

$$ N(t) \le \frac{\varLambda }{\mu } +\left[ N(0)-\frac{\varLambda }{\mu }\right] e^{- \mu t}$$

In particular, if \(N(0)\le \frac{\varLambda }{\mu }\), then \(N(t) \le \frac{\varLambda }{\mu }\). Hence \(\varPhi \) is positively-invariant and an attractor so that no solution path leaves through any boundary of \(\varPhi \) [23].

3.2 Positivity of Solutions

In order for the tuberculosis infection model (1) to be epidemiological realistic, it is essential to demonstrate that all the state variables are positive at all times.

Let initial data be

Theorem 2

\( \{(S, E, I, T) \ge 0\} \in \varPhi . \)

Then, the solution set \( \{S(t), E(t), I(t), T(t)\} \) of the model system (1) is non-negative for all \( t > 0. \)

Proof

As in Obasi and Mbah [24] from the non-linear system of model system (1) we take the first equation

$$ \frac{dS}{dt}= \varLambda -\mu S -\beta S I $$
$$\begin{aligned} \frac{dS}{dt}\ge - ( \mu +\beta I)S \end{aligned}$$
(4)
$$\begin{aligned} \Rightarrow \frac{dS}{S} \ge - ( \mu +\beta I) dt. \end{aligned}$$
(5)

integrating (5) gives

$$\begin{aligned} S(t) \ge S(0) e^ {\int -(\mu +\beta I) dt} \ge 0. \end{aligned}$$
(6)

In the same way, it can be verified that \(E(t) > 0\), \( I(t) > 0\) and \( T(t) > 0\) for all \(t > 0\) [21].

Thus, the disease is uniformly consistent for every positive solution. The above result can also be proved by using the approach in [25].

The system (1) stands for the dynamic transmission of TB in humans; hence, all the related parameters are taken to be positive. As a result, the following positivity and invariance results must hold.

It is assumed that Eq. (2) admits a positive equilibrium \(N_0\) that satisfies \( \varLambda =\mu N\) with \(N_0\) represents population equilibrium in the absence of disease. It is also assumed that this equilibrium is asymptotically stable and unique \(N_0 > 0\). This implies that the total population will still be in equilibrium while the epidemic is spreading. Therefore, Eq. (1) can be considered if \( S+E+I+T = N_0.\)

The system of Eqs. (1) is not solvable analytically because of the non-linearities. Instead, we can eliminate the variable T in order to reduce system (1) into three dimensional system. In particular, we set \( T = N_0 - S - E -I\) can be written as:

$$\begin{aligned} \begin{array}{l} {\frac{dS}{dt} =\mu N_0 -\mu S- \beta S I } \\ \\ {\frac{dE}{dt} =\beta S I - p\beta EI -\left( \kappa +\mu \right) E}+ \sigma \beta I(N_0 - S - E -I) \\ \\ {\frac{dI}{dt} = p\beta EI+ \kappa E -\left( \mu + r \right) I} \\ \\ \end{array} \end{aligned}$$
(7)

3.3 Analysis of Disease-Free Equilibrium (DFE), \( P _0 \), and Basic Reproduction Number \(R_0\)

The disease-free equilibrium (DFE) state, \( P _0 \) is a steady state solution where there is no infection in the community. Disease class can be described as the infected human population. Taking the first equation of (3) with \(E=I=0\) into consideration, we arrive at:

$$ \mu N - \mu S =0 $$

i.e.,

$$ S = N _0$$

Then, the disease free equilibrium (DFE) state \( P _0 \) is given by (S, E, I) = \((N _0 , 0, 0).\) Diekmann et al. [26] define basic reproduction number, \( R_0\) as the effective number of secondary infections caused by a primary infected individual. To obtain the basic reproduction number, we employed next generation matrix method by [27], where F is the matrix of the new infection terms and V the matrix of the transition terms. The matrices F and V are determined from the coefficients of E and I, in the second and the last equations of the system (7). Starting with the newly infective classes, the model equations can then be written as:

$$\begin{aligned}&{\frac{dE}{dt}= \beta SI -p\beta E I -\left( \mu + k\right) E - \sigma \beta I(E+I)}, \end{aligned}$$
(8)
$$\begin{aligned}&{\frac{dI}{dt} = p\beta E I + kE-\left( \mu +r \right) I} \end{aligned}$$
(9)
$$ F = \left( \begin{array}{c} \beta S \\ 0 \end{array} \right) , V = \left( \begin{array}{cc} (\mu + \kappa ) &{} 0 \\ -k &{} (\mu + r) \end{array} \right) $$

Next, the Jacobian matrix of F and V at the disease free equilibrium \( (N_0, 0, 0)\) is obtained to give:

$$ F = \begin{bmatrix} 0 &{} \beta N_0 \\ 0 &{} 0 \end{bmatrix}, V = \begin{bmatrix} (\mu + \kappa ) &{} 0 \\ - k &{} (\mu + r) \end{bmatrix} $$

It is always known that for any two by two matrix for example, \( \ A\, =\left[ \begin{array}{cc} a &{} b \\ c &{} d\end{array}\right] , \) its inverse can be obtained by:

$$\begin{aligned} \ A^{-1}= \frac{1}{ad -bc} \left[ \begin{array}{cc} {d} &{} {-b} \\ -c &{} a \end{array}\right] . \end{aligned}$$
(10)

In a similar way, the inverse of V can be obtained as given below:

$$\begin{aligned} V^{-1}= \frac{1}{(\mu +\kappa )(\mu +r) - 0} \left[ \begin{array}{cc} {(\mu +r)} &{} 0 \\ k &{} {(\mu + \kappa ) } \end{array}\right] =\left[ \begin{array}{cc} \frac{1}{(\mu + \kappa )} &{} {0} \\ \frac{\kappa }{(\mu +\kappa )(\mu +r)} &{} \frac{1}{(\mu + r) } \end{array}\right] \end{aligned}$$
(11)

then, we now compute the product of F and \( V^{-1}\), which becomes,

$$\begin{aligned} \ FV^{-1}= \left[ \begin{array}{cc} {0 } &{} \beta N_0\\ {0}&{} {0} \end{array}\right] \left[ \begin{array}{cc} \frac{1}{(\mu +\kappa )} &{} {0} \\ \frac{k}{ (\mu +\kappa )(\mu +r)} &{} \frac{1}{(\mu +r) } \end{array}\right] \end{aligned}$$
(12)
$$\begin{aligned} \ FV^{-1} =\left[ \begin{array}{cc} {\frac{\beta \kappa N_0}{(\mu + \kappa ) (\mu + r) } } &{} {\frac{1 }{(\mu + r) } }\\ {0} &{} {0} \end{array}\right] . \end{aligned}$$
(13)

Basic reproduction number is the spectral radius of \(FV^{-1}\) [26, 28]. It must be considered when analyzing any epidemiological model [27]. Thus, \(R_0\) for this epidemiological system is:

$$\begin{aligned} R_0 = \frac{\beta \kappa N_0}{(\mu +\kappa )(\mu +r)}. \end{aligned}$$
(14)

4 Stability and Bifurcation Analysis

The Jacobian matrix \(\varSigma \) of the system (7) at endemic equilibrium \((S^*, E^*, I^*)\) is given by

$$\begin{aligned} \varSigma = \begin{pmatrix} -\mu - \beta I^* &{} 0 &{} -\beta S^* \\ -\sigma \beta I^*+ \beta I^* &{} -p \beta I^* -\sigma \beta I^* -(\mu + \kappa ) &{} \beta (1-\sigma )S^*-(p+\sigma )\beta E^*+\sigma \beta (N_0-2 I^*) \\ 0 &{} p \beta I^* +\kappa &{} p \beta E^*-(\mu +r) \end{pmatrix}. \end{aligned}$$
(15)

For the endemic equilibrium points, setting the right hand sides of the equations in model (7) to zero we have:

$$\begin{aligned} \begin{array}{l} {\mu N_0 -\mu S^*- \beta S I^* =0} \\ \\ { \beta (1-\sigma ) S^* I^*- (p+\sigma )\beta E^*I^* -\left( \kappa +\mu \right) E^* + \sigma \beta I^*(N_0-I^*)=0} \\ \\ {p\beta E^*I^*+ \kappa E^* -\left( \mu + r \right) I^* =0} \\ \\ \end{array} \end{aligned}$$
(16)

For endemic equilibrium P = \((S^*,E^*,I^*)\), from first and last equations of (16)

$$\begin{aligned} S^*=\frac{\mu N_0}{(\mu +\beta I^*)} \end{aligned}$$
(17)
$$\begin{aligned} E^*=\frac{(\mu +r)I^*}{(\kappa + p \beta I^*)} \end{aligned}$$
(18)

Substituting (17) and (18) into Eq. (16), the endemic equilibrium conditions become a cubic polynomial equation of \(I^*\) which is given below:

$$\begin{aligned} f(I) = n_1 I^*{^3} + n_2 I^*{^2} + n_3 I^* + n_4 = 0 \end{aligned}$$
(19)

where

$$ \begin{array}{l} n_1 = p \sigma \beta \\ n_2 = p \sigma N_0 (\beta _0 -\beta )\\ n_3 = (p \mu +\kappa \sigma )N_0 (\frac{\beta _1}{\beta }-1)\\ n_4 = \mu (\mu +r)(\mu + \kappa )\frac{(1-R_0)}{\beta ^2} \end{array} $$

where

$$R_0 = \frac{\beta \kappa N_0}{(\mu +\kappa )(\mu +r)}$$

and \( \beta _0, \beta _1 \) are two threshold parameters as follows:

$$ \begin{array}{l} \beta _0 = \frac{(p+\sigma )(\mu +r)+\sigma (\kappa +p \mu )}{p \sigma N_0}\\ \beta _1= \frac{\mu (\mu + r)(p+\sigma +1)+\kappa (\mu +r + \mu \sigma )}{(p \mu + \kappa \sigma )N_0} \end{array} $$

It is clear the \(I^*\) is the positive real roots of the polynomial (19). Currently, number of possible positive real roots of the cubic polynomial (19), depend on the signs of \(n_2, n_3 \,, and \,, n_4\).

4.1 Local Asymptotic Stability (LAS) of Disease Free Equilibrium Point \(P_0\)

Theorem 3

The disease free equilibrium state, \( P_0 \) of the system (7) is LAS when \( R_0 < 1 \) and otherwise unstable.

Proof

Consider the model system (7)

$$\begin{aligned} f_1 = \frac{d S}{dt }, f_2 = \frac{dE}{dt}, f_3 = \frac{d I}{dt }, \end{aligned}$$
(20)

then, the Jacobian of the model system (7) will be given by:

$$\begin{aligned} \varSigma (P_0) = \left( \begin{array}{ccc} \frac{\partial f_1}{\partial S} &{} \frac{\partial f_1}{\partial E} &{} \frac{\partial f_1}{\partial I} \\ \frac{\partial f_2}{\partial S} &{}\frac{\partial f_2}{\partial E} &{} \frac{\partial f_2}{\partial I} \\ \frac{\partial f_3}{\partial S} &{} \frac{\partial f_3}{\partial E}&{} \frac{\partial f_3}{\partial I} \end{array}\right) \end{aligned}$$
(21)

at equilibrium point \((P_0),\) the Jacobian becomes;

$$\begin{aligned} \varSigma (P_0) =\left( \begin{array}{ccc} - \mu &{} 0 &{} - \beta S \\ \beta I &{} - (\kappa +\mu ) &{} \beta S+ \sigma \beta R\\ 0 &{} \kappa &{} - (\mu +r) \end{array}\right) \end{aligned}$$
(22)

Evaluating the (22) at the \(P_0\) to ascertain the LAS of the system yield;

$$\begin{aligned} \varSigma (P_0) =\left( \begin{array}{ccc} - \mu &{} 0 &{} - \beta N_0 \\ 0 &{} - (\kappa +\mu ) &{} \beta N_0\\ 0 &{} \kappa &{} - (\mu +r) \end{array}\right) \end{aligned}$$
(23)

Calculate the eigenvalues of the Jacobian, evaluated at the equilibrium point (in this case, the \(P_0\)) \((\varSigma (P_0)\), thus: The eigenvalue of (23) are given by

$$ \left| \varSigma P_{0} -\alpha I\right| \, = 0 $$

where \(\varSigma (P_{0})\) represents Jacobian matrix at disease free equilibrium, \(\alpha \) is the characteristic equation of the matrix while I is the identity matrix. The characteristics equation of the resulting Jacobian from (23) is given by:

$$\begin{aligned} \varSigma (P_0) = \begin{vmatrix} - \mu - \alpha&0&-\beta N_0 \\ 0&-( \kappa +\mu ) - \alpha&\beta N_0 \\ 0&\kappa&- (\mu +r) - \alpha \end{vmatrix} =0. \end{aligned}$$
(24)

Thus, the characteristics equation of (24) are given by

$$ (- \mu - \alpha ) \left[ -(\mu +\kappa ) - \alpha )(- (\mu +r) - \alpha )-\kappa \beta N_0\right] =0 $$
$$ ( \mu + \alpha ) \left[ ( \mu +\kappa )(\mu +r)+( \kappa +\mu +\mu +r)\alpha +\alpha ^{2}-\kappa \beta N_0\right] =0$$
$$ ( \mu + \alpha ) \left[ \alpha ^{2}+( \kappa + 2\mu +r)\alpha +(\mu +\kappa )(\mu +r)- \kappa \beta N_0\right] =0$$
$$ ( \mu + \alpha ) \left[ \alpha ^{2}+( \kappa + 2\mu +r)\alpha +(\mu +\kappa )(\mu +r)\left( 1-\frac{\kappa \beta N_0}{( \mu +\kappa )(\mu +r)} \right) \right] =0$$
$$\begin{aligned} ( \mu + \alpha ) \left[ \alpha ^{2}+( \kappa + 2\mu +r)\alpha +(\mu +\kappa )(\mu +r)(1-R_0)\right] =0 \end{aligned}$$
(25)

From Eq. (25)

$$ (( \mu + \alpha ) = f(\alpha )) $$

therefore

$$\begin{aligned} f(\alpha )= \delta _0 \alpha ^{2}+ \delta _1 \alpha +\delta _2. \end{aligned}$$
(26)

where

\(\delta _0=1,\) \(\delta _1 =( \kappa + 2\mu +r)\alpha ,\) \(\delta _2 = (\mu +\kappa )(\mu +r)(1-R_0).\)

In order to show the LAS of DFE, we set up conditions that will allow the quadratic equation (26) to have negative real roots. In this case, we apply the Routh-Hurwitz (R-H) Criterion.

Clearly, from Eq. (26), \(\delta _0=1>0,\) \(\delta _1 =( \kappa + 2\mu +r)\alpha >0,\) while \(\delta _2 = (\mu +\kappa )(\mu +r)(1-R_0)>0\) if and only if \(R_0 <1.\) Therefore, disease–free equilibrium is locally asymptotically stable when \(R_0 <1\) and unstable when \(R_0 >1.\)

5 Bifurcation Analysis and Numerical Simulation Studies

Bifurcation analysis is an essential tool that enables systematic identification of where dynamics of interest can be located in the parameter space [29]. The important parameters that play crucial roles in the system are varied in order to understand dynamical behaviours of the model. These parameters are:

  • Basic Reproduction number, \(R_0 \): this term is one of epidemiological value that plays a critical role in epidemics [27, 30,31,32].

  • Exogenous re-infection rate, p: this quantity refers to when a previously infected individual (in dormant stage) in an exposed class acquire new infection from another infectious person, as a result of low level of immunity [12].

  • Transmission rate \( \beta \): this term is the extent of transmission probability of the disease due to contact with infectious individuals [33].

Table 1 Parameter and values used for the model (7)
Full size table

This section presents some findings from our numerical simulation analysis. We also highlight our bifurcation analysis results to demonstrate the bifurcational changes in dynamics through the occurrence of distinct bifurcations. The appearance and stability of different branches of (DFE and EEP) equilibria are analyzed as \(\beta \) and p are changed. Numerical simulation and bifurcation analysis are performed using MATLAB and XPPAUT [39], respectively. Figure 2 illustrates the bifurcation diagram of the system (7) as the basic reproduction number \((R_0)\) varies against the infected population (I). The first (top-left) diagram of Fig. 2 depicts the bifurcation diagram at \(\beta \) = 1.7. In general, there are several branches of steady states: (i) the upper branch corresponds to stable endemic equilibria, EEP; (ii) the middle branch represents unstable EEP; (iii) the lower branch corresponds disease free equilibria, DFE, which can be stable or unstable depending on the magnitudes of \(R_0\). As in our theoretical analysis section, this \(R_0\) quantity can be calculated using Eq. (14). Our bifurcation analysis results also reveal the occurrence of two threshold quantities, i.e., transcritical (BP, with this bifurcation occurs when \(R_0=1\)) and saddle-node (LP) bifurcations.

When \(R_0>1\), only EEP is stable and this situation leads to an outbreak of TB disease. Also noticed is that as basic reproduction number decreases and lies below LP point i.e., \(R_0<LP\), DFE is stable in this case; consequently, this situation leads to elimination of the disease. To further understand the transmission dynamics of system (3), we plot some time series diagrams in Fig. 3 as transmission rate \(\beta \) changes. As can be seen in the top left and right diagrams, one of the possibilities when the magnitudes of \(\beta \) are high is that this situation would lead to the persistence of TB disease (i.e., the trajectories converge to EEP) in this epidemiological system. However, as the transmission rate \(\beta \) decreases, this results in small \(R_0\) quantities as shown by the bottom-left (respectively, bottom-right) of Fig. 3 with \(\beta =1.5\) (respectively, \(\beta =1\)) and \(R_0=0.4104\) (respectively, \(R_0=0.2736\)); consequently, the TB disease is eradicated and DFE is stable in a long run.

Furthermore, other interesting dynamics are realized when \( LP<R_0<1\), whereby alternative steady states phenomenon emerges. In this case, the outcomes of this epidemiological system depend on initial conditions and the unstable EEP (middle branch) acts as a basin boundary separating the two stable (DFE and EEP) equilibria. Hence, the trajectories will converge to either DFE (elimination of disease) or EEP (outbreaks of TB), depending on the initial conditions. For example, an initial condition below the unstable EEP (basin boundary) will converge to DFE. Otherwise, the trajectories will shift and converge to EEP. To demonstrate these possible outcomes, the time series diagrams in Fig. 4 are plotted using distinct initial conditions. It can be seen that when \(\beta =1.7\) (with other parameter values fixed as in Table 1) and \(R_0=0.4651\), this situation is equivalent to a bifurcation diagram in the top left of Fig. 2 where alternative steady states occur. In this case, the trajectories converge to either EEP (outbreaks of TB: Fig. 4 left) or DFE (elimination of disease: Fig. 4 right), depending on the choice of initial conditions.

A closer investigation of our bifurcation analysis results in Fig. 2 demonstrate that the interaction between saddle-node and transcritical bifurcations leads to contrasting observations in the model (7). As the value of transmission rate \( \beta \) decreases, we observe that the frequency of alternative steady states phenomenon diminishes and eventually eliminated under \(R_0\)-variation. This is evident when we examine the fifth (bottom-left) and sixth (bottom-right) diagrams of Fig. 2: the two bifurcation points, namely BP and LP, approach each other and finally coalesce. Consequently, alternative stable states incident disappear and the trajectories would converge to a stable equilibrium of the system; for instance, as \(\beta =1.5\), EEP (respectively, DFE) is stable when \(R_0>1\) (respectively, \(R_0<1\)) and this situation causes an outbreak (respectively, elimination) of TB disease.

Fig. 2
figure 2

Bifurcation diagram of system model (7), there is different types of behaviour as the bifurcation parameter \(\beta \) changes from the top left, different values of \(\beta \) are used in clockwise direction respectively: values are \(\beta = 1.7\), \(\beta = 1.69\), \(\beta = 1.67\), \(\beta = 1.65\), \(\beta = 1.63\), \(\beta = 1.61\), while other parameters values are fixed \( \mu \) = 0.15, \( N_0 = 5\), \(p = 0.5\), \(\kappa = 0.02\), \(\sigma = 0.7 \), \(r = 2\). The label LP corresponds to saddle node bifurcation, BP correspond to transcritical bifurcation, EEP corresponds to endemic equilibrium point and DFE correspond to disease free equilbrium. These graphs are computed using Matlab

Full size image
Fig. 3
figure 3

Simulation results showing the impact of transmission rate \((\beta )\) on the spread of tuberculosis. The values of transmission rate are set to be \(\beta = 2.5,\) \(\beta = 2,\) \(\beta = 1.5,\) \(\beta = 1,\) in clockwise direction respectively while other parameters values are \( \mu = 0.15\), \( N_0 = 5\), p = 0.5 k = 0.02, \(\sigma = 0.7 \), r = 2 and the initial conditions S(0) = 2.5, E(0) = 2 and I(0) = 1. These plots are computed by numerical continuation XPPAUT

Full size image
Fig. 4
figure 4

Time series plots of system (7) showing the endemic equilibrium points (EEP) left and disease free equilibrium (DFE) right with the initial conditions of (S(0), E(0), I(0)) = (3.5, 2.5, 4) and (2.5, 2,1) at the parameter values \(\mu = 0.15,\) \(N_0 = 5\), \( \beta =1.7\), \(\sigma = 0.7,\) \(k = 0.02\), \(p = 0.5\), \(r = 2\). These plots are computed by numerical continuation XPPAUT

Full size image
Fig. 5
figure 5

Bifurcation diagram of system model (7), there is different types of behaviour as the bifurcation parameter p changes from the top left, different values of p are used: values are from 0.4 to 0.51 in clockwise direction respectively while other parameters values are fixed \( \mu \) = 0.15,\( N_0 = 5\), \(\beta = 1.69 \), \(\kappa = 0.02\), \(\sigma = 0.7 \), \(r = 2\). The label LP corresponds to saddle node bifurcation, BP corresponds to transcritical bifurcation, EEP corresponds to endemic equilibrium point and DFE corresponds to disease free equilibrium. These graphs are computed using Matlab

Full size image

To examine the influence of the force of exogenous reinfection on the dynamical behaviour of the model, we performed one-parameter bifurcation analysis as shown in Fig. 5. These findings demonstrate some bifurcation diagrams of system (7) with y-axis representing infected population (I) and x-axis corresponding to basic reproduction number \((R_0)\) as parameter p changes.

Similar to our previous observation, there are some branches of steady states where the upper (respectively, middle) branch corresponds to stable (respectively, unstable) EEP. In addition, there occurs lower branch of equilibrium for DFE, which can be stable or unstable, depending on the magnitudes of \(R_0\). The appearances of transcritical (BP) and saddle-node (LP) bifurcations are also observed. As p increases (from top to bottom diagrams), we notice that the alternative stable states region first vanishes and then emerges. The bi-stable region gets wider (i.e., occurs at more values of \(R_0\)) the force of exogenous re-infection (p) gets higher (see bottom left and right diagrams); in this case, when \( LP<R_0<1\), the outcomes of system (7) determined by the alternative stable states phenomenon with the trajectories converging to either DFE (elimination of disease) or EEP (outbreaks of TB), depending on the initial conditions. It is realized that the interaction between these distinct bifurcations can shape the overall dynamics of the epidemiological system (7).

6 Discussion and Conclusion

In this present paper, the influences of transmission rate, \(\beta ,\) and exogenous re-infection, p, on the dynamical behaviors of TB outbreaks have been investigated. It is observed from the simulation and bifurcation analysis results that the threshold quantity known as basic reproduction number \( R_0\) is very critical when determining the persistence and exclusion of the epidemic. By using bifurcation analysis, we observed the occurrences of transcritical and saddle node bifurcations in the system. The interplay between these two local bifurcations shapes the overall dynamics of the system and determines the outbreaks of TB disease. In general, the interaction between saddle-node and transcritical bifurcations is also considered in other biological systems such as Mohd et al. [36,37,38] and Kooi et al. [40]. We conclude that different epidemiological forces, such as the transmission rate \(\beta \) and exogenous re-infection, p, exert significant effects on the transmission dynamics of TB. We suggest that future research should focus on mitigating their joint impacts on the society.