Experiments on nonlinear vibrations of a combined structure with segments of beams and a disc subjected to axial tensile force

Abstract

This paper presents experimental results on nonlinear vibrations of a combined structure with segments of beams and a disc, which is a fundamental model of a micro scanner. Both ends of the structure are clamped for deflection and one of the ends of the structure is constrained with an axial spring. Under an axial tensile force, the structure is excited with lateral periodic acceleration. Sweeping the excitation frequency, nonlinear frequency response curves are obtained. In the typical frequency region, non-periodic responses are generated. The responses are inspected by the Fourier spectrum, the Poincaré projection, the maximum Lyapunov exponents and the principal component analysis. The non-periodic responses are confirmed as chaotic responses coupled with torsional and the lowest flexural modes of the combined structure.

1 Introduction

Micro electro mechanical system (MEMS) is widely used for sensors or actuators in electronic appliances and information appliances. One of the MEMS structures is a micro scanner. The micro scanner has a shape of a combined structure with segments of beams and a plate. As the plate, a rectangular or a circular plate is used. Thickness of the structure is sufficiently thin to a length of the structure. With resonant responses of a torsional mode of the structure, the structure reflects light beam to a wide range. If a torsional angle of the resonant responses is large, nonlinear coupled vibrations between the torsional mode and the flexural mode might be generated on the structure by the nonlinear vibrations. Furthermore, chaotic responses might be generated in a specific condition of forcing amplitude and frequency. These nonlinear or chaotic responses of the micro scanners reduce the quality of scanning. To design the micro scanner having good accuracy, it is important to investigate nonlinear vibrations of the structure.

The micro scanner consists of segments of beams and a plate. The nonlinear vibrations of a beam have been investigated by many researchers. Yamaki et al. [1, 2] investigated nonlinear frequency responses of a clamped–clamped beam by changing a initial axial displacement. Nagai et al. [3] conducted experiments on nonlinear vibrations, especially on chaotic vibrations, of a post-buckled beam with clamped–clamped boundary conditions. Chaotic vibrations of the post buckled beam are analyzed by Maruyama et al. [4] in detail to investigate modal contributions in the chaotic response. The nonlinear vibrations of a plate are also investigated by many researchers. Nonlinear vibrations of a clamped rectangular plate subjected to in-plane displacement are investigated analytically and experimentally by Yamaki et al. [5, 6]. Chang et al. [7] analyzed a nonlinear and chaotic vibrations of a simply supported rectangular plate. Onozato et al. [8] conducted experiments on chaotic vibrations of a rectangular plate subjected in-plane compressive force. Nonlinear vibrations of a clamped circular plate is analyzed by Sridhar et al. [9, 10]. Experimental and analytical studies of nonlinear vibrations of a clamped circular plate subjected to initial in-plane displacement are reported by Yamaki et al. [11, 12]. The dynamic responses of a micro scanner are investigated by some researches. Khatami and Rezazadeh [13] analyzed dynamic responses of a torsional mirror subjected to electrostatic force and mechanical shock. Shabani et al. [14] analyzed nonlinear vibrations of a electro static torsional actuator near the pull-in condition. Ataman and Urey [15] and Ataman et al. [16] investigated nonlinear frequency responses of comb-driven micro scanners. In theses studies, an analytical model of the micro scanner is assumed to be combination of springs and a rigid plate. For the experimental studies on nonlinear vibrations of the micro scanner, it seems to the authors that detailed investigation of the nonlinear vibrations coupled with the torsional and flexural modes has not been reported.

As mentioned above, nonlinear coupling between the torsional vibration and the flexural vibration should be made clear to improve the design of micro scanners. To the best of the author’s knowledge, nonlinear vibration analyses on complex-shaped structures are not developed at present. Thus, it would be important to show the conditions of the generation of nonlinear coupled vibration and modal contribution of the torsional and the flexural modes by the experiment. These experimental results would be valuable foundations to develop the analysis on nonlinear vibrations of the complex-shaped structures.

In this paper the nonlinear vibrations of the combined structure with segments of the beams and the disc are investigated. The structure is fundamental model of a micro scanner. Both ends of the structure are clamped for deflection. One of the ends of the structure is elastically constrained with the axial spring. The structure is subjected to axial forces by the axial spring. First, natural frequencies of the torsional mode and the lowest flexural mode of the structure are measured by changing the axial forces. Under typical tensile axial forces, the configuration of the structure and characteristics of restoring force of the structure are obtained. Next, the structure is subjected to periodic acceleration laterally under the axial tensile force. A frequency response curve is obtained by sweeping excitation frequency. Non-periodic responses are generated in a typical frequency. The responses are inspected by the Fourier spectrum, the Poincaré projection and the maximum Lyapunov exponents. To investigate the modal contribution to the non-periodic responses, the principal component analysis is adapted to the time histories with a length of long time period. The time histories are measured at multiple positions, simultaneously. Furthermore, time histories of the contribution ratio are obtained from calculations of principal component analysis with time histories cut out from the time histories with a length of long time period.

2 Combined structure

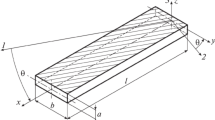
The combined structure and its fixture are shown in Fig. 1. The dimensions and the material properties of the structure are shown in Table 1. The structure consists of two segments of beams and a segment of a disc. The segment of the disc is located at the center of the structure. Both ends of the structure are clamped on the fixture. The length between clamped edges is $L=157.5$ $\mathrm {mm}$. The breadth of the beam is $b=13.5$ $\mathrm {mm}$ and the diameter of the disc is $D=99$ $\mathrm {mm}$. The ratio of the diameter of the disc to the length between the clamped edges is $D/L=0.63$. The corners between the beam and the disc are smoothed with radius 10mm. For the test specimen of the structure, a phosphor-bronze sheet with the thickness $h=0.15$ $\mathrm {mm}$ is used. Material properties of the sheet are measured as the Young’s modulus $E=81$ $\mathrm {GPa}$ and the mass density $\rho = 8.5\times 10^3$ $\mathrm {kg / m^3}$. To improve measuring accuracy of the deflection, the both surfaces of the structure are painted with acrylic lacquer of white color. The thickness of the structure including the painted layer is $h'=0.21$ $\mathrm {mm}$. The Cartesian coordinate system is defined by $x$-axis along the longitudinal direction, $y$-direction along the clamped edge and $z$-axis vertical to the surface of the structure.

Fig. 1

The combined structure and the fixture

Table 1 The dimensions and the material properties of the structure

The fixture consists of two fixing devices which are the rigid block and the movable table. The rigid block is firmly fixed on the base frame by bolts. The movable table has two parallel elastic plates as an axial spring on the slide block. The slide block can move on the base frame to the $x$-direction by turning a screw. One end of the structure is fixed on the on the rigid block and the other end is fixed on the movable table. Consequently, the boundary condition of the structure is clamped laterally at the both ends and elastically constrained in the axial direction. When the slide block moves in $x$-direction, the axial force $n_{x}$ is loaded on the structure. The axial force can be calculated from the strain measured by strain gauges which are glued on the axial springs. The spring constant of the elastic plates is measured as $k_{s}=13\times 10^{3}$ $\mathrm {N/m}$ from the relation between deflections of the elastic plates and concentrated forces.

3 Procedure of experiments

3.1 Measurement of fundamental poroperties

As fundamental properties of the structure linear natural frequencies, modes of vibration, configuration of the structure and characteristics of restoring force of the structure are obtained under the gravitational force. First, the linear natural frequencies of the lowest flexural mode and the torsional mode are obtained. Applying periodic acoustic pressure on the structure, resonant response with small amplitude is generated on the structure. The resonant response is measured by a laser displacement sensor and is inspected by a digital voltmeter and a spectrum analyzer. The natural frequencies of the structure are obtained by an inspection of the amplitude of the resonant response. Under the acoustic pressure at the natural frequency, the modes of vibration are obtained by scanning the amplitude and the phase difference between the response and acoustic pressure. By changing the axial force, the natural frequencies are measured. Then, the configuration of the structure and characteristics of restoring force are measured under some axial forces. The configuration of the structure is measured by the laser displacement sensor. As the characteristics of restoring force, the relation between the static deflection $\bar{W}_{s}$ and a concentrated force $Q_{s}$ is obtained. The concentrated force is loaded on the structure by a load cell. Pressing the structure with the load cell, the structure deflects to an equilibrium position of elastic force between the structure and the load cell. At the equilibrium position, the static deflection and the concentrated force are recorded.

3.2 Procedure of vibration test

A schematic diagram and an actual view of vibration test apparatus are shown in Figs. 2 and 3, respectively. Whole instruments of the vibration test are numbered from 1 to 16. The excitation is provided by the instruments as numbered from 1 to 5. The exciter controller 1 (B&K 1050) generates a sinusoidal periodic signal, where the frequency of the periodic signal can be swept with the resolution of 1 mHz. The periodic signal is amplified with the power amplifier 2 (B&K 2708). The electromagnetic exciter 3 (B&K 4802) drives the exciter head 4 (B&K 4818). The electromagnetic exciter has the maximum amplitude of periodic force 1780 N. The structure is fixed on the exciter head through the base frame. Periodic acceleration is loaded on the structure through the fixture. The accelerometer pickup 5 (B&K 4371) fixed on the base frame detects the acceleration acting on the structure. The signal of the acceleration is fed back to the controller 1. Then, during a sweep of the excitation frequency, the amplitude of periodic acceleration can be kept to a prescribed constant level larger than the lower limit depending on the weight of a fixture and a specimen (approximately $2\,\mathrm {m/s^2}$ for this specimen).

Fig. 2

Schematic diagram of vibration apparatus

Fig. 3

Actual view of vibration apparatus

Dynamic deflections $W$ of the structure are measured with the instruments of the laser displacement sensor from 6 to 8 (Keyence LC2400 series). The laser displacement sensors can measure the response at most 5kHz. Relative displacement of the structure to the base frame is detected with the laser displacement sensors 6 and 7. The sensor 6 detects the periodic displacement of the base frame. The sensor 7 measures the dynamic deflection of the structure and the periodic displacement of the base frame. The controller 8 subtracts the two signals. With this subtraction, the pure dynamic deflection of the structure can be detected. The laser displacement sensors 7 are set on the sliding table 9 and the sensor moves above the surface of the structure. The instruments from 10 to 16 are the measuring devices of signal processing and data analysis. Nonlinear frequency response of the structure is obtained by sweeping the excitation frequency. The dynamic deflections of the structure detected by the laser sensors are transformed to the amplitude in a root mean square value with the digital voltmeter 10 (ADCMT 7461A). The excitation frequency applied on the structure is counted with the digital frequency counter 11 (Advantest TR5822) through the periodic signal from the exciter controller 1. The amplitude of the dynamic response and the excitation frequency are transferred to the computer 12 (Dell inspiron). Then, the nonlinear frequency response curve is obtained. In the experiment, the excitation frequency is swept with the sweep rate $0.01\,\mathrm {Hz/sec}$ to avoid transient effects on the nonlinear response. Time histories of nonlinear response at multiple positions are recorded simultaneously with the multi-channel recorder 13 (YOKOGAWA DL750) and are transmitted to the computer 12. The multi-channel recorder has a resolution of 16-bit. With the computer the Fourier spectrum, the maximum Lyapunov exponents and results of principal component analysis are obtained. The Poincaré projection of the response is obtained by the following step. Dynamic deflection of the response is transformed to velocity by the differentiation amplifier 14. The set of the deflection and the velocity is recorded sequentially once in every period of the excitation. Synchronized with the period of excitation acceleration, a pulsating signal is generated with the phase meter 15 (B&K 2971) and the delayed pulse oscillator 16 (NF Elec. Instr.1930). The set of aforementioned deflection and velocity of the nonlinear response is recorded by the multi-channel recorder in each trigger by the pulsating signal and is transmitted to the computer as the Poincaré projection.

3.3 Evaluation of nonlinear and chaotic vibrations

The nonlinear and the chaotic responses of the structure are evaluated by the Fourier spectrum, the Poincaré projection, the maximum Lyapunov exponents and results of principal component analysis. By calculations with the time histories the Fourier spectrum, the maximum Lyapunov exponents and results of principal component analysis are obtained.

The Fourier spectrum detects frequency components involved in the time history of the response. The Poincaré projection of the chaotic response shows the distributed pattern. The maximum Lyapunov exponents $\lambda _\mathrm {max}$ can determine whether a non-periodic response is chaos. If the maximum Lyapunov exponents converge to a positive value as an increase of embedding dimension, the response can be confirmed as chaos. The maximum Lyapunov exponents are calculated with the procedure proposed by Wolf et al. [17]. In the experiment, $e$-dimensional pseudo-phase space is composed with time-delay coordinates from a time histories, where $e$ is the embedding dimension [18]. A component of the pseudo-phase space is a sequential time history chosen partially from the time response which has a fixed time delay from the former component. A trajectory in the pseudo-phase space is constructed from the single time response of the structure from an arbitrary start time. Two trajectories, which initially have sufficiently small distance, are selected as the fiducial trajectory and the nearby trajectory. The exponential growth rate of the distance between the two trajectories is calculated in each infinitesimal time interval. The exponential growth rate is averaged in the long time interval, then the maximum Lyapunov exponents can be estimated. The principal component analysis [19] enables the estimation of the modal pattern and corresponding contribution ratio in the response of the structure. In the principal component analysis, the covariance matrix of the simultaneous time histories of the response at multiple positions on the structure is calculated. The covariance matrix is transformed to an orthogonal matrix, which results in the eigenvalue problem of the covariance matrix. The eigenvector $\phi _{i}$ represents the modal pattern and the corresponding eigenvalue denotes the contribution of the modal pattern to the response. Contribution ratio $\mu _{i}$ is the ratio of eigenvalues of the $i$th modal pattern to the all modal patterns.

3.4 Thermal control

The fundamental properties and the dynamic responses of the structure are affected by changes of the temperature of the base frame and the structure. To avoid changes of the fundamental properties and dynamic response, the temperatures of the base frame and the vicinity of the structure are controlled.

The structure is set in an air chamber which is surrounded by air-formed sheet. The temperature in the chamber is controlled by an air conditioner and an electric heater. Consequently, the temperature in the vicinity of the structure is stabilized. The base frame of the structure is warmed because heat of the exciter is conducted through the exciter head. To avoid conduction of the heat, a cooling plate is set between the base frame and the exciter head. The cooling plate has holes which water run through. Changing the temperature of the water, the temperature of the base frame is stabilized. Through the experiments, the temperatures of the base frame and the vicinity of the structure are controlled within the $20 \pm 1$ $^\circ$C.

3.5 Non-dimensional notations

To discuss the results of the experiments, the following non-dimensional notations are introduced:

$$\begin{aligned}&\xi =x/L,\eta =y/D,\\&[w_s, \bar{w}_s, w] = [W_s, \bar{W}_s, {W}]/h,\\&n_x=N_x L^2/EI, [p_s, p_d] =[g, a_d]\rho A L^4/EIr,\\&\quad q_s=Q_s L^3 /EIr,\\&[\omega _\mathrm {ex}, \omega _{mn}] =[f_\mathrm {ex}, f_{mn}](2\pi /\Omega _0), \tau =\Omega _0 t. \end{aligned}$$

In the foregoing, $r=\sqrt{I/A}$ and $\Omega _0 = (1 / L^2)\sqrt{EI / \rho A}$ are used, where $I$ and $A$ indicate the moment of inertia of cross section and the area of the segments of the beam, respectively. In the above notations, $\xi$ and $\eta$ are the non-dimensional coordinate along $x$-axis and $y$-axis, respectively. The symbol $w_s$ indicates non-dimensional notation of the static deflection $W_s$ from the $z=0$, while the symbols $\bar{w}_s$ and $w$ indicate non-dimensional notations of the static deflection $\bar{W}_s$ and the dynamic deflection ${W}$ from the equilibrium position under the gravitational force and the axial force, respectively. Notation $n_x$ is the non-dimensional axial force where $N_x$ represents the force on the cross section. The notations $p_s$ and $p_d$ are the non-dimensional gravitational acceleration $g$ and the non-dimensional amplitude of the periodic acceleration $a_d$. The notation $q_s$ is the non-dimensional concentrated force. The symbols $\omega _\mathrm {ex}$ and $\omega _{mn}$ are the non-dimensional excitation frequency and the linear natural frequencies of the mode $(m,n)$. The indices $m$ and the $n$ show the number of nodal lines which are perpendicular to the $\xi$ and $\eta$ directions, respectively. The symbol $\tau$ denotes the non-dimensional time.

4 Experimental results and discussion

4.1 Fundamental properties of the structure

Changing the axial forces on the structure, the linear natural frequencies are measured. Relation between the axial forces and the linear natural frequencies is shown in Fig. 4. The ordinate show the natural frequencies $\omega _{mn}$ of mode $(m,n)$. The abscissa indicates the axial forces. Natural frequencies of the mode $(0,0)$ and the mode $(0,1)$, which correspond to the lowest flexural mode and the torsional mode, are marked by circles and squares, respectively. To load the axial compressive force on the structure, the axial force ${n_x}$ is decreased from ${n_x}=0$ to the negative direction. As the decrease of the axial force ${n_x}$, the natural frequency $\omega _{00}$ is slightly decreased first and then is increased after $\omega _{00}$ shows a minimum value at ${n_x}=-7$. In contrast, the natural frequency $\omega _{01}$ takes a minimum value when the structure is subjected to the axial tensile force. The absolute value of the axial compressive force $n_x=-7$, to which the $\omega _{00}$ shows the minimum value, is taken as a critical force $n_{cr}=7$ of the buckling.

Fig. 4

Natural frequencies of the structure under axial forces $n_{x}$

The configuration of structure and the characteristics of restoring force of the structure are measured under the axial force $n_{x}=0$, $350$ and $700$, which correspond to $n_{x}/n_{cr}=0$, $50$ and $100$, respectively. Fig. 5a and b show the configuration of the structure. The static deflection $w_{s}$ under axial force $n_{x}/n_{cr}= 0$, $50$ and $100$ is marked as circles, squares and triangles, respectively. In the Fig. 5a, which shows the configuration of the structure along the $\xi$ direction at $\eta =0$, the static deflection at the center of the structure is about 8 times to the thickness of the structure under the axial force $n_{x}/n_{cr}=0$. Increasing the axial tensile force, the static deflection decreases to about the thickness of the structure under the axial tensile force $n_{x}/n_{cr}=50$ and $100$. The configuration of the structure is almost symmetrical with respect to $\xi =0.5$ in the 3 cases of the axial force $n_{x}/n_{cr}=0$, $50$ and $100$. Configuration of the structure along the $\eta$ direction at $\xi =0.5$ is shown in Fig. 5b. Under the axial force $n_{x}/n_{cr}=0$, direction of the static deflection at both edges of the structure is different with respect to $\eta =0$. Increasing the axial tensile force, the static deflection of the both edges shows same direction due to decrease in the deflection at the $\eta =0$. Furthermore, a difference of the static deflection between both edges decreases.

Fig. 5

Configurations of the structure under axial tensile forces, a along the $\xi$ direction at $\eta =0$, b along the $\eta$ direction at $\xi =0.5$

Figure 6a and b shows characteristics of restoring force of the structure. The abscissa shows the static deflection $\bar{w}_s$, while the ordinate shows the concentrated force $q_{s}$. The static deflections $\bar{w}_{s}$ under axial force $n_{x}/n_{cr}= 0$, $50$ and $100$ are marked by circles, squares and triangles, respectively. In Fig. 6a, the static deflection $\bar{w}_s$ is measured at $(\xi ,\eta )=(0.3, 0)$ under the concentrated force at $(\xi ,\eta )=(0.5, 0)$ to obtain the characteristics of the restoring force corresponding to the lowest flexural mode. As can be seen in Fig. 6a, the characteristics of restoring force have slight nonlinearity under the axial force $n_{x}/n_{cr}= 0$, $50$ and $100$. The gradient of the restoring force increases as an increase of the axial tensile force. In Fig. 6b, the static deflection $\bar{w}_s$ is measured at $(\xi ,\eta )=(0.5, -0.45)$ under the concentrated force at $(\xi ,\eta )=(0.5, 0.45)$ to obtain the characteristics of the restoring force corresponding to the torsional mode. Under the axial force $n_{x}/n_{cr}=0$, increasing the concentrated force $q_s$ to the positive direction the restoring force shows large gradient of curve. Decreasing the concentrated force to the negative direction, the gradient of curve of restoring force decreases. Under the axial tensile force $n_{x}/n_{cr}=50$ and $100$, the structure shows almost linear characteristics of restoring force. Furthermore, the restoring forces in the each axial tensile force $n_{x}/n_{cr}=50$ and $100$ are almost similar. Thus, the effect of increase in the axial tensile force on the characteristics of restoring force of the structure is small.

Fig. 6

Characteristics of the restoring force of the structure, a $\bar{w}_s$ is measured at $(\xi ,\eta )=(0.3, 0)$ under $q_{s}$ at $(\xi ,\eta )=(0.5, 0)$, b $\bar{w}_s$ is measured at $(\xi ,\eta )=(0.5, -0.45)$ under $q_{s}$ at $(\xi , \eta )=(0.5, 0.45)$

Under the axial tensile force $n_{x}/n_{cr}=100$, the structure shows the most symmetric configuration and slight nonlinear characteristics of restoring force in the three cases of the axial forces. In the experiment, the excitation of the structure is conducted under the axial tensile force $n_{x}/n_{cr}=100$. The linear modes of vibration and the natural frequencies of the structure under the axial tensile force $n_{x}/n_{cr}=100$ are shown in Table 2. In the table, a dashed line indicates a nodal line.

Table 2 The modes of vibration and the natural frequencies of the structure under $n_x/n_{cr}=100$

4.2 Frequency response curve

Applying the axial tensile force $n_{x}/n_{cr}=100$ to the structure, the frequency response curve is obtained under excitation amplitude $p_{d}=3\times 10^3$ ($a_{d}=4 \mathrm {m/s^2}$). The excitation frequency is swept near the natural frequency of the mode $(0,0)$. The frequency response curve, which is measured at $(\xi ,\eta ) = (0.7, 0.3)$, is shown in Fig. 7. The ordinate indicates the amplitude $w_{\mathrm {rms}}$ of the dynamic deflection $w$ with a root mean square value. The abscissa indicates the excitation frequency $\omega _\mathrm {ex}$. The linear natural frequency of the mode $(0, 0)$ is also indicated by the circle on the abscissa. The frequency response curve shows large amplitude resonances with the type of a hardening spring. It can be observed that the nonlinearity of the frequency response curve is strong even for this relatively lower amplitude of excitation. Furthermore, non-periodic response can be seen along the large amplitude resonances. In this experiment, the non-periodic response at the excitation frequency $\omega _\mathrm {ex}=40.6$ is examined in detail.

Fig. 7

Frequency response curve under $p_{d} = 3\times 10^3$

4.3 Nonlinear vibrations

The time history, the Fourier spectrum and the Poincaré projection of the dynamic response are obtained under excitation frequency $\omega _\mathrm {ex}=40.6$. The measured point of the response is selected at $(\xi ,\eta ) = (0.7, 0.3)$. The dynamic deflection $w$ is shown in Fig. 8a related to the time ratio $\tau /\tau _\mathrm {e}$ normalized by excitation period $\tau _\mathrm {e}$. The envelope of the dynamic response is irregularly modulated. The Fourier spectrum of the dynamic response is shown in Fig. 8b. The ordinate shows the amplitude $A$ of the spectrum scaled by decibel, while the abscissa denotes the non-dimensional frequency $\omega$. The linear natural frequencies of the structure are indicated by the circles on the abscissa. Broadband spectra can be seen in Fig. 8b. Distinguished peak spectra of the response are detected at the excitation frequency $\omega _\mathrm {ex}$ and the vicinity of the half of the excitation frequency $(1/2) \omega _\mathrm {ex}$. The Poincaré projection is show in Fig. 8c, in which the response of the dynamic deflection $w$ and the velocity $w_{,\omega \tau }$ are potted. Points of the projection are distributed in wide region.

Fig. 8

The nonlinear response a time history, b Fourier spectrum, c Poincaré projection under $p_{d} = 3\times 10^3$, $\omega _\mathrm {ex}=40.6$

The maximum Lyapunov exponents $\lambda _\mathrm {max}$ are calculated from the time history, which is measured at the position $(\xi ,\eta ) = (0.7, 0.3)$ and under the excitation frequency $\omega _\mathrm {ex}=40.6$. The maximum Lyapunov exponents $\lambda _\mathrm {max}$ are shown related to the embedding dimension $e$ in Fig. 9. As the embedding dimension increases at $e=10$, the maximum Lyapunov exponent $\lambda _\mathrm {max}$ is converged to $\lambda _\mathrm {max}=1$ to $1.3$. As the maximum Lyapunov exponent is converged to the positive value, the dynamic response is confirmed as the chaotic response.

Fig. 9

Maximum Lyapunov exponent related to embedding dimension under $p_{d} = 3\times 10^3$, $\omega _\mathrm {ex}=40.6$

To investigate the modes of vibration and related contribution ratio, which contribute to the chaotic response, principal component analysis is applied to the time histories of the response. Under the excitation frequency $\omega _\mathrm {ex}=40.6$, the time histories are measured at the position $(\xi , \eta )=(0.1,0.05)$, $(0.3,-0.3)$, $(0.5,0)$, $(0.7,0.3)$ and $(0.9, -0.05)$, simultaneously. The length of the time histories used in the principal component analysis is selected as 1,500 times to the excitation period $\tau _\mathrm {e}$. The modal patterns and related contribution ratios $\mu _i$ are shown in Table 3. The modal patterns are presented by height and direction of black cones in the figure which corresponds to the components of the eigenvector $\phi _i$. The modal pattern corresponding to the mode $(0, 0)$ shows the largest contribution ratio $\mu _1$ of 76.9 % to the chaotic response. The modal pattern corresponding to the mode $(0,1)$ shows second larger contribution ratio $\mu _2$ of 22.2 %. The third to fifth larger contribution ratios are relatively small. Thus, the mode $(0,0)$ and mode $(0,1)$ contribute to the chaotic response, predominantly.

Table 3 Contribution ratio and modal patterns to the chaotic response under $p_{d} = 3\times 10^3$, $\omega _\mathrm {ex}=40.6$

To investigate the time histories of the contribution ratios of the mode $(0,0)$ and mode $(0,1)$, the principal component analysis is adapted to time histories with short time intervals, which are cut out from the time histories with the length of $1500 \tau _\mathrm {e}$. Length of the short time intervals is taken as $30\tau _\mathrm {e}$. The time histories of the contribution ratios are shown in Fig. 10. The contribution ratios of the modal patterns corresponding to the mode $(0,0)$ and mode $(0,1)$ are marked as circles and squares, respectively. The circles and squares are plotted in the middle of the short time intervals. The chaotic response involves three kinds of response. When the time ratio $\tau /\tau _\mathrm {e}$ is 0–210 and 330–660, the modal pattern corresponding to the mode $(0,0)$ shows dominant contribution ratio of about 90 %. When the time ratio $\tau /\tau _\mathrm {e}$ is 210–330, the modal patterns corresponding to the mode $(0,1)$ and modes $(0,0)$ contribute to the chaotic response, predominantly. When the time ratio $\tau /\tau _\mathrm {e}$ is 660–990, contribution ratio of the modal patterns corresponding to the mode $(0,0)$ and the mode $(0,1)$ is exchanged irregularly.

Fig. 10

Time histories of the contribution ratios corresponding to mode $(0,0)$ and mode $(0,1)$ under $p_{d} = 3\times 10^3$, $\omega _\mathrm {ex}=40.6$

5 Conclusion

Experimental results are presented on nonlinear vibrations of the combined structure with segments of the beams and the disc. The structure is subjected to axial tensile force. Under lateral periodic acceleration, the nonlinear responses of the structure are measured in the vicinity of the linear natural frequency of the lowest flexural mode. Main results are summarized as follows:

• 1. The chaotic response coupled with the lowest flexural mode and the torsional mode is generated on the structure in the vicinity of the natural frequency of the lowest flexural mode.

• 2. Applying principal component analysis to the time histories of the chaotic response divided into the short time intervals, the chaotic response involves three kinds of responses: The response with the dominant contribution of the lowest flexural mode, the response with predominant contribution of the lowest flexural mode and the torsional mode and the response with exchange of contribution between the lowest flexural mode and the torsional mode.