Nonclassical Vibrations of a Monoclinic Composite Strip

Abstract

A mathematical model of damped flexural–torsional vibrations of monoclinic composite strip of constant-length rectangular cross section is proposed. The model is based on the refined Timoshenko beam-bending theory, the theory of generalized Voigt–Lekhnitskii torsion, and the elastic–viscoelastic correspondence principle in the linear theory of viscoelasticity. A two-stage method for solving a coupled system of differential equations is developed. First, using the Laplace transform in spatial variable, real natural frequencies and natural forms are found. To determine the complex natural frequencies of the strip, the found real values are used as their initial values of natural frequencies, and then the complex frequencies are calculated by the method of third-order iterations. An assessment is given of the reliability of the mathematical model and method of numerical solution performed by comparing calculated and experimental values of natural frequencies and loss factors. The results of a numerical study of the effect of angles of orientation of reinforcing fibers and lengths by the values of natural frequencies and loss factors for free–free and cantilever monoclinic stripes are discussed. It is shown that, for the free–free strip, the region of mutual transformation eigenmodes of coupled vibration modes arise for quasi-bending and -twisting vibrations of either even or odd tones. In the cantilever strip of the region of mutual transformation of eigenforms of coupled modes, vibrations occur for both even and odd tones.

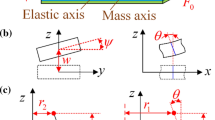
1. The main advantage of monoclinic composites is the possibility to create adaptive constructions on their base, which are able to respond to changes in external influences. Such constructions primarily include an adaptive composite wing and blade systems, which provide the best correspondence with an inhomogeneous oncoming flow of liquid or gas by means of selection of compositions and structures for the most appropriate realization of the effect of flexural–torsional coupling [1]. Adaptive composite structures of the bearing surfaces of aircraft [2], rotor blades of wind and tidal turbines [3, 4], and propeller blades [5, 6] are known. The creation of such constructions requires a deep understanding of nonclassical peculiarities of their reaction to external dynamic influences: the dependence of self-model and self-vibration frequencies, as well as dissipative properties, on reinforcement orientation. The simplest object that allows these characteristics to be demonstrated is a cantilever strip cut from a plate of unidirectional composite at an arbitrary angle to the reinforcement direction (Fig. 1). As another reason for increased interest in studying nonclassical effects generated by flexural–torsional vibrations of monoclinic composite strips, it is necessary to note the problem of development of experimental methods of determination of elastic and dissipative properties of orthotropic composites by measured values of natural frequencies and loss factors of various vibration modes of free-free test samples [7–9]. Despite the existence of numerous works devoted to vibrations of orthotropic composite beams, reference data on free flexural–torsional vibrations are extremely poor. At the same time, most papers are devoted to the creation of mathematical models and numerical investigations of elastic vibrations, in which internal friction is not taken into account [10–14]. The latter circumstance was the reason for writing this work.

Fig. 1.

Monoclinic composite rod.

2. A quasi-uniform composite strip of constant-length rectangular cross section is considered, the reinforcing fibers of which are oriented in direction θ relative to median axis x. A mathematical model of attenuating flexural–torsional vibrations is constructed on the basis of the refined Timoshenko beam-bending theory [15], the theory of generalized Voigt–Lekhnitskii torsion [16, 17] and the elastic–viscoelastic correspondence principle in the form of complex modules [18, 19]. Assuming that vibrations have a quasi-harmonic character, the coupled set of differential motion equations is denoted as

$$\begin{gathered} \frac{{{{d}^{4}}w}}{{d{{x}^{4}}}} + \rho {{\omega }^{2}}\left[ {\left( {\frac{1}{{{{E}_{x}}}} + \frac{1}{{k{{G}_{{xz}}}}}} \right)\frac{{{{d}^{2}}w}}{{d{{x}^{2}}}} + \frac{1}{{{{E}_{x}}}}\left( {\rho {{\omega }^{2}}\frac{1}{{k{{G}_{{xz}}}}} - \frac{A}{{{{I}_{y}}}}} \right)w - \frac{{{{\mu }_{{x,xy}}}{{I}_{p}}}}{{2{{G}_{{xy}}}{{I}_{y}}}}\frac{{d\Phi }}{{dx}}} \right] = 0, \\ \frac{{{{d}^{2}}\Phi }}{{d{{x}^{2}}}} + \rho {{\omega }^{2}}\frac{{{{I}_{p}}}}{{\bar {C}}}\Phi + \frac{{{{\mu }_{{xy,x}}}}}{2}\frac{d}{{dx}}\left[ {\frac{{{{d}^{2}}w}}{{d{{x}^{2}}}} + \rho {{\omega }^{2}}\frac{w}{{k{{G}_{{xz}}}}}} \right] = 0, \\ \end{gathered} $$

(1)

where w is the linear displacement of the strip axis towards the z axis; Φ is the torsion angle; E_x = E_x(θ) is the complex elasticity modulus in the direction of the x axis; G_xy = G_xy(θ) is the complex shear modulus in reinforcement plane xy; G_xz = G_xz(θ) is the complex modulus of interlayer shear in plane xz; μ_x, xy = μ_x, xy(θ) and μ_xy, x = μ_xy, x(θ) are coefficients of mutual influence of the first and second kind; k is the shear coefficient, which depends on the shape of the cross section (for a rectangular cross section, k = 5/6); A is the area of the strip cross section; I_y is the moment of inertia of the strip cross section relative to the y axis; I_p is the polar moment of inertia of the strip cross section; ω is the angular vibration frequency; ρ is the density of the material; and is the $\bar {C}$ torsional rigidity in generalized torsion without bending of the strip axis calculated by the formula [17]

$$\bar {C} = \frac{{{{a}^{3}}b{{{\bar {G}}}_{{xy}}}}}{3}\left[ {1 - \frac{{192}}{{{{\pi }^{5}}}}\frac{a}{b}\sqrt {\frac{{{{{\bar {G}}}_{{xy}}}}}{{{{G}_{{xz}}}}}} \sum\limits_{n = 0}^\infty {\frac{1}{{{{{(2n + 1)}}^{5}}}}\tanh \left( {\frac{{(2n + 1)\pi b}}{{2a}}\sqrt {\frac{{{{G}_{{xz}}}}}{{{{{\bar {G}}}_{{xy}}}}}} } \right)} } \right],$$

where ${{\bar {G}}_{{xy}}}$ = G_xy/(1 − μ_x, xy · μ_xy, x) is the “pure” complex shear modulus in the xy axis [16].

The boundary conditions are written for the free end as

$$\frac{{{{d}^{3}}w}}{{d{{x}^{3}}}} + \rho {{\omega }^{2}}\left( {\frac{1}{{{{E}_{x}}}} + \frac{1}{{k{{G}_{{xz}}}}}} \right)\frac{{dw}}{{dx}} - \rho {{\omega }^{2}}\frac{{{{\mu }_{{x,xy}}}{{I}_{p}}}}{{2{{G}_{{xy}}}{{I}_{y}}}}\Phi = 0,$$

$$\frac{{{{d}^{2}}w}}{{d{{x}^{2}}}} + \rho {{\omega }^{2}}\frac{1}{{k{{G}_{{xz}}}}}w = 0,$$

(2)

$$\frac{{d\Phi }}{{dx}} = 0$$

and for the fixed end as

$$w = 0,\quad \frac{{dw}}{{dx}} = 0,\quad \Phi = 0.$$

(3)

Analysis of differential set of equations (1) implies that coupling of the flexural–torsional vibrations of a monoclinic strip is conditioned by the difference of mutual-influence coefficients μ_x, xy(θ) and ${{\mu }_{{xy,x}}}(\theta )$ from zero at θ ≠ 0° and 90°. At θ = 0° and 90°, we have ${{\mu }_{{x,xy}}}$ = ${{\mu }_{{xy,x}}}$ = 0 and coupled set (1) is split into two independent equations. The first of these equations describes transversal vibrations of an orthotropic Timoshenko beam, and the second describes torsional vibrations of an orthotropic rod of rectangular cross section with constant length:

$$\frac{{{{d}^{4}}w}}{{d{{x}^{4}}}} + \rho {{\omega }^{2}}\left[ {\left( {\frac{1}{{{{E}_{x}}}} + \frac{1}{{k{{G}_{{xz}}}}}} \right)\frac{{{{d}^{2}}w}}{{d{{x}^{2}}}} + \frac{1}{{{{E}_{x}}}}\left( {\rho {{\omega }^{2}}\frac{1}{{k{{G}_{{xz}}}}} - \frac{A}{{{{I}_{y}}}}} \right)w} \right] = 0,$$

(4)

$$\frac{{{{d}^{2}}\Phi }}{{d{{x}^{2}}}} + \rho {{\omega }^{2}}\frac{{{{I}_{p}}}}{{\bar {C}}}\Phi = 0.$$

(5)

3. Complex self frequencies are determined in two steps. First, a real eigenvalue problem is solved, which makes it possible to determine the self frequencies and natural modes of vibrations of an elastic monoclinic composite strip. Real eigenvalues of coupled set of differential equations (1) with boundary conditions (2), (3) are determined using the Laplace transformation of functions w and Φ by variable x. Simple transformations lead to the bicubic algebraic equation

$$\Delta (p) = 0,$$

(6)

the roots of which allow obtaining exact expressions for the images and, then, the originals of functions w(x) and Φ(x). The originals of w(x) and Φ(x) contain the initial values of functions w(x), w'(x), and Φ(x) at x = 0: w₀ = w(0), w₁ = w'(0), and Φ₀ = Φ(0). Submitting found functions w(x) and Φ(x) to the boundary conditions at x = l, we obtain a uniform set of equations for w₀, w₁, and Φ₀. The necessary and sufficient condition of the existence of a nontrivial solution of this set is equality of its determinant to zero det(ω²) = 0.

Equation (6) represents the sought frequency equation. Natural frequencies of flexural–torsional vibrations ω are determined using the method of sequential approximations: setting of frequency ω allows solving Eq. (6) and calculating det(ω²).

The frequency is then changed and the cycle is repeated. If at a new value of frequency ω the determinant det(ω²) changes its sign, then thereafter the problem is reduced to decreasing the interval between the old and new values of ω. This procedure is repeated until natural frequency ω with the required accuracy is obtained. After determination of w₀, w₁, and Φ₀, eigenfunctions are calculated from the uniform system (up to normalization), which make it possible to identify the found frequency.

In the case of attenuating natural vibrations of monoclinic strip, the sought frequencies have the form of complex numbers and the aforementioned method is inapplicable to finding them.

Thus, let us select complex number ω⁽⁰⁾ as an initial approximation to the sought complex frequency, the real part of which is equal to the frequency of elastic natural vibrations with modules equal to real parts of corresponding complex modules and the imaginary part of which is equal to an arbitrary value within the limits of the expected loss factor. We then construct the iteration sequence

$${{\omega }^{{(k + 1)}}} = {{\omega }^{{(k)}}} - \frac{{F({{\omega }^{{(k)}}})}}{{F{\kern 1pt} '({{\omega }^{{(k)}}})}} - \frac{{{{F}^{2}}({{\omega }^{{(k)}}})F{\kern 1pt} ''({{\omega }^{{(k)}}})}}{{2F{\kern 1pt} {{'}^{3}}({{\omega }^{{(k)}}})}}.$$

It converges with the third order to the desired frequency; i.e., the error at the next step is approximately equal to the cube of the previous error [20].

It is impossible to determine the required derivatives exactly; thus, they are found approximately by formulas of numerical differentiation of the second order of accuracy,

$$F{\kern 1pt} '(z) \approx \frac{{F(z + {{h}_{z}}) - F(z - {{h}_{z}})}}{{2{{h}_{z}}}},\quad F{\kern 1pt} ''(z) \approx \frac{{F(z + {{h}_{z}}) - 2F(z) + F(z - {{h}_{z}})}}{{h_{z}^{2}}},$$

with a suitable choice of step h_z depending on point z.

At each iteration step, it is required to calculate the value of the high-order determinant three times, which determines the main running time of the program. The values of the loss factor of the k-th self-vibration mode are determined by the values of the real and imaginary parts of k-th complex natural frequency using the formula η_k = 2 Im ω_k/Re ω_k .

4. The appropriateness of the mathematical model of flexural–torsional vibrations and the proposed numeric solution of differential equations (1) was evaluated by comparing calculated and experimental values of natural frequencies and loss factors of the lowest vibration tones of free-free strips. The strips were cut from fiber-glass plates (a = 0.00976 m, b = 0.02524 m, l = 0.295 m, ρ = 1650 kg/m³), the values of the elastic–dissipative characteristics of which were determined experimentally.

When conducting the numerical and experimental investigations, angle of orientation of the strip axis relative to the direction of the reinforcing tissue θ varied. The solid lines in Fig. 2 present calculated dependences of natural frequencies f_i cal = f_i cal(θ) and loss factors η_i cal = η_i cal(θ) (i = $\overline {1,7}$).

Fig. 2.

Comparison of (a) computed and experimental values of natural frequencies and (b–d) loss factors of the lowest vibration tones of the free-free strip.

Dots designate similar experimental values f_i exp = f_i exp(θ) and η_i exp = η_i exp(θ) at θ = 0°, 15°, 30°, 45°, 60°, 75°, and 90°. Comparison of the obtained results allows noting that there is a good agreement between calculated and experimental values. Divergences Δf_i = [( f_i cal/f_i exp) – 1] × 100% and Δη_i = [(η_i cal/η_i exp) – 1] × 100% do not exceed the values |Δf_i| = 2.7% and |Δη_i| = 19% for all the considered vibration tones (i = $\overline {1,7}$) at θ ∈ [0°, 90°].

5. Numerical investigations of the influence of orientation angles of reinforcing fibers and the length of the rod on the values of free-free frequencies and loss factors were carried out for free-free and cantilever monoclinic strips of rectangular cross section (a = 0.005 m, b = 0.02 m) from unidirectional carbon plastic (ρ = 1581.5 kg/m³, Re E₁/Re E₂ ≈ 38). Vibration modes were identified in the basis of their own forms.

First, let us investigate the influence of orientation angle of reinforcing fibers θ ∈ [0°, 90°] on the parameters of attenuating flexural–torsional vibrations using the example of a monoclinic strip with length l = 0.2 m = const. Figures 3 and 4 present diagrams of dependences f_i = f_i(θ) and η_i = η_i(θ) (solid lines) for the lowest tones of flexural–torsional vibrations of free-free and cantilever monoclinic strips (i = $\overline {1,5}$). The same figures also show dependences of partial natural frequencies and partial loss factors of flexure vibrations ${{\bar {f}}_{i}}$ = ${{\bar {f}}_{i}}(\theta )$ and ${{\bar {\eta }}_{i}}$ = ${{\bar {\eta }}_{i}}(\theta )$ (i = $\bar {1}$, $\bar {2}$, …, dotted lines) and torsional vibrations ${{\tilde {f}}_{i}}$ = ${{\tilde {f}}_{i}}(\theta )$, ${{\tilde {\eta }}_{i}}$ = ${{\tilde {\eta }}_{i}}(\theta )$ (i = $\tilde {1}$, $\tilde {2}$, …, dashed lines) of orthotropic strip of the same geometry. Values of functions ${{\bar {f}}_{i}}$ = ${{\bar {f}}_{i}}(\theta )$ and ${{\bar {\eta }}_{i}}$ = ${{\bar {\eta }}_{i}}(\theta )$ were found from solving Eq. (4), and values of functions ${{\tilde {f}}_{i}}$ = ${{\tilde {f}}_{i}}(\theta )$ and ${{\tilde {\eta }}_{i}}$ = ${{\tilde {\eta }}_{i}}(\theta )$ were found from solution of Eq. (5).

Fig. 3.

(a) Dependences of natural frequencies and (b–f) loss factors of the free-free monoclinic strip on angle θ.

Fig. 4.

(a) Dependences of natural frequencies and (b–f) loss factors of the cantilever monoclinic strip on angle θ.

Combined analysis of the results presented in Figs. 3 and 4 allows it to be concluded that, at θ $\geqslant$ 30°, natural frequencies and loss factors of coupled vibrations can be characterized as quasi-flexure (with weakly pronounced torsional deformations) or quasi-torsional (with weakly pronounced flexural deformations). At the same time, functions f_i = f_i(θ) and η_i = η_i(θ) are well approximated on segment θ ∈ [30°, 90°] by functions ${{\bar {f}}_{i}}$ = ${{\bar {f}}_{i}}(\theta )$, ${{\bar {\eta }}_{i}}$ = ${{\bar {\eta }}_{i}}(\theta )$ and ${{\tilde {f}}_{i}}$ = ${{\tilde {f}}_{i}}(\theta )$, ${{\tilde {\eta }}_{i}}$ = ${{\tilde {\eta }}_{i}}(\theta )$.

Nonclassical effects on half-open segment θ ∈ (0°, 30°] are conditioned by the fast growth of the values of function |μ_x, xy(θ) · μ_xy, x(θ)| in the indicated range of variation of argument θ. These effects are manifested in the appearance of areas of mutual transformation of eigenforms of coupled vibration modes.

For an unsupported strip of the area of mutual transformation, this occurs on segments with fuzzy boundaries [θ₁, θ₂], the conditional centers of which are located at the points of intersection of the dependences of partial natural frequencies of flexure and torsional vibrations or even or odd tones (Fig. 3). In areas of mutual transformation of their own forms of related modes, vibrations of flexural–torsional interaction are more noticeable. The maximum effect (strong interaction) occurs in the equal numbers of the tones of partial flexure and torsional vibrations.

Let us return to the results of numerical calculations of the free-free strip (Fig. 3). It is needs to be noted that the eigenform of the first mode of coupled vibrations, which at θ ∈ (0°, 90°) is identified as the first quasi-flexural mode, degenerates into the first flexural mode at θ = 0°, 90°, since ${{\mu }_{{x,xy}}}$(0°) · ${{\mu }_{{xy,x}}}$(0°) = ${{\mu }_{{x,xy}}}$(90°) · ${{\mu }_{{xy,x}}}$(90°) = 0. The influence of flexural torsion on open segment θ ∈ (0°, 90°) is confirmed by the difference of diagrams of functions f₁ = f₁(θ) and η₁ = η₁(θ) (curves 1 in Figs. 3a, 3b) and ${{\bar {f}}_{1}}$ = ${{\bar {f}}_{1}}(\theta )$ and ${{\bar {\eta }}_{1}}$ = ${{\bar {\eta }}_{1}}(\theta )$ (curves $\bar {1}$ in Figs. 3a, 3b).

An increase in vibration tone causes mutual transformations of eigenforms of the coupled modes. This is evidenced by the appearance of points of intersection of graphs of functions ${{\bar {f}}_{i}}$ = ${{\bar {f}}_{i}}(\theta )$ and ${{\tilde {f}}_{i}}$ = ${{\tilde {f}}_{i}}(\theta )$ (curves $\bar {2}$, $\tilde {2}$ and $\bar {3}$, $\tilde {3}$, curves $\bar {4}$, $\tilde {2}$ and $\bar {3}$, $\tilde {1}$ in Fig. 3a) inside areas restricted by functions f_m = f_m(θ) and f_n = f_n(θ) (curves 3, 4 and 2, 5 in Fig. 3a).

Intersection of graphs of functions ${{\bar {f}}_{2}}$ = ${{\bar {f}}_{2}}(\theta )$ and ${{\tilde {f}}_{2}}$ = ${{\tilde {f}}_{2}}(\theta )$ at point θ ≈ 4° indicates that mutual transformation of eigenforms of the third and fourth coupled modes of flexural–torsional vibrations begins on a segment with fuzzy boundaries adjacent to it by axis θ as a result of strong interaction. Thus, at θ > 4°, the eigenform of the third coupled mode is transformed into the eigenform of the fourth coupled mode and vice versa. On a segment with a conventional center at point θ ≈ 15°, the process of mutual transformation of the eigenforms of the third and fourth modes is complemented by the process of mutual transformation of the eigenforms of the fourth and seventh modes (not shown in Fig. 3a) of coupled vibrations. This is confirmed by interaction of graphs of functions ${{\bar {f}}_{4}}$ = ${{\bar {f}}_{4}}(\theta )$ and ${{\tilde {f}}_{2}}$ = ${{\tilde {f}}_{2}}(\theta )$ at point θ ≈ 15°. Therefore, at θ > 15°, the eigenform of the fourth mode is transformed into the eigenform of the seventh coupled mode. The process of mutual transformations finally stops at θ = 90°. Thus, the eigenform of the fourth mode of coupled vibrations at θ = 0° is identical to that of the third mode of coupled vibrations at θ = 90° (second flexural). Two mutual transformations on segment θ ∈ [0°, 30°] result in the identity of the eigenform of the seventh mode of coupled vibrations at θ = 0° to that of the fourth mode of coupled vibrations at θ = 90° (fourth flexural).

Similarly, strong interaction between fifth and sixth coupled vibration modes occurs on a segment with a conventional center at point θ ≈ 7°, which is confirmed by intersections of graphs of functions ${{\bar {f}}_{3}}$ = ${{\bar {f}}_{3}}(\theta )$ and ${{\tilde {f}}_{3}}$ = ${{\tilde {f}}_{3}}(\theta )$ at point θ ≈ 4°. The indicated flexural–torsional interaction generates mutual transformation of coupled vibration modes. An increase in angle θ on a segment with a conventional center at point θ ≈ 18° leads to mutual transformation of the second and fifth coupled modes of flexural–torsional vibrations. Therefore, at θ > 18°, the eigenform of the second coupled mode is transformed into that of the fifth coupled mode and vice versa. As a result of the described mutual transformations of the eigenform of the second mode of coupled vibrations at θ = 0° is identical to the eigenform of the fifth mode of coupled vibrations at θ = 90° (first torsional). In turn, the eigenform of the sixth mode of coupled vibrations at θ = 0° is identical to the eigenform of the second mode of coupled vibrations at θ = 90° (third flexural).

Obviously, besides the influence of the character of changing of functions f_i = f_i(θ), mutual transformations of eigenforms of coupled modes of flexural–torsional vibrations will also influence the character of changing of functions η_i = η_i(θ).

Analysis of the dependences presented in Figs. 3c–3f allows concluding that, outside the areas of mutual transformations of eigenforms, loss factors of coupled vibration modes are satisfactorily approximated by those of corresponding partial vibration modes. In the areas of mutual transformations of eigenforms, loss factors of partial vibration modes do not describe the loss factors of coupled vibration modes even qualitatively. In particular, on segment θ ∈ [0°, 7°], function η₂ = η₂(θ) is well approximated by function ${{\tilde {\eta }}_{1}}$ = ${{\tilde {\eta }}_{1}}(\theta )$; on segment θ ∈ [20°, 90°], it is well approximated by function ${{\bar {\eta }}_{3}}$ = ${{\bar {\eta }}_{3}}(\theta )$ (curves 2, $\bar {3}$, 1 in Fig. 3c). At the same time, in the area of mutual transformation of the eigenforms of the second and fifth coupled modes of flexural–torsional vibrations (θ ∈ [7°, 20°]), divergences between functions η₂ = η₂(θ) and ${{\bar {\eta }}_{3}}$ = ${{\bar {\eta }}_{3}}(\theta )$, ${{\tilde {\eta }}_{1}}$ = ${{\tilde {\eta }}_{1}}(\theta )$ significantly increase.

Graphs of functions η_i = η_i(θ) presented in Figs. 3b–3f imply that ${{\bar {\eta }}_{4}}(0^\circ )$ > ${{\bar {\eta }}_{3}}(0^\circ )$ > ${{\bar {\eta }}_{2}}(0^\circ )$ > ${{\bar {\eta }}_{1}}(0^\circ )$ > ${{\eta }_{x}}(0^\circ )$ = η₁. This result is conditioned by the increasing influence of deformation of transversal shear by values of f_i = f_i(0°) and η_i = η_i(0°) with increasing vibration tone, since relation E_x(0°)/G_xz(0°) = E₁/G₁₃ is maximal on segment θ ∈ [0°, 90°]. Maximal values of functions ${{\bar {\eta }}_{i}}$ = ${{\bar {\eta }}_{i}}(\theta )$ are reached on segment θ ∈ [25°, 30°], where the potential energy of deformation is dominated by the component responsible for shear in the reinforcement plane; i.e., the influence of the viscoelastic matrix on the energy dissipation is maximal. The global minimum of functions ${{\bar {\eta }}_{i}}$ = ${{\bar {\eta }}_{i}}(\theta )$ is reached at θ = 0°, since in this case the potential energy of rod deformation is mainly determined by the potential energy of deformation of elastic reinforcing fibers. Maximums of functions ${{\tilde {\eta }}_{i}}$ = ${{\tilde {\eta }}_{i}}(\theta )$ at θ = 0°, 90° are also conditioned by the dominating influence of shear in the plane of reinforcement (viscoelastic matrix) of the potential energy of rod deformation.

Let us proceed to analysis of the results of numerical studies of a cantilever monoclinic strip. We note right away that, in contrast to the unsupported strip, in the cantilever strip, areas of mutual transformation of the eigenforms of coupled vibration modes appear on segments with conventional centers at the points of intersection of the dependences of partial flexural and partial torsional natural frequencies of both even and odd vibration tones (Fig. 4). This difference is generated by a change in the boundary conditions, which is symmetric for the unsupported strip and asymmetric for the cantilever strip.

The dependences presented in Fig. 4 imply that, at all θ ∈ [0°, 90°], the first mode of coupled vibrations of the monoclinic strip is quasi-flexural; it degenerates into the first flexural mode at θ = 0°, 90° (curves 1, $\bar {1}$ in Fig. 4).

The second mode, which is identified as first torsional at θ = 0°, is transformed into the first quasi-torsional mode with growth of θ (θ > 0°). The intersection of the graphs of functions ${{\bar {f}}_{2}}$ = ${{\bar {f}}_{2}}(\theta )$ and ${{\tilde {f}}_{1}}$ = ${{\tilde {f}}_{1}}(\theta )$ (curves $\tilde {1}$, $\bar {2}$ in Fig. 4) at point θ ≈ 7° indicates that mutual transformation of the eigenforms of the second (first quasi-torsional) and third (second quasi-flexure) coupled modes of flexural–torsional vibrations begins on a segment adjacent to it. Therefore, at θ > 7°, the eigenform of the second coupled mode is transformed into that of the third coupled mode (second quasi-flexural) and the eigenform of the third coupled mode is transformed into the eigenform of second (first quasi-torsional) coupled mode. In this way, at θ > 7°, the second coupled mode is identified as the second quasi-flexural mode, which degenerates into the second flexural vibration mode at θ = 90°. On a segment with a conventional center at point θ ≈ 19°, the process of mutual transformation of the eigenforms of the second and third modes is complemented by the process of mutual transformation of the eigenforms of the third (first quasi-torsional) and fourth (third quasi-flexural) modes of coupled vibrations. This is confirmed by the intersection of graphs of functions ${{\bar {f}}_{3}}$ = ${{\bar {f}}_{3}}(\theta )$ and ${{\tilde {f}}_{1}}$ = ${{\tilde {f}}_{1}}(\theta )$ at point θ ≈ 19°. As a result, at θ > 19°, the eigenform of the third coupled mode is transformed into the eigenform of the fourth coupled mode and the third quasi-flexural mode, is degenerates into the third flexural vibration mode at θ = 90°. Similar behavior is also observed for vibrations of higher tones.

6. The influence of the length of the strip on the parameters of its attenuating vibrations was studied using the example of a monoclinic, free-free strip, the reinforcing fibers of which are oriented at angle θ = 15° relative to the x axis. When carrying out numerical experiments, the strip length was varied in the range of l ∈ [0.05; 0.40] m. The results are shown in Fig. 5. Since the partial natural frequencies of bending and torsional vibrations are inversely proportional to different degrees of strip length (${{\bar {f}}_{i}}$ ~ ${{l}^{{ - 2}}}$, ${{\tilde {f}}_{i}}$ ~ ${{l}^{{ - 1}}}$), for clarity, the dependences of the natural frequencies on the strip length are presented in the coordinate system log  f_i = log  f_i(log l). In this coordinate system, the partial natural frequencies of flexural and torsional vibrations are characterized by two families of curves that differ in the rate of change (slope) of the function when its argument changes (Fig. 5a).

Fig. 5.

(a) Dependences of natural frequencies and (b) loss factors of the lowest tones of flexural–torsional vibrations of an free-free monoclinic strip at θ = 15° on length l.

Analysis of the results presented in Fig. 5 allows it to be concluded that the eigenforms of coupled vibrations at a sufficiently large strip length (l = 0.4 m) can be characterized as quasi-flexural (with weakly pronounced torsional deformations) or as quasi-torsional. At the same time, the eigenforms of the first, second, third, and fifth tone correspond to the first, second, third, and fourth quasi-flexural vibration modes, while the eigenform of the fourth tone corresponds to the first quasi-torsional vibration mode. Natural frequencies f_i = f_i(0.4 m) and loss factors η_i = η_i(0.4 m) of coupled vibration modes are well approximated by corresponding partial frequencies ${{\bar {f}}_{i}}$ = ${{\bar {f}}_{i}}$(0.4 m) and ${{\tilde {f}}_{i}}$ = ${{\tilde {f}}_{i}}$(0.4 m) and partial loss factors ${{\bar {\eta }}_{i}}$ = ${{\bar {\eta }}_{i}}$(0.4 m) and ${{\tilde {\eta }}_{i}}$ = ${{\tilde {\eta }}_{i}}$(0.4 m). With a decrease in the differences in rod length between the values of f_i = f_i(l) and ${{\bar {f}}_{i}}$ = ${{\bar {f}}_{i}}(l)$, ${{\tilde {f}}_{i}}$ = ${{\tilde {f}}_{i}}(l)$ while η_i = η_i(l) and ${{\bar {\eta }}_{i}}$ = ${{\bar {\eta }}_{i}}(l)$, ${{\tilde {\eta }}_{i}}$ = ${{\tilde {\eta }}_{i}}(l)$ increase, and at l = 0.1 m eigenforms of all the five vibration tones are identified as coupled flexural–torsional. In addition, on a segment with fuzzy boundaries, the conventional center of which is located at point l = 0.24 m, mutual transformation of the eigenforms of the third and fourth coupled modes of flexural–torsional vibrations occurs. Therefore, at l < 0.24 m, the eigenform of the third coupled mode is transformed into that of the fourth coupled mode and the eigenform of the fourth coupled mode into the eigenform of the third coupled mode.