Identification of the bridge moving loads based on fractional conjugate gradient method

Abstract

This paper proposes a bridge moving load identification method based on the fractional conjugate gradient (FCG) method to address the low identification accuracy of traditional conjugate gradient methods. Firstly, the mathematical framework for detecting the moving load in the vehicle-bridge system is established by utilizing both the time-domain deconvolution technique and modal superposition approach. Secondly, the derivation of the discrete moving load identification system matrix equation enables its formulation as an unconstrained optimization problem. Finally, the load information is obtained iteratively by the FCG method. Experimental results demonstrate that, compared with the Hestenes–Stiefel conjugate gradient (HSCG) method, the Flether–Reeves conjugate gradient (FRCG) method, and the Polak–Ribire–Polyak conjugate gradient (PRPCG) method, the FCG method has faster identification speed, smaller identification error, and higher identification accuracy and noise resistance in identifying bridge moving loads at different noise levels.

1 Introduction

The safety and reliability of bridge structures are directly related to the development of society and the economy as a whole. With the rapid development of the national economy, traffic volume increasing, vehicle high-speed driving, and overloading during service, it can adversely affect the safety of bridges and also pose a significant threat to their integrity and stability [1,2,3]. In the field of bridge engineering, identifying and monitoring moving loads effectively and studying the impact of bridge vibration and damage on operational performance have become urgent and important problems that need to be solved [4,5,6]. Since the problem of self-loading identification is first introduced, scholars have conducted extensive research and achieved numerous results. Law et al. proposed an improved time-domain method (TDM) to identify bridge moving loads and used singular value decomposition (SVD) to solve the noise-sensitive problem [7]. Chen et al. subsequently proposed a bridge moving load identification method based on truncated singular value decomposition methods, segmental polynomial truncation singular value decomposition method and pre-processing least squares QR decomposition method, which increases the identification accuracy of moving loads to a certain extent [8,9,10]. Liu et al. identified spatio-temporally coupled distributed dynamic loads using blind source separation and orthogonal matching pursuit, and obtained its spatial distribution and temporal history [11]. Wang et al. proposed a new fast-converging iterative regularization method, which successfully identified dynamic loads on stochastic structures [12]. Liu et al. proposed a power spectral density identification method for steady-state random excitation, considering the impact of multisource uncertainty, used a two-step weighted regularization strategy and response superposition-decomposition principle, and improved the accuracy and efficiency of load identification using an adaptive dimensionality reduction Chebyshev model and the first-order Taylor series [13]. He et al. proposed an L1-norm regularization load identification method based on redundant extended cosine dictionaries, which efficiently identifies complex dynamic loads with good noise resistance [14]. Chen et al. proposed a new method for identifying dynamic loads at the interface between spacecraft and rocket using BP neural network, which further optimized the accuracy of identifying dynamic loads at the interface [15]. Li et al. combined the extended Kalman filter method with the least squares estimation method to identify unknown loads acting on time-varying structures, which more accurately estimated the parameter values of unknown loads on time-varying structures [16]. Qiao et al. used a cubic B-spline expansion function to propose a moving load identification method with high accuracy and the ability to overcome the ill-conditioning problem. This method has strong robustness to noise and uncertainty in data and can reduce estimation errors [17]. Liu et al. proposed a method to identify complex loads acting on a cantilever beam at multiple points, which reduced the data processing difficulty and improved the accuracy of load identification [18]. However, due to the complexity and uncertainty of engineering structures, existing load identification methods require strong data processing capabilities [19] and precise system response data. They are also sensitive to sensor layout. Incorrect sensor placement may also affect the accuracy of the identification results. The conjugate gradient algorithm can solve most of the above problems and has advantages such as fast computation speed and good convergence [20,21,22,23]. Wang et al. used the conjugate gradient method to identify multisource excitation forces [24]. Luo et al. introduced a bridge moving load identification technique based on an improved conjugate gradient method, which solved the noise-sensitive problem of time-domain method and the poor numerical performance of traditional conjugate gradient methods [25].

Although the moving load identification method based on the traditional conjugate gradient method is effective and reliable, it still has drawbacks such as low identification accuracy, poor noise resistance at high noise levels, and slow identification speed. Recently, the fractional-order model has become a major hotspot [26,27,28]. Compared with integer-order models, its advantages are excellent in describing the memory and genetic characteristics of various processes [29]. Because the order is fractional, the simulation results can more accurately describe the dynamic characteristics of the system. Based on this, this paper proposes a bridge moving load identification method based on the fractional conjugate gradient (FCG) algorithm, which avoids the selection of regularization parameters and does not introduce complex objective functions. Firstly, a mathematical model for moving load identification is established using the time-domain deconvolution method and modal superposition method. Secondly, by constructing an appropriate optimization objective function, the problem is transformed into a high-dimensional unconstrained optimization problem. Then, the FCG method is used to solve this optimization problem to obtain the load information. Finally, the effectiveness of the proposed method is verified through numerical simulations, and the impact of noise and sensor configuration on mobile load identification is also studied.

2 Basic theory of load identification

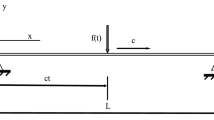
Figure 1 shows the vehicle-bridge system model, which makes the following assumptions simplify actual engineering problems: (1) The bridge satisfies small deformation theory, Hooke’s law, Navier hypothesis, and Saint-Venant’s principle; (2) the bridge has uniform cross-section and constant mass per unit length; (3) the velocity of the moving load is constant, and it moves from left to right; and (4) the bridge’s damping is proportional to the vibration speed.

Fig. 1

The model diagram of vehicle-bridge system

Based on these assumptions, the displacement response $f\left( t \right)$ of the bridge under the moving load $u\left( {x,t} \right)$ can be expressed as:

$$\begin{aligned} \delta \left( {x - ct} \right) f\left( t \right)= & {} C\frac{{\partial u\left( {x,t} \right) }}{{\partial t}} + \rho \frac{{{\partial ^2}u\left( {x,t} \right) }}{{\partial {t^2}}}\nonumber \\{} & {} + EI\frac{{{\partial ^4}u\left( {x,t} \right) }}{{\partial {t^4}}} \end{aligned}$$

(2.1)

where: $x$ represents the distance from the left end of the bridge; $t$ represents time; $c$ is the constant vehicle speed; $u\left( {x,t} \right)$ represents the displacement of the bridge at position $x$ and time $t$; $f\left( t \right)$ represents the moving load; $C$ represents the viscous damping parameter; $E$ represents the Young’s modulus; $I$ represents the moment of inertia; $\delta \left( {x - ct} \right)$ represents the Dirac $\delta$ function; and $\rho$ represents the density of the beam.

Using modal superposition method and time-domain deconvolution method, we can obtain the structural response:

$$\begin{aligned} u\left( {x,t} \right)= & {} \sum \limits _\mathrm{{n}}^\infty {\frac{2}{{L\rho \omega _n^d}}} \sin \frac{{\pi nx}}{L} \nonumber \\{} & {} \times \int _0^t {{e^{ - {\xi _n}{\omega _n}\left( {t - \tau } \right) }}} \sin \left[ {\omega _n^d\left( {t - \tau } \right) } \right] \sin \frac{{\pi nc\tau }}{L}f\left( \tau \right) d\tau , \end{aligned}$$

(2.2)

in which, $n$ represents the modal order; $L$ represents the bridge span; ${\xi _n} = \frac{C}{{2\rho {\omega _n}}}$; ${\omega _n} = \frac{{{n^2}{\pi ^2}}}{{{L^2}}}\sqrt{\frac{{EI}}{\rho }}$; $\omega _n^d = {\omega _n}\sqrt{1 - \xi _n^2}$; and $\tau$ is the integration variable. The bridge bending moment response $m\left( {x,t} \right)$ and acceleration response $a\left( {x,t} \right)$ can be, respectively, obtained from the displacement response $u\left( {x,t} \right)$, as follows:

$$\begin{aligned} m\left( {x,t} \right) = - EI\frac{{{\partial ^2}u\left( {x,t} \right) }}{{\partial {x^2}}},a\left( {x,t} \right) = \frac{{{d^2}u\left( {x,t} \right) }}{{d{t^2}}}, \end{aligned}$$

(2.3)

where

$$\begin{aligned} \frac{{{\partial ^2}u\left( {x,t} \right) }}{{\partial {x^2}}} = \sum \limits _{\mathrm{{n = 1}}}^\infty { - \frac{{2{\pi ^2}{n^2}}}{{{L^3}\rho \omega _n^d}}} \sin \frac{{\pi nx}}{L}\int _0^t {{e^{ - {\xi _n}{\omega _n}\left( {t - \tau } \right) }}} \sin \left[ {\omega _n^d\left( {t - \tau } \right) } \right] \sin \frac{{\pi nc\tau }}{L}f\left( \tau \right) d\tau , \end{aligned}$$

(2.4)

$$\begin{aligned} \frac{{{d^2}u\left( {x,t} \right) }}{{d{t^2}}} = \sum \limits _{\mathrm{{n = 1}}}^\infty {\frac{2}{{L\rho }}} \sin \frac{{\pi nx}}{L}\left[ {\sin \frac{{\pi nc\tau }}{L}f\left( t \right) + \int _0^t {\ddot{h}\left( {t - \tau } \right) f\left( t \right) \sin \frac{{\pi nc\tau }}{L}d\tau } } \right] , \end{aligned}$$

(2.5)

in which

$$\begin{aligned} \ddot{h}\left( t \right) = \frac{1}{{\omega _n^d}}{e^{ - {\xi _n}{\omega _n}t}}\left\{ {\left[ {{{\left( {{\xi _n}{\omega _n}} \right) }^2} - {\omega _n}^2} \right] \sin \left( {\omega _n^dt} \right) + \left( { - 2{\xi _n}{\omega _n}\omega _n^d} \right) \cos \left( {\omega _n^dt} \right) } \right\} , \end{aligned}$$

(2.6)

Then, we discrete (2.4) and (2.5) into a matrix form. If the acceleration response is measured separately, we can obtain

$$\begin{aligned} \mathop {{{\ddot{u}}_{}}}\limits _{N \times 1} = \mathop {{U_{}}}\limits _{N \times ({N_k} - 1)} \cdot \mathop f\limits _{({N_k} - 1) \times 1}. \end{aligned}$$

(2.7)

If the bending moment response is measured separately, we can obtain

$$\begin{aligned} \mathop {{m_{}}}\limits _{(N - 1) \times 1} = \mathop {{M_{}}}\limits _{(N - 1) \times ({N_k} - 1)} \cdot \mathop f\limits _{({N_k} - 1) \times 1}. \end{aligned}$$

(2.8)

If both bending moment and acceleration responses are measured simultaneously, they can be used together to identify the driving force. By scaling the variables $m$ in (2.7) and $\ddot{u}$ in (2.8) to non-dimensional units, we obtain

$$\begin{aligned} \left[ \begin{array}{l} M/\left\| m \right\| \\ U/\left\| {\ddot{u}} \right\| \end{array} \right] f = \left\{ \begin{array}{l} m/\left\| m \right\| \\ \ddot{u}/\left\| {\ddot{u}} \right\| \end{array} \right\} \end{aligned}$$

(2.9)

in which, $M$ and $U$ are matrices of the vehicle-bridge system; $m$ and $\ddot{u}$ are matrices of bending moment and acceleration response, respectively. In the time domain, the load identification problem in (2.9) can ultimately be transformed into the following equation:

$$\begin{aligned} Af = Y, \end{aligned}$$

(2.10)

in which, $A$ represents the system matrix that is related to the vehicle-bridge parameters; $Y$ represents the response vector of bending moment, acceleration response, or their combination at measurement points on the bridge; and $f$ represents the time series vector of moving loads. The specific forms of these matrices can be found in [7].

3 The fractional conjugate gradient method

The load identification problem can be transformed into the problem about solving matrix equation $AF = Y$. By formulating the corresponding objective function, the original issue can be converted into a high-dimensional unconstrained optimization problem:

$$\begin{aligned} \mathop {\min }\limits _{w \in {R^n}} H(x), \end{aligned}$$

(3.1)

Here, ${{R^n}}$ represents the n-dimensional Euclidean space, and $H(x)$ is a continuously differentiable function:

$$\begin{aligned} H(x) = \frac{1}{2}{x^T}Ax + {x^T}Y, \end{aligned}$$

(3.2)

The conjugate gradient method is commonly used to solve optimization problems. This method can be used to solve (3.1), and its iterative formula is expressed as

$$\begin{aligned} {x_{i + 1}} = {x_i} + {\alpha _i}{d_i},i = 0,1,2, \cdots ..., \end{aligned}$$

(3.3)

where $i$ represents the number of iterations; ${x_i}$ represents the solution of step $i$; ${\alpha _i}$ represents the step size; ${d_i}$ represents the search direction

$$\begin{aligned} {d_i} = \left\{ \begin{array}{l} - {g_i},\mathrm{{ }}i = 1\\ - {g_i} + {\beta _i}{d_{i - 1}},i \ge 2. \end{array} \right. \end{aligned}$$

(3.4)

We assure ${g_i}$ represents the gradient of $H(x)$ at $x = {x_k}$, and ${\beta _i}$ is a scalar used to adjust the direction. Different conjugate gradient algorithms use different ${\beta _i}$.

The scalar ${\beta _i}$ for adjusting the search direction in the FCG method proposed in this article is given by the following formula:

$$\begin{aligned} {\beta _i} = \left\{ {\begin{array}{*{20}{l}} {\frac{{g_i^T\left( {{g_i} - \frac{{{{\left\| {{g_i}} \right\| }^p}}}{{{{\left\| {{g_{i - 1}}} \right\| }^p}}}{g_{i - 1}}} \right) }}{{d_i^T\left( {{g_i} - {g_{i - 1}}} \right) }},g_i^T{g_{i - 1}} \ge 0}\\ {\frac{{g_i^T\left( {{g_i} + \frac{{{{\left\| {{g_i}} \right\| }^p}}}{{{{\left\| {{g_{i - 1}}} \right\| }^p}}}{g_{i - 1}}} \right) }}{{d_i^T\left( {{g_i} - {g_{i - 1}}} \right) }},g_i^T{g_{i - 1}} < 0} \end{array}} \right. \end{aligned}$$

(3.5)

where $p$ denotes the fractional order. The maximum number of iterations in the moving force identification calculation process is set to N = 7000, with a precision indicator of $e = {10^{ - 6}}$. If $N>7000$ or $\left\| {{g_i}} \right\| \le e$, the algorithm immediately stops iterating, yielding the identification result; otherwise, it continues iterating until a convergent solution is obtained. Based on (3.5), the detailed calculation process of the moving force identification using the proposed IFCG algorithm in this paper is illustrated in Fig. 2. The fundamental steps are described as follows:

• Step 1: Construct (2.7) using the time-domain deconvolution method and the modal superposition principle;

• Step 2: Formulate the objective function (3.1), transforming the problem of identifying moving loads into an unconstrained optimization problem;

• Step 3: Set initial values: ${x_0} = 0, {g_0} = b, i = 0, {d_0} = {g_0}, N=7000, e={10^{ - 6}}$;

• Step 4: Calculate the step size $\alpha _i$ using ${\alpha _i} = ({g_i},{g_i})/({d_i},A{d_i})$;

• Step 5: Update $x_i$ using (3.3);

• Step 6: Calculate the residual through ${g_{i + 1}} = {g_i} - {g_i}{d_i}$; if $\left\| {{g_{i+1}}} \right\| \le e$, the iteration ends, and the result $x_i$ is output. Otherwise, proceed to the next step;

• Step 7: Calculate the directional scalar $\beta _i$ using (3.5).

• Step 8: Update the search direction $d_i$ using ${d_{i + 1}} = {g_{i + 1}} + {\beta _i}{d_i}$.

• Step 9: If $i \le N$, end the iteration and output the result $x_i$; otherwise, return to Step 4.

Fig. 2

The calculation flowchart of FCG method

4 Load identification and result analysis

4.1 Parameter selection and setting

The structural parameters of the bridge model are given as follows: the flexural stiffness ($EI$) is $1.27 \times {10^{11}}\mathrm{{N}}\;\mathrm{{m}^2}$; the density $\rho _\mathrm{{A}}$ is $1.2 \times {10^4}\; \mathrm{{kg/m}}$; and the span of the beam is 40 m. The initial three resonant frequencies of the beam are 3.2 Hz, 12.8 Hz, and 28.8 Hz, respectively. The vehicle parameters are given as follows: the vehicle’s moving speed is 40 m/s, the distance between the front and rear axles is 4 m, and the sampling frequency is 200 Hz.

The time history of the moving load on the front and rear axles of the vehicle is, respectively:

$$\begin{aligned} \begin{array}{l} {F_1}\left( t \right) = 20\left[ {1 + 0.2\sin \left( {10\pi t} \right) + 0.08\sin \left( {40\pi t} \right) } \right] ,\\ {F_2}\left( t \right) = 20\left[ {1 - 0.2\sin \left( {10\pi t} \right) + 0.08\sin \left( {50\pi t} \right) } \right] . \end{array} \end{aligned}$$

(4.1)

Considering the possible influence of errors and noise interference in the actual measurement process, this article adopts the method of simulating random noise to generate the response obtained from actual measurements:

$$\begin{aligned} {b_\text {simulate}} = {b_\text {true}}\left( {1 + nl \times {N_\text {noise}}} \right) \end{aligned}$$

(4.2)

in which, ${b_\text {true}}$ represents the simulated true response; ${b_\text {simulate}}$ represents the measured response after simulating the noise interference; $nl$ represents the noise level; ${N_\text {noise}}$ represents the random Gaussian white noise.

To streamline the load identification process, acceleration and bending moment sensors are strategically deployed at specific positions along the bridge span, namely at 1/4, 1/2, and 3/4 intervals. For ease of reference, $M$ is used to represent the moment response, and $A$ represents the acceleration response. For example, $M14$ denotes the bending moment response at the 1/4-span position, while $A34$ represents the acceleration response at the 3/4-span position, and so on for other positions. The efficiency of load identification will be assessed by measuring the number of required iterations, and the time required for each iteration will be kept constant across the different methods. A lower number of iterations will signify a more rapid load identification process.

Fig. 3

Number of recognition iterations for four p values at different noise levels

Fig. 4

The recognition accuracy of four p values at different noise levels

In this study, the accuracy of the load identification process is assessed by utilizing the relative percentage error (RPE). The RPE is computed using the following formula:

$$\begin{aligned} \text {RPE} = \frac{{\left\| {{F_\text {iden}} - {F_\text {true}}} \right\| }}{{\left\| {{F_\text {true}}} \right\| }}, \end{aligned}$$

(4.3)

where ${F_\text {true}}$ is the true load, and ${F_\text {iden}}$ is the estimated load.

The following discussion is conducted regarding the selection of the fractional order $p$ in (3.5): under different noise levels and using a sensor configuration of $M14 \& M12 \& M34 \& A14 \& A12 \& A34$, the value of $p$ can be evaluated based on the number of accuracy of load identification and iterations results for both the front and rear axles. The specific results are shown in Figs. 3 and 4.

Based on the analysis of the load identification accuracy and iteration time in Figs. 3 and 4, it is observed that p = 1/2 leads to a faster load identification speed and better identification accuracy. Therefore, in the subsequent analysis, p = 1/2 will be selected for load identification.

4.2 The analysis of the identification results

To validate the anti-noise performance and accuracy of the proposed algorithm, this paper conducted simulation experiments on the load identification of front and rear axles by selecting six different sensor configurations and 21 noise levels (0–20% noise level, with a step of 1%). Identification error is used as the evaluation index to evaluate the precision of the load identification outcomes. Meanwhile, the FCG method is compared with other conjugate gradient methods such as Hestenes–Stiefel conjugate gradient method (HSCG), Fletcher–Reeves conjugate gradient method (FRCG), and Polak–Ribire–Polyak conjugate gradient method (PRPCG) in terms of identification accuracy and identification speed. The specific identification results are shown in Figs. 5 and 6. The specific experimental results for the error in identifying the front and rear axis load and the number of iterations for the four methods can be found in Tables 1, 2, and 3.

Table 1 Identification error of front axle moving load by four methods under three noise levels under different sensor configurations

Table 2 Identification error of rear axle moving load by four methods under three noise levels under different sensor configurations

Table 3 Iterations of four methods for load identification at different noise levels under different sensor configurations

Fig. 5

The error of four kinds of conjugate gradient methods in load identification results

Fig. 6

The iterations of four different methods under different sensor positions

As shown in Fig. 5a, when using only the acceleration to identify the load, the identification errors of the four methods are similar, but the FCG method shows slightly better identification accuracy than other methods at low noise levels. From the results in Figs. 5b and 6b, when using only the torque to identify the load, the identification errors of the FCG method and the HSCG method are much smaller than the other two methods, especially at high noise levels, and the iteration numbers of the FCG method are significantly lower than those of the HSCG method. Additionally, when combining the acceleration and torque, all methods show the stability in load identification. As shown in Figs. 5c–f and 6c–f, there were no significant jumps in identification error among these methods, indicating the stability in load identification. Furthermore, when analyzing the identification accuracy under high noise levels, the identification error of the FCG method is significantly lower than that of the FRCG method, PRPCG method, and HSCG method, and the iteration numbers required for the FCG method are much lower than the other three methods, indicating that its identification accuracy and speed are better than other methods. In conclusion, the proposed FCG method has a high identification accuracy and speed under high noise levels and is not dependent on sensor configurations.

To quantitatively analyze the identification accuracy of the FCG method, this paper chooses the sensor configuration of $M14 \& M12 \& M34 \& A14 \& A12 \& A34$ and used four methods to identify the load on the front and rear axles at six different noise levels. The identification results are shown in Fig. 7.

Fig. 7

The identified results of front and rear axle loads using four methods at different noise levels

As shown in Fig. 7, in the absence of noise, all four methods successfully achieve accurate load identification. However, as the noise level increases to 5%, the FRCG method experiences a reduction in identification accuracy, whereas the remaining three methods still accurately identify the load. Upon reaching a noise level of 10%, the FRCG method exhibits significant identification errors, while the PRPCG method demonstrates relatively smaller errors. On the other hand, the FCG method and HSCG method retain their ability to accurately identify the load. At the maximum noise level of 20%, all four methods encounter identification errors, but the FCG method exhibits comparatively smaller errors compared to the other methods. These results indicate that the FCG method has high identification accuracy and strong robustness.

5 Conclusion

• (1) This paper applies the proposed FCG to identifiy moving loads on bridges with six different sensor arrangements. When using bending moment and acceleration for load identification, the FRCG method and the PRPCG method achieve higher identification accuracy than the proposed FCG method at low noise level. However, at high noise level, the identification error of the proposed FCG method is lower than that of the HSCG method, the FRCG method, and the PRPCG method, indicating that the FCG method exhibits higher identification accuracy and robustness in high noise environment.

• (2) The proposed FCG method exhibits a significant advantage in identification speed, showing a faster identification speed than the FRCG method, the PRPCG method, and the HSCG method. This indicates that the FCG method performs more efficiently and quickly in handling large-scale data, which is highly beneficial for applications that require rapid processing of large amounts of data.

• (3) The load identification method proposed based on the FCG method can accurately identify moving loads on bridges and has high identification speed, robustness, and universality without sacrificing identification accuracy. The present method has broad application prospects in the practical monitoring and maintenance of bridges.