Introduction

Dynamic information about moving load on the bridge is closely related to structural design, reliability analysis, fault diagnosis, and other engineering problems. In most practical engineering problems, it is difficult or impossible to directly measure moving loads acting on the bridge structure. However, the dynamic responses of the bridge are easier to obtain without damaging the bridge structure, so the load information can be obtained in an indirect way, i.e., moving force identification (MFI). After decades of research by many scholars, a variety of moving load identification methods have been developed. According to different identification methods, it can be divided into direct method, basis function expansion method, regularization method, function approximation method, intelligent calculation method, and so on.

The direct method is mainly based on the basic theory of structural vibration to deduce and establish the mathematical equation of MFI. Then matrix inverse method or least square method is used to solve the equation directly. For example, Law et al. [1] proposed the time-domain method to identify the moving load on the bridge from the acceleration and bending moment response. Huang et al. [2] transformed the differential equation of bridge structure vibration into the general form of precise integration, and then obtained the precise integration method for MFI. Hou et al. [3] introduced the idea of precise integration method into the symplectic algorithm to establish a symplectic precise integration method for MFI. Liu et al. [4] proposed a new method called time-domain Galerkin method for investigating the structural dynamic load identification problems. Because the MFI is a typical inverse problem, in the case of measurement error or noise interference, the direct method will encounter the problem of ill-conditioned [5], leading to a large deviation in the identification results. Therefore, the direct method is difficult or impossible to be applied in engineering practice.

For the ill-conditioned problem of moving load identification, the regularization methods have been developed by introducing reasonable additional information as the constraint. For example, Qiao et al. [6] used Tikhonov regularization method to overcome the ill-conditioned problem of bridge moving load identification. Based on integer-order Tikhonov regularization technique, Wang et al. [7] proposed a new fractional Tikhonov regularization technique. Subsequently, Liu et al. [8] constructed an improved fractional order filtering factor and proposed an improved fractional order Tikhonov regularization method. Based on singular value decomposition, Chen et al. [9, 10] proposed the truncated generalized singular value decomposition method and piecewise polynomial truncated singular value decomposition method for moving force identification. Chen et al. [11] developed a novel preconditioned least-square QR-factorization method for moving force identification. Based on the Arnoldi process, Krylov subspace method and generalized minimal residual method, Chen et al. [12] proposed a preconditioned range restricted generalized minimal residual method for moving force identification. Based on sparse regularization technique, Pan et al. [13] proposed a novel moving load identification method. Qiao et al. [14] developed a general sparse regularization method based on minimizing l1-norm of the coefficient vector of basis functions. He et al. [15] proposed a novel modified regularization method to solve the ill-posed problem and mitigate the error propagation of random dynamic loads identification. Feng et al. [16] proposed a novel sparse Kalman filter recursive algorithm to localize and reconstruct the forces in time domain. Based on the redundant concatenated dictionary and weighted-norm regularization method, Wang et al. [17] proposed a hybrid method for MFI. Regularization methods are widely studied because they can improve the ill-conditioned problem of inverse problems, but the constraints introduced by regularization method need to be determined in advance. The regularization parameter plays a role in regulating the constraints. If the regularization parameter is too large, it will lead to excessive constraints; if it is too small, it cannot improve the ill-condition of the inverse problem. Therefore, regularization parameters should be selected reasonably according to practical engineering problems, which are the shortcomings of the regularization method.

The main idea of the basis function expansion method is to expand the unknown moving load using the known function, and transform the problem of load identification into the problem of selecting the basis function coefficient. For example, Qiao et al. [18] proposed an efficient basis function expansion method based on wavelet multi-resolution analysis using cubic B-spline scaling functions as basis functions. Qiao et al. [19] developed a regularized cubic B-spline collocation method for identifying the impact force time history, which overcomes the deficiency of the ill-posed problem. Qiao et al. [20] proposed a novel method based on the discrete cosine transform in the time domain for force identification, which overcomes the deficiency of the ill-posedness of the transfer matrix. Liu et al. [21] proposed an analytical method to identify dynamic loads acting on stochastic structures based on the Gegenbauer polynomial expansion theory and regularization method, and also investigated the parallelotope-formed evidence theory model [22]. There are two key points in identifying moving loads by the basis function method: one is the selection of load basis function type and the other one is the selection of the number of basis function. In fact, the basis function expansion method is a special regularization method.

The main idea of the function approximation method is to use the known basis function to fit the deflection of the measured point, and then obtain the velocity and acceleration from the deflection differentiation. Then the acceleration, velocity, and displacement are substituted into the dynamic equation of the structure to identify the load acting on the bridge. For example, Yuan et al. [23] used the polynomial function, trigonometric function, and their combination to approximate the deflection of measured points. Jiang et al. [24] proposed a cubic spline curve fitting method to identify the moving load of the bridge. However, the identification accuracy of different approximation functions is quite different.

The main idea of intelligent calculation method is to transform the identification of moving load into an optimization problem, and use the heuristic algorithms or optimization algorithm to solve the problem. For example, Chen et al. [25] developed a modified preconditioned conjugate gradient method for moving force identification by preconditioned conjugate gradient methods with a modified Gram–Schmidt algorithm. Chisari et al. [26] proposed an identification approach based on genetic algorithm. Based on the firefly algorithm, Pan et al. [27] presented a novel method for moving force identification. Zhou et al. [28] applied least-squares support vector machine to identify the inverse model. Then based on this inverse model, the operational responses were adopted to determine the real-time excitation force. Zhou et al. [29] proposed a novel impact load identification method of nonlinear structures using deep Recurrent Neural Network.

In addition to the above load identification methods, many scholars have also proposed many other methods. For example, Li et al. [30] proposed an online dynamic load identification algorithm based on an extended Kalman filter. Pinkaew [31] proposed the updated static component regularization technique for moving force identification. Yang et al. [32] studied the application of strain influence line method to moving load identification. Qian et al. [33] proposed a novel moving load identification method based on the bending moment influence line. Liu et al. [34] proposed a novel and efficient method utilizing blind source separation and orthogonal matching pursuit. Jiang et al. [35] proposed a novel time-domain algorithm based on the Newmark-b method.

In fact, the direct method is simple, straightforward, and clear, but the MFI results are not reliable when there is measurement error and noise interference. Regularization methods can improve the ill-conditioned problem of load identification. However, the regularization parameter selection needs to be considered. Moreover, the basis function expansion method has the same limitation. The function approximation method is insensitive to noise, but its identification accuracy is excessively dependent on the basic function type. Meanwhile, error accumulation occurs when velocity and acceleration are obtained from the deflection approximated by the function approximation method, which brings the inevitable error to the identification results. Although intelligent calculation methods avoid the shortcomings of the above methods, they require a large amount of data for network training or model construction, which is costly and time consuming, and cannot be used for real-time load identification. According to the discussion above, a new conjugate gradient method is established for MFI of vehicle–bridge system, which is based on the ideas of existing method in [36]. The proposed method does not need to select regularization parameters in advance and model construction and training. Meanwhile, it has the advantages of fast convergence and small storage space which reduces the cost of load identification and improves the speed of load identification. In addition, the iterative process has regularization effect, so the proposed method has anti-noise property. In a word, the proposed method can improve the ill-conditioned problem of load identification and identify the moving load on the bridge efficiently and quickly.

This paper is organized as follows. “Moving Force Identification in Time Domain” section describes the basic theory of the moving load identification of vehicle–bridge system. The modified conjugate gradient (MCG) method is established in “Establishment of Modified Conjugate Gradient Method” section. In “Proof of Global Convergence” section, the global convergence of the MCG method is proved by mathematical theory. The preconditioned technique is introduced in “Theory of Preconditioned Modified Conjugate Gradient (PMCG)” section. Numerical simulations are carried out to investigate the stability and effectiveness of the proposed method in “Numerical Simulation” section. Finally, some conclusions are summarized in “Conclusion” section.

Background of Theory

Moving Force Identification in Time Domain

As shown in Fig. 1, the vehicle–bridge system is modeled as a Bernoulli–Euler simply supported beam subjected to unknown time-varying forces [1]. Assuming that the force f(t) moves from left to right at a constant velocity, the motion equation in terms of the modal coordinate \({q_n}(t)\) can be written as

$$\begin{aligned} {\ddot{q}_n}(t) + 2{\xi _n}{\omega _n}{\dot{q}_n}(t) + \omega _n^2{q_n}(t) = \frac{2}{{\rho L}}{p_n}(t), \end{aligned}$$
(1)

where \({\xi _n}\) is the n-th modal damping ratio; \({p_n}(t) = f(t)\sin (\frac{{n\pi ct}}{L})\) is the modal force; \({\omega _n}\) is the \(n-th\) modal frequency; \(\rho \) is the density of the beam; L is the span of the beam. Based on modal superposition and time-domain deconvolution, the dynamic deflection v(x, t) of the beam at point x and time t can be obtained as

$$\begin{aligned} v(x,t)= & {} \sum \limits _{n = 1}^\infty {\frac{2}{{\rho L\omega _n^\prime }}\sin \frac{{n\pi x}}{L}} \int _0^t {e^{ - {\xi _n}{\omega _n}(t - \tau )}}\nonumber \\{} & {} \sin \left[ {\omega _n^\prime \left( {t - \tau } \right) } \right] \sin \frac{{n\pi c\tau }}{L}f\left( \tau \right) d\tau , \end{aligned}$$
(2)

where \(\omega _n^\prime = {\omega _n}\sqrt{(1 - \xi _n^2)} \).

Fig. 1
figure 1

Moving force identification model with a Bernoulli–Euler simply supported beam

Full size image

The acceleration and bending moment response can be obtained by v(x, t). Then according to the relationship between dynamic response and moving force, which together with the discretization and dimensionless processing, the following equation is formed:

$$\begin{aligned} Aw = r, \end{aligned}$$
(3)

where A is the vehicle–bridge system matrix, w is the moving force vector, and r is the dynamic response vector. The specific form of A and r can be referred to [1], which will not be repeated here.

Establishment of Modified Conjugate Gradient Method

It can be seen from “Moving Force Identification in Time Domain” section that the load identification problem is finally transformed into the solution of the high-dimensional equation. To facilitate the calculation, the original equation is usually transformed into the following symmetric positive definite equations

$$\begin{aligned} Aw = r \Leftrightarrow Kw = b, \end{aligned}$$
(4)

where \(K = {A^T}A\), \(b = {A^T}r\).

By constructing the corresponding objective function, the problem about solving large system of linear equations \(Kw=b\) can be transformed into an unconstrained optimization problem

$$\begin{aligned} \mathop {\min }\limits _{w \in {R^n}} H(w), \end{aligned}$$
(5)

where H(w) represents the objective function, which is defined as

$$\begin{aligned} H(w) = \frac{1}{2}{w^T}Kw - {w^T}b. \end{aligned}$$
(6)

As we all know, the conjugate gradient algorithm is a common optimization method which has the characteristics of small storage space and fast convergence. Therefore, the conjugate gradient method can be used for load identification, and the iteration form can be expressed as

$$\begin{aligned} {w_{i + 1}} = {w_i} + {\alpha _i}{d_i},\quad i = 0,1,2, \ldots , \end{aligned}$$
(7)

where \({\alpha _i}\) is the step length and \({d_i}\) is the search direction. This step size \({\alpha _i}\) is often obtained by the Wolfe line search method. The search direction \({d_i}\) is defined as

$$\begin{aligned} {d_i} = \left\{ {\begin{array}{*{20}{c}} { - {g_i},}&{}\quad {i = 1}\\ { - {g_i} + {\beta _i}{d_{i - 1}},}&{}\quad {i \ge 2}\end{array}} \right. , \end{aligned}$$
(8)

where \({g_i}\) is the gradient of H(w) and \({\beta _i}\) is a scalar. Different parameters \({\beta _i}\) correspond to different conjugate gradient methods. There are many different conjugate gradient methods, such as HS conjugate gradient [37], RPR conjugate gradient [38], and DY conjugate gradient [39], which are given by \(\beta _i^{HS} = \frac{{g_i^T({g_i} - {g_{i - 1}})}}{{d_{i - 1}^T({g_i} - {g_{i - 1}})}}\), \(\beta _i^{PRP} = \frac{{g_i^T({g_i} - {g_{i - 1}})}}{{{{\left\| {{g_{i - 1}}} \right\| }^2}}}\) and \(\beta _i^{DY} = \frac{{{{\left\| {{g_i}} \right\| }^2}}}{{d_{i - 1}^T({g_i} - {g_{i - 1}})}}\), respectively. Different conjugate gradient methods have different properties. In fact, the DY method has good convergence property, and the PRP method and the HS method have good numerical performance. Based on this idea, many new conjugate gradient methods are derived. Such as VHS [40], VRPR [41], and MDY [42], which are given by \(\beta _i^{{\textrm{VHS}}} = \frac{{{{\left\| {{g_i}} \right\| }^2} - \frac{{\left\| {{g_i}} \right\| }}{{\left\| {{g_{k - 1}}} \right\| }}\left| {g_i^T{g_{i - 1}}} \right| }}{{d_{i - 1}^T({g_i} - {g_{i - 1}})}}\), \(\beta _i^{{\textrm{VPRP}}} = \frac{{g_i^T({g_i} - \frac{{\left\| {{g_i}} \right\| }}{{\left\| {{g_{i - 1}}} \right\| }}{g_{i - 1}})}}{{{{\left\| {{g_{i - 1}}} \right\| }^2}}}\) and \(\beta _i^{{\textrm{MDY}}} = \frac{{g_i^T({g_i} - \frac{{g_i^T{d_{i - 1}}}}{{{{\left\| {{d_{i - 1}}} \right\| }^2}}}{d_{i - 1}})}}{{d_{i - 1}^T({g_i} - {g_{i - 1}})}}\), respectively.

Based on the analysis above, this paper proposes a modified conjugate gradient method, in which \({\beta _i}\) is defined as

$$\begin{aligned} {\beta _i} = \left\{ {\begin{array}{*{20}{c}} {\frac{{g_i^T({g_i} - \mu \frac{{{d_{i - 1}}g_i^T}}{{{{\left\| {{d_{i - 1}}} \right\| }^2}}}{d_{i - 1}})}}{{d_{i - 1}^T({g_i} - {g_{i - 1}})}}}&{}\quad {g_i^T{g_{i - 1}} \ge 0,}\\ {\frac{{g_i^T({g_i} + \mu \frac{{{d_{i - 1}}g_i^T}}{{{{\left\| {{d_{i - 1}}} \right\| }^2}}}{d_{i - 1}})}}{{d_{i - 1}^T({g_i} - {g_{i - 1}})}}}&{}\quad {g_i^T{g_{i - 1}} < 0.} \end{array}} \right. \end{aligned}$$
(9)

where \( 0< \mu < 1 \) is a variable parameter.

In this paper, the step size \(\alpha _i\) is determined by the following standard Wolfe line search

$$\begin{aligned} H({x_i} + {\alpha _i}{d_i}) - H({x_i}) \le \delta {\alpha _i}g_i^T{d_i}, \end{aligned}$$
(10)
$$\begin{aligned} g{({x_i} + {\alpha _i}{d_i})^T}{d_i} \ge \sigma g_i^T{d_i} , \end{aligned}$$
(11)

where \(0< \delta< \sigma < 1\). We can name the conjugate gradient method based on (9–11) as the modified conjugate gradient method.

Throughout the paper, we make the following assumptions:

  • (AC1): The objective function H(w) has a lower bound on the level set \(\Omega = \{ w \in {R^n}|H(w) \le H({w_1})\} \), where \({w_1}\) is the initial point.

  • (AC2): The objective function H(w) is continuously differentiable in some neighborhood U of \(\Omega \), in which the gradient is Lipchitz continuous, and that is to say there exists a constant \(L > 0,\) such that

    $$\begin{aligned} \left\| {g(w) - g(y)} \right\| \le L\left\| {w - y} \right\| ,\quad \forall w,y \in \Omega . \end{aligned}$$
    (12)

The new conjugate gradient algorithm is given as follows:

  • Step 1: Select an initial point \({w_1} \in {R_n}\), set \(i: = 1,\varepsilon > 0,{d_1} = - {g_1};\) if \(\left\| {{g_1}} \right\| \le \varepsilon \), then stop.

  • Step 2: Compute the step length \({\alpha _i}\) by the standard Wolfe line search such that \({\alpha _i}\) satisfies the formula (10)–(11).

  • Step 3: Calculate \({w_{i + 1}}\) by the formula (7); if \(\left\| {{g_{i + 1}}} \right\| \le \varepsilon \), then stop.

  • Step 4: Compute \({\beta _i}\) by the formula (9), and generate \({d_{i + 1}}\) by the formula (8).

  • Step 5: Let \(i = i + 1\); go to step 2.

Proof of Global Convergence

Lemma 1

Suppose that (AC1) and (AC2) hold. The parameter \({\beta _i}\) comes from formula (9), and let the sequences \({{\textrm{g}}_i}\) and \({d_i}\) be generated by the new conjugate gradient algorithm. If \({{\textrm{g}}_i} \ne 0\), \({\mu } \in [0,1]\) for \(i \ge 1\), then \({\textrm{g}}_{_i}^T{d_i} < 0.\)

Proof

Case (1) if \(\mu = 0\), then \({\beta _i} = \beta _i^{DY}\).

Case (2) if \(i = 1\), then \(g_1^T{d_1} = - {\left\| {{g_1}} \right\| ^2} < 0\). The conclusion holds.

Assume that \(g_{i - 1}^T{d_{i - 1}} < 0\) is true for \(i - 1\) and \(i \ge 2\), from (11), we have

$$\begin{aligned} d_{i- 1}^T({g_i} - {g_{i - 1}}) \ge (\sigma - 1)g_{i - 1}^T{d_{i - 1}}> 0. \end{aligned}$$
(13)

Define \({\eta _i}\) as the angle between the \({g_i}\) and \({d_{i - 1}}\) vectors, then

$$\begin{aligned} \cos {\eta _i} = \frac{{g_i^T{d_{i - 1}}}}{{\left\| {{g_i}} \right\| \left\| {{d_{i - 1}}} \right\| }}. \end{aligned}$$
(14)

If \(g_i^T{g_{i - 1}} \ge 0\), then we take the inner product of both sides of (8) with vector \(g_i^T\). According to (9) and (11), we have

$$\begin{aligned} \begin{aligned} \frac{{{{\left\| {{d_i}} \right\| }^2}}}{{{{(g_i^T{d_i})}^2}}}&= \frac{{\beta _i^2{{\left\| {{d_{i - 1}}} \right\| }^2}}}{{{{(g_i^T{d_i})}^2}}} - \frac{2}{{g_i^T{d_i}}} - \frac{{{{\left\| {{g_i}} \right\| }^2}}}{{{{(g_i^T{d_i})}^2}}}\\&= \frac{{\beta _i^2{{\left\| {{d_{i - 1}}} \right\| }^2}}}{{{{(g_i^T{d_i})}^2}}} + \frac{1}{{{{\left\| {{g_i}} \right\| }^2}}}{\left( \frac{1}{{\left\| {{g_i}} \right\| }} + \frac{{\left\| {{g_i}} \right\| }}{{g_i^T{d_i}}}\right) ^2}\\&\le \frac{{\beta _i^2{{\left\| {{d_{i - 1}}} \right\| }^2}}}{{{{(g_i^T{d_i})}^2}}} + \frac{1}{{{{\left\| {{g_i}} \right\| }^2}}}. \end{aligned} \end{aligned}$$
(15)

If \(g_k^T{g_{k - 1}} < 0\), we have

$$\begin{aligned} \begin{aligned} g_i^T{d_i}&= - {\left\| {{g_i}} \right\| ^2} + {\beta _i}g_i^T{d_{i - 1}}\\&= - {\left\| {{g_i}} \right\| ^2} + \frac{{g_i^T\left( {g_i} - \frac{{\mu {d_{i - 1}}g_i^T{d_{i - 1}}}}{{{{\left\| {{d_{i - 1}}} \right\| }^2}}}\right) }}{{d_{i - 1}^T({g_i} - {g_{i - 1}})}}g_i^T{d_{i - 1}}\\&= \frac{{ - {{\left\| {{g_i}} \right\| }^2}d_{i - 1}^T{g_i} + {{\left\| {{g_i}} \right\| }^2}d_{i - 1}^T{g_{i - 1}} + {{\left\| {{g_i}} \right\| }^2}g_i^T{d_{i - 1}} - \frac{{\mu g_i^T{d_{i - 1}}g_i^T{d_{i - 1}}}}{{{{\left\| {{d_{i - 1}}} \right\| }^2}}}g_i^T{d_{i - 1}}}}{{d_{i - 1}^T({g_i} - {g_{i - 1}})}}\\&= \frac{{{{\left\| {{g_i}} \right\| }^2}d_{i - 1}^T{g_{i - 1}} - \mu {{\left\| {{g_i}} \right\| }^2}{{\cos }^2}{\eta _i} \cdot g_i^T{d_{i - 1}}}}{{d_{i - 1}^T({g_i} - {g_{i - 1}})}}\\&\le \frac{{{{\left\| {{g_i}} \right\| }^2}g_{i - 1}^T{d_{i - 1}}({\mathrm{1 - }}\sigma \mu {{\cos }^2}{\eta _i})}}{{d_{i - 1}^T({g_i} - {g_{i - 1}})}} < 0. \end{aligned} \end{aligned}$$
(16)

By mathematical induction, we know that Lemma 1 is true. \(\square \)

Lemma 2

Suppose that (AC1) and (AC2) hold. If the step length \({\alpha _i}\) satisfies the standard Wolfe line search (10) and (11), then we have

$$\begin{aligned} 0 \le {\beta _i} \le \frac{{g_i^T{d_i}}}{{g_{i - 1}^T{d_{i - 1}}}}. \end{aligned}$$
(17)

Proof

From the formula (9) and the angle \({\eta _i}\), we have

$$\begin{aligned} {\beta _i}= & {} \frac{{{{\left\| {{g_i}} \right\| }^2}(1 - \mu {{\cos }^2}{\eta _i})}}{{d_{i - 1}^T({g_i} - {g_{i - 1}})}} \ge 0, (g_i^T{g_{i - 1}} \ge 0), \end{aligned}$$
(18)
$$\begin{aligned} {\beta _i}= & {} \frac{{{{\left\| {{g_i}} \right\| }^2}(1 + \mu {{\cos }^2}{\eta _i})}}{{d_{i - 1}^T({g_i} - {g_{i - 1}})}} \ge 0, (g_i^T{g_{i - 1}} < 0). \end{aligned}$$
(19)

Therefore, \({\beta _i} \ge 0\).

Exploiting Lemma 1, we obtain

$$\begin{aligned} {\beta _i}= & {} \frac{{{{\left\| {{g_i}} \right\| }^2}(1 - \mu {{\cos }^2}{\eta _i})}}{{d_{i - 1}^T({g_i} - {g_{i - 1}})}} \le \frac{{{{\left\| {{g_i}} \right\| }^2}(1 - \sigma \mu {{\cos }^2}{\eta _i})}}{{d_{i - 1}^T({g_i} - {g_{i - 1}})}} \nonumber \\\le & {} \frac{{g_i^T{d_i}}}{{g_{i - 1}^T{d_{i - 1}}}}, (g_i^T{g_{i - 1}} \ge 0), \end{aligned}$$
(20)
$$\begin{aligned} {\beta _i}= & {} \frac{{{{\left\| {{g_i}} \right\| }^2}(1 + \mu {{\cos }^2}{\eta _i})}}{{d_{i - 1}^T({g_i} - {g_{i - 1}})}} \le \frac{{{{\left\| {{g_i}} \right\| }^2}(1 + \sigma \mu {{\cos }^2}{\eta _i})}}{{d_{i - 1}^T({g_i} - {g_{i - 1}})}} \nonumber \\\le & {} \frac{{g_i^T{d_i}}}{{g_{i - 1}^T{d_{i - 1}}}},(g_i^T{g_{i - 1}} < 0). \end{aligned}$$
(21)

In summary, \({\beta _i} \le \frac{{g_i^T{d_i}}}{{g_{i - 1}^T{d_{i - 1}}}}\). So, \(0 \le {\beta _i} \le \frac{{g_i^T{d_i}}}{{g_{i - 1}^T{d_{i - 1}}}}\), and that is to say, Lemma 2 holds. \(\square \)

Theorem 1

Suppose that (AC1) and (AC2) hold. Considering any iteration of the formula (8), where the \({d_i}\) is a descent direction and the step length \({\alpha _i}\) satisfies the standard Wolfe line search conditions, then we have

$$\begin{aligned} \sum \limits _{i \ge 1} {\frac{{{{(g_i^T{d_i})}^2}}}{{{{\left\| {{d_i}} \right\| }^2}}}} < + \infty . \end{aligned}$$
(22)

Proof

From Lemma 1, we have \(g_i^T{d_i} < 0\). By the formula (11), we get

$$\begin{aligned} d_i^T({g_{i - 1}} - {g_i}) \ge (\sigma - 1)g_i^T{d_i} > 0. \end{aligned}$$
(23)

From (AC2), it follows that

$$\begin{aligned} d_i^T({g_{i - 1}} - {g_i}) \le L{\alpha _i}{\left\| {{d_i}} \right\| ^2}. \end{aligned}$$
(24)

Thus, we can obtain

$$\begin{aligned} {\alpha _i} \ge \frac{{(\sigma - 1)g_i^T{d_i}}}{{L{{\left\| {{d_i}} \right\| }^2}}}. \end{aligned}$$
(25)

Because the sequences \({H_i}\) is monotonic decreasing and convergent, we get

$$\begin{aligned} {H_i} - {H_{i - 1}}\ge & {} - \delta {\alpha _i}g_i^T{d_i} \ge \frac{{{\mathrm{- }}\delta (\sigma - 1)(g_i^T{d_i})}}{{L{{\left\| {{d_i}} \right\| }^2}}} \nonumber \\= & {} \frac{{\delta (1 - \sigma )}}{L}\frac{{{{(g_i^T{d_i})}^2}}}{{{{\left\| {{d_i}} \right\| }^2}}}. \end{aligned}$$
(26)

Taking the limit of the sum of both sides of formula (26), we have

$$\begin{aligned} \sum \limits _{i \ge 1} {\frac{{\delta (1 - \sigma )}}{L}\frac{{g_i^T{d_i}{^{{\textrm{2}}}}}}{{{{\left\| {{d_i}} \right\| }^2}}}}\le & {} \sum \limits _{i \ge 1} ({H_i} - {H_{i - 1}}) \nonumber \\= & {} {H_1} - \mathop {\lim }\limits _{x \rightarrow \infty } {H_i} < + \infty . \end{aligned}$$
(27)

Therefore, the formula (22) holds, that is, Theorem 1 is true. \(\square \)

Theorem 2

Suppose that (AC1) and (AC2) hold. The step length \({\alpha _i}\) is generated by the standard Wolfe line search conditions, and Lemma 1 holds. \({\beta _i}\) is the parameter of the formula (9). Then we have

$$\begin{aligned} \mathop {\lim }\limits _{i \rightarrow \infty } \inf \left\| {{g_i}} \right\| = 0. \end{aligned}$$
(28)

Proof

Assume by the contradiction that the formula (28) does not hold. For all i, there exists a constant \(\lambda > 0\), such that

$$\begin{aligned} \left\| {{g_i}} \right\| \ge \lambda . \end{aligned}$$
(29)

Rearranging \({d_i} = - {g_i} + {\beta _i}{d_{i - 1}}\) into \({d_i} +{g_i}= {\beta _i}{d_{i - 1}},\) and squaring both sides, we can obtain

$$\begin{aligned} {\left\| {{d_i}} \right\| ^2} = \beta _i^2{\left\| {{d_{i - 1}}} \right\| ^2} - 2g_i^T{d_i} - {\left\| {{g_i}} \right\| ^2}. \end{aligned}$$
(30)

Dividing the above formula by \({(g_i^T{d_i})^2},\) we get

$$\begin{aligned} \begin{aligned} \frac{{{{\left\| {{d_i}} \right\| }^2}}}{{{{(g_i^T{d_i})}^2}}}&= \frac{{\beta _i^2{{\left\| {{d_{i - 1}}} \right\| }^2}}}{{{{(g_i^T{d_i})}^2}}} - \frac{2}{{g_i^T{d_i}}} - \frac{{{{\left\| {{g_i}} \right\| }^2}}}{{{{(g_i^T{d_i})}^2}}}\\&= \frac{{\beta _i^2{{\left\| {{d_{i - 1}}} \right\| }^2}}}{{{{(g_i^T{d_i})}^2}}} + \frac{1}{{{{\left\| {{g_i}} \right\| }^2}}} - {\left( \frac{1}{{\left\| {{g_i}} \right\| }} + \frac{{\left\| {{g_i}} \right\| }}{{g_i^T{d_i}}}\right) ^2}\\&\le \frac{{\beta _i^2{{\left\| {{d_{i - 1}}} \right\| }^2}}}{{{{(g_i^T{d_i})}^2}}} + \frac{1}{{{{\left\| {{g_i}} \right\| }^2}}}. \end{aligned} \end{aligned}$$
(31)

From the formula (17) of Lemma 2, we have

$$\begin{aligned} \begin{aligned} \frac{{{{\left\| {{d_i}} \right\| }^2}}}{{{{(g_i^T{d_i})}^2}}}&\le \frac{{{{(g_i^T{d_i})}^2}}}{{{{(g_{i - 1}^T{d_{i - 1}})}^2}}}\frac{{{{\left\| {{d_{i - 1}}} \right\| }^2}}}{{{{(g_i^T{d_i})}^2}}} + \frac{1}{{{{\left\| {{g_i}} \right\| }^2}}} \\&= \frac{{{{\left\| {{d_{i - 1}}} \right\| }^2}}}{{{{(g_{i - 1}^T{d_{i - 1}})}^2}}} + \frac{1}{{{{\left\| {{g_i}} \right\| }^2}}}. \end{aligned} \end{aligned}$$
(32)

From the formula (8), we can get

$$\begin{aligned} {d_1} = - {g_1}. \end{aligned}$$
(33)

Thus, we have

$$\begin{aligned} \frac{{{{\left\| {{d_1}} \right\| }^2}}}{{{{(g_1^T{d_1})}^2}}} = \frac{1}{{{{\left\| {{g_1}} \right\| }^2}}}. \end{aligned}$$
(34)

By recursion, we have

$$\begin{aligned} \frac{{{{\left\| {{d_i}} \right\| }^2}}}{{{{(g_i^T{d_i})}^2}}} \le \sum \limits _{j = 1}^i {\frac{1}{{{{\left\| {{g_j}} \right\| }^2}}}} \le \frac{i}{{{\lambda ^2}}}. \end{aligned}$$
(35)

That is,

$$\begin{aligned} \frac{{{{(g_i^T{d_i})}^2}}}{{{{\left\| {{d_i}} \right\| }^2}}} \ge \frac{{{\lambda ^2}}}{i}. \end{aligned}$$
(36)

Summing both sides of the above formula, we can obtain

$$\begin{aligned} \sum \limits _{i \ge 1} {\frac{{{{(g_i^T{d_i})}^2}}}{{{{\left\| {{d_i}} \right\| }^2}}}} \ge {\lambda ^2}\sum \limits _{i \ge 1} {\frac{1}{i}} = + \infty . \end{aligned}$$
(37)

This contradicts (22). So, Theorem 2 holds. \(\square \)

Theory of Preconditioned Modified Conjugate Gradient (PMCG)

It is well known that conjugate gradient method converges slowly when cond(K) is large. Therefore, the preconditioned technology is introduced to deal with this problem. The main idea of the preconditioned technology is to transform the original problem into an equivalent problem that is easy to solve, and its equivalent transformation is given as follows:

$$\begin{aligned} Kw = b \Leftrightarrow {\widetilde{K}}{\widetilde{w}} = {\widetilde{b}}, \end{aligned}$$
(38)

where, \({\widetilde{K}} = {Q^{ - 1}}K{Q^{ - T}},\) \({\widetilde{w}} = {Q^T}w\), \({\widetilde{b}} = {Q^{ - 1}}b\). Q represents the preconditioned matrix, and its selection method can be found in [43]. In this paper, the diagonal matrix is chosen as the preconditioned matrix. Through this equivalent transformation, if \(cond({\widetilde{K}}) < cond(K)\), the solving speed of conjugate gradient algorithm will be improved.

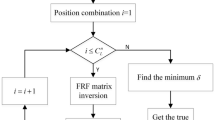
Based on MCG algorithm and the preconditioned technology, the PMCG algorithm can be established. The computation flowchart of the PMCG algorithm is shown in Fig. 2. In the following simulation experiment, the convergence control error \(\varepsilon \) of the conjugate gradient method is set to 10e-5 and the maximum number of iterations maxiter is set to 5000.

Fig. 2
figure 2

The flowchart of the PMCG algorithm

Full size image

Numerical Simulation

Problem Description

As shown in Fig. 1, a Bernoulli–Euler simply supported beam subjected to moving force is investigated to evaluate the performances of the proposed algorithm in this paper. The beam has a span of 40 m, and the parameters of the beam are given as: the flexural rigidity \(EI = 1.274916 \times {10^{11}}\,\hbox {N}\, {\hbox {m}^2}\); the density of unit length \(\rho = 12{,}000\,\hbox {kg}\, {\hbox {m}^{ - 1}}\); the first three natural frequencies of the beam are \(3.2\,\hbox {Hz}, 12.8\,\hbox {Hz}\) and \(28.8\,\hbox {Hz}\), respectively. The parameters of the vehicle are given as follows: the speed of vehicle moving is \(40\,\hbox {m} \,\hbox {s}^{ - 1}\); the distance between two axles is 4 m. The analysis frequency ranges from 0 to 40 Hz. The sampling frequency is selected as 200 Hz. Biaxial time-varying force identification with six different cases is investigated. The moving force is given as follows:

$$\begin{aligned} {F_1}(t)= & {} 20[1 + 0.1\sin (8\pi t) + 0.05\sin (20\pi t)]({kN}),\nonumber \\ {F_2}(t)= & {} 20[1 - 0.1\sin (8\pi t) + 0.05\sin (24\pi t)]({kN}). \end{aligned}$$
(39)

There are measurement error and noise interference in the practical engineering, so the polluted responses with the random noise are given as

$$\begin{aligned} {b_{{\textrm{simulate}}}}{\mathrm{= }}{b_{{\textrm{true}}}}({\mathrm{1 + }}\, nl \times {N_{{\textrm{noise}}}}), \end{aligned}$$
(40)

where, \({b_{{\textrm{true}}}}\) is the real response of simulation; \({b_{{\textrm{simulate}}}}\) represents the polluted measured response; nl represents the noise level, which is selected as 0–20% in subsequent studies; \({N_{{\textrm{noise}}}}\) is the random white Gaussian noise.

The acceleration and bending moment sensors are located at 1/4,  1/2, and 3/4 of the bridge span, respectively. For convenience, M14 represents the bending moment response of 1/4 bridge span, J12 represents the acceleration response of 1/2 bridge span, and so on. The load identification speed will be evaluated by the number of iterations. The relative percentage error (RPE) is adopted as the criterion to evaluate the accuracy of load identification, and the calculation formula is given as

$$\begin{aligned} RPE = \frac{{\left\| {{f_{{\textrm{iden}}}} - {f_{{\textrm{true}}}}} \right\| }}{{\left\| {{f_{{\textrm{true}}}}} \right\| }} \times 100\%, \end{aligned}$$
(41)

where \(f_{{\textrm{true}}}\) represents the true load; \(f_{{\textrm{iden}}}\) represents the load from MFI.

Parameter Selection

As can be seen from the description in “Background of Theory” section, there is a variable parameter \(\mu \) in the PMCG method, which needs to be selected appropriately. The parameter \(\mu \) is usually selected by the posterior RPE criterion, which can be described as:

$$\begin{aligned} {\hbox {RPE}}({\mu _{{\textrm{optimal}}}}) = \mathop {{\textrm{min}}}\limits _{0< \mu < 1} \{ {\hbox {RPE}}(\mu )\}, \end{aligned}$$
(42)

where \({\hbox {RPE}}(\mu )\) represents the relative percentage error of the identified load by PMCG when the variable parameter is \(\mu \), which is defined as follows:

$$\begin{aligned} {\hbox {RPE}}(\mu ) = \frac{{\left\| {{F_{\mu ,{\textrm{identification}}}} - {F_{{\textrm{true}}}}} \right\| }}{{\left\| {{F_{{\textrm{true}}}}} \right\| }}, \end{aligned}$$
(43)

where \({F_{\mu ,{\textrm{identification}}}}\) represents the load identified by the PMCG method when the parameter is \(\mu \), and \({F_{{\textrm{true}}}}\) represents the true load.

However, in practical engineering, the true load \({F_{{\textrm{ture}}}}\) required in RPE criterion is generally unknown. Therefore, a new equivalent evaluation criterion named as response relative percentage error (RRPE) can be adopted, and it can be expressed as

$$\begin{aligned} {\hbox {RRPE}}({\mu _{{\textrm{optimal}}}}) = \mathop {\min }\limits _{0< \mu < 1} \{ {\hbox {RRPE}}(\mu )\}, \end{aligned}$$
(44)

where \({\hbox {RRPE}}(\mu )\) represents the relative percentage error between the measured response and the reconstructed response when the parameter is \(\mu \), which can be expressed as:

$$\begin{aligned} {\hbox {RRPE}}(\mu ) = \frac{{\left\| {{R_{\mu ,{\textrm{reconstruction}}}} - {R_{{\textrm{measurement}}}}} \right\| }}{{\left\| {{R_{{\textrm{measurement}}}}} \right\| }}, \end{aligned}$$
(45)

where \({R_{{\textrm{measurement}}}}\) represents the measured response, and \({R_{\mu ,{\textrm{reconstruction}}}}\) represents the reconstructed response from the load identified by the PMCG when the parameter is \(\mu \).

For the iterative method, the number of iterations has a linear relationship with the identification speed. Therefore, it is necessary to take the number of iterations as the evaluation criterion, and its mathematical expression is given as

$$\begin{aligned} Iterations(\;{\mu _{{\textrm{optimal}}}}) = \mathop {\min }\limits _{0< \mu < 1} \{ Iterations(\mu )\}, \end{aligned}$$
(46)

where \(Iterations(\mu )\) represents the number of iterations when the parameter is \(\mu \).

The sensor configuration is selected as M14 &M12 &M34 &J14 &J12 &J34, and the parameters are chosen by the above two posterior parameter selection criteria under five different noise levels. The number of iterations of load identification corresponding to different \(\mu \) is shown in Fig. 3. It can be seen from Fig. 3 that the iteration number of PMCG is relatively low when \(\mu \) is between 0.87 and 0.99. Similarly, the relative percentage error of the reconstruction response corresponding to different \(\mu \) is shown in Fig. 4. As can be seen from Fig. 4, when \(\mu \) is between 0.84 and 0.99, the reconstruction response of load identified by PMCG is more consistent with the measured response. It can be seen from the above description that when the variable parameter \(\mu \) is between 0.87 and 0.99, PMCG has good numerical performances and convergence, so the variable parameter \(\mu \) is selected as 0.98 in the following analysis.

Fig. 3
figure 3

The iteration number criterion

Full size image
Fig. 4
figure 4

Reconstructed response relative percentage error criterion

Full size image

Moving Force Identification and Results Analysis

The accuracy of load identification is affected by the measurement error and noise, so it is necessary to study the anti-noise ability of the proposed algorithm. Generally, the identification error is used to assess the accuracy of load identification results. To verify the accuracy of the proposed PMCG, 6 different sensor configurations are selected to perform load identification under 21 different noise levels, and PMCG is compared with 6 different preconditioned conjugate gradient methods. Figures 5 and 6 show the RPE of front and rear axle loads identified by seven methods respectively. It can be seen from Fig. 5 that the errors of PMCG, perconditioned modified DY conjugate gradient (PMDYCG), and perconditioned HS conjugate gradient (PHSCG) in identifying the front axle load are very close under various noise and different sensor configurations. Meanwhile, in most cases, the errors of PMCG, PMDYCG, and PHSCG are lower than those of other four methods. The identification error of seven methods increases with the increase of noise, but the error of PMCG, PMDYCG, and PHSCG increases less than that of the other four methods. Similarly, the same conclusion can be drawn from Fig. 6.

Fig. 5
figure 5

Comparison on RPE of front axle loads identified by seven methods under different sensor placement

Full size image
Fig. 6
figure 6

Comparison on RPE of rear axle loads identified by seven methods under different sensor placement

Full size image

For the iterative method, the number of iterations has a linear relationship with the calculation time, so it is necessary to reduce the number of iterations for real-time load identification. Meanwhile, reducing the number of iterations can effectively decrease the cost of MFI. The number of iterations of seven methods in different sensor configurations and with different noise levels is shown in Fig. 7. It can be observed in Fig. 7 that the number of iterations of perconditioned DY conjugate gradient (PDYCG) and perconditioned VHS conjugate gradient (PVHSCG) methods is significantly lower than those of the other five methods, which indicate that the convergence speed of PDYCG and PVHSCG is much faster than that of other methods. Conversely, the number of iterations of the perconditioned PRP conjugate gradient (PPRPCG) and perconditioned VPRP conjugate gradient (PVPRPCG) almost reaches the preset maximum (5000). In addition, it can be obviously seen that the number of iterations of PMCG method is lower than PMDYCG and PHSCG.

Fig. 7
figure 7

Comparison on the number of iterations of MFI by seven methods under different sensor placement

Full size image

Table 1 lists the average number of iterations and average identification errors of 7 methods under 21 different noise levels. In this table, the last row is the average number of iterations and the mean error of the biaxial load identification for all the above sensors configurations and all the noise situations. As can be seen from Table 1, PDYCG and PVHSCG have the least average number of iterations, which indicates that their identification speed is fast. The average error of PMCG, PMDYCG, and PHSCG is small, which indicates that their identification accuracy is good. Based on the results in Table 1, it can be seen that compared with PMDYCG and PHSCG, the average number of iterations of PMCG is reduced by about 62.37% and 39.95%, respectively; compared with PDYCG and PVHSCG, the front axle load identification errors of PMCG are decreased by 20.82% and 20.23%, and the rear axle load identification error of PMCG is decreased by 15.31% and 15.79%, respectively; compared with PPRPCG and PVPRPCG, the average number of iterations of PMCG is reduced by 86.77% and 86.77%, the front axle load identification errors are reduced by 24.29% and 16.53%, and the rear axle load identification errors are reduced by 18.10% and 13.52%, respectively. The above data analysis shows that the PMCG method reduces the average number of iterations and improves the speed of load identification on the premise of ensuring the identification accuracy.

Table 1 The comparison of the average number of iterations and average identification RPE (%)
Full size table

Figure 8 shows the comparison between the true load and the identified load by seven methods from the combined responses (\( M14 \& M12 \& M34 \& J14 \& J12 \& J34\)). As shown in Fig. 8, when the noise level is 0%, all seven methods can accurately identify the moving load. When the noise level increases to 5%, seven methods can identify the load, but all of them have a slight deviation. When the noise level increases to 10%, all the seven methods have large error, but the identification error of PMCG, PDYCG, PMDYCG, and PHSCG is, respectively, smaller than PVPRPCG, PPRPCG, and PVHSCG. When the noise level reaches the extreme value 20%, the identification error of PMCG, PMDYCG, and PHSCG is less than that of PDYCG, PPRPCG, PVPRPCG, and PVHSCG. The above results also demonstrate that PMCG, PMDYCG, and PHSCG have high identification accuracy and strong robustness.

Fig. 8
figure 8

The identification results of seven methods under different noise levels

Full size image

Spectrum Analysis

As we all know, the moving load is a special dynamic load whose main dynamic characteristics contain frequency and corresponding amplitude. To verify the accuracy of PMCG in identifying the moving loads, the spectrum analysis is carried out to study the moving loads identified by PMCG. First, the dynamic characteristics (frequency and amplitude) of simulated true loads and the identified loads are obtained by frequency spectrum analysis. Then the amplitude relative percentage error (ARPE) between the load identified by PMCG and the exact values is caculated by:

$$\begin{aligned} ARPE = \frac{{\left\| {{A_{{\textrm{identification}}}} - {A_{{\textrm{true}}}}} \right\| }}{{\left\| {{A_{{\textrm{true}}}}} \right\| }} \times 100\% \end{aligned}$$
(47)

where \(A_{{\textrm{identification}}}\) represents the amplitude of the load identified by PMCG, and \(A_{{\textrm{true}}}\) represents the exact values.

The sensor configuration is selected as \( M14 \& M12 \& M34 \& J14 \& J12 \& J34\). The moving loads are identified by PMCG under five different noise levels, and the spectral analysis of the loads is also performed. The spectrum analysis diagram is shown in Fig. 9, and the amplitude corresponding to the principal frequency and amplitude errors is shown in Table 2, and the relationship between the ARPE of each frequency component and noise is shown in Fig. 10. According to Fig. 9, when the noise level is 0%, PMCG can accurately obtain the main frequency and the corresponding amplitude of the moving load. As the noise level increases from 0 to 10%, PMCG can accurately obtain the main frequency, but the corresponding amplitude error of the main frequency increases gradually. When the noise level increases to 15%, PMCG can also obtain the main frequency characteristic, and the corresponding amplitude error increases further. At the same time, the appearance of other frequency components interferes with the identification of high-frequency components of moving loads. When the noise level increases to 20%, the static component can still be identified accurately, and the amplitude error of the low-frequency component increases further, but the high-frequency component cannot be identified. It can be found more clearly from Table 2 and Fig. 10 that PMCG can accurately identify the static component of the biaxial load under various noise levels; the amplitude error of low-frequency component is linear with noise; the amplitude error of high-frequency component also has a linear relationship with noise, but the slope is large, and the error increases faster. Even in the absence of noise, the amplitude identification accuracy of high-frequency components is low.

Table 2 The comparison of amplitude and ARPE (%)
Full size table
Fig. 9
figure 9

The frequency spectrogram of the identified loads by PMCG under different noise levels

Full size image
Fig. 10
figure 10

Relationship between APRE of each frequency component and noise

Full size image

Conclusion

A new PMCG algorithm based on improved gradient operator and preconditioned technology is proposed for MFI of bridge structure. The time-domain deconvolution technology and modal superposition method transform the moving load identification problem into the solution of large linear equations problem. Then it is transformed into an equivalent linear equations problem by the preconditioned technology. Finally, the moving load identification problem is solved by the proposed conjugate gradient method. Meanwhile, the identification situation of different load components is studied by the frequency spectrum analysis method. Numerical simulations are carried out for the verification of the proposed method. Some conclusions can be given as follows:

  1. 1.

    Compared with the preconditioned conjugate gradient method with good convergence property, such as PDYCG and PVHSCG, PMCG has higher identification accuracy. Compared with the conjugate gradient method with good numerical performance, such as PMDYCG and PHSCG, PMCG reduces the number of optimization iterations and improves the identification speed of moving load identification on the premise of ensuring accuracy.

  2. 2.

    For sensor configuration, only using acceleration responses as the input responses of load identification can achieve fast identification, but the identification accuracy is low. Using the combination of acceleration and bending moment responses as the input responses of load identification can accurately identify the moving load.

  3. 3.

    As for the different frequency components of moving loads, PMCG has high identification accuracy for static and low-frequency components of loads, and the amplitude deviation of low-frequency components is linear with the noise level. Under the condition of low noise level, the low-frequency components can be accurately obtained, which can be used for dynamic weighing of low-frequency moving loads.

In the future, we will apply the proposed algorithm into more complex moving load identification problems with viscoelastic boundary conditions and different ground foundation conditions. To verify the feasibility of practical engineering application of the proposed algorithm, experimental verification will be performed in the next step working.