1 Introduction

In the high-speed operation of common turbo-machineries, the flow of the lubricating liquid film in the bearing lubricating cavity will generate a considerable film Reynolds number, so the flow in the bearing clearance may get into transition flow or even become turbulent case. Though lubricating flow is turbulent, many numerical simulations or research ignore turbulent effects or reduce the model to be a simplified laminar case. Neglecting turbulent flow would lead to significant failure results in simulation or a miss of undesired vibrations in the study of turbo-rotating mechanical systems. Therefore, turbulent flow phenomena should be considered in studying rotor-bearing system dynamics. Some studies [1,2,3,4,5] focus on analyzing the turbulent flow effect in turbo-machineries and prove that ignorance would bring serious mistakes in predicting dynamic behaviors or designing turbo-machineries. In addition, turbo-machineries operating at high speed may also cause the lubrication flow in the bearing gap to enter a turbulent flow situation. Some effects, such as rub impact between the rotor and stator, may be formed at high rotating speeds and would cause the failure of the bearing-rotor system. Zhang et al. [6] developed a novel indicator considering force, velocity, and phase information over time intervals based on vibration power flow theory. Through the theoretical analysis of collision faults, the energy response of the rotor system and the law between input power and collision are obtained. At the same time, fault severity detection is achieved using the proposed indicators. Liu et al. [7] proposed a new evaluation method—the weighted contribution rate of the nonlinear output frequency response function. This method is an extension of traditional indicators based on nonlinear output frequency response functions, trying to obtain new indicators with higher recognition of faults. Simulation and experimental results demonstrate the sensitivity of the new index to frictional impact faults. Besides, some literature [8,9,10,11,12,13] also emphasized and explained the significance and severity of rub impact occurring in the bearing-rotor systems.

Some studies focused on applying some algorithms to improve the efficiency of fault diagnosis of bearing-rotor systems, e.g., Li et al. [14, 15] presented an enhanced selective integration deep learning method based on the beetle antennae search (BAS) algorithm to adaptively select the optimal class-specific thresholds. Experimental bearing data are used to verify the effectiveness of the proposed method. Zhang et al. [16] introduced the piezoelectric energy harvester to study the bearing-rotor system. Rotational energy is harvested from rotating machines by installing arc-shaped piezoelectric sheets between the outer ring of rolling bearings and the bearing housing. The proposed piezoelectric energy harvester can not only power the sensor but also has the capability of bearing fault detection. Yu et al. [17,18,19] published a series of research papers focusing on fault detection of turbo-machineries and also proved that its theory is reasonable and the applicability of their studies. Some exciting and excellent published documents, e.g., [20,21,22,23,24,25], proposed practical methods to detect and control turbo-machineries’ faults.

Wang et al. [26] presented the integral magnetorheological dampers (IMRDs) to replace the traditional magnetorheological dampers. Research results show that the oil film pressure in each bearing area can be adjusted independently with the current, resulting in changes in the direction and magnitude of the oil film force. In addition, different oil film-bearing areas contribute to the stiffness and damping of IMRD. In some cases, IMRD can provide pure damping with negligible stiffness. In addition, magnetorheological fluids with huge journal eccentricity ratios are prone to produce strong nonlinearity; however, compared with traditional MRD, the IMRD proposed here can significantly reduce the nonlinearity level. Zaccardo et al. [27] employed active magnetic dampers (AMDs) to overcome the inherent trade-offs associated with squeeze-film dampers. The AMD's design, fabrication, and experimental demonstrated the reduction of lateral rotor vibration in high-speed rotating shafts through the critical speed. The squeeze-film damper is a helpful application to enhance the performance of stability of bearings and also suppress the amplitude and irregularity of turbo-machineries. Chang-Jian et al. [28] presented a model of a hybrid squeeze-film damper to study the nonlinear dynamics of the rotor-bearing system lubrication with couple stress fluid, and they found that the rotor dynamic responses of the system will be more stable by using a hybrid squeeze-film damper and lubricated with couple stress fluid. Ashtekar et al. [29] investigated the dynamics of a turbocharger supported by deep groove and angular contact ball bearing with a squeeze-film damper, and they found that the damper plays an important role not only in improving turbocharger dynamics but also in extending the bearing life. Giovanni [30] proposed a bifurcation analysis of the dynamics of an unbalanced rigid rotor supported by two-lobe wave bearings with squeeze-film dampers. Some non-periodic behaviors are found in this study. Chang-Jian [31] applied the porous squeeze-film damper to improve the dynamic stability of gear-bearing systems and proved that the usage of a porous squeeze-film damper would be helpful in the design and development of a gear-bearing system for rotating machinery that operates at highly rotational speed and highly nonlinear regimes. Han and Ding [32] used both the linear damping support and squeeze-film damper support to study the dynamic characteristics of the rotor/ball-bearing system during maneuvers. Using a squeeze-film damper could suppress sub- and super-harmonic resonances. Hsu et al. [33] studied the nonlinear dynamic of a turbine generator with a squeeze-film damper, considering the effect of flywheel eccentricity and squeeze-film damper will fail to support the rotor in a specific range of rotor speed but enlarged as the flywheel eccentricity increases at the same time.

While turbo-machineries operate with high rotational speed, lubricating flow in bearing housing may be transition or even turbulent. Therefore, these systems' damping effect should differ from the viscous damping effect; the quadratic damping case would be more suitable. Applying squeeze-film dampers into turbo-machineries could remarkably enhance dynamic characteristics, according to the literature review, as shown in the above paragraph. We will analyze the nonlinear dynamic responses for the turbulent rotor-bearing system with quadratic damping. We will prove that the hybrid squeeze-film damper can suppress aperiodic responses and even chaotic cases. The dynamic trajectories, power spectra, Poincaré maps, bifurcation diagrams, the maximum Lyapunov exponent, and fractal dimension are applied to analyze the rotor-bearing system. Besides we also used PD controllers in the hydrostatic chambers to control the rotor-bearing system.

2 Mathematical modeling

2.1 Modified Reynolds equation under turbulent flow assumption

Based on the assumption of turbulent flow, the modified Reynolds equation in the hydrodynamic lubrication theory may be performed as.

$$\frac{\partial }{{R\partial \theta }}\left( {\frac{{h^{3} G_{\theta } }}{\mu }\frac{{\partial p}}{{R\partial \theta }}} \right) + \frac{\partial }{{\partial z}}\left( {\frac{{h^{3} G_{z} }}{\mu }\frac{{\partial p}}{{\partial z}}} \right) = \frac{U}{2}\frac{{\partial h}}{{R\partial \theta }} + \frac{{\partial h}}{{\partial t}}$$
(1)

where \(U = R\omega\), \(\frac{1}{{G_{\theta } }} = 12 + 0.0260({\text{Re}}^{*} )^{0.8265}\), \(\frac{1}{{G_{z} }} = 12 + 0.0198({\text{Re}}^{*} )^{0.741}\)[1], \(h = c(1 + \varepsilon \cos (\gamma - \varphi (t))) = c(1 + \varepsilon \cos \theta )\), \(\frac{\partial h}{{\partial \theta }} = - c\varepsilon \sin \theta\), \(\frac{\partial h}{{\partial t}} = c\dot{\varepsilon }\cos \theta + c\varepsilon \dot{\varphi }\sin \theta\), \(\varepsilon = \frac{e}{c}\) and \({{\text{Re}}}^{*}\) is local Reynolds number (\({{\text{Re}}}^{*}=\frac{\rho Uh}{\mu }\)). Thus, the Reynolds equation considering the turbulent flow effect can be rewritten as

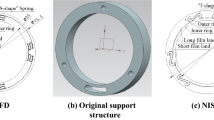
$$\frac{\partial }{{R^{2} \partial \theta }}\left( {\frac{{h^{3} G_{\theta } }}{\mu }\frac{\partial p}{{\partial \theta }}} \right) + \frac{\partial }{\partial z}\left( {\frac{{h^{3} G_{z} }}{\mu }\frac{\partial p}{{\partial z}}} \right) = - \frac{\omega c\varepsilon \sin \theta }{2} + (c\dot{\varepsilon }\cos \theta + c\varepsilon \dot{\varphi }\sin \theta )$$
(2)

Figure 1 represents the supporting region of HSFD, and it should be divided into three regions, i.e., static pressure region, rotating direction dynamic pressure region, and axial direction active pressure region. In the pressure area of the static pressure chamber, the angle relative to the bearing center is \(\beta\), and the pressure is a fixed value, i.e., \(P_{c,i}\)(\(i = 1,2,3,4\)). In the circumferential sealing oil groove dynamic pressure area of HSFD (\(- a \le z \le a\)), the long bearing theory is assumed \(\left( {\frac{\partial p}{{\partial z}} = 0} \right)\), and Eq. (2) could be modified to be

$$\frac{\partial }{{R^{2} \partial \theta }}\left( {\frac{{h^{3} G_{\theta } }}{\mu }\frac{\partial p}{{\partial \theta }}} \right) = - \frac{\omega c\varepsilon \sin \theta }{2} + (c\dot{\varepsilon }\cos \theta + c\varepsilon \dot{\varphi }\sin \theta )$$
(3)
Fig. 1
figure 1

The distribution of static and dynamic pressure in HSFD

Full size image

The modified Reynolds equation for Eq. (3) will then be solved with the boundary condition of the dynamic pressure region to acquire the pressure distribution \(p_{0} (\theta )\). The part of the pressure zone in the axial oil sealing surface for HSFD (\(\left( {a \le \left| z \right| \le \frac{L}{2}} \right)\)), the short bearing theory is assumed \(\left( {\frac{\partial p}{{\partial \theta }} = 0} \right)\), and the equation will be

$$\frac{\partial }{\partial z}\left( {\frac{{h^{3} G_{z} }}{\mu }\frac{\partial p}{{\partial z}}} \right) = - \frac{\omega c\varepsilon \sin \theta }{2} + (c\dot{\varepsilon }\cos \theta + c\varepsilon \dot{\varphi }\sin \theta )$$
(4)

Solving Eq. (4) with the boundary conditions \(\left\{ {\begin{array}{*{20}l} {z = \pm L/2,\;P_{a} (\theta , \pm L/2) = 0\quad \quad \quad \quad \quad \quad \quad \quad \quad } \\ {z = \pm a,\;P_{a} (\theta , \pm a) = P_{0} (\theta ) = \left\{ \begin{gathered} P_{c,i} ; \theta_{i1} - \beta \le \theta \le \theta_{i1} \hfill \\ P_{d,i} ; \theta_{i1} \le \theta \le \theta_{i2} \hfill \\ \end{gathered} \right.} \\ \end{array} } \right.\)

and then the dynamic pressure distribution in the axis direction will be obtained. The formula of pressure distribution in the whole supporting region will finally be established.

2.2 The resulting damper force for HSFD

Based on the above conditions of pressure distribution, the instant oil film pressure distribution considering turbulent flow is introduced as follows.

The instant pressure in a rotating direction within the range of \(- a \le z \le a\) is

$$p_{0} (\theta ) = \left\{ \begin{gathered} p_{c,i}; \frac{\pi }{2}(i - 1) - \frac{\beta }{2} - \phi_{b} \le \theta \le \frac{\pi }{2}(i - 1) + \frac{\beta }{2} - \phi_{b} \hfill \\ p_{d,i} (\theta );\frac{\pi }{2}(i - 1) + \frac{\beta }{2} - \phi_{b} \le \theta \le \frac{\pi }{2}i - \frac{\beta }{2} - \phi_{b} \hfill \\ \end{gathered} \right.,{\text{i}} = {1},{2},{3},{4}.$$
(5)

where

$$p_{d,i} (\theta ) = p_{c,i} + \int\limits_{{\theta_{i1} }}^{\theta } {\frac{{\left[ {\frac{{\mu R^{2} \omega c\varepsilon \cos \theta }}{2} + \mu R^{2} (c\dot{\varepsilon }\sin \theta - c\varepsilon \dot{\varphi }\cos \theta )} \right]}}{{c^{3} (1 + \varepsilon \cos \theta )^{3} G_{\theta } }}{\text{d}}\theta } + c_{1} \int\limits_{{\theta_{i1} }}^{\theta } {\frac{1}{{c^{3} (1 + \varepsilon \cos \theta )^{3} G_{\theta } }}{\text{d}}\theta } ,{\text{i}} = {1},{2},{3},{4,}$$
(6)
$$c_{1} = \frac{{p_{c,i + 1} - p_{c,i} - \int_{{\theta_{i1} }}^{{\theta_{i2} }} {\frac{{\left[ {\frac{{\mu R^{2} \omega c\varepsilon \cos \theta }}{2} + \mu R^{2} (c\dot{\varepsilon }\sin \theta - c\varepsilon \dot{\varphi }\cos \theta )} \right]}}{{c^{3} (1 + \varepsilon \cos \theta )^{3} G_{\theta } }}{\text{d}}\theta } }}{{\int_{{\theta_{i1} }}^{{\theta_{i2} }} {\frac{1}{{c^{3} (1 + \varepsilon \cos \theta )^{3} G_{\theta } }}{\text{d}}\theta } }},$$
$$\theta_{i1} = (i - 1)\frac{\pi }{2} + \frac{\beta }{2} - \phi_{b}, \quad{\text{i}} = {1},\;{2},\;{3},\;{4}.$$

The instant pressure in the axis direction within the range is

$$p_{a} (\theta ,z) = \left( {\frac{L}{2} - \left| z \right|} \right)\left\{ {\left[ {\Lambda_{1} (\theta )\dot{\phi }_{b} \varepsilon + \Lambda_{2} (\theta )\dot{\varepsilon }} \right]\left( {a - \left| z \right|} \right) + p_{0} (\theta )\frac{1}{L/2 - a}} \right\}.$$
(7)

where.

$$\Lambda_{1} (\theta ) = \frac{\mu c\sin \theta }{{2c^{3} (1 + \varepsilon \cos \theta )^{3} G_{z} }};\Lambda_{2} (\theta ) = \frac{\mu c\cos \theta }{{2c^{3} (1 + \varepsilon \cos \theta )^{3} G_{z} }}.$$

The instant oil film forces of each part of the elements are determined by integrating Eqs. (5) and (7) over the area of the journal sleeve. For the static pressure region, the forces in the radial direction and tangential direction will be

$$\left\{ {\begin{array}{*{20}c} {F_{{{\text{rs}}}} = \sum\limits_{i = 1}^{4} {p_{c,\;i} 2aR\left[ {\sin \left( {\frac{\pi }{2}(i - 1) + \frac{\beta }{2} - \phi_{b} } \right) - \sin \left( {\frac{\pi }{2}(i - 1) - \frac{\beta }{2} - \phi_{b} } \right)} \right]} } \\ {F_{\tau s} = \sum\limits_{i = 1}^{4} {p_{c,\;i} 2aR\left[ {\cos \left( {\frac{\pi }{2}(i - 1) - \frac{\beta }{2} - \phi_{b} } \right) - \cos \left( {\frac{\pi }{2}(i - 1) + \frac{\beta }{2} - \phi_{b} } \right)} \right]} } \\ \end{array} } \right.,$$
(8)

For the rotating direction dynamics pressure region, the forces in the radial direction and tangential direction will be

$$\left\{ {\begin{array}{*{20}c} {F_{{{\text{rd}}}} = \sum\limits_{i = 1}^{4} {\int\limits_{{\theta_{i1} }}^{{\theta_{i2} }} {2aRp_{d,i} (\theta )\cos \theta \;{\text{d}}\theta } } } \\ {F_{\tau d} = \sum\limits_{i = 1}^{4} {\int\limits_{{\theta_{i1} }}^{{\theta_{i2} }} {2aRp_{d,i} (\theta )\sin \theta \;{\text{d}}\theta } } } \\ \end{array} } \right.,$$
(9)

For the axial direction dynamic pressure region, the forces in the radial direction and tangential direction will be

$$\left\{ {\begin{array}{*{20}c} {F_{ra} = \int\limits_{z = - L/2}^{z = - a} {\int\limits_{\theta = 0}^{\theta = 2\pi } {p_{a} (\theta ,z)R\cos \theta \;{\text{d}}\theta {\text{d}}z} } + \int\limits_{z = L/2}^{z = a} {\int\limits_{\theta = 0}^{\theta = 2\pi } {p_{a} (\theta ,z)R\cos \theta \;{\text{d}}\theta {\text{d}}z} } } \\ {F_{\tau a} = \int\limits_{z = - L/2}^{z = - a} {\int\limits_{\theta = 0}^{\theta = 2\pi } {p_{a} (\theta ,z)R\sin \theta \;{\text{d}}\theta \;{\text{d}}z} } + \int\limits_{z = L/2}^{z = a} {\int\limits_{\theta = 0}^{\theta = 2\pi } {p_{a} (\theta ,z)R\sin \theta \;{\text{d}}\theta {\text{d}}z} } } \\ \end{array} } \right.,$$
(10)

The resulting damper forces in the radial direction (\(F_{r}\)) and tangential (\(F_{\tau }\)) direction are determined by the summation of the above-supporting forces, and they could be performed as follows, respectively.

$$\left\{ {\begin{array}{*{20}c} {F_{{\text{r}}} = F_{{{\text{rs}}}} + F_{{{\text{rd}}}} + F_{{{\text{ra}}}} } \\ {F_{\tau } = F_{\tau s} + F_{\tau d} + F_{\tau a} } \\ \end{array} } \right.,$$
(11)

2.3 Dynamic equations for turbulent bearing-rotor system under quadratic damping with a hybrid squeeze-film damper

Before we introduce the dynamic equations for turbulent bearing-rotor system under quadratic damping with HSFD, some assumptions are given:

  1. (a)

    The bearing mass is concentrated in the geometric center.

  2. (b)

    The rotor and the bearing are axisymmetric.

  3. (c)

    The rotor speed is constant.

  4. (d)

    The rotor, bearing, and shaft are rigid bodies.

  5. (e)

    The effect of torsional vibration of the rotating shaft is neglected.

  6. (f)

    The torque of the shaft and the disk is negligible.

Figure 2 shows a rigid rotor supported by two-hybrid squeeze-film dampers under turbulent flow and quadratic damping considerations. The strongly nonlinear dynamic equations of the rotor geometric center in the Cartesian coordinate system under the above assumptions can be written as

Fig. 2
figure 2

Schematic illustration of hybrid squeeze-film damper mounted on the rotor-bearing system

Full size image
$$\left\{\begin{array}{l}M\ddot{X}+C\dot{X}\left|\dot{X}\right|+KX=M\uprho {\Omega }^{2}{\text{cos}} \, \omega t+{F}_{x}+K{X}_{0}\\ M\ddot{Y}+C\dot{Y}\left|\dot{Y}\right|+KY=M\rho {\Omega }^{2}{\text{sin}} \, \omega t+{F}_{y}+K{Y}_{0}\end{array}\right.$$
(12)

O-XYZ is the fixed coordinate system fixed at the bearing center Ob, M represents the mass of the rotor, C is the rotor external quadratic damping, K is the spring coefficient of restoring force, \(\rho\) is the eccentric displacement of the rotor mass, \(\Omega\) is the rotational speed of the rotating shaft, \({F}_{x}\) and \({F}_{y}\) are the oil film force under turbulent flow effect in the x and y directions, X0 and Y0 are the initial deformation of the centering spring in the x and y directions, respectively (i.e., the initial displacement of the journal center). The non-dimensional equations will be introduced with the non-dimensional parameters defined below.

$$\begin{gathered} x = X/c,y = Y/c,x_{0} = X_{0} /c,y_{0} = Y_{0} /c,\frac{{\text{d}}}{{{\text{d}}t}} = \Omega \frac{{\text{d}}}{{{\text{d}}\phi }},s = \frac{\Omega }{{\Omega_{n} }},\Omega_{n}^{2} = \frac{K}{M},\beta = \rho /c,f = \frac{c}{{\sqrt {KM} }},\alpha = \frac{{6\mu R^{2} L^{2} }}{{Mc^{3} \Omega_{n} }}, \hfill \\ \sigma_{1} = \frac{{XF_{r} - YF_{\tau } }}{\varepsilon },\sigma_{2} = \frac{{XF_{r} + YF_{\tau } }}{\varepsilon } \hfill \\ \end{gathered}$$

where \({F}_{r}\) and \({F}_{\tau }\) are the resulting bearing forces in the radial and tangential directions and could be obtained from Eq. (11). Then, Eq. (12) become

$$\left\{\begin{array}{l}{x}^{{\prime}{\prime}}+\frac{f}{s}{x}^{\prime}\left|{x}^{\prime}\right|+\frac{1}{{s}^{2}}x=\beta {\text{cos}} \, \phi +\frac{\alpha {\sigma }_{1}}{s}+\frac{1}{{s}^{2}}{x}_{0}\\ {y}^{{\prime}{\prime}}+\frac{f}{s}{y}^{\prime}\left|{y}^{\prime}\right|+\frac{1}{{s}^{2}}y=\beta {\text{sin}} \, \phi +\frac{\alpha {\sigma }_{2}}{s}+\frac{1}{{s}^{2}}{y}_{0}\end{array}\right.$$
(13)

Equation (13) is a nonlinear dynamic system describing a turbulent bearing-rotor system under quadratic damping with a hybrid squeeze-film damper, and the approximate solution for the coupled nonlinear differential equation can be carried out by numerical method, i.e., the fourth-order Runge–Kutta method.

2.4 PD controller design

To control the hybrid squeeze-film damper bearing, two pairs of PD controllers are applied in the hydrostatic chambers to stabilize the HSFD bearing-rotor system. The pressure difference between hydrostatic chambers 1 and 3 is assumed to be \(\Delta p_{1} = k_{p} x + k_{d} \dot{x}\), and the pressure difference of hydrostatic chambers 2 and 4 is considered to be \(\Delta p_{2} = k_{p} y + k_{d} \dot{y}\). The controllable pressure distributions in the hydrostatic chambers are

$$p_{c,1} = p_{s} - \Delta p_{1} ,p_{c,2} = p_{s} - \Delta p_{2} ,p_{c,3} = p_{s} + \Delta p_{1} \;{\text{and}}\;p_{c,4} = p_{s} + \Delta p_{2} .$$
(14)

Substituting the pressure distributions in the hydrostatic chambers, i.e., (14), into Eqs. (8)–(11), the resulting damper forces in the radial and tangential directions can be obtained.

3 Results and discussions

To ensure the data used corresponds to the steady state, the time series data of the first 800 revolutions of the system are deliberately excluded from the dynamic behavior. Besides, the time step for direct numerical integration is designated to be π/300, and the tolerance is appointed to 0.0001. Standard tools for analyzing nonlinear dynamic characteristics are dynamic trajectories, power spectra, Poincaré maps, bifurcation diagrams, fractal dimension, and the maximum Lyapunov exponent. The Lyapunov exponent of a dynamic system characterizes the rate of separation of infinitesimally close trajectories and provides a useful test for the presence of chaos. In a chaotic system, the points of nearby trajectories starting initially within a sphere of radius \({\varepsilon }_{0}\) form after time t an approximately ellipsoidal distribution with semi-axes of length \({\varepsilon }_{j}(t)\). The Lyapunov exponents of a dynamic system are defined by\({\lambda }_{j}=\underset{t\to \infty }{{\text{lim}}}\frac{1}{t}log\frac{{\varepsilon }_{j}(t)}{{\varepsilon }_{0}}\), where \({\lambda }_{j}\) denotes the rate of divergence of the nearby trajectories. The exponents of a system are usually ordered into a Lyapunov spectrum, i.e., \({\lambda }_{1}>{\lambda }_{2}>...>{\lambda }_{m}\). A positive value of the maximum Lyapunov exponent (\({\lambda }_{1}\)) is generally taken as an indication of chaotic motion [34,35,36,37]. Chaotic vibration in a system is generally detected using either the Lyapunov exponent or the fractal dimension property. The Lyapunov exponent test can be used for both dissipative and non-dissipative (i.e., conservative) systems, but is not easily applied to the analysis of experimental data. Conversely, the fractal dimension test can only be used for dissipative systems, but is easily applied to experimental data [38]. In contrast to Fourier transform-based techniques and bifurcation diagrams, which provide only a general indication of the change from periodic motion to chaotic behavior, dimensional measures allow chaotic signals to be differentiated from random signals. Although many dimensional measures have been proposed, the most commonly applied measure is the correlation dimension dG defined by Grassberger and Proccacia due to its computational speed and the consistency of its results. However, before the correlation dimension of a dynamic system flow can be evaluated, it is first necessary to generate a time series of one of the system variables using a time-delayed pseudo-phase-plane method. Assume an original time series of xi = {x(iτ); i = 1,2,3,…N}, where τ is the time delay (or sampling time). If the system is acted upon by an excitation force with a frequency ω, the sampling time, τ, is generally chosen such that it is much smaller than the driving period. The delay coordinates are then used to construct an n-dimensional vector X = (x(jτ), x[(j + 1) τ], x[(j + 2) τ],….., x[(j + n−1) τ]), where j = 1,2,3,…(N−n + 1). The resulting vector comprises a total of (N−n + 1) vectors, which are then plotted in an n-dimensional embedding space. Importantly, the system flow in the reconstructed n-dimensional phase space retains the system’s dynamic characteristics in the original phase space. In other words, if the system flow has the form of a closed orbit in the original phase plane, it also forms a closed path in the n-dimensional embedding space. Similarly, if the system exhibits a chaotic behavior in the original phase plane, its path in the embedding space will also be chaotic. The characteristics of the attractor in the n-dimensional embedding space are generally tested using the function \(\sum_{i,j=1}^{N}H(r-\left|{x}_{i}-{x}_{j}\right|)\) to determine the number of pairs (i, j) lying within a distance |xi − xj|< r in\({\left\{{x}_{i}\right\}}_{i=1}^{N}\), where H denotes the Heaviside step function, N represents the number of data points, and r is the radius of an n-dimensional hyper-sphere. For many attractors, this function exhibits a power law dependence on r as r → 0, i.e., \(c(r)\propto {r}^{{d}_{G}}\). Therefore, the correlation dimension, dG, can be determined from the slope of a plot of [log c(r)] versus [log r]. Grassberger and Proccacia [39] showed that the correlation dimension represents the lower bound to the capacity or fractal dimension dc and approaches its value asymptotically when the attracting set is distributed more uniformly in the embedding phase space. A set of points in the embedding space is considered fractal if its dimension has a finite non-integer value. Otherwise, the attractor is referred to as a ‘strange attractor.’ To establish the nature of the attractor, the embedding dimension is progressively increased, causing the slope of the characteristic curve to approach a steady state value. This value determines whether the system has a fractal or strange attractor structure. If the dimension of the system flow is found to be fractal (i.e., to have a non-integer value), the system is judged to be chaotic.

The bifurcation diagram of the rotor geometric center using dimensionless rotational speed ratio s as bifurcation parameter (s = 0.1–10.1) can be found in Fig. 3b. Moreover, the dynamic trajectory, power spectrum, and Poincaré section are also attached to show which dynamic behaviors they are (Fig. 3a). The bifurcation diagram reveals that the dynamic responses behave 1T-period and 2T-period at low rotational speeds. That may be because HSFD plays a vital role in suppressing aperiodic motions. We could also check from the dynamic trajectory, power spectrum, and Poincaré section (just one single point), so we could say that it is a 1T periodic response at s = 1.0 and behaves in subharmonic motions with a 2T period at s = 4.0. Even though the system is under strong nonlinear effects, including quadratic damping, nonlinear oil film force, and turbulent flow, the dynamic behaviors persist in periodic motions until s > 6.0, when the system breaks from periodic motion and enters non-periodic motion. The dynamic behaviors perform aperiodic ones in the bifurcation diagram with increasing rotational speed, the dynamic trajectory is aperiodic, the power spectrum is rich and broad, and the closed curves present in the Poincaré section at s = 6.8 and s = 8.8, so the quasi-periodic motions are found at higher rotational speeds by observing those diagrams. In Fig. 4, we use the dimensionless unbalanced parameter β as a bifurcation parameter to discuss dynamic responses in a bifurcation diagram for the rotor geometric center. The bifurcation diagram suggests that periodic, subharmonic, and chaotic motions exist in the rotor geometric center (Fig. 4a). Therefore, dynamic trajectory, power spectrum, and Poincaré section are also applied to identify those trajectories clearly (Fig. 4b). At first, a disordered course could be found in the dynamic orbit, and then numerous excitation frequencies could also be found in power spectra at β = 0.11. Then, the return points in the Poincaré section are a geometrically fractal structure. We could determine that the dynamic response is chaotic for β = 0.11. Besides, the dynamic responses are quasi-periodic at β = 0.25, 7T-periodic at β = 0.40, 5T-periodic at β = 0.56 and 3T-periodic at β = 0.60. The Lyapunov exponent and the fractal dimension are vital tools to verify whether the dynamic response performs chaos. Therefore, we apply them to detect the dynamic response for β = 0.11 in Fig. 5. The maximum Lyapunov exponent is positive. The fractal dimensions show the plot of (log c(r)) vs. (log r) for different embedding dimensions at β = 0.11. It is clear that as the embedding dimension is increased, the linear part of the slope approaches a constant value, 1.25 for β = 0.11, so we prove again that the dynamic response is a chaotic motion at β = 0.11. The pressure distributions in the four oil chambers, i.e., \({p}_{c,1},{p}_{c,2},{p}_{c,3}\) and \({p}_{c,4}\) are also shown in Fig. 6. The pressure distribution in the static pressure chamber at β = 0.11 without active control is aperiodic.

Fig. 3
figure 3figure 3

a Orbit, power spectrum and Poincaré section at s = 1.0, 4.0, 6.8, and 8.8 b Bifurcation diagram of the rotor geometric center using dimensionless rotational speed ratio s as bifurcation parameter (s = 0.1–10.1)

Full size image
Fig. 4
figure 4figure 4

a Orbit, power spectrum, and Poincaré section at β = 0.11, 0.25, 0.40, 0.56, and 0.60 b Bifurcation diagram of the rotor geometric center using dimensionless unbalance parameter β as bifurcation parameter (β = 0.001–1.00)

Full size image
Fig. 5
figure 5

Fractal Dimension and Lyapunov Exponent with β = 0.11

Full size image
Fig. 6
figure 6

Pressure distribution in the static pressure chamber at β = 0.11 without active control

Full size image

The PD controllers with two pairs are constructed in the hydrostatic chambers to stabilize and control the HSFD-equipped bearing-rotor system. They are assuming that the pressure difference between hydrostatic chambers 1 and 3 is and the pressure difference between hydrostatic chambers 2 and 4 is. The controllable pressure distributions in the hydrostatic chambers are defined as \(p_{c,4} = p_{s} + \Delta p_{2}\). Then substituting \({p}_{c,1},{p}_{c,2}, {p}_{c,3}\) and \({p}_{c,4}\) into equations, and the resulting damper forces in the radial and tangential directions can be obtained and used to avoid the system operating in a chaotic motion, e.g., when the dimensionless unbalance parameter β = 0.11, an increased proportional gain is applied to control this system by the active control method we have published [40] shown in Fig. 7. It can be seen that the rotor trajectory is 1T-periodic motion at β = 0.11 with the proportional gain \(k_{p} = 75000\) demonstrated in the rotor trajectory (8(a)), Poincaré section (8(b)), and power spectrum (8(c)). The pressure distributions in the static pressure chambers are also performed periodically for \({p}_{c,1}, {p}_{c,2}, {p}_{c,3}\) and \({p}_{c,4}\) in Fig. 8d–g.

Fig. 7
figure 7

The flow rate control structure of HSFD [12]

Full size image
Fig. 8
figure 8

Synchronous motion of rotor trajectory at β = 0.11 with \(k_{p} = 75000\) a Rotor trajectory; b Poincaré section c power spectrum of rotor trajectory; d–g Pressure distributions for Pc,1, Pc,2, Pc,3, and Pc,4 in the static pressure chambers

Full size image

4 Conclusion

The nonlinear dynamic analysis of a turbulent bearing-rotor system under quadratic damping equipped with HSFD is presented in this study. Due to the strongly nonlinear effect inclusive of the nonlinear oil film force and quadratic damping, the dynamic responses of these systems would perform aperiodic potions, so we take HSFD to suppress the aperiodic motions, which works effectively. We use two bifurcation parameters, i.e., dimensionless speed ratio and dimensionless unbalance parameter, to plot the bifurcation diagrams, and we found abundant harmonic, subharmonic, quasi-periodic, and even chaotic motions with dynamic trajectories, power spectrum, Poincaré maps, Lyapunov exponent, and fractal dimension, simultaneously. We also use the PD controllers constructed in the hydrostatic chambers to control the bearing-rotor system and avoid chaotic motions. The results of this study enhance our understanding of the importance of turbulent journal bearings, considering quadratic damping and the application of HSFD and active control. The analysis of the model would help improve turbo-machineries and related industrial applications in designing or operating.