The stability analysis of a two-spool rotor system undergoing rub-impact

Abstract

The main objective of the present paper is to determine the influence of rub parameters on the stability of a two-spool rotor system undergoing rub-impact. The parameters such as rotor–stator contact stiffness, coefficient of friction and clearance are varied for understanding their effects on the system response and stability. Moreover, the analysis is performed for two modes of rotor operations, namely co-rotation and counter-rotation, and determines their impacts on rotor–stator rubbing. A time variational method is employed to predict the nonlinear response of the system with a perturbation function applied at the steady-state solution points to investigate their stability. Two types of bifurcations, namely limit point and Neimark–Sacker bifurcations, are observed in the response by monitoring the Floquet exponents of the perturbed system. As the coefficient of friction is increased, the early onset of NS bifurcation has happened and the system enters into the quasi-periodic regime early. However, when the contact stiffness and clearance values are increased, the onset of NS bifurcation is delayed. It is also observed that the response characteristics of the co- and counter-rotating systems are entirely different. The separation between forward and backward whirling frequencies is reduced for the counter-rotating system due to the cancellation of gyroscopic moments. In addition, for the same set of parameters, the counter-rotating system enters into the quasi-periodic regime quickly once the disk starts rubbing.

1 Introduction

Rub-impact is a common fault observed in rotating machinery, generated as a consequence of tight clearance between rotating and stationary components. It creates unwanted vibrations in the machinery which may reduce its performance under different operating conditions. The aircraft engines are composed of multi-spool rotors that will induce multiple excitations when they are subjected to unbalanced forces and external excitations. As a result, the dynamic behavior of such machines appears to be more complicated in the presence of rub-impact. In literature, most of the works related to rub-impact are carried out using single-spool rotor models [1]. However, the information received from a single-spool rotor model won’t be sufficient enough to predict the response behavior of an aircraft engine model since it has a two-spool configuration. For the analysis of such machines, a dual-rotor model will be appropriate which consists of two co-axial rotors that are connected together using inter-shaft bearings. Both the rotors spin at different speeds with their ratio may not be an integer. The presence of inter-shaft bearings makes the behavior of the dual-rotor model unique and results in the coupling of both rotor vibrations.

The detailed studies on rub-impact in dual-rotor systems are started recently. Yang et al. [2] constructed an experimental test-rig and studied the vibration characteristics of a dual-rotor system undergoing rub-impact. A dynamic model is also developed and obtained the response behavior under fixed point rubbing. It is observed that the response of the dual-rotor model under rub-impact not only contains the excitation frequency components but also includes their linear combinations. Later, Wang et al. [3] also observed similar results when an experimental and numerical analysis is performed. Moreover, the effects of different model parameters such as rotational speed ratio, initial clearance, mass eccentricity and inter-shaft stiffness on the dynamic response are also presented in detail. Yang et al. [4, 5] extended the analysis by incorporating multi-unbalances and multi-fixed-point rubbing in the dual-rotor model. In this model, the casing and disks are painted with softer coatings; hence, a Lankarani–Nikravesh model [6] is used to calculate the impact force between contact points. Multi-periodic and quasi-periodic motions are observed in the response due to the multi-fixed point rubbing. Lu et al. [7] modified the dual-rotor model by incorporating a ball bearing in place of linear bearing and studied the effects of bearing clearance on the primary resonance of the system. Using a similar kind of dual-rotor model, Gao et al. [8] investigated the effects of barrel roll maneuver on rub-impact phenomenon numerically and experimentally. Coupled bending and torsional motions are observed in which the rub-impact stiffness affected the bending vibration while the friction coefficient influenced the torsional vibration. Meantime, Wang et al. [9] developed a dual-rotor blade-casing (DRBC) model by including a thin-walled casing and rigid blades in a simple dual-rotor model. The vibration signals are measured from the casing surface, and certain periodic impact characteristics are noticed in the signal with its frequency equal to the product of the rotational frequency and the numbers of blades. Later, Yang et al. [10] studied the vibration behaviors of a DRBC system undergoing pedestal looseness and rub-impact faults simultaneously. It is found that the pedestal looseness results in a pulsating kind of vibration with a large amplitude and induces the rub-impact early.

Generally, the vibration characteristics of a rotor model undergoing rub-impact are obtained using numerical integration schemes. However, it is very time-consuming in finding the steady-state response behavior of a large degree of freedom (DOF) model subjected to rub. In such problems, a multi-harmonic balance method (MHBM) with alternating frequency–time (AFT) technique is found to be an appropriate solution procedure. It generates the results at a faster rate compared to numerical integration schemes and traces the unstable branches beyond the bifurcation points with the help of continuation procedures. Sun et al. [11] developed an 8-DOF model of a dual-rotor system and investigated the effects of system parameters such as rotational speed ratio, mass eccentricity and inter-shaft stiffness. The disks are modeled as lumped masses with the bearings represented using the linear springs. Later, Hou et al. [12] continued the analysis by replacing the linear springs with ball bearings at the inter-shaft location. A resonance hysteresis phenomenon is observed in the frequency–response curve when the clearance of inter-shaft ball bearing is increased. Bifurcation and stability analysis is also carried out when the rotor system is subjected to constant excitation and rub-impact [13]. Since the MHBM-AFT is a frequency domain technique, Hsu’s method is used to predict the stability and bifurcation nature of the system. A more improved dual-rotor model is proposed by Sun et al. [14] in which a sophisticated geometrical structure of the jet engine is considered by finite solid element modeling. The total size of the FE model is reduced using an efficient model reduction technique called component mode synthesis (CMS). The model provided a better understanding of the nonlinear dynamical behaviors of the real complicated dual-rotor aero-engine undergoing rub-impact. Moreover, this research works showed the efficiency of the MHBM-AFT method compared to numerical integration. However, this method has some limitations when more than two excitation frequencies are present in the system. In such problems, the AFT procedure becomes complex since the formulation of the multi-dimensional fast Fourier transform (FFT) is very complicated. Hence, Guskov and Thouverez [15] introduced an adjusted harmonic balance method (AHBM) in which the response is expressed in terms of a one-dimensional Fourier series by taking the greatest common divisor of the excitation frequencies as the fundamental frequency. It is observed that this method performed the stability analysis at a faster rate and provided results similar to that of the MHBM-AFT. However, the method requires a higher number of harmonics for capturing the complete nonlinear phenomena, which in turn makes the formulation tedious. In addition, the alternate transformation between the frequency and time domains consumes more time when the number of state variables in the nonlinear function is high.

A new time-domain technique called the time variational method (TVM) is introduced by Rook [16] which didn’t require the alternate transformation between the frequency and time domains during the calculation of the Jacobian and nonlinear forces. Later, Krishna and Padmanabhan [17, 18] used the same method for investigating the response behavior of nonlinear, multi-DOF mechanical systems subjected to external excitations. In their work, the performance of the TVM is compared with that of the existing numerical techniques, and a good agreement is obtained. Recently, Prabith and Krishna [19] extended the TVM in multiple frequency excitation problems by expressing the excitation force in terms of a fundamental frequency which is the greatest common divisor of the approximated frequency components. The method is applicable to all the multi-frequency excitation problems and proved to be effective in handling the system with more than two excitation frequencies. Hence, it can be applied for the analysis of the dual-rotor systems as well. In this method, the stability of the response is determined by applying a perturbation at the steady-state solution point and checking the eigenvalues of the perturbed dynamical system.

The nature of rotor response and its stability is highly dependent on the direction of rotor rotations. There are some studies in the literature that compared the dynamic characteristics of co- and counter-rotating rotors. From the studies, it is observed that the critical speeds of the counter-rotating system are slightly less than that of the co-rotating system due to the low gyroscopic effects [20,21,22]. Wang et al. [20] compared the responses of the co- and counter-rotating dual-rotor systems when they are subjected to nonlinear forces of squeeze film dampers. It is noticed that the frequency components that are appeared in the response are quite different for co- and counter-rotating rotors. Later, Ma et al. [21] noticed that the motion trajectories of the rotor under rub-impact is influenced by the direction of rotor rotations. For the same set of model parameters, a petal-like trajectory is observed for the counter-rotating system whereas multiple circles are obtained for the co-rotating systems. It indicates that the stability and bifurcation nature of the dual-rotor model are significantly affected by the direction of rotor rotation. In addition, the effects of rub parameters on the stability and onset of bifurcation need to be explored in detail for both modes of rotor rotations. Hence, the objectives of the present work are highlighted as follows.

Fig. 1

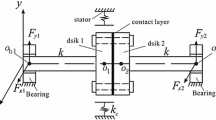
The schematic diagram of a two-spool rotor system [23]

Table 1 Properties of the symmetric bearings used in the model [23]

Table 2 Properties of the disks used in the model [23]

• introduce the TVM in predicting the steady-state response of a two-spool rotor system undergoing rub-impact.

• perform the stability analysis by applying a perturbation at the steady-state solution point and determine the bifurcation points by monitoring the Floquet exponents.

• investigate the effects of the direction of rotor rotations (co- and counter-rotation) on the stability of the rubbing response.

• perform the parametric analysis and obtain the influence of rub parameters such as the rotor–stator contact stiffness, coefficient of friction and clearance on the stability and onset of bifurcation points.

The present paper is organized into nine sections. After introduction, Sect. 2 describes the mechanical model of the two-spool rotor system. In this section, the parameters and structure of the dual-rotor model are provided. Section 3 explains the methodology formulation in which the model reduction technique, the TVM and the stability theory are described. In Sect. 4, the finite element (FE) modeling of the two-spool rotor model is carried out and the unbalance responses are obtained during co- and counter-rotations. Section 5 provides the validation of the proposed methodology with the experimental results published in a reference article. In Sect. 6, the nonlinear dynamic responses of the two-spool rotor model undergoing rub-impact are explained during co- and counter-rotations. Sections 7 and 8 describe the stability analysis and the parametric analysis, respectively. Finally, Sect. 9 presents conclusions.

2 Mechanical model of the two-spool rotor system

The two-spool rotor system shown in Fig. 1 is composed of a pair of co-axial rotors that are connected together using an inter-shaft bearing [23]. The presence of inter-shaft bearing couples the vibrations of both the rotors and leads to combined harmonic responses. The inner rotor is made up of a long and slender shaft which is supported at the ends using two symmetric bearings, whereas the outer rotor consists of a hollow shaft whose one end is connected to the frame through a symmetric bearing and the other end is connected to the inner rotor through an inter-shaft bearing. The outer rotor is spinning at a speed that is 1.2 times the speed of the inner rotor (speed ratio $\kappa = 1.2$).

The following assumptions are made to perform the nonlinear dynamic analysis,

• 1. All the bearings are modeled using linear springs and viscous dampers.

• 2. All the disks are rigid and are represented using lumped masses with moments of inertias equal in X and Y directions.

• 3. No coatings are applied on the casing and disk surfaces

• 4. The axial and torsional vibrations are small, hence ignored.

Tables 1 and 2 give the details of the bearings and disks used in the model. The complete rotor model is cyclically symmetric with the elastic modulus as 207 GPa, the Poisson’s ratio as 0.3 and the mass density as 8300 $kg/m^3$. The geometric properties of the shafts are given in Table 3. Disk 1 and 3 have mass unbalances of magnitude 0.0001 kgm each that forces the rotors to whirl during their operation. When the amplitude of whirling exceeds the clearance $\delta$, disk 2 impacts the stator, and the system behavior becomes nonlinear. The stator is assumed as a rigid ring with a rotor–stator contact stiffness $k_c$. The friction at the contact interface is modeled according to Coulomb’s frictional law, without considering the thermal effect and the material removal. The nonlinear forces along X and Y directions due to rub-impact can be expressed as,

$$\begin{aligned} \begin{aligned}&f_{nx}=\Theta k_c \Big [1-\frac{\delta }{r}\Big ](x-\mu \text {sign} (v_{rel}) y) \\&f_{ny}=\Theta k_c \Big [1-\frac{\delta }{r}\Big ](\mu \text {sign} (v_{rel}) x+ y)\\&\text {where} \quad v_{rel} = \omega r_{disk} + v_{tang} \end{aligned} \end{aligned}$$

(1)

$r_{disk}$ is the radius of the disk, $\omega$ is the angular velocity of the disk, $\mu$ is the coefficient of friction, and $v_{tang}$ is the instantaneous tangential velocity of whirling at the contact point. Its direction is depended on the sense of whirling. x, y and r are the instantaneous positions along X, Y directions and whirling radius, respectively. $\Theta$ is a switching function that is equal to one when contact occurs and equal to zero when no contact occurs.

Table 3 Geometric properties of the shafts used in the model [23]

3 Methodology formulation

The governing equations of a two-spool rotor system having N DOF can be expressed in FE formulation as,

$$\begin{aligned}&\mathbf{M} \ddot{\mathbf{x }}+\mathbf{C} \dot{\mathbf{x }}+ \mathbf{G} (\omega _1,\omega _2) \dot{\mathbf{x }}+\mathbf{K} \mathbf{x} +\mathbf {F}_{nl}(\mathbf {x},t)\nonumber \\&\quad =\mathbf {F} (\omega _1,\omega _2,t) \end{aligned}$$

(2)

where $\mathbf{M}$, $\mathbf{C}$, $\mathbf{G}$ and $\mathbf{K}$ constitute the mass, damping, gyroscopic and stiffness matrices respectively. The mass matrix $\mathbf{M}$ is symmetric with its elements including the translatory and rotary inertia components of the shafts as well as the disks. The damping matrix $\mathbf{C}$ may be symmetric or non-symmetric, decided by the nature of the bearings and the internal damping of the shafts. The gyroscopic matrix $\mathbf{G}$ is a skew-symmetric matrix, involving the gyroscopic effects of both the shafts and the disks. The stiffness matrix $\mathbf{K}$ is symmetric in nature with its elements containing the stiffnesses of shaft and bearings (assuming no cross-coupled terms). The vector $\mathbf{x}$ is of size $N \times 1$, representing the physical DOFs of the complete FE model. $\mathbf {F}_{nl}$ and $\mathbf {F}$ are the corresponding nonlinear and external force vectors respectively. $\omega _1$ and $\omega _2$ are the angular velocities of the inner and outer rotors respectively with their ratio need not be an integer. As a result, the response of the two-spool rotor system may not be periodic with respect to the external excitations. However, it can be made periodic by expressing the external excitations in terms of a frequency $\omega _0$ which is the greatest common divisor of the approximated frequency components [19] as given,

$$\begin{aligned} \omega _0=\frac{\tilde{\omega }_j}{p_j},\quad j=1,2 \quad p_j\in {\mathbb {N}} \end{aligned}$$

(3)

where $\tilde{\omega }_j$ is the approximated value of ${\omega }_j$ obtained by approximating the irrational excitation frequencies to rational ones. Now, by using the relation $\tau =\omega _0 t$, Eq. (2) is transformed into a new time scale as expressed below,

$$\begin{aligned} \omega _0^2 \mathbf{M} \mathbf{x }''+\omega _0 \mathbf{C} \mathbf{x }'+\omega _0^2 \tilde{\mathbf{G }} \mathbf{x }' +\,\mathbf{K} \mathbf{x} +\mathbf {F}_{nl}(\mathbf{x} ,\tau )=\mathbf {F}(\tau ) \end{aligned}$$

(4)

where $\mathbf{x }'$ and $\mathbf{x }''$ are the first and second derivatives of $\mathbf{x }$ with respect to $\tau$. $\tilde{\mathbf{G }}$ is a constant matrix such that it is no longer a function of $\omega _1$ and $\omega _2$.

3.1 Model reduction

Since the rubbing happens at disk position only, it won’t be advisable to use the nonlinear solution technique to all the DOFs, as it increases the computational expense. Hence, a model reduction technique based on component mode synthesis is employed to lower the size of the FE model [17]. In this technique, the complete FE model is partitioned into two components, namely primary and secondary components. All the nonlinear nodes with their boundary nodes are assembled in the primary component and the remaining nodes are included in the secondary component. The primary component is retained in its physical coordinates, whereas the secondary component is reduced using the Craig–Bampton sub-structuring. The equation of motion for the secondary component is written as,

$$\begin{aligned} \omega _0^2 \mathbf{M} _\mathbf{s } \mathbf{x} _\mathbf{s }''+\omega _0 \mathbf{C} _\mathbf{s } \mathbf{x} _\mathbf{s }'+\omega _0^2 \tilde{\mathbf{G }}_\mathbf{s } \mathbf{x} _\mathbf{s }'+\mathbf{K} _\mathbf{s } \mathbf{x} _\mathbf{s }=\mathbf{F} _\mathbf{s } \end{aligned}$$

(5)

where ‘s’ stands for the secondary component. The coordinate vector $\mathbf{x} _\mathbf{s }$ is partitioned into boundary and interior coordinates as,

$$\begin{aligned} \mathbf{x} _\mathbf{s }=\begin{Bmatrix} \mathbf{x} _\mathbf{s }^i\\ \mathbf{x} _\mathbf{s }^b \end{Bmatrix} \end{aligned}$$

(6)

where $\mathbf{x} _\mathbf{s }^i$ are the interior coordinates and $\mathbf{x} _\mathbf{s }^b$ are the boundary coordinates including the DOFs corresponding to the disks and the interface node. Now, Eq. (5) is rewritten as

$$\begin{aligned}&\omega _0^2 \begin{bmatrix} \mathbf{M} _\mathbf{s }^{ii} &{} \mathbf{M} _\mathbf{s }^{ib} \\ \mathbf{M} _\mathbf{s }^{bi} &{} \mathbf{M} _\mathbf{s }^{bb} \end{bmatrix} \begin{Bmatrix} \mathbf{x} _\mathbf{s }^i\\ \mathbf{x} _\mathbf{s }^b \end{Bmatrix}'' + \omega _0 \begin{bmatrix} \mathbf{C} _\mathbf{s }^{ii} &{} \mathbf{C} _\mathbf{s }^{ib} \\ \mathbf{C} _\mathbf{s }^{bi} &{} \mathbf{C} _\mathbf{s }^{bb} \end{bmatrix} \begin{Bmatrix} \mathbf{x} _\mathbf{s }^i\\ \mathbf{x} _\mathbf{s }^b \end{Bmatrix}'\nonumber \\&\quad +\,\omega _0^2 \begin{bmatrix} \tilde{\mathbf{G }}_\mathbf{s }^{ii} &{} \tilde{\mathbf{G }}_\mathbf{s }^{ib} \\ \tilde{\mathbf{G }}_\mathbf{s }^{bi} &{} \tilde{\mathbf{G }}_\mathbf{s }^{bb} \end{bmatrix} \begin{Bmatrix} \mathbf{x} _\mathbf{s }^i\\ \mathbf{x} _\mathbf{s }^b \end{Bmatrix}'+ \begin{bmatrix} \mathbf{K} _\mathbf{s }^{ii} &{} \mathbf{K} _\mathbf{s }^{ib} \\ \mathbf{K} _\mathbf{s }^{bi} &{} \mathbf{K} _\mathbf{s }^{bb} \end{bmatrix} \begin{Bmatrix} \mathbf{x} _\mathbf{s }^i\\ \mathbf{x} _\mathbf{s }^b \end{Bmatrix}= \begin{Bmatrix} \mathbf{0} \\ \mathbf{F} _\mathbf{s }^b \end{Bmatrix}\nonumber \\ \end{aligned}$$

(7)

By using the Craig–Bampton sub-structuring, the interior DOFs are transformed into a set of modal coordinates as given below,

$$\begin{aligned} \begin{Bmatrix} \mathbf{x} _\mathbf{s }^i\\ \mathbf{x} _\mathbf{s }^b \end{Bmatrix}= \begin{bmatrix} \Phi &{} \Psi \\ \mathbf{0} &{} \mathbf{I} \end{bmatrix} \begin{Bmatrix} \mathbf{q} _\mathbf{s }\\ \mathbf{x} _\mathbf{s }^b \end{Bmatrix}=\mathbf{T} _s \bar{\mathbf{x }}_\mathbf{s } \end{aligned}$$

(8)

where $\mathbf{q} _\mathbf{s }$ represents the modal coordinates and $\mathbf{T} _s$ constitutes the transformation matrix including the retained normal modes $\Phi$ and constraint mode $\Psi$ such that,

$$\begin{aligned} \begin{aligned} \Phi ^T \mathbf{M} _\mathbf{s }^{ii}\Phi&= \bar{\mathbf{M }}_\mathbf{s }^{ii}\\ \Phi ^T \mathbf{C} _\mathbf{s }^{ii}\Phi&= \bar{\mathbf{C }}_\mathbf{s }^{ii}\\ \Phi ^T \tilde{\mathbf{G }}_\mathbf{s }^{ii}\Phi&= \bar{\mathbf{G }}_\mathbf{s }^{ii}\\ \Phi ^T \mathbf{K} _\mathbf{s }^{ii}\Phi&= \bar{\mathbf{K }}_\mathbf{s }^{ii}\\ \Psi&= -(\mathbf{K} _\mathbf{s }^{ii})^{-1}{} \mathbf{K} _\mathbf{s }^{ib} \end{aligned} \end{aligned}$$

(9)

The number of retained modes is chosen based on a convergence study and it is very much less than the total DOFs of the FE model. Now, Eq. (8) is substituted in Eq. (7) and is pre-multiplied with the transpose of $\mathbf{T} _s$ to get the reduced equations of motion of the secondary component as,

$$\begin{aligned} \omega _0^2 \bar{\mathbf{M }}_\mathbf{s } \bar{\mathbf{x }}_\mathbf{s }''+\omega _0 \bar{\mathbf{C }}_\mathbf{s } \bar{\mathbf{x }}_\mathbf{s }'+\omega _0^2 \bar{\mathbf{G }}_\mathbf{s } \bar{\mathbf{x }}_\mathbf{s }'+\bar{\mathbf{K }}_\mathbf{s } \bar{\mathbf{x }}_\mathbf{s }=\bar{\mathbf{F }}_\mathbf{s } \end{aligned}$$

(10)

where $\bar{\mathbf{M }}_\mathbf{s }$, $\bar{\mathbf{C }}_\mathbf{s }$, $\bar{\mathbf{G }}_\mathbf{s }$ and $\bar{\mathbf{K }}_\mathbf{s }$ are the reduced mass, damping, gyroscopic and stiffness matrices of the secondary component, respectively. $\bar{\mathbf{F }}_\mathbf{s }$ is the reduced force vector. Now, the equation of motion for the primary component is written as,

$$\begin{aligned} \omega _0^2 \mathbf{M} _\mathbf{p } \mathbf{x} _\mathbf{p }''+\omega _0 \mathbf{C} _\mathbf{p } \mathbf{x} _\mathbf{p }'+\omega _0^2 \tilde{\mathbf{G }}_\mathbf{p } \mathbf{x} _\mathbf{p }'+\mathbf{K} _\mathbf{p } \mathbf{x} _\mathbf{p }+\mathbf{F} _{nl\mathbf{p} }=\mathbf{F} _\mathbf{p }\nonumber \\ \end{aligned}$$

(11)

The primary component is retained in physical coordinates. However, an identity matrix transformation is performed to keep the procedure the same as that of the secondary component. The transformed equation of motion is written as,

$$\begin{aligned} \omega _0^2 \bar{\mathbf{M }}_\mathbf{p } \bar{\mathbf{x }}_\mathbf{p }''+\omega _0 \bar{\mathbf{C }}_\mathbf{p } \bar{\mathbf{x }}_\mathbf{p }'+\omega _0^2 \bar{\mathbf{G }}_\mathbf{p } \bar{\mathbf{x }}_\mathbf{p }'+\bar{\mathbf{K }}_\mathbf{p } \bar{\mathbf{x }}_\mathbf{p }+\bar{\mathbf{F }}_{nl\mathbf{p} }=\bar{\mathbf{F }}_\mathbf{p }\nonumber \\ \end{aligned}$$

(12)

Finally, Eqs. (10) and (12) are assembled together to get the reduced equations of motion of the two-spool rotor model as,

$$\begin{aligned} \omega _0^2 \bar{\mathbf{M }} \bar{\mathbf{x }}''+\omega _0 \bar{\mathbf{C }} \bar{\mathbf{x }}'+\omega _0^2 \bar{\mathbf{G }} \bar{\mathbf{x }}'+\bar{\mathbf{K }} \bar{\mathbf{x }}+\bar{\mathbf{F }}_{nl} (\bar{\mathbf{x }}) = \bar{\mathbf{F }} \end{aligned}$$

(13)

where $\bar{\mathbf{M }}$, $\bar{\mathbf{C }}$, $\bar{\mathbf{G }}$ and $\bar{\mathbf{K }}$ are the reduced mass, damping, gyroscopic and stiffness matrices of the two-spool rotor model. The size of these matrices is $N_{size} \times N_{size}$, where $N_{size} = (n_p+m+n_s^b-n)$, $n_p$ is the size of the primary component, n is the nodal DOF, $n_s^b$ is the number of boundary coordinates in the secondary component and m is the number of retained modes. $\bar{\mathbf{F }}_{nl}$ and $\bar{\mathbf{F }}$ are the corresponding nonlinear and external force vectors, respectively, of size $N_{size} \times 1$.

3.2 Time variational method

The time variational method (TVM) is a semi-analytic technique that is generally employed for solving periodic and single excitation problems. Fortunately, Eq. (13) is equivalent to a periodic, single excitation problem with a fundamental frequency $\omega _0$. A detailed description of the TVM is available in the paper by Rook [16]. According to this method, the response, nonlinear function and external force are approximated using the basis function as given below,

$$\begin{aligned}&\bar{\mathbf{x }}(\tau )=\hat{\mathbf{X }} . \chi (\tau ) \ \bar{\mathbf{F }}_{nl}(\tau )=\hat{\mathbf{F }}_{nl}.\chi (\tau ) \nonumber \\&\quad \bar{\mathbf{F }}(\tau )=\hat{\mathbf{F }}.\chi (\tau ) \end{aligned}$$

(14)

where $\chi (\tau )$ maybe a wavelet scaling function or a finite element shape function. In this paper, a cubic spline function is used as the basis function that has a good convergence rate compared to the other functions due to the narrow banded structure of the differentiation matrices [16]. In Eq. (14), $\hat{\mathbf{X }}$ represents a matrix whose ith row denotes the ith DOF value calculated at discrete time points. Its column size is equal to the number of discrete time points $N_p$ taken for the analysis. Similarly, $\hat{\mathbf{F }}$ and $\hat{\mathbf{F }}_{nl}$ are the external and nonlinear force matrices calculated at discrete time points, respectively. The substitution of Eq. (14) in Eq. (13) and then, applying the Galerkin method, a weak residual form of Eq. (13) is obtained as

$$\begin{aligned}&\mathbf{R} (\hat{\mathbf{x }})=\big [\omega _0 ^2 \big (\bar{\mathbf{M }}\otimes \mathbf{D} ^{(2)}\big )+\omega _0 \big (\bar{\mathbf{C }}\otimes \mathbf{D} ^{(1)}\big )\nonumber \\&\quad +\omega _0^2 \big (\bar{\mathbf{G }}\otimes \mathbf{D} ^{(1)}\big )+\big (\bar{\mathbf{K }}\otimes \mathbf{D} ^{(0)}\big )\big ]\hat{\mathbf{x }}\nonumber \\&\quad +\big (\mathbf{I} \otimes \mathbf{D} ^{(0)}\big )\big (\hat{\mathbf {f}}_{nl}(\hat{\mathbf{x }})-\hat{\mathbf {f}}\big ) = 0 \end{aligned}$$

(15)

where $\hat{\mathbf{x }}= \text {vec} (\hat{\mathbf{X }}^T)$, $\hat{\mathbf{f }}_{nl} = \text {vec} (\hat{\mathbf{F }}_{nl}^T)$ and $\hat{\mathbf{f }} = \text {vec} (\hat{\mathbf{F }}^T)$. $\otimes$ is the Kronecker product and vec ( ) is the vectorize operator that stacks the columns of the matrix operated upon. Equation (15) is a set of nonlinear algebraic equations of size $N_p N_{size}$ and are solved using the Newton–Raphson method. In order to obtain the frequency response of the system, a suitable continuation procedure can be adopted for tracing the unstable branches beyond the bifurcation. This is achieved by incorporating a tracing equation in Eq. (15) as given below,

$$\begin{aligned} \mathbf {R}_1(\hat{\mathbf{x }},\omega _0)= \begin{Bmatrix} \mathbf {R}(\hat{\mathbf{x }},\omega _0)\\ \bar{\mathbf {R}}(\hat{\mathbf{x }},\omega _0) \end{Bmatrix}=0 \end{aligned}$$

(16)

In this paper, a hyper-sphere-based continuation algorithm is used for getting a future solution. It is performed by predicting and correcting the assumed solution along the surface of a hyper-sphere of radius $\bar{r}$ with its center at $\hat{\mathbf{x }}_c$ which is the previous steady-state point. The tracing equation of the hyper-sphere based continuation algorithm is written as,

$$\begin{aligned} \bar{\mathbf {R}}(\hat{\mathbf{x }},\omega _0)=(\hat{\mathbf{x }}^2-\hat{\mathbf{x }}_c^2)+(\omega _0^2-\omega _{0c}^2)-\bar{r}^2 = 0 \end{aligned}$$

(17)

As explained earlier, the TVM has certain advantages and disadvantages over existing solution techniques. A comparison of the proposed methodology with the existing techniques is provided in Table 4.

Table 4 Comparison of the proposed methodology with the existing techniques [1]

3.3 Stability theory

In this paper, the local stability of the solution points is determined by introducing a small perturbation $\epsilon (\tau )$ around the steady-state solution point $\bar{\mathbf{x }}^*$. As a result, Eq. (13) is modified as,

$$\begin{aligned}&\omega _0^2 \bar{\mathbf{M }} (\bar{\mathbf{x }}^*+\epsilon )''+\omega _0 \bar{\mathbf{C }} (\bar{\mathbf{x }}^*+\epsilon )'+\omega _0^2 \bar{\mathbf{G }} (\bar{\mathbf{x }}^*+\epsilon )'\nonumber \\&\quad +\bar{\mathbf{K }} (\bar{\mathbf{x }}^*+\epsilon )+\bar{\mathbf{F }}_{nl}(\bar{\mathbf{x }}^*+\epsilon ) = \bar{\mathbf{F }} \end{aligned}$$

(18)

By linearizing the nonlinear force $\bar{\mathbf{F }}_{nl}$ around $\bar{\mathbf{x }}^*$ using the Taylor series expansion, Eq. (18) is changed as,

$$\begin{aligned}&\omega _0^2 \bar{\mathbf{M }} (\bar{\mathbf{x }}^*+\epsilon )''+\omega _0 \bar{\mathbf{C }} (\bar{\mathbf{x }}^*+\epsilon )'+\omega _0^2 \bar{\mathbf{G }} (\bar{\mathbf{x }}^*+\epsilon )'\nonumber \\&\quad +\bar{\mathbf{K }} (\bar{\mathbf{x }}^*+\epsilon )+\bar{\mathbf{F }}_{nl}(\bar{\mathbf{x }}^*)+\frac{\partial \bar{\mathbf{F }}_{nl} (\bar{\mathbf{x }}^*)}{\partial \bar{\mathbf{x }}} \epsilon = \bar{\mathbf{F }} \end{aligned}$$

(19)

Since $\bar{\mathbf{x }}^*$ is an equilibrium point,

$$\begin{aligned} \omega _0^2 \bar{\mathbf{M }} \bar{\mathbf{x }}^{*''}+\omega _0 \bar{\mathbf{C }} \bar{\mathbf{x }}^{*'}+\omega _0^2 \bar{\mathbf{G }} \bar{\mathbf{x }}^{*'}+\bar{\mathbf{K }} \bar{\mathbf{x }}^*+\bar{\mathbf{F }}_{nl}(\bar{\mathbf{x }}^*)-\bar{\mathbf{F }}= 0 \end{aligned}$$

(20)

Hence, the remaining perturbation equation is written as,

$$\begin{aligned} \omega _0^2 \bar{\mathbf{M }} \epsilon ''+\omega _0 \bar{\mathbf{C }} \epsilon '+\omega _0^2 \bar{\mathbf{G }} \epsilon '+\bar{\mathbf{K }} \epsilon +\frac{\partial \bar{\mathbf{F }}_{nl} (\bar{\mathbf{x }}^*)}{\partial \bar{\mathbf{x }}} \epsilon = 0\nonumber \\ \end{aligned}$$

(21)

According to the Floquet theory, $\epsilon (\tau ) = e^{\lambda \tau } \phi (\tau )$, where $\lambda$ is the eigenvalue and $\phi (\tau )$ is a periodic function. By substituting this expression and its derivatives into Eq. (21), the modified equation is written as,

$$\begin{aligned}&\Big \{\mathbf{[ }\omega _0^2 \bar{\mathbf{M }} \phi \mathbf{] } \lambda ^2 + \mathbf{[ }2\omega _0^2 \bar{\mathbf{M }} \phi ' + \omega _0 \bar{\mathbf{C }} \phi + \omega _0^2 \bar{\mathbf{G }} \phi \mathbf{] } \lambda \nonumber \\&+ \mathbf{[ }\omega _0^2 \bar{\mathbf{M }} \phi ''+\omega _0 \bar{\mathbf{C }} \phi '+\omega _0^2 \bar{\mathbf{G }} \phi '+\bar{\mathbf{K }} \phi +\frac{\partial \bar{\mathbf{F }}_{nl} (\bar{\mathbf{x }}^*)}{\partial \bar{\mathbf{x }}} \phi \mathbf{] }\Big \} \nonumber \\&\qquad e^{\lambda \tau } = 0 \end{aligned}$$

(22)

Now, the periodic function $\phi (\tau )$ is expressed in terms of the basis function as $\phi (\tau )=\hat{\Phi }. \chi (\tau )$. Substitution of this expression into Eq. (22) and following the Galerkin procedure, a quadratic eigenvalue equation is obtained as,

$$\begin{aligned} \begin{aligned}&(\lambda ^2\Xi _2 + \lambda \Xi _1 + \Xi _0 )\hat{\Phi } = 0 \,\, \text {where}\\&\quad \Xi _2 = \omega _0^2 \big (\bar{\mathbf{M }}\otimes \mathbf{D} ^{(0)}\big )\\&\quad \Xi _1 = 2\omega _0^2 \big (\bar{\mathbf{M }}\otimes \mathbf{D} ^{(1)}\big ) + \omega _0 \big (\bar{\mathbf{C }}\otimes \mathbf{D} ^{(0)}\big )\\&\quad + \omega _0^2 \big (\bar{\mathbf{G }}\otimes \mathbf{D} ^{(0)}\big )\\&\quad \Xi _0 = \omega _0 ^2 \big (\bar{\mathbf{M }}\otimes \mathbf{D} ^{(2)}\big )+\omega _0 \big (\bar{\mathbf{C }}\otimes \mathbf{D} ^{(1)}\big )\\&\quad +\omega _0^2 \big (\bar{\mathbf{G }}\otimes \mathbf{D} ^{(1)}\big )+\big (\bar{\mathbf{K }}\otimes \mathbf{D} ^{(0)}\big )+\big (\mathbf{I} \otimes \mathbf{D} ^{(0)}\big ) \frac{\partial \hat{\mathbf{f }}_{nl} }{\partial \hat{\mathbf{x }}} \end{aligned} \end{aligned}$$

(23)

Even though Eq. (23) provides $2 N_p N_{size}$ eigenvalues, only $2 N_{size}$ eigenvalues have physical meaning. Hence, the first $2 N_{size}$ eigenvalues with the smallest imaginary part can be calculated instead of determining the complete set of eigenvalues. The system is stable when real parts of the first $2 N_{size}$ eigenvalues are negative, while it is unstable when at least one of them is positive. The advantage of this method is that all the terms in Eq. (23) are determined during each iteration of the continuation procedure, and hence, the stability analysis can be performed along with the continuation procedure that saves a lot of time.

4 Rotor FE modeling and dynamic analysis

In this study, the two-spool rotor system is completely modeled using one-dimensional finite elements. Mainly, Timoshenko beam elements are used for discretizing the shafts with rotary inertia, shearing and gyroscopic effects are taking into account. Each node is having 4 DOFs: two translational and two rotational displacements. The complete model is discretized into 13 elements with a total of 52 DOFs. Later, its size is reduced using the model reduction technique as explained in the previous section. The component mode partition of the dual-rotor model is shown in Fig. 2, and its details are given in Table 5.

Fig. 2

Component mode partition of the rotor

Table 5 The details of the model reduction of dual-rotor model

Table 6 Natural frequencies of the two-spool rotor model under non-rotating condition

In two-spool rotors, there are two modes of rotor operations possible: co-rotation in which both the rotors spin in the same direction and counter-rotation in which one rotor spins in the opposite direction to the other. In this paper, both the modes of rotor operations are analyzed.

4.1 Co-rotation

In this mode of rotor operation, the rotors are co-rotating with a speed ratio of $\kappa = 1.2$; hence, the approximated excitation frequency components and their common divisor $\omega _0$ can be determined as,

$$\begin{aligned} \frac{\tilde{\omega }_2}{\tilde{\omega }_1}=\frac{6}{5}=1.2 \quad \omega _0=\frac{\tilde{\omega }_1}{5}=\frac{\tilde{\omega }_2}{6} \end{aligned}$$

(24)

Now, by expressing the external excitations in terms of $\omega _0$, the TVM can be utilized for finding the responses. At first, the modal analysis is performed to determine the natural frequencies of the system. The first five natural frequencies of the system under the non-rotating condition are given in Table 6. However, for a rotating system, the natural frequencies vary with the rotor speed due to the presence of the gyroscopic effect. This variation is displayed through the Campbell diagram. Figure 3a, b shows the Campbell diagrams of the two-spool rotor system when excited by the inner and outer rotors, respectively. Due to the presence of gyroscopic effects, the whirl frequencies split into forward and backward whirls. The critical speeds of the system are obtained by noting the rotational speeds at the crossing points of the frequency curves with the synchronous excitation line (1x). They are listed in Table 7. For each mode of vibration, there are two critical speeds corresponding to the forward and the backward whirl motions as listed in Table 7.

Fig. 3

Campbell diagram of the two-spool rotor model (co-rotation)

Table 7 Critical speeds of the two-spool rotor model (co-rotation)

4.2 Counter-rotation

In this mode of rotor operation, one rotor rotates in the opposite direction to the other with a speed ratio of $\kappa = -1.2$. The approximated excitation frequency components and their common divisor $\omega _0$ can be determined as,

$$\begin{aligned} \frac{\tilde{\omega }_2}{\tilde{\omega }_1}=-\frac{6}{5}=-1.2 \quad \omega _0=\frac{\tilde{\omega }_1}{5}=-\frac{\tilde{\omega }_2}{6} \end{aligned}$$

(25)

The Campbell diagrams for this mode of operation are shown in Fig. 4, and the corresponding critical speeds are listed in Table 8. While comparing the critical speeds of the co- and counter-rotating systems, it is observed that the forward speeds are smaller and backward speeds are larger for the counter-rotating system. It means that the separation between the forward and backward speeds are reduced. This behavior can be seen in the Campbell diagrams as well where the forward and backward speeds are close to each other for the counter-rotating system compared to the co-rotating system. This happens mainly due to the cancellation of the gyroscopic moments of the two rotors during the counter-rotation.

Figures 3 and 4 also give a comparison of the Campbell diagrams of the complete and the reduced models. It shows the effectiveness of the model reduction technique. A perfect matching is observed between the results of both models.

4.3 Unbalance response

The presence of mass unbalances in disks 1 and 3 produces centrifugal forces in the rotors that will lead to rotor whirling during their operation. Initially, by assuming no stationary components in the system, it is possible to study the nature of whirling and the frequency contents in it. Since both the rotors are excited together, the system response will contain both of the frequency components. In this paper, the TVM is used for determining the unbalance responses under two-frequency excitation. The number of discrete-time points $N_p$ is taken as 200. In order to validate its performance, the system response is compared with that of the MHBM-AFT. Figure 5 shows the unbalance responses of the inner rotor at disk 2 position under two-frequency excitations. A good agreement is observed between the results of the TVM and MHBM.

Fig. 4

Campbell diagram of the dual-rotor model (counter-rotation)

Table 8 Critical speeds of the dual-rotor model (counter-rotation)

Fig. 5

The response of the inner rotor at disk 2 position when mass unbalances are at disk 1 and 3

Figure 5a, b shows the unbalance responses during co-rotation and counter-rotation, respectively. Only forward whirling modes are excited since all the bearings used in the model are symmetric in nature. The peaks A and C represent the resonance when the rotating speed is equal to $\frac{1}{1.2}$ times the critical speeds of the model with respect to the outer rotor excitations. The peaks B and D correspond to the resonance when the rotating speed becomes equal to the critical speeds of the model with respect to the inner rotor excitation.

Fig. 6

Orbit plot and the FFT of the rotor displacements during co-rotation of rotors

In order to analyze the whirling nature and the frequency content, the orbit plot and the FFT diagrams are constructed for different rotating speeds of the rotors. Due to the lack of space, the responses at some of the rotating speeds are discussed. Figures 6 and 7 show the orbit plots and the FFT diagrams during the co- and counter-rotation of the rotors, respectively. In Figs. 6 and 7, the FFTs are plotted for the vertical responses measured at disk 2 position. It is observed that the rotor response contains the combinations of the inner and outer rotor excitations. Generally, the linear combinations of the inner and outer rotor excitations are expressed as $i \omega _1 + j \omega _2$. For simplicity, it can be denoted using (i, j), where i and j are integers. Since the unbalance response is linear, (1,0) and (0,1) components are observed in the rotor displacements as shown in Figs. 6 and 7. The direction of the rotor whirl can be obtained from the orbit plot. It is seen that during co-rotation, the inner and outer rotors (disk 2 and disk 4) whirls in the same direction as the rotor rotation (in an anti-clockwise direction) for all the values of rotating speeds. However, during counter-rotation, the whirling nature of the rotors is different at different rotating speeds. It can be observed from Fig. 7a, c that when the rotating speed lies in the region of resonance with respect to the outer rotor excitation, both rotors whirl in the same spin direction as the outer rotor, i.e., in the clockwise direction. But, when the rotor speed is in the region of resonance with respect to the inner rotor excitation, both rotors whirl in the same spin direction as the inner rotor, i.e., in an anti-clockwise direction, as shown in Fig. 7b. It indicates that the direction of whirling is dependent on the value of rotating speed when the rotors are counter-rotating.

Fig. 7

Orbit plot and the FFT of the rotor displacements during counter-rotation of rotors

5 Validation of the methodology using experimental results

In order to verify the proposed methodology in nonlinear rub analysis, a dual-rotor system from ref. [2] is analyzed. Using the proposed technique, a dynamic model of the given rotor system is developed and its results are compared with that of the numerical and experimental investigations from Ref. [2]. The details of model parameters are given in Ref. [2]. The Timoshenko beam elements are utilized for developing the FE models of the low pressure (LP) and high pressure (HP) shafts. A fixed elastic limiter is used as the stator representing the convex protuberance on the casing. The disk and the fixed limiter are applied with softer coatings and several local contacts happen during the orbital motion. Hence, a Lankarani–Nikravesh model is employed to obtain the contact force generated between the compressor disk and the fixed limiter. In ref. [2], the numerical integration technique is used to acquire the rubbing response, whereas, in the present study, the TVM is utilized. As a result, the computation time is significantly reduced since the TVM provides the steady-state response directly.

Initially, the linear response of the system without a rub-impact is studied. Figures 8 and 9 show the comparison of the results of the present study with the numerical and experimental results from ref. [2]. From Figs. 8 and 9, it is clear that the numerical results of the present study are well matched with numerical and experimental results from ref. [2].

Fig. 8

Vertical vibration of the LP compressor disk at $\omega _1=216.8$ rad/s and $\kappa = 1.2$ a present study b numerical study from ref. [2]

Fig. 9

Vertical vibration of the LP compressor disk at $\omega _1=252.6$ rad/s and $\omega _2=301.2$ rad/s a present study b experiment from ref. [2]

Once rub-impact happens, the system response becomes nonlinear and different combinations of excitation frequencies can be seen in the frequency spectrum. Figure 10 shows the comparison of the frequency spectra obtained from the present study and ref. [2]. A clear agreement is obtained between the numerical results of the present study and ref. [2]. However, a slight variation is observed with the experimental results. The frequency dispersion that is observed in the experimental result is not obtained in the numerical results. Still, the amplitudes and frequencies of both results have good matching.

Fig. 10

Frequency spectra of the LP compressor disk displacement at $\omega _1 = 184.1$ rad/s after rub-impact a present study b numerical study from ref. [2] c experimental study from ref. [2]

Fig. 11

Response at disk 2 position when rotors are co-rotating

Fig. 12

Response at disk 2 position when rotors are counter-rotating

Fig. 13

Response at disk 4 position when rotors are co-rotating

Fig. 14

Response at disk 4 position when rotors are counter-rotating

Fig. 15

Orbit plot and the FFT of the rotor displacements during co-rotation of rotors (after rub-impact)

Fig. 16

Orbit plot and the FFT of the rotor displacements during counter-rotation of rotors (after rub-impact)

The comparison study in this section clearly ensures the validity of the proposed methodology. Hence, it is employed for the nonlinear dynamic analysis of the two-spool rotor system undergoing rub-impact. It is explained in the following section.

6 Rub-impact in the two-spool rotor system

As the whirling amplitude of the rotor exceeds the clearance at disk 2 position, it contacts the stator during a rotor orbit. As a result, the nature of the rotor response changes significantly. In order to study this nonlinear behavior, The TVM is employed by taking the number of discrete time points $N_p$ as 300. Figures 11 and 12 show the rubbing responses of the rotor at disk 2 position when it is undergoing co-rotation and counter-rotation, respectively. The system parameters are taken as $k_c$ = 5 $\times$ $10^6$ N/m, $\delta$ = 0.1 mm and $\mu$ = 0.01. As the rotor touches the stator, a rightward bending is observed along with a resonance shift which is happening mainly due to the addition of contact stiffness. In a speed range of [0,15000] rpm, four contact regions are noticed in the response which are zoomed in Figs. 11 and 12. When rotors are co-rotating, the initial contact happened at $\omega _1$ = 6096.3 rpm, whereas for the counter-rotation, it happened at $\omega _1$ = 3882 rpm. It indicates that for the same set of system parameters, the counter-rotating system undergoes early rub-impact. This is due to the lower critical speeds of the counter-rotating system compared to the co-rotating system. The validation of the TVM with the MHBM-AFT is also displayed in Figs. 11 and 12. The MHBM-AFT technique is utilized by taking the number of harmonics as 5. A good agreement is obtained between the results of both methods.

In order to verify the coupling of the inner and outer rotor vibrations, the responses are determined at the disk 4 position as well. They are shown in Figs. 13 and 14. It is observed that the outer rotor also experiences a similar kind of rightward bending as the inner rotor, even though it doesn’t undergo any rub-impact. It shows the coupling of the inner and outer rotor vibrations which is mainly occurring due to the presence of the inter-shaft bearing. Moreover, it is also noticed that the amplitude of the outer rotor response is slightly larger than that of the inner rotor.

Figures 15 and 16 show the orbit plots and FFT diagrams of the co- and counter-rotating systems during rub-impact. They are determined at certain rotational speeds that are marked as points a, b and c in Figs. 11 and 12. These diagrams will help to understand the motion types and frequency contents in the response during rub-impact. It is observed that both the rotors are orbiting in a circular path and are exceeding the clearance space, indicating the synchronous full annular rub at disk 2. While noticing the FFT diagrams, it is found that in addition to (1,0) and (0,1) components, other components such as (1,-2), (2,-1), (2,-3) and (3,-2) are also seen in the response. However, their amplitudes are very small compared to that of the excitation frequency components (1,0) and (0,1). The additional components are appearing mainly due to the presence of nonlinearities, induced as a result of rub. More details of the post-rub effects will be obtained after performing the stability analysis and parametric analysis. They are discussed in the next sections.

7 Stability analysis

The stability analysis of the synchronous full annular rub response is performed using the theory as described in Sect. 3.3. In this analysis, the system is slightly perturbed from the steady-state solution point and the eigenvalues of the perturbed system are determined. The system is said to be stable when the real parts of the first $2N_{size}$ eigenvalues are negative. Figure 17 shows the stability diagrams of the rub-impact regions during co-rotation. Since the non-contact region is always stable, it isn’t displayed in the stability diagram. In Fig. 17, the stable part is represented using the continuous line, whereas the unstable part is represented using the dotted line. The bifurcations appearing in the system are determined by monitoring the Floquet exponents. The first $2N_{size}$ eigenvalues of the perturbed system become equal to the Floquet exponents when a sufficient number of time points $N_p$ are taken for the TVM during the stability analysis. Two types of bifurcations, namely limit point (LP) and Neimark–Sacker (NS) bifurcations, are observed in the response and are denoted using circle and triangle markers, respectively. An LP bifurcation is detected when at least one of the Floquet exponents crosses the imaginary axis of the complex plane along the real axis, whereas the NS bifurcation is identified when a pair of Floquet exponents crosses the imaginary axis as a pair of complex conjugates [24, 25]. The NS bifurcation indicates a transition from periodic to the quasi-periodic regime, whereas the LP bifurcation points out a sudden jump phenomenon.

Fig. 17

Stability analysis of the synchronous rub response when rotors are co-rotating

Figure 18 shows the real parts of the eigenvalues during the first two rub-impact regions. The speed at which the real parts became positive is indicated in Fig. 18 with its amplitude. It actually happened at $\omega _1$ = 6263.3 rpm and the response is stable until this particular speed. An NS bifurcation is detected at $\omega _1$ = 6263.3 rpm by monitoring the Floquet exponents of the system. Figure 19a shows the Floquet exponents of the system before and after NS bifurcation. It is seen that a pair of Floquet exponents crossed the imaginary axis as a pair of complex conjugates that confirms the occurrence of NS bifurcation at $\omega _1$ = 6263.3 rpm. As a result, a quasi-periodic regime can be initiated from this bifurcation point. However, the proposed methodology is unable to capture the quasi-periodic regime, since the quasi-periodicity contains the irrational frequency components that are unknown. As the speed is increased, the periodic response becomes unstable and it is shown by the dotted line in Fig. 17. At $\omega _1$ = 6596 rpm, an LP bifurcation is identified which indicates the presence of a sudden jump phenomenon. In order to verify this, the Floquet exponents are determined and displayed in Fig. 19b. It is observed that one of the Floquet exponents crossed the imaginary axis along the real axis. It confirms the occurrence of LP bifurcation at $\omega _1$ = 6596 rpm. At this speed, the quasi-periodic regime also coexists, that is the reason for seeing a pair of Floquet exponents crossing the imaginary axis as a pair of complex conjugates in Fig. 19b. Similar to the first peak, the NS and LP bifurcations are observed for the other peaks as well. It should also be noted that the orbit plots and FFT diagrams that are shown in Fig. 15 are stable, periodic responses.

Fig. 18

Real parts of the eigenvalues during the first two rub-impact regions (co-rotation)

Fig. 19

Floquet exponents in the vicinity of NS and LP bifurcations (co-rotation)

The stability analysis is performed for the counter-rotating system as well. It is shown in Fig. 20. The periodic response became unstable when the rotational speed reached $\omega _1$ = 3883.3 rpm. It is visible from Fig. 21 in which the real parts of the eigenvalues are plotted against the rotor speed. An NS bifurcation is detected at $\omega _1$ = 3883.3 rpm and the response became unstable during the remaining contact period. It should be noted that the orbit plots and FFT diagrams displayed in Fig. 16 represent the unstable, periodic response. As the speed is increased, an LP bifurcation is identified at $\omega _1$ = 4130.6 rpm and a sudden jump phenomenon can happen at this speed. The Floquet exponents in the vicinity of the NS and LP bifurcations are shown in Fig. 22 and it verifies the occurrence of the NS and LP bifurcations. For the other peaks as well, the system became unstable immediately after the contact. Hence it can be stated that for the same set of system parameters, the NS bifurcation and the onset of the quasi-periodic regime are happening early for the counter-rotation.

Fig. 20

Stability analysis of the synchronous rub response when rotors are counter-rotating

Fig. 21

Real parts of the eigenvalues during the first two rub-impact regions (counter-rotation)

Fig. 22

Floquet exponents in the vicinity of NS and LP bifurcations (counter-rotation)

During co-rotation, two additional small peaks are observed in the response between 10885-10892 rpm and 11038-11043 rpm. They are analyzed using the stability diagrams, FFT spectra and orbit plots. In Fig. 23, the orbit plots and FFT diagrams are determined at the stable regions of the response, marked as points a and b. While observing the frequency components, it is seen that an additional (2,-1) component is also present in the response besides (1,0) and (0,1) components. Due to the presence of this frequency component, two additional peaks are appearing in the response. Since the damping in the model is very low, the (2,-1) component also dominates in the response along with the excitation frequency components. Some other frequency components are also existing in the frequency spectrum; however, their effects are not visible due to their low amplitudes. From the orbit plots, it is seen that the rotors are whirling in multiple orbits and they are moving in and out of the clearance space. It also indicates the presence of multiple frequency components in the response. During this motion, the rub-impact happens occasionally, indicating the partial rub.

Fig. 23

Stability diagram, FFT spectrum and orbit plot of the two additional small peaks

In order to understand more about these small peaks, they are analyzed by varying the coefficient of friction and contact stiffness, as shown in Fig. 24. The coefficient of friction is varied between 0.1 and 0.5, while the contact stiffness is varied between $1 \times 10^6$ N/m and $10 \times 10^6$ N/m. It is observed that when the coefficient of friction is increased, the amplitudes of the peaks are diminishing. It indicates that the magnitude of (2,-1) component is reducing as the value of $\mu$ is increased. However, when the contact stiffness is increased, the peaks are becoming more visible and they diminish for smaller values of the contact stiffness. As a result, it can be stated that the small peaks are appearing due to the (2,-1) frequency component and are more visible when the coefficient of friction is low and contact stiffness is high.

Fig. 24

Variations in the small peaks when the coefficient of friction and contact stiffness are changed

8 Parametric analysis

In order to understand the effect of different rub parameters such as coefficient of friction, rotor–stator contact stiffness and clearance on the stability of the rubbing responses, a parametric analysis is conducted. The response curves are plotted for different values of a parameter by keeping the others constant. The bifurcation points are detected for each set of rub parameters and are compared in this section. It is also noted that the damping values of all the bearings are increased to 1000 Ns/m in order to get visible variations in the stability. This is due to the fact that for the small damping values such as 100 Ns/m, the rubbing responses were mostly unstable during counter-rotation, even for small values of the friction coefficient as seen in Fig. 20. Hence, it won’t be possible to understand the variations in the stability with respect to the parameters.

8.1 Effect of coefficient of friction

The influence of rotor–stator interface friction on the rubbing response is investigated by varying the coefficient of friction. Other parameters such as contact stiffness ($k_c$ = 5$\times$ $10^6$ N/m) and clearance ($\delta$ = 0.1 mm) are kept as constants during the analysis. Figure 25 shows the variations in the onset of NS bifurcations when rotors are co-rotating. The first two resonant peaks are only displayed because the other peaks occupy within the clearance space due to the increased damping. It is observed that the range of rightward bending is shortened as the coefficient of friction is increased. This may due to the increased friction losses happening due to the increased resistance. Significant variations are observed in the stability when $\mu$ is increased from 0.05 to 0.2. For $\mu = 0.05$ and 0.08, the NS bifurcation is not at all occurring in the first peak, however, it is happened to occur as the $\mu$ is increased. The NS bifurcation is detected at $\omega _1$= 6171 rpm for $\mu$ = 0.1, whereas it is identified at $\omega _1$= 6113 rpm for $\mu$ = 0.2. It indicates that the onset points of NS bifurcation are happening early as the coefficient of friction is increased. It is represented using an arrow mark in Fig. 25, pointing the direction of NS bifurcation as $\mu$ is increased.

The variations in the onset of NS bifurcation during counter-rotation are shown in Fig. 26. In the case of counter-rotation, the values of the coefficient of friction are taken smaller compared to the co-rotation, because the rubbing responses are mostly unstable for larger values of the coefficient of friction. Hence, there won’t be any visible variations in the stability when the coefficient of friction is changed. As a result, the $\mu$ is varied in the range of 0.001 and 0.05. While analyzing Fig. 26, it is noticed that the system response shows similar nature as the co-rotation. The onset points of NS bifurcation are happening early when $\mu$ is increased.

Fig. 25

Variations in the onset of NS bifurcation when the coefficient of friction is increased (co-rotation)

Fig. 26

Variations in the onset of NS bifurcation when the coefficient of friction is increased (counter-rotation)

In order to verify whether any changes are happening in the frequency contents during the variation of coefficient of friction, the FFT diagrams are plotted. Figure 27 shows the comparison of frequency components for the two different values of $\mu$. By observing Fig. 27, it is seen that the same frequency components are present in the responses for both values of $\mu$.

Fig. 27

Comparison of the FFT’s of the rotor responses for two different values of $\mu$

8.2 Effect of rotor–stator contact stiffness

The effect of contact stiffness on the response is analyzed by varying the value of $k_c$. Figures 28 and 29 show the variations in the rubbing responses for different values of contact stiffness. From Figs. 28 and 29, it is observed that the extent of rightward bending is increased as the value of $k_c$ is increased. It indicates that the stator with hard surfaces is suppressing the whirling amplitude. Moreover, the onset of NS bifurcation points is getting delayed as the contact stiffness is increased. It is shown by the direction of arrow in Figs. 28 and 29. This nature is the same for both co- and counter-rotations.

Fig. 28

Variations in the onset of NS bifurcation when the contact stiffness is increased (co-rotation)

Fig. 29

Variations in the onset of NS bifurcation when the contact stiffness is increased (counter-rotation)

The frequency contents in the responses for different values of $k_c$ are compared using the FFT diagrams. Figure 30 shows the comparison plot for $k_c = 3 \times 10^6$ N/m and $k_c = 10 \times 10^6$ N/m at different rotating speeds. It is observed that the responses contain similar frequency components for both values of $k_c$ with a slight difference in their amplitudes.

Fig. 30

Comparison of the FFT’s of the rotor responses for $k_c = 3 \times 10^6$ N/m and $k_c = 10 \times 10^6$ N/m

8.3 Effect of clearance

The clearance between disk 2 and its stator is varied and the corresponding response behavior is plotted as shown in Figs. 31 and 32. It is observed that the range of rightward bending is shortened as the clearance is increased. Moreover, for both co-rotation and counter-rotation, the onset of NS bifurcation points is delayed when the clearance between rotor and stator is increased. Major portion of the rubbing responses are stable for large clearances as seen in Figs. 31 and 32.

Fig. 31

Variations in the onset of NS bifurcation when the clearance is increased (co-rotation)

Fig. 32

Variations in the onset of NS bifurcation when the clearance is increased (counter-rotation)

9 Conclusion

In this paper, the stability analysis of a two-spool rotor system undergoing rub-impact is performed. The TVM is used to obtain the steady-state, periodic responses of the system. The main advantage of the TVM is that it doesn’t require alternate transformations between the frequency and time domains during the calculation of the nonlinear Jacobian matrix, as compared to the MHBM-AFT method. It helped in determining the nonlinear force and the Jacobian matrix directly from the displacement vector since all the variables are expressed in the time domain.

The analysis is carried out by developing a one dimensional FE model of a dual-rotor system using the Timoshenko beam elements. Later, its size is reduced using an efficient model reduction technique based on component mode synthesis. In this technique, the whole system is categorized into two components, namely primary and secondary components. All the nonlinear DOFs along with their boundary DOFs are included in the primary component whereas the remaining linear DOFs are assembled in the secondary component. This technique helped to reduce the computational time by executing the analysis only on the nonlinear DOFs. The accuracy of the reduced model is checked with that of the complete model by comparing the Campbell diagrams. Good matching is obtained which indicates that the reduced model is accurate enough.

Two modes of rotor operations, namely co-rotation and counter-rotation, are included in the analysis to study their effects on the response behavior. The Campbell diagrams and the unbalance responses of the dual-rotor model are determined for both modes of rotor operations. From the Campbell diagrams, it is observed that the critical speeds are different for both co- and counter-rotations. For counter-rotation, the forward critical speeds are smaller, and backward critical speeds are larger compared to that of co-rotation. This is mainly due to the cancellation of the gyroscopic moments in the case of counter-rotation. Moreover, during the counter-rotation, the direction of whirling is dependent on the value of rotating speed. When the rotating speed is in the range of resonance with respect to the outer rotor excitation, both the rotors whirled in the same spin direction as the outer rotor, whereas when the speed is in the range of resonance with respect to the inner rotor excitation, both the rotors whirled in the same spin direction as the inner rotor. However, during the co-rotation, the whirling always happens in one direction irrespective of the rotating speed.

When contact is initiated, a rightward bending of the response curve is observed as it touches the stator. Due to the presence of inter-shaft bearing, the coupling of the inner and outer rotor vibrations have happened. As a result, the outer rotor also showed a similar rightward bending, although it didn’t undergo any rub-impact. The stability of each solution point is assessed using a technique based on the Floquet theory. A hyper-sphere based continuation algorithm is used to obtain the response beyond the bifurcation points. The Floquet exponents are monitored during the continuation procedure in order to detect the bifurcation points. Mainly, LP and NS bifurcations are observed in the responses when the rotor touched the stator. It is observed that the direction of rotor rotation has a significant effect on the onset of NS bifurcation. For the same set of system parameters, the onset of NS bifurcation happened early for the counter-rotating system compared to the co-rotating system.

Finally, a parametric analysis is conducted to investigate the effect of different rub parameters on the rubbing response. The parameters such as the coefficient of friction, rotor–stator contact stiffness and clearance are varied individually by keeping the others constant. It is found that when the coefficient of friction is increased, the range of rightward leaning is shortened. In addition, the early onset of NS bifurcation is observed as the co-efficient of friction is increased. However, when the contact stiffness is increased, the rightward bending of the response is increased and the onset of NS bifurcation is delayed. For clearance as well, the onset of NS bifurcation is delayed as the gap between rotor and stator is increased.