Train-structure interaction for high-speed trains using a full 3D train model

Abstract

In high-speed trains, the driving safety and passenger comfort of the railway vehicle are negatively affected due to the problem of interaction between the train and the bridge. Among these problems are rail irregularities, flexible foundation effect, and external effects such as wind load and seismic loads. In this study, the dynamic interaction between the full train model modeled as 31-degrees of freedom and the bridge that can be modeled according to the Euler–Bernoulli beam theory was studied. The motion equations of the train and bridge beams have been derived with the Lagrange method, and the motion equations obtained have been solved with the fourth-degree Runge–Kutta method. The results obtained in this method were confirmed by two case studies previously conducted. The first four natural frequencies of the beam calculated using bridge parameters were determined, and the resonance velocities, which are the critical velocities of the beam-train system corresponding to this determined frequency, were calculated. Moving at resonance velocities, the train causes maximum acceleration amplitudes, especially in low damped beams. In this study, maximum dynamic responses were determined at variable velocities of the train, and it was understood that critical velocities were an essential concept in train-bridge interaction. It has also been found that well-damped beams reduce maximum dynamic responses. As a result, it was found that car body mass, bridge length, and train velocity significantly affect the combined train–bridge dynamic interaction.

1 Introduction

With the development of the use of high-speed trains, the research in this area is rapidly increasing. Today, high-speed trains are preferred for faster transportation. Researchers are working on the rail system vehicles that reach higher velocities to shorten the transportation time. The velocity of the high-speed train on the 4072 km long Shinkansen line in Japan was measured as 320 km/h. The longest high-speed train line in the world is located in China with 30,000 km, and this train can go up to 400 km/h. The highest velocity in history is maglev trains with 603 km/h in Japan using magnetic levitation technology [1]. While these increased velocities provide a significant advantage in reducing travel times, there are also disadvantages brought about by high velocities.

The most important of these disadvantages is vibration. Vibrations adversely affect passenger comfort and transportation safety. Train vibrations originating from the ground are the leading type. At the same time, ground vibration creates noise and damages the surrounding structures [2]. Another example of ground-based vibration is rail irregularities. Due to the wear of the rail profile on the railway lines, contact problems occur between the rail and the wheel [3, 4]. While these ground-based vibrations affect passenger comfort more, external vibrations threaten both comfort and driving safety. Wind and earthquake effects can be shown as external vibrations. The high-speed train's exposure to strong winds with a velocity of more than 25 m/s during bridge crossings creates a gravely serious safety concern [5]. Therefore, wind barriers are usually installed in windy areas to ensure the driving safety of high-speed trains [6, 7]. In addition, since railway bridges are located on highly long columns, it creates excessive vibrations in a possible earthquake, and there is the risk of the derailment of the train [8, 9]. High-speed trains derailed and crashed during the Kaohsiung earthquake in Taiwan in 2010 and the Niigata earthquake in Japan in 2014 [10].

Several studies have been conducted on the interaction between railway bridges and trains. The trains and bridges can be considered as independent systems. Railway bridges can be modeled as a beam. There are Euler–Bernoulli, Timoshenko, Rayleigh, and Shear beam theories in the literature [11, 12]. Timoshenko beam model is preferred in studies examining the shear deformation, bending deformation, linear and rotary inertia effect of beams [13,14,15,16]. Euler–Bernoulli [17] beam model is preferred when parameters such as shear deformation and rotary inertia effect are not taken into account, and the beam height is negligible compared to the beam length. In his study, Esen conducted the vibration analysis of the Timoshenko beam, which was simply supported on a two-parameter ground, using the finite element method [18]. Within the scope of Euler–Bernoulli beam theory, Chen et al. [19] examined high-frequency vibration analysis of beams exposed to axial force. In another study, lateral vibrations of beams under the influence of rotational motion were examined [20]. In the literature, the Euler–Bernoulli beam model is used for beams forced to random dynamic loading, except for axial and rotational forces [21]. The force applied by the railway vehicle passing over the bridge beam, which will be examined within the scope of this study, is assumed to be the moving load. Dynamic analysis of Euler–Bernoulli beams exposed to moving loads was performed using an isogeometric approach [22]. The isogeometric approach has been expressed as a robust and reliable tool for simulating and solving related engineering problems. Dixit used Euler–Bernoulli and Timoshenko beam theories to compare the dynamic response of damaged beams and compared their results with each other [23]. As a result, he found that the Timoshenko beam theory gave better results in determining the dynamic response since it includes shear deformation and rotary inertia effect compared to the Euler–Bernoulli beam theory. Heydari et al. examined forced bending vibration analysis for damaged short beams and used the Timoshenko beam as a beam model. They compared the results they obtained with the Euler–Bernoulli model. Their study showed that the Timoshenko beam model is more advantageous for use in short beams [24].

In order to model railway vehicles, (TBI)s are taken with a high degrees of freedom (DOF). The simplest known vehicle model is a 2-DOFs spring damping system consisting of only the vehicle body and the wheel [25]. However, this (DOFs) model is not adequate for numerical solutions. Train models can also be modeled as a quarter, half, or full models for ease of application. Mızrak and Esen [26], using numerical and experimental methods, examined the dynamic effects of wagon mass and train velocity on a quarter railway vehicle model with 5-DOFs consisting of a car body, bogie, and two wheelsets. There are also 6-DOFs models obtained by adding seats to the quarter railway vehicle model [27]. Wang et al. [28] analyzed the half-railway vehicle model consisting of two bogies, four wheelsets, and the car body using FEM for train-track analysis. In order to get more accurate results by considering all factors in the train model, the 3-D full train model is used [29]. In the full train model, lateral displacements, roll, and yaw movements can also be examined. Zhu et al. controlled the lateral displacement of the 17-degrees full railway vehicle using active suspension systems for the ride quality of the trains [30]. In the study [5], the authors have been modeled 27-DOFs full railway vehicle model with 2-bogies and 4-axles and bridge structure to investigate the effect of the wind action upon railway vehicle dynamic in time domain using computer simulation and studied running safety, stability of the train vehicles. The study [31] investigates that non-stationary random vibration of 3D time-dependent train-bridge systems subjected to multi-point earthquake excitations, including wave passage effect, is investigated using the pseudo-excitation method 27-DOFs full vehicle model. On the other hand, in the study [32], train-bridge coupled vibration system has been investigated random dynamic responses of the 3D train-bridge coupled system with random parameters, including parameters of the bridge materials.

Analytical and numerical methods are available in previous studies for train-bridge interaction (TBI). The finite element method (FEM) is the most common numerical method. Both train and bridge can usually be modeled using FEM. In addition, the Mode superposition method [33, 34] and Newmark β method [35] can also be used to figure out the motion equations of the combined train-bridge model. However, it should be considered that the time step size used for the analysis of train rail movement in these methods increases the solution time and the required computer memory.

Most of the studies given in above generally include low-speed vehicles, simple vehicle, and simple bridge models, whereas the high and very high-speed train has been grooving up worldwide, and there is no satisfying study to explain the interaction between these railway vehicles and structures on which railway vehicles are moving. The organizations that are likely to do this study do not present their studies because of privacy and know-how. In this study, as can see Fig. 1, the interaction between a 3-D complex railway vehicle with 31-DOFs to be considered moving at high-speeds and bridge has been modeled, and the analysis result is investigated for different velocity and different system parameters according to the presented theory which is not implemented to full train and bridge interaction problem before.

Fig. 1

Schematic illustration of TBI system

In the analysis results, the dynamic behavior of the railway vehicle body has been investigated in detail in terms of vibration amplitude of acceleration considering interval of the train velocity 2–200 m/s and the dynamic transverse displacement of the bridge is presented. Significantly, the time-dependent dynamic contact forces, which are very important in train bridge interaction, have been investigated, and analysis results are given in the study. Furthermore, the vibration responses of the high-speed train body and bogies have been analyzed in two axes, and the analysis results are presented. The effect of the bridge span length in the dynamic interaction has been investigated, and the results are examined. The novelty of the presented study, unlike the other studies given in above, the dynamic equation of motion of the interaction between the 31-DOF full railway vehicle and bridge substructure has been obtained using Lagrange equation then, the equation of motion of the entire system has been transformed to state-space form with the state variables, and finally, for the solution of the equation of the motion, fourth-order Runge–Kutta algorithm has been used in the time domain, and some critical parameters which affect railway vehicle and bridge dynamics such as railway vehicle body mass, vehicle velocity, bridge span length, and contact forces have been investigated in detail.

2 Mathematical modeling of train and bridge

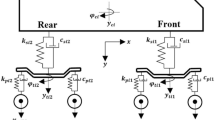
In Fig. 2, to model the TBI, the bridge beam can be modeled according to the simply supported Euler–Bernoulli beam theorem and the full train model moving with a constant velocity of 31-DOFs are shown.

Fig. 2

Mathematical model of railway vehicle and bridge a side view, b top view and c front view

In Fig. 1, the simply supported Euler–Bernoulli beam model and the train bridge interaction for the train model are explained with a drawing. Train model consists of the car body, front bogie, rear bogie, and wheelsets. The parameters of the train and bridge model seen in Fig. 2 are given in Table 1. In this study, the direction of movement of the train was chosen along the x-axis. All vertical displacements are shown along the y-axis, while lateral displacements are shown along the z-axis.

Table 1 The parameters of full high-speed train and bridge models

In Fig. 2, the displacement and rotation movements are represented as r₁₂ and Ө₁₂, respectively. Here, the first index represents the train parts such as the car body, the bogies, and the wheel, and the second index represents the direction of the train parts, such as x, y, z. r_cy shows the vertical displacement of the car body, while r_cz shows the lateral displacement of the car body. r_b1y, r_b1z, r_b2y, and r_b2z represent the vertical displacement of the front bogie, lateral displacement of the front bogie, vertical displacement of the rear bogie, and lateral displacement of the rear bogie, respectively. The vertical displacement of the wheelsets of the front bogie is defined as r_w1y, r_w2y, the lateral displacement is determined as r_w1z, r_w2z, the vertical displacement of the rear bogie wheelset is defined as r_w3y, r_w4y, and its lateral displacement is defined as r_w3z, r_w4z.

The train’s rolling, pitching and yawing movement is assumed to be around the x-axis, z-axis, and y-axis, respectively. The pitching is of the car body, the front bogie and the rear bogie are shown as Ө_cz, Ө_b1z ve Ө_b2z, respectively. The rolling motion of the car body, the front bogie, the rear bogie, and the wheelsets are shown as Ө_cx, Ө_b1x, Ө_b2x, ve Ө_wx, respectively. The yawing movement of the car body, the front bogie, the rear bogie, and the wheelsets are shown as Ө_cy, Ө_b1y, Ө_b2y, ve Ө_wy, respectively.

m_c, m_b1, m_b2, and m_w parameters represent the car body mass, front bogie mass, rear bogie mass, and wheel mass, respectively. The parameters I_cz, I_b1z, I_b2z represent the mass moment of inertia around the pitch motion of the car body, the front body, and the rear body, respectively. I_cx, I_b1x, I_b2x, I_wx correspond to the mass moment of inertia around the roll motion of the car body, the front body and the rear body, and wheelsets, respectively. Similarly, I_cy, I_b1y, I_b2y, I_wy define the mass moment of inertia around the yaw motion of the car body, the front body and the rear body, and wheelsets, respectively. The distances l_b1, l_b2 represent the distance between the car body center of mass and the front bogie center of mass and the distance between the car body center of mass and the rear body of mass. The distances l_w1 and l_w2 represent the distance of the front wheel to the center of the bogie mass and the distance of the rear wheel to the center of the bogie. Likewise, distances l_w3, l_w4 represent the distance of the front wheel to the center of the rear bogie mass and the distance of the rear wheel to the center of the rear bogie, respectively. While the parameters k_w1y, k_w2y, k_w3y, and k_w4y represent the suspension spring coefficient in the y-axis, between each bogie and wheels, respectively. The parameters k_w1z, k_w2z, k_w3z, and k_w4z represent the suspension spring coefficient in the z-axis.

Similarly, while the parameters c_w1y, c_w2y, c_w3y, and c_w4y correspond to the suspension damping coefficient in the y-axis, the parameters c_w1z, c_w2z, c_w3z, and c_w4z correspond to the damping coefficient of the suspension in the z-axis. In addition, whereas the parameters k_b1y and k_b2y represent the suspension spring coefficient in the y-direction, between the front and rear bogie and car body. The parameters c_b1y and c_b2y represent the suspension damping coefficient. Likewise, whereas the parameter k_b1z and k_b2z represent the suspension spring coefficient in the z-direction, the parameters c_b1z and c_b2z represent the damping coefficient of the suspension in the z-axis. The vertical movement of the bridge, w_b(x,t), represents the displacement of any x point of the bridge beam at any t time, with reference to the point where the train enters the bridge. v represents the movement of the train at a constant velocity from left to right of the bridge beam. The following assumptions have been accepted for the TBI analysis.

• The bridge is modeled as a simply supported beam according to Euler–Bernoulli beam theory.

• The railway vehicle is modeled with 31-DOFs.

• Only one vehicle passes over the bridge at constant velocity v.

• Train wheels are always in contact with the bridge beam and do not jump.

• The rigidity of the rail subsystem has been added to the rigidity of the flexible bridge structure used in the study.

With these assumptions, the kinetic and potential energies of the TBI seen in Fig. 2 are given in the equations below:

$$E_{k} = \frac{1}{2}\left[ \begin{gathered} \int\limits_{0}^{L} {\mu_{R} \left[ {\dot{w}_{R,b}^{2} \left( {x,t} \right)} \right]{\text{d}}x + } \int\limits_{0}^{L} {\mu_{L} \left[ {\dot{w}_{L,b}^{2} \left( {x,t} \right)} \right]{\text{d}}x} + m_{c} \dot{r}_{cy}^{2} + m_{c} \dot{r}_{cz}^{2} + I_{cz} \dot{\theta }_{cz}^{2} + I_{cx} \dot{\theta }_{cx}^{2} + I_{cy} \dot{\theta }_{cy}^{2} + m_{b1} \dot{r}_{b1y}^{2} \hfill \\ + m_{b1} \dot{r}_{b1z}^{2} + I_{b1z} \dot{\theta }_{b1z}^{2} + I_{b1x} \dot{\theta }_{b1x}^{2} + I_{b1y} \dot{\theta }_{b1y}^{2} + m_{b2} \dot{r}_{b2y}^{2} + m_{b2} \dot{r}_{b2z}^{2} + I_{b2z} \dot{\theta }_{b2z}^{2} + I_{b2x} \dot{\theta }_{b2x}^{2} + I_{b2y} \dot{\theta }_{b2y}^{2} \hfill \\ + m_{w} \dot{r}_{w1y}^{2} + m_{w} \dot{r}_{w1z}^{2} + I_{w1x} \dot{\theta }_{w1x}^{2} + I_{w1y} \dot{\theta }_{w1y}^{2} + m_{w} \dot{r}_{w2y}^{2} + m_{w} \dot{r}_{w2z}^{2} + I_{w2x} \dot{\theta }_{w2x}^{2} + I_{w2y} \dot{\theta }_{w2y}^{2} + m_{w} \dot{r}_{w3y}^{2} \hfill \\ + m_{w} \dot{r}_{w3z}^{2} + I_{w3x} \dot{\theta }_{w3x}^{2} + I_{w3y} \dot{\theta }_{w3y}^{2} + m_{w} \dot{r}_{w4y}^{2} + m_{w} \dot{r}_{w4z}^{2} + I_{w4x} \dot{\theta }_{w4x}^{2} + I_{w4y} \dot{\theta }_{w4y}^{2} \hfill \\ \end{gathered} \right]$$

(1a)

$$E_{p} = \frac{1}{2}\left[ \begin{gathered} \int\limits_{0}^{L} {E_{R} I_{R} \left[ {w_{R,b}^{\prime \prime 2} \left( {x,t} \right)} \right]{\text{d}}x} + \int\limits_{0}^{L} {E_{L} I_{L} \left[ {w_{L,b}^{\prime \prime 2} \left( {x,t} \right)} \right]{\text{d}}x} \hfill \\ + \,k_{b1y} \left[ {\left[ {r_{cy} - r_{b1y} + \theta_{cz} l_{b1} - \theta_{cx} a + \theta_{b1x} a} \right]^{2} + \left[ {r_{cy} - r_{b1y} + \theta_{cz} l_{b1} + \theta_{cx} a - \theta_{b1x} a} \right]^{2} } \right] \hfill \\ + \,k_{b2y} \left[ {\left[ {r_{cy} - r_{b2y} - \theta_{cz} l_{b2} - \theta_{cx} a + \theta_{b2x} a} \right]^{2} + \left[ {r_{cy} - r_{b2y} - \theta_{cz} l_{b2} + \theta_{cx} a - \theta_{b2x} a} \right]^{2} } \right] \hfill \\ + \,k_{w1y} \left[ {\left[ {r_{b1y} - r_{w1y} + \theta_{b1z} l_{w1} - \theta_{b1x} d + \theta_{w1x} d} \right]^{2} + \left[ {r_{b1y} - r_{w1y} + \theta_{b1z} l_{w1} + \theta_{b1x} d - \theta_{w1x} d} \right]^{2} } \right] \hfill \\ + \,k_{w2y} \left[ {\left[ {r_{b1y} - r_{w2y} - \theta_{b1z} l_{w2} - \theta_{b1x} d + \theta_{w2x} d} \right]^{2} + \left[ {r_{b1y} - r_{w2y} - \theta_{b1z} l_{w2} + \theta_{b1x} d - \theta_{w2x} d} \right]^{2} } \right] \hfill \\ + \,k_{w3y} \left[ {\left[ {r_{b2y} - r_{w3y} + \theta_{b2z} l_{w3} - \theta_{b2x} d + \theta_{w3x} d} \right]^{2} + \left[ {r_{b2y} - r_{w3y} + \theta_{b2z} l_{w3} + \theta_{b2x} d - \theta_{w3x} d} \right]^{2} } \right] \hfill \\ + \,k_{w4y} \left[ {\left[ {r_{b2y} - r_{w4y} - \theta_{b2z} l_{w4} - \theta_{b2x} d + \theta_{w4x} d} \right]^{2} + \left[ {r_{b2y} - r_{w4y} - \theta_{b2z} l_{w4} + \theta_{b2x} d - \theta_{w4x} d} \right]^{2} } \right] \hfill \\ + \,2k_{bz} \left[ {\left[ {r_{cz} - r_{b1z} - \theta_{cx} h_{c} - \theta_{b1x} h_{b} } \right]^{2} + \left[ {r_{cz} - r_{b2z} - \theta_{cx} h_{c} - \theta_{b2x} h_{b} } \right]^{2} } \right] \hfill \\ + \,2k_{wz} \left[ {r_{b1z} - r_{w1z} - \theta_{b1x} h_{w} } \right]^{2} + 2k_{wz} \left[ {r_{b1z} - r_{w2z} - \theta_{b1x} h_{w} } \right]^{2} + 2k_{wz} \left[ {r_{b2z} - r_{w3z} - \theta_{b2x} h_{w} } \right]^{2} \hfill \\ + \,2k_{wz} \left[ {r_{b2z} - r_{w4z} - \theta_{b2x} h_{w} } \right]^{2} + 2k_{bx} \left[ {\left[ {\theta_{cy} e - \theta_{b1y} f} \right]^{2} + \left[ {\theta_{cy} e - \theta_{b2y} f} \right]^{2} } \right] \hfill \\ + \,2k_{wx} \left[ {\left[ {\theta_{b1y} s - \theta_{w1y} s} \right]^{2} + \left[ {\theta_{b1y} s - \theta_{w2y} s} \right]^{2} } \right] + 2k_{wx} \left[ {\left[ {\theta_{b2y} s - \theta_{w3y} s} \right]^{2} + \left[ {\theta_{b2y} s - \theta_{w4y} s} \right]^{2} } \right] \hfill \\ \end{gathered} \right]$$

(1b)

$$D = \frac{1}{2}\left[ \begin{gathered} \int\limits_{0}^{L} {c_{R} \dot{w}_{R,b}^{2} } (x,t){\text{d}}x + \int\limits_{0}^{L} {c_{L} \dot{w}_{L,b}^{2} } (x,t){\text{d}}x \hfill \\ + \;c_{b1y} \left[ {\left[ {\dot{r}_{cy} - \dot{r}_{b1y} + \dot{\theta }_{cz} l_{b1} - \dot{\theta }_{cx} a + \dot{\theta }_{b1x} a} \right]^{2} { + }\left[ {\dot{r}_{cy} - \dot{r}_{b1y} + \dot{\theta }_{cz} l_{b1} + \dot{\theta }_{cx} a - \dot{\theta }_{b1x} a} \right]^{2} } \right] \hfill \\ + \;c_{b2y} \left[ {\left[ {\dot{r}_{cy} - \dot{r}_{b2y} - \dot{\theta }_{cz} l_{b2} - \dot{\theta }_{cx} a + \dot{\theta }_{b2x} a} \right]^{2} + \left[ {\dot{r}_{cy} - \dot{r}_{b2y} - \dot{\theta }_{cz} l_{b2} + \dot{\theta }_{cx} a - \dot{\theta }_{b2x} a} \right]^{2} } \right] \hfill \\ + \;c_{w1y} \left[ {\left[ {\dot{r}_{b1y} - \dot{r}_{w1y} + \dot{\theta }_{b1z} l_{w1} - \dot{\theta }_{b1x} d + \dot{\theta }_{w1x} d} \right]^{2} + \left[ {\dot{r}_{b1y} - \dot{r}_{w1y} + \dot{\theta }_{b1z} l_{w1} + \dot{\theta }_{b1x} d - \dot{\theta }_{w1x} d} \right]^{2} } \right] \hfill \\ + \;c_{w2y} \left[ {\left[ {\dot{r}_{b1y} - \dot{r}_{w2y} - \dot{\theta }_{b1z} l_{w2} - \dot{\theta }_{b1x} d + \dot{\theta }_{w2x} d} \right]^{2} + \left[ {\dot{r}_{b1y} - \dot{r}_{w2y} - \dot{\theta }_{b1z} l_{w2} + \dot{\theta }_{b1x} d - \dot{\theta }_{w2x} d} \right]^{2} } \right] \hfill \\ + \;c_{w3y} \left[ {\left[ {\dot{r}_{b2y} - \dot{r}_{w3y} + \dot{\theta }_{b2z} l_{w3} - \dot{\theta }_{b2x} d + \dot{\theta }_{w3x} d} \right]^{2} + \left[ {\dot{r}_{b2y} - \dot{r}_{w3y} + \dot{\theta }_{b2z} l_{w3} + \dot{\theta }_{b2x} d - \dot{\theta }_{w3x} d} \right]^{2} } \right] \hfill \\ + \;c_{w4y} \left[ {\left[ {\dot{r}_{b2y} - \dot{r}_{w4y} - \dot{\theta }_{b2z} l_{w4} - \dot{\theta }_{b2x} d + \dot{\theta }_{w4x} d} \right]^{2} + \left[ {\dot{r}_{b2y} - \dot{r}_{w4y} - \dot{\theta }_{b2z} l_{w4} + \dot{\theta }_{b2x} d - \dot{\theta }_{w4x} d} \right]^{2} } \right] \hfill \\ + \;{\text{2c}}_{bz} \left[ {\left[ {\dot{r}_{cz} - \dot{r}_{b1z} - \dot{\theta }_{cx} h_{c} - \dot{\theta }_{b1x} h_{b} } \right]^{2} + \left[ {\dot{r}_{cz} - \dot{r}_{b2z} - \dot{\theta }_{cx} h_{c} - \dot{\theta }_{b2x} h_{b} } \right]^{2} } \right] \hfill \\ + \;2c_{wz} \left[ {\dot{r}_{b1z} - \dot{r}_{w1z} - \dot{\theta }_{b1x} h_{w} } \right]^{2} + {\text{2c}}_{wz} \left[ {\dot{r}_{b1z} - \dot{r}_{w2z} - \dot{\theta }_{b1x} h_{w} } \right]^{2} + {\text{2c}}_{wz} \left[ {\dot{r}_{b2z} - \dot{r}_{w3z} - \dot{\theta }_{b2x} h_{w} } \right]^{2} \hfill \\ + \;{\text{2c}}_{wz} \left[ {\dot{r}_{b2z} - \dot{r}_{w4z} - \dot{\theta }_{b2x} h_{w} } \right]^{2} + 2c_{bx} \left[ {\left[ {\dot{\theta }_{cy} e - \dot{\theta }_{b1y} f} \right]^{2} + \left[ {\dot{\theta }_{cy} e - \dot{\theta }_{b2y} f} \right]^{2} } \right] \hfill \\ + \;2c_{wx} \left[ {\left[ {\dot{\theta }_{b1y} s - \dot{\theta }_{w1y} s} \right]^{2} + \left[ {\dot{\theta }_{b1y} s - \dot{\theta }_{w2y} s} \right]^{2} } \right] + 2c_{wx} \left[ {\left[ {\dot{\theta }_{b2y} s - \dot{\theta }_{w3y} s} \right]^{2} + \left[ {\dot{\theta }_{b2y} s - \dot{\theta }_{w4y} s} \right]^{2} } \right] \hfill \\ \end{gathered} \right]$$

(1c)

In Eq. (1a–c), μ_R and μ_L are the parameters of the mass of the unit length of the right and left bridge beam, respectively. E_RI_R and E_LI_L are the flexural rigidity of the right and left bridge beams. On the other hand, the dissipation function of the full railway vehicle model and flexible structure coupled system can be obtained by Eq. (1c) considering the physical model given Fig. 2.

The parameters, c_R and c_L, given in Eq. (1c) represent the equivalent viscous damping coefficient of the Euler–Bernoulli right and left bridge beam with the simply supported boundary condition given in Fig. 2. The expression Galerkin functions for both bridge beam, w_R,b(x,t) and w_L,b(x,t), which is the displacement of any x point on the beam at any time t, is given below:

$$w_{R,b} (x,t) = \sum\limits_{i = 1}^{n} {\varphi_{i} } (x)q_{i} (t),\quad w_{L,b} (x,t) = \sum\limits_{i = 1}^{n} {\varphi_{i + n} } (x)q_{i + n} (t), \,$$

(2)

$$\dot{w}_{R,b} (x,t) = \sum\limits_{i = 1}^{n} {\varphi_{i} } (x)\dot{q}_{i} (t),\quad \dot{w}_{L,b} (x,t) = \sum\limits_{i = 1}^{n} {\varphi_{i + n} } (x)\dot{q}_{i + n} (t), \,$$

(3)

$$w^{\prime\prime}_{R,b} (x,t) = \sum\limits_{i = 1}^{n} {\varphi^{\prime\prime}_{i} } (x)q_{i} (t),\quad w^{\prime\prime}_{L,b} (x,t) = \sum\limits_{i = 1}^{n} {\varphi^{\prime\prime}_{i + n} } (x)q_{i + n} (t),$$

(4)

Here, the parameter q is the generalized coordinate representing the displacement of the bridge beam structure, φ represents the oscillation form obtained with simply supported boundary conditions of the bridge beam. The parameter n defines the mode number of the simply supported bridge beams. The mode function of bridge beam is given by Eq. (5) as shown below:

$$\varphi_{i} (x) = \sqrt{\frac{2}{L}} \sin \left( {\frac{i\pi x}{L}} \right),\quad \, i = 1,2, \ldots ,n.$$

(5)

The conditions of orthogonality between these oscillation mode shapes are given in Eq. (6), where ẟ_ij represents Kronecker delta.

$$\int\limits_{0}^{L} {\mu \varphi_{i} (x)\varphi_{j} } (x){\text{d}}x = N_{i} \delta_{ij} , \,$$

(6a)

$$\, \int\limits_{0}^{L} {EI\varphi^{\prime\prime}_{i} (x)} \varphi^{\prime\prime}_{j} (x){\text{d}}x = \Pi_{i} \delta_{ij}$$

(6b)

Lagrange expression is the distinction between kinetic energy and potential energies obtained in Eq. (1a, b). Lagrange expression can be defined as (L = E_k− E_p).

$$\frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{\partial L}{{\partial {\dot{\mathbf{\eta }}}_{{\mathbf{k}}} (t)}}} \right) - \frac{\partial L}{{\partial {{\varvec{\upeta}}}_{{\mathbf{k}}} (t)}} + \frac{\partial D}{{\partial {\dot{\mathbf{\eta }}}_{{\mathbf{k}}} (t)}} = 0 \, ,\quad k = 1,2,3, \ldots ,31.$$

(7)

$$\frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{\partial L}{{\partial {\dot{\mathbf{q}}}_{{\mathbf{i}}} (t)}}} \right) - \frac{\partial L}{{\partial {\mathbf{q}}_{{\mathbf{i}}} (t)}} + \frac{\partial D}{{\partial {\dot{\mathbf{q}}}_{{\mathbf{i}}} (t)}} = Q_{i} \, , \, \begin{array}{*{20}c} {i = 1,2, \ldots ,n. \, \Rightarrow {\text{ For the right bridge beam}}} \\ {i = n + 1,n + 2, \ldots ,2n. \, \Rightarrow {\text{ For the left bridge beam}}} \\ \end{array} \,$$

(8)

$$ {\mathbf{\eta (}}t{\mathbf{)}} = \left\{ \begin{gathered} r_{cy} \, r_{cz} \, \theta_{cz} \, \theta_{cx} \, \theta_{cy} \, r_{b1y} \, r_{b1z} \, \theta_{b1z} \, \theta_{b1x} \, \theta_{b1y} \, r_{b2y} \, r_{b2z} \, \theta_{b2z} \, \theta_{b2x} \, \theta_{b2y} \, r_{w1y} \, r_{w1z} \hfill \\ \theta_{w1x} \, \theta_{w1y} \, r_{w2y} \, r_{w2z} \, \theta_{w2x} \, \theta_{w2y} \, r_{w3y} \, r_{w3z} \, \theta_{w3x} \, \theta_{w3y} \, r_{w4y} \, r_{w4z} \, \theta_{w4x} \, \theta_{w4y} \hfill \\ \end{gathered} \right\}^{{\text{T}}} , \, $$

(9)

$${\mathbf{q}}(t) = \left\{ {q_{1} (t) \, q_{2} (t) \, q_{3} (t) \, \ldots \, q_{2n} (t)} \right\}^{{\text{T}}} ,$$

(10)

Generalized coordinates of train and bridge beams are given as in Eqs. (9–10). Here, whereas η represents the train’s generalized coordinates with 31-DOFs, the parameter q defines generalized coordinates of the two-simple supported bridge beam. Since each bridge beam has a first four vibrations mode in this study, eight generalized coordinates are given. The effect and defining of the number of mode function is explained in Sect. 3.2

$$Q_{i} = \int\limits_{0}^{L} {\varphi_{i} (x)f_{ci} (x,t){\text{d}}x,\quad i = 1,2,. \ldots ,2n,}$$

(11)

The motion equation of the 31-DOFs train model seen in Fig. 2 was obtained using the orthogonality conditions given in Eq. (6) and the Galerkin’s approach of the beam displacement expressed in Eqs. (2–4). Some equations of motion for car body, front and rear bogies, wheels and bridge are given below:

The vertical acceleration of the car body can be obtained as follow:

$$\begin{aligned} \ddot{r}_{cy} = & - 2c_{b1y} /m_{c} \left[ {\dot{r}_{cy} - \dot{r}_{b1y} + \dot{\theta }_{cz} l_{b1} } \right] - 2c_{b2y} /m_{c} \left[ {\dot{r}_{cy} - \dot{r}_{b2y} - \dot{\theta }_{cz} l_{b2} } \right] \\ & - 2k_{b1y} /m_{c} \left[ {r_{cy} - r_{b1y} + \theta_{cz} l_{b1} } \right] - 2k_{b2y} /m_{c} \left[ {r_{cy} - r_{b2y} - \theta_{cz} l_{b2} } \right] \\ \end{aligned}$$

(12a)

Response of the right bridge beam is written as Eq. (12b)

$$\begin{aligned} \ddot{q}_{i(t)} = & - S_{1} q_{i(t)} /N_{1} - c_{1} \dot{q}_{i(t)} /N_{1} \\ & + \varphi_{i} (\xi_{1R} ,t)/N_{1} \left[ {c_{w1y} \left[ {\dot{r}_{b1y} - \sum\limits_{i = 1}^{n} {\varphi_{i} (\xi_{1R} ,t)\dot{q}_{i} } + \dot{\theta }_{b1z} l_{w1} - \dot{\theta }_{b1x} d + \dot{\theta }_{w1x} d} \right] + k_{w1y} \left[ {r_{b1y} - \sum\limits_{i = 1}^{n} {\varphi_{i} (\xi_{1R} ,t)q_{i} } + \theta_{b1z} l_{w1} - \theta_{b1x} d + \theta_{w1x} d} \right] - fg_{1} } \right] \\ & + \varphi_{i} (\xi_{2R} ,t)/N_{1} \left[ {c_{w2y} \left[ {\dot{r}_{b1y} - \sum\limits_{i = 1}^{n} {\varphi_{i} (\xi_{2R} ,t)\dot{q}_{i} } - \dot{\theta }_{b1z} l_{w2} - \dot{\theta }_{b1x} d + \dot{\theta }_{w2x} d} \right] + k_{w2y} \left[ {r_{b1y} - \sum\limits_{i = 1}^{n} {\varphi_{i} (\xi_{2R} ,t)q_{i} } - \theta_{b1z} l_{w2} - \theta_{b1x} d + \theta_{w2x} d} \right] - fg_{2} } \right] \\ & + \varphi_{i} (\xi_{3R} ,t)/N_{1} \left[ {c_{w3y} \left[ {\dot{r}_{b2y} - \sum\limits_{i = 1}^{n} {\varphi_{i} (\xi_{3R} ,t)\dot{q}_{i} } + \dot{\theta }_{b2z} l_{w3} - \dot{\theta }_{b2x} d + \dot{\theta }_{w3x} d} \right] + k_{w3y} \left[ {r_{b2y} - \sum\limits_{i = 1}^{n} {\varphi_{i} (\xi_{3R} ,t)q_{i} } + \theta_{b2z} l_{w3} - \theta_{b2x} d + \theta_{w3x} d} \right] - fg_{3} } \right] \\ & + \varphi_{i} (\xi_{4R} ,t)/N_{1} \left[ {c_{w4y} \left[ {\dot{r}_{b2y} - \sum\limits_{i = 1}^{n} {\varphi_{i} (\xi_{4R} ,t)\dot{q}_{i} } - \dot{\theta }_{b2z} l_{w4} - \dot{\theta }_{b2x} d + \dot{\theta }_{w4x} d} \right] + k_{w4y} \left[ {r_{b2y} - \sum\limits_{i = 1}^{n} {\varphi_{i} (\xi_{4R} ,t)q_{i} } - \theta_{b2z} l_{w4} - \theta_{b2x} d + \theta_{w4x} d} \right] - fg_{4} } \right] \\ \end{aligned}$$

(12b)

The vertical acceleration of the rear wheelset has been formulated as follow:

$$\ddot{r}_{w2z} = 2c_{wz} /m_{w} \left[ {\dot{r}_{b1z} - \dot{r}_{w2z} - \dot{\theta }_{b1x} h_{w} } \right] + 2k_{wz} /m_{w} \left[ {r_{b1z} - r_{w2z} - \theta_{b1x} h_{w} } \right]$$

(12c)

Angular acceleration of rear bogie around the x-axis is given by Eq. (12d).

$$\begin{aligned} \ddot{\theta }_{b2x} = & 2c_{b2y} a^{2} /I_{b2x} \left[ {\dot{\theta }_{cx} - \dot{\theta }_{b2x} } \right] + c_{w3y} d/I_{b2x} \left[ {2\dot{\theta }_{w3x} d - \varphi_{i} (\xi_{3R} ,t)\dot{q}_{i} + \varphi_{i} (\xi_{3L} ,t)\dot{q}_{i} - 2\dot{\theta }_{b2x} d} \right] \\ & + \;c_{w4y} d/I_{b2x} \left[ {2\dot{\theta }_{w4x} d - \varphi_{i} (\xi_{4R} ,t)\dot{q}_{i} + \varphi_{i} (\xi_{4L} ,t)\dot{q}_{i} - 2\dot{\theta }_{b2x} d} \right] + 2k_{b2y} a^{2} /I_{b2x} \left[ {\theta_{cx} - \theta_{b2x} } \right] \\ & + \;k_{w3y} d/I_{b2x} \left[ {2\theta_{w3x} d - \varphi_{i} (\xi_{3R} ,t)q_{i} + \varphi_{i} (\xi_{3L} ,t)q_{i} - 2\theta_{b2x} d} \right] \\ & + \;k_{w4y} d/I_{b2x} \left[ {2\theta_{w4x} d - \varphi_{i} (\xi_{4R} ,t)q_{i} + \varphi_{i} (\xi_{4L} ,t)q_{i} - 2\theta_{b2x} d} \right] \\ \end{aligned}$$

(12d)

On the other hand, the vertical acceleration of the front bogie is obtained by Eq. (12e).

$$\begin{aligned} \ddot{r}_{b1y} = & 2c_{b1y} /m_{b1} \left[ {\dot{r}_{cy} - \dot{r}_{b1y} + \dot{\theta }_{cz} l_{b1} } \right] - c_{w1y} /m_{b1} \left[ {2\dot{r}_{b1y} - \varphi_{i} (\xi_{1R} ,t)\dot{q}_{i} - \varphi_{i} (\xi_{1L} ,t)\dot{q}_{i} + 2\dot{\theta }_{b1z} l_{w1} } \right] \\ & - \;c_{w2y} /m_{b1} \left[ {2\dot{r}_{b1y} - \varphi_{i} (\xi_{2R} ,t)\dot{q}_{i} - \varphi_{i} (\xi_{2L} ,t)\dot{q}_{i} - 2\dot{\theta }_{b1z} l_{w2} } \right] + 2k_{b1y} /m_{b1} \left[ {r_{cy} - r_{b1y} + \theta_{cz} l_{b1} } \right] \\ & - \;k_{w1y} /m_{b1} \left[ {2r_{b1y} - \varphi_{i} (\xi_{1R} ,t)q_{i} - \varphi_{i} (\xi_{1L} ,t)q_{i} + 2\theta_{b1z} l_{w1} } \right] \\ & - \;k_{w2y} /m_{b1} \left[ {2r_{b1y} - \varphi_{i} (\xi_{2R} ,t)q_{i} - \varphi_{i} (\xi_{2L} ,t)q_{i} - 2\theta_{b1z} l_{w2} } \right] \\ \end{aligned}$$

(12e)

The angular acceleration of the car body around the z-axis is governed by Eq. (12f).

$$\begin{aligned} \ddot{\theta }_{cz} = & - 2c_{b1y} l_{b1} /I_{cz} \left[ {\dot{r}_{cy} - \dot{r}_{b1y} + \dot{\theta }_{cz} l_{b1} } \right] + 2c_{b2y} l_{b2} /I_{cz} \left[ {\dot{r}_{cy} - \dot{r}_{b2y} - \dot{\theta }_{cz} l_{b2} } \right] \\ & - \;2k_{b1y} l_{b1} /I_{cz} \left[ {r_{cy} - r_{b1y} + \theta_{cz} l_{b1} } \right] + 2k_{b2y} l_{b2} /I_{cz} \left[ {r_{cy} - r_{b2y} - \theta_{cz} l_{b2} } \right] \\ \end{aligned}$$

(12f)

In Eq. (12b), the second-order equation of the right bridge beam is given. Here, the f_g value shows the static forces applied to the bridge beam by the train and is calculated as in Eq. (13a). Here, wh represents the number of wheels of the train going over the bridge beam. On the other hand, other static contact forces on the train body and bogies are obtained by Eq. (13b–c). The parameters f_b and f_t represent the static forces of bogies and train body, respectively.

$$f_{g} = \frac{{\left( {m_{c} + \sum\nolimits_{i = 1}^{2} {m_{b,i} + } \sum\nolimits_{i = 1}^{8} {m_{w,i} } } \right)g}}{wh}$$

(13a)

$$f_{b} = \frac{{\left( {m_{c} + \sum\nolimits_{i = 1}^{2} {m_{b,i} } } \right)g}}{2}$$

(13b)

$$f_{t} = m_{c} g$$

(13c)

The parameter g given by Eq. (13a–c), as shown above represents gravitational acceleration.

3 Numerical analysis

3.1 Numerical verification examples

The equations of motion for the entire train and bridge model are obtained using the Lagrange method in Eqs. (7–8). A total of 39 s-order differential equations, 31 belonging to the train and 8 equations belonging to the bridge, were created. These equations are reduced to 78 first-order differential equations with the help of state-space forms. Then, to solve these equations, the fourth-order Runge–Kutta method was used by means of “Appendix 1”. The dynamic responses that occurred during the passage of the high-speed train over the bridge, which can be modeled as the Euler–Bernoulli beam, were analyzed with the commercial analysis program MATLAB. The parameters of the train and bridge beam used by [30, 36] in the literature for analysis in this study are given in Table 1. In order to verify the results of the analysis, a comparison was made with the results of the studies in the literature. In both solutions compared, all parameters were selected the same. The motion equation of the train bridge models in the literature was analyzed by the Newmark method [17, 37]. However, in this study, the second-order differential equations were reduced to the first-order equation in the state-space form and analyzed with the Runge–Kutta method. Two cases were examined for comparison; in the first case, the elasticity module of the beam was taken as E = 2.87 GPa, the inertia moment of the cross-sectional area was taken as I = 2.9 m⁴, the mass of unit length of the beam was taken as µ = 2303 kg/m, beam length was taken as L = 25 m, sprung mass was taken as M_v = 5.75 tons, spring rating was accepted as k_v = 1595 kN/m, and the system was assumed as undamped.

In the second verification case, which connected to the body of the wheel through spring and damping elements, the elasticity module of the beam was taken as E = 2.943 GPa, the inertia moment of the cross-sectional area was taken as I = 8.65 m⁴, the mass of unit length of the beam was taken as µ = 36 tons/m, beam length was taken as L = 30 m, sprung mass was taken as M_v = 540 tons, spring coefficient was accepted as k_v = 41,350 kN/m, and the system was assumed as undamped. Distance between two wheels was taken as d = 17.5 m, and the train speed was taken as 27.78 m/s. The comparative result of the method used in this study with the examples given in Fig. 3 is shown in Fig. 4. The results of both validation examples and the method used in this study were quite similar. In Fig. 4, the comparison of the presented study with literature studies [38, 39], considering two cases sprung mass model (1-DOF) and suspended rigid beam model (2-DOFs) including moving load case too. According to the figure for case 2 given in Fig. 4b, it is clearly seen that there is some difference between the proposed study and Yang and Wu [39] in terms of bridge structure midpoint vertical displacement because of the reason explained in this study. One of the biggest reasons the occurring this difference between the presented study and Yang and Wu [39] is taking into different mode numbers in the calculation of the flexible structure transverse dynamic effect of moving vehicle or moving load. For example, in the study Yang and Wu [39], for calculation of the beam deflection, the only first mode of the flexible beam has been considered and analytically and Newmark’s finite difference technique is used for the numerical analysis, which has a significant effect upon determining bridge and vehicle dynamic. In other words, in the presented study, the first four modes of the flexible beam have been taken into, and the fourth-order Runge–Kutta algorithm is used for the numerical analyses in the time domain.

Fig. 3

a Verification case 1 and b case 2

Fig. 4

a Displacement at the midpoint of beam for verification case 1 and b displacement at midpoint of beam for case 2

In the analysis, the railway vehicle and the bridge parameters were taken as in Table 1. However, these values do not remain constant in the actual model. For example, the mass of the railway vehicle changes depending on whether the wagon is filled with passengers. Similarly, bridge parameters are of great importance for bridge engineering. The length of the bridge over which the high-speed train passes cannot be considered constant, as seen in Fig. 1, and different bridge lengths change the train-bridge dynamic interaction. When the train enters the bridge at a certain velocity, the bridge is forced to vibrate. If this velocity equals the resonance frequency of the bridge, the bridge oscillations are quite high. Train velocity, which corresponds to the resonance frequency, is called critical velocity at which the train is not desired to travel. Before starting the analysis, the displacement modes of the bridge beam have been determined. In this study, it was seen that the first four modes of bridge beam are satisfactory. The natural frequency calculation of the beam is given in Eq. (14) [40], where ω represents the circular natural frequency of the beam.

$$\omega_{j}^{2} = \frac{{j^{4} \pi^{4} EI}}{{\mu L^{4} }} \, ({\text{rad/s}}),$$

(14)

In Eq. (14), the circular natural frequency of the beam is given. In Eq. (15), the beam vibration frequency is calculated.

$$f_{j} = \frac{{\omega_{j} }}{2\pi } = \frac{{j^{2} \pi }}{{2L^{2} }}\sqrt {\frac{EI}{\mu }} \, ({\text{Hz}})$$

(15)

According to Eq. (15), the first four vibration modes of the right and left bridge beam can be calculated as in Table 2.

Table 2 First four vibration modes of the right and left bridge beam

The force frequency f_v of the train and the natural frequency f_b of the bridge are called speed parameters. If f_v and f_b are equal, resonance occurs. The resonance causes the periodic motion amplitudes of the train passing over the bridge to increase. The most crucial characteristic length for the resonance caused by the train passing over the bridge beam is the length of the train [41]. The critical velocity of the beam-train system, v_cr, causing resonance is given in Eq. (16) [42].

$$v_{cr,j} = \frac{{df_{b,j} }}{i}$$

(16)

In Eq. (16), f_b,j represents the jth natural frequency of the bridge beam. Expression d stands for the distance between the front wheel of the front bogie and the rear wheel of the rear bogie. i represents the number of half oscillation cycles [37, 43]. Length d is calculated as l_b1 + l_b2 + l_w1 + l_w4 = 20 m using Table 1. Thus, critical velocities of the beam-train system for the first four modes of the bridge are determined as in Table 2.

3.2 The effect of the mode number used in the study upon railway vehicle and bridge dynamic

In this section, it will be examined how the vibration mode number of bridges that can be modeled according to the Euler–Bernoulli beam theory changes the TBI. In Sect. 2, the vibration mode frequencies of the simply supported bridge beams are introduced. Determining the vibration response of flexible structures such as bridges at specific frequencies or natural frequencies is very important in examining forced vibrations. Therefore, in this section, both bridge and train dynamics are examined by considering the first eight vibration modes of the simply supported bridge beam.

In Fig. 5, the vertical displacement and acceleration of the train body and the deflection of the bridge midpoint are given according to the different mode numbers (n = 1–8). The root mean square (RMS) values of the graphs given in Fig. 5 according to each mode number are given in Table 3. As can be seen from the graphs, the responses of train and bridge are almost the same for all modes of bridge beams.

Fig. 5

Effect of bridge beam mode number upon train-bridge dynamic response

Table 3 Comparison of the bridge mode number (n) upon the dynamic response of train and bridge beam

Considering only one vibration mode of the bridge beam and the first two vibration modes, the relative error value in the vertical displacement value of the train is 1.2%. If the first three modes are included, there is only a relative error value of 0.1024% compared to the results including the first two modes. With the inclusion of the first four vibration frequencies of the bridge beam, the value of the relative error is negligibly low, and it is observed that the results do not change much with the inclusion of subsequent vibration modes. As a result, it is seen that the first four vibration modes of the bridge beam examined in this study are pretty sufficient for the accuracy of the study.

3.3 The effect of time step upon dynamic responses of the train and bridge

In this study, the equations of motion of the train-bridge system given in Eq. (12a–f) are solved precisely and accurately by the Runge–Kutta method. In this context, the selection of the time step is an important concept. In some studies, the use of different time steps has been preferred to solve the equations of motion of the bridge and train. For example, Zhu et al. [44] adopted a fine time-step for the train subsystem and track subsystem due to the high-frequency wheel-rail contact and adopted a coarse time-step for the bridge subsystem due to low-frequency vibration. Froio et al. [45], in their study on the determination of maximum beam displacements, applied an automatic calculation method to evaluate the time step for each simulation. They also used the HHT-α implementation method [46] to achieve the numerical solution of the initial-value problem. An implicit formulation for this method is given as follow:

$$m.\ddot{r}_{k + 1} + \left( {1 + \alpha } \right).c.\dot{r}_{k + 1} - \alpha .c.\dot{r}_{k} + \left( {1 + \alpha } \right).r_{k + 1} - \alpha .r_{k + 1} = \left( {1 + \alpha } \right).F_{k + 1} - \alpha .F_{k} \quad k = 0,1, \ldots ,N - 1$$

(17)

$$r_{k + 1} = r_{k} + \Delta t.\dot{r}_{k} + \Delta t^{2} .\left[ {\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}} - \beta } \right).r_{k} + \beta .r_{k + 1} } \right]$$

(18)

$$\dot{r}_{k + 1} = \dot{r}_{k} + \Delta t.\left[ {\left( {1 - \gamma } \right).\ddot{r}_{k} + \gamma .\ddot{r}_{k + 1} } \right]$$

(19)

where m and c are the mass and damping coefficient, respectively. $r_{k}$, $\dot{r}_{k}$, and $\ddot{r}_{k}$ are the displacement, velocity, and acceleration response at the k^th time-step, respectively. F is the vector of external forces. N is the number of time steps, $\Delta t = \frac{\tau }{N}$. Where, the parameter $\tau$ is the time needed for the train to leave the bridge completely. $\alpha$, $\beta$, and $\gamma$ are parameters of the algorithm. Hilber et al. [46] suggested $- {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}} \le \alpha \le 0$, $\gamma > 0.5$ and $\beta \ge 0.25.\left( {\gamma + 0.5} \right)^{2}$ parameters to ensure stability and accuracy in the given method. Here, the parameter HHT-α, that indicates the high-frequency numerical distribution ratio, can be chosen equal to α = − 0.1.

The HHT-α method presented by Hilbert et al. [46] in determining the time step size is briefly introduced above. In this study, before starting the analysis, solution step time was determined as Δt. It is adequate to take Δt = 10^–2 in the analysis. Choosing the solution step time smaller does not change the results obtained and increases the analysis time considerably. In order for all wheelsets to contact the bridge (l_b1 + l_b2 + l_w1 + l_w4)/v = 0.24 s time is needed. The time needed for the train to leave the bridge completely is (L + l_b1 + l_b2 + l_w1 + l_w4)/v = 0.84 s. The total analysis time was taken as five times the time required for the entire train to leave the bridge, and the dynamic response of the bridge was examined after the train left the bridge.

In this context, the displacement and acceleration values of the train body and the dynamic response of the bridge midpoint in 4 different time steps (Δt = 0.2, 0.1, 0.01, 0.001 s) according to the position of the train while passing over the bridge are given in Figs. 6 and 7. RMS values of the bridge’s midpoint displacement and the train body displacement are given in Table 4. According to Table 4, if the train speed is 300 km/h when the time step size is 0.001, the RMS of the displacement value of the bridges’ midpoint is 0.01699 m, when the time step size is 0.01, this value is 0.01693 m, and the relative difference is only 0.35%. However, when the time spent by the computer software program for the solution for both step times is considered, there is a sixfold difference. The effect of the proposed time step in the study is examined in Figs. 6 and 7 when the train speed is 300 km/h and 50 km/h. Considering the fast or slow movement of the train according to both graphs, it is stated that the determined time step size is the most appropriate. As a result, choosing the solution step time more minor does not change the results obtained and increases the analysis time considerably. Similarly, for the train body displacement, the results are also the same.

Fig. 6

Effect of time step size (Δt) on dynamic responses of the train body and bridge in case of train velocity = 50 km/h a vertical displacement of train body, b vertical acceleration of train body and c displacement of bridge midpoint

Fig. 7 

Effect of time step size (Δt) on dynamic responses of the train body and bridge in case of train velocity = 300 km/h a vertical displacement of train body, b vertical acceleration of train body and c displacement of bridge midpoint

Table 4 Effect of time step size Δt upon solution accuracy for bridge midpoint displacement and train body displacement

3.4 Train and railway vehicle dynamic responses for constant velocity

In Figs. 8, 9 and 10, dynamic responses of car body and bogies are given for the train traveling at a constant velocity on the bridge beam. In Fig. 8a, b, vertical and lateral displacement graphs of the car body and bogies are given. The train leaves the bridge after, 0.84 s and after this time, the vibration and displacement of the train decrease.

Fig. 8

Dynamic responses of car body, front and rear bogies a vertical displacement and b lateral displacement

Fig. 9

Dynamic responses of car body, front and rear bogies a rotation of pitch motion and b rotation of roll motion

Fig. 10

Dynamic responses of car body, front and rear bogies a vertical acceleration and b lateral acceleration

When Fig. 8a is examined, the maximum displacement of the rear bogie and car body occurs at 0.73 s, and the maximum displacement of the front bogie is 0.55 s, which is 0.18 s before the rear bogie. This is due to the distance between the wheel in the front bogie and the wheel in the rear bogie. Figure 8b shows lateral displacements for the car body, front bogie, and the rear bogie. The maximum displacement of the car body and front bogie was at 0.76 s, and 53.3 m after the car body entered the bridge. The maximum displacement of the rear bogie was at 0.5 s, and 31.67 m after the car body entered the bridge. In Fig. 9, the pitching and rolling movements of the car body, front bogie and the rear bogie are given. The rolling motion is due to the dynamic response distinction between the right bridge beam and the left bridge beam, which can be seen in Fig. 11.

Fig. 11

Dynamic responses of beams

The vertical and lateral accelerations of the car body, front bogie, and rear bogie are given in Fig. 10. The maximum vertical acceleration of the car body was found as 52.5 m after the train entered the bridge, and 0.84 m/s², while the maximum lateral acceleration was found as 60 m after the car body entered the bridge and 0.0048 m/s². The maximum vertical displacement and maximum acceleration of the car body occurred almost in the same position of the bridge. The maximum lateral acceleration of the front and rear bogie was found to be 0.032 m/s² and 0.06 m/s², respectively. This vertical acceleration of the car body exceeds the acceleration values affecting humans according to ISO 2631 standard, and according to this standard, the low comfortable acceleration value is 0.49 m/s², and the medium comfortable acceleration value is 0.37 m/s² [26].

3.5 Train and railway vehicle dynamic responses for different car body masses

In this section, car body mass, one of the most important parameters in TBI, will be examined. Train velocity is constant and taken as 300 km/h. Four different car body masses, (m_c = 20, 40, 60, 80 tons), were examined. In Figs. 12 and 13, the displacement and acceleration of the car body in different masses are given.

Fig. 12

The compare of effect of car body mass on the car body dynamic responses a vertical displacement and b lateral displacement

Fig. 13

The compare of effect of car body mass on the car body dynamic responses a vertical acceleration and b lateral acceleration

When Fig. 12 is examined, it can be noticed that as the mass of the car body increases, vertical displacements increase. However, it is also detected that the lateral displacements decrease with the increase in the car body mass. Also, a detail seen in Fig. 12 is that as the car body mass increases, the maximum displacement time shifts to the right. This means that the natural frequency of the train bridge system is related to the car body mass. For example, if m_c = 20–40–60–80 tons, the maximum displacement times were determined to be 0.64 s, 0.71 s, 0.76 s, and 0.8 s, respectively. Similarly, in Fig. 13, vertical acceleration and lateral acceleration rise as the car body mass increases.

In Fig. 14, the displacement of the right and left bridge beam center point is given. After the car body passes 38.3 m over the bridge, the maximum displacement of the right bridge beam is 0.58 s, and its value is 0.046 m. The left bridge was calculated as 0.83 s and 0.0748 m, which is when the train leaves the bridge. After this time, the bridge beam is in free vibration, and the bridge vibrations are damped.

Fig. 14

The compare of effect of car body mass on the beam dynamic responses a left beam midpoint displacement and b right beam midpoint displacement

3.6 Effect of train velocity upon train and railway vehicle dynamic responses

In Figs. 15, 16 and 17, the car body, front and rear bogie displacement, rotation, and acceleration values are given when the train speed changes from 2 to 200 m/s at 0.5 m/s intervals. When Fig. 15a is examined, it can be seen that the maximum displacement of car and bogies peaked in two places, the first of which occurred when the train speed was 18 m/s, and the other was 45 m/s. According to Table 2, the value of 18 m/s is quite close to the first critical velocity of the beam-train system. Similarly, whereas the maximum pitching movement of the car body in Fig. 16 is determined to be at 65 m/s, the maximum vertical acceleration of the car body in Fig. 17 is 69 m/s, which are quite close to the second critical speed of the beam-train system. In Fig. 15b, the maximum lateral displacement of the rear bogie occurs when the train speed is 168.5 m/s, and it is known that the train is very close to the third critical velocity according to Table 2.

Fig. 15

The effect of train velocity upon dynamic response a vertical displacement and b lateral displacement

Fig. 16

The effect of train velocity upon dynamic response a pitch motion and b roll motion

Fig. 17

The effect of train velocity upon dynamic response a vertical acceleration and b lateral acceleration

The dynamic amplification factor (DAF) of the beam mid-point is given in Fig. 18. DAF is the ratio of the maximum displacement of the bridge beam center point to the displacement of the bridge beam center point due to the mass of the train if the train passes over the bridge; it is found using the expression DAF = R_d(x)/R_s(x). The maximum displacement of the bridge center point is found using R_s = FL³/48EI formula, where F is the total weight of the train. When Fig. 18 is examined, it can be seen that three different damping ratios are given for the bridge beam. These are determined as ζ = 0.47%, 2.36%, 4.72% for the right beam and ζ = 0.57%, 2.88%, 5.77% for the left beam. The maximum DAF of beams has increased in two places. These occur at 18.5 m/s and 71.5 m/s, the critical velocities of the beam-train system for the left beam.

Fig. 18

The comparison of the effect of the bridge damping ζ on DAF a DAF for right beam and b DAF for left beam

One of the essential factors affecting the TBI is the car body mass. When the trainload increases, the forces applied to the bridge beam increase. In Figs. 19 and 20, the displacement and rotation movements of the car body are given for increasing train speed and different car body mass.

Fig. 19

Displacement of car body for increasing velocity and different car body mass a vertical displacement of car body and b lateral displacement of car body

Fig. 20

Displacement of car body for increasing velocity and different car body mass a pitch motion of car body and b roll motion of car body

When Fig. 19 is examined, the vertical displacement of the car body increases as the car body mass increases. However, in contrast, lateral displacement decreases with increasing mass. In Fig. 19a, the maximum vertical displacement of the car body occurs at 40 m/s if the car body mass is 20 tons, while it is seen that it is at 45 m/s for the other masses. When Fig. 19b is examined, the maximum lateral displacement of the car body occurs at 15.5 m/s and 45 m/s, which are very close to the first two critical velocities of the beam-train system, and after this velocity, lateral displacement decreases as the velocity of the train increases.

The rotational movements of the car body are given in Fig. 20. The maximum pitching movement of the car body is at 76 m/s close to the second critical velocity of the beam-train system, and it is at 2.51 × 10^–3 rad value. In Fig. 21, it is seen how the change of train velocity and body mass affects the car body acceleration, and accordingly, the vertical acceleration increases with the increase in the mass, while the lateral acceleration decreases with the increase in the mass. However, after about 120 m/s of train velocity, the effect of the mass is reversed, and vertical acceleration decreases when mass increases.

Fig. 21

Acceleration of car body for increasing velocity and different car body mass a vertical acceleration of car body and b lateral acceleration of car body

The vertical acceleration of the car body exceeds 0.49 m/s², which is considered to be low comfort according to ISO 2631 standards, when the train goes with a speed of 74.9 m/s, the second critical velocity for the left bridge beam-train system. In Fig. 21b, the maximum lateral acceleration is quite close to the third critical velocity of the beam-train system, 178.5 m/s, according to Table 2. If the speed is about 150 m/s, the lateral acceleration is 0.015 m/s² regardless of the mass.

Railway bridges are essential parameters in terms of bridge engineering. Therefore, in Figs. 22, 23, 24 and 25, the dynamic responses of bridge beams at different lengths for train bodies are examined. Four different beam lengths, 30–40–50–60 m, were studied. An examination of Fig. 22 shows that both vertical and lateral displacements change as the bridge length increases. The first four critical velocities of the beam-train system for the all bridge length can be determined in Table 5. Figure 23 shows the pitching and rolling movement of the car body. According to this graph, the angle of rotation increases with increased bridge length. If the length of the bridge is 30 m, according to Table 5. The maximum pitching movement is quite close to the first critical velocity of the beam-train system. Similarly, if the length of the bridge is 40–50–60 m, the maximum pitching movement occurs at speeds close to the first and second.

Fig. 22

Displacement of car body for increasing velocity and different bridge beam length a vertical displacement of car body and b lateral displacement of car body

Fig. 23

Rotation of car body for increasing velocity and different bridge beam length a pitch motion of car body and b roll motion of car body

Fig. 24

Acceleration of car body for increasing velocity and different bridge beam length a vertical acceleration of car body and b lateral acceleration of car body

Fig. 25

Displacement of bridge beams for increasing velocity and different bridge beam length a right bridge midpoint displacement and b left bridge midpoint displacement

Table 5 The first four critical velocities of the beam-train system for different bridge length

In Fig. 25, the maximum displacement of the bridge midpoint according to the bridge length is given. Accordingly, the maximum displacement amount increases as the length of the bridge beam increases, and the maximum displacement amount of the bridge midpoint occurs at lower speeds as the bridge length increases. As seen in Eq. (14), the main reason for this is that the natural frequency of the bridge depends on the length of the bridge.

In Fig. 24, the vertical acceleration of the car body increases as the length of the bridge increases, while the lateral acceleration remains almost the same.

3.7 Dynamic contact forces analysis

In this section, the vertical contact forces of the train body, bogies and wheel-rail due to train-bridge couple vibrations during the passage of the high-speed train over the bridge are analyzed by considering the speed of the train and the length of the train. When the high-speed train passes over the bridge, static forces occur in the contact area due to the train’s weight, while dynamic forces occur due to the instantaneous acceleration of the train parts due to the moving train. Therefore, the value of the contact forces is obtained by adding the static force and the dynamic force. In this section, the formulation of the train body, bogies and wheel-rail contact forces is presented in “Appendix 2”.

In Fig. 26, the train body, bogies, and rail-wheel contact forces are given in the time domain according to the train speed being constant and 300 km/h. When Fig. 26a is examined, the maximum contact force acting on the train body was 3.94 × 10⁵ N in 0.6 s, while the minimum contact force was 3.91 × 10⁵ N in 0.89 s. These determined values are quite similar to the vertical acceleration graph of the train body given in Fig. 10. Again, the same situation is the same for the vertical contact force values of the front and rear bogies. It is understood from this that in addition to the static forces caused by the mass, the dynamic forces of the vertical accelerations due to the TBI are added to the total contact force.

Fig. 26

The responses of the contact forces a contact force of train body, b contact force of bogies, c contact force of right wheels and d contact force of left wheels

In Figs. 27, 28 and 29, the contact forces of the train have been investigated according to four different bridge lengths (L = 30, 40, 50, 60 m) and the train speed being in the range of 2–200 m/s. As can be seen from the figures, the contact forces increase with the increase in the bridge length. However, in some graphics, the contact forces reach their maximum value at certain speeds. For example, in Fig. 27a, b, the maximum contact force of the bogies occurs at the low speeds of the train, while in Fig. 27c, the maximum contact force of the train body occurs at the medium speeds of the train. According to this graph, the train speeds at which the maximum contact forces of the train's body occur change as the bridge length changes. In other words, in this case, as mentioned in the previous sections, the critical speed concept of the beam-train system becomes essential. Therefore, just as vertical accelerations increase at these critical speeds, the vertical contact forces also increase. Right and left wheel-rail contact forces are given in Figs. 28 and 29, respectively. According to these graphs, if the train speed is 40 m/s or less, the contact forces are pretty high, while the contact forces are relatively low as the train speed increases.

Fig. 27

Effect of train velocity and bridge length on contact force a front bogie contact force, b rear bogie contact force and c train body contact force

Fig. 28

Effect of train velocity and bridge length on contact force a front bogie (Right wheel 1) contact force, b front bogie (Left wheel 1) contact force, c front bogie (Right wheel 2) contact force and d front bogie (Left wheel 2) contact force

Fig. 29

Effect of train velocity and bridge length on contact force a front bogie (Right wheel 3) contact force, b front bogie (Left wheel 3) contact force, c front bogie (Right wheel 4) contact force and d front bogie (Left wheel 4) contact force

4 Conclusion

In this study, dynamic analysis of the railway bridges has been conducted, which can be modeled as Euler–Bernoulli beams with 31-DOFs full railway vehicle model, in terms of the constant speed of the train, different car body masses, and different bridge lengths. For this purpose, the mathematical model of the bridge beam and full railway vehicle model was created, and the motion equations were obtained with the Lagrange method according to the model established. Dynamic responses of all train parts were found using the fourth-order Runge–Kutta method. The comparison was conducted with two different models in the literature to verify the study, and the results were found to be very similar. The results of the TBI at the end of the study are given below.

• In this study, dynamic responses were obtained quickly due to solving the motion equations created for TBI using the Runge–Kutta method.

• If the train speed is constant and 300 km/h, the maximum responses of the car body and rear bogie are almost identical, while the maximum dynamic response of the front bogie seems to have been slightly earlier.

• In the study, it is seen that the bridge parameters affect the bridge behavior. Therefore, when the frequency of the train passing over the bridge is equal to the natural frequency of the bridge, the bridge is resonant, and the bridge oscillations increase significantly. In addition, critical velocities depending on the natural frequency of the bridge are determined, and it is observed that dynamic responses increase at critical velocities.

• The effect of the body mass m_c of the train and the bridge length L on the train-bridge dynamics were examined in four different values. With the increase in both values, the vertical displacement of the car body increases, while the lateral displacement decreases with the increase in mass.

• Moreover, in this study, contact forces have been examined on wheels, bogies and train body considering train velocity and bridge length. While most of the contact forces are static forces, consisting of the mass of the train parts, dynamic forces occur due to the vertical accelerations caused by the interaction when the train passes over the bridge. Therefore, the contact force’s graphs are quite similar to vertical acceleration responses. Also, the maximum contact force values occur when the train speed is close to the critical speeds of the train-beam system.

With the proposed method to analyze interaction 3-D full model railway vehicle and flexible structure likewise bridge beam given in this study, one can simulate easily complex, nonlinear, and multi-parameter physical systems without costly and time-consuming experimental study.

Appendices

Appendix 1

Thirty-nine motion equations have been converted to seventy-eight first-order equations using the variables given in “Appendix 1”.

$$\begin{array}{llll} {{x_1} = {r_{cy}} \gg {{\dot x}_1} = {{\dot r}_{cy}} = {x_2}} \hfill & {{\text{ }}{x_{18}} = {{\dot \theta }_{b1x}} \gg {{\dot x}_{18}} = {{\ddot \theta }_{b1x}}} \hfill & {{x_{35}} = {\theta _{w1x}} \gg {{\dot x}_{35}} = {{\dot \theta }_{w1x}} = {x_{36}}} \hfill & {{x_{52}} = {{\dot \theta }_{w3x}} \gg {{\dot x}_{52}} = {{\ddot \theta }_{w3x}}} \hfill \\ {{x_2} = {{\dot r}_{cy}} \gg {{\dot x}_2} = {{\ddot r}_{cy}}} \hfill & {{x_{19}} = {\theta _{b1y}} \gg {{\dot x}_{19}} = {{\dot \theta }_{b1y}} = {x_{20}}} \hfill & {{x_{36}} = {{\dot \theta }_{w1x}} \gg {{\dot x}_{36}} = {{\ddot \theta }_{w1x}}} \hfill & {{x_{53}} = {\theta _{w3y}} \gg {{\dot x}_{53}} = {{\dot \theta }_{w3y}} = {x_{54}}} \hfill \\ {{x_3} = {r_{cz}} \gg {{\dot x}_3} = {{\dot r}_{cz}} = {x_4}} \hfill & {{x_{20}} = {{\dot \theta }_{b1y}} \gg {{\dot x}_{20}} = {{\ddot \theta }_{b1y}}} \hfill & {{x_{37}} = {\theta _{w1y}} \gg {{\dot x}_{37}} = {{\dot \theta }_{w1y}} = {x_{38}}{\text{ }}} \hfill & {{x_{54}} = {{\dot \theta }_{w3y}} \gg {{\dot x}_{54}} = {{\ddot \theta }_{w3y}}} \hfill \\ {{x_4} = {{\dot r}_{cz}} \gg {{\dot x}_4} = {{\ddot r}_{cz}}{\text{ }}} \hfill & {{x_{21}} = {r_{b2y}} \gg {{\dot x}_{21}} = {{\dot r}_{b2y}} = {x_{22}}} \hfill & {{x_{38}} = {{\dot \theta }_{w1y}} \gg {{\dot x}_{38}} = {{\ddot \theta }_{w1y}}} \hfill & {{x_{55}} = {r_{w4y}} \gg {{\dot x}_{55}} = {{\dot r}_{w4y}} = {x_{56}}} \hfill \\ {{x_5} = {\theta _{cz}} \gg {{\dot x}_5} = {{\dot \theta }_{cz}} = {x_6}{\text{ }}} \hfill & {{x_{22}} = {{\dot r}_{b2y}} \gg {{\dot x}_{22}} = {{\ddot r}_{b2y}}} \hfill & {{x_{39}} = {r_{w2y}} \gg {{\dot x}_{39}} = {{\dot r}_{w2y}} = {x_{40}}{\text{ }}} \hfill & {{x_{56}} = {{\dot r}_{w4y}} \gg {{\dot x}_{56}} = {{\ddot r}_{w4y}}} \hfill \\ {{x_6} = {{\dot \theta }_{cz}} \gg {{\dot x}_6} = {{\ddot \theta }_{cz}}} \hfill & {{x_{23}} = {r_{b2z}} \gg {{\dot x}_{23}} = {{\dot r}_{b2z}} = {x_{24}}} \hfill & {{x_{40}} = {{\dot r}_{w2y}} \gg {{\dot x}_{40}} = {{\ddot r}_{w2y}}} \hfill & {{x_{57}} = {r_{w4z}} \gg {{\dot x}_{57}} = {{\dot r}_{w4z}} = {x_{58}}} \hfill \\ {{x_7} = {\theta _{cx}} \gg {{\dot x}_7} = {{\dot \theta }_{cx}} = {x_8}{\text{ }}} \hfill & {{x_{24}} = {{\dot r}_{b2z}} \gg {{\dot x}_{24}} = {{\ddot r}_{b2z}}} \hfill & {{x_{41}} = {r_{w2z}} \gg {{\dot x}_{41}} = {{\dot r}_{w2z}} = {x_{42}}} \hfill & {{x_{58}} = {{\dot r}_{w4z}} \gg {{\dot x}_{58}} = {{\ddot r}_{w4z}}} \hfill \\ {{x_8} = {{\dot \theta }_{cx}} \gg {{\dot x}_8} = {{\ddot \theta }_{cx}}} \hfill & {{x_{25}} = {\theta _{b2z}} \gg {{\dot x}_{25}} = {{\dot \theta }_{b2z}} = {x_{26}}} \hfill & {{x_{42}} = {{\dot r}_{w2z}} \gg {{\dot x}_{42}} = {{\ddot r}_{w2z}}} \hfill & {{x_{59}} = {\theta _{w4x}} \gg {{\dot x}_{59}} = {{\dot \theta }_{w4x}} = {x_{60}}} \hfill \\ {{x_9} = {\theta _{cy}} \gg {{\dot x}_9} = {{\dot \theta }_{cy}} = {x_{10}}{\text{ }}} \hfill & {{x_{26}} = {{\dot \theta }_{b2z}} \gg {{\dot x}_{26}} = {{\ddot \theta }_{b2z}}} \hfill & {{x_{43}} = {\theta _{w2x}} \gg {{\dot x}_{43}} = {{\dot \theta }_{w2x}} = {x_{44}}} \hfill & {{x_{60}} = {{\dot \theta }_{w4x}} \gg {{\dot x}_{60}} = {{\ddot \theta }_{w4x}}} \hfill \\ {{x_{10}} = {{\dot \theta }_{cy}} \gg {{\dot x}_{10}} = {{\ddot \theta }_{cy}}{\text{ }}} \hfill & {{\text{ }}{x_{27}} = {\theta _{b2x}} \gg {{\dot x}_{27}} = {{\dot \theta }_{b2x}} = {x_{28}}} \hfill & {{x_{44}} = {{\dot \theta }_{w2x}} \gg {{\dot x}_{44}} = {{\ddot \theta }_{w2x}}{\text{ }}} \hfill & {{x_{61}} = {\theta _{w4y}} \gg {{\dot x}_{61}} = {{\dot \theta }_{w4y}} = {x_{62}}} \hfill \\ {{x_{11}} = {r_{b1y}} \gg {{\dot x}_{11}} = {{\dot r}_{b1y}} = {x_{12}}} \hfill & {{x_{28}} = {{\dot \theta }_{b2x}} \gg {{\dot x}_{28}} = {{\ddot \theta }_{b2x}}{\text{ }}} \hfill & {{\text{ }}{x_{45}} = {\theta _{w2y}} \gg {{\dot x}_{45}} = {{\dot \theta }_{w2y}} = {x_{46}}} \hfill & {{x_{62}} = {{\dot \theta }_{w4y}} \gg {{\dot x}_{62}} = {{\ddot \theta }_{w4y}}} \hfill \\ {{x_{12}} = {{\dot r}_{b1y}} \gg {{\dot x}_{12}} = {{\ddot r}_{b1y}}} \hfill & {{x_{29}} = {\theta _{b2y}} \gg {{\dot x}_{29}} = {{\dot \theta }_{b2y}} = {x_{30}}} \hfill & {{\text{ }}{x_{46}} = {{\dot \theta }_{w2y}} \gg {{\dot x}_{46}} = {{\ddot \theta }_{w2y}}} \hfill & {{x_{63}} = {q_1} \gg {{\dot x}_{63}} = {{\dot q}_1} = {x_{64}}} \hfill \\ {{x_{13}} = {r_{b1z}} \gg {{\dot x}_{13}} = {{\dot r}_{b1z}} = {x_{14}}} \hfill & {{x_{30}} = {{\dot \theta }_{b2y}} \gg {{\dot x}_{30}} = {{\ddot \theta }_{b2y}}} \hfill & {{x_{47}} = {r_{w3y}} \gg {{\dot x}_{47}} = {{\dot r}_{w3y}} = {x_{48}}} \hfill & {{x_{64}} = {{\dot q}_1} \gg {{\dot x}_{64}} = {{\ddot q}_1}} \hfill \\ {{x_{14}} = {{\dot r}_{b1z}} \gg {{\dot x}_{14}} = {{\ddot r}_{b1z}}{\text{ }}} \hfill & {{x_{31}} = {r_{w1y}} \gg {{\dot x}_{31}} = {{\dot r}_{w1y}} = {x_{32}}{\text{ }}} \hfill & {{x_{48}} = {{\dot r}_{w3y}} \gg {{\dot x}_{48}} = {{\ddot r}_{w3y}}{\text{ }}} \hfill & \vdots \hfill \\ {{x_{15}} = {\theta _{b1z}} \gg {{\dot x}_{15}} = {{\dot \theta }_{b1z}} = {x_{16}}} \hfill & {{x_{32}} = {{\dot r}_{w1y}} \gg {{\dot x}_{32}} = {{\ddot r}_{w1y}}} \hfill & {{x_{49}} = {r_{w3z}} \gg {{\dot x}_{49}} = {{\dot r}_{w3z}} = {x_{50}}} \hfill & \vdots \hfill \\ {{x_{16}} = {{\dot \theta }_{b1z}} \gg {{\dot x}_{16}} = {{\ddot \theta }_{b1z}}} \hfill & {{x_{33}} = {r_{w1z}} \gg {{\dot x}_{33}} = {{\dot r}_{w1z}} = {x_{34}}} \hfill & {{x_{50}} = {{\dot r}_{w3z}} \gg {{\dot x}_{50}} = {{\ddot r}_{w3z}}} \hfill & {{x_{62 + (2n - 1)}} = {q_n} \gg {{\dot x}_{62 + (2n - 1)}} = {{\dot q}_n} = {x_{62 + 2n}}} \hfill \\ {{x_{17}} = {\theta _{b1x}} \gg {{\dot x}_{17}} = {{\dot \theta }_{b1x}} = {x_{18}}} \hfill & {{x_{34}} = {{\dot r}_{w1z}} \gg {{\dot x}_{34}} = {{\ddot r}_{w1z}}{\text{ }}} \hfill & {{x_{51}} = {\theta _{w3x}} \gg {{\dot x}_{51}} = {{\dot \theta }_{w3x}} = {x_{52}}} \hfill & {{x_{62 + (2n)}} = {{\dot q}_n} \gg {{\dot x}_{62 + (2n)}} = {{\ddot q}_n}} \hfill \\ \end{array}$$

(20)

When Equations are written in state-space form with state variables given by Eq. (20), together with the motions of equation belonging to other coordinates, the following is obtained:

$${\dot{\mathbf{X}}}(t) = A(t){\mathbf{X}}(t) + f(t),$$

(21)

$${\mathbf{X}}(t) = \left\{ {x_{1} \, x_{2} \, \ldots \, x_{62 + (2n - 1)} \, x_{62 + 2n} } \right\}^{{\text{T}}} ,$$

(22)

Four repetitive coefficients of the Runge–Kutta method are written as follow for the differential equation system, comprising of a total of sixty-two first-degree differential equations:

$$\begin{array}{*{20}l} {k_{1(1)}^{i} = f\left( {t_{i} ,x_{1(i)} , \, x_{2(i)} , \, x_{3(i)} , \ldots ,x_{62 + 4n(i)} } \right),} \hfill \\ \vdots \hfill \\ {k_{1(62 + 2n)}^{i} = f\left( {t_{i} ,x_{1(i)} , \, x_{2(i)} , \, x_{3(i)} , \ldots ,x_{62 + 4n(i)} } \right),} \hfill \\ \end{array}$$

(23)

$$\begin{array}{*{20}l} {k_{2(1)}^{i} = f\left( {t_{i} + \frac{1}{2}\Delta t,x_{1(i)} + \frac{1}{2}k_{1(1)}^{i} \Delta t, \, x_{2(i)} + \frac{1}{2}k_{1(2)}^{i} \Delta t, \, x_{3(i)} + \frac{1}{2}k_{1(3)}^{i} \Delta t, \ldots ,x_{62 + 4n(i)} + \frac{1}{2}k_{1(62 + 4n)}^{i} \Delta t} \right),} \hfill \\ \vdots \hfill \\ {k_{2(62 + 2n)}^{i} = f\left( {t_{i} + \frac{1}{2}\Delta t,x_{1(i)} + \frac{1}{2}k_{1(1)}^{i} \Delta t, \, x_{2(i)} + \frac{1}{2}k_{1(2)}^{i} \Delta t, \, x_{3(i)} + \frac{1}{2}k_{1(3)}^{i} \Delta t, \ldots ,x_{62 + 4n(i)} + \frac{1}{2}k_{1(62 + 4n)}^{i} \Delta t} \right),} \hfill \\ \end{array}$$

(24)

$$\begin{array}{*{20}l} {k_{3(1)}^{i} = f\left( {t_{i} + \frac{1}{2}\Delta t,x_{1(i)} + \frac{1}{2}k_{2(1)}^{i} \Delta t, \, x_{2(i)} + \frac{1}{2}k_{2(2)}^{i} \Delta t,x_{3(i)} + \frac{1}{2}k_{2(3)}^{i} \Delta t, \ldots ,x_{62 + 4n(i)} + \frac{1}{2}k_{2(62 + 4n(i))}^{i} \Delta t} \right),} \hfill \\ \vdots \hfill \\ {k_{3(62 + 2n)}^{i} = f\left( {t_{i} + \frac{1}{2}\Delta t,x_{1(i)} + \frac{1}{2}k_{2(1)}^{i} \Delta t, \, x_{2(i)} + \frac{1}{2}k_{2(2)}^{i} \Delta t,x_{3(i)} + \frac{1}{2}k_{2(3)}^{i} \Delta t, \ldots ,x_{62 + 4n(i)} + \frac{1}{2}k_{2(62 + 4n)}^{i} \Delta t} \right),} \hfill \\ \end{array}$$

(25)

$$\begin{array}{*{20}l} {k_{4(1)}^{i} = f\left( {t_{i} + \Delta t,x_{1(i)} + k_{3(1)}^{i} \Delta t, \, x_{2(i)} + k_{3(2)}^{i} \Delta t, \, x_{3(i)} + k_{3(3)}^{i} \Delta t, \ldots ,x_{12 + 2n(i)} + k_{3(62 + 4n)}^{i} \Delta t} \right),} \hfill \\ \vdots \hfill \\ {k_{4(62 + 2n)}^{i} = f\left( {t_{i} + \Delta t,x_{1(i)} + k_{3(1)}^{i} \Delta t, \, x_{2(i)} + k_{3(2)}^{i} \Delta t,x_{3(i)} + k_{3(3)}^{i} \Delta t, \ldots ,x_{62 + 4n(i)} + k_{3(62 + 4n)}^{i} \Delta t} \right),} \hfill \\ \end{array}$$

(26)

$$\begin{array}{*{20}l} {x_{1(i + 1)} = x_{1(i)} + \frac{\Delta t}{6}\left( {k_{1(1)}^{i} + 2k_{2(1)}^{i} + 2k_{3(1)}^{i} + k_{4(1)}^{i} } \right)} \hfill \\ {x_{2(i + 1)} = x_{2(i)} + \frac{\Delta t}{6}\left( {k_{1(2)}^{i} + 2k_{2(2)}^{i} + 2k_{3(2)}^{i} + k_{4(2)}^{i} } \right)} \hfill \\ \vdots \hfill \\ {x_{(62 + 2n)(i + 1)} = x_{(62 + 2n)(i)} + \frac{\Delta t}{6}\left( {k_{1(62 + 2n)}^{i} + 2k_{2(62 + 2n)}^{i} + 2k_{3(62 + 2n)}^{i} + k_{4(62 + 2n)}^{i} } \right)} \hfill \\ \end{array}$$

(27)

Appendix 2

Static forces acting on wheelsets, bogies, and train body is given Eqs. (13a–c). Total contact forces have been obtained using motion equation of 31-DOFs full railway vehicle model and bridge beam as below:

The vertical force of the center of the wheelsets center is given Eq. (28), whereas the torque of the wheelset’s center is formulated as Eq. (29).

$${\mathbf{F}}_{wk} = \dot{r}_{wky} m_{w} - 2c_{wky} \left( {\dot{r}_{bjy} - \dot{r}_{wky} + \dot{\theta }_{bjz} l_{wk} } \right) - 2k_{wky} \left( {r_{bjy} - r_{wky} + \theta_{bjz} l_{wk} } \right)\quad k = 1,2 - 3,4 j = 1,2$$

(28)

$$\begin{aligned} {{\varvec{\uptau}}}_{wk} = & \ddot{\theta }_{wkx} I_{wkx} - c_{wky} d\left( {2\dot{\theta }_{bjx} d - \varphi_{i} (\xi_{kL} ,t)\dot{q}_{i} + \varphi_{i} (\xi_{kR} ,t)\dot{q}_{i} - 2\dot{\theta }_{wkx} d} \right) \ldots \quad k = 1,2 - 3,4 j = 1,2 \\ & - \;k_{wky} d\left( {2\theta_{bjx} d - \varphi_{i} (\xi_{kL} ,t)q_{i} + \varphi_{i} (\xi_{kR} ,t)q_{i} - 2\theta_{wkx} d} \right) \\ \end{aligned}$$

(29)

The forces at the points of contact of right and left wheels are expressed as follow:

$$F_{rwk} = f_{g} + F_{wk} + \frac{{\tau_{wk} }}{{l_{r} }}\quad k = 1, \ldots ,4.$$

(30)

$$F_{lwk} = f_{g} + F_{wk} - \frac{{\tau_{wk} }}{{l_{r} }}\quad k = 1, \ldots ,4.$$

(31)

The contact forces of front and rear bogies are defined as follow:

$$\begin{aligned} F_{fb} = & f_{b} + \ddot{r}_{b1y} m_{b1} - 2c_{b1y} \left( {\dot{r}_{cy} - \dot{r}_{b1y} + \dot{\theta }_{cz} l_{b1} } \right) + c_{w1y} \left( {2\dot{r}_{b1y} - \varphi_{i} (\xi_{1R} ,t)\dot{q}_{i} - \varphi_{i} (\xi_{1L} ,t)\dot{q}_{i} + 2\dot{\theta }_{b1z} l_{w1} } \right) \ldots \\ & + c_{w2y} \left( {2\dot{r}_{b1y} - \varphi_{i} (\xi_{2R} ,t)\dot{q}_{i} - \varphi_{i} (\xi_{2L} ,t)\dot{q}_{i} - 2\dot{\theta }_{b1z} l_{w2} } \right) - 2k_{b1y} \left( {r_{cy} - r_{b1y} + \theta_{cz} l_{b1} } \right) \ldots \\ & + k_{w1y} \left( {2r_{b1y} - \varphi_{i} (\xi_{1R} ,t)q_{i} - \varphi_{i} (\xi_{1L} ,t)q_{i} + 2\theta_{b1z} l_{w1} } \right)... \\ & + k_{w2y} \left( {2r_{b1y} - \varphi_{i} (\xi_{2R} ,t)q_{i} - \varphi_{i} (\xi_{2L} ,t)q_{i} - 2\theta_{b1z} l_{w2} } \right) \\ \end{aligned}$$

(32)

$$\begin{aligned} F_{rb} = & f_{b} + \ddot{r}_{b2y} m_{b2} - 2c_{b2y} \left( {\dot{r}_{cy} - \dot{r}_{b2y} - \dot{\theta }_{cz} l_{b2} } \right) + c_{w3y} \left( {2\dot{r}_{b2y} - \varphi_{i} (\xi_{3R} ,t)\dot{q}_{i} - \varphi_{i} (\xi_{3L} ,t)\dot{q}_{i} + 2\dot{\theta }_{b2z} l_{w3} } \right) \ldots \\ & + \,c_{w4y} \left( {2\dot{r}_{b2y} - \varphi_{i} (\xi_{4R} ,t)\dot{q}_{i} - \varphi_{i} (\xi_{4L} ,t)\dot{q}_{i} - 2\dot{\theta }_{b2z} l_{w4} } \right) - 2k_{b2y} \left( {r_{cy} - r_{b2y} - \theta_{cz} l_{b2} } \right) \ldots \\ & + \,k_{w3y} \left( {2r_{b2y} - \varphi_{i} (\xi_{3R} ,t)q_{i} - \varphi_{i} (\xi_{3L} ,t)q_{i} + 2\theta_{b2z} l_{w3} } \right) \ldots \\ & + \,k_{w4y} \left( {2r_{b2y} - \varphi_{i} (\xi_{4R} ,t)q_{i} - \varphi_{i} (\xi_{4L} ,t)q_{i} - 2\theta_{b2z} l_{w4} } \right) \\ \end{aligned}$$

(33)

Similarly, the contact force act on the train body is given as follow:

$$\begin{aligned} F_{tb} = & f_{t} + \ddot{r}_{cy} m_{c} + 2c_{b1y} \left( {\dot{r}_{cy} - \dot{r}_{b1y} + \dot{\theta }_{cz} l_{b1} } \right) + 2c_{b2y} \left( {\dot{r}_{cy} - \dot{r}_{b2y} - \dot{\theta }_{cz} l_{b2} } \right) \ldots \\ & { + }\,2k_{b1y} \left( {r_{cy} - r_{b1y} + \theta_{cz} l_{b1} } \right) + 2k_{b2y} \left( {r_{cy} - r_{b2y} - \theta_{cz} l_{b2} } \right) \\ \end{aligned}$$

(34)