Introduction

Railway transportation is one of the fastest-growing modes of transportation for both inter and intra-city movements. The rise in metro facilities, monorail, tram services and high-speed trains globally is clearly at par with the recent technological advancements in railway engineering. Most developing economies such as India, Brazil [1], Turkey, and Saudi Arabia, are developing new high-speed corridors. At the same time, they want to exploit the maximum capacity of their existing massive rail infrastructures comprising railway tracks, trains, stations and bridges. Indian Railways is no exception and is currently focused on updating its existing infrastructure, increasing the speed of the current passenger and freight trains and introducing new high-speed corridors [2]. Simultaneously, the Indian Railways is working to utilise the existing bridge and track capacity to run the train at a higher speed. As a result, it is critical to investigate the impact of high-speed trains on existing infrastructure. Railway bridges are an essential element of the railway infrastructure, and it is crucial to examine the impact of high-speed trains on bridge dynamics and performance [3]. The current study focuses on the train–track–bridge interaction [4] of a composite steel–concrete bridge in the context of, but not limited to, Indian Railways. The emphasis is on examining the dynamic behaviour of existing bridge structures under the effect of high-speed trains, evaluating the train’s safety in terms of ride comfort, and analysing the high-speed train’s environmental impact on the nearby structures and human settlements.

The study of railway dynamics is a subject of great interest and is still being explored due to the complexities in train–bridge interaction behaviour [5]. The high-speed train produces a considerable vibration on the bridge structure, which affects the bridge’s serviceability and is also a concern for train vehicle safety, reducing passenger ride comfort [6]. The steel–concrete composite bridges are used extensively for the high-speed railway network in developed countries such as Japan, China, and European nations due to significant advantages related to the structure’s design, durability, and cost. However, it is necessary to check and evaluate the problems associated with dynamic effects and interaction phenomenon, fatigue loading, structural modelling and damage assessment [7]. The bridge resonance, in particular, is among various response characteristics that is of interest mainly due to the structural safety of the bridge [8, 9]. Due to their lightness and damping capacities, composite bridges can experience resonance-induced vibration at speeds slower than the design speed [10].

Liu et al. [11] studied the fatigue assessment of the composite Sesia viaduct and identified train speed and mass ratio as significant factors that determine the dynamic effect. Adam et al. [12] analysed the dynamic response of compound bridges under moving loads. Nguyen et al. [13] presented the analytical models for dynamic analysis of short skew bridges under moving loads and found that the degree of skewness has an important influence on the vertical displacement but hardly on the vertical acceleration of the bridge. Hoorpah [14] studied the dynamic analysis of high-speed railway composite bridges in France. Sieffert et al. [15] studied the application of a diaphragm at midspan on the static and dynamic behaviour of a composite railway bridge and concluded that a diaphragm is not necessary except for accidental lateral loads. Melo et al. [16] performed the train-bridge system’s dynamic analysis, considering the non-linear behaviour of the track–deck interface. Matsuoka et al. [17] focused on the dynamic simulation and critical assessment of a composite bridge in a high-speed railway for a case study of the Sesia viaduct. Shibeshi and Roth [18] conducted a dynamic analysis of a 77-year-old single-span steel truss railway bridge using experimental, analytical and three-dimensional finite element analysis.

The periodic loading due to moving train gives rise to the driving and dominant frequencies. When these frequencies or their integral multiples match the fundamental frequency of the bridge, there is amplification in the bridge’s global response [19, 20], which might affect the bridge’s and train’s serviceability [21, 22]. The passenger ride comfort can decrease substantially due to amplification in the bridge response. Ride comfort depends on several factors such as bridge span length, train speed, train compartment length, vehicle suspension, etc. [23,24,25]. Ride comfort can be measured using Sperling’s ride index based on the Wz method (Werzungzahl) [26], ISO 2631 standard [27] and the European method [28].

The environmental impact of high-speed trains is another critical area that needs attention. The effect of high-speed trains is always portrayed as an environment-friendly mode of transportation [29]. However, high-frequency noise and low-frequency vibration originating at the wheel–rail interface interfere with equipment working, affect the structure’s durability [30, 31] close to the rail track and causes a nuisance in the nearby facilities [32,33,34] demanding the application of suitable mitigation measures [35]. The Federal Transit Administration [36] (FTA) has issued guidelines to limit the intensity of train-induced vibrations. The methods for controlling train-induced vibration are divided into three stages: generation, propagation, and reception. The primary approach is to dampen the vibrations at the source, and the track structure’s elastic support absorbs the energy transmitted owing to ground vibration propagation [37]. Proper vibration assessment in train–track–bridge interactions requires an accurate description of track structures. The modelling of layered track structure requires complex iterative models [38, 39]; however, analysis can be simplified using simple viscoelastic foundations [40].

Further, an efficient and accurate numerical model for the vehicle is necessary to model the load transfer between train and track [41]. The interaction between train and bridge is basically divided into three categories based on the modelling strategy adopted, i.e. moving load, moving mass and moving spring-damper system model. The moving load model [42] is the simplest and most efficient but cannot consider the train–bridge interaction effect, which can be studied using the moving mass model [43]. The moving mass spring damper system [44, 45] combines lumped masses, rigid bars, and spring and dashpot, considering interaction and vehicle motion.

In the comprehensive discussion above, it is clear that bridge dynamics has been a topic of interest from the early days, and continuous research in this field is necessary with the advancement in railway technology. The two-dimensional (2D) finite element method (FEM) [46, 47] is used to develop the train–track–bridge interaction model with the application of the coupled approach [48]. The moving mass-spring-damper system is used for vehicle modelling. The properties of Linke Hofmann Busch (LHB) trains and composite steel–concrete railway bridges of Indian Railways are used for parametric studies. The modelling strategy adopted is discussed in Sect. 2, and validation of the numerical model is shown in Sect. 3. The ride comfort is discussed in Sect. 4, and parametric analysis is performed in Sect. 5. Finally, the significant outcomes are discussed in Sect. 6.

The Train–Track–Bridge Dynamic Interaction Model

The dynamic interaction model is developed using the 2D FEM and solved using numerical techniques based on the dynamic interaction one proposed by Zhai and Cai [49]. The analysis is bifurcated into two separate subsystems, i.e. vehicle and track–bridge. The interaction between the two subsystems is accomplished by the wheel–rail interaction forces that arise at the interface [41].

Train System

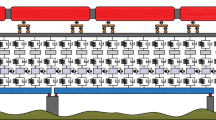
The properties of the LHB air-conditioned (AC) two-tier German-designed broad gauge (BG) coach with a seating capacity of 48 [50, 51] is used to assess the ride comfort and evaluate the dynamic response of a bridge at critical locations. The multibody dynamics concept [52, 53] is used to model a train where a vehicle’s degrees of freedom (DOFs) are assigned to the vehicle’s body’s motion. The train running on the bridge at a constant speed combines several carriages and locomotives. Figure 1 illustrates a train’s numerical model where each component, i.e. carbody, bogie and wheelset, is modelled as a rigid body connected by spring and damper elements. Each carbody and bogies have vertical and pitch displacement, and for each wheelset, only vertical displacement is considered. Thus, a total of 10 DOFs is established for a 4-axle train vehicle. Here, \(y_{ci}\) is the vertical displacement of an ith carbody \(\left( {i = 1 - 10} \right)\); \(y_{tij}\) is the vertical displacement of jth bogie of an ith carbody \(\left( {j = 1 - 2} \right)\); \(\varphi_{ci}\) is the pitch displacement of an ith carbody; \(\varphi_{tij}\) is the pitch displacement of jth bogie of an ith carbody; \(y_{wijl}\) is the vertical displacement of lth wheelset of jth bogie of an ith carbody \(\left( {l = 1 - 4} \right)\).

Fig. 1
figure 1

10 DOFs 4-axle vehicle model

Full size image

However, the vertical displacement of the wheelset is restrained by the rail displacement, reducing the vehicle-independent DOFs to six. The 10 LHB coaches are considered in the present work, and their technical specifications are shown in Table 1. The mass matrix \(M_{v}\) of a vehicle with the order \(\left( {6 \times N_{v} } \right) \times \left( {6 \times N_{v} } \right)\) is written as follows;

$$M_{v} = {\text{diag}}\left[ {\begin{array}{*{20}c} {M_{v1} } & {M_{v2} } & \cdots & {M_{v10} } \\ \end{array} } \right],$$
(1)

here \(M_{vi}\) is a mass matrix of an ith vehicle and can be written as follows;

$$M_{vi} = {\text{diag}}\left[ {\begin{array}{*{20}c} {m_{{\text{c}}} } & {j_{{\text{c}}} } & {m_{{{\text{br}}}} } & {j_{{{\text{br}}}} } & {m_{{{\text{bf}}}} } & {j_{{{\text{bf}}}} } \\ \end{array} } \right],$$
(2)

here subscripts r and f represent the rear and front bogie.

Table 1 Technical specifications of LHB coaches [50, 51]
Full size table

The stiffness matrix \(K_{v}\) of a vehicle with the order \(\left( {6 \times N_{v} } \right) \times \left( {6 \times N_{v} } \right)\) is written as follows;

$$K_{v} = {\text{diag}}\left[ {\begin{array}{*{20}c} {K_{v1} } & {K_{v2} } & \cdots & {K_{v10} } \\ \end{array} } \right],$$
(3)

here \(K_{vi}\) is a stiffness matrix of an ith vehicle and can be written as follows;

$$K_{v1} = \left[ {\begin{array}{*{20}c} {2k_{{\text{s}}} } & { - k_{{\text{s}}} L_{1} + k_{{\text{s}}} L_{2} } & { - k_{{\text{s}}} } & 0 & { - k_{{\text{s}}} } & 0 \\ { - k_{{\text{s}}} L_{1} + k_{{\text{s}}} L_{2} } & {k_{{\text{s}}} L_{1}^{2} + k_{{\text{s}}} L_{2}^{2} } & {k_{{\text{s}}} L_{1} } & 0 & { - k_{{\text{s}}} L_{2} } & 0 \\ { - k_{{\text{s}}} } & {k_{{\text{s}}} L_{1} } & {k_{{\text{s}}} + 2k_{{\text{p}}} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {2k_{{\text{p}}} L_{{\text{b}}}^{2} } & 0 & 0 \\ { - k_{{\text{s}}} } & { - k_{{\text{s}}} L_{2} } & 0 & 0 & {k_{{\text{s}}} + 2k_{{\text{p}}} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {2k_{{\text{p}}} L_{{\text{b}}}^{2} } \\ \end{array} } \right].$$
(4)

The damping matrix \(C_{v}\) of a vehicle with the order \(\left( {6 \times N_{v} } \right) \times \left( {6 \times N_{v} } \right)\) is written as follows;

$$C_{v} = {\text{diag}}\left[ {\begin{array}{*{20}c} {C_{v1} } & {C_{v2} } & \cdots & {C_{v10} } \\ \end{array} } \right],$$
(5)

here \(C_{vi}\) is a stiffness matrix of an ith vehicle and can be written as follows;

$$C_{v1} = \left[ {\begin{array}{*{20}c} {2c_{{\text{s}}} } & { - c_{{\text{s}}} L_{1} + c_{{\text{s}}} L_{2} } & { - c_{{\text{s}}} } & 0 & { - c_{{\text{s}}} } & 0 \\ { - c_{{\text{s}}} L_{1} + c_{{\text{s}}} L_{2} } & {c_{{\text{s}}} L_{1}^{2} + c_{{\text{s}}} L_{2}^{2} } & {c_{{\text{s}}} L_{1} } & 0 & { - c_{{\text{s}}} L_{2} } & 0 \\ { - c_{{\text{s}}} } & {c_{{\text{s}}} L_{1} } & {c_{{\text{s}}} + 2c_{{\text{p}}} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {2c_{{\text{p}}} L_{{\text{b}}}^{2} } & 0 & 0 \\ { - c_{{\text{s}}} } & { - c_{{\text{s}}} L_{2} } & 0 & 0 & {c_{{\text{s}}} + 2c_{{\text{p}}} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {2c_{{\text{p}}} L_{{\text{b}}}^{2} } \\ \end{array} } \right].$$
(6)

The use of a 2D train numerical model is only suitable to study the vertical vibrations, and the lateral dynamics is neglected, in the present study. The use of 2D analysis is motivated by the assumption that the vertical bridge vibration will primarily affect the vertical response of the vehicle. Moreover, the comparison of 2D and 3D vehicle models carried out by Arvidsson et al. [25] shows an excellent agreement of the wheel–rail force between the 2D and 3D models.

Bridge Systems

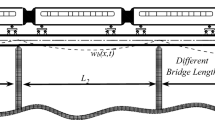
The present analysis uses composite girder railway bridges designed for a 25t loading of three different span lengths. The ballasted track system shown in Fig. 2 is primarily used by the Indian railways for surface and elevated corridors. The track system consists of rail, rail pads, sleepers, and ballast. In a dynamic coupled analysis, the track is crucial because it transfers load from the wheels to the bridge deck and reduces vibration. The schematic layout of a simply supported composite railway bridge is shown in Fig. 3a and b. It consists of two—I shape riveted steel girders, horizontal and vertical brace systems, concrete deck slabs, sleepers and rail systems.

Fig. 2
figure 2

Ballasted track system

Full size image
Fig. 3
figure 3

Schematic representation of a bridge. a Side view. b Cross-sectional view

Full size image

The concept of a 2D FEM is used to model track and bridge structures. Since the train–bridge interaction problem lies in an elastic range, a reduced model of a composite bridge is used to simplify an analysis in which steel girders are replaced with equivalent concrete structures using the modulus of elasticity. The fundamental behaviour of simply supported bridges can be described by the 2D Euler Bernoulli beams’ dynamic behaviour [54,55,56]. Hence, the bridge structure is modelled as an Euler beam divided into several elements of equal lengths with elastic supports. The bridge’s mass is assumed to be a cumulative mass of the bridge structure, and there is no vertical displacement in columns and foundations. Moreover, shear deformation is neglected and only bending is considered in a beam. These assumptions are equitable here as only the dynamic vibration of the bridge structure and vehicle dynamic behaviour are analysed. An embankment of equal length lies on the bridge’s left and right side, and a rail is resting on a viscoelastic foundation for the entire length. The equivalent stiffness and damping of the viscoelastic foundation are calculated for soft to stiff pads using a spring analogy where rail pads, sleeper and ballast are considered in a series combination [57]. This simplification reduces the analysis’s complexity and includes the effect of rail pads, sleeper, and ballast in the viscoelastic foundation. The bridge structures’ global mass, stiffness and damping matrices are formulated using the classical 2D finite element theory discussed in several published literature [55, 58, 59].

It is to be noted here that, the use of 2D numerical model for the bridge neglects the torsional mode of vibrations in the bridge. However, this assumption holds good for the bridges having a torsional frequency much larger than the vertical vibration frequency. A 3D model of the considered bridges shows the ratio of torsional to vertical frequency as 5, which justifies the use of 2D model as per Eurocode EN 1990:2002 + A1 [60].

Train–Track–Bridge Coupling

The train and bridge subsystems are coupled together to form a dynamic coupled train–track–bridge interaction model. As shown in Fig. 4, the train moves at a constant speed on a rail beam resting on a viscoelastic foundation. The embankment provided in a model ensures that the vehicle reaches a dynamic equilibrium before reaching a bridge [61].

Fig. 4
figure 4

Train–track–bridge coupled system

Full size image

The train–track–bridge coupled equations of motion solution are based upon time history integral techniques performed using numerical integration such as Newmark-β and Wilson-θ methods [62]. Xia. et al. [59] discussed three different methodologies for analysing train–bridge interaction problems, i.e. the direct coupling iteration method [63], in which equations of motion of various subsystems are established as a unified system. The in-time-step iteration method [64], where train and bridge systems are solved separately, and interaction is achieved through wheel–rail interaction forces. It is required that both the train and bridge systems fulfil the convergence requirement. The intersystem iteration method [65] is similar to the previous process; the only difference lies in convergence criteria. The wheel–rail interaction forces are used as an index for convergence judgment. Direct coupling is adopted in the present work to analyse the dynamic interaction between train, track and bridge. Each of the subsystems is defined by the second-order differential equation. The corresponding equation of a unified system in a submatrix form is represented by Eq. 7.

$$\left[ {\begin{array}{*{20}c} {M_{v} } & 0 & 0 \\ 0 & {M{}_{T}} & 0 \\ 0 & 0 & {M_{B} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\ddot{X}_{v} } \\ {\ddot{X}_{T} } \\ {\ddot{X}_{B} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {C_{v} } & {C_{VT} } & 0 \\ {C_{TV} } & {C_{T} } & {C_{TB} } \\ 0 & {C_{BT} } & {C_{B} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\dot{X}_{v} } \\ {\dot{X}_{T} } \\ {\dot{X}_{B} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {K_{v} } & {K_{VT} } & 0 \\ {K_{TV} } & {K_{T} } & {K_{TB} } \\ 0 & {K_{BT} } & {K_{B} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {X_{v} } \\ {X_{T} } \\ {X_{B} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {F_{v} } \\ {F_{T} } \\ {F_{B} } \\ \end{array} } \right\}$$
(7)

Here, M, K, and C represent the global mass, stiffness and damping matrix of a system, together with the external force vector F solved for the X DOFs. The subscript v, T and B stand for a vehicle, track and bridge, respectively. The interaction between train and track is represented by matrices having subscript VT or TV and between track and bridge by subscript BT or TB. The detailed derivation of these matrices can be found in papers [66, 67]. The coupling terms in Eq. (7) depend on the beam element’s shape function and mechanical properties of the system. They are time-dependent terms, which means that their value must be updated at each time step of numerical integration. In the coupled approach, the DOFs of a wheel are integrated with the rail’s DOFs. As a result, wheel masses are added to the track’s mass matrix (\(M_{T}\)) at each time step [45]. The external force vector is the combined effect of gravity load and dynamic excitation due to the track profile at the wheel–rail interface [20, 68, 69]. The wheel–rail interaction forces are included in the formulation as an internal force in the coupled approach. The dynamic Eq. (7) is solved using the Newmark-β method to obtain the train, track and bridge responses. The damping in a bridge is defined using the Ryleigh Damping, in which the damping matrix is a linear combination of mass and stiffness matrix and is represented as follows;

$$C = \alpha \left[ M \right] + \beta \left[ K \right]$$
(8)
$$\alpha = \frac{{2D\omega_{1} \omega_{2} }}{{\omega_{1} + \omega_{2} }}{\text{ and }}\beta = \frac{2D}{{\omega_{1} + \omega_{2} }},$$
(9)

here, \(\omega_{1}\) and \(\omega_{2}\) are the first and second circular natural frequencies of a bridge [70], and D is a damping ratio of 2% for the first and second bridge mode. The finite element model of rail and simply supported bridge is discretised in an element size of 0.5 m. The sensitivity analysis highlighted that a time step of 0.001 s gives a stable solution and is selected for numerical simulation.

Track Irregularity

The track irregularity profiles are generated using the power spectral density functions (Eq. 10) provided by the Federal Railroad Administration [71]. A sample profile of track irregularity along the track’s longitudinal direction shown in Fig. 5 is generated using the trigonometric series or spectral representation method [55] for grades 1–6. The grade 6 track irregularity sample is used in the present work.

$$S_{v} \left( \omega \right) = KA\frac{{\omega_{c}^{2} }}{{\left( {\omega^{2} + \omega_{c}^{2} } \right)\omega^{2} }}\left( {{\text{cm}}^{2} {\text{/rad/m}}} \right).$$
(10)
Fig. 5
figure 5

Track irregularity

Full size image

Validation of the Numerical Model

The numerical model is validated by the results published in the literature [67]. The analysis is done for a train running speed of 10–110 m/s with an increment of 2 m/s. The time step of analysis is fixed to 0.0005 s for each speed, and train and track properties are taken from Ref. [67] (readers can refer to Tables 1 and 2 of Ref. [67] for train and track properties, respectively). Figure 6 compares the maximum value of bridge midpoint displacement and acceleration obtained from the numerical model with published work at various speeds. It can be seen that the numerical model is correctly predicting the outcome.

Fig. 6
figure 6

Validation of the numerical model a comparison of maximum midpoint displacement, b comparison of maximum midpoint acceleration

Full size image

Ride Comfort

The train ride comfort is evaluated using Sperling’s ride index (SI) [72], a well-known parameter in railway dynamics, to assess passengers’ ride comfort. The SI is a low-cost computational technique compared to the other ride comfort indexes such as EN or UIC, which require a minimum of 5 min of acceleration time history. The stepwise methodology to evaluate SI is shown in Fig. 7.

Fig. 7
figure 7

Methodology to compute ride comfort index

Full size image

The vertical car body acceleration is transformed to a frequency domain using the fast Fourier transform (FFT). Eventually, the Sperling frequency filter \(\left( {B\left( f \right)} \right)\) shown in Eq. (11) is applied to obtain the weighted car body acceleration in the frequency domain. The weighted acceleration in the time domain is acquired through inverse Fourier transform (IFT).

$$B\left( f \right) = \left\{ {0.588\left[ {\frac{{1.911f^{2} + \left( {0.25f^{2} } \right)^{2} }}{{\left( {1 - 0.277f^{2} } \right)^{2} + \left( {1.563f - 0.0368f^{3} } \right)^{2} }}} \right]^{0.5} } \right\}.$$
(11)

The SI (WZ) is obtained using Eq. (12). Here, \(a_{{{\text{rms}}}}\) is the root mean square of the weighted acceleration in a time domain.

$$W_{Z} = 4.42\left( {a_{{{\text{rms}}}} } \right)^{0.3} .$$
(12)

The ride comfort conditions defined as per the range of SI are given in Table 2, and it is clear that for moderate and comfortable conditions, SI should be below 2.5.

Table 2 Ride comfort scales [73]
Full size table

The flexibility in a carbody is represented by an equivalent free-free Euler–Bernoulli beam, with a constant section and uniformly distributed mass to consider the vertical bending modes. Several authors have used flexible models to evaluate the ride index. The literature review highlighted that for low and medium speed upto 250 km/h, not much difference is observed between the rigid and flexible car body models. However, for higher speed and low frequency of the first flexural mode, a significant difference is observed in ride index value for the rigid and flexible car body models. The study by Bokaeian et al. [74] highlighted the effect of bending flexural modes of the car body on the ride index. They concluded that the first bending flexural mode has the highest influence on the vehicle’s ride quality. Moreover, the ride quality index is not affected significantly by flexural modes for the velocities between 140 and 250 km/h. However, for a train speed higher than 250 km/h, the effect of bending modes on the ride quality index becomes clear. The study by Kunpeng et al. [75] shows that car-body flexibility has little influence on bridge responses and vehicle running safety indices but greatly influences car-body accelerations. Dumitriu and Dihoru [76] showed that the contribution of the bending vibration is noticeable at high velocities, and at low bending vibration frequency difference is more vivid. Dumitriu and Cruceanu [77] highlighted the significance of the vertical symmetrical bending of the car body on the vehicle’s dynamic response, mainly at high velocities, and the ride comfort is greatly affected should the frequency of this vibration mode is lower than 10 Hz. Zhou et al. [78] concluded that at frequencies higher than 7 Hz, ride quality has the same value for rigid and flexible car body.

Parametric Study

The parametric analysis is carried out on the developed dynamically coupled numerical model to study the dynamic behaviour and performance of existing steel–concrete composite railway bridges. The various parameters, i.e. train speed, bridge span length and track properties that affect the dynamic response of the train–track–bridge system, are discussed elaborately in the present work. As mentioned in Sect. 2.1, the ten identical LHB coaches travelling at a constant speed over the simply supported composite bridge are considered for the parametric analysis. As discussed in Sect. 2.2, composite railway bridges of short (19.40 m), medium (25.280 m) and long (31.90 m) span lengths are considered for the parametric study and their equivalent mechanical properties are reported in Table 3. The properties of the ballasted track structure currently in use in the Indian Railways calculated using the spring analogy are elaborated in Table 4. The overall stiffness and damping of ballasted track structure increase from R1 to R6.

Table 3 Bridge and rail mechanical properties
Full size table
Table 4 Properties of ballasted track structure
Full size table

Dynamic Behaviour of Train–Track–Bridge System

The bridge responses are evaluated at different speeds ranging from 2 m/s (7.2 km/h) to 110 m/s (396 km/h) for varying track properties and various span lengths to study the dynamic behaviour of the bridge structures under the influence of LHB trains. The maximum displacement and acceleration obtained at the midpoint of a bridge using a validated numerical model at different speeds for various span lengths are shown in Fig. 8. The displacement and acceleration increase with an increase in train speed and reaches a peak value at a bridge’s resonance speed for all the span lengths. Further, with an increase in span length, bridges’ flexural rigidity and stiffness increase, leading to a decrease in acceleration amplitude, as shown in Fig. 8. It is also interesting that, except at higher speeds where amplitude somewhat fluctuates with a change in track parameters, the influence of track stiffness and damping on bridge response is insignificant.

Fig. 8
figure 8

Bridge midpoint displacement for span length of a 19.4 m, c 25.28 m, e 31.9 m and bridge midpoint acceleration for span length of b 19.4 m, d 25.28 m, f 31.9 m

Full size image

The resonance property is an essential natural characteristic that governs the bridge design [43]. The train loading mainly excites two types of frequencies in the bridge structures, i.e. driving and dominant frequencies. Driving frequencies [79] depend on the vehicle’s duration of crossing the bridge, and dominant frequencies [80] arise due to repeated loads. Mathematically, driving frequencies \(\left( {f_{{{\text{dr}}}} } \right)\) can be represented as, \(f_{{{\text{dr}}}} = nv/2L^{\prime}\) and dominant frequencies \(\left( {f_{{{\text{do}}}} } \right)\) can be represented as, \(f_{{{\text{do}}}} = nv/L_{{\text{c}}}\) [81] where \(L_{{\text{c}}}\) denotes the characteristic length of a vehicle compartment (24 m), \(v\) is the train speed in m/s, and \(n = 1, 2, 3, \ldots , \infty\) represents a higher harmonic frequency. The driving frequencies are contained in the bridge dynamic response due to a single moving vehicle, and when these frequencies approach the bridge fundamental frequency, amplification in the bridge response occurs, giving rise to the critical speed. The current study focuses on the dynamic behaviour of railway bridges associated with repeated loads induced by multiple cars passing through. These repeated loads give rise to dominant frequencies. When a dominant frequency or its integral multiple approaches the bridge fundamental frequency, the bridge response is amplified.

The speed parameter \(S_{k}\), defined as the ratio of the exciting frequency to the frequency of the beam is another critical factor considered in bridge dynamics and is represented using the following expression,

$$S_{k} = \frac{k\pi v}{{\omega_{k} L^{\prime}}},$$
(13)

here \(\omega_{k}\) is the kth natural frequency of the simply supported bridge structure. The speed parameter \(S_{1}\) of the first mode [82] primarily governs the maximum dynamic response of the beam travelled by the vehicle. Further, Yang et al. [83] showed that for the given compartment length and span length, the resonant speed parameter could be found as;

$$S_{1} = \frac{{L_{{\text{c}}} }}{{2nL^{\prime}}}.$$
(14)

The resonance may occur at \(S_{1} = 0.50L_{{\text{c}}} /L^{\prime},0.250\quad L_{{\text{c}}} /L^{\prime},0.167\quad L_{{\text{c}}} /L^{\prime},0.125\quad L_{{\text{c}}} /L^{\prime},...\) by letting \(n = 1, 2, 3, \ldots , \infty\) in Eq. (14). The time and frequency domain comparisons of midpoint displacement of the bridge of various span lengths are shown in Fig. 9, and the critical frequencies are shown in Table 5.

Fig. 9
figure 9

Comparison of bridge midpoint displacement and frequency spectrum for span length of a, b 19.4 m; c, d 25.28 m; e, f 31.9 m

Full size image
Table 5 Critical frequencies
Full size table

The resonance takes place when the integral multiple of the dominant frequency \(f_{{{\text{do}}}}\) matches the fundamental frequency of the bridge. Moreover, as seen in Table 5, the speed parameter \(S_{1}\) obtained from Eq. (13) satisfies Eq. (14) for \(n = 4\) at resonance condition. Further, the frequency plot shown in Fig. 9b, d and f shows enlarged peaks of dominant frequencies. Moreover, at resonance speed, as seen from Fig. 9a, c and e, a clear amplification can be seen in the bridge’s midpoint response; however, bridge deflection closely resembles the trainload pattern at all other speeds.

Dynamic Impact Factor of Bridges

The dynamic effect of a running train is higher in bridge members than normal static load, and this effect is considered in the bridge design codes as an impact factor (I) [84]. The impact factor depends on several factors, including bridges’ and vehicles’ dynamic characteristics and actions [85]. Mathematically, the impact factor is represented by the following expression,

$$I = \frac{{d_{{{\text{dyn}}}} - d_{{{\text{sta}}}} }}{{d_{{{\text{sta}}}} }},$$
(15)

here \(d_{{{\text{dyn}}}}\) and \(d_{{{\text{sta}}}}\) are the maximum dynamic and static displacement of the midpoint of a bridge evaluated at different speeds, respectively. In most design codes, span length is identified as a critical factor affecting the dynamic response of a bridge structure and is an essential parameter of bridge design. Numerous design codes evaluate impact factors in terms of span length; for instance, RDSO [86] suggests Eq. (16) to consider the impact factor of a single span track subjected to a maximum speed of 160 kmph (44.4 m/s);

$$I = 0.15 + \frac{8}{6 + L}.$$
(16)

AASTHO manual recommends Eq. (17) for impact factor;

$$I = \frac{15.24}{{L + 38.1}} < 30\% .$$
(17)

Iranian code suggests Eq. (18) for evaluating impact factor;

$$I = \left\{ {\begin{array}{*{20}c} {\frac{1.44}{{\sqrt L - 0.2}} + 0.82:{\text{ Good maintenance}}} \\ {\frac{2.16}{{\sqrt L - 0.2}} + 0.73{\text{ : Other situations}}} \\ \end{array} } \right..$$
(18)

The American Railway Engineering and Maintenance-of-Way Association (AREMA) has proposed Eq. (19) for calculating the impact factor in steel railway bridges;

$$I = \left\{ {\begin{array}{*{20}c} {40 - \frac{{3L^{2} }}{148.6}} & {L \le 24} \\ {16 + \frac{182.9}{{L - 9.1}}} & {L \ge 24} \\ \end{array} } \right..$$
(19)

The bridge impact factors obtained from the validated model are shown in Fig. 10, and the comparison of impact factors of different standards is given in Table 6.

Fig. 10
figure 10

Bridge impact factor for span length of a 19.4 m, b 25.28 m, c 31.9 m

Full size image
Table 6 Bridge impact factor
Full size table

It can be seen that the impact factor of the bridge is below the limitation set by different standards except at the resonance condition. Further, it can be observed that the impact factor decreases with an increase in span length. Moreover, multiple or single-tuned mass dampers can be used to counter the effect of resonance in composite bridges [87, 88]. However, the application of tuned mass dampers is beyond the scope of the present study.

Environmental Impact of High-Speed Train

Several standards are available worldwide to evaluate and supervise the vibrations generated inside a structure due to railways. As discussed in the International standard ISO 2631-1-1997 [27], the frequency weighting technique is adopted to evaluate the vertical vibration acceleration level (VAL) in decibel (dB). The evaluated vibration levels are compared with the Chinese standard GB 10070-88 [89] limits listed in Table 7 for various application scopes.

Table 7 Classification and vibration limits [89]
Full size table

The vibration levels are evaluated using the acceleration responses generated on the bridge structure. The vibration levels produced near railway lines or inside the structures near the high-speed corridors are assumed to be comparable to a vibration level generated at the bridge structure [57]. The VAL for the long-span bridge is relatively lower in magnitude than short and medium-span bridges, as seen in Fig. 11. In addition, in general, a steep rise can be seen in VAL until resonance occurs, and after that, a gradual increase is observed. Moreover, the VAL for all the span lengths surpasses the threshold limit of 80 dB mentioned in Table 7, which may cause damage to the nearby structures and affect human comfort. Besides this, obtained vibration levels are compared with the vibration level criteria curve of FTA [36] shown in Fig. 11d, and it can be seen that the vibration level surpasses the limit for each type of land use. Thus it becomes imperative to adopt vibration mitigation measures [35] on or near the track to reduce train-induced vibrations’ adverse effects.

Fig. 11
figure 11

Vibration level for span length of a 19.4 m, b 25.28 m, c 31.9 m. d Vibration level criteria curve for detailed vibration analysis

Full size image

Ride Comfort of LHB Coaches

The ride comfort of vehicles is of great concern for the trains travelling at high speed on the bridges [90]. In the present analysis, the SI explained in Sect. 4 is calculated at various speeds and track properties for short, medium, and long-span bridges to assess the ride comfort of the vehicles. The SI evaluated for different conditions is shown in Fig. 12, and it is clear that ride comfort varies considerably with the span length and track properties. For all the span lengths, a steep rise in ride index value can be seen upto 40 kmph, and after that, a gradual decline can be seen with an increase in the train speed.

Fig. 12
figure 12

Sperling’s Ride Index for span length of a 19.4 m, b 25.28 m, c 31.9 m

Full size image

Moreover, it can be seen that the train’s ride comfort surpasses the threshold value \(\left( {{\text{Wz}} = 2.5} \right)\) at a very low speed for medium and long-span railway bridges, but for small-span bridges ride index lies well below the threshold value, owing to the fact that low frequencies generated in medium and long-span bridges amplify the train vibration modes. Furthermore, a general observation is that ride comfort improves with an increase in track damping and stiffness at the same speed.

Conclusions

The present work investigated the efficiency of existing steel–concrete composite railway bridges subjected to a high-speed train. A coupled approach based on the two-dimensional finite element method has been used to develop the train–track–bridge dynamic interaction model. The generalised research has been carried out using the case study of Indian Railways. The dynamic performance of the existing composite girder railway bridge is adequate to operate the high-speed train; however, the critical assessment of the railway bridge is necessary under resonance conditions. The ride comfort estimated using Sperling’s ride index has shown significant variation with span length and is “clearly noticeable” at medium and high speeds for all span lengths. Moreover, the vibration level generated due to high-speed trains has exceeded the limitations set by FTA and GB 10070-88 for various land use categories. This might annoy residents and cause minor damage to nearby structures unless some mitigation measures are used. In addition, research highlights that increasing the stiffness and damping of the track from R1 to R6 has no considerable effect on the bridge response. However, ride comfort has improved with an increase in track damping and stiffness at the same speed.

It is worth noting that although some assumptions related to the modelling of bridges and trains have limited the application of the proposed model, the presented approach has effectively simplified the calculation of the complex interaction of the train–track–bridge system.