1 Introduction

The non-Newtonian fluid has various applications in science and technology [1,2,3]. Theoretical studies give the important information related to investigation and modeling of mass and energy transfer in non-Newtonian fluids [4,5,6]. Generally, the flow behavior of non-Newtonian fluids is much complex as compare to Newtonian fluids. Non-Newtonian fluids such as polymeric solutions, muddy, coal-water, inks, blood and oils [7,8,9] contained a nonlinear relationship between viscous shear stress and velocity gradient. Such type of fluids is generally used in chemical and polymer processing, namely bubbles absorption, composite and molten plastic foam processing, etc. Rheological features of non-Newtonian fluids are commonly used in biomedical and biological devises. Generally, non-Newtonian fluid models lead the constitutive nonlinear stress–strain relation, which lead the nonlinear equations of motion. It is clearly noted that non-Newtonian fluids model cannot be addressed by a single constitutive equation between shear rate and shear stress. Due to such reason, some famous non-Newtonian models proposed by various authors such as: Akbar et al. [10] used the asymmetric channel for the peristaltic flow of Williamson nano-fluid. They used fifth-order Runge–Kutta–Fehlberg method to solve the nonlinear differential equations and presented some important results in the form of streamlines, velocity and temperature profiles. Slips effects on peristaltic flow of Jeffery’s fluid in an asymmetric channel were discussed by Akbar and Nadeem [11]. They concluded that the pressure is an increasing function of Hartmann number, perturbation, thermal slip and relaxation parameter. Ellahi [12] examined the slip effects on Oldroyd eight constant fluid in a channel, and Homotopy analysis method was implemented to solve the nonlinear boundary value problem. Analytical study of flow of Casson fluid over an exponentially shrinking sheet under the effects of magnetic field was investigated by Nadeem et al. [13]. Alamri et al. [14] used the Cattaneo–Christov heat flux model in the flow of second grade fluid over a stretching cylinder to explores the heat transfer characteristics. The effects of inclined magnetic field and heat transfer analysis on peristaltically induced motion of particle through uniform channel were analyzed by Bhatti et al. [15]. The effects of mass and bioheat transfer on MHD two-phase Sisko fluid inside the porous channel were determined by Bhatti et al. [16]. They used the homotopy perturbation method to find the series solution of the modeled equations. Ellahi et al. [17] investigated the combined effects of slip and entropy generation on MHD boundary layer flow over a moving plate. Hassan et al. [18] utilized the Dupuit–Forchheimer and Darcy’s law models for the investigation of heat transfer phenomena of nano-fluid in a porous wavy surface. Effects of magnetic dipole and suction on the viscoelastic fluid over a stretching sheet were explored by Majeed et al. [19]. A numerical investigation of free convection flow inside a porous inclined rectangular conduit under the effect of surface radiation was analyzed by Shirvan et al. [20]. They employed finite volume method for the solution of couple nonlinear partial differential equations. Hassan et al. [21] obtained the analytical expression of velocity and temperature profiles for Cu–Ag/water hybrid nanofluids inside the inverted cone. Yousaf et al. [22] performed the shooting method for the study of thermal boundary layer flow of non-Newtonian fluid over an exponentially permeable stretching sheet.

Extensive literature can be seen in which many models have been proposed to account the viscosity’s dependence on temperature of the fluid. For this, there are two famous models are noted in the literature, namely Reynolds and Vogel’s models. Some, useful studies on variable viscosity models are presented in the next paragraph.

Turkyilmazoglu [23, 24] used the variable physical properties to account the magnetic and thermal radiation effects over rotating porous body. Bhatti et al. [25] examined the effects of slip condition and variable viscosity on clot blood model. Ellahi and Riaz [26] investigated the effects of variable properties on third-grade fluid in a pipe and presented the explicit analytical solution of the problem. In another study, Ellahi [27] examined the effects of magnetohydrodynamic flow of third-grade fluid inside the tube under the different viscosity models. He used the homotopic analysis method to predict the important results.

Power-law model is mostly use to predict the behavior of non-Newtonian fluids. Mathematically, the power-law model looks like simple model but having some restriction over Eyring–Powell fluids. In modern era, numerous researchers have used the Powel-Eyring fluid model and illustrated the various aspects. For this, Hayat et al. [28] used the series solution method to find the solution of nonlinear modeled equations of Eyring–Powell fluid and highlighted the important results. Hayat et al. [29] analyzed the effects of magnetic field, heat generation/absorption and thermal radiation on Eyring–Powell fluid over a stretching cylinder. Finite difference numerical technique was performed by Akbar et al. [30] to capture the effects of magnetic field on flow of Eyring–Powell fluid over a stretching surface. Nadeem and Saleem [31] employed the optimal homotopy analysis method to solve the nonlinear partial differential equations of Eyring–Powell fluid model and pointed out some useful results. The effects of physical parameters on MHD Eyring–Powell fluid over a rotating surface were investigated by Khan et al. [32]. Hayat et al. [33] applied the homotopy approach for the investigation of Eyring–Powell fluid over a stretching sheet under the effects of Brownian motion and magnetic field.

According to Ellahi et al. [34], the non-Newtonian fluid models are divided into three different classes, namely integral, rate types and differential. The Eyring–Powell fluid model has certain advantages over other non-Newtonian models like Power-law model because it shows Newtonian behavior against low and high shear rates. The Eyring–Powell fluid model is derived from kinematic theory rather than empirical relation, due to this reason it is favorite over other non-Newtonian fluid models. Such model characterizes the behavior of viscoelastic suspension and polymeric solutions against extensive ranges of shear rates. In the present study, the Eyring–Powell fluid inside the pipe under the effects of magnetic field is incorporated. To our best knowledge, there is no investigation available that deals with the flow of temperature dependent Eyring–Powell fluid in a pipe. Such type of flow configuration is commonly used in polymeric liquids, slurries and food stuffs, etc. [35]. In this investigation, the motivation emanates from a desire to realize the effects of magnetic field on Eyring–Powell fluid in a pipe. The shooting method based on Newton method [36, 37] is implemented to find the solution of considered problem. The important results of present study are highlights with the help of plots.

2 Problem formulation

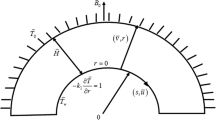
Let us consider the steady-state fully developed, incompressible one-dimensional MHD flow of Eyring–Powell fluid inside a pipe. It is assumed that the fluid is flowing inside the pipe is electrical conducting fluid with applied uniform magnetic field \(\varvec{B}_{0}\). Further, we have neglected the electric and induced magnetic. The fluid flow inside the pipe is due to constant pressure gradient. The geometry of the present problem is shown in Fig. 1. However, here the rheology of fluid flowing in the pipe is characterized by Erying–Powell model. In particular, the analysis is carried out for three different viscosity models.

Fig. 1
figure 1

Geometry of the considered study

Full size image

The Cauchy-stress tensor for the current study is [38]

$${\mathbf{S}} = \left[ {\mu + \frac{1}{{K_{2} }}\frac{{\text{Sinh}^{ - 1} \left( {K_{3} \dot{\psi }} \right)}}{{\dot{\psi }}}} \right]{\mathbf{A}}_{1} ,\quad {\text{where}}\quad \dot{\psi } = \sqrt {\frac{1}{2}{\text{tra}}\left( {{\mathbf{A}}_{1}^{2} } \right)} .$$
(1)

Powell and Erying [38] present the relation given in Eq. (1). With the help of \(\text{Sinh}^{ - 1}\) approximation

$$\text{Sinh}^{ - 1} \left( {K_{3} \dot{\psi }} \right) \cong K_{3} \dot{\psi } - \frac{1}{6}\left( {K_{3} \dot{\psi }} \right)^{3} ,\quad \left| {K_{3} \dot{\psi }} \right| \ll 1.$$
(2)

The new form of Eq. (1) is

$${\mathbf{S}} = \left[ {\mu + \text{A} - \frac{B}{6}\dot{\psi }^{2} } \right]{\mathbf{A}}_{1} ,\quad B \ll 1,$$
(3)

where \(A = \frac{{K_{3} }}{{K_{2} }}\) and \(B = \frac{{K_{3}^{3} }}{{K_{2} }}\).

The velocity and temperature fields are defined by the given expression

$${\mathbf{V}} = \left[ {0,0,w\left( r \right)} \right],$$
(4)
$$\theta = \theta \left( r \right).$$
(5)

In view of Eq. (4), the stress tensor has the following form

$${\mathbf{S}} = \left( {\mu + A - \frac{B}{6}\left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{2} } \right)\left( {\begin{array}{*{20}c} 0 & 0 & {\left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)} \\ 0 & 0 & 0 \\ {\left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)} & 0 & 0 \\ \end{array} } \right).$$
(6)

It is noted that from above equation, \(S_{rz} \left( {S_{zr} } \right)\) only non-vanishing components of stress tensor S

$$S_{rz} = S_{zr} = \left( {\mu + A - \frac{B}{6}\left( {\frac{dw}{dr}} \right)^{2} } \right)\left( {\frac{dw}{dr}} \right).$$
(7)

In the present situation, equations of continuity and conservation of momentum are given by

$$\frac{\partial w}{\partial z} = 0,$$
(8)
$$0 = - \frac{\partial p}{\partial z} + \frac{1}{r}\frac{\partial }{\partial r}\left( {rS_{rz} } \right) - \sigma B_{0} w,$$
(9)

Substituting the values \(S_{rz}\) into Eq. (9), we have

$$\frac{1}{r}\frac{\text{d}}{{{\text{d}}r}}\left( {\mu r\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right) + \frac{1}{r}\frac{\text{d}}{{{\text{d}}r}}\left( {r\left( {A\frac{{{\text{d}}w}}{{{\text{d}}r}} - \frac{B}{6}\left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{3} } \right)} \right) - \sigma B_{0} w = \frac{{{\text{d}}p}}{{{\text{d}}z}}.$$
(10)

The energy equations in the present problem take the following form:

$$\frac{\mu }{k}\left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{2} + \frac{A}{k}\left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{2} - \frac{B}{6k}\left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{4} + \frac{{{\text{d}}^{2} \theta }}{{{\text{d}}r^{2} }} + \frac{1}{r}\frac{{{\text{d}}\theta }}{{{\text{d}}r}} = 0.$$
(11)

The boundary conditions of Eqs. (10) and (11) are

$$w = 0,\quad \theta = \theta_{w} ,\quad {\text{at}}\quad r = R,\quad {\text{and}}\quad \frac{{{\text{d}}w}}{{{\text{d}}r}} = \frac{{{\text{d}}\theta }}{{{\text{d}}r}} = 0\quad {\text{at}}\quad r = 0.$$
(12)

With the help of normalized quantities [4], the new form of Eqs. (10)–(12) are:

$$\frac{1}{{\bar{r}}}\frac{\text{d}}{{{\text{d}}\bar{r}}}\left( {\bar{\mu }\bar{r}\frac{{{\text{d}}w}}{{{\text{d}}\bar{r}}}} \right) + \frac{1}{{\bar{r}}}\frac{\text{d}}{{{\text{d}}\bar{r}}}\left( {\bar{r}\left( {A\frac{{{\text{d}}\bar{w}}}{{{\text{d}}\bar{r}}} - \frac{B}{6}\left( {\frac{{{\text{d}}\bar{w}}}{{{\text{d}}\bar{r}}}} \right)^{3} } \right)} \right) - M_{e}^{2} \bar{w} = C,$$
(13)
$$\frac{{{\text{d}}^{2} \bar{\theta }}}{{{\text{d}}\bar{r}^{2} }} + \frac{1}{{\bar{r}}}\frac{{{\text{d}}\bar{\theta }}}{{{\text{d}}\bar{r}}} + \frac{{\bar{\mu }}}{k}\left( {\left( {\frac{{{\text{d}}\bar{w}}}{{{\text{d}}\bar{r}}}} \right)^{2} + \frac{A}{{\bar{\mu }}}\left( {\frac{{{\text{d}}\bar{w}}}{{{\text{d}}\bar{r}}}} \right)^{2} - \frac{B}{{6\bar{\mu }}}\left( {\frac{{{\text{d}}\bar{w}}}{{{\text{d}}\bar{r}}}} \right)^{4} } \right) = 0,$$
(14)
$$\bar{w} = 0,\quad \bar{\theta } = 0\quad at\quad \bar{r} = 1,\quad and\quad \frac{{d\bar{w}}}{{d\bar{r}}} = \frac{{d\bar{\theta }}}{{d\bar{r}}} = 0\quad at\quad \bar{r} = 0.$$
(15)

where \(M_{e}^{2} = {\raise0.7ex\hbox{${\sigma B_{0} R}$} \!\mathord{\left/ {\vphantom {{\sigma B_{0} R} {\mu_{0} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\mu_{0} }$}}\) is the magnetic parameter.

It is noted that the momentum equation will be different against different viscosity models such form is defined separately in separate section.

2.1 Constant viscosity model

For this case, \(\bar{\mu } = 1\), and Eq. (13) becomes

$$\frac{\text{d}}{{{\text{d}}\bar{r}}}\left( {\bar{r}\frac{{{\text{d}}\bar{w}}}{{{\text{d}}\bar{r}}}} \right) + M\frac{\text{d}}{{{\text{d}}\bar{r}}}\left( {\bar{r}\left( {\frac{{{\text{d}}\bar{w}}}{{{\text{d}}\bar{r}}}} \right)\left( {1 - \chi^{*} \left( {\frac{{{\text{d}}\bar{w}}}{{{\text{d}}\bar{r}}}} \right)^{2} } \right)} \right) = \bar{r}\left( {C + M_{e}^{2} \,\bar{w}} \right),$$
(16)

where \(M = \frac{A}{{\mu_{0} }},\chi^{*} = \frac{{K_{3}^{2} w_{0}^{2} }}{{6\mu_{0} R^{2} }}.\)

2.2 Reynold’s model

According to this model \(\mu \left( \theta \right) = \mu_{0} e^{ - n\theta }\) therefore \(\bar{\mu } = e^{{ - n\theta_{w} }} e^{{ - L\bar{\theta }}}\) and

$$\begin{aligned}& e^{{ - L\bar{\theta }}} \frac{1}{{\bar{r}}}\frac{\text{d}}{{{\text{d}}\bar{r}}}\left( {\bar{r}\frac{{{\text{d}}\bar{w}}}{{{\text{d}}\bar{r}}}} \right) - Le^{{ - L\bar{\theta }}} \frac{{{\text{d}}\bar{\theta }}}{{{\text{d}}\bar{r}}}\frac{{{\text{d}}\bar{w}}}{{{\text{d}}\bar{r}}}\\&\quad + \frac{M}{{\bar{r}}}\frac{\text{d}}{{{\text{d}}\bar{r}}}\left( {\bar{r}\left( {\frac{{{\text{d}}\bar{w}}}{{{\text{d}}\bar{r}}} - \chi^{*} \left( {\frac{{{\text{d}}\bar{w}}}{{{\text{d}}\bar{r}}}} \right)^{3} } \right)} \right) - M_{e}^{2} \bar{w} = C, \end{aligned}$$
(17)

where \(\chi^{*} = \frac{{K_{3}^{2} w_{0}^{2} }}{{6\mu^{*} R^{2} }}\) and \(\mu^{*} = \mu_{0} e^{{ - n\theta_{w} }}\). For this case \(\lambda\) in Eq. (11) is defined by \(\lambda = {\raise0.7ex\hbox{${\mu^{*} w_{0}^{2} }$} \!\mathord{\left/ {\vphantom {{\mu^{*} w_{0}^{2} } {k\left( {\theta_{m} - \theta_{w} } \right)}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${k\left( {\theta_{m} - \theta_{w} } \right)}$}}\).

2.3 Vogel’s model

For this model \(\mu \left( \theta \right) = \mu_{0} e^{{\left( {\frac{X}{{Y + \bar{\theta }}}} \right)}}\) or \(\bar{\mu } = e^{{\theta_{w} }} e^{{\left( {\frac{X}{{Y + \bar{\theta }}} - \theta_{w} } \right)}}\). Thus dimensionless equation of motion in this case is

$$\begin{aligned} & e^{{\left( {\frac{X}{{Y + \bar{\theta }}} - \theta_{w} } \right)}} \frac{1}{{\bar{r}}}\frac{\text{d}}{{{\text{d}}\bar{r}}}\left( {\bar{r}\frac{{{\text{d}}\bar{w}}}{{{\text{d}}\bar{r}}}} \right) - \frac{X}{{\left( {Y + \bar{\theta }} \right)^{2} }}e^{{\left( {\frac{X}{{Y + \bar{\theta }}} - \theta_{w} } \right)}} \frac{{{\text{d}}\bar{\theta }}}{{{\text{d}}\bar{r}}}\frac{{{\text{d}}\bar{w}}}{{{\text{d}}\bar{r}}} \\&\quad+ \frac{M}{{\bar{r}}}\frac{\text{d}}{{{\text{d}}\bar{r}}}\left( {\bar{r}\left( {\frac{{{\text{d}}\bar{w}}}{{{\text{d}}\bar{r}}} - \chi^{*} \left( {\frac{{{\text{d}}\bar{w}}}{{{\text{d}}\bar{r}}}} \right)^{3} } \right)} \right) - M_{e}^{2} \bar{w} = C, \\ \end{aligned}$$
(18)

where \(\mu^{*} = \mu_{0} e^{{\theta_{w} }} .\)

The boundary conditions of Eqs. (16)–(18) are

$$\bar{w} = 0\quad {\text{at}}\quad \bar{r} = 1,\quad {\text{and}}\quad \frac{{{\text{d}}\bar{w}}}{{{\text{d}}r}} = 0\quad {\text{at}}\quad \bar{r} = 0.$$
(19)

The shooting method is selected for the solution of the given boundary value problems. The detail of shooting method is present in the next section.

3 Numerical solution

It is noted that the analytical solution of each system in each case is not possible due to nonlinearity and coupling appear in each equation. Due to this reason, the boundary value problem of an ordinary differential equations is solved with numerical technique (shooting method). Various techniques have been implemented to obtain the solution of complex rheological models which are cited in introduction section. The main problem noted with such type of techniques is that when you discretize the differential equations into system of algebraic equations it is time consuming and we get highly nonlinear algebraic structure. Particularly, it takes penalty of time when we enhance the interval and number of mesh points to attain the accuracy. The shooting method based on Runge–Kutta scheme of order 4 combined with Newton–Raphson’s method, based on step-by-step technique in which we use previous solution to approximate the next one. In this scheme, all the differential equations have unit order. This numerical scheme is very eminent, less time consuming, stable and rapidly convergent as explained in [39,40,41,42,43,44,45,46,47,48,49,50]. In some cases, when we have physical constraints on dependent variable, the iterative numerical solution of discretized nonlinear boundary value problems by using Newton–Raphson method is divergent. In this scenario, we prefer to use shooting method. The graphical results and discussion are given in next section. The flowchart is presented below to show the short view of this method that how to work this method. For the employment of the shooting method, first of all we want to transform the achieved system of equation of the constant viscosity case, such as

$$\frac{{{\text{d}}\bar{w}}}{{{\text{d}}\bar{r}}} = \bar{f}_{1} ,$$
(20)
$$\frac{{{\text{d}}^{2} \bar{w}}}{{{\text{d}}\bar{r}^{2} }} = \frac{{{\text{d}}\bar{f}_{1} }}{{{\text{d}}\bar{r}}},$$
(21)
$$\frac{{{\text{d}}\bar{\theta }}}{{{\text{d}}\bar{r}}} = \bar{f}_{2} ,$$
(22)
$$\frac{{{\text{d}}^{2} \bar{\theta }}}{{{\text{d}}\bar{r}^{2} }} = \frac{{{\text{d}}\bar{f}_{2} }}{{{\text{d}}\bar{r}}}.$$
(23)
$$\frac{{{\text{d}}\bar{f}_{1} }}{{{\text{d}}\bar{r}}} = \frac{{\left[ {\bar{r}\left( {C + M_{e}^{2} \bar{w}} \right) + M\chi^{*} \bar{f}_{1}^{3} - \left( {1 + M} \right)\bar{f}_{1} } \right]}}{{\bar{r}\left[ {\left( {1 + M} \right) - 3M\chi^{*} \bar{f}_{1}^{2} } \right]}},$$
(24)
$$\frac{{{\text{d}}\bar{f}_{2} }}{{{\text{d}}\bar{r}}} = - \left[ {\frac{{\bar{f}_{2} }}{{\bar{r}}} + \lambda \bar{f}_{1}^{2} \left( {1 + M - M\chi^{*} \bar{f}_{1}^{2} } \right)} \right],$$
(25)
$$\bar{w}\left( 0 \right) = k,\quad \bar{f}\left( 0 \right) = 0,\quad \bar{\theta }\left( 0 \right) = l,\quad \bar{g}\left( 0 \right) = 0.$$
(26)

In above (26), k and l represent the unknown slopes (missing conditions) and these are pick as boundary conditions at unity are fulfilled. In the numerical implementation of shooting method, we face singularity at \(\bar{r} = 0\). In fact, we need \(\bar{w}^{\prime \prime } \left( 0 \right)\) and \(\bar{\theta }^{\prime \prime } \left( 0 \right)\) to start Runge–Kutta fourth-order method. By using L’Hospital’s rule, we computed the values of

$$\bar{w}^{\prime \prime } \left( 0 \right) = \frac{{M_{e}^{2} \bar{w}_{0} + C}}{{2\left( {1 + M} \right)}},$$
(27)

and

$$\bar{\theta }^{\prime \prime } \left( 0 \right) = 0.$$
(28)
figure a

4 Results and discussion

In this portion, we intend to explore the obtained results. Here, we focused velocity \(w\left( r \right)\) and temperature \(\theta \left( r \right)\) through variation in some important parameters. The nonlinear boundary value problem is solved with the help of eminent shooting method based on Newton–Raphson method. Total eight figures are plotted in this section in which Figs. 2 and 3 are for constant case, Figs. 4, 5, 6 and 7 are for the case of temperature dependent viscosity (Reynolds and Vogel’s model), and absolute errors between numerically computed velocity and temperature are depicted in Fig. 8. In each figure, left panel is for the velocity and right panel for the temperature profiles. Figure 2 predicts the effects of magnetic parameter \(M_{e}\) on velocity and temperature profiles, respectively. From the figure, it can be seen that the velocity and temperature profile decreases with increasing the values of magnetic parameter \(M_{e}\). It is evident that when magnetic forces or Lorentz forces (friction forces) are dominating over viscous forces as a result the velocity of the fluid is showing decreasing trend against magnetic parameter and boundary layer thickness is also decreases. Figure 3 illustrates the behavior of Eyring–Powell parameter M on velocity and temperature fields. It scrutinized that the velocity and temperature decays through M. Physically, for increasing the values of M, the viscosity of the fluid will decrease; therefore, the resistance in the fluid particle decreases and less heat is produced. The effects of magnetic parameter \(M_{e}\) on velocity and temperature fields are highlighted in Fig. 4 for the case of Reynolds model. It is noted that the effects of magnetic parameter are similar as we have shown for the case of constant viscosity model. Basically, the velocity and temperature fields are decreasing function of magnetic parameter for both cases namely, constant and Reynods model cases. Figure 5 depicts the effects of pressure gradient on velocity and temperature profiles. It is clearly noted that both velocity and temperature profiles rises via magnitude of the pressure gradient. It is noted that when C becomes negative, the velocity of the fluid is going maximum at the center of the pipe physically which means that thickness of the velocity boundary layer decreases. Figure 6 illustrates the effects of \(M_{e}\) on \(w\left( r \right)\) and \(\theta \left( r \right)\) for the case of Vogel’s model. It is clearly noted that the velocity and temperature profiles having similar trend against the values of magnetic parameter \(M_{e}\) as we discussed into previous two cases. The effects of parameter Y are presented in Fig. 7. The velocity and temperature fields are also increases with increasing the value of Y. To verify the numerical results obtained from shooting method, we solve numerically the same problem via pseudo-spectral collocation method for different cases. The absolute errors between numerically computed velocity and temperature are depicted in Fig. 8. The numerically values of velocity and temperature for \(M_{e} = 1, 2, 3\) are four and five digits accurate comparing with pseudo-spectral collocation method.

Fig. 2
figure 2

Effects via \(M_{e}\) on \(w\) and \(\theta\)

Full size image
Fig. 3
figure 3

Effects via \(M\) on \(w\) and \(\theta\)

Full size image
Fig. 4
figure 4

Effects via \(M_{e}\) on \(w\) and \(\theta\)

Full size image
Fig. 5
figure 5

Effects via \(C\) on \(w\) and \(\theta\)

Full size image
Fig. 6
figure 6

Effects via \(M_{e}\) on \(w\) and \(\theta\)

Full size image
Fig. 7
figure 7

Effects via \(Y\) on \(w\) and \(\theta\)

Full size image
Fig. 8
figure 8

Absolute error in velocity and temperature for \(M_{e} = 1, 2, 3\)

Full size image

5 Conclusions

The steady-state MHD Eyring–Powell fluid inside the infinite long pipe is discussed here through numerically. The coupled nonlinear ordinary differential equations arise from the mechanics of fluid. The simulations are constructed for both constant and variable viscosity models. The effects of some important parameters on velocity \(w\left( r \right)\), and temperature \(\theta \left( r \right)\) are noted with the help of plots. The major outcomes are listed below:

  • The velocity and temperature fields are diminishing with increasing \(M_{e}\) in all cases, namely constant, Reynolds and Vogel’s models.

  • Both velocity and temperature profiles rise via magnitude of the pressure gradient and material parameter Y.

  • The validity of our numerical results due to shooting method is presented by comparing them with the numerical results produced by pseudo-spectral collocation method. Relative absolute errors are plotted and achieved accuracies are of the order four and five in w and \(\theta,\) respectively.