Computational study of non-Newtonian Eyring–Powell fluid from a vertical porous plate with biot number effects

Abstract

In this article, the nonlinear, steady-state boundary layer flow and heat transfer of an incompressible Eyring–Powell non-Newtonian fluid from a vertical porous plate is investigated. The transformed conservation equations are solved numerically subject to physically appropriate boundary conditions using a second-order versatile, implicit finite-difference Keller Box technique. The numerical code is validated with previous studies. The influence of a number of emerging non-dimensional parameters, namely Eyring–Powell rheological fluid parameters (ε), the local non-Newtonian parameter based on length scale x (δ), Prandtl number (Pr), Biot number (γ) and dimensionless tangential coordinate (ξ) on velocity and temperature evolution in the boundary layer regime are examined in detail. Furthermore, the effects of these parameters on surface heat transfer rate and local skin friction are also investigated. It is found that the velocity is reduced with increasing ε but temperature is increased. Increasing δ enhances velocity but reduces temperature. The increasing γ is observed to enhance both velocity and temperature. And an increasing Prandtl number Pr is found to decrease both velocity and temperature.

1 Introduction

For a long time, there has been considerable interest in non-Newtonian fluids. This is because non-Newtonian fluids are found to be of great commercial importance. Examples of such fluids include coal–oil slurries, shampoo, paints, clay coating and suspensions, grease, cosmetic products, custard, physiological liquids (blood, bile, synovial fluid), etc. The classical equations employed in simulating Newtonian viscous flows, i.e. the Navier–Stokes equations fail to simulate a number of critical characteristics of non-Newtonian fluids. Hence several constitutive equations of non-Newtonian fluids have been presented over the past decades. The relationship between the shear stress and rate of strain in such fluids are very complicated in comparison to viscous fluids. The viscoelastic features in non-Newtonian fluids add more complexities in the resulting equations when compared with Navier–Stokes equations. Significant attention has been directed at mathematical and numerical simulation of non-Newtonian fluids. Recent investigations have implemented, respectively, the Casson model [1], second-order Reiner-Rivlin differential fluid models [2], Eringen micro-morphic models [3], Maxwell fluid flow model [4], Carreau fluid model [5], Nanofluid model [6], Williamson Nanofluid model [7] and Jeffery’s viscoelastic fluid model [8].

Convective heat transfer has also mobilized substantial interest owing to its importance in industrial and environmental technologies including energy storage, gas turbines, nuclear plants, rocket propulsion, geothermal reservoirs, photovoltaic panels, etc. The convective boundary condition has also attracted some interest and this usually is simulated via a Biot number in the wall thermal boundary condition. Recently, Ishak [9] discussed the similarity solutions for flow and heat transfer over a permeable surface with convective boundary condition. Aziz [10] provided a similarity solution for laminar thermal boundary layer over a flat surface with a convective surface boundary condition. Aziz [11] further studied hydrodynamic and thermal slip flow boundary layers with an iso-flux thermal boundary condition. The buoyancy effects on thermal boundary layer over a vertical plate subject a convective surface boundary condition was studied by Makinde and Olanrewaju [12]. Further analyses include Makinde and Aziz [13]. Gupta et al. [14] used a variational finite element to simulate mixed convective-radiative micropolar shrinking sheet flow with a convective boundary condition. Swapna et al. [15] studied convective wall heating effects on hydromagnetic flow of a micropolar fluid. Makinde et al. [16] studied cross diffusion effects and Biot number influence on hydromagnetic Newtonian boundary layer flow with homogenous chemical reactions and MAPLE quadrature routines. Bég et al. [17] analysed Biot number and buoyancy effects on magnetohydrodynamic thermal slip flows. Subhashini et al. [18] studied wall transpiration and cross-diffusion effects on free convection boundary layers with a convective boundary condition. Hayat et al. [19] presented a simple isothermal Nanofluid flow model through a porous space of homogeneous–heterogeneous reactions under the physically acceptable convective type boundary conditions. Ahmad and Mustafa [20] addressed the rotating flow of Nanofluids induced by an exponentially stretching sheet. They implemented the convective boundary conditions to inspect the thermal boundary layer. Junaid et al. [21] considered the three-dimensional rotating flow of Nanofluid induced by a convectively heated deformable surface. They used the shooting approach combined with fifth-order Runge–Kutta method to determine the velocity and temperature distributions above the sheet. Junaid et al. [22] theoretically studied the boundary layer flow of Nanofluid past an exponentially stretching sheet.

An interesting non-Newtonian model developed for chemical engineering systems is the Eyring–Powell fluid model. This rheological model has certain advantages over the other non-Newtonian formulations, including simplicity, ease of computation and physical robustness. Furthermore, it is deduced from kinetic theory of liquids rather than the empirical relation. Additionally, it correctly reduces to Newtonian behavior for low and high shear rates [23]. Several communications utilizing the Eyring–Powell fluid model have been presented in the scientific literature. Hayat et al. [24] numerically studied the chemical reaction and double stratification effects in the flow induced by a nonlinear stretching surface with variable thickness of Eyring–Powell liquid. They examined the heat transfer by considering non-Fourier heat flux model. Najeeb et al. [25] presented the two-layer Eyring–Powell fluid flow in a vertical channel along with nanoparticles using homotopy analysis method. Hayat et al. [26] reported the magnetohydrodynamic boundary layer flow of Powel-Eyring Nanofluid past a non-linear stretching sheet of variable thickness. Khalil-Ur-Rehman et al. [27] analyzed the magnetohydrodynamic boundary layer stagnation point flow of Eyring–Powell fluid induced by an inclined stretching cylindrical surface in the presence of both mixed convection and Joule heating effects using fifth-order Runge–Kutta algorithm with shooting scheme. Waqas et al. [28] investigated the heat and mass transfer in stagnation point flow of PowellEyring liquid due to stretched cylinder using homotopy analysis method. They considered the non-Fourier double-diffusion characteristics that feature the thermal and concentration relaxation factors. Hina et al. [29] explored the peristaltic flow of Eyring–Powell fluid through curved passage with complaint walls in the presence of viscous dissipation and thermophoresis effects using perturbation technique. Hayat et al. [30] investigated the influence of Hall currents on peristaltic transport of conducting Eyring–Powell fluid in an inclined symmetric channel in the presence of Joule heating effect and velocity and thermal slip effects using perturbation technique. Hayat et al. [31] also communicated the magnetohydrodynamic flow of Eyring–Powell nanomaterial bounded by a nonlinear stretching sheet for small magnetic Reynolds number using homotopy analysis method. Other studies on Eyring–Powell fluid include Bhatti et al. [32], Abdul gaffar et al. [33–36].

The objective of the present study was to investigate the laminar boundary layer flow and heat transfer of an Eyring–Powell non-Newtonian fluid from a vertical porous plate. The non-dimensional equations with associated dimensionless boundary conditions constitute a highly nonlinear, coupled two-point boundary value problem. An implicit finite difference “Keller box” scheme is implemented to solve the problem. The effects of the emerging thermophysical parameters, namely the rheological parameters (ε,δ), Biot number (γ), Prandtl number (Pr) on the velocity, temperature, local skin friction and heat transfer rate (local Nusselt number) characteristics are studied. The present problem has to the authors’ knowledge not appeared thus far in the scientific literature and is relevant to polymeric manufacturing processes.

2 Non-Newtonian constituive Eyring–Powell fluid model

In the present study a subclass of non-Newtonian fluids known as the Eyring–Powell fluid is employed owing to its simplicity. Mathematically, the Eyring–Powell model is given as

$$A = - pI + \varGamma ,$$

(1)

where the extra stress tensor Γ is defined as

$$\varGamma = \mu A_{1} + \frac{1}{{\beta \mathop \gamma \limits^{.} }}\sinh^{ - 1} \left( {\frac{1}{C}\mathop \gamma \limits^{.} } \right)A_{1}$$

(2)

Here μ is dynamic viscosity, β and C are the rheological Eyring–Powell fluid model [37] parameters. Considering the second-order approximation of the sinh⁻¹ function as

$$\sinh^{ - 1} \left( {\frac{1}{C}\mathop \gamma \limits^{.} } \right) \cong \frac{1}{C}\mathop \gamma \limits^{.} - \frac{1}{6}\left( {\frac{1}{C}\mathop \gamma \limits^{.} } \right)^{3} ,\,\,\,\,\,\,\,\,\left| {\frac{1}{C}\mathop \gamma \limits^{.} } \right| \ll 1$$

(3)

Therefore, Eq. (2) takes the form

$$\varGamma = \left( {\mu + \frac{1}{\beta C}} \right)A_{1} - \frac{1}{{6\beta C_{3} }}\left( {\mathop \gamma \limits^{.} } \right)^{2} A_{1} ,$$

(4)

where $\mathop \gamma \limits^{.} = \sqrt {\frac{1}{2}trA_{1}^{2} }$ and the kinematical tensor A ₁ is $A_{1} = \nabla V + \left( {\nabla V} \right)^{T}.$

The introduction of the appropriate terms into the flow model is considered next. The resulting boundary value problem is found to be well-posed and permits an excellent mechanism for the assessment of rheological characteristics on the flow behaviour.

3 Mathematical flow model

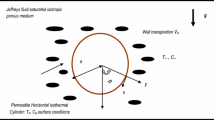
Steady, double-diffusive, laminar, incompressible, buoyancy-driven convection flow and heat transfer of an Eyring–Powell from a vertical porous plate are illustrated in Fig. 1. Both plate and Eyring–Powell fluid are initially maintained at the same temperature. Instantaneously it is raised to a temperature $T_{w} \left( { > T_{\infty } } \right)$, where the latter (ambient) temperature of the fluid remains constant. The x-coordinate is measured from the leading edge of the plate and the y-coordinate is measured normal to the plate. The corresponding velocities in the x and y directions are u and v, respectively. The gravitational acceleration g, acts vertically downwards. The Boussineq approximation holds, i.e. the density variation is only experienced in the buoyancy term in the momentum equation. Introducing the boundary layer approximations, the equations of mass, momentum and energy can be written as follows:

Fig. 1

Physical model

$$\frac{\partial u}{\partial x} + \frac{\partial u}{\partial y} = 0$$

(5)

$$u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = \left( {\nu + \frac{1}{\rho \beta C}} \right)\frac{{\partial^{2} u}}{{\partial y^{2} }} - \frac{1}{{2\rho \beta C^{3} }}\left( {\frac{\partial u}{\partial y}} \right)^{2} \frac{{\partial^{2} u}}{{\partial y^{2} }} + g\beta_{1} \left( {T - T_{\infty } } \right)$$

(6)

$$u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \alpha \frac{{\partial^{2} T}}{{\partial y^{2} }}$$

(7)

The Eyring–Powell fluid model introduces a mixed derivative into the momentum boundary layer in Eq. (6). The non-Newtonian effects feature in the shear terms only of Eq. (6) and not the convective (acceleration) terms. The third term on the right-hand side of Eq. (6) represents the thermal buoyancy force and couples the velocity field with the temperature field Eq. (7). Viscous dissipation effects are neglected in the model. In Eqs. (5)–(7), u and $v$ are the velocity components in the x and y directions, respectively, and all the parameters are defined in nomenclature.

The appropriate boundary conditions are

$$\begin{aligned} {\text{At }}y = 0,\quad u = 0,\quad v = - V_{w} ,\,\quad - k\frac{\partial T}{\partial y} = h_{w} \left( {T_{w1} - T} \right)\,, \hfill \\ As\,\,y \to \infty ,\,\quad u \to 0,\,\quad T \to T_{\infty } \hfill \\ \end{aligned}$$

(8)

where $V_{w}$ denotes the uniform transpiration (blowing or suction) velocity at the surface of the vertical plate, $k$ is the thermal conductivity, $h_{w}$ is the convective heat transfer coefficient and $T_{w1}$ is the convective fluid temperature. To transform the boundary value problem to a dimensionless one, we introduce a stream function ψ defined by the Cauchy–Riemann equations, $u = \frac{\partial \psi }{\partial y}$ and $v = - \frac{\partial \psi }{\partial x}$, and therefore, the mass conservation Eq. (5) is automatically satisfied. In order to render the governing equations and the boundary conditions in dimensionless form, the following dimensionless variables are introduced into Eqs. (6), (7) and (8):

$$\begin{aligned} \xi = \frac{{V_{0} x}}{\nu }Gr_{x}^{ - 1/4} ,\,\quad \eta = \frac{y}{x}Gr_{x}^{1/4} ,\,\quad \psi = 4\nu Gr_{x}^{1/4} \left( {f\left( {\xi ,\eta } \right) + \frac{1}{4}\xi } \right),\,\quad \theta \left( {\xi ,\eta } \right) = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }} \hfill \\ \Pr = \frac{\nu }{\alpha },\quad Gr_{x} = \frac{{g\beta_{1} \left( {T_{w} - T_{\infty } } \right)x^{3} }}{{4\nu^{2} }},\quad \varepsilon = \frac{1}{\mu \beta C},\quad \delta = \frac{{8\nu^{2} }}{{C^{2} x^{4} }}Gr_{x}^{3/2} \hfill \\ \end{aligned}$$

(9)

The resulting momentum and energy boundary layer equations take the following form:

$$\left( {1 + \varepsilon } \right)f'''\, + \left( {3f + \xi } \right)f'' - 2\left( {f'} \right)^{2} + \theta - \varepsilon \delta \left( {f''} \right)^{2} f'''\,\, = \,\xi \left( {f'\frac{\partial f'}{\partial \xi } - f''\frac{\partial f}{\partial \xi }} \right)$$

(10)

$$\frac{\theta ''}{ \Pr } + \left( {3f + \xi } \right)\theta ' = \xi \left( {f'\frac{\partial \theta }{\partial \xi } - \theta '\frac{\partial f}{\partial \xi }} \right)$$

(11)

The corresponding non-dimensional boundary conditions for the collectively fifth order, multi-degree partial differential equation system defined by Eqs. (10), (11) assume the following form:

$$\begin{aligned} At\,\,\,\,\,\,\eta = 0,\,\,\,\,\,\,\,f = f_{w} ,\,\,\,\,\,\,\,f' = 0,\,\,\,\,\,\,\,\theta = 1 + \frac{\theta '}{\gamma } \hfill \\ As\,\,\,\,\,\eta \to \infty ,\,\,\,\,f' \to 0,\,\,\,\,\theta \to 0 \hfill \\ \end{aligned}$$

(12)

Here primes denote the differentiation with respect to η. $\gamma = \frac{{xh_{w1} }}{k}Gr_{x}^{ - 1/4}$ is the Biot number. $f_{w} = \frac{{ - \,V_{w} x}}{{3\nu \,\sqrt[4]{{Gr_{x} }}}}$ is the suction/injection parameter. The wall thermal boundary condition in (12) corresponds to convective cooling. The skin-friction coefficient (shear stress at the Plate surface) and Nusselt number (heat transfer rate) can be defined using the transformations described above with the following expressions:

$$Gr_{x}^{ - 3/4} C_{f} = \left( {1 + \varepsilon } \right)f''(\xi ,0) - \frac{\varepsilon }{3}\delta \left( {f''(\xi ,0)} \right)^{3}$$

(13)

$$Gr_{x}^{ - 1/4} Nu = - \theta '\left( {\xi ,0} \right)$$

(14)

The location, ξ ~ 0, corresponds to the vicinity of the lower stagnation point on the plate. For this scenario, the model defined by Eqs. (10), (11) contracts to an ordinary differential boundary value problem:

$$\left( {1 + \varepsilon } \right)f'''\, + 3ff'' - 2\left( {f'} \right)^{2} + \theta - \varepsilon \delta \left( {f''} \right)^{2} f'''\,\, = 0$$

(15)

$$\frac{\theta ''}{ \Pr } + 3f\theta ' = 0$$

(16)

The general model is solved using a powerful and unconditionally stable finite difference technique introduced by Keller [38]. The Keller-box method has a second-order accuracy with arbitrary spacing and attractive extrapolation features.

4 Numerical solution with Keller box implict method

The Keller-Box implicit difference method is implemented to solve the nonlinear boundary value problem defined by Eqs. (10), (11) with boundary conditions (12). This technique, despite recent developments in other numerical methods, remains a powerful and very accurate approach for parabolic boundary layer flows. It is unconditionally stable and achieves exceptional accuracy [38]. Recently this method has been deployed in resolving many challenging, multi-physical fluid dynamics problems. These include magnetohydrodynamics applications of Keller’s method reviewed in Bég [39], micropolar Nanofluid transport from a horizontal circular cylinder [40], Nanofluid transport from a sphere [41],Walter’s B viscoelastic flows [42], hyperbolic-tangent convection flows from curved bodies [43], Jeffrey’s elasto-viscous boundary layers [44] and magnetic Williamson fluids [45]. The Keller-Box discretization is fully coupled at each step which reflects the physics of parabolic systems—which are also fully coupled. Discrete calculus associated with the Keller-Box scheme has also been shown to be fundamentally different from all other mimetic (physics capturing) numerical methods, as elaborated by Keller [38]. The Keller Box Scheme comprises four stages.

• 1. Reduction of the Nth order partial differential equation system to N first-order Equations.

• 2. Finite Difference Discretization.

• 3. Quasilinearization of Non-Linear Keller Algebraic Equations.

• 4. Block-tridiagonal Elimination of Linear Keller Algebraic Equations.

Step 1: Reduction of the Nth order partial differential equation system to N first order equations

Equations (8)–(9) subject to the boundary conditions (10) are first cast as a multiple system of first order differential equations. New dependent variables are introduced:

$$u(x,y) = f',\quad v(x,y) = f'',\quad s(x,y) = \theta ,\quad t(x,y) = \theta '$$

(17)

These denote the variables for velocity, temperature and concentration, respectively. Now Eqs. (10), (11) are solved as a set of fifth-order simultaneous differential equations:

$$f^{{\prime }} = u$$

(18)

$$u^{{\prime }} = v$$

(19)

$$\theta ' = \,\,t$$

(20)

$$\left( {1 + \varepsilon } \right)v' + \left( {3f + \xi } \right)v - 2u^{2} + s - \varepsilon \delta v^{2} v' = \xi \left( {u\frac{\partial u}{\partial \xi } - v\frac{\partial f}{\partial \xi }} \right)$$

(21)

$$\frac{t'}{\Pr } + \left( {3f + \xi } \right)t = \xi \left( {u\frac{\partial s}{\partial \xi } - t\frac{\partial f}{\partial \xi }} \right),$$

(22)

where primes denote differentiation with respect to η. In terms of the dependent variables, the boundary conditions become

$$\begin{aligned} At\,\,\,\,\,\,\eta = 0,\,\,\,\,\,\,\,f = 0,\,\,\,\,\,\,\,f' = 0,\,\,\,\,\,\,\,\theta = 1 + \frac{\theta '}{\gamma } \hfill \\ As\,\,\,\,\,\,\eta \to \infty ,\,\,\,\,\,\,\,f' \to 0,\,\,\,\,\,\,\,\theta \to 0 \hfill \\ \end{aligned}$$

(23)

Step 2: Finite difference discretization

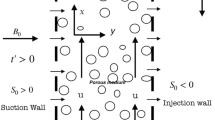
A two-dimensional computational grid is imposed on the ξ-η plane as sketched in Fig. 2. The stepping process is defined by

Fig. 2

Grid meshing and a Keller box computational cell

$$\eta_{0} = 0,\,\,\,\,\,\eta_{j} = \eta_{j - 1} + h_{j} ,\,\,\,\,\,\,j = 1,\,2, \ldots ,\,J,\,\,\,\,\,\,\eta_{J} \equiv \eta_{\infty }$$

(24)

$$\xi^{0} = 0,\,\,\,\,\,\xi^{n} = \xi^{n - 1} + k_{n} ,\,\,\,\,\,\,n = 1,\,2,\, \ldots ,\,N,$$

(25)

where k _n and h _j denote the step distances in the ξ and η directions, respectively. If $g_{j}^{n}$ denotes the value of any variable at $\left( {\eta_{j} ,\xi^{n} } \right)$, then the variables and derivatives of Eqs. (18)–(22) at $\left( {\eta_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} ,\xi^{{n - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right)$ are replaced by

$$g_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}^{{n - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} = \frac{1}{4}\left( {g_{j}^{n} + g_{j - 1}^{n} + g_{j}^{n - 1} + g_{j - 1}^{n - 1} } \right)$$

(26)

$$\left( {\frac{\partial g}{\partial \eta }} \right)_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}^{{n - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} = \frac{1}{{2h_{j} }}\left( {g_{j}^{n} - g_{j - 1}^{n} + g_{j}^{n - 1} - g_{j - 1}^{n - 1} } \right)$$

(27)

$$\left( {\frac{\partial g}{\partial \xi }} \right)_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}^{{n - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} = \frac{1}{{2k^{n} }}\left( {g_{j}^{n} - g_{j - 1}^{n} + g_{j}^{n - 1} - g_{j - 1}^{n - 1} } \right)$$

(28)

The resulting finite-difference approximation of Eqs. (18)–(22) for the mid-point $\left( {\eta_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} ,\xi^{n} } \right)$, takes the following form:

$$h_{j}^{ - 1} \left( {f_{j}^{n} - f_{j - 1}^{n} } \right) = u_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}^{n}$$

(29)

$$h_{j}^{ - 1} \left( {u_{j}^{n} - u_{j - 1}^{n} } \right) = v_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}^{n}$$

(30)

$$h_{j}^{ - 1} \left( {\theta_{j}^{n} - \theta_{j - 1}^{n} } \right) = t_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}^{n}$$

(31)

$$\begin{aligned} \left( {1 + \varepsilon } \right)\left( {v_{j} - v_{j - 1} } \right) + \left( {3 + \alpha } \right)\frac{{h_{j} }}{4}\left( {f_{j} + f_{j - 1} } \right)\left( {v_{j} + v_{j - 1} } \right) + \xi \frac{{h_{j} }}{2}\left( {v_{j} + v_{j - 1} } \right) - \left( {2 + \alpha } \right)\frac{{h_{j} }}{4}\left( {u_{j} + u_{j - 1} } \right)^{2} \hfill \\ + \frac{{h_{j} }}{2}\left( {s_{j} + s_{j - 1} } \right) - \frac{\varepsilon \delta }{4}\left( {v_{j} + v_{j - 1} } \right)^{2} \left( {v_{j} - v_{j - 1} } \right) + \frac{{\alpha h_{j} }}{2}v_{j - 1}^{n - 1} \left( {f_{j} + f_{j - 1} } \right) - \frac{{\alpha h_{j} }}{2}f_{j - 1}^{n - 1} \left( {v_{j} + v_{j - 1} } \right)\,\,\,\, = \,\,\,\,\left[ {R_{1} } \right]_{j - /12}^{n - 1} \hfill \\ \end{aligned}$$

(32)

$$\begin{aligned} \frac{1}{\Pr }\left( {t_{j} - t_{j - 1} } \right) + \frac{{\left( {3 + \alpha } \right)h_{j} }}{4}\left( {f_{j} + f_{j - 1} } \right)\left( {t_{j} + t_{j - 1} } \right) + \xi \frac{{h_{j} }}{2}\left( {t_{j} + t_{j - 1} } \right)\, - \frac{{\alpha h_{j} }}{4}\left( {u_{j} + u_{j - 1} } \right)\left( {s_{j} + s_{j - 1} } \right) \hfill \\ + \frac{{\alpha h_{j} }}{2}s_{j - 1/2}^{n - 1} \left( {u_{j} + u_{j - 1} } \right) - \frac{{\alpha h_{j} }}{2}u_{j - 1/2}^{n - 1} \left( {s_{j} + s_{j - 1} } \right) - \frac{{\alpha h_{j} }}{2}f_{j - 1/2}^{n - 1} \left( {t_{j} + t_{j - 1} } \right)\,\, + \,\,\frac{{\alpha h_{j} }}{2}t_{j - 1/2}^{n - 1} \left( {f_{j} + f_{j - 1} } \right)\,\, = \,\,\left[ {R_{2} } \right]_{j - 1/2}^{n - 1} , \hfill \\ \end{aligned}$$

(33)

where the following notation applies:

$$\alpha = \frac{{\xi^{{n - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}{{k_{n} }}$$

(34)

$$\left[ {R_{1} } \right]_{j - 1/2}^{n - 1} = - h_{j} \left[ \begin{array}{l} \left( {1 + \varepsilon } \right)\left( {v'} \right)_{j - 1/2}^{n - 1} + \left( {3 - \alpha } \right)f_{j - 1/2}^{n - 1} v_{j - 1/2}^{n - 1} + \xi v_{j - 1/2}^{n - 1} - \,\left( {2 - \alpha } \right)\left( {u_{j - 1/2}^{n - 1} } \right)^{2} \,\\ + s_{j - 1/2}^{n - 1} \, - \varepsilon \delta \left( {v^{2} } \right)_{j - 1/2}^{n - 1} \left( {v'} \right)_{j - 1/2}^{n - 1} \hfill \end{array} \right]$$

(35)

$$\left[ {R_{2} } \right]_{j - 1/2}^{n - 1} = - h_{j} \left[ {\frac{1}{\Pr }\left( {t'} \right)_{j - 1/2}^{n - 1} + \left( {3 - \alpha } \right)f_{j - 1/2}^{n - 1} t_{j - 1/2}^{n - 1} + \xi t_{j - 1/2}^{n - 1} + \alpha \,u_{j - 1/2}^{n - 1} s_{j - 1/2}^{n - 1} } \right]$$

(36)

The boundary conditions are

$$f_{0}^{n} = u_{0}^{n} = 0,\,\,\,\,\,\,\,\,\,s_{0}^{n} = 1,\,\,\,\,\,\,\,\,u_{J}^{n} = 0,\,\,\,\,\,\,\,\,\,v_{J}^{n} = 0,\,\,\,\,\,\,\,s_{J}^{n} = 0\,$$

(37)

Step 3: Quasilinearization of non-linear Keller algebraic equations

Assuming $f_{j}^{n - 1} ,u_{j}^{n - 1} ,v_{j}^{n - 1} ,s_{j}^{n - 1} ,t_{j}^{n - 1}$ to be known for $0 \le j \le J$, then Eqs. (29)–(33) constitute a system of 5 J + 5 equations for the solution of 5 J + 5 unknowns $f_{j}^{n} ,u_{j}^{n} ,v_{j}^{n} ,s_{j}^{n} ,t_{j}^{n} , \quad j = 0, \, 1, \, 2, \ldots , \, J$. This non-linear system of algebraic equations is linearized by means of Newton’s method as explained in Keller [38] and Prasad [46].

Step 4: Block-tridiagonal elimination of linear Keller algebraic equations

The linearized system is solved by the block-elimination method owing to its block-tridiagonal structure. The block-tridiagonal structure generated consists of block matrices. The complete linearized system is formulated as a block matrix system, where each element in the coefficient matrix is a matrix itself, and this system is solved using the efficient Keller-box method. The numerical results are strongly influenced by the number of mesh points in both directions. After some trials in the η-direction (radial coordinate) a larger number of mesh points are selected, whereas in the ξ-direction (tangential coordinate) significantly less mesh points are necessary. η _max has been set at 15 and this constitutes an adequately large value at which the prescribed boundary conditions are satisfied. ξ _max is set at 3.0 for the simulations. Mesh independence has been comfortably attained in the simulations. The numerical algorithm is executed in MATLAB on a PC. The method demonstrates excellent stability, convergence and consistency, as elaborated by Keller [38].

5 Numerical results and interpretation

Comprehensive solutions have been obtained and are presented in Tables 1, 2, 3, 4, 5 and Figs. 3, 4, 5, 6, 7, 8. The numerical problem comprises two independent variables (ξ,η), two dependent fluid dynamic variables (f,θ) and five thermo-physical and body force control parameters, namely $\varepsilon ,\,\delta ,\,\gamma ,\,{\text{Pr, }}\xi$. The following default parameter values, i.e. ε = 0.1, δ = 0.1, γ = 0.3, Pr = 0.71, ξ = 1.0 are prescribed (unless otherwise stated). Furthermore, the influence of stream-wise (transverse) coordinate on heat transfer characteristics is also investigated.

Table 1 Values of $f^{\prime\prime}(\xi ,0)$ and $- \theta^{\prime}(\xi ,0)$ for different $\varepsilon {\text{ and Pr}}$ $\left( {\delta = 0.1, \, \gamma { = 0} . 3 , { }\xi { = 1} . 0} \right)$

Table 2 Values of $f^{\prime\prime}(\xi ,0)$ and $- \theta^{\prime}(\xi ,0)$ for different $\varepsilon {\text{ and Pr}}$ $\left( {\delta = 0.1, \, \gamma { = 0} . 3 , { }\xi { = 1} . 0} \right)$

Table 3 Values of $f^{\prime\prime}(\xi ,0)$ and $- \theta^{\prime}(\xi ,0)$ for different $\delta {\text{ and Pr}}$ $\left( {\delta = 0.1, \, \gamma { = 0} . 3 , { }\xi { = 1} . 0} \right)$

Table 4 Values of $f^{\prime\prime}(\xi ,0)$ and $- \theta^{\prime}(\xi ,0)$ for different $\delta {\text{ and Pr}}$ $\left( {\delta = 0.1, \, \gamma { = 0} . 3 , { }\xi { = 1} . 0} \right)$

Table 5 Numerical Values of $f^{\prime\prime}(\xi ,0)$ (in brackets) and skin friction coefficient $C_{f}$ for different values of δ and ε

Fig. 3

a Influence of γ on velocity profiles, b influence of γ on temperature profiles

Fig. 4

a Influence of ε on velocity profiles, b influence of ε on temperature profiles

Fig. 5

a Influence of δ on velocity profiles, b influence of δ on temperature profiles

Fig. 6

a Influence of Pr on velocity profiles, b influence of Pr on temperature profiles

Fig. 7

a Influence of ξ on velocity profiles, b influence of ξ on temperature profiles

Fig. 8

a Influence of ξ and on velocity profiles, b influence of ξ and on temperature profiles

In Tables 1, 2, we present the influence of the Eyring–Powell fluid parameter, ε, on the skin friction and heat transfer rate, along with a variation in Prandtl number (Pr). With increasing ε, the skin friction is enhanced. The parameter ε is inversely proportional to the dynamic viscosity of the non-Newtonian fluid. There as ε is elevated, viscosity will be reduced and this will induce lower resistance to the flow at the surface of the plate, i.e. accelerate the flow leading to an escalation of shear stress. Furthermore, this trend is sustained at any Prandtl number. However, an increase in Prandtl number markedly reduces the shear stress magnitudes. Similarly increasing ε is observed to reduce heat transfer rates, again at all Prandtl numbers, whereas it strongly accentuates heat transfer rates. Magnitudes of shear stress are always positive indicating that flow reversal (backflow) never arises.

Tables 3, 4 document results for the influence of the local non-Newtonian parameter (based on length scale x), i.e. δ and also the Prandtl number (Pr) on skin friction and heat transfer rate. Skin friction is generally decreased with increasing δ. However, heat transfer rate (i.e. local Nusselt number function) is found to be enhanced with increasing δ. $\delta = \frac{{8\nu^{2} }}{{C^{2} x^{4} }}Gr_{x}^{3/2}$ and inspection of this definition shows that the direct proportionality of δ to kinematic viscosity (ν) (with all other parameters being maintained constant) will generate a strong resistance to the flow leading to a deceleration. i.e. drop in shear stresses. Conversely, the direct proportionality of δ to Grashof number (Gr) will imply that thermal buoyancy forces are enhanced as δ increases, and this will cause a boost in heat transfer by convection from the plate surface manifesting with the greater heat transfer rates observed in Tables 3 and 4. These tables also show that with an increase in the Prandtl number, Pr, the skin friction is also depressed, whereas the heat transfer rate is elevated.

Table 5 presents the Keller box numerical values of the missing condition $f^{\prime\prime}(\xi ,0)$ (in brackets) and skin friction C _f for various values of δ and ε. It is found that skin friction is reduced with increasing values of δ. Furthermore, the skin friction C _f is observed to be increased with a rise in the Eyring–Powell fluid parameter (ε) for all values of the local non-Newtonian parameter (δ).

Table 6 shows the comparison values of the present study with those obtained by Hossain et al. [47] for natural convection heat transfer along a vertical porous plate and are found to be in excellent agreement.

Table 6 Comparison values of $f^{\prime\prime}(\xi ,0)$ and $- \theta '\left( {\xi ,0} \right)\,$ for different values of ξ with ε = δ = 0.0, γ = 0.3, Pr = 1.0

Figure 3a, b depicts the evolution of velocity $\left( {f'} \right)$ and temperature $\left( \theta \right)$ functions with a variation in Biot number, $\gamma$. Dimensionless velocity component (Fig. 3a) is considerably enhanced with increasing $\gamma$. In Fig. 3b, an increase in Biot number is also seen to considerably enhance temperature throughout the boundary layer regime. For γ < 1, i.e. small Biot numbers, the regime is frequently designated as being “thermally simple” and there is a presence of more uniform temperature fields inside the boundary layer and the plate surface. For γ > 1 thermal fields are anticipated to be non-uniform within the solid body. The Biot number effectively furnishes a mechanism for comparing the conduction resistance within a solid body to the convection resistance external to that body (offered by the surrounding fluid) for heat transfer. We also note that a Biot number in excess of 0.1, as studied in Fig. 3a, b, corresponds to a “thermally thick” substance, whereas Biot number less than 0.1 implies a “thermally thin” material. Since γ is inversely proportional to thermal conductivity (k), as γ increases, thermal conductivity will be reduced at the plate surface and this will lead to a decrease in the rate of heat transfer from the boundary layer to within the plate, manifesting in a rise in temperature at the plate surface and in the body of the fluid the maximum effect will be sustained at the surface, as witnessed in Fig. 3b. However for a fixed wall convection coefficient and thermal conductivity, Biot number as defined in $\gamma = \frac{{xh_{w} }}{k}Gr_{x}^{ - 1/4}$ is also directly inversely proportional to the local Grashof (free convection) number. As local Grashof number increases generally the enhancement in buoyancy causes a deceleration in boundary layer flows; however, as Biot number increases, the local Grashof number must decrease and this will induce the opposite effect, i.e. accelerate the boundary layer flow, as shown in Fig. 3a.

Figure 4a, b illustrates the effect of Eyring–Powell fluid parameterε, on the velocity $\left( {f'} \right)$ and temperature $\left( \theta \right)$ distributions through the boundary layer regime. Velocity is significantly decreased with increasing $\varepsilon$ at larger distance from the plate surface owing to the simultaneous drop in dynamic viscosity. Conversely, temperature is consistently enhanced with increasing values of $\varepsilon$. The mathematical model reduces to the Newtonian viscous flow model as $\varepsilon \to 0$ and $\delta \to 0$. The momentum boundary layer equation in this case contracts to the familiar equation for Newtonian mixed convection from a plate, viz

$$f'''\, + \left( {3f + \xi } \right)f'' - 2\left( {f'} \right)^{2} + \theta \,\, = \,\xi \left( {f'\frac{\partial f'}{\partial \xi } - f''\frac{\partial f}{\partial \xi }} \right).$$

(38)

The thermal boundary layer Eq. (9) remains unchanged. In Fig. 4b, temperatures are clearly minimized for the Newtonian case (ε = 0) and maximized for the strongest non-Newtonian case (ε = 1.0). The non-Newtonian parameter ε (=1/[μβC]) is evidently inversely proportional to the viscosity and also to $\beta$ and C (Eyring–Powell rheological fluid parameters). As ε is increased, the material viscosity, therefore, will decrease which would aid momentum development. Similarly the parameters $\beta$ and C are simultaneously reduced (they are strongly linked to viscosity) and the overall effect is a boost in material viscosity. This results in reduction in the ε magnitude which manifests in marked deceleration in the flow as shown in Fig. 4a. With decreased momentum diffusion rates the velocity boundary layer thickness is decreased. Thermal diffusion is conversely enhanced and the fluid heated (Fig. 4b), resulting in a thickening in the thermal boundary layer.

Figure 5a, b depicts the velocity $\left( {f'} \right)$ and temperature $\left( \theta \right)$ distributions with increasing local non-Newtonian fluid parameter $\delta$. Very little tangible effect is observed in Fig. 5a, although there is a very slight increase in velocity with increase in $\delta$. Similarly, there is only a very slight depression in temperature magnitudes in Fig. 5b with a rise in $\delta$.This parameter is defined as ν ²Re ³ _x /(2C ² x ⁴), features in a single negative term in Eq. (8), viz, -εδ(f ^// ) ² f ^///, unlike ε, rheological parameter which also appears in the shear term, −(1 + ε)² f ^///. This parameter also features viscosity which effectively is decreased weakly and induces a slight acceleration in the flow. Therefore, the momentum boundary layer thickness is decreased slightly, whereas the thermal boundary layer thickness is marginally reduced.

Figure 6a, b depicts the profiles for velocity $\left( {f'} \right)$ and temperature $\left( \theta \right)$ for various values of Prandtl number, Pr. It is observed that an increase in the Prandtl number significantly decelerates the flow, i.e. velocity decreases. Also increasing Prandtl number is found to decelerate the temperature. The solutions to denser fluids, i.e. water-based solvents, very low-density spray paints [48], etc. Prandtl number must be varied, as this is the only non-dimensional parameter which categorizes thermofluid properties. For example, Pr = 5 corresponds closely to actual characteristics for chlorofluorocarbon halomethance (CFC) which is used in aerosol spray propellants. Pr = 7 represents certain paint-thinners as well as water at room temperature. Prandtl number defines the ratio of viscous diffusion to thermal diffusion in the boundary layer regime. For Pr > 1, momentum diffusivity will exceed thermal diffusivity, but for Pr < 1, thermal diffusivity will exceed momentum diffusivity. Increasing Pr is known to significantly depress temperatures in the boundary layer, as elaborated in Incropera and DeWitt [49] and Schlichting [50]. Pr signifies the ratio of momentum diffusivity to thermal diffusivity. Pr is the most important parameter in heat transfer analysis as it corresponds to actual physical properties of fluids unlike the vast majority of other dimensionless thermofluid numbers. Higher Pr values imply a thinner thermal boundary layer thickness and more uniform temperature distributions across the boundary layer. Hence the thermal boundary layer will be much reduced in thickness compared with the hydrodynamic (momentum) boundary layer. Pr < 1 corresponds to greater thermal diffusion rate compared with momentum diffusion rate. A lower Pr (Pr = 0.71, i.e. gas) implies that the fluid possess higher thermal conductivity (and an associated thicker thermal boundary layer structure) so that heat can diffuse away from the fluid to the plate surface faster than for higher Pr fluid (Pr = 7.0, i.e. liquids associated with thinner boundary layers).

Figure 7a, b depicts the velocity $\left( {f'} \right)$ and temperature $\left( \theta \right)$ distributions with radial coordinate, for various transverse (stream wise) coordinate values, ξ along with the variation in the fluid parameter $\varepsilon$. Clearly, from these figures it can be seen that as suction parameter ξ increases, the maximum fluid velocity decreases. This is due to the fact that the effect of the suction is to take away the warm fluid on the vertical plate and thereby decrease the maximum velocity with a decrease in the intensity of the natural convection rate. Figure 7b shows the effect of the local suction parameter on the temperature profiles. It is noticed that the temperature profiles decrease with an increase in the suction parameter and as the suction is increased, more warm fluid is taken away and this the thermal boundary layer thickness decreases. It is also seen that with an increase in $\varepsilon$, the impedance offered by the fibers of the porous medium will increase and this will effectively decelerate the flow in the regime, as testified to by the evident decrease in velocities shown in Fig. 7a.

Figure 8a, b depicts the velocity $\left( {f'} \right)$ and temperature $\left( \theta \right)$ distributions with radial coordinate, for various transverse (stream wise) coordinate values, ξ, along with the variation in the fluid parameter $\delta$. Clearly, from these figures it can be seen that as suction parameter ξ increases, the maximum fluid velocity decreases. This is due to the fact that the effect of the suction is to take away the warm fluid on the vertical plate and thereby decrease the maximum velocity with a decrease in the intensity of the natural convection rate. Figure 8b shows the effect of the local suction parameter on the temperature profiles. It is noticed that the temperature profiles decrease with an increase in the suction parameter and as the suction is increased, more warm fluid is taken away and this the thermal boundary layer thickness decreases.

Figure 9a, b depicts the influence of the Biot number, γ, on the dimensionless skin friction coefficient and heat transfer rate at the plate surface. The skin friction at the plate surface is seen to enhance greatly with rising γ values. This is principally attributable to the decrease in Grashof (free convection) number which results in an acceleration in the boundary layer flow, as elaborated by Chen and Chen [51]. Heat transfer rate (local Nusselt number) is also enhanced with increasing γ, as computed in Fig. 9b.

Fig. 9

a Influence of γ on velocity profiles, b influence of γ on temperature profiles

Figure 10a, b presents the influence of Eyring–Powell fluid parameter, ε, on dimensionless skin friction coefficient and heat transfer rate at the plate surface. It is observed that the dimensionless skin friction is elevated with the increase in ε, i.e. the boundary layer flow is accelerated with decreasing viscosity effects in the non-Newtonian regime. Conversely, the surface heat transfer rate is substantially decreased with increasing ε values. Decreasing viscosity of the fluid (induced by increasing the ε value) reduces thermal diffusion as compared with momentum diffusion. A decrease in heat transfer rate at the wall implies less heat is convected from the fluid regime to the plate, thereby heating the boundary layer and enhancing temperatures.

Fig. 10

a Influence of ε on velocity profiles, b influence of ε on temperature profiles

Figure 11a, b illustrates the influence of the local non-Newtonian parameter, δ, on the dimensionless skin friction coefficient and heat transfer rate. The skin friction (Fig. 11a) at the plate surface is reduced with increasing δ, however, only for very large values of the transverse coordinate, ξ. The flow is, therefore, strongly accelerated along the curved plate surface far from the lower stagnation point. Heat transfer rate (local Nusselt number) is increased with increasing δ, again at large values of ξ, as computed in Fig. 11b.

Fig. 11

a Influence of δ on velocity profiles, b influence of δ on temperature profiles

6 Conclusions

Numerical solutions have been presented for the boundary-driven flow and heat transfer of non-Newtonian Eyring–Powell fluid from a vertical porous plate. The Keller-box implicit second-order accurate finite difference numerical scheme has been utilized to efficiently solve the transformed, dimensionless velocity and thermal boundary layer equations, subject to realistic boundary conditions. A comprehensive assessment of the effects of Eyring–Powell fluid parameter (ε), local non-Newtonian parameter (δ), Biot number (γ), Prandtl number (Pr) and dimensionless tangential coordinate (ξ) on thermo-fluid characteristics has been conducted. Excellent correlation with previous studies has been demonstrated testifying to the validity of the present code. Generally, very stable and accurate solutions are obtained with the present finite difference code. The numerical code is able to solve nonlinear boundary layer equations very efficiently and, therefore, shows excellent promise in simulating transport phenomena in other non-Newtonian fluids. It is, therefore, presently being employed to study micropolar fluids and viscoplastic fluids which also simulate accurately many chemical engineering working fluids in curved geometrical systems. The present study has also neglected time effects. Future simulations will also address transient polymeric boundary layer flows and will be presented soon.