1 Introduction

Analysis of non-Newtonian liquids is important due to its involvement in current applications. Such examples include blood at low sheer rate, emulsion, mud, chyme, organic product purée, chemicals, sugar game plan and shampoos. No single equation can predict the diverse characteristics of non-Newtonian materials. Thus, different logical models have been proposed by the researchers. Maxwell is one subclass of rate-type fluids. This fluid model predicts time relaxation impacts. Such effects cannot be expected by differential fluids. Maxwell liquid model is particularly helpful for polymers of low molecular weight. Fetecau and Fetecau [1] obtained analytical solution of flow of Maxwell liquid bounded by an infinite plate. Some current investigations predicting flow of Maxwell liquid have been elucidated in Refs. [2,3,4,5,6,7,8,9].

Nanoliquids can massively help the heat exchange qualities of working liquids. The heat transport wonder is a crucial procedure in designing and in this manner improvement in heat exchange angles prompts to propel the productivity of bunches of procedures. In like manner, the nanoliquids have a few applications for example as coolants, heat exchangers, sun-based water warming, cooling of electronic types of gear, chillers, icebox coolers, space vehicles, atomic reactors, smaller scale channel heat sinks and ointments. Nanofluid term was right off the bat presented by Choi [10]. From there on, test and hypothetical examinations on nanofluid’s heat exchange perspectives are finished by Buongiorno [11]. Afterward, much information has been presented on this topic can be found in Refs. [12,13,14,15,16,17,18,19,20,21,22,23,24,25]. The magneto-nanoliquids are the liquids that have both magnetic and fluid qualities. These materials have pivotal part in optical switches, modulators, optical gratings and especially in optical fiber channels. The attractive nanoparticles are very noticeable in pharmaceutical, disease treatment, tumor investigation, sink drift partition and many more. The current takes a shot at magneto-nanofluids are exhibited in Refs. [26,27,28,29,30].

Activation energy can be portrayed as the tiniest required imperativeness that reactants must get before a substance reaction can happen. Mass transport process by substance reaction with approving essentialness routinely met in applications including mechanics of water and oil emulsions, geothermal supplies, compound portraying and sustenance getting ready. Makinde et al. [31] addressed the heat transport behavior in porous flat plate by considering the effect of radiation and activation energy. Maleque [32] examined the exothermic and endothermic chemical reactions in MHD viscous liquid by considering Arrhenius activation energy. Awad et al. [33] elaborated binary chemical reaction and activation energy in an unsteady rotating fluid. Casson liquid flow past a stretching and shrinking surface with binary chemical reaction was numerically analyzed by Abbas et al. [34]. Shafique et al. [35] studied the flow of Maxwell liquid in rotating frame with activation energy and chemical reaction. Mustafa et al. [36] present the magneto-nanoliquid over a vertical sheet by accounting the activation energy and chemical reaction.

Convective point of confinement condition is mostly used to describe a direct convective heat exchange condition for no less than one scientific component in heat. Heat transport examination with convective point of confinement conditions is evoked in methodology, for instance, heat essentialness storing, gas turbines and nuclear plants. In context of the above examination, Aziz [37] studied the heat transport phenomenon in boundary layer flow by taking convective-type boundary condition. His study reveals that similarity solutions are possible only when convective heat transport associated with the hot liquid on the lower sheet surface is proportional to \(x^{ - 1/2}\). Numerous scientists [38,39,40,41,42] have examined the flow and heat transfer of viscous/non-Newtonian fluids via convective-type boundary condition.

In the above literatures and applications, we noted that activation energy can be realized as energy barrier that separates two minima of potential energy which has to be overcome by reactants to initiate a chemical reaction. So that we are going to analyze the chemical reaction and activation energy effects in Maxwell nanoliquid flow. The aspects of Brownian movement and thermophoretic are retained due to consideration of nanofluid model. The problem is dealt with convective boundary condition and passively controlled mass flux. The transformed non-dimensional equations are solved numerically using spectral relaxation scheme because it gives a better accuracy on coarser grids which significantly improves the speed of the convergence. Validation of computations has been visualized through comparative benchmark.

2 Statement of problem

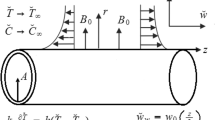
Model of the problem is presented in Fig. 1. Here steady two-dimensional Maxwell liquid flow by stretching surface is considered. Here the flow occupies to \(y > 0\), sheet velocity \(U_{\text{w}} (x) = bx,\;b > 0\) and \(x\)-axis taken along the sheet. Uniform magnetic field \(B_{0}\) is applied normal to the sheet. Influences of activation energy and chemical reaction are accounted in mass transfer. Convective surface temperature is denoted by \(T_{\text{f}}\), and heat transport coefficient is \(h_{\text{f}}\). Nanoparticles normal flux at the surface is passively controlled. Under the above assumptions, the rheological model of continuity, momentum, energy and mass equations are

$$\nabla \cdot V = 0,$$
(1)
$$\rho_{\text{f}} (V \cdot \nabla )V = - \nabla p + \nabla \cdot S,$$
(2)
$$\rho_{\text{p}} c_{\text{p}} (V \cdot \nabla T) = k\nabla^{2} T + \rho_{\text{f}} c_{\text{f}} \left[ {D_{\text{B}} \nabla C \cdot \nabla T + \frac{{D_{T} }}{{T_{\infty } }}(\nabla T)^{2} } \right],$$
(3)
$$(V \cdot \nabla C) = D_{B} \nabla^{2} C + \frac{{D_{T} }}{{T_{\infty } }}\nabla^{2} T - k_{\text{r}}^{2} (C - C_{\infty } )\left( {\frac{T}{{T_{\infty } }}} \right)^{n} \exp \left( {\frac{ - Ea}{\kappa T}} \right).$$
(4)

From Eq. (2), last term \(S\) represents the extra stress tensor and for Maxwell fluid, it satisfies \(S + \lambda_{1} \frac{DS}{Dt} = \mu A^{*}\). Here \(A^{*} = \nabla V + (\nabla V)^{t}\) for first Rivlin–Ericksen tensor, \(\lambda_{1}\) for time relaxation of liquid. Also third term on RHS of Eq. (4) represents modified Arrhenius formula in which \(k_{r}^{2}\) for rate of reaction [35], \(Ea\) for activation energy, \(\kappa\) for Boltzmann constant and \(n\) dimensionless fitted rate constant which lies in the range \(- 1 < n < 1\).

Fig. 1
figure 1

Flow model and coordinate system

Full size image

After the boundary layer approximations, one has [26, 29]:

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0,$$
(5)
$$u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = \nu \frac{{\partial^{2} u}}{{\partial y^{2} }} + k_{0} \left( {u^{2} \frac{{\partial^{2} u}}{{\partial x^{2} }} + v^{2} \frac{{\partial^{2} u}}{{\partial y^{2} }} + 2uv\frac{{\partial^{2} u}}{\partial x\partial y}} \right) - \frac{{\sigma B_{0}^{2} }}{\rho }\left( {u + k_{0} v\frac{\partial u}{\partial y}} \right)$$
(6)
$$u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \alpha \left( {\frac{{\partial^{2} T}}{{\partial y^{2} }}} \right)\, + \tau \left\{ {D_{\text{B}} \left( {\frac{\partial C}{\partial y}\frac{\partial T}{\partial y}} \right) + \left( {\frac{{D_{T} }}{{T_{\infty } }}} \right)\left[ {\left( {\frac{\partial T}{\partial y}} \right)^{2} } \right]} \right\},$$
(7)
$$u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} = D_{\text{B}} \frac{{\partial^{2} C}}{{\partial y^{2} }} + \left( {\frac{{D_{T} }}{{T_{\infty } }}} \right)\left( {\frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) - k_{\text{r}}^{2} (C - C_{\infty } )\left( {\frac{T}{{T_{\infty } }}} \right)^{n} \exp \left( {\frac{ - Ea}{\kappa T}} \right),$$
(8)

Imposed boundary conditions are [40]:

$$\begin{aligned} u = U_{\text{w}} (x),\quad v = 0,\quad - k\frac{\partial T}{\partial y} = h_{\text{f}} (T_{\text{f}} - T),\quad D_{B} \frac{\partial C}{\partial y} + \frac{{D_{T} }}{{T_{\infty } }}\frac{\partial T}{\partial y} = 0\,({\text{passive}}\,{\text{control}}\,{\text{of}}\,\phi )\;{\text{at}}\;y = 0 \hfill \\ u \to 0,\quad T \to T_{\infty } ,\quad C \to C_{\infty } \,{\text{as}}\,y \to \infty \hfill \\ \end{aligned}$$
(9)

Defined variables [15, 17]:

$$\varsigma = \left( {\frac{{U_{\text{w}} }}{\nu x}} \right)^{1/2} y,\quad f(\varsigma ) = \frac{\psi }{{(x\nu U_{\text{w}} )^{1/2} }},\quad \theta (\varsigma ) = \frac{{T - T_{\infty } }}{{T_{\text{f}} - T_{\infty } }},\quad \phi (\varsigma ) = \frac{{C - C_{\infty } }}{{C_{\infty } }}({\text{passive}}\,{\text{control}}\,{\text{of}}\,\phi )$$
(10)

and making use of (10), Eqs. (5–8) are reduced to following non-dimensional equations

$$\frac{{{\text{d}}^{3} f}}{{{\text{d}}\varsigma^{3} }} + f\frac{{{\text{d}}^{2} f}}{{{\text{d}}\varsigma^{2} }} - \left( {\frac{{{\text{d}}f}}{{{\text{d}}\varsigma }}} \right)^{2} - M^{2} \frac{{{\text{d}}f}}{{{\text{d}}\varsigma }} + MKf\frac{{{\text{d}}^{2} f}}{{{\text{d}}\varsigma^{2} }} + K\left( {f^{2} \frac{{{\text{d}}^{3} f}}{{{\text{d}}\varsigma^{3} }} - 2f\frac{{{\text{d}}f}}{{{\text{d}}\varsigma }}\frac{{{\text{d}}^{2} f}}{{{\text{d}}\varsigma^{2} }}} \right) = 0,$$
(11)
$$\frac{1}{\Pr }\frac{{{\text{d}}^{2} \theta }}{{{\text{d}}\varsigma^{2} }} + f\frac{{{\text{d}}\theta }}{{{\text{d}}\varsigma }} + Nb\frac{{{\text{d}}\theta }}{{{\text{d}}\varsigma }}\frac{{{\text{d}}\phi }}{{{\text{d}}\varsigma }} + Nt\left( {\frac{{{\text{d}}\theta }}{{{\text{d}}\varsigma }}} \right)^{2} = 0,$$
(12)
$$\frac{{{\text{d}}^{2} \phi }}{{{\text{d}}\varsigma^{2} }} + Scf\frac{{{\text{d}}\phi }}{{{\text{d}}\varsigma }} + \frac{Nt}{Nb}\frac{{{\text{d}}^{2} \theta }}{{{\text{d}}\varsigma^{2} }} - Sc\sigma (1 + \delta \theta )^{n} \phi \exp \left( {\frac{ - E}{1 + \delta \theta }} \right) = 0.$$
(13)

Corresponding boundary conditions become

$$\begin{aligned} f(\varsigma ) = & 0,\quad \frac{{{\text{d}}f}}{{{\text{d}}\varsigma }} = 1,\quad \frac{{{\text{d}}\theta }}{d\varsigma } = - Bi(1 - \theta (\varsigma )),\quad Nb\frac{{{\text{d}}\phi }}{{{\text{d}}\varsigma }} + Nt\frac{{{\text{d}}\theta }}{{{\text{d}}\varsigma }} = 0\;{\text{at}}\;\varsigma = 0 \\ & \;\frac{{{\text{d}}f}}{{{\text{d}}\varsigma }} \to 0,\quad \theta (\varsigma ) \to 0,\quad \phi (\varsigma ) \to 0\;{\text{as}}\;\varsigma \to \infty \\ \end{aligned}$$
(14)

Here key parameters of the extended study are \(M\)—Hartmann number, \(K\)—elastic parameter, \(\Pr\)—Prandtl number, \(Nb\)—Brownian movement, \(Nt\)—thermophoretic, \(Sc\)—Schmidt number, \(Bi\)—Biot number, \(\sigma\)—reaction rate, \(E\)—activation energy and \(\delta\)—temperature difference. These can be expressed as

$$\begin{aligned} M = & \frac{{\sigma B_{0}^{2} }}{\rho b},\quad K = bk_{0} ,\quad \Pr = \frac{\nu }{\alpha },\quad Nb = \frac{{\tau D_{\text{B}} C_{\infty } }}{\nu },\quad Nt = \frac{{\tau D_{T} (T_{\text{w}} - T_{\infty } )}}{{\nu T_{\infty } }}, \\ Sc = & \frac{\nu }{{D{}_{\text{B}}}},\quad \sigma = \frac{{k_{\text{r}}^{2} }}{b},\quad E = \frac{Ea}{{\kappa T_{\infty } }},\quad \delta = \frac{{T_{\text{w}} - T_{\infty } }}{{T_{\infty } }},\quad Bi = \left( {\frac{\nu }{b}} \right)^{1/2} \frac{{h_{\text{f}} }}{k}. \\ \end{aligned}$$

The skin friction factor and wall temperature and concentration gradients are defined as

$$C_{\text{f}} = \frac{{\tau_{\text{w}} }}{{\rho_{\text{f}} U_{\text{w}}^{2} (x)}},\quad Nu = \frac{{xq_{\text{w}} }}{{\alpha (T_{\text{w}} - T_{\infty } )}},\quad Sh = \frac{{xq_{\text{m}} }}{{D_{\text{B}} (C_{\text{w}} - C_{\infty } )}},$$
(15)

where \(\tau_{\text{w}}\) is wall shear stress, \(q_{\text{w}}\) the heat flux and \(q_{m}\) the mass flux, i.e.,

$$\tau_{\text{w}} = \mu (1 + K)\left( {\frac{\partial u}{\partial y}} \right)_{y = 0} ,\quad q_{\text{w}} = - k\left( {\frac{\partial T}{\partial y}} \right)_{y = 0} ,\quad q_{\text{w}} = - D_{\text{B}} \left( {\frac{\partial C}{\partial y}} \right)_{y = 0} .$$
(16)

Use of Eq. (10) in (16) yields [45]:

$$\text{Re}_{x}^{1/2} C_{f} = (1 + K)f^{\prime \prime } (0),\quad \text{Re}_{x}^{ - 1/2} Nu = - \theta^{\prime } (0),\quad \text{Re}_{x}^{ - 1/2} Sh = \frac{Nt}{Nb}\theta^{\prime } (0).$$
(17)

3 Method of solution

The nonlinear Eqs. (11–14) are coupled, and ordinary differential equations and hence numerical solutions via spectral relaxation method are computed. To apply this method, first we set \(\frac{{{\text{d}}f}}{{{\text{d}}\varsigma }} = f^{\prime } = g\) and the governing Eqs. (11–14) are reduced to

$$f^{\prime } = g,$$
(18)
$$g^{\prime \prime } + fg^{\prime } - g^{2} - M^{2} g + MKfg^{\prime } + K(f^{2} g^{\prime \prime } - 2gg^{\prime } ) = 0,$$
(19)
$$\frac{{\theta^{\prime \prime } }}{\Pr } + f\theta^{\prime } + Nb\theta^{\prime } \phi^{\prime } + Nt\theta^{\prime 2} = 0,$$
(20)
$$\phi^{\prime \prime } + Scf\phi^{\prime } + \frac{Nb}{Nt}\theta^{\prime \prime } - Sc\sigma (1 + \delta \theta )^{n} \exp \left( {\frac{ - E}{1 + \delta \theta }} \right)\phi = 0,$$
(21)

also the boundary conditions become

$$\begin{aligned} f(0) = 0,\, \, g(0) = 1,\, \, \theta^{\prime } (0) = - Bi(1 - \theta (0)),\,{\text{ Nb}}\phi^{\prime } (0) + Nt\theta^{\prime } (0) = 0, \hfill \\ g(\infty ) \to 0,\,\,\,\theta (\infty ) \to 0,\,\,\phi (\infty ) \to 0.\, \hfill \\ \end{aligned} .$$
(22)

The spectral relaxation iteration procedure for the present problem can be written as

$$f_{r + 1}^{\prime } = g_{r,}$$
(23)
$$(1 + Kf_{r}^{2} )g_{r + 1}^{\prime \prime } + (1 + MK)f_{r} g_{r + 1}^{\prime } - 2Kg_{r + 1} g_{r}^{\prime } - M^{2} g_{r + 1} = g_{r}^{2} ,$$
(24)
$$\frac{{\theta_{r + 1}^{\prime \prime } }}{\Pr } + f_{r + 1} \theta_{r + 1}^{\prime } = - Nt\theta_{r}^{\prime 2} ,$$
(25)
$$\phi_{r + 1}^{\prime \prime } + Scf_{r + 1} \phi_{r + 1}^{\prime } - Sc\sigma (1 + \delta \theta_{r + 1} )\exp \left( {\frac{ - E}{{1 + \delta \theta_{r + 1} }}} \right)\phi_{r + 1} = - \frac{Nb}{Nt}\theta_{r + 1}^{\prime \prime } ,$$
(26)
$$\begin{aligned} f_{r + 1} (0) = 0,\, \, g_{r + 1} (0) = 1,\, \, \theta_{r + 1}^{\prime } (0) = - Bi(1 - \theta_{r + 1} (0)),\,{\text{ Nb}}\phi_{r + 1}^{\prime } (0) + N\theta_{r + 1}^{\prime } (0) = 0, \hfill \\ g_{r + 1} (\infty ) \to 0,\,\,\,\theta_{r + 1} (\infty ) \to 0,\,\,\phi_{r + 1} (\infty ) \to 0.\, \hfill \\ \end{aligned}$$
(27)

Since \(\varsigma\) varies from \(\varsigma_{0} \,\,{\text{to}}\,\,\varsigma_{\infty }\), let \(\xi = \frac{2\varsigma }{{\varsigma_{\infty } }} - 1\) be the domain mapped into the interval [1, − 1] and grid points are defined as \(\xi_{i} = \cos \left( {\frac{\pi j}{N}} \right)\), where \(N\) represents the number of grid points and \(j = 1,2,3, \ldots ,N\). Now applying the Chebyshev pseudo-spectral method to the above equations, the following iterative equations are obtained.

$$P_{1} f_{r + 1}^{{}} = E_{1} ,\,\,f_{r + 1} (\xi_{N} ) = 0,$$
(28)
$$P_{2} g_{r + 1} = E_{2} ,g_{r + 1} (\xi_{N} ) = 1 + \delta g_{r + 1}^{\prime } (\xi_{N} ),g_{r + 1} (\xi_{0} ) = 0,$$
(29)
$$P_{3} \theta_{r + 1} = E_{3} ,\theta_{r + 1}^{\prime } (\xi_{N} ) = - Bi(1 - \theta_{r + 1} (\xi_{N} )),\theta_{r + 1} (\xi_{0} ) = 0,$$
(30)
$$P_{4} \phi_{r + 1} = E_{4} ,Nb\phi_{r + 1}^{\prime } (\xi_{N} ) + N\theta_{r + 1}^{\prime } (\xi_{N} ) = 0,\phi_{r + 1} (\xi_{0} ) = 0,$$
(31)

where

$$P_{1} = D,\quad E_{1} = g_{r}$$
(32)
$$P_{2} = D^{2} + (1 + MK){\text{diag}}\,f_{r + 1} D + K{\text{diag}}\,f_{r}^{2} D^{2} - (2Kg_{r}^{\prime } + M^{2} )I,\quad E_{2} = g_{r}^{2} ,$$
(33)
$$P_{3} = \frac{{D^{2} }}{\Pr } + {\text{diag}}\,f_{r + 1} D,\,\,E_{3} = - Nt\theta_{r}^{\prime 2} ,$$
(34)
$$P_{4} = D^{2} + Sc\,{\text{diag}}\,f_{r + 1} D - Sc\sigma (1 + \delta \theta )^{n} \exp \left( {\frac{ - E}{1 + \delta \theta }} \right)I,\quad E_{4} = - \frac{Nb}{Nt}\theta_{r + 1}^{\prime \prime } .$$
(35)

In the above expressions, \(I\) and \(D\) represent the identity and differentiation matrices. The above matrix system of equations is solved iteratively with a proper initial guesses of \(f_{0} (\varsigma ),\,g_{0} (\varsigma ),\,\theta_{0} (\varsigma )\,\,{\text{and}}\,\phi_{0} (\varsigma )\). To solve these equations, an in-house code has been developed in MATLAB program and it is successfully validated with the standard benchmark solutions before obtaining the simulations.

4 Results and discussion

First we checked the accuracy of numerical computations. For this case, we made a comparative analysis (see Table 1) with the available literature and found that present results coincide with the results of Khan and Pop [12] and Kandasamy et al. [43]. Also we made a graphical comparison with Makinde and Aziz [44] in the absence of \(\,K = M = E = \delta = \sigma = n.\) Further, Table 2 presents the values of wall temperature and concentration gradients for \(E,\delta ,\sigma\) and \(n.\) It is noted that temperature gradient and concentration gradient are increased with larger \(E\) but the opposite trend is found for \(\delta ,\sigma\) and \(n\). Important aspect of this study is Biot number. It is clearly observed from Table 3 that increasing values of \(Bi\)(0.1–50) enhance both the wall temperature gradient and wall concentration gradient. Additionally increment of \(Bi\) from 100 to 100,000 has just minor impact. Thus, as \(Bi\) has so large value then there is no significant changes. The much larger Biot number has no significant impact that at high scale, the influence of heat transfer coefficient is very lesser on temperature of liquid.

Table 1 Validation results of the present numerical method
Full size table
Table 2 Computational values of wall temperature gradient and wall concentration gradient when \(Nb = Nt = 0.3,\,\Pr = 7,\,K = M = Bi = 0.5\) and \(Sc = 10\)
Full size table
Table 3 Computational values of wall temperature gradient and wall concentration gradient when \(Nb = Nt = 0.3,\,\Pr = 7,\,K = M = n = 0.5,\,E = \sigma = \delta = 1\) and \(Sc = 10\)
Full size table

Essential key parameter of this model is elastic parameter which is displayed in Fig. 2. It is obviously observed that expansion of \(K\) is to increase the velocity field. Additionally this figure reveals that \(K = 0\) gives an outcome for consistent liquid. This increase is due to an enhancement in relaxation time factor which is directly related to \(K.\) Figure 3 is plotted to exhibit the impact of Hartmann number on liquid velocity. It demonstrates that expansion of \(M\) diminishes the velocity of liquid. This happens due to magnetic force normal to electrically directing liquid which can create drag-like force named as Lorentz force. This force is demonstration in course inverse to that of flow which has tendency to block its movement. Figure 4 demonstrates the impacts of \(M\) and \(K\) on skin friction coefficient. It is noticed that for higher estimations of \(K\), the skin friction coefficient displays the amplifying conduct relating to the increasing estimations of \(M\).

Fig. 2
figure 2

Effect of \(K\) on velocity field

Full size image
Fig. 3
figure 3

Effect of \(M\) on velocity field

Full size image
Fig. 4
figure 4

Effect of \(K\,\,{\text{and}}\,M\) on friction factor

Full size image

The curves of temperature and concentration profiles with specific values of \(Nt\) are portrayed in Fig. 5. Greater values of \(Nt\) lead to higher temperature and its related thermal boundary layer thickness. The reason is \(Nt\) produce a stronger thermophoretic force which is accountable to transfer the nanoparticles in the ambient fluid. Moreover, it is observed that higher estimations of \(Nt\) lead to reduce the concentration profile. Figure 6 shows that larger value of \(Nb\) leads to increment in the concentration profile. This has exactly inverse behavior when the activation energy is absent.

Fig. 5
figure 5

Effect of \(Nt\) on temperature and concentration fields

Full size image
Fig. 6
figure 6

Effect of \(Nb\) on concentration field

Full size image

Figures 7, 8, 9 and 10 are displayed to show the impact of \(Sc,E,\delta\) and \(\sigma\) on concentration fields. It is observation from Fig. 7 that an increment of \(Sc\) leads to stronger concentration. As we know that \(Sc\) is based on Brownian diffusivity. Thus, an enhancement in \(Sc\) corresponds to decrease in Brownian diffusivity which leads to lower concentration field. Figure 8 presents the effect of \(E\) on \(\phi (\zeta )\). An increment of activation energy \(E\) gives stronger concentration and its related layer thickness. Influence of \(\delta\) on concentration is depicted in Fig. 9. It shows that higher values of \(\delta\) lead to stronger concentration field. Opposite behavior can be seen for \(\sigma\) which portrayed in Fig. 10.

Fig. 7
figure 7

Effect of \(Sc\) on concentration field

Full size image
Fig. 8
figure 8

Effect of \(E\) on concentration field

Full size image
Fig. 9
figure 9

Effect of \(\delta\) on concentration field

Full size image
Fig. 10
figure 10

Effect of \(\sigma\) on concentration field

Full size image

Influence of Biot number on temperature distribution is displayed in Fig. 11. It is noticed that higher values of \(Bi\) give an increment in temperature. Physically, temperature gradient applied on the sheet wall implies the proportion representing the temperature inside a body shifts significantly while the body heats or cools over a period. Generally if \(Bi < 1\), it treated as regular temperature inside the wall and \(Bi > 1\) gives the irregular temperature at the wall. Further the variations of \(Bi\) and Pr on wall temperature gradient are plotted in Fig. 12. Increase in Prandtl number and Biot number enhances temperature at the wall. Higher values of Prandtl number decrease the temperature curve which is displayed in Fig. 13.

Fig. 11
figure 11

Effect of \(Bi\) on concentration field

Full size image
Fig. 12
figure 12

Effect of \(Bi\,\,{\text{and}}\,\,\Pr\) on wall temperature gradient

Full size image
Fig. 13
figure 13

Comparison of the present work with the existing work

Full size image

5 Concluding remarks

Here we studied the influences of activation energy, chemical reaction, convective boundary condition and passive control of nanoparticles in flow of Maxwell magneto-nanoliquid. Activation energy can be portrayed as the tiniest required imperativeness that reactants must get before a substance reaction can happen. Mass transport process by substance reaction with approving essentialness routinely met in applications including mechanics of water and oil emulsions, geothermal supplies, compound portraying and sustenance getting ready. Present problem has a great application in engineering and technological field for example geothermal reservoirs, water mechanism and food processing.

Major findings are recorded as:

  • Increment in elastic parameter leads to stronger velocity field but inverse effect for Hartmann number.

  • Higher values of Brownian diffusion parameter promotes the concentration field but reverse effect via thermophoresis parameter.

  • Increase in Schmidt number, reaction parameter and temperature difference parameter enhances the concentration field but opposite behavior for activation energy.

  • Effects of Prandtl and Biot number on temperature are similar qualitatively.